Micro-Distortion Detection of Lidar Scanning Signals Based on Geometric Analysis
Abstract
1. Introduction
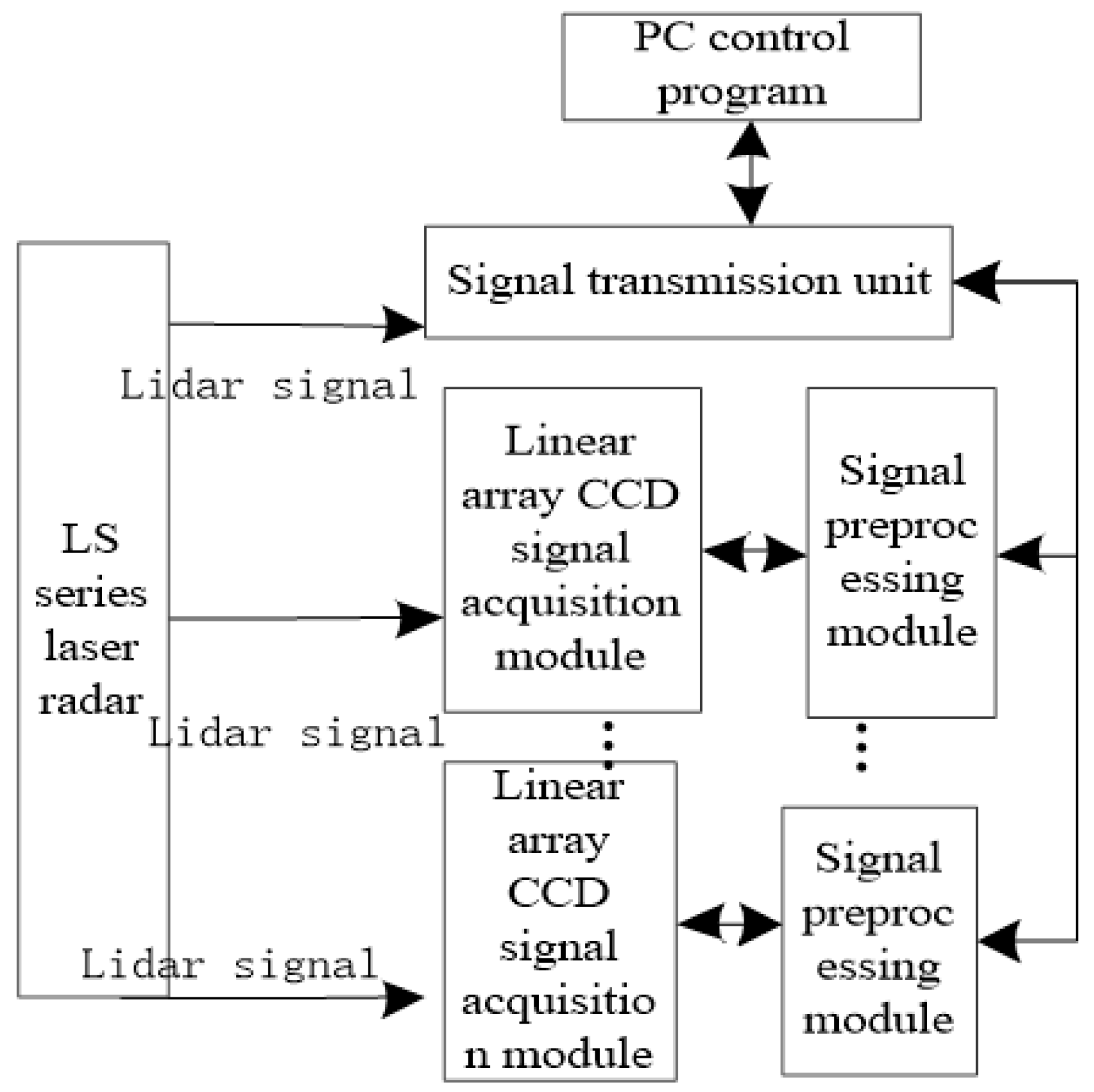
2. Hardware Support for the Technology
2.1. Overall Framework of the Technology
2.2. Development of Linear Array CCD Module
2.3. Signal Preprocessing Module
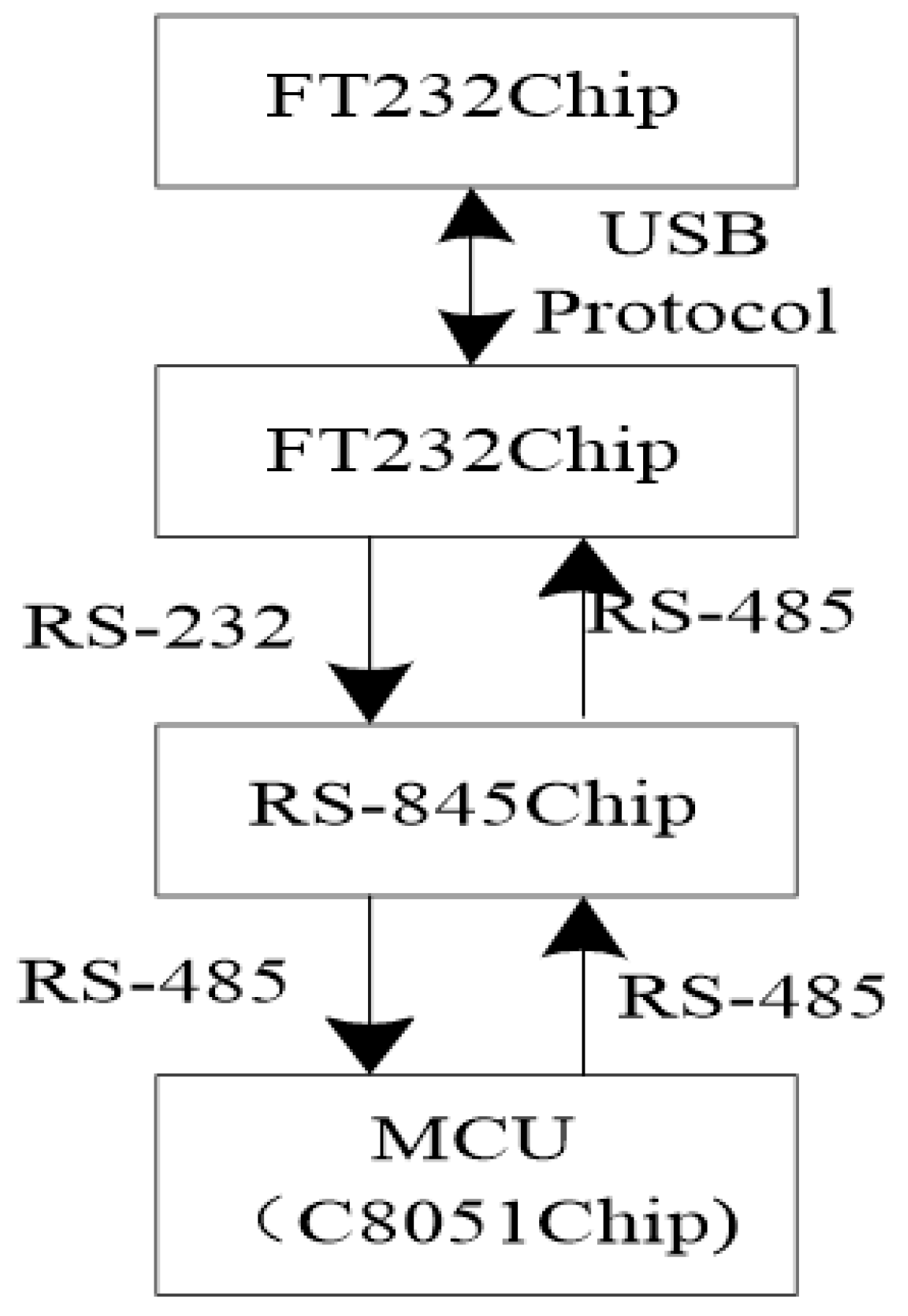
2.4. Signal Transmission Unit
3. Feature Matching Algorithm for Micro-Distortion Signal Based on Geometric Statistics
3.1. Frequency Matching of Micro-Distortion Based on Geometric Statistical Algorithm
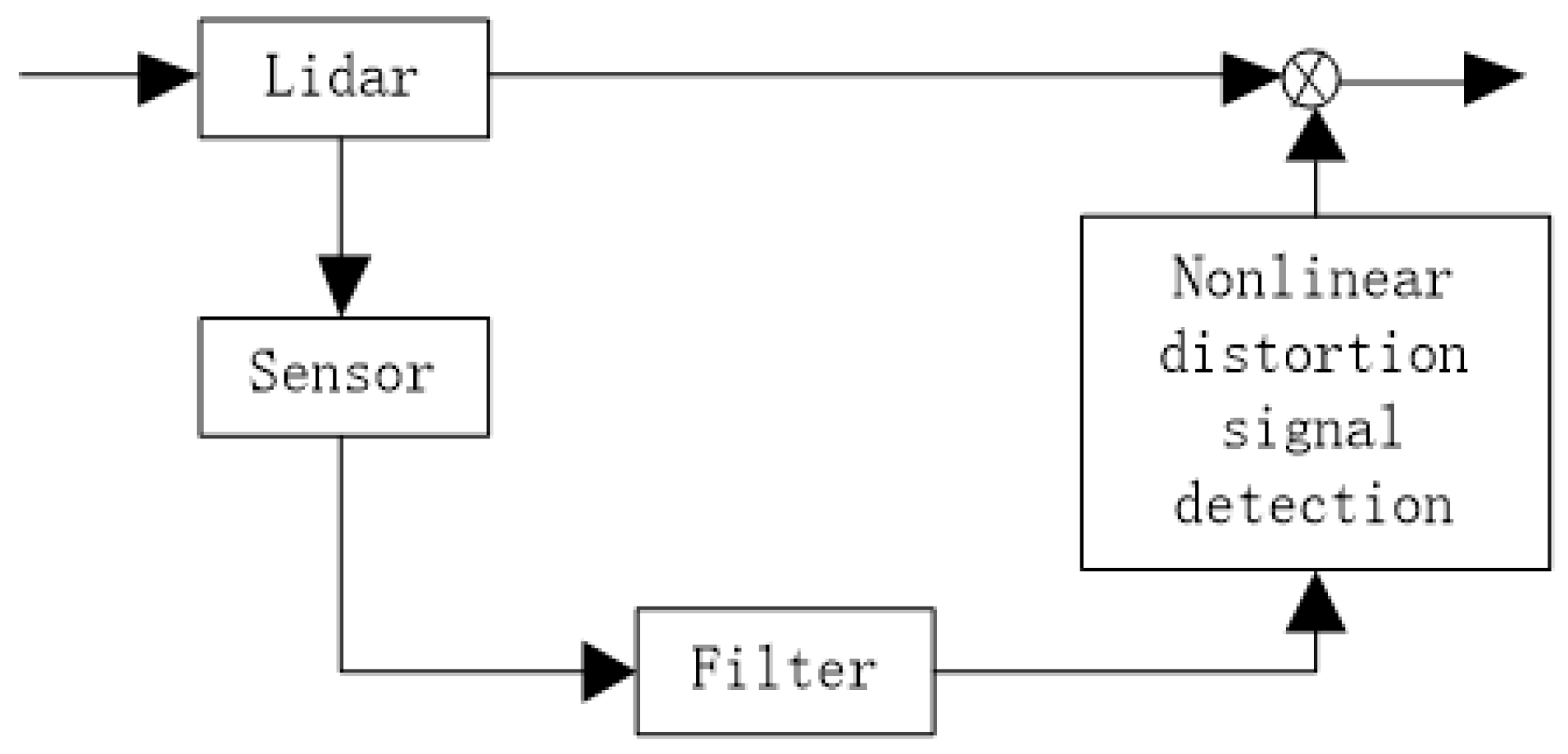
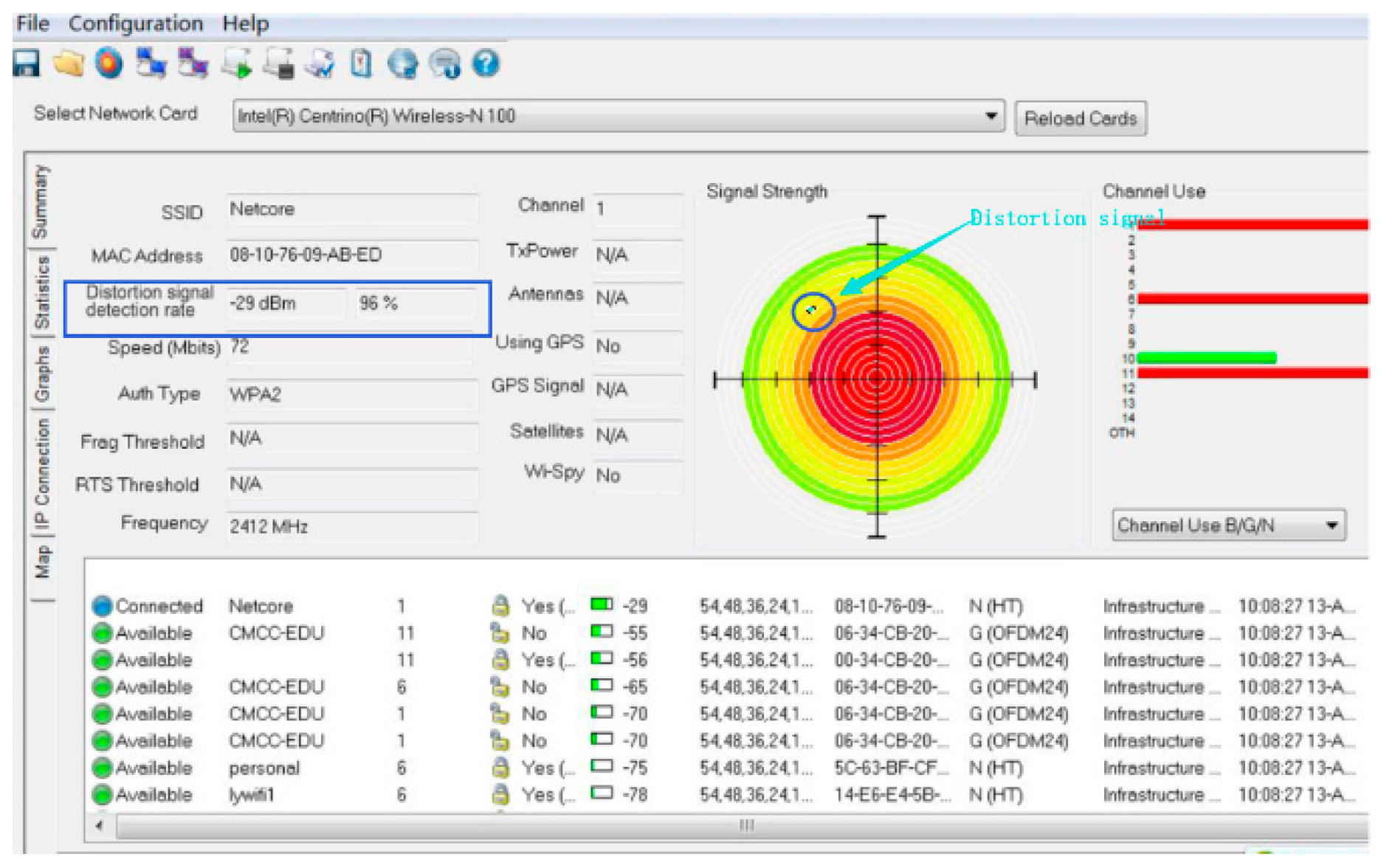
3.2. Nonlinear Micro-Distortion Signal Detection
3.3. Distortion Correction of Lidar Scanning Micro
- (1)
- In order to improve the performance of the control host, the sensor design of the entire lidar needs to use the clock as the corrective drive, and the controller uses the event as the corrective drive.
- (2)
- Data is scanned in a single package.
- (3)
- The local scanning state of the micro-distortion signal is controllable.
4. Results and Analysis of Simulation Experiments
5. Conclusions
- (1)
- (2)
- (3)
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Aubry, A.; Maio, A.D.; Pallotta, L.A. Geometric Approach to Covariance Matrix Estimation and its Applications to Radar Problems. IEEE Trans. Signal Process. 2018, 66, 907–922. [Google Scholar] [CrossRef]
- Muqaibel, A.H.; Abdalla, A.T.; Alkhodary, M.T.; Alawsh, S.A. Through-the-wall radar imaging exploiting Pythagorean apertures with sparse reconstruction. Digit. Signal Process. 2017, 61, 86–96. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, C.; Wan, J.; Dou, Z. A Novel Dynamic Spectrum Access Framework Based on Reinforcement Learning for Cognitive Radio Sensor Networks. Sensors 2016, 16, 86–96. [Google Scholar]
- Rakesh, P.R.; Narayanan, G. Investigation on Zero-Sequence Signal Injection for Improved Harmonic Performance in Split-Phase Induction Motor Drives. IEEE Trans. Ind. Electron. 2017, 64, 2732–2741. [Google Scholar] [CrossRef]
- Lin, Y.; Zhu, X.; Zheng, Z.; Dou, Z.; Zhou, R. The individual identification method of wireless device based on dimensionality reduction and machine learning. J. Supercomput. 2017, 75, 3010–3027. [Google Scholar] [CrossRef]
- Liu, S.; Bai, W.; Zeng, N.; Wang, S. A Fast Fractal Based Compression for MRI Images. IEEE Access 2019, 7, 62412–62420. [Google Scholar] [CrossRef]
- Piazzo, L.; Raguso, M.C.; Seu, R.; Mastrogiuseppe, M. Signal enhancement for planetary radar sounders. Electron. Lett. 2019, 55, 153–155. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, C.; Li, L. Influences of optical-spectrum errors on excess relative intensity noise in a fiber-optic gyroscope. Opt. Commun. 2018, 410, 504–513. [Google Scholar] [CrossRef]
- Lupi, S.M.; Galinetto, P.; Cislaghi, M.; y Baena, A.R.; Scribante, A.; y Baena, R.R. Geometric distortion of panoramic reconstruction in third molar tilting assessments: A comprehensive evaluation. Dentomaxillofacial Radiol. 2018, 47, 20170467. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Lu, S.; Tang, Y. Research on panoramic point cloud data acquisition technology based on ASODVS. J. Comput. Meas. Control 2014, 22, 2284–2287. [Google Scholar]
- Hua, X.; Cheng, Y.; Wang, H.; Qin, Y.; Li, Y. Geometric means and medians with applications to target detection. IET Signal Process. 2017, 11, 711–720. [Google Scholar] [CrossRef]
- Gui, R.; Wang, W.Q.; Cui, C.; So, H.C. Coherent Pulsed-FDA Radar Receiver Design with Time-Variance Consideration: SINR and CRB Analysis. IEEE Trans. Signal Process 2017, 66, 200–214. [Google Scholar] [CrossRef]
- Le, Z.; Wang, X. Super-Resolution Delay-Doppler Estimation for OFDM Passive Radar. IEEE Trans. Signal Process. 2017, 65, 2197–2210. [Google Scholar]
- Zhang, Y.; Pan, S. Broadband Microwave Signal Processing Enabled by Polarization-Based Photonic Microwave Phase Shifters. IEEE J. Quantum Electron. 2018, 54, 1–12. [Google Scholar] [CrossRef]
- Engels, F.; Heidenreich, P.; Zoubir, A.M.; Jondral, F.K.; Wintermantel, M. Advances in Automotive Radar: A framework on computationally efficient high-resolution frequency estimation. IEEE Signal Process. Mag. 2017, 34, 36–46. [Google Scholar] [CrossRef]
- Wanchun, L.; Qiu, T.; Chengfeng, H.; Yingxiang, L. Location algorithms for moving target in non-coherent distributed multiple-input multiple-output radar systems. IET Signal Process. 2017, 11, 503–514. [Google Scholar] [CrossRef]
- Pan, Z.; Liu, S.; Sangaiah, A.K.; Muhammad, K. Visual attention feature (VAF): A novel strategy for visual tracking based on cloud platform in intelligent surveillance systems. J. Parallel Distrib. Comput. 2018, 120, 182–194. [Google Scholar] [CrossRef]
- Cheng, Z.; Liao, B.; He, Z.; Li, Y.; Li, J. Spectrally Compatible Waveform Design for MIMO Radar in the Presence of Multiple Targets. IEEE Trans. Signal Process. 2018, 66, 3543–3555. [Google Scholar] [CrossRef]
- Duan, K.; Wang, Z.; Xie, W.; Chen, H.; Wang, Y. Sparsity-based STAP algorithm with multiple measurement vectors via sparse Bayesian learning strategy for airborne radar. IET Signal Process. 2017, 11, 544–553. [Google Scholar] [CrossRef]
- Zhang, W.; Fu, Y.; Nie, L.; Zhao, G.; Yang, W.; Yang, J. Parameter estimation of micro-motion targets for high-range-resolution radar using high-order difference sequence. IET Signal Process. 2018, 12, 1–11. [Google Scholar] [CrossRef]


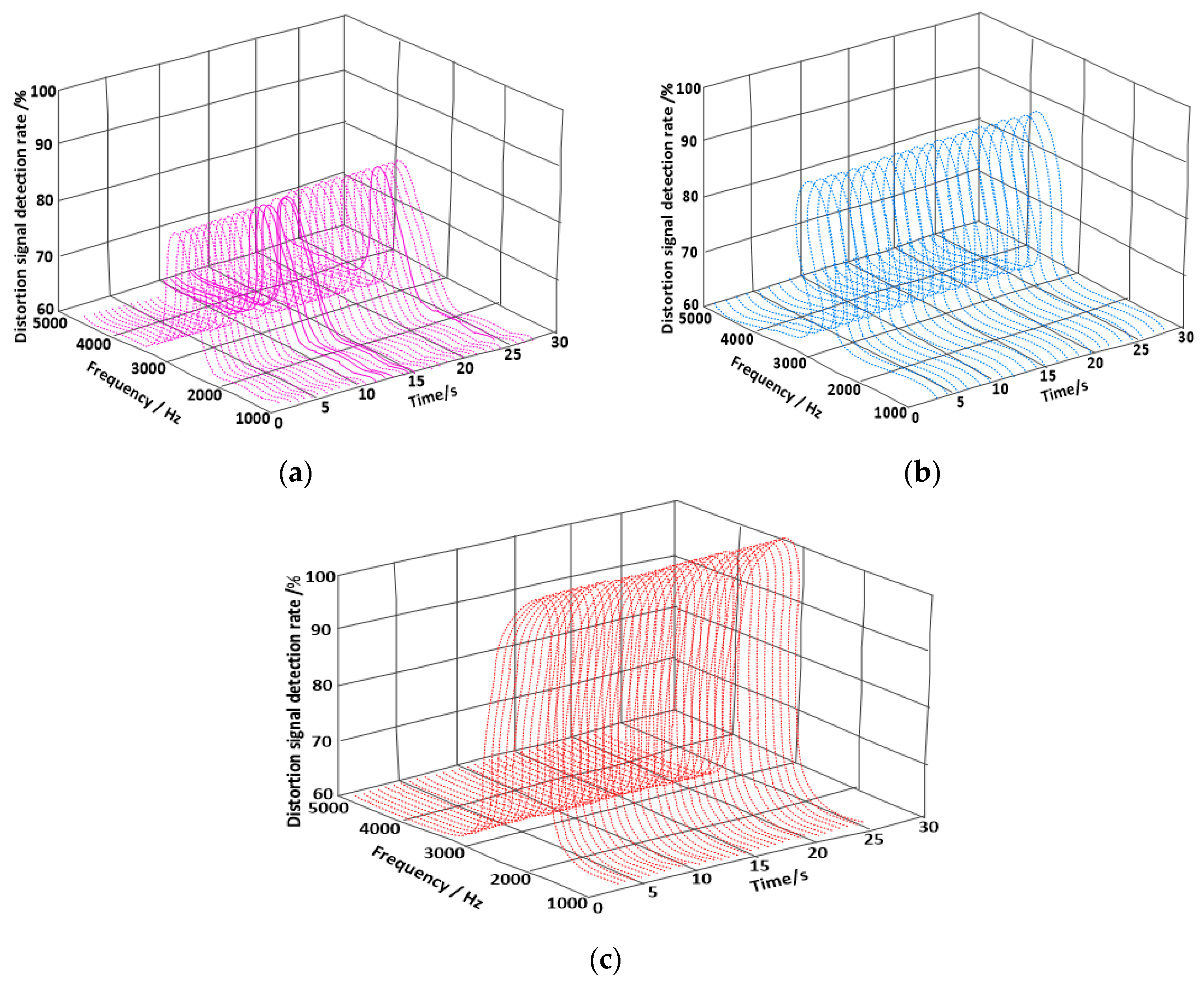
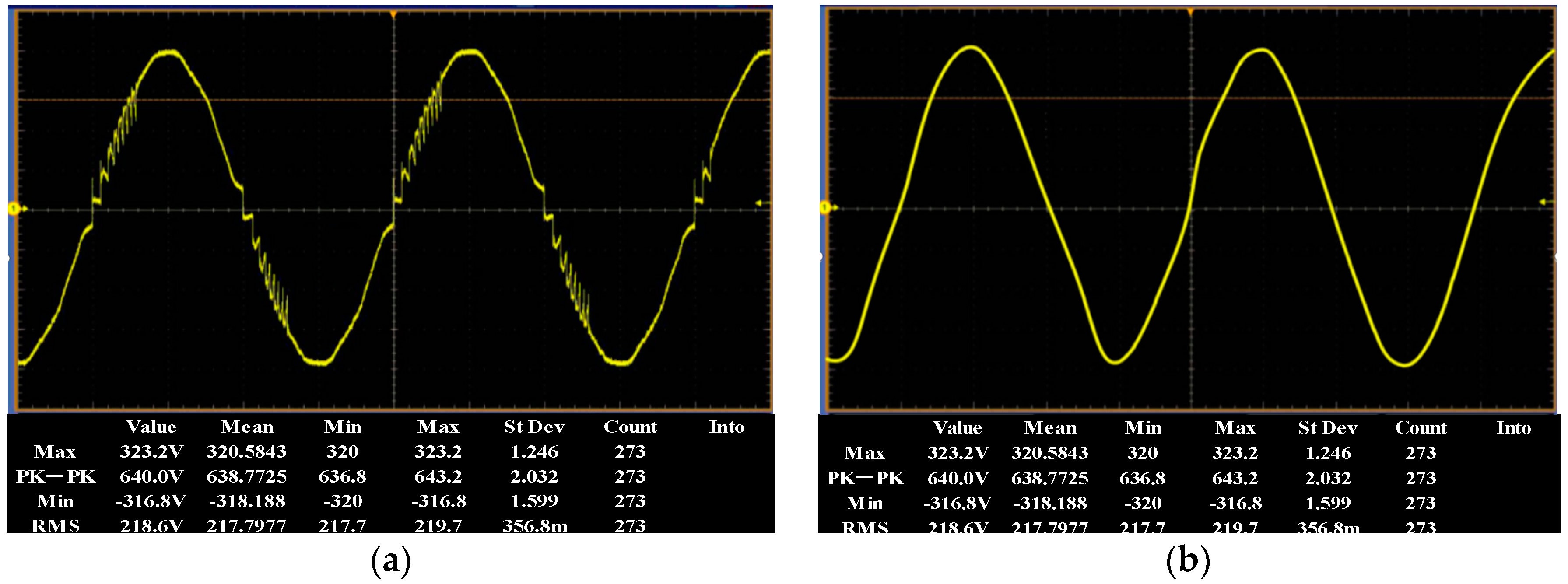
| Number of Experiments/Time | Proposed Method/s | Literature [8] Method/s | Literature [9] Method/s |
|---|---|---|---|
| 1 | 2.13 | 2.58 | 3.03 |
| 2 | 2.16 | 2.64 | 3.09 |
| 3 | 2.08 | 2.52 | 2.94 |
| 4 | 2.09 | 2.53 | 2.95 |
| 5 | 2.12 | 2.56 | 3.02 |
| 6 | 2.15 | 2.63 | 3.07 |
| 7 | 2.10 | 2.54 | 3.96 |
| 8 | 2.14 | 2.60 | 3.05 |
| 9 | 2.13 | 2.59 | 3.04 |
| 10 | 2.11 | 2.26 | 2.99 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Chen, X.; Li, Y.; Cheng, X. Micro-Distortion Detection of Lidar Scanning Signals Based on Geometric Analysis. Symmetry 2019, 11, 1471. https://doi.org/10.3390/sym11121471
Liu S, Chen X, Li Y, Cheng X. Micro-Distortion Detection of Lidar Scanning Signals Based on Geometric Analysis. Symmetry. 2019; 11(12):1471. https://doi.org/10.3390/sym11121471
Chicago/Turabian StyleLiu, Shuai, Xiang Chen, Ying Li, and Xiaochun Cheng. 2019. "Micro-Distortion Detection of Lidar Scanning Signals Based on Geometric Analysis" Symmetry 11, no. 12: 1471. https://doi.org/10.3390/sym11121471
APA StyleLiu, S., Chen, X., Li, Y., & Cheng, X. (2019). Micro-Distortion Detection of Lidar Scanning Signals Based on Geometric Analysis. Symmetry, 11(12), 1471. https://doi.org/10.3390/sym11121471






