Feature Selection of Grey Wolf Optimizer Based on Quantum Computing and Uncertain Symmetry Rough Set
Abstract
:1. Introduction
2. Theoretical Basis of Combinatorial Optimization Feature Selection Algorithm
2.1. Uncertain Symmetry Rough Set
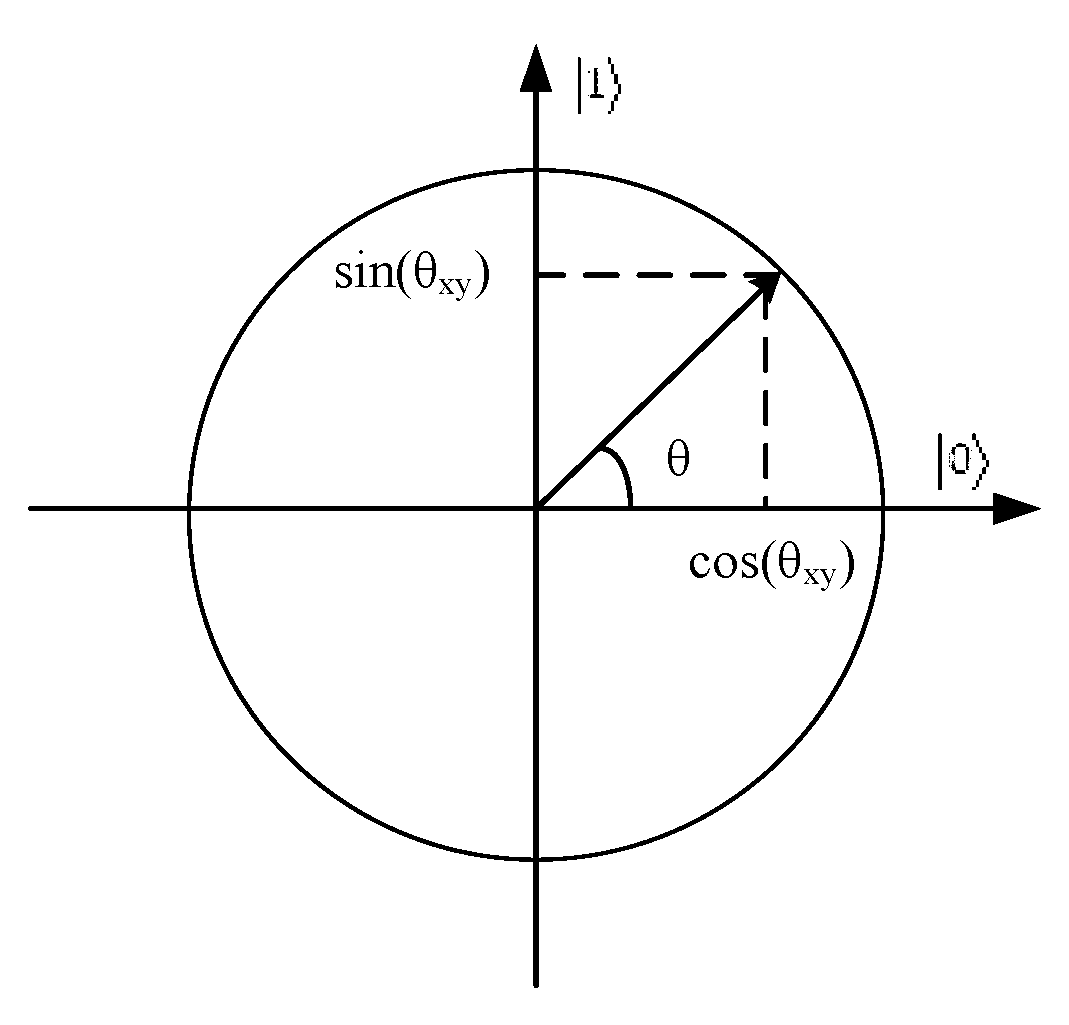
2.2. Quantum Computing
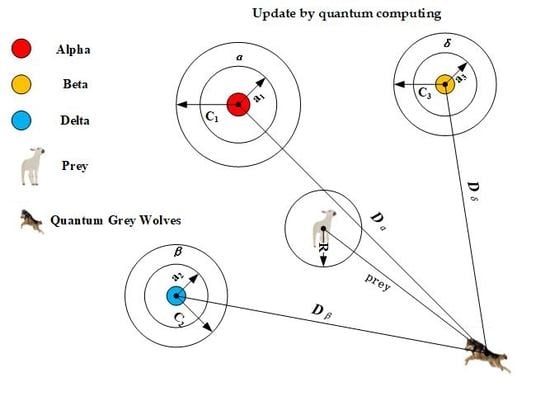
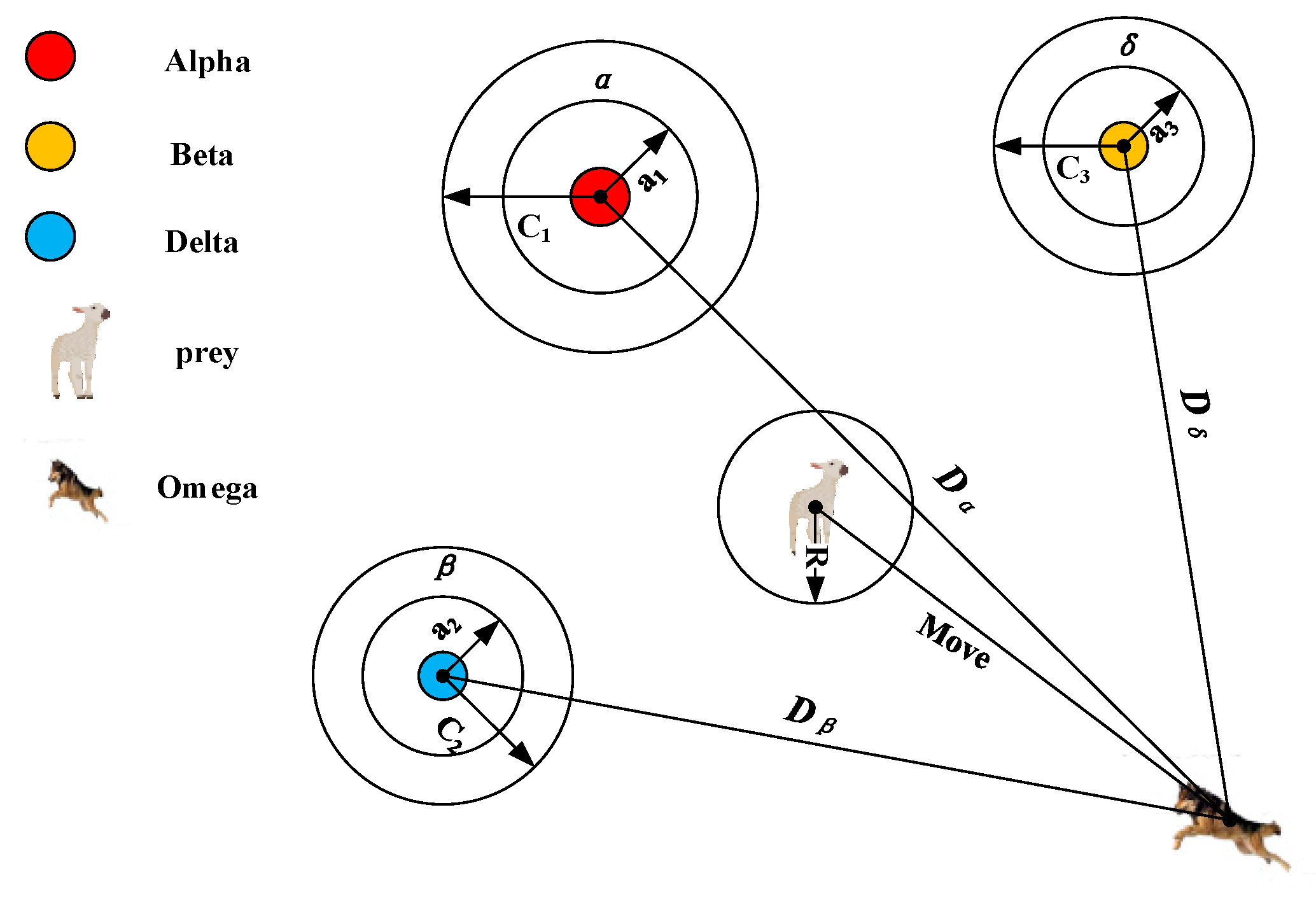
2.3. Grey Wolf Optimizer
3. Grey Wolf Optimizer Based on Quantum Computing and Rough Set
| Algorithm 1. QCGWORS process |
| Input: An extended Information System: F Output: optimal feature subset 1. Initialize n quantum grey wolf individuals using (34); 2. Get the group of n binary grey wolves from 3. Search the minimal feature subset of each binary Wolf by the Algorithm 3; 4. corresponding of binary wolf using (26); 5. while (t < maximum iterations) 6. for i=1:q (all q binary grey wolf individuals) do 7. Evaluate the feature subset ; 8. Update the best feature subset ; 9. end for 10. end while 11. return end while 12. return |
3.1. Rough Set Evaluation Function
3.2. Quantum Representation of Grey Wolf Individual
3.3. Quantum Computing in Feature Selection
3.4. Quantum Measurement in the Proposed Algorithm
| Algorithm 2. Quantum measurement in the proposed algorithm |
| Input:: Quantum Grey individual, C= {}: Conditional feature set Output:: Binary Grey Wolf Individual, : Feature Subset 1. ← 2. for each qubit y of do 3. real value r is generated between [0, 1]; 4. if r > then 5. ← 1; 6. R ←∪; 7. else 8. ← 0; 9. end if 10. end for 11. return |
3.5. Update Position of Binary Grey Wolves
| Algorithm 3. Process of updating the binary wolves’ position |
| Input: I: Information System Output: minimum condition feature subset 1. Calculate the fitness of 2. Initialize search wolf for Alpha, Beta, and Delta. 3. Initialize parameters a, A and C. 4. while (t <Max iterations) 5. for each Omega wolf 6. calculate the fitness function (26) value of the 7. for each search wolf 8. if there is a search wolf(Alpha, Beta, Delta) position that needs to be replaced 9. Update parameters a, A and C. 10. Update the current search wolf position 11. end if 12. end For 13. end For 14. end while 15. return Alpha wolf, |
4. Experiments
4.1. Experimental Setup
4.1.1. Classical Part Preparation
4.1.2. Quantum Part Preparation
- It can initialize the qubits and rearrange the qubits if needed;
- It can easily construct the superposition state of qubits;
- It can give abstraction to the quantum operator to easily format the quantum, such as NOT gate, quantum rotation gate, Hadamard gate, and other gate operation;
- It can simplify quantum measurement operation to obtain the definite state of the qubit;
- It can randomly generate correlation matrices, including unitary matrices.
4.2. Analysis of Experimental Data
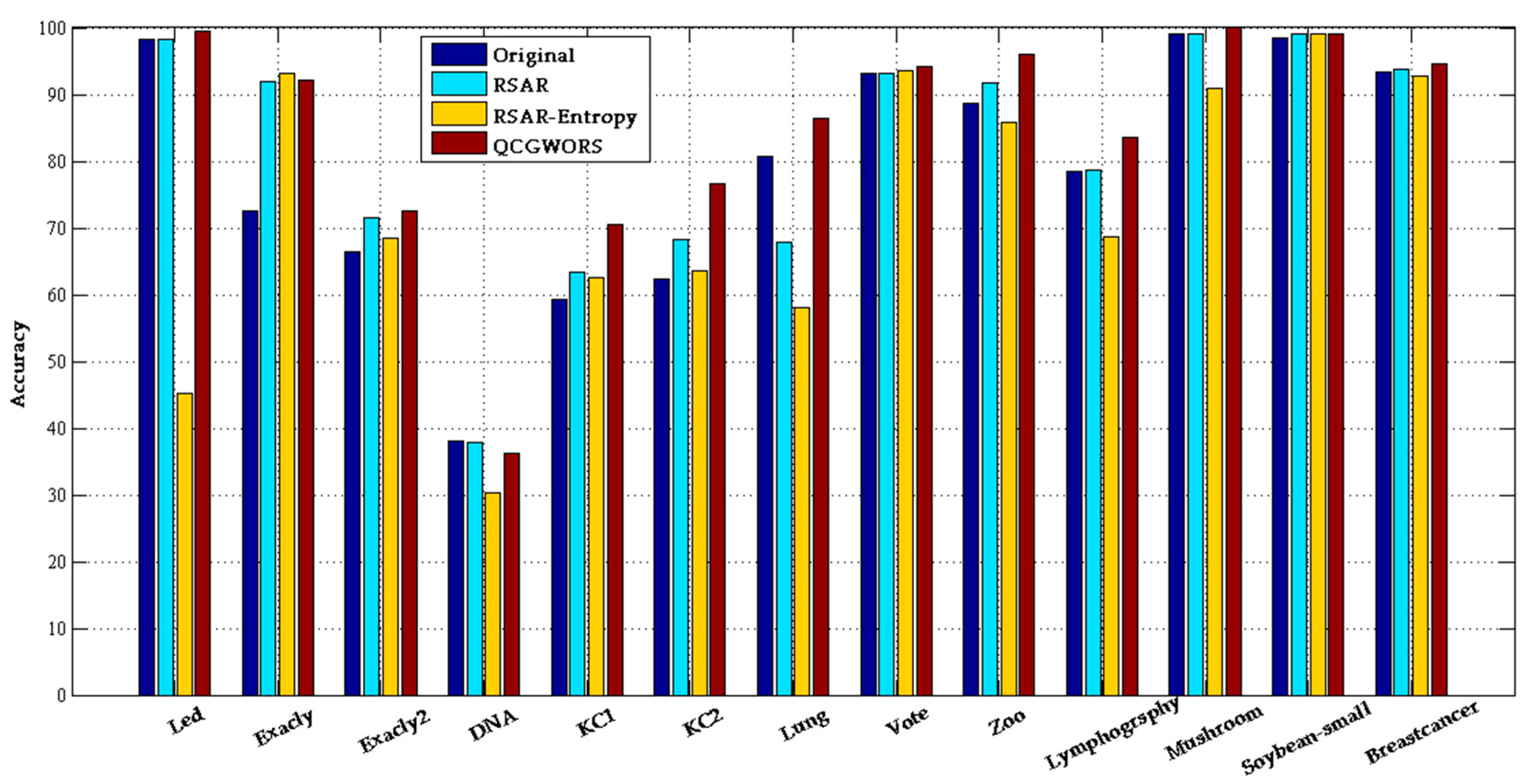
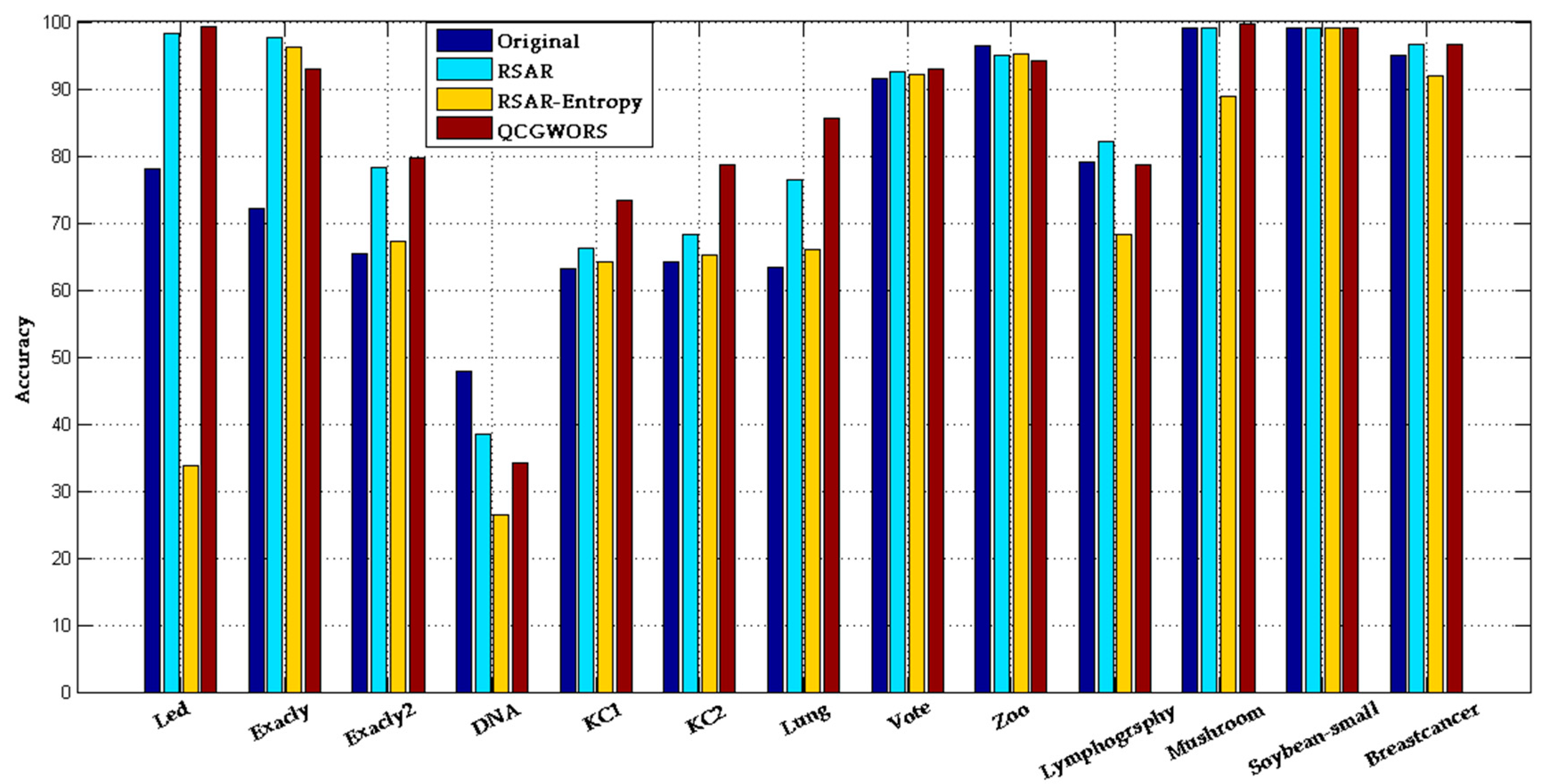
4.2.1. QCGWORS Improved Classification Accuracy Experiment
4.2.2. Rough Set Evaluation and Comparison Experiment
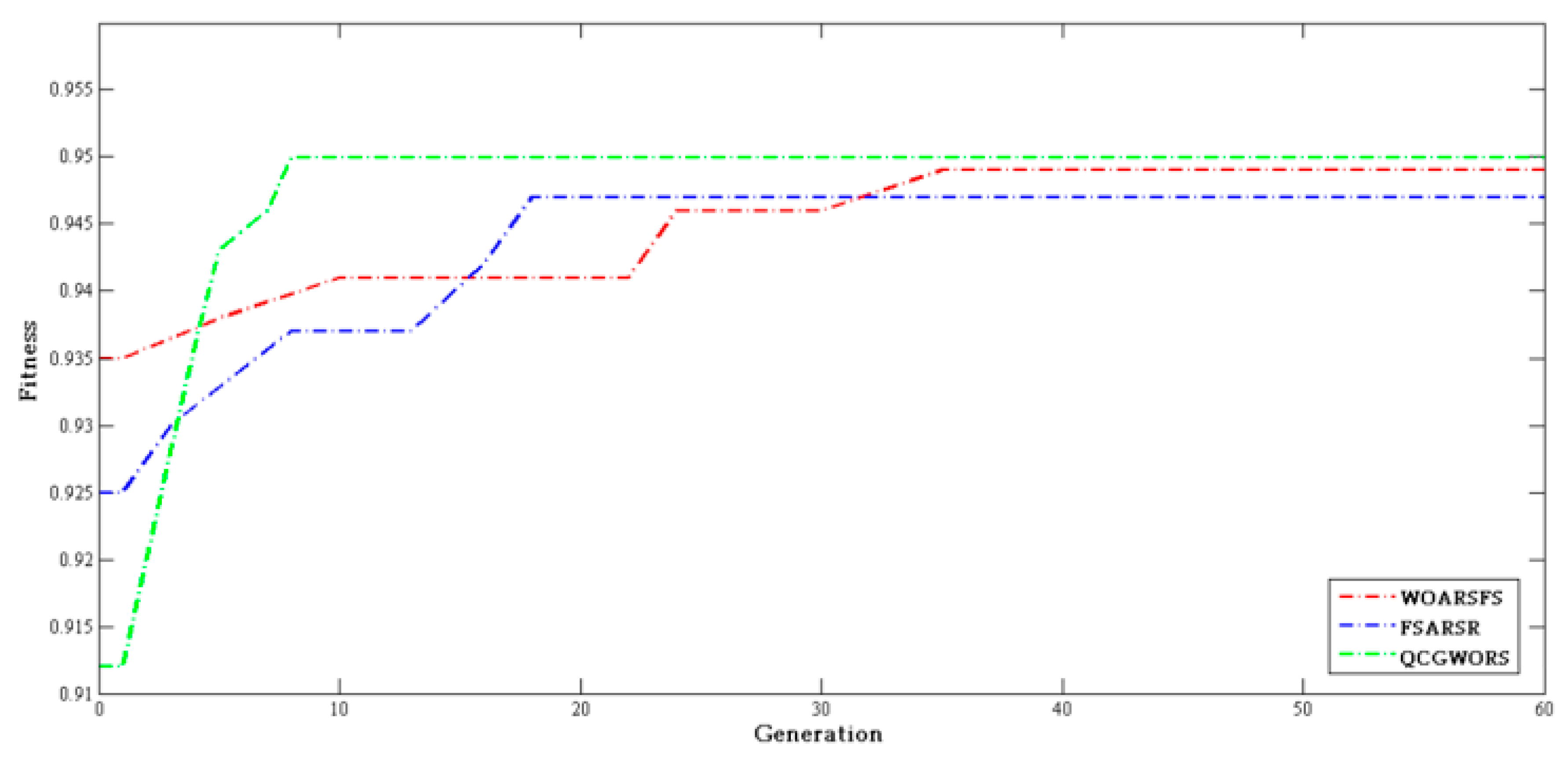
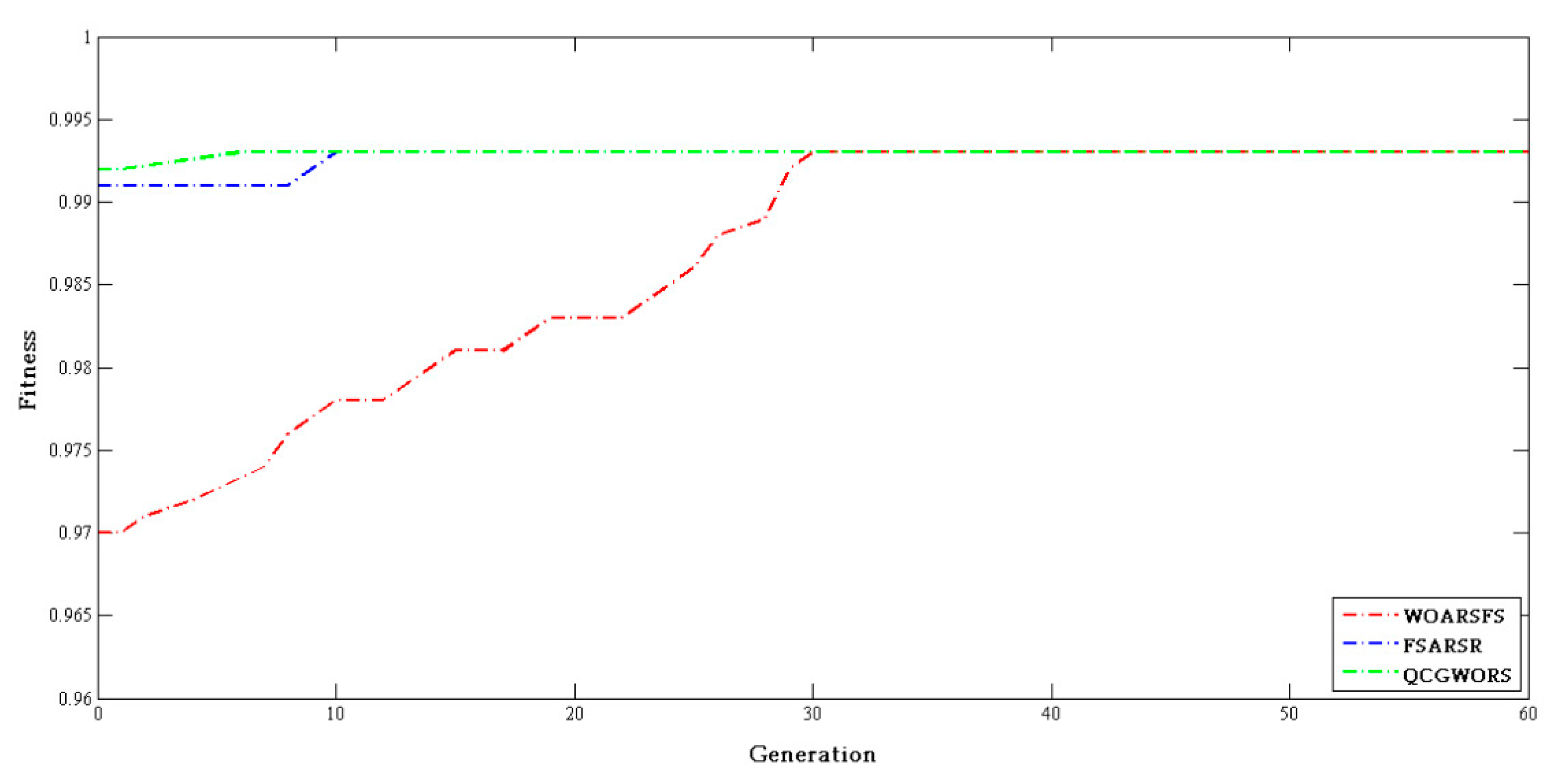
4.2.3. Swarm Intelligence Algorithm Comparison Experiment
4.2.4. Experiment on the Effect of Quantum Part in Feature Selection
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- References Davies, S.; Russell, S. NP-completeness of searches for smallest possible feature sets. In Proceedings of the AAAI Symposium on Intelligent Relevance, Berkeley, CA, USA, 4–6 February 1994; pp. 37–39. [Google Scholar]
- Gheyas, I.; Smith, L. Feature subset selection in large dimensionality domains. Pattern Recognit. 2010, 43, 5–13. [Google Scholar] [CrossRef]
- Vergara, J.; Estévez, P. A review of feature selection methods based on mutual information. Neural Comput. Appl. 2014, 24, 175–186. [Google Scholar]
- Mao, Y.; Zhou, X.B.; Xia, Z.; Yin, Z.; Sun, Y.X. Survey for study of feature selection algorithms. Pattern Recognit. Artif. Intell. 2007, 20, 211–218. [Google Scholar]
- Gan, J.; Hasan, B.; Tsui, C. A filter-dominating hybrid sequential forward floating search method for feature subset selection in high-dimensional space. Int. J. Mach. Learn. Cybern. 2014, 5, 413–423. [Google Scholar] [CrossRef]
- Kohavi, R.; John, G.H. Wrappers for Feature Subset Selection. Artif. Intell. 1997, 97, 273–324. [Google Scholar] [CrossRef]
- Pawlak, Z.; Skowron, A. Rough sets: Some extensions. Inf. Sci. 2007, 177, 28–40. [Google Scholar] [CrossRef]
- Pawlak, Z.; Skowron, A. Rudiments of rough sets. Inf. Sci. 2007, 177, 3–27. [Google Scholar] [CrossRef]
- Kryszkiewicz, M. Rough set approach to incomplete information systems. Inf. Sci. 1998, 112, 39–49. [Google Scholar] [CrossRef]
- Mi, J.S.; Wu, W.Z.; Zhang, W.X. Approaches to knowledge reduction based on variable precision rough set model. Inf. Sci. 2004, 159, 255–272. [Google Scholar] [CrossRef]
- Jinming, Q.; Kaiquati, S. F-rough law and the discovery of rough law. J. Syst. Eng. Electron. 2009, 20, 81–89. [Google Scholar]
- Hu, Q.; Yu, D.; Liu, J.; Wu, C. Neighborhood rough set based heterogeneous feature subset selection. Inf. Sci. 2008, 178, 3577–3594. [Google Scholar] [CrossRef]
- Stefanowski, J.; Tsoukias, A. Incomplete information tables and rough classification. Comput. Intell. 2001, 17, 545–566. [Google Scholar] [CrossRef]
- Qian, Y.; Liang, J.; Li, D.; Wang, F.; Ma, N. Approximation reduction in inconsistent incomplete decision tables. Knowl. Based Syst. 2010, 23, 427–433. [Google Scholar] [CrossRef]
- Yang, X.; Chen, Z.; Dou, H.; Zhang, M.; Yang, J. Neighborhood system based rough set: Models and attribute reductions. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2012, 20, 399–419. [Google Scholar] [CrossRef]
- Degang, C.; Changzhong, W.; Qinghua, H. A new approach to attribute reduction of consistent and inconsistent covering decision systems with covering rough sets. Inf. Sci. 2007, 177, 3500–3518. [Google Scholar] [CrossRef]
- Teng, S.H.; ZHOU, S.L.; SUN, J.X.; Li, Z.Y. Attribute reduction algorithm based on conditional entropy under incomplete information system. J. Natl. Univ. Def. Technol. 2010, 32, 90–94. [Google Scholar]
- Ren, Y.G.; Wang, Y.; Yan, D.Q. Rough Set Attribute Reduction Algorithm Based on GA. Comput. Eng. Sci. 2006, 47, 134–136. [Google Scholar]
- Long, N.C.; Meesad, P.; Unger, H. Attribute reduction based on rough sets and the discrete firefly algorithm. In Recent Advances in Information and Communication Technology; Springer: Berlin, Germany, 2014; pp. 13–22. [Google Scholar]
- Wang, X.; Yang, J.; Teng, X.; Xia, W.; Jensen, R. Feature selection based on rough sets and particle swarm optimization. Pattern Recognit. Lett. 2007, 28, 459–471. [Google Scholar] [CrossRef]
- Inbarani, H.H.; Azar, A.T.; Jothi, G. Supervised hybrid feature selection based on PSO and rough sets for medical diagnosis. Comput. Methods Programs Biomed. 2014, 113, 175–185. [Google Scholar] [CrossRef]
- Bae, C.; Yeh, W.C.; Chung, Y.Y.; Liu, S.L. Feature selection with intelligent dynamic swarm and rough set. Expert Syst. Appl. 2010, 37, 7026–7032. [Google Scholar] [CrossRef]
- Chen, Y.; Miao, D.; Wang, R. A rough set approach to feature selection based on ant colony optimization. Pattern Recognit. Lett. 2010, 31, 226–233. [Google Scholar] [CrossRef]
- Jensen, R.; Shen, Q. Fuzzy-rough data reduction with ant colony optimization. Fuzzy Sets Syst. 2005, 149, 5–20. [Google Scholar] [CrossRef]
- Ke, L.; Feng, Z.; Ren, Z. An efficient ant colony optimization approach to attribute reduction in rough set theory. Pattern Recognit. Lett. 2008, 29, 1351–1357. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, Q.; Xu, H. Finding rough set reducts with fish swarm algorithm. Knowl. Based Syst. 2015, 81, 22–29. [Google Scholar] [CrossRef]
- Luan, X.Y.; Li, Z.P.; Liu, T.Z. A novel attribute reduction algorithm based on rough set and improved artificial fish swarm algorithm. Neurocomputing 2016, 174, 522–529. [Google Scholar] [CrossRef]
- Yamany, W.; Emary, E.; Hassanien, A.E.; Schaefer, G.; Zhu, S.Y. An innovative approach for attribute reduction using rough sets and flower pollination optimisation. Procedia Comput. Sci. 2016, 96, 403–409. [Google Scholar] [CrossRef]
- Chen, Y.; Zeng, Z.; Lu, J. Neighborhood rough set reduction with fish swarm algorithm. Soft Comput. 2017, 21, 6907–6918. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Schuld, M.; Sinayskiy, I.; Petruccione, F. An introduction to quantum machine learning. Contemp. Phys. 2015, 56, 172–185. [Google Scholar] [CrossRef]
- Yu, L.; Liu, H. Efficient feature selection via analysis of relevance and redundancy. J. Mach. Learn. Res. 2004, 5, 1205–1224. [Google Scholar]
- Swiniarski, R.W.; Skowron, A. Rough set methods in feature selection and recognition. Pattern Recognit. Lett. 2003, 24, 833–849. [Google Scholar] [CrossRef]
- Benioff, P. The computer as a physical system: A microscopic quantum mechanical Hamiltonian model of computers as represented by Turing machines. J. Stat. Phys. 1980, 22, 563–591. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I. Quantum computation and quantum information. Am. J. Phys. 2002, 70, 558–694. [Google Scholar] [CrossRef]
- Manju, A.; Nigam, M.J. Applications of quantum inspired computational intelligence: A survey. Artif. Intell. Rev. 2014, 42, 79–156. [Google Scholar] [CrossRef]
- Zouache, D.; Nouioua, F.; Moussaoui, A. Quantum-inspired firefly algorithm with particle swarm optimization for discrete optimization problems. Soft Comput. 2016, 20, 2781–2799. [Google Scholar] [CrossRef]
- Jensen, R.; Shen, Q. Finding Rough Set Reducts with Ant Colony Optimization. J. Fussy Sets Sys. 2003, 49, 15–22. [Google Scholar]
- Wang, G.; Yu, H.; Yang, D.C. Decision table reduction based on conditional information entropy. Chin. J. Comput. Chin. Ed. 2002, 25, 759–766. [Google Scholar]
- Tharwat, A.; Gabel, T.; Hassanien, A.E. Classification of toxicity effects of biotransformed hepatic drugs using whale optimized support vector machines. J. Biomed. Inform. 2017, 68, 132–149. [Google Scholar] [CrossRef]
- Tóth, G. QUBIT4MATLAB V3. 0: A program package for quantum information science and quantum optics for MATLAB. Comput. Phys. Commun. 2008, 179, 430–437. [Google Scholar]

| u | v | w | d | |
|---|---|---|---|---|
| 0 | 1 | 1 | 0 | |
| 1 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 0 | |
| 0 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 0 | |
| 0 | 0 | 0 | 0 |
| No. | Dataset | Features | Samples |
|---|---|---|---|
| 1 | Led | 24 | 2000 |
| 2 | Exactly | 13 | 1000 |
| 3 | Exactly2 | 13 | 1000 |
| 4 | DNA | 57 | 318 |
| 5 | KC1 | 22 | 2109 |
| 6 | KC2 | 21 | 522 |
| 7 | Lung | 56 | 32 |
| 8 | Vote | 16 | 300 |
| 9 | Zoo | 16 | 101 |
| 10 | Lymphography | 18 | 148 |
| 11 | Mushroom | 22 | 8124 |
| 12 | Soybean-small | 35 | 47 |
| 13 | Breast cancer | 9 | 699 |
| Dataset | ORIGINAL | QCGWORS | ||||
|---|---|---|---|---|---|---|
| Features | RF | KNN | Features | RF | KNN | |
| Led | 24 | 98.20 ± 0.50 | 77.99 ± 0.8 | 5 | 99.57 ± 0.32 | 99.31 ± 0.25 |
| Exactly | 13 | 72.53 ± 2.50 | 72.14 ± 0.7 | 6 | 92.23 ± 0.90 | 93.05 ± 0.30 |
| Exactly2 | 13 | 66.51 ± 1.50 | 65.38 ± 0.5 | 10 | 72.56 ± 0.05 | 79.63 ± 0.7 |
| DNA | 57 | 37.96 ± 213 | 77.80 ± 0.9 | 5 | 36.25 ± 0.23 | 34.09 ± 0.10 |
| KC1 | 22 | 59.23 ± 2.51 | 61.14 ± 2.92 | 8 | 70.42 ± 0.16 | 73.42 ± 1.37 |
| KC2 | 21 | 62.25 ± 2.17 | 64.25 ± 1.92 | 5 | 76.61 ± 0.23 | 78.61 ± 0.81 |
| Lung | 56 | 80.78 ± 0.27 | 63.28 ± 2.64 | 4 | 86.35 ± 0.16 | 85.53 ± 0.74 |
| Vote | 16 | 93.08 ± 0.63 | 91.62 ± 0.65 | 8 | 94.12 ± 0.69 | 92.88 ± 0.42 |
| Zoo | 16 | 88.74 ± 1.03 | 96.34 ± 0.43 | 5 | 96.06 ± 0.14 | 94.21 ± 0.40 |
| Lymphography | 18 | 78.38 ± 2.20 | 79.07 ± 1.52 | 7 | 83.49 ± 2.01 | 78.75 ± 1.22 |
| Mushroom | 22 | 99.00 ± 1.07 | 99.00 ± 0.10 | 4 | 99.03 ± 0.10 | 99.71 ± 0.10 |
| Soybean-small | 35 | 98.47 ± 2.53 | 99.00 ± 0.10 | 2 | 99.00 ± 0.10 | 99.00 ± 0.10 |
| Breast cancer | 9 | 93.44 ± 6.56 | 94.94 ± 0.51 | 4 | 94.65 ± 0.73 | 96.59 ± 0.34 |
| Average | 25 | 79.12 | 77.80 | 6 | 85.17 | 85.59 |
| Dataset | ‘RSAR’ | ‘RSAR-Entropy’ | ‘QCGWORS’ |
|---|---|---|---|
| Led | 6,1,2,4,3,5 | 6,11,24,19,22,8,18,21,9,16,7,1 | 1,2,3,4,5 |
| Exactly | 1,2,3,4,5,11,7,9 | 3,5,7,1,4,8,9,11 | 1,3,5,7,9,11 |
| Exactly2 | 1,2,3,4,10,9,6,8,7,5 | 2,3,8,6,13,12,5,10,11,4,7 | 1,2,3,4,5,6,7,8,9,10 |
| DNA | 1,16,45,24,57,2,3 | 18,42,14,49,9,25 | 5,19,22,26,33 |
| KC1 | 4,2,5,8,9,7,10,11,1,6 | 1,5,2,7,3,11,4,21,15,18 | 2,4,5,6,7,8,11,18 |
| KC2 | 2,4,5,8,7,18,11,6 | 2,5,6,8,7,4,1,18,5 | 2,4,5,7,8 |
| Lung | 1,42,7,4 | 3,9,4,36,13,15 | 3,9,24,42 |
| Vote | 1,4,12,16,11,3,13,2,9 | 9,16,8,14,5,10,13,2,15,4,6 | 1,2,3,4,9,11,13,16 |
| Zoo | 4,13,12,6,8 | 6,13,1,8,7,5,15,14,12,3 | 3,4,6,8,13 |
| Lymphography | 2,18,14,13,16,15 | 1,18,14,5,12,11,16,2 | 8,6,2,13,14,18,15 |
| Mushroom | 5,20,8,12,3 | 14,1,9,3,6 | 5,12,20,22 |
| Soybean-small | 4,22 | 23,22 | 23,22 |
| Breast cancer | 1,7,2,6 | 1,3,4,9 | 1,6,5,8 |
| Dataset | Original | RSAR | RSAR-Entropy | QCGWORS |
|---|---|---|---|---|
| Led | 24 | 6 | 11 | 5 |
| Exactly | 13 | 8 | 8 | 6 |
| Exactly2 | 13 | 10 | 11 | 10 |
| DNA | 57 | 7 | 6 | 5 |
| KC1 | 22 | 11 | 10 | 8 |
| KC2 | 21 | 7 | 9 | 5 |
| Lung | 56 | 4 | 5 | 4 |
| Vote | 16 | 9 | 11 | 8 |
| Zoo | 16 | 5 | 10 | 5 |
| Lymphography | 18 | 6 | 8 | 7 |
| Mushroom | 22 | 5 | 5 | 4 |
| Soybean-small | 35 | 2 | 2 | 2 |
| Breast cancer | 24 | 6 | 11 | 5 |
| Algorithm | Parameters |
|---|---|
| WOARSFS | Population size = 20, = 0.9, = 0.1, |
| FSARSR | Population size = 20, = 0.9, = 0.1 |
| QCGWORS | Population size = 20, = 0.9,= 0.1, |
| Dataset | Features | WOARSF | FSARSR | QCGWORS |
|---|---|---|---|---|
| Led | 24 | 6 | 5 | 5 |
| Exactly | 13 | 7 | 6 | 6 |
| Exactly2 | 13 | 11 | 10 | 10 |
| DNA | 57 | 6 | 7 | 5 |
| KC1 | 22 | 8 | 9 | 8 |
| KC2 | 21 | 5 | 6 | 5 |
| Lung | 56 | 4 | 4 | 4 |
| Vote | 16 | 9 | 9 | 9 |
| Zoo | 16 | 6 | 5 | 5 |
| Lymphography | 18 | 7 | 8 | 7 |
| Mushroom | 22 | 4 | 5 | 4 |
| Soybean-small | 35 | 2 | 2 | 2 |
| Breast cancer | 24 | 6 | 5 | 5 |
| Dataset | Feature | GWORS | QGWORS | ||||
|---|---|---|---|---|---|---|---|
| RF | KNN | Feature | RF | KNN | Feature | ||
| Lung | 56 | 84.03 ± 0.22 | 85.21 ± 0.81 | 4 | 86.35 ± 0.16 | 85.53 ± 0.74 | 4 |
| DNA | 57 | 35.13 ± 0.20 | 33.78 ± 0.10 | 7 | 36.25 ± 0.23 | 34.09± 0.10 | 5 |
| Vote | 16 | 91.41 ± 0.29 | 90.64 ± 0.45 | 8 | 93.12 ± 0.69 | 92.88 ± 0.42 | 8 |
| Breast cancer | 24 | 92.21 ± 0.28 | 93.91 ± 0.57 | 5 | 94.65 ± 0.73 | 96.59 ± 0.34 | 4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, G.; Wang, H.; Jia, D.; Wang, Q. Feature Selection of Grey Wolf Optimizer Based on Quantum Computing and Uncertain Symmetry Rough Set. Symmetry 2019, 11, 1470. https://doi.org/10.3390/sym11121470
Zhao G, Wang H, Jia D, Wang Q. Feature Selection of Grey Wolf Optimizer Based on Quantum Computing and Uncertain Symmetry Rough Set. Symmetry. 2019; 11(12):1470. https://doi.org/10.3390/sym11121470
Chicago/Turabian StyleZhao, Guobao, Haiying Wang, Deli Jia, and Quanbin Wang. 2019. "Feature Selection of Grey Wolf Optimizer Based on Quantum Computing and Uncertain Symmetry Rough Set" Symmetry 11, no. 12: 1470. https://doi.org/10.3390/sym11121470
APA StyleZhao, G., Wang, H., Jia, D., & Wang, Q. (2019). Feature Selection of Grey Wolf Optimizer Based on Quantum Computing and Uncertain Symmetry Rough Set. Symmetry, 11(12), 1470. https://doi.org/10.3390/sym11121470