1. Introduction
Pictorial composition is one of the most important concepts in art and design [
1,
2,
3,
4,
5]. It concerns the harmonious arrangement of components of an artwork into a unified whole. Of the various principles of composition, geometric or static bilateral symmetry is one of the simplest ones, i.e., the exact duplication of elements about the medial vertical axis. Pictures and designs with this property are usually pleasing to look at [
6]. However, also non-symmetric pictures can be aesthetically appealing. Therefore, in order to maintain symmetry as a general principle of good composition, it has been assumed that such pictures often have some hidden symmetry, i.e., are symmetric with respect to the perceptual weights of the elements in a picture. This kind of symmetry has been called aesthetic symmetry [
7], or dynamic symmetry [
8] and is closely related to the concept of perceptual balance [
9].
In his influential book on design, Ross [
1] provided a rather general definition of balance by stating that a balanced arrangement of elements in a picture “… is a Harmony of Positions due to the coincidence of two centers, the center of the attractions and the center of the framing” (p. 24). Obviously, this definition treats both horizontal and vertical balance equally. However, such a two-dimensional concept of balance, where both dimensions are combined and treated equally, has been investigated empirically only recently [
10,
11,
12,
13,
14,
15,
16]. The first empirical studies on balance were mainly concerned with the horizontal arrangement of elements in a picture, although some researchers also examined vertical balance [
17].
With respect to horizontal balance, it has been assumed that a picture is liked, if the perceptual weights on one side of a picture counterbalance those on the other side. Thus, the elements in a picture are considered as weights on a beam scale, or seesaw. This mechanical metaphor has often been applied to investigate how balanced a picture is. McManus et al. [
18], for instance, asked their participants to position a fulcrum underneath a picture so that the perceptual weights in the picture were horizontally balanced. If a picture is well balanced towards the midline, then the fulcrum should be placed underneath the center of the frame. McManus et al. found, however, that for many pictures the balance point was slightly left of center.
This example demonstrates that mechanical balance can be a helpful metaphor for investigating perceptual balance. However, its application is based on several assumptions. First of all, it has to be assumed that persons attribute weights to each element in a picture. This is not implausible, because by lifting real objects in our everyday activities, we steadily associate their weight with certain object features such as color, brightness, or other properties. Nevertheless, measuring the perceptual weights of picture elements is not straightforward, unless one makes simplifying assumptions. For instance, if one believes that brightness plays a crucial role for the perceptual weight of an object, then a simple approach is to assume that dark elements are heavier than bright ones, and, given an equal brightness, that large elements are heavier than small ones. Accordingly, the weight of an object can be computed by a simple gray-value integration method, i.e., by integrating the gray values over the object’s area (e.g., [
14]). This type of perceptual weight has to be distinguished from weights based on higher level properties such as perceptual salience, which is related to visual attention [
19,
20]. However, irrespective of how weight is determined, we further have to assume that persons are able to perceive the common center of ‘mass’ of all the perceptual element weights in a picture. At least for simple configurations, it has been shown that this assumption is justified [
21,
22].
Early experimental research on perceptual balance [
7,
23] tested the mechanical metaphor and found more or less support. Although the methods and procedures applied in these studies were state of the art at that time, from our perspective, they are improvable. Moreover, they were rather effortful, and therefore, only a few participants were observed. Therefore, the aim of the present study was to repeat some of the early experiments with modern methods and more participants to examine to what extent the early results are replicable.
As far as we know, the first experimental study on perceptual balance was conducted by Edgar Pierce [
7] during his time as a graduate student in Hugo Münsterberg’s lab at Harvard University. Pierce was concerned with the question: “Can a feeling of symmetry, that is, of aesthetical equality of the two halves, remain when the two sides are not geometrically identical, and if so, what are the conditions under which this can result—what variations of one side seem aesthetically equal to the variations of the other side?” (p. 484).
For his experiments, he used a 100 × 100 cm board covered with a black rubber surface. It had two invisible slits from one side to the other, which were used to hold and move objects by means of a slider on the backside. In one of the simpler arrangements, the physical midline was marked with a permanent 20 cm long white line. A 10 cm long vertical line was positioned on the right half of the display at a fixed distance of 20 cm from the midline, while there were movable objects such as a star, a square, or a vertical line on the left side, respectively. The experimenter could slide the movable object alternately towards and from the midline and the participants were asked to say “stop” when it reached the most “agreeable” position. After this decision, the participants were asked whether the composition gave any aesthetical feeling of symmetry or balance.
As a result, some participants made adjustments in accord with mechanical balance. For instance, a variable short line was stopped at a greater distance from the center than a long vertical line, whereas others ignored the size differences and simply placed the variable element at the laterally symmetric location. Further persons chose locations closely related to the golden section.
Despite noting individual differences, Pierce [
7] derived some general relations from his results. For instance, he concludes that a short line must be farther out than a long one, a thin line farther out than a bold line, etc. Thus, by and large, Pierce’s results can be interpreted as supporting the concept of mechanical balance.
A few years later, Ethel Puffer [
23], who was also a graduate student in Hugo Münsterberg’s Harvard Psychology Lab, criticized Pierce’s [
7] study for several reasons. First, by explicitly asking his participants whether the adjusted configuration was balanced, Pierce excluded any other possibility than that of mechanical balance. Second, by permanently showing a line at the center, he strongly accentuated the midline and divided the frame into two clearly visible halves. Finally, by focusing on averaged data, performance was not represented adequately, given the large individual differences.
In her own study on symmetry and balance, Puffer [
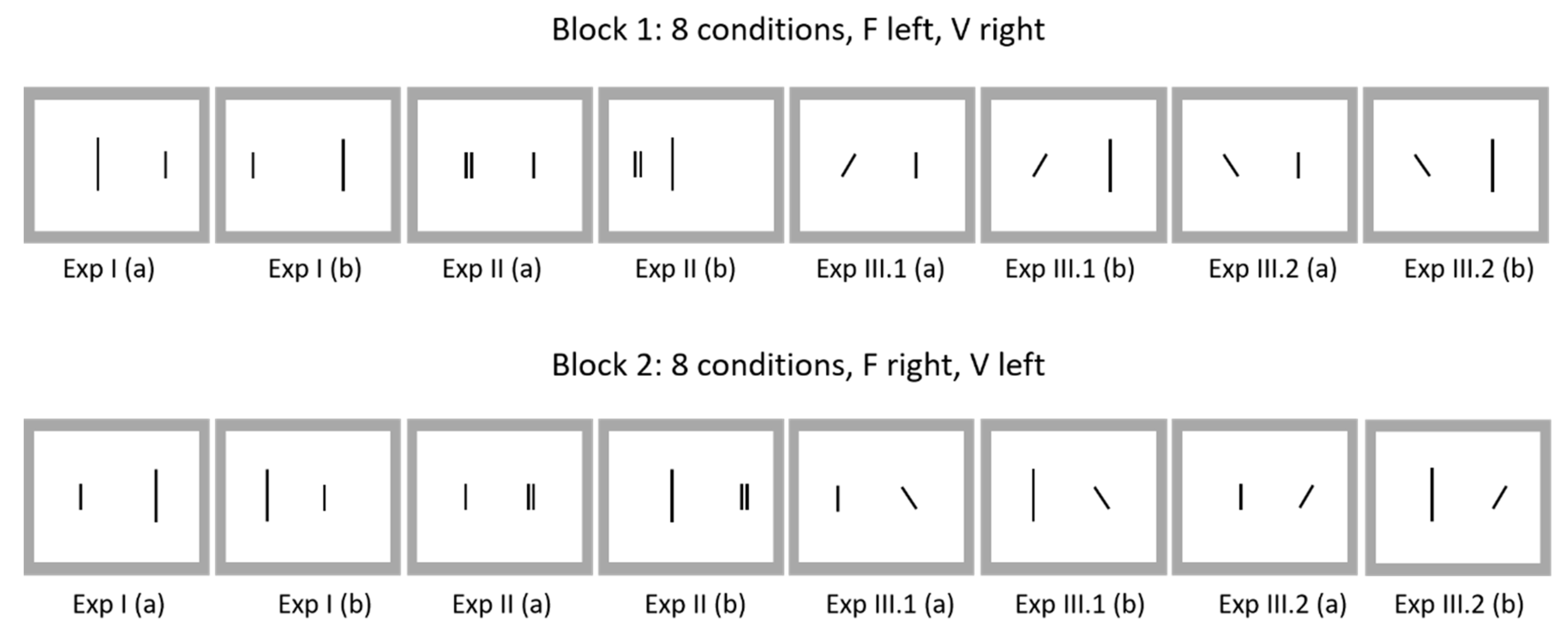
23] used arrangements of lines and other figures that were attached to a rectangular black surface (60 × 40 cm) with a gray frame (see
Figure 1). There was a fixed element F on one side (left or right) of the surface, and a variable element V on the other side. F was placed successively at different distances from the center, respectively. In her various experiments, Puffer used elements of different size (short, long, or double lines), elements that suggested movement (oblique or curved lines), elements that arouse what she called “intrinsic interest”, i.e., attracted attention, and elements with perspective depth. In all cases, Puffer’s nine participants were asked to horizontally move the variable element V, which was always a vertical long or short line, until they found a position that made the arrangement most aesthetically pleasing. Finding such a position of V was the result of a long series of trials, so that each participant made only about ten choices per hour. They were never asked whether the resulting arrangement was balanced.
Overall, Puffer’s results provided little support for mechanical balance as a design principle. As in Pierce’s study, there were large individual differences, which is why she did not compute averages but discussed her results on an individual level. Some persons behaved in accord with mechanical balance, at least in some conditions, whereas others even placed V close to F on the same side, which is incompatible with mechanical balance.
The preferred positions also depended on the element type. Preference for mechanical balance occurred most often when F was oblique (Exp. III, see
Figure 2). For lines of different sizes (Exp. I (a) and I (b), see
Figure 2), in some cases there was even a reversal of mechanical balance. For instance, with a short fixed line near the center, a larger movable line was positioned at a greater distance. For double lines (Exp. II, see
Figure 2), reversals were even more pronounced. However, they only occurred when mechanical balance would have brought both elements near the center of the frame. From the comments of her participants, Puffer concluded that they considered the whole picture and often tried to avoid a large black space. In any case, even if mechanical balance was reversed, the participants had a feeling of equilibrium.
In addition to the preference for mechanical balance and its reversal, there were also other preferred positions. Some of them were close to the center, while others approached bilateral symmetry. The latter, however, did not occur for double lines.
Taken together, Puffer’s results do not support mechanical balance as an important principle of aesthetic composition. Nevertheless, they have been interpreted as compatible with this metaphor (e.g., [
5,
24]). Since the exact role of mechanical balance for composition is still under dispute, the purpose of the current study was to repeat some of Puffer’s pioneering experiments with modern methods and a larger sample of participants.
3. Experiment 2
This experiment was similar to Experiment 1, except that all trials, i.e., also the F locations, were randomized in each block. If positional carry-over effects between trials have been responsible for the frequent closeness in our first experiment, then this principle should be applied less frequently in the present experiment.
Moreover, because we proposed the centering hypothesis only ex post facto in Experiment 1, this experiment was also an opportunity to see whether this result can be replicated.
3.1. Method
Forty persons (14 males, 26 females; mean age 24.2, SD = 6.20), mostly students from different disciplines of the University of Konstanz, were recruited via our local online system as in Experiment 1. They participated for a voucher worth €3. No participant had previously participated in Experiment 1. The procedure was identical to that of Experiment 1, except that the F locations were randomized.
3.2. Results
The data set of one participant was incomplete due to technical issues, and additionally three participants reported a small displacement between the variable line and the mouse cursor. Therefore, their data were excluded from the analysis (remaining 36 participants: 14 males, mean age 24.3, SD = 6.52).
The data were analyzed in the same way as in Experiment 1. The results of the statistical tests with respect to the four hypotheses are shown in
Table 2. As can be seen, tests for mechanical balance are significant only in one of 24 conditions tested, and this was a condition where the location for balance coincides with that for symmetry. Whereas symmetry was significant four times, closeness was again by far the most frequently applied strategy (11 of 24 test were significant). The majority of significant tests occurred with oblique F and short V, but again also for double-line F. This time, centering was significant only in two main conditions, and only for one F location, respectively. One of these conditions was double-short, where we included the F location closest to the center. Insofar, this result should be taken with care.
Concerning our overall analyses, the rate ratios for balance was 1.14, p = 0.161, for symmetry 1.51, p < 0.001, for closeness 4.63, p < 0.001, and for centering 1.65, p < 0.001. Even if we ignore the problematic double-short condition for the latter strategy (see above), the ratio is still significant, 1.43, p < 0.001.
3.2.1. Adjustment Times
The trimmed mean adjustment times for the eight conditions were: 5.21 (2.70), 5.29 (3.05), 5.66 (2.94), 5.60 (3.36), 4.84 (2.90), 5.12 (3.58), 5.08 (3.27), and 4.90 (2.88) s. Their average is 5.21 s (3.09 s). Across all trials, the adjustment times sum up to 6.95 min.
3.2.2. Individual Performance
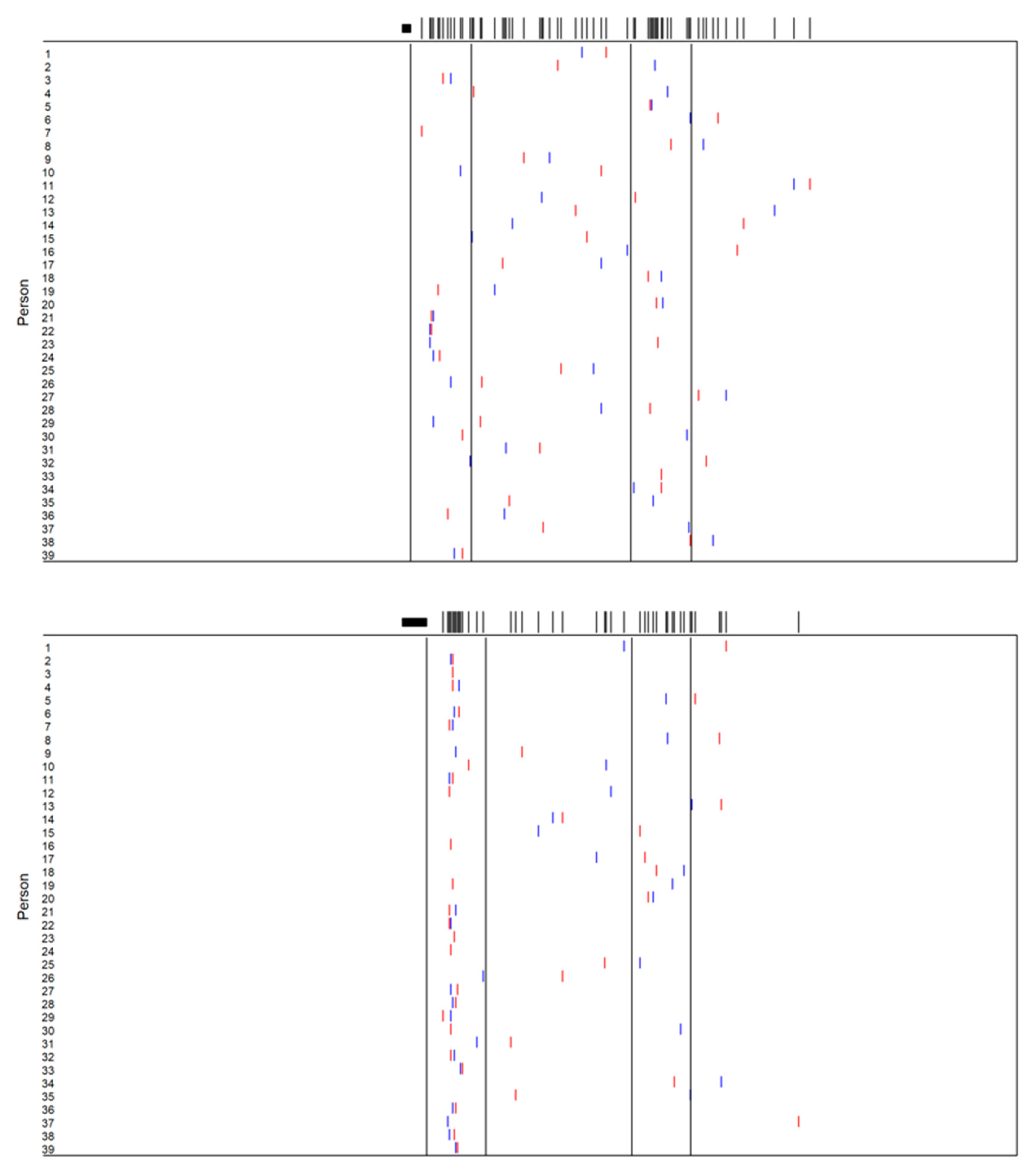
As in the previous experiment, we analyzed how many participants preferred the symmetry or closeness strategy. As a result, five persons produced a symmetric arrangement more often, whereas 22 placed more lines in accord with the closeness hypothesis. Nine persons could not be assigned to either of the two strategies.
Figure 7 illustrates these findings.
3.3. Discussion
Even though the F locations were randomized in this experiment, the results are, by and large, similar to those from the previous experiment. Different from our expectation, closeness was not only again the most frequently applied strategy, its dominance was even more pronounced than in Experiment 1. The analysis of the individual data revealed that more than half of the participants (22 of 36) preferred closeness over symmetry. These results demonstrate that the frequency of closeness in Experiment 1 was not due to carry-over effects caused by the stepwise increase of the distance between the fixed element and the midline.
Symmetry and centering also occurred less frequently than in our previous experiment. Centering was significant only in two tests, compared to nine tests in Experiment 1. Nevertheless, the overall tests were again significant for both strategies, indicating that they still played some role. In line with Experiment 1, there was again no evidence for the application of mechanical balance.
4. General Discussion
The aim of the present study was to repeat some of the experiments on symmetry and balance conducted by Ethel Puffer [
23] more than a century ago. She used a large (60 × 80 cm) board with an element of a certain form attached on one side at a fixed location and asked her nine participants to position a variable line so that the configuration was aesthetically most pleasing. Here, we updated her method and used an online experiment, where the variable line had to be moved on a screen with a computer mouse. A first striking difference in performance between the two experiments was that Puffer’s participants took about 6 min for each adjustment, whereas ours spent only about 5 s. Despite these large differences in adjustment times and the whole setup, some of the results obtained in Experiment 1 were similar.
First of all, as in Puffer, we found little to no evidence for the application of mechanical balance as a principle for producing aesthetically pleasing compositions. Rather, geometric symmetry was applied as principle, in the sense that participants often moved the variable element to a position that was laterally symmetric to that of the fixed element, but without paying attention to size and form differences between the fixed and variable elements. A similar performance was observed by Pierce, [
7] as well as by Puffer [
23]. A possible reason of why size and form differences were largely ignored could have been that they were relatively small. This is supported by the fact that symmetry was practically absent for double lines, which differed most in this respect. That lateral symmetry played an important role as design principle might have several reasons. For instance, there is not only a relatively high general preference for symmetry, it is also relatively easy to realize. This corresponds to the idea that people prefer symmetry, because it facilitates fluent processing, which generates positive subjective feelings [
28].
Furthermore, after visual inspection of our data, we had the impression that participants often placed the variable line at the center of the frame. Therefore, we also considered centering as a strategy, which was confirmed by our statistical analysis.
An unexpected result was that the variable line was often placed very close to the fixed element. Although Puffer had already reported that some of her participants placed the variable line near the fixed element, it occurred by far not as frequently as in our experiment. Here, closeness occurred for almost all element types. Moreover, the analysis of individual performance revealed that several participants exclusively used closeness as a strategy. Moreover, more participants preferred closeness over symmetry than vice versa. How can the strong tendency to produce closeness be explained? Puffer concluded from comments of her participants that they wanted to construct a configuration without necessarily forming a figure. Moreover, for them the clustered elements were set off against the blackness on the other side. Puffer had the impression that the black space on the opposite side had some meaning such as a deep vista or an expanse of sky.
Although Puffer’s account of closeness is interesting, we questioned that it accounts for the frequent application of this principle in our first experiment. Therefore, we hypothesized that the stepwise increase of the distance between the fixed element and the midline in combination with the short adjustment times might have produced carry-over effects from the shortest distance, where closeness is an obvious strategy, to longer distances.
To test our hypothesis, we conducted a second experiment, which was similar to the first one, except that the location of the fixed element and the element type were randomized across trials. As a result, the number of significant tests decreased substantially for all of our hypotheses (from 29 in Experiment 1, to 17 in Experiment 2, counting tests for overlapping hypotheses only once). The largest decrease occurred for centering, which was now practically absent. However, different from our expectation, closeness occurred again very frequently. The relative number of persons that preferred closeness over symmetry even increased. These results indicate that the stepwise procedure had an effect on the frequency of use of specific design principles, but that it was not responsible for the strong tendency in Experiment 1 to produce compositions based on closeness.
What else could explain the high frequency of closeness in our experiments? One reason might be that this principle was also relatively easy to apply, presumably, even easier than symmetry, and therefore strongly met the needs of our participants who are used to act quickly on the computer. However, an alternative and more plausible account is to assume that the participants adopted a specific perspective. The comments given by our participants suggest that some of them took a local perspective, i.e., focused more on composing a pleasing configuration from the elements, which usually resulted in closeness, while others adopted a global perspective and tried to produce a pleasing picture as a whole. Given these two perspectives, it is reasonable to assume that our computer-based method, where the participants had to focus on the variable line to drag it to another position, and where we had no control of the viewing distance, favored a local perspective, and, therefore, the production of closeness. The situation might be similar to drawing, where a local focus is also particularly useful [
29]. This account might explain the difference between our and Puffer’s results with respect to the frequency of closeness.
As already mentioned, similar to Puffer, we found only weak support for mechanical balance—at least if one does not assume empty space to have perceptual weight. This result could also have been due to our specific method. Both Puffer’s and our study applied the method of production, which is one of the three methods, besides the method of choice and the method of use, proposed by Fechner [
30]. The method of production has the advantage that it offers a large range of possibilities. In contrast, if the method of choice is applied for investigating balance, the researcher presents a more and a less balanced configuration and asked the participants which one they prefer. In such situations the more balanced one is usually preferred, and it is concluded that balance is important, and that people generally prefer balanced pictures. The present study, however, shows, as did Puffer’s study a century ago, that even for relatively simple arrangements, almost no person produces mechanically balanced configurations, when she or he is free also to apply other principles. One reason could be that balance is more difficult to produce than symmetry and closeness. Perhaps, art experts might have produced more balanced compositions, because of their knowledge about balance, and because they prefer symmetry less than non-experts [
31,
32].
If the positive role of mechanical balance for liking was only measurable in settings where all other variables are held constant, the importance of balance as a design principle was largely reduced. However, the attraction of balance as an aesthetic principle might depend on the applied method and the stimuli. As mentioned in the Introduction, more recent experiments did not restrict their investigation to the horizontal balance of simple elements, but examined to what extent the center of mass of multiple and more complex elements deviates from the center of the frame irrespective of direction [
10,
11,
12,
13,
14,
15,
16]. All these studies find support for a positive relation between balance and liking.
Interestingly, also for this two-dimensional approach, there is a study that used the method of production. Locher et al. [
33] asked their participants to construct interesting and pleasant designs from nine identical shapes of different sizes within a square frame located on a table. As a result, for most of the compositions the center of gravity was close to the geometric center of the frame.
Taken together, these results indicate that the answer to whether balance is an important design principle or not, depends on the stimulus material and the specific task. If multiple elements can be positioned freely in a frame, then mechanical balance is usually taken into account. In this case the geometric center of a display functions as an “anchor” around which the construction is organized [
2]. However, if there are only two elements in a frame, and one of them is fixed on one side, and the other can be moved along the horizontal midline only, then there are other, more attractive principles for designing a pleasing composition, such as closeness and lateral symmetry of the location of these two elements no matter whether the composition as a whole is balanced or not.