Riemann-Symmetric-Space-Based Models in Screening for Gene Transfer Polymers
Abstract
1. Introduction
2. Materials and Methods
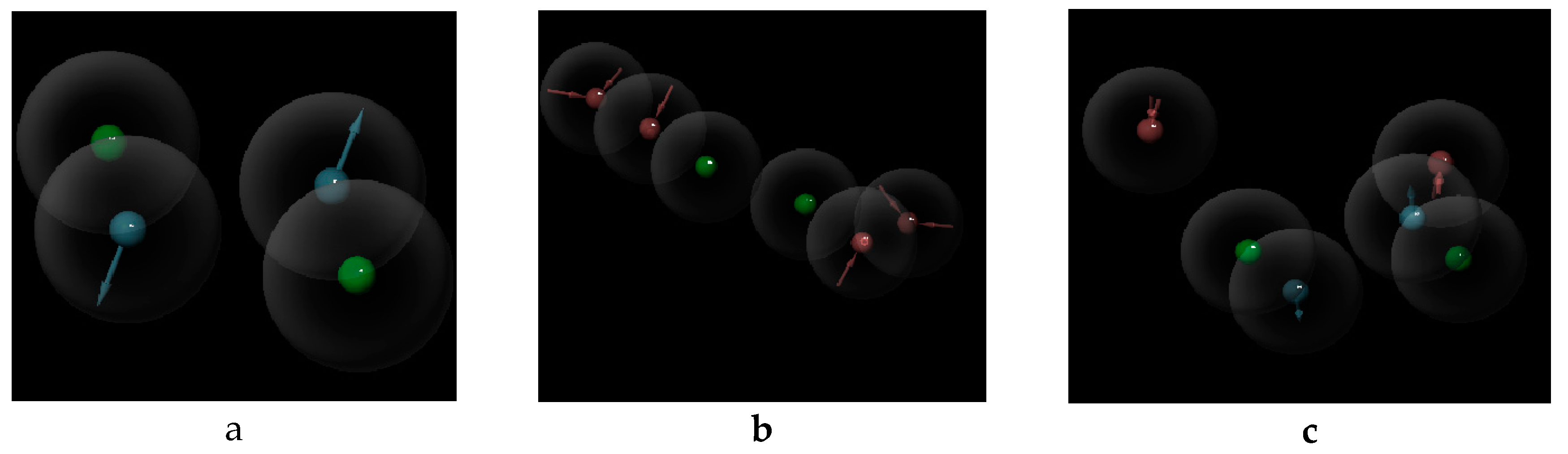
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mary, B.; Maurya, S.; Kumar, M.; Bammidi, S.; Kumar, V.; Jayandharan, G.R. Molecular engineering of Adeno-associated virus capsid improves its therapeutic gene transfer in murine models of hemophilia and retinal degeneration. Mol. Pharm. 2019, 16, 4738–4750. [Google Scholar] [CrossRef] [PubMed]
- Aartsma-Rus, A.; van Putten, M. The use of genetically humanized animal models for personalized medicine approaches. Dis. Model. Mech. 2019, 13, 041673. [Google Scholar] [CrossRef] [PubMed]
- Contin, M.; Garcia, C.; Dobrecky, C.; Lucangioli, S.; D’Accorso, N. Advances in drug delivery, gene delivery and therapeutic agents based on dendritic materials. Future Med. Chem. 2019, 11, 1791–1810. [Google Scholar] [CrossRef] [PubMed]
- Richard, B.; Ho-Fung, C.; Jóhannes, R. Characteristics of known drug space. Natural products, their derivatives and synthetic drugs. Eur. J. Med. Chem. 2010, 45, 5646–5652. [Google Scholar]
- Anderson, D.G.; Peng, W.; Akinc, A.; Naushad, H.; Kohn, A.; Pandera, R.; Langer, R.; Sawicli, A.J. A polymer library approach to suicide gene therapy for cancer. Proc. Natl. Acad. Sci. USA 2004, 9, 16028–16033. [Google Scholar] [CrossRef] [PubMed]
- Beata, S.; Mircea, V.D.; Mihai, V.P.; Ireneusz, P.G. Docking linear ligands to glucose oxidase. Int. J. Mol. Sci. 2016, 17, 1796. [Google Scholar]
- Nguyen, L.H.; Nguyen, T.H.; Truong, T.N. Quantum Mechanical-Based Quantitative Structure-Property Relationships for Electronic Properties of Two Large Classes of Organic Semiconductor Materials: Polycyclic Aromatic Hydrocarbons and Thienoacenes. ACS Omega 2019, 4, 7516–7523. [Google Scholar] [CrossRef] [PubMed]
- Mathematica; Version 8.0; Wolfram Research, Inc.: Champaign, IL, USA, 2010.
- Schrödinger Release Prime; Schrödinger LLC: New York, NY, USA, 2009.
- Akhiezer, D.N.; Vinberg, E.B. Weakly symmetric spaces and spherical varieties. Transf. Groups 1999, 4, 3–24. [Google Scholar] [CrossRef]
- Wolf Joseph, A. Spaces of Constant Curvature, 5th ed.; McGraw–Hill: New York, NY, USA, 1999. [Google Scholar]
- Conway John, B. Functions of One Complex Variable, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1978. [Google Scholar]
- Arfken, G. Mathematical Methods for Physicists, 3rd ed.; Academic Press: Orlando, FL, USA, 1985; pp. 397–399. [Google Scholar]
- Morse, P.M.; Feshbach, H. Methods of Theoretical Physics, Part I; McGraw-Hill: New York, NY, USA, 1953; pp. 391–392, 399–401. [Google Scholar]
- Trott, M. The Mathematica Guidebook for Programming; Springer: Berlin/Heidelberg, Germany, 2004; pp. 188–191. [Google Scholar]
- Weisstein, E.W. “Branch Point” from MathWorld—A WolframWeb Resource. Available online: http://mathworld.wolfram.com/BranchPoint.html (accessed on 5 December 2018).
- Majumdar, S.; Basak, S.C.; Lungu, C.N.; Diudea, M.V.; Grunwald, G.D. Mathematical structural descriptors and mutagenicity assessment: A study with congeneric and diverse datasets. SAR QSAR Environ. Res. 2018, 29, 579–590. [Google Scholar] [CrossRef] [PubMed]
- Petitjean, M. A definition of symmetry. Symmetry Cult. Sci. 2007, 18, 99–119. [Google Scholar]
- Lungu, C.N. C-C chemokine receptor type 3 inhibitors: Bioactivity prediction using local vertex invariants based on thermal conductivity layer matrix. Stud. Univ. Babes-Bolyai Chem. 2018, 63, 177–188. [Google Scholar] [CrossRef]
- Lungu, C.N.; Diudea, M.V.; Putz, M.V. Ligand shaping in induced fit docking of MraY inhibitors. Polynomial discriminant and Laplacian operator as biological activity descriptors. Int. J. Mol. Sci. 2018, 18, 1377. [Google Scholar] [CrossRef] [PubMed]
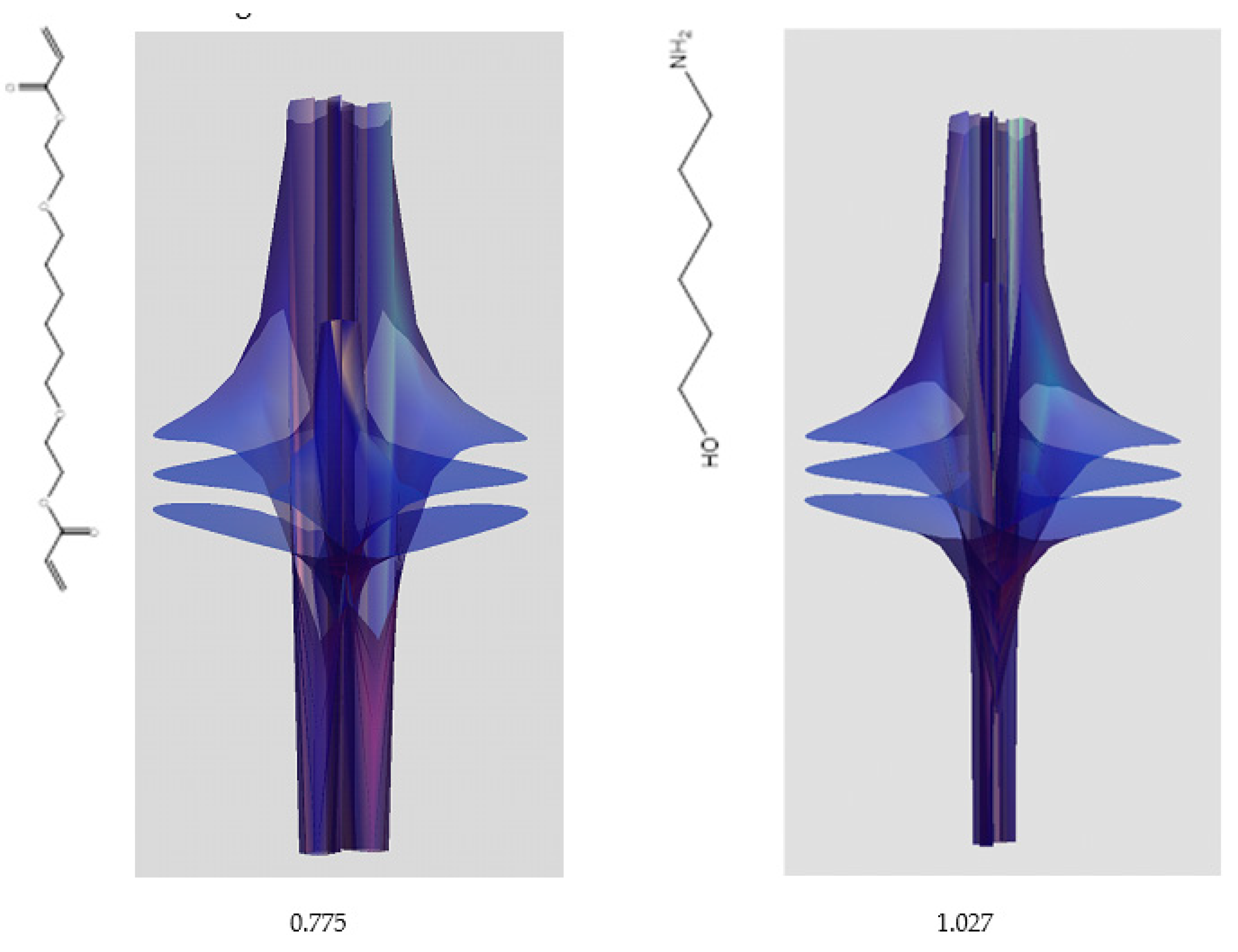
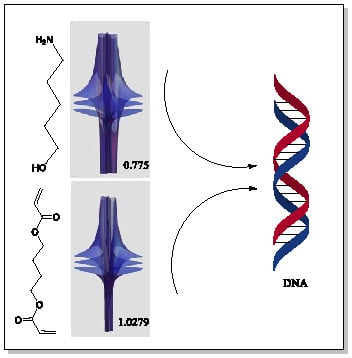
| Item | Monomers with Proven Gene Transfer Capabilities |
|---|---|
| 1 | 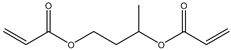 |
| 2 | 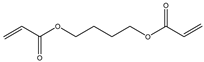 |
| 3 | 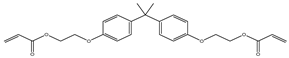 |
| 4 | 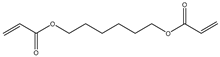 |
| 5 | 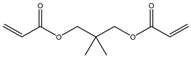 |
| 6 | 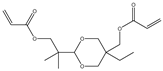 |
| 7 |  |
| 8 |  |
| 9 | 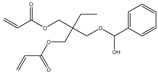 |
| 10 | 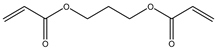 |
| 11 |  |
| 11 |  |
| 12 |  |
| 13 | 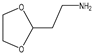 |
| 14 | 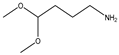 |
| 15 | 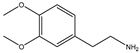 |
| 16 |  |
| 17 | 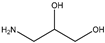 |
| 18 | 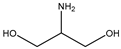 |
| 19 |  |
| 20 |  |
| 21 |  |
| 22 | 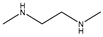 |
| 23 | 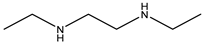 |
| 24 | 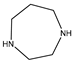 |
| 25 | 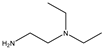 |
| 26 |  |
| 27 | 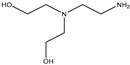 |
| 28 | 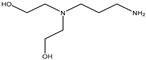 |
| 29 |  |
| Monomer Equations | |
|---|---|
| # | Coordinate Based Equations |
| 1 | ∂H(−13.4 + 19H) |
| 2 | ∂H(−2.2 + 18.5H) |
| 3 | ∂H(−13.0 + 28H) |
| 4 | ∂H(−13.6 + 14H) |
| 5 | ∂H(−2.4 + 15H) |
| 6 | ∂H(−2.6 + 15H) |
| 7 | ∂H(−4.9 + 17H) |
| 8 | ∂H(−15.5 + 20H) |
| 9 | ∂H(−4.5 + 23H) |
| 10 | ∂H(−4.3 + 18H) |
| 11 | ∂H(−19.1 + 24H) |
| 12 | ∂H(−3.4 + 19H) |
| 13 | ∂H(−3.7 + 24H) |
| 14 | ∂H(−2.4 + 21H) |
| 15 | ∂H(−4.6 + 26H) |
| 16 | ∂H(−4.0 + 2.8H) |
| 17 | ∂H(6.8H) |
| 18 | ∂H(−1.8 + 19H) |
| 19 | ∂H(−1.9 + 795.2H) |
| 20 | ∂H(−13.4 + 28H) |
| 21 | ∂H(−28.7 + 28H) |
| 22 | ∂H(−16.7 + 59H) |
| 23 | ∂H(83.1H) |
| 24 | ∂H(−10.8 + 31H) |
| 25 | ∂H(25H) |
| 26 | ∂H(31H) |
| 27 | ∂H(−7.3 + 323.5H) |
| 28 | ∂H(398.6H) |
| 29 | ∂H(−5.8 + 49H) |
| # | Equations for Computing Riemann Surfaces |
|---|---|
| 1 | z (−13.4 + 19 z)^(1/(z (−13.4 + 19 z))) |
| 2 | z (−2.2 + 18.5z)^(1/(z (−2.2 + 18.5z))) |
| 3 | z (−13.0 + 28z)^(1/(z (−13.0 + 28z))) |
| 4 | z (−13.6 + 14 z)^(1/(z (−13.6 + 14z))) |
| 5 | z (−2.4 + 15 z)^(1/(z (−2.4 + 15 z))) |
| 6 | z (−2.6 + 15z)^(1/(z (−2.6 + 15z))) |
| 7 | z (−4.9 + 17z)^(1/(z (−4.9 + 17z))) |
| 8 | z (−15.5 + 20z)^(1/(z (−15.5 + 20z))) |
| 9 | z (−4.5 + 23z)^(1/(z (−4.5 + 23 z))) |
| 10 | z (−4.3 + 18z)^(1/(z (−4.3 + 18z))) |
| 11 | z (−19.1 + 24z)^(1/(z (−19.1 + 24z))) |
| 12 | z (−3.4 + 19 z)^(1/(z (−3.4 + 19z))) |
| 13 | z (−3.7 + 24 z)^(1/(z (−3.7 + 24z))) |
| 14 | z (−2.4 + 21z)^(1/(−2.4 + 21 z))) |
| 15 | z (−4.6 + 26z)^(1/(z (−4.6 + 26 z))) |
| 16 | z (−4.0 + 2.8 z)^(1/(z (−4.0 + 28 z))) |
| 17 | z (6.8 z)^(1/(z (6.8 z))) |
| 18 | z (−1.8 + 19z)^(1/(z (−1.8 + 19 z))) |
| 19 | z (−1.9 + 795.2 z)^(1/(z (−1.9 + 795.2 z))) |
| 20 | z (−13.4 + 28 z)^(1/(z (−13.4 + 28 z))) |
| 21 | z (−28.7 + 28 z)^(1/(z (−28.7 + 28 z))) |
| 22 | z (−16.7 + 59 z)^(1/(z (−16.7 + 59 z))) |
| 23 | z ( 83.1 z)^(1/(z (83.1 z))) |
| 24 | z (−10.8 + 31 z)^(1/(z (−10.8 + 31 z))) |
| 25 | z (25 z)^(1/(z ( 25 z))) |
| 26 | z (31 z)^(1/(z ( 31z))) |
| 27 | z (−7.3 + 323.5 z)^(1/(z (−7.3 + 323.5 z))) |
| 28 | z ( 398.6 z)^(1/(z (398.6 z))) |
| 29 | z (−5.8 + 49 z)^(1/(z (−5.8 + 49 z))) |
| Riemann Surfaces | ||
|---|---|---|
| 1 | 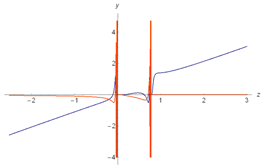 | 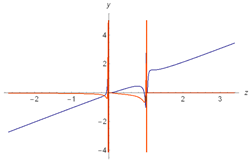 |
| 2 | 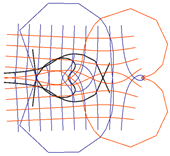 | 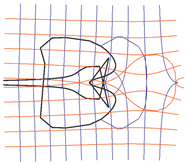 |
| 3 |  |  |
| 4 |  |  |
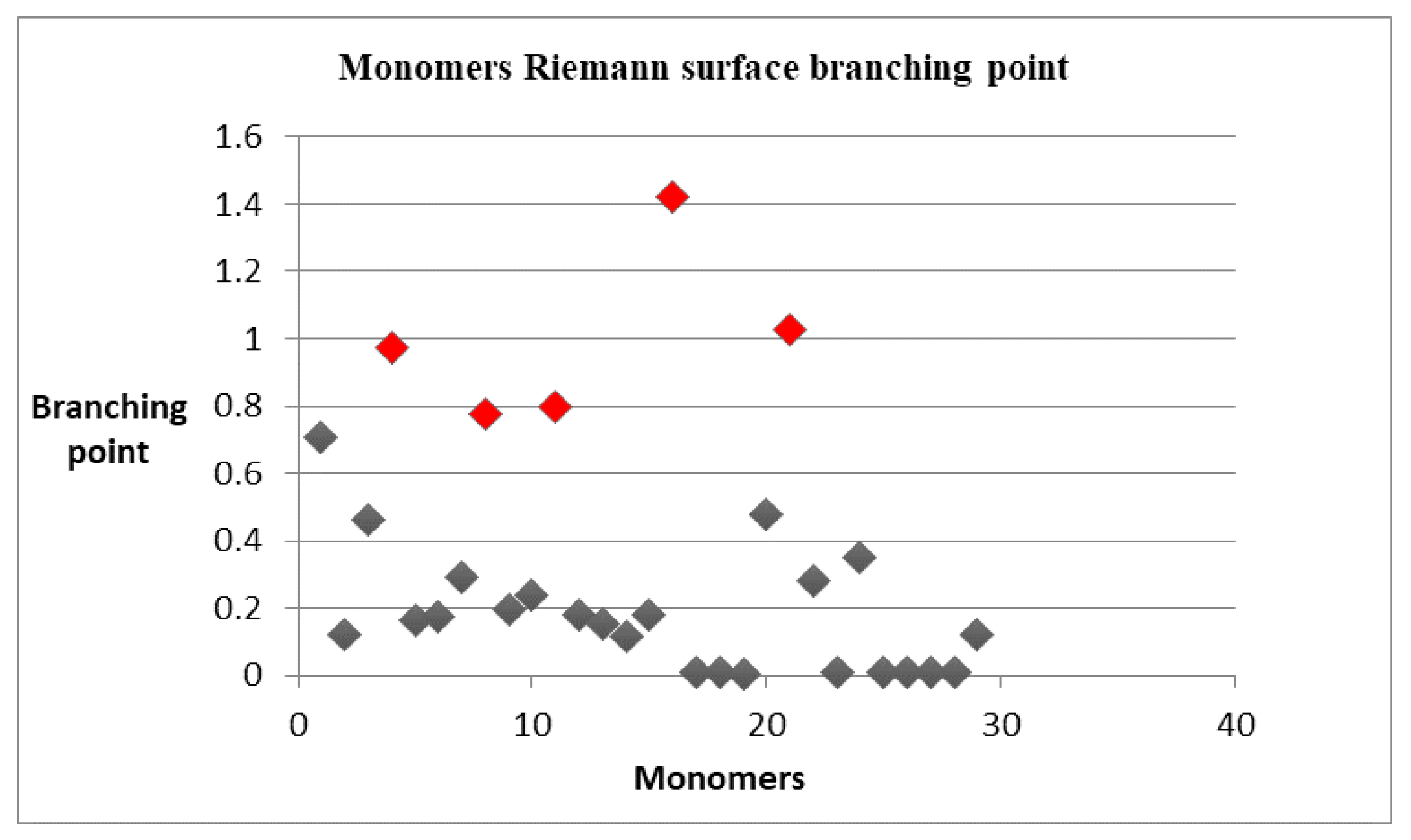
| 5 | 0.7754 | 1.027 |
| 6 | # 8 | # 21 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lungu, C.N.; Grudzinski, I.P. Riemann-Symmetric-Space-Based Models in Screening for Gene Transfer Polymers. Symmetry 2019, 11, 1466. https://doi.org/10.3390/sym11121466
Lungu CN, Grudzinski IP. Riemann-Symmetric-Space-Based Models in Screening for Gene Transfer Polymers. Symmetry. 2019; 11(12):1466. https://doi.org/10.3390/sym11121466
Chicago/Turabian StyleLungu, Claudiu N., and Ireneusz P. Grudzinski. 2019. "Riemann-Symmetric-Space-Based Models in Screening for Gene Transfer Polymers" Symmetry 11, no. 12: 1466. https://doi.org/10.3390/sym11121466
APA StyleLungu, C. N., & Grudzinski, I. P. (2019). Riemann-Symmetric-Space-Based Models in Screening for Gene Transfer Polymers. Symmetry, 11(12), 1466. https://doi.org/10.3390/sym11121466