Abstract
In this work, a stratiform metamaterial is arranged as multiple periods of metal-dielectric symmetrical film stack to provide precise equivalent refractive index and admittance. There are multiple solutions of equivalent refractive index retrieved from the characteristic matrix of the film stack. The correct refractive index is derived by connecting different branches of solution at different ranges of wavelength or thickness of the dielectric layer. The refractive index of an Ag-TiO2 five-layered symmetrical film stack shown in previous work is demonstrated to be positive real instead of negative real. The associated type I iso-frequency curve supports negative refraction. In order to extend the operating wavelength of type I metamaterial, the number of the metal-dielectric symmetrical film stack is increased to reduce the thickness of the dielectric film to approach subwavelength requirement.
1. Introduction
A metamaterial with a negative index of refraction has been predicted to be effective for constructing a perfect lens [1]. Archetypical left-handed metamaterials comprise split rings as inductive-capacitive resonators, which support the simultaneous reversal of electric and magnetic responses to light at microwave frequencies [2]. Using advanced lithographic nanofabrication, the scales of resonators were shrunk to exhibit a left-handed response to light at higher frequencies, such as infrared or visible frequencies [3]. Recently, a stratiform metamaterial that comprises metal film (M) and dielectric film (D) was developed for transverse magnetic (TM) polarization mode [4]. Light incident on the side of this stack will couple to waveguide modes [5,6]. The anti-symmetry mode of the transverse electric field in a plasmonic waveguide composed of metal film (M)/dielectric film (D)/metal film (M) (MDM) causes a negative group velocity at frequencies greater than the surface plasmon resonance frequency [6]. A combination of a pair of typical MDM waveguides as a waveguide composed of metal film (M)/dielectric film (D)/metal film (M)/dielectric film (D)/metal film (M) (MDMDM) results in electric-field coupling between adjacent MDM waveguides. The symmetrical electric field distribution leads to a positive coupling constant, thus the stack exhibits backward wave phenomenon.
In 2014, a film stack comprising TiO2 and Ag films alternately was claimed to yield an index of negative unity over a wide range of incidence angles at a wavelength of 363.8 nm [7]. Later, whether the negative refraction in the TiO2-Ag multilayer came from a negative index of refraction was questioned and discussed. The negative refraction also occurs in a hyperbolic metamaterial. Hyperbolic metamaterials have been developed for more than 10 years. In most cases, hyperbolic metamaterials are metal-dielectric multilayers [8,9]. Its property is described by a diagonal permittivity tensor. The principal permittivities are roughly estimated using effective medium approximation [10]. The signs of the two tangential permittivities are the same, but the signs of its tangential and vertical permittivities are opposite. Accordingly, there are two kinds of hyperbolic shaped isofrequency curves (type I and type II) [11]. A previous work on the decomposition of the Bloch wave in the layered structure into a number of harmonics showed that the iso-frequency curve of the main harmonic mode corresponds to the type I hyperbolic metamatrerial [12]. The negative refraction of energy is invoked by the shape of the iso-frequency contour [11]. Therefore, the multilayer is a hyperbolic metamaterial, and light propagation is mainly dominated by right-handed harmonics with a positive phase index.
Although the relevant works have explained the wave phenomenon in a metal-dielectric multilayer, a comprehensive design method for negative refraction is still required. A multilayer with precise optical constants, including refractive index and admittance, are necessary for a metamaterial design because, in real applications, both transmission and reflection are affected by both optical constants. In this work, a stratiform metamaterial is designed by arranging a multilayer composed of multiple periods of metal-dielectric symmetrical film stack (SFS). Based on the calculation of characteristic film matrixes [13], the metal-dielectric symmetrical film stack is equivalent to a layer with the equivalent refractive index and admittance that can be derived precisely by choosing the correct solution from a multi-branch of solution [14,15]. The refractive index versus angle of incidence can be used to plot a precise iso-frequency curve that indicates whether the stratiform metamaterial is a hyperbolic metamaterial. A type I hyperbolic metamaterial supports negative refraction from normal incidence to a certain oblique angle of incidence. In order to apply to real applications, the transmission is taken into account by considering the extinction coefficient and admittance [16].
2. Methods
Exploiting thin-film optics, symmetrical film stacks have been widely designed for edge filters [17]. An all-dielectric symmetrical film stack is equivalent to a single layer with an equivalent refractive index that is a function of wavelength , thicknesses, and refractive indexes of all constituent films. The equivalent refractive index is pure real and pure imaginary in different wavelength ranges, providing passband and stopband characteristics, respectively. An edge filter was designed across the passband and stopband. The equivalent model of a metal-dielectric symmetrical film stack was still valid, thus the product of characteristic film matrixes of the constituent thin films yielded a resultant matrix that had the same form of that of a single layer. Figure 1 shows the equivalent model of 3 symmetrical films composed of film A and film B. Equation (1) shows the product of 3 characteristic film matrixes of the symmetrical structure: film A/film B/film A (ABA).
where and (j = A, B) are the phase and admittance of each layer of the stack. The equivalent phase thickness of the stack and the equivalent admittance Eeq were complex. At normal incidence, the equivalent refractive index Neq is derived from the phase thickness through the relationship . Both Eeq and Neq can be tailored separately. Both Eeq and Neq are represented with the equivalent permittivity εeq and the equivalent permeability as and , respectively. According to effective medium approximation, the equivalent refractive index and admittance of a metal-dielectric composite are generally complex. In case of oblique incidence and TM polarization state, the equivalent phase thickness should be . Figure 1 shows the equivalent scheme of a 3-layered symmetrical film stack ABA. The θeq is the equivalent angle of refraction in the film stack. The and are thicknesses of film A and film B, respectively. The and are angles of refraction in film A and film B, respectively. The equivalent admittance for TM polarization should be modified as . The product of the 3 characteristic film matrixes ABA is shown in Equation (2).
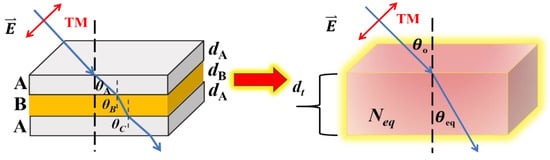
Figure 1.
The equivalent model of a three-layered symmetrical film stack.
The permittivity εeq can be retried from the matrix elements firstly through Equation (3).
The equivalent angle of refraction can be derived through the law of refraction (N0 and θ0 are the refractive indexes of the cover medium and angle of incidence, respectively), as shown in Equation (4).
Next, we can get the equivalent refractive index Neq shown in Equation (5).
Finally, we can have the equivalent permeability μeq and admittance .
In this work, the time-dependent phase factor of a propagating harmonic wave takes the form ( is the angular frequency) and an absorbing material has a refractive index n-ik. Unlike an all-dielectric symmetrical film stack, most metal–dielectric symmetrical film stacks have a different equivalent refractive index and equivalent admittance because the equivalent permeability is not unity for most metal–dielectric composites in subwavelength scale. Both and can be tailored separately for novel applications [16]. In a previous work, a 7-layered metal-dielectric symmetrical film stack was designed and fabricated to have an near unity and an with large imaginary part that was comparable to that of a metal. Such a layered metamaterial can couple most incident light into the upper interface and dissipate its energy with a very small thickness [18].
It is noted that there were multi-solutions for the phase thickness and refractive index. There were multiple branches of solutions of equivalent phase thickness retrieved from matrix element M11: (m = 0, The correct solution should satisfy the 3 criteria: (1) The real part of the equivalent admittance should be positive; (2) the imaginary part of the equivalent refractive index should be negative; (3) both and as functions of wavelength or any constitutive parameter should be continuous [19]. It is particular that a specific branch was unable to satisfy the criteria over the whole wavelengths. The continuity of the real part of the equivalent refractive index as a function of wavelength or any constitutive parameter required choosing different branches for regions separated by the discontinuous points. For a metal-dielectric SFS in the form of MDM…DM, a m-th branch was chosen thus that the at thickness of dielectric layer equal to the refractive index of metal. The m-th branch was correct for the range form to its first discontinuous point at . The at thickness d larger than relied on a branch next to the m-th branch to connect the m-th branch at to keep the continuous condition till its discontinuous point at . The correct branch for the thickness d larger than was chosen to keep continuous at the .
3. Results
A five-layered SFS of Ag (33 nm)/TiO2 (28 nm)/Ag (30 nm)/TiO2 (28 nm)/Ag (33 nm) in a previous work [7] was examined here. Such SFS was claimed to have a negative index around -1 at a wavelength of 363.8 nm. The refractive indexes of Ag and TiO2 were 0.0785-1.59i and 2.8-0.05i, respectively. The equivalent versus thickness of TiO2 from 0 nm to 60 nm at normal incidence with branch (m = 0) is shown in Figure 2a. At the thickness of d = 0 nm, the index of refraction was 0.0785, which was the real part of the refractive index of Ag. It means that the branch m = 0 was correct from d = 0 nm to its first discontinuous point at = 22 nm. At the thickness of d = 28 nm in Figure 2a, the index of refraction was −1.058, which was the proposed value of negative index. However, the index of refraction after = 22 nm needed to be connected with another branch (m = 1), as shown in Figure 2b. For the branch (m = 1), there was a discontinuous point at = 37 nm, thus the index after d = 37 nm was connected with branch (m = −1), as shown in Figure 2c. Figure 2d shows the correct real part of as a function of d from d = 0 nm to d = 60 nm.
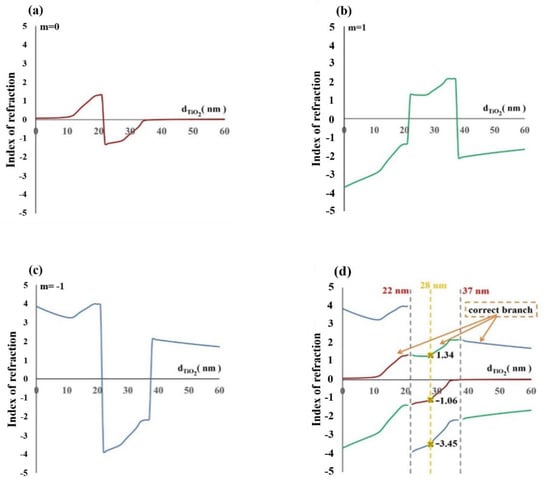
Figure 2.
Equivalent of branches (a) m = 0, (b) m = 1, and (c) m = −1; (d) The correct as a function of d.
Figure 3a shows both the real part and imaginary part of as a function of d. The at d = 28 nm was 1.34 and the versus the angle of incidence is shown in Figure 3b. With the correct as a function of angle of incidence. The iso-frequency curve (IFC) in Figure 3c represents the wave vector component versus the other component . The wave vector component along the interface is denoted as that is decided by the incident wave vector and continuous across each interface of a multilayer. The other wave vector component perpendicular to the interface is that can be derived through dispersion relation, as shown in Equation (8).
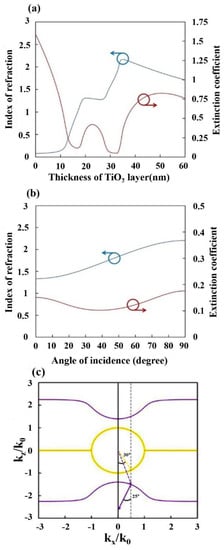
Figure 3.
(a) Correct and as functions of d, (b) correct and as functions of angle of incidence at d = 28 nm, (c) the iso-frequency curve, the yellow and purple lines are cover medium and hyperbolic metamaterial, respectively. The dotted arrows and solid arrows represent wave vector and ray vector, respectively.
The IFC shows that the multilayer is a type I hyperbolic metamaterial. Compared with the IFC estimated by effective permittivity tensor, the IFC calculated using the SFS equivalent model is precise. The ray vector derived from the IFC demonstrates that the imaging using the multilayer as a flat lens was based on the negative refraction instead of the nature of the negative index of refraction.
Here an SFS arrangement was used to design a type I hyperbolic metamaterial in order to provide a precise iso-frequency curve. High transmission at normal incidence was necessary for a type I metamaterial. The thicknesses of the metal and dielectric films needed to be within the subwavelength scale. However, the type I iso-frequency curve of an alternatively arranged metal–dielectric multilayer usually occurs at short wavelengths around the plasmonic resonate wavelength of the metal at which the permittivity of the metal film lead to low loss [20,21]. Besides the requirement of refractive index for type I isofrequency curve, the admittance should match to environment (air in this work) from normal incidence to an oblique angle to support the function of imaging. In order to overcome the frequency restriction for the occurrence of negative refraction, the type I hyperbolic metamaterial composed of Ag and Ta2O5 films was designed at a wavelength of 600 nm. According to our previous work [22], a thin metal film can be inserted between two metal films to perform a huge admittance locus and admittance matching to achieve high transmission property. The method, called modified Fabry-Perot (FP) design, can be extended to any odd-numbered metal–dielectric film stack. At a wavelength of 600 nm, the silver film usually takes 10 nm to 20 nm to achieve the modified FP design. Therefore, each silver film in the film stack was set to have the same thickness of 20 nm for the five-layered symmetrical film stack MDMDM = Ag/Ta2O5/Ag/Ta2O5/Ag. The optical constants of Ag and Ta2O5 were adopted from the commercial optical thin-film software (Essential Macleod) [23].
Figure 4a shows and as functions as functions of from 0 nm to 200 nm. Three branches of were selected for the three ranges of (0 nm,87 nm), (87 nm,117 nm), and (117 nm,200 nm). At 113 nm, equivalent extinction coefficient had a minimum value of 0.011 and equivalent index of refraction was 1.815. There were two ranges of corresponding to low (<0.1), which were from = 68 nm to = 80 nm and from = 99 nm to = 115 nm. With respect to real applications, the equivalent admittance needed to be considered too. Figure 4b plots and as functions of . High transmission required a small imaginary part of the admittance . At 108 nm, has a minimum magnitude of 0.091 and was 4.078. The mismatch of the real part of the admittance between the cover medium and SFS can be improved through index-matching coatings to reduce reflection at the upper and bottom interfaces. For low-magnitude (), varied from 1.246 to 3.118 and 1.024 to 8.98 occurred during the ranges of ( 67 nm, 74 nm) and (100 nm, 113 nm), respectively. The ranges of for low and low considerably overlaped, thus a multilayer with low loss could be derived by tuning the dielectric layer within both ranges. The as a function of and angle of incidence is shown in Figure 4c. The maximum is 2.156 at and =126 nm. At the range of between 67 nm and 74 nm, the versus showed that the SFS was equivalent to a dielectric–like anisotropic medium. The versus showed near type I hyperbolic shape at the range from 100 nm to 113 nm. The optimum transmission for the metamaterial in air was considered here. The transmittance of Air/SFS/Air was greater than from to . The thickness was tuned in the range that corresponded to type I hyperbolic metamaterial to yield a maximum of 47.56% at 100 nm. Figure 4d plots the iso-frequency curve of Ag (20 nm)/Ta2O5 (100 nm)/Ag (20 nm)/Ta2O5 (100 nm)/Ag (20 nm), where was the wave vector in free space. Unlike a smooth and typical hyperbolic curve, the ratio kept around 1.2 within the range of between and . It means that the reflected or diffracted ray vector was perpendicular to the interface for the parallel-to-interface component of the wave vector during the aforementioned range.
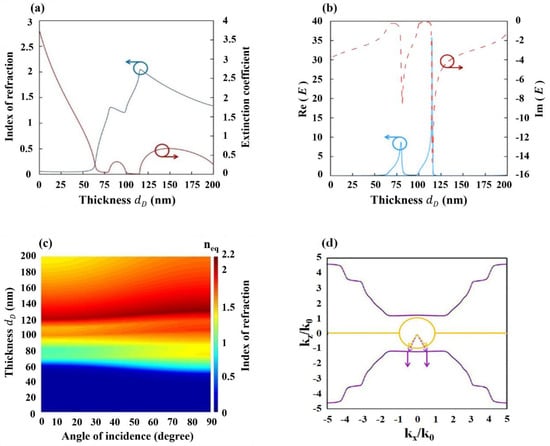
Figure 4.
(a) and as functions of dD of five-layered MDMDM at a wavelength of 600 nm, (b) and as functions of dD of five-layered MDMDM a wavelength of 600 nm, (c) as a function of dD and angle of incidence at a wavelength of 600 nm, (d) the iso-frequency curve of Ag(20 nm)/Ta2O5 (100 nm)/Ag (20 nm)/ Ta2O5 (100 nm)/Ag (20 nm). The dotted arrows and solid arrows represent wave vector and ray vector, respectively.
The procedure for constructing the aforementioned modified FP SFS can be executed for a seven-layered MDMDMDM for a wavelength of 600 nm with 20 nm-thick Ag films and equally thick Ta2O5 films. Figure 5a shows and as functions of . Figure 5b shows and as functions of . There are three ranges of corresponding to low ( < 0.1), which were (64 nm, 67 nm), (83 nm, 97 nm), and (108 nm, 117 nm). The thickness of the dielectric layer in the seven-layered SFS with a low extinction coefficient was less than that of MDMDM. At 113 nm, had a minimum magnitude of 0.1327 and the was 4.2736. varied from 1.28 to 4.02 and 2.037 to 9.053 at a low-magnitude (), which ranges were (84 nm, 92 nm) and ( 110 nm, 116 nm), respectively. The as a function of and angle of incidence is shown in Figure 5c. The type I hyperbolic metamaterial occurred at and ranged from 75 nm to 80 nm. The maximum of 46.49 % occurred at 85 nm, and the corresponding iso-frequency curve is shown in Figure 5d. The optimum thickness for type I iso-frequency curve was shifted from 100 nm in MDMDM structure to 80 nm here in MDMDMDM structure. Compared with the five-layered case, the ratio keeps around 1.1 within a smaller range of between and .
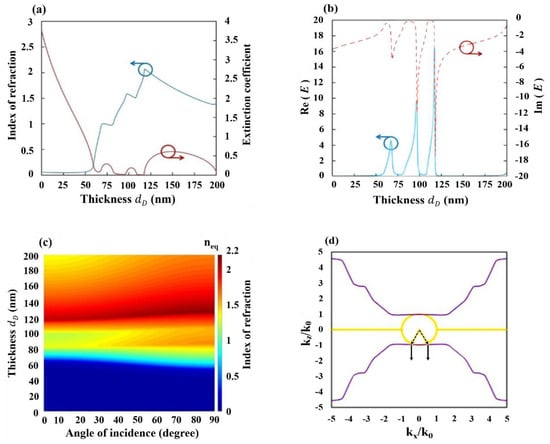
Figure 5.
(a) and as functions of dD of seven-layered MDMDM at a wavelength of 600 nm, (b) and as functions of dD of seven-layered MDMDM a wavelength of 600 nm, (c) as a function of dD and angle of incidence at a wavelength of 600 nm, (d) the iso-frequency curve of Ag (20 nm)/Ta2O5 (85 nm)/Ag (20 nm)/ Ta2O5 (85 nm)/Ag (20 nm). The dotted arrows and solid arrows represent wave vector and ray vector, respectively.
4. Conclusions
In conclusion, the equivalent model of a symmetrical film stack was applied to calculate the precise equivalent refractive index and admittance. In order to satisfy the criteria of branch selection, the correct branch solution of the refractive index was only valid for a certain range of wavelength or thickness of the dielectric layer. We clarify that the previous stratiform metamaterial is a type I hyperbolic metamaterial instead of a negative index medium. Based on the modified Fabry-Perot design for a metal-dielectric multilayer, a low loss hyperbolic metamaterial can be designed for an odd-numbered metal-dielectric symmetrical film stack. It is demonstrated that the required thickness of dielectric film for a type I metamaterial can be reduced by increasing the number of films in a symmetrical film stack. A metal-dielectric multilayer should be arranged as a multiple symmetrical film stack to exhibit the exact optical property. The method we proposed here can be applied to design a hyperbolic metamaterial in a precise and more flexible way.
Author Contributions
Y.-J.J. conceived the design method and supervised the data analysis. Y.-J.J. wrote the manuscript. W.-C.L. performed the calculations. W.-C.L. analyzed and checked all computational data.
Funding
Ministry of Science and Technology, Taiwan No. MOST 108-2221-E-027-100-MY3.
Acknowledgments
This work was supported by grants from the National Taipei University of Technology and the Ministry of Science and Technology, Taiwan.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Pendry, J.B. Negative Refraction Makes a Perfect Lens. Phys. Rev. Lett. 2000, 85, 3966–3969. [Google Scholar] [CrossRef] [PubMed]
- Shelby, R.A.; Smith, D.R.; Schultz, S. Experimental Verification of a Negative Index of Refraction. Science 2001, 292, 77–79. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhang, X. Metamaterials: A new frontier of science and technology. Chem. Soc. Rev. 2011, 40, 2494–2507. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Litchinitser, N.M.; Zhou, J. Indefinite by Nature: From Ultraviolet to Terahertz. ACS Photonics 2014, 1, 293–303. [Google Scholar] [CrossRef]
- Lu, L.; Simpson, R.E.; Valiyaveedu, S.K. Active hyperbolic metamaterials: Progress materials and design. J. Opt. 2018, 20, 103001. [Google Scholar] [CrossRef]
- Verhagen, E.; de Waele, R.; Kuipers, L.; Polman, A. Three-dimensional negative index of refraction at optical frequencies by coupling plasmonic waveguides. Phys. Rev. Lett. 2010, 105, 223901. [Google Scholar] [CrossRef]
- Xu, T.; Agrawal, A.; Abashin, M.; Chau, K.J.; Lezec, H.J. All-angle negative refraction and active flat lensing of ultraviolet light. Nature 2013, 497, 470–474. [Google Scholar] [CrossRef]
- Yin, X.; Zhu, H.; Guo, H.; Deng, M.; Xu, T.; Gong, Z.; Li, X.; Hang, Z.H.; Wu, C.; Li, H.; et al. Hyperbolic Metamaterial Devices for Wavefront Manipulation. Laser Photonics Rev. 2019, 13, 1800081. [Google Scholar] [CrossRef]
- Agranovich, V.M.; Kravtsov, V.E. Notes on crystal optics of superlattices. Solid State Commun. 1985, 55, 85–90. [Google Scholar] [CrossRef]
- Hoffman, A.J.; Alekseyev, L.; Howard, S.S.; Franz, K.J.; Wasserman, D.; Podolskiy, V.A.; Narimanov, E.E.; Sivco, D.L.; Gmachl, C. Negative refraction in semiconductor metamaterials. Nat. Mater. 2007, 6, 946–950. [Google Scholar] [CrossRef]
- Poddubny, A.; Iorsh, I.; Belov, P.; Kivshar, Y. Hyperbolic metamaterials. Nat. Photonics 2013, 7, 948–957. [Google Scholar] [CrossRef]
- Maas, R.; Verhagen, E.; Parsons, J.; Polman, A. Negative refractive index and higher-order harmonics in layered metallodielectric optical metamaterials. ACS Photonics 2014, 1, 670–676. [Google Scholar] [CrossRef]
- Macleod, H.A. Thin-Film Optical Filters, 4th ed.; CRC Press: Boca Raton, FL, USA, 2010; pp. 177–187. [Google Scholar]
- Smith, D.R.; Vier, D.C.; Koschny, T.; Soukoulis, C.M. Electromagnetic parameter retrieval from inhomogeneous metamaterials. Phys. Rev. E 2005, 71, 036617. [Google Scholar] [CrossRef] [PubMed]
- Kildishev, A.V.; Cai, W.; Chettiar, U.K.; Yuan, H.-K.; Sarychev, A.K.; Drachev, V.P.; Shalaev, V.M. Negative refractive index in optics of metal–dielectric composites. J. Opt. Soc. Am. B 2006, 23, 423–433. [Google Scholar] [CrossRef]
- Jen, Y.-J.; Lin, M.-J.; Wu, H.-M.; Liao, H.-S.; Dai, J.-W. An interference coating of metamaterial as an ultrathin light absorber in the violet-to-infrared regime. Opt. Express 2013, 21, 10259–10268. [Google Scholar] [CrossRef] [PubMed]
- Epstein, L.I. The design of optical filter. J. Opt. Soc. Am. 1952, 42, 806–810. [Google Scholar] [CrossRef]
- Jen, Y.J.; Liu, W.C.; Chen, T.K.; Lin, S.W.; Jhang, Y.C. Design and deposition of a metal-like and admittance-matching metamaterial as an ultra-thin perfect absorber. Sci. Rep. 2017, 7, 3076. [Google Scholar] [CrossRef]
- Jen, Y.J.; Lakhtakia, A.; Yu, C.W.; Jhou, J.J.; Wang, W.H.; Lin, M.J.; Wu, H.M.; Liao, H.S. Silver/silicon dioxide/silver sandwich films in the blue-to-red spectral regime with negative-real refractive index. Appl. Phys. Lett. 2011, 99, 181117. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, C.; Yang, F.; Liang, G.; Li, Q.; Guo, L.J. Plasmonic Lithography Utilizing Epsilon Near Zero Hyperbolic Metamaterial. ACS Nano 2017, 11, 9863–9868. [Google Scholar] [CrossRef]
- Jen, Y.J.; Lee, C.C.; Lu, K.H.; Jheng, C.Y.; Chen, Y.J. Fabry-Perot based metal-dielectric multilayered filters and metamaterials. Opt. Express 2015, 23, 33008–33017. [Google Scholar] [CrossRef]
- Zhu, P.; Shi, H.; Guo, L.J. SPPs Coupling Induced Interference in Metal/dielectric Multilayer Waveguides and Its Application for Plasmonic Lithography. Opt. Express 2012, 20, 12521–12529. [Google Scholar] [CrossRef] [PubMed]
- Essential Macleod by Thin Film Center Inc. Available online: http://www.thinfilmcenter.com (accessed on 25 March 2013).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).