Investigation of High-Efficiency Iterative ILU Preconditioner Algorithm for Partial-Differential Equation Systems
Abstract
1. Introduction
2. Decomposition Strategy
- and is a unit matrix, .
3. Analysis of Convergence
3.1. Preliminary
3.2. Proposition and Theorem
- .
4. Parallel Implementations
4.1. Storage Method
4.2. Circulating
5. Results Analysis of Numerical Examples
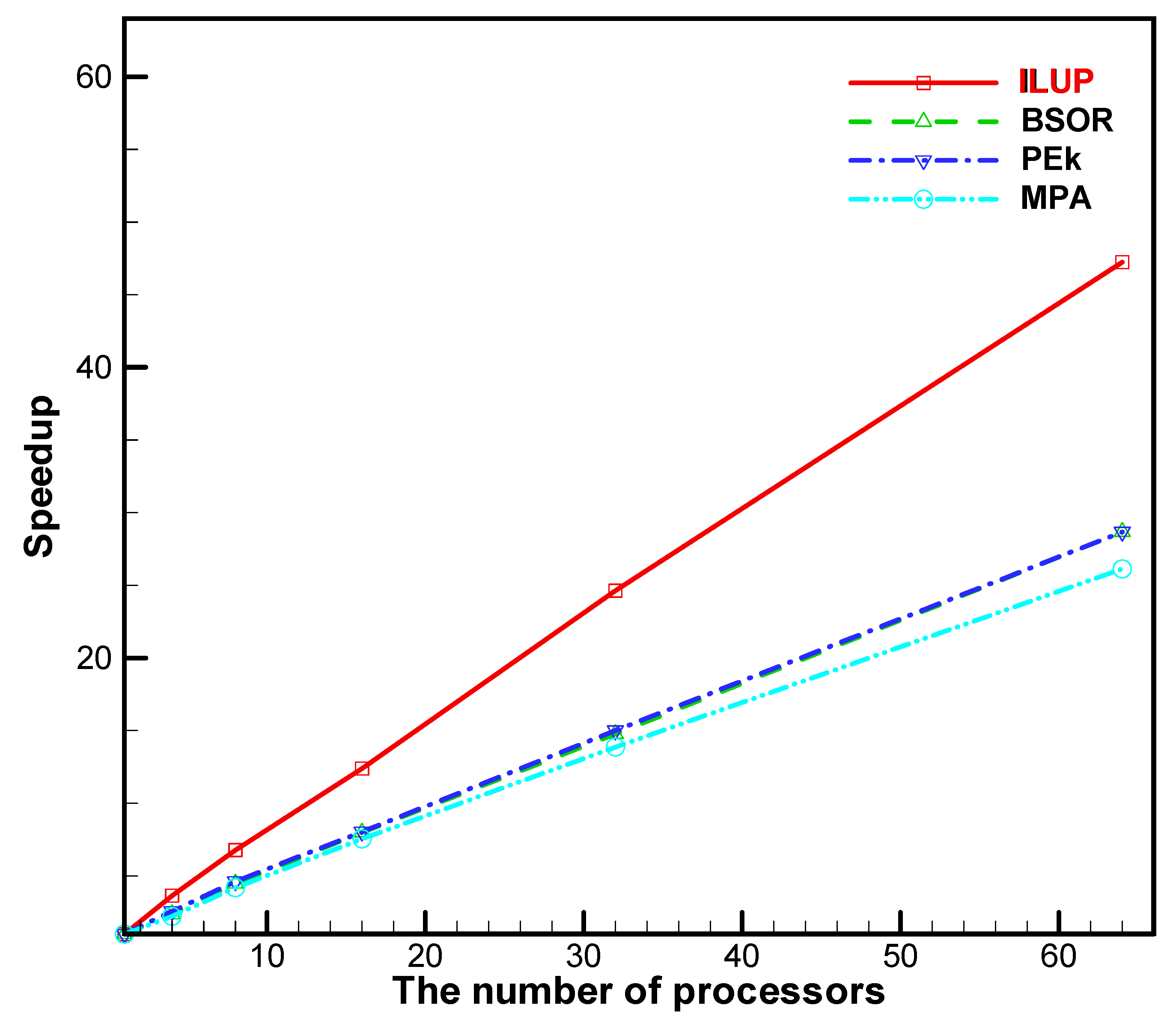
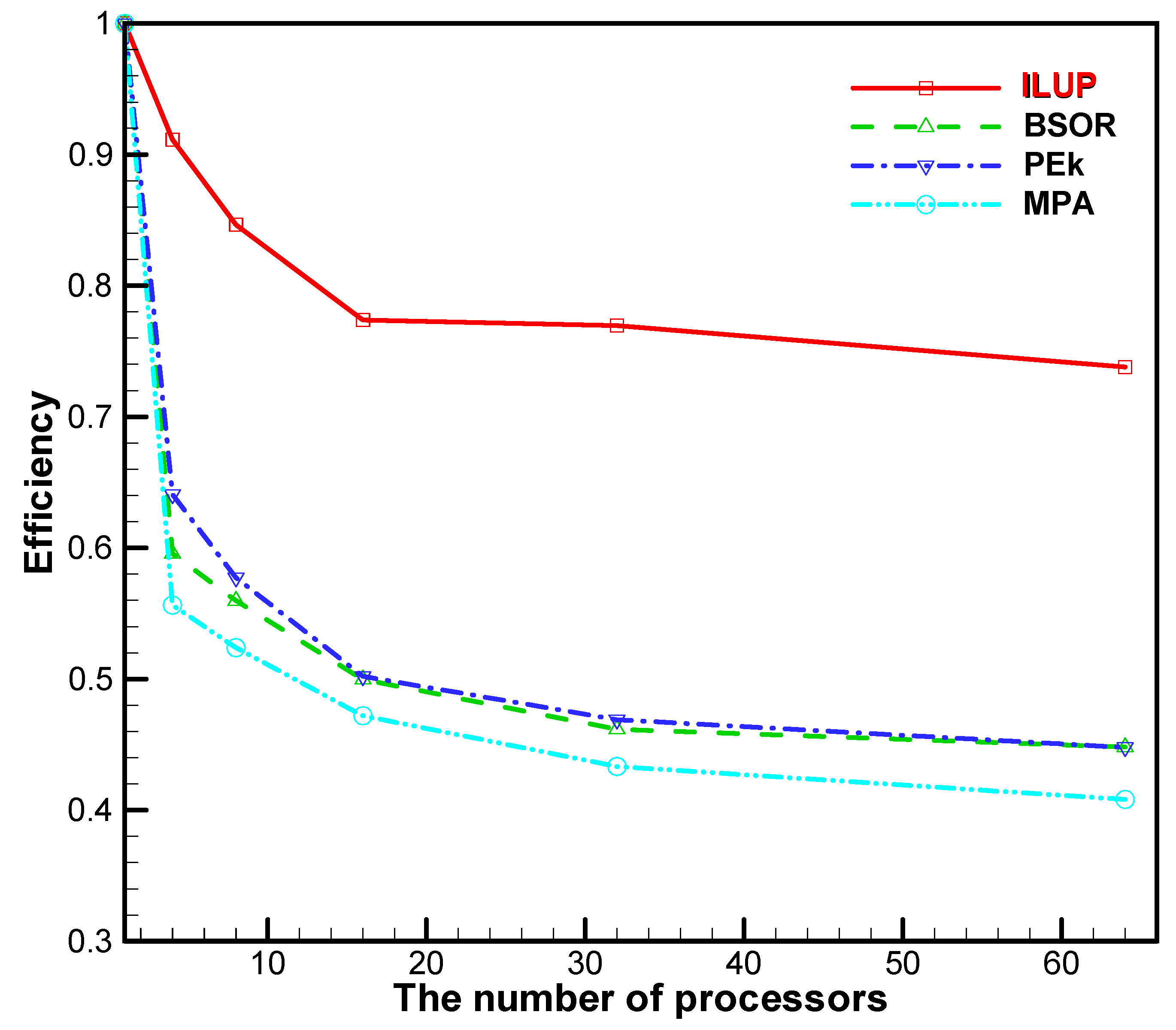
5.1. Results Analysis of the Large-Scale System of Equations
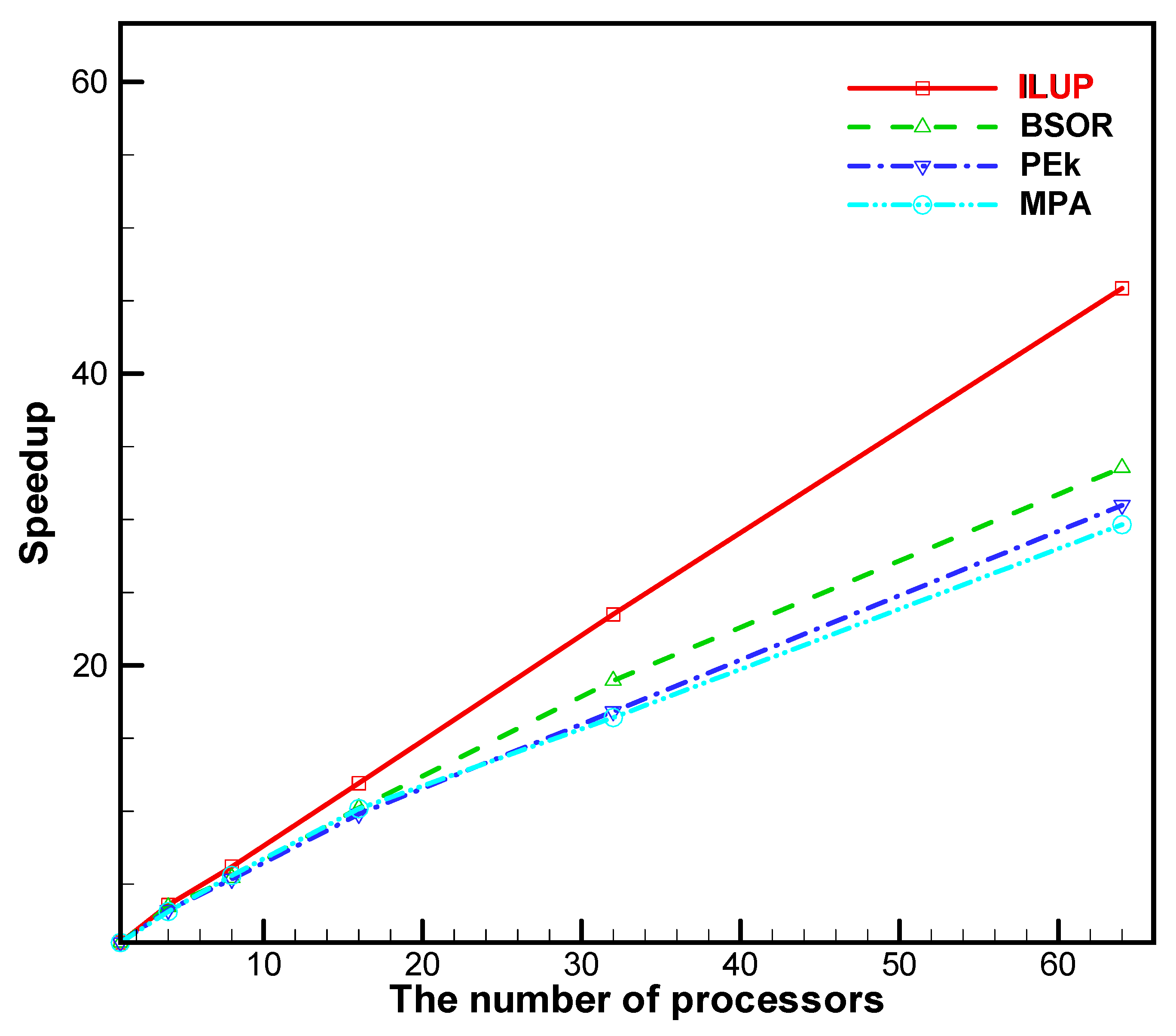
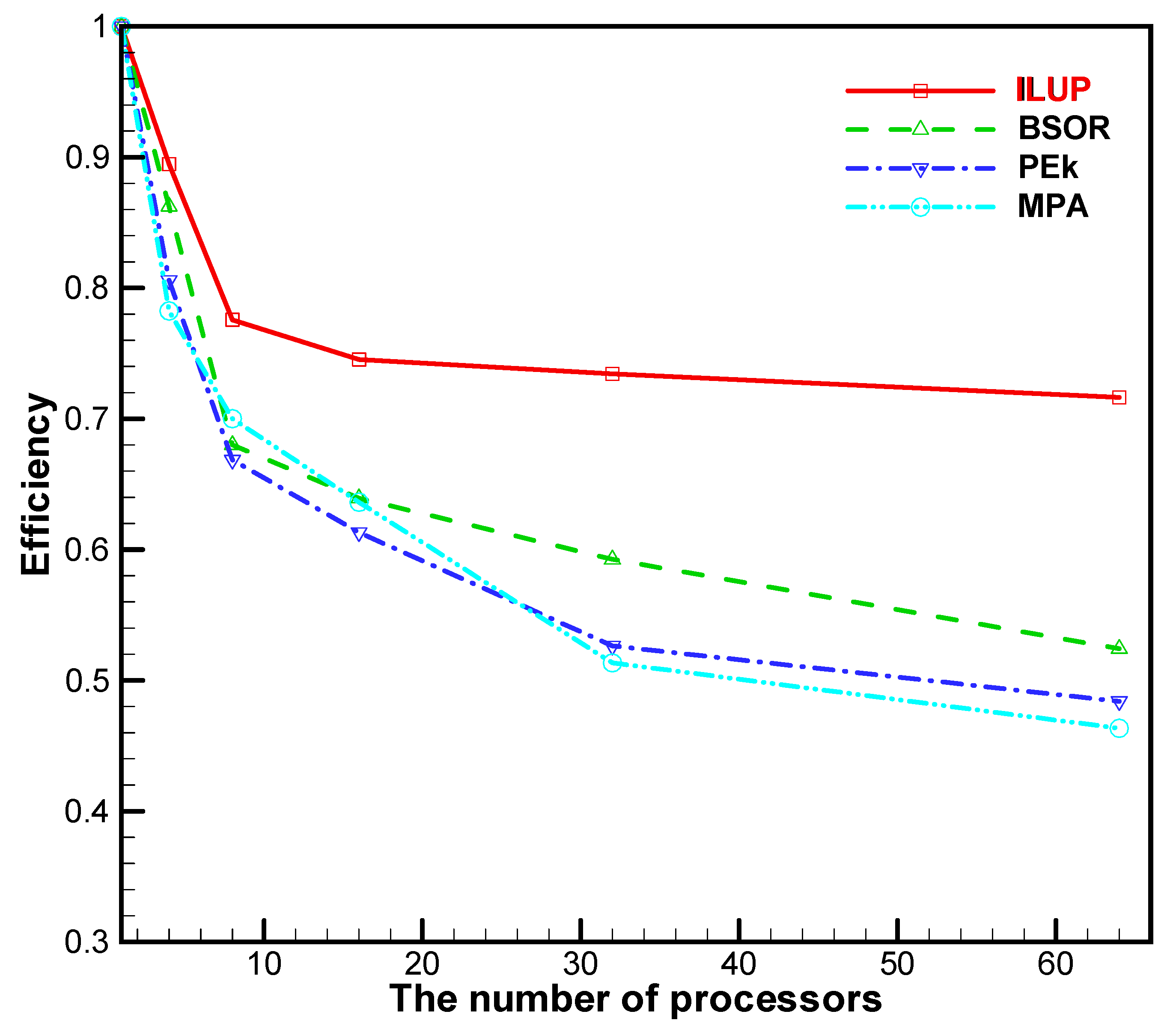
5.2. Results Analysis of the Partial-Differential Equations
- and
- ,
6. Conclusions
- The ILUP algorithm for the large-scale system of equations and partial-differential equation systems was performed on different multi-CPU cores. The numerical results show that the solutions are consistent with the theory.
- From Example 1, when is neither positive nor an M-matrix, the ILUP algorithm still converges.
- No matter the number of processors, the parallel efficiency of the ILUP algorithm is preferable. The parallel efficiency of the ILUP algorithm is higher than that of the other three algorithms. For example, the parallel efficiency of the ILUP algorithm achieves a value of above 73.8% (as seen in Table 5), which is higher than that for any other algorithm, including the BSOR method [10], the PEk method [40], and the MPA algorithm [2]. Obviously, the ILUP algorithm has the superiority of producing exceedingly high parallel efficiency values.
Author Contributions
Funding
Conflicts of Interest
References
- Polizzi, E.; Sameh, A.H. A parallel hybrid banded system solver: The spike algorithm. Parallel Comput. 2006, 32, 177–194. [Google Scholar] [CrossRef]
- Yun, J.H. Convergence of nonstationary multi-splitting methods using ILU factorizations. J. Comput. Appl. Math. 2005, 180, 245–263. [Google Scholar] [CrossRef][Green Version]
- Zhang, B.L.; Gu, T.X. Numerical Parallel Computational Theory and Method; Defense Industry Press: Beijing, China, 1999; pp. 161–168. [Google Scholar]
- Wu, J.; Song, J.; Zhang, W.; Li, X. Parallel incomplete factorization pre-conditioning of block-tridiagonal linear systems with 2-D domain decomposition. Chin. J. Comput. Phys. 2009, 26, 191–199. [Google Scholar]
- Duan, Z.; Yang, Y.; Lv, Q.; Ma, X. Parallel strategy for solving block-tridiagonal linear systems. Comput. Eng. Appl. 2011, 47, 46–49. [Google Scholar]
- Fan, Y.; Lv, Q. The parallel iterative algorithms for solving the block-tridiagonal linear systems. J. Basic Sci. Text. Coll. 2010, 23, 174–179. [Google Scholar]
- El-Sayed, S.M. A direct method for solving circulant tridiagonal block systems of linear equations. Appl. Math. Comput. 2005, 165, 23–30. [Google Scholar] [CrossRef]
- Bai, Z. A class of parallel decomposition-type relaxation methods for sparse systems of linear equations. Linear Algebra Appl. 1998, 282, 1–24. [Google Scholar]
- Cui, X.; Lv, Q. A parallel algorithm for block-tridiagonal linear systems. Appl. Math. Comput. 2006, 173, 1107–1114. [Google Scholar] [CrossRef]
- Cui, X.; Lv, Q. A parallel algorithm for band linear systems. Appl. Math. Comput. 2006, 181, 40–47. [Google Scholar]
- Akimova, E.; Belousov, D. Parallel algorithms for solving linear systems with block-tridiagonal matrices on multi-core CPU with GPU. J. Comput. Sci. 2012, 3, 445–449. [Google Scholar] [CrossRef]
- Terekhov, A.V. A fast parallel algorithm for solving block-tridiagonal systems of linear equations including the domain decomposition method. Parallel Comput. 2013, 39, 245–258. [Google Scholar] [CrossRef]
- Ma, X.; Liu, S.; Xiao, M.; Xie, G. Parallel algorithm with parameters based on alternating direction for solving banded linear systems. Math. Probl. Eng. 2014, 2014, 752651. [Google Scholar] [CrossRef]
- Terekhov, A. A highly scalable parallel algorithm for solving Toeplitz tridiagonal systems of linear equations. J. Parallel Distrib. Comput. 2016, 87, 102–108. [Google Scholar] [CrossRef]
- Gu, B.; Sun, X.; Sheng, V.S. Structural minimax probability machine. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 1646–1656. [Google Scholar] [CrossRef]
- Zhou, Z.; Yang, C.N.; Chen, B.; Sun, X.; Liu, Q.; Wu, Q.M.J. Effective and efficient image copy detection with resistance to arbitrary rotation. IEICE Trans. Inf. Syst. 2016, E99, 1531–1540. [Google Scholar] [CrossRef]
- Deng, W.; Zhao, H.; Liu, J.; Yan, X.; Li, Y.; Yin, L.; Ding, C. An improved CACO algorithm based on adaptive method and multi-variant strategies. Soft Comput. 2015, 19, 701–713. [Google Scholar] [CrossRef]
- Deng, W.; Zhao, H.; Zou, L.; Li, G.; Yang, X.; Wu, D. A novel collaborative optimization algorithm in solving complex optimization problems. Soft Comput. 2016, 21, 4387–4398. [Google Scholar] [CrossRef]
- Tian, Q.; Chen, S. Cross-heterogeneous-database age estimation through correlation representation learning. Neurocomputing 2017, 238, 286–295. [Google Scholar] [CrossRef]
- Xue, Y.; Jiang, J.; Zhao, B.; Ma, T. A self-adaptive artificial bee colony algorithm based on global best for global optimization. Soft Comput. 2018, 22, 2935–2952. [Google Scholar] [CrossRef]
- Yuan, C.; Xia, Z.; Sun, X. Coverless image steganography based on SIFT and BOF. J. Internet Technol. 2017, 18, 435–442. [Google Scholar]
- Qu, Z.; Keeney, J.; Robitzsch, S.; Zaman, F.; Wang, X. Multilevel pattern mining architecture for automatic network monitoring in heterogeneous wireless communication networks. China Commun. 2016, 13, 108–116. [Google Scholar]
- Chen, Z.; Ewing, R.E.; Lazarov, R.D.; Maliassov, S.; Kuznetsov, Y.A. Multilevel preconditioners for mixed methods for second order elliptic problems. Numer. Linear Algebra Appl. 1996, 3, 427–453. [Google Scholar] [CrossRef]
- Liu, H.; Yu, S.; Chen, Z.; Hsieh, B.; Shao, L. Sparse matrix-vector multiplication on NVIDIA GPU. Int. J. Numer. Anal. Model. Ser. B 2012, 2, 185–191. [Google Scholar]
- Liu, H.; Chen, Z.; Yu, S.; Hsieh, B.; Shao, L. Development of a restricted additive Schwarz preconditioner for sparse linear systems on NVIDIA GPU. Int. J. Numer. Anal. Model. Ser. B 2014, 5, 13–20. [Google Scholar]
- Chen, Z.; Liu, H.; Yang, B. Parallel triangular solvers on GPU. In Proceedings of the International Workshop on Data-Intensive Scientific Discovery (DISD), Shanghai, China, 2–4 June 2013. [Google Scholar]
- Yang, B.; Liu, H.; Chen, Z. GPU-accelerated preconditioned GMRES solver. In Proceedings of the 2nd IEEE International Conference on High Performance and Smart Computing (IEEE HPSC), Columbia University, New York, NY, USA, 8–10 April 2016. [Google Scholar]
- Liu, H.; Yang, B.; Chen, Z. Accelerating the GMRES solver with block ILU (K) preconditioner on GPUs in reservoir simulation. J. Geol. Geosci. 2015, 4, 1–7. [Google Scholar]
- Barrett, R.; Berry, M.; Chan, T.F.; Demmel, J.; Donato, J.; Dongarra, J.; Eijkhout, V.; Pozo, R.; Romine, C.; Vander, V.H. Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods, 2nd ed.; SIAM: Philadelphia, PA, USA, 1994. [Google Scholar]
- Saad, Y. Iterative Methods for Sparse Linear Systems, 2nd ed.; SIAM: Philadelphia, PA, USA, 2003. [Google Scholar]
- Cai, X.C.; Sarkis, M.A. restricted additive Schwarz preconditioner for general sparse linear systems. Math. Sci. Fac. Publ. 1999, 21, 792–797. [Google Scholar] [CrossRef]
- Ascher, U.M.; Greif, C. Computational methods for multiphase flows in porous media. Math. Comput. 2006, 76, 2253–2255. [Google Scholar]
- Hu, X.; Liu, W.; Qin, G.; Xu, J.; Yan, Y.; Zhang, C. Development of a fast auxiliary subspace pre-conditioner for numerical reservoir simulators. In Proceedings of the Society of Petroleum Engineers SPE Reservoir Characterisation and Simulation Conference and Exhibition, Abu Dhabi, UAE, 9–11 October 2011. [Google Scholar]
- Cao, H.; Tchelepi, H.A.; Wallis, J.R.; Yardumian, H.E. Parallel scalable unstructured CPR-type linear solver for reservoir simulation. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 9–12 October 2005. [Google Scholar]
- NVIDIA Corporation. CUSP: Generic Parallel Algorithms for Sparse Matrix and Graph. Available online: http://code.google.com/p/cusp-library (accessed on 25 December 2008).
- Chen, Z.; Zhang, Y. Development, analysis and numerical tests of a compositional reservoir simulator. Int. J. Numer. Anal. Mode. 2009, 5, 86–100. [Google Scholar]
- Klie, H.; Sudan, H.; Li, R.; Saad, Y. Exploiting capabilities of many core platforms in reservoir simulation. In Proceedings of the SPE RSS Reservoir Simulation Symposium, Bali, Indonesia, 21–23 February 2011. [Google Scholar]
- Chen, Y.; Tian, X.; Liu, H.; Chen, Z.; Yang, B.; Liao, W.; Zhang, P.; He, R.; Yang, M. Parallel ILU preconditioners in GPU computation. Soft Comput. 2018, 22, 8187–8205. [Google Scholar] [CrossRef]
- Varga, R.S. Matrix Iterative Analysis; Science Press: Beijing, China, 2006; pp. 91–96. [Google Scholar]
- Zhang, K.; Zhong, X. Numerical Algebra; Science Press: Beijing, China, 2006; pp. 70–77. [Google Scholar]
| P | 1 | 4 | 8 | 16 | 32 | 64 |
| T | 119.1036 | 32.6697 | 17.5870 | 9.6202 | 4.8371 | 2.5217 |
| I | 233 | 237 | 238 | 238 | 238 | 238 |
| S | 3.6457 | 6.7723 | 12.3806 | 24.6231 | 47.2324 | |
| E | 0.9114 | 0.8465 | 0.7738 | 0.7695 | 0.7380 | |
| P | 1 | 4 | 8 | 16 | 32 | 64 |
| T | 112.0383 | 47.0284 | 25.0183 | 14.0130 | 7.5833 | 3.9065 |
| I | 211 | 216 | 216 | 216 | 216 | 216 |
| S | 2.3824 | 4.4783 | 7.9953 | 14.7743 | 28.6800 | |
| E | 0.5956 | 0.5598 | 0.4997 | 0.4617 | 0.4481 |
| P | 1 | 4 | 8 | 16 | 32 | 64 |
| T | 114.3098 | 44.5992 | 24.7489 | 14.2286 | 7.6159 | 3.9878 |
| I | 224 | 227 | 227 | 227 | 227 | 227 |
| S | 2.5630 | 4.6188 | 8.0338 | 15.0094 | 28.6649 | |
| E | 0.6408 | 0.5773 | 0.5021 | 0.4690 | 0.4479 |
| P | 1 | 4 | 8 | 16 | 32 | 64 |
| T | 103.597 | 46.547 | 24.716 | 13.717 | 7.472 | 3.9564 |
| I | 172 | 174 | 174 | 174 | 174 | 174 |
| S | 2.2256 | 4.1915 | 7.5525 | 13.8647 | 26.1254 | |
| E | 0.5564 | 0.5239 | 0.4720 | 0.4333 | 0.4082 |
| Compared List | ILUP Algorithm | Block Successive over Relaxation Method [10] | Pseudo-Elimination Method with Parameter k [40] | Multi-Splitting Algorithm [2] |
|---|---|---|---|---|
| Speedup | 47.2324 | 28.6800 | 28.6649 | 26.1254 |
| Parallel Efficiency | 0.7380 | 0.4481 | 0.4479 | 0.4082 |
| P | 1 | 4 | 8 | 16 | 32 | 64 |
| T | 121.7960 | 34.0280 | 19.6270 | 10.2140 | 5.1830 | 2.6565 |
| I | 578 | 560 | 560 | 560 | 560 | 560 |
| S | 3.5793 | 6.2055 | 11.9244 | 23.4991 | 45.8483 | |
| E | 0.8948 | 0.7757 | 0.7453 | 0.7343 | 0.7164 | |
| P | 1 | 4 | 8 | 16 | 32 | 64 |
| T | 144.8230 | 41.9830 | 26.6220 | 14.1590 | 7.6370 | 4.3165 |
| I | 779 | 793 | 793 | 793 | 793 | 793 |
| S | 3.4496 | 5.4400 | 10.2283 | 18.9633 | 33.5510 | |
| E | 0.8624 | 0.6800 | 0.6393 | 0.5926 | 0.5242 |
| P | 1 | 4 | 8 | 16 | 32 | 64 |
| T | 157.7210 | 48.9280 | 29.4860 | 16.0790 | 9.3640 | 5.0917 |
| I | 786 | 798 | 798 | 798 | 798 | 798 |
| S | 3.2235 | 5.3490 | 9.8091 | 16.8433 | 30.9764 | |
| E | 0.8059 | 0.6686 | 0.6131 | 0.5264 | 0.4840 |
| P | 1 | 4 | 8 | 16 | 32 | 64 |
| T | 180.6459 | 57.7139 | 32.2524 | 17.7462 | 10.9967 | 6.0917 |
| I | 824 | 838 | 838 | 838 | 838 | 838 |
| S | 3.1300 | 5.6010 | 10.1794 | 16.4273 | 29.6547 | |
| E | 0.7825 | 0.7001 | 0.6362 | 0.5134 | 0.4634 |
| Compared List | ILUP Algorithm | Block Successive over Relaxation Method [10] | Pseudo-Elimination Method with Parameter k [40] | Multi-Splitting Algorithm [2] |
|---|---|---|---|---|
| Speedup | 45.8483 | 33.5510 | 30.9764 | 29.6547 |
| Parallel Efficiency | 0.7164 | 0.5242 | 0.4840 | 0.4634 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Y.-H.; Wang, L.-H.; Jia, Y.; Li, X.-G.; Yang, X.-X.; Chen, C.-C. Investigation of High-Efficiency Iterative ILU Preconditioner Algorithm for Partial-Differential Equation Systems. Symmetry 2019, 11, 1461. https://doi.org/10.3390/sym11121461
Fan Y-H, Wang L-H, Jia Y, Li X-G, Yang X-X, Chen C-C. Investigation of High-Efficiency Iterative ILU Preconditioner Algorithm for Partial-Differential Equation Systems. Symmetry. 2019; 11(12):1461. https://doi.org/10.3390/sym11121461
Chicago/Turabian StyleFan, Yan-Hong, Ling-Hui Wang, You Jia, Xing-Guo Li, Xue-Xia Yang, and Chih-Cheng Chen. 2019. "Investigation of High-Efficiency Iterative ILU Preconditioner Algorithm for Partial-Differential Equation Systems" Symmetry 11, no. 12: 1461. https://doi.org/10.3390/sym11121461
APA StyleFan, Y.-H., Wang, L.-H., Jia, Y., Li, X.-G., Yang, X.-X., & Chen, C.-C. (2019). Investigation of High-Efficiency Iterative ILU Preconditioner Algorithm for Partial-Differential Equation Systems. Symmetry, 11(12), 1461. https://doi.org/10.3390/sym11121461






