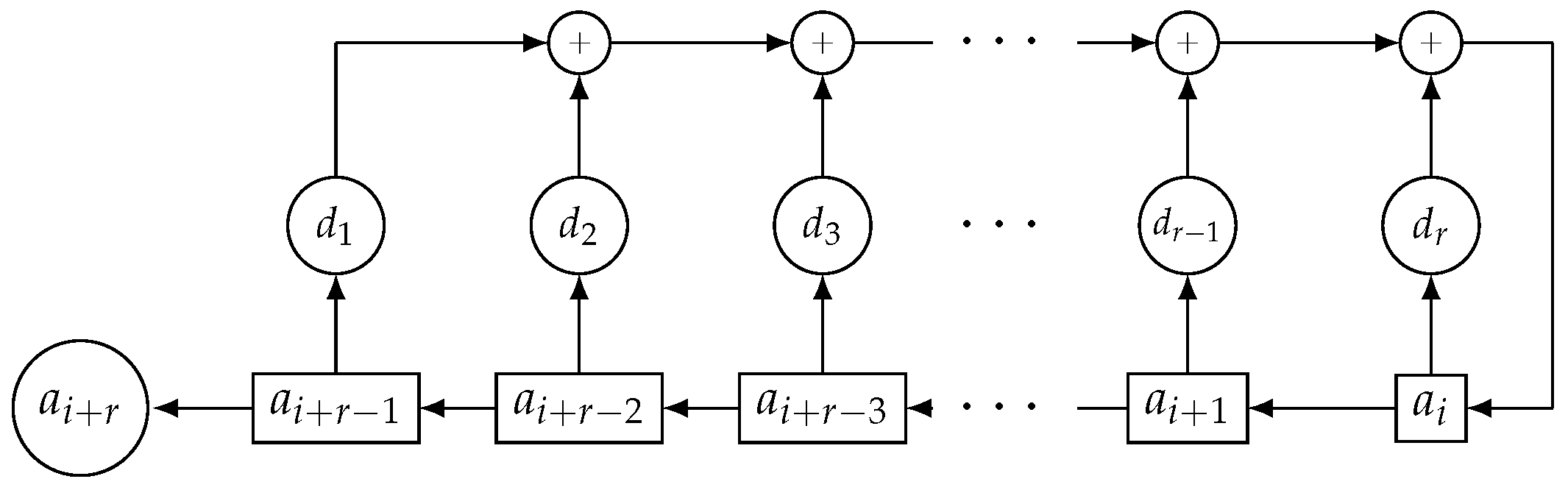
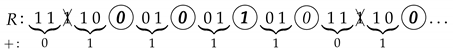Furthermore, the family of GSS-sequences is analysed with the family of statistical tests FIPS 140-2, provided by the National Institute of Standards and Technology (NIST), as well as with the Lempel-Ziv Compression Test. In both cases the sequences have passed the tests.
5.1. Graphical Testing
In this section, the main graphical tests used in Reference [
9], are applied to the GSS-sequences, from which their cryptographic properties can be analyzed.
The results obtained for GSS-sequences of length bits, is presented. These sequences are generated by the GSSG from a maximal-length LFSR with the 24-degree characteristic polynomial and whose initial state is the identically 1 vector of length 24.
The tests were performed with bit sequences. Most of the tests works associating every eight bits in an octet, obtaining sequences of samples of 8 bits; with the exception of the Linear complexity test that works with just one bit and the Chaos game that works associating the bits two by two.
Next, the results of graphical tests to study the randomness of our sequences is shown.
1. Return map
Return map [
10] tries to measure visually the entropy of the sequence, that is, allows to detect the existence of some useful information about the parameters used in the design of pseudo-random generators [
36]. This test, that customarily is used in theory of dynamic systems, is also a powerful tool in cryptanalysis.
Basically, it consists of a graph of the points of the sequence as a function of and, under certain conditions, allows us to obtain the value of the parameters of a pseudo-random sequence, defeating the security of the cryptosystem under analysis. The result should be a distribution of points where you cannot guess neither trends, nor figures, nor lines, nor symmetry, nor patterns.
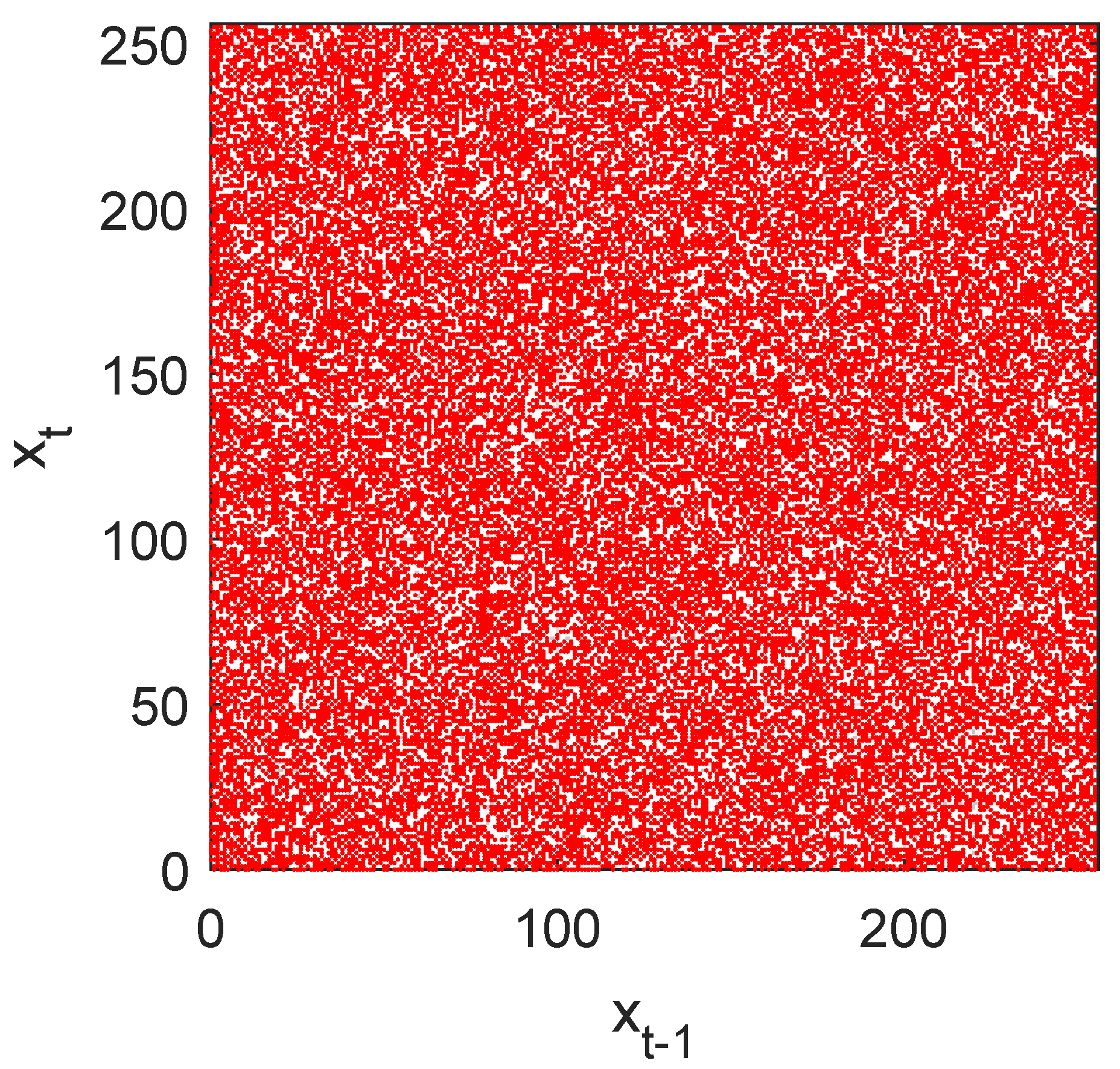
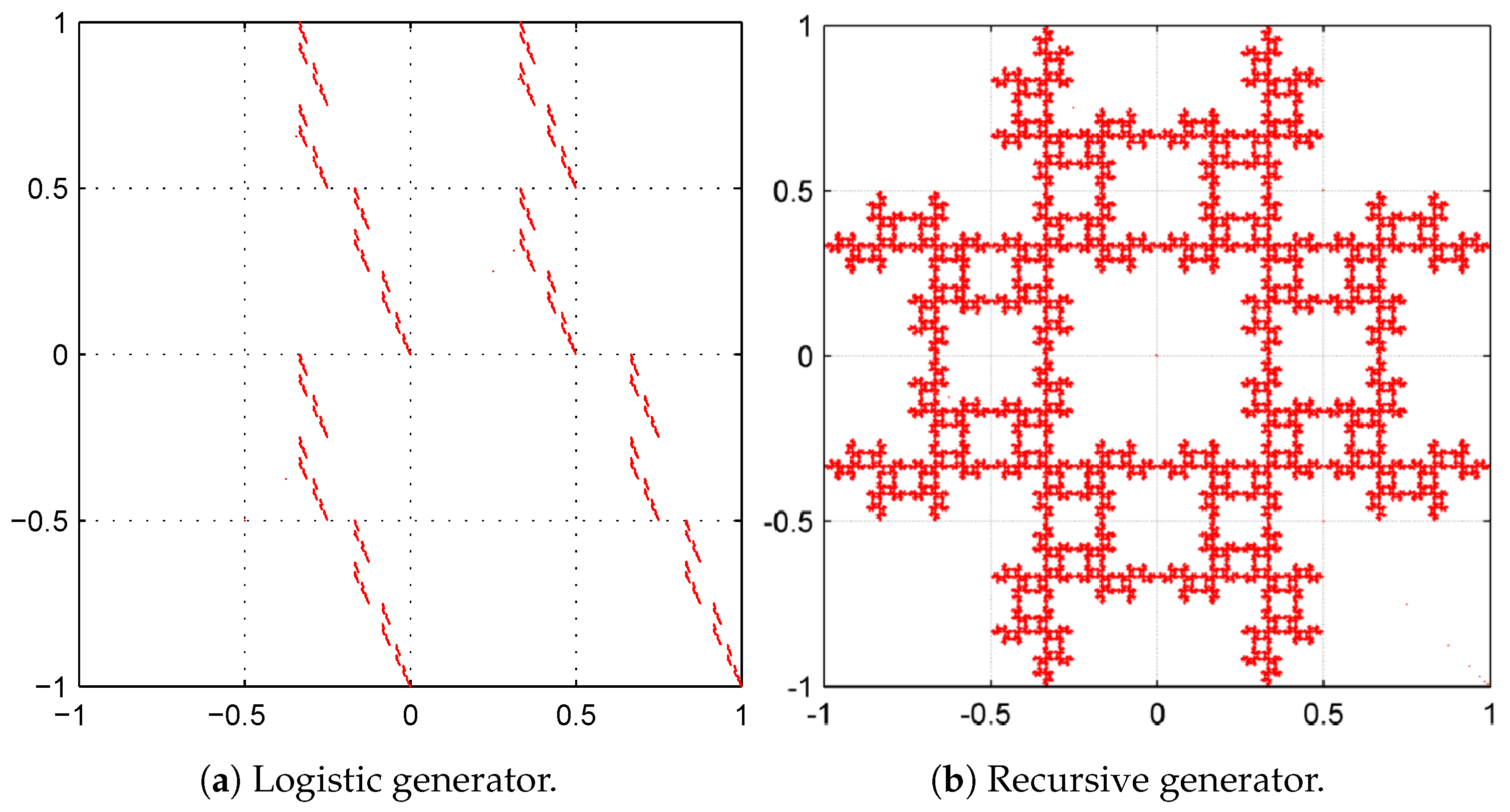
Figure 2 shows the return map of our GSS-sequence as a disordered cloud, which does not provide any useful information for its cryptanalysis.
Figure 3a,b are the return applications of two imperfect generators where the lack of randomness can be neatly observed. Indeed, these maps present clear patterns that permit to determine the generator function and the parameter values.
2. Linear Complexity
The linear complexity (
) is considered as a measure of the unpredictability of a pseudo-random sequence and is a widely used metric of the security of a keystream sequence [
37]. We have used the Berlekamp-Massey algorithm [
38] to compute this parameter. If the characteristic polynomial of the LFSR is primitive [
32], then it is known as maximal-length LFSR; moreover, its output sequence has period
, where
L is the degree of the characteristic polynomial.
must be as large as possible, that is, its value has to be very close to half the period [
39],
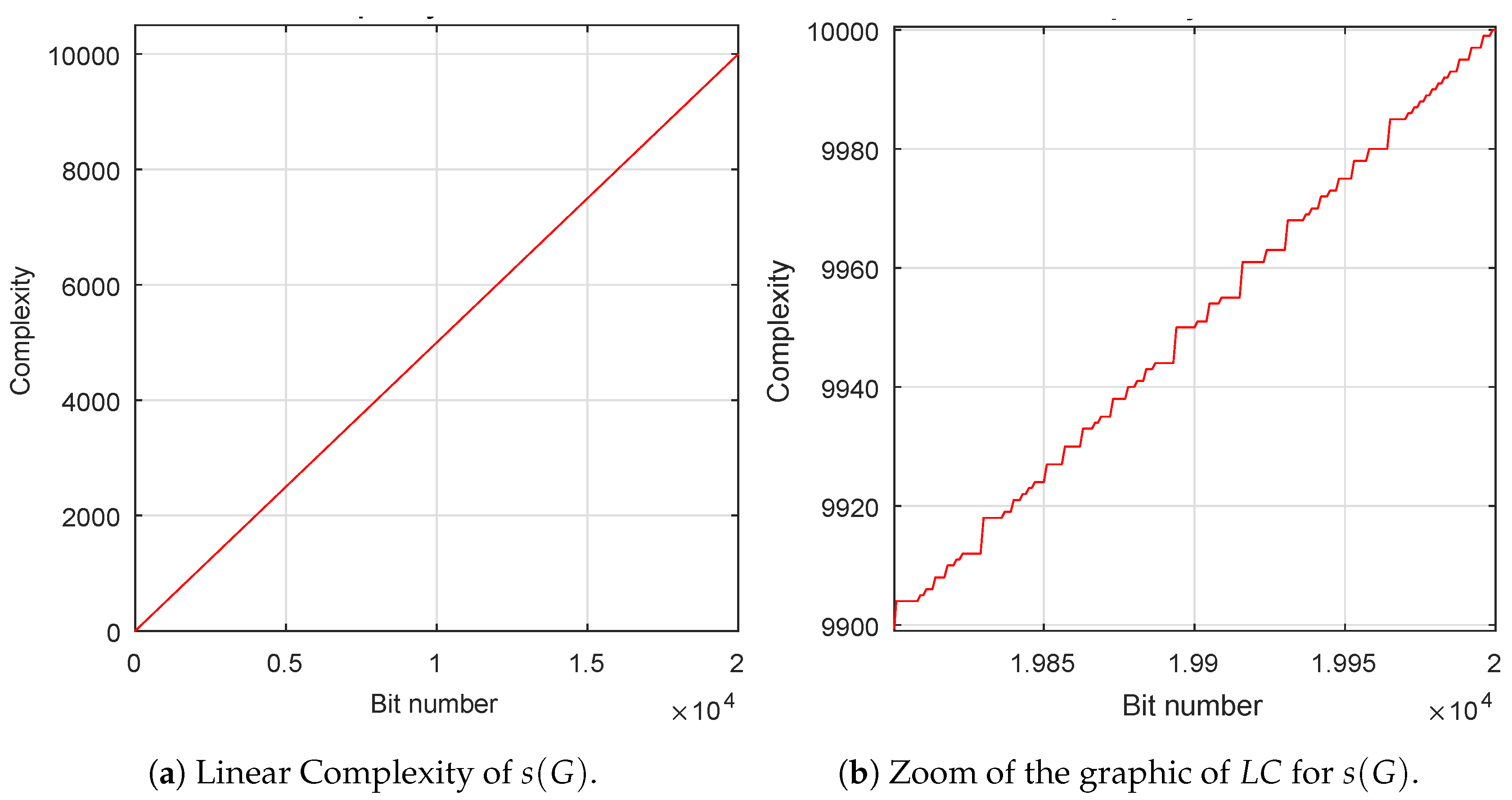
. From
Figure 4a, it can be deduced that the value of the linear complexity of the first 20,000 bits of the sequence is just half its length, 10,000 and, from
Figure 4b is observed that
is
irregularly close to the
-line, being
l the length of the sequence.
3. Shannon Entropy and Min-Entropy
The entropy of a sequence is defined as a measure of the amount of information of a process measured in bits or as a measure of the uncertainty of a random variable. From these two possible interpretation, the quality of the output sequence or the input of a random number generator can be described, respectively.
Shannon’s entropy is measured based on the average probability of all the values that the variable can take. A formal definition can be presented as follows,
Definition 2. Let X be a random variable that takes on the values . Then the Shannon’s entropy is defined aswhere Pr(·) represents probability. If the process is a sequence of integers modulo m perfectly random, then its entropy is equal to n. As in the case at hand , the entropy of a random sequence must be close to bit per octet.
The min-Entropy is only measured based on the probability of the more frequent occurrence value of the variable. It is recommended by the NIST SP B standard for True Random Number Generators (TRNG).
In order to determine if the proposed generator is considered perfect from these entropies values, according to Reference [
40] for a sequence of
octets, it must obtain a Shannon entropy value greater or equal than
bits per octet and a min-entropy greater or equal to
bits per octet. In this case the following values are obtained:
| Shannon entropy (measured) | = | bits per octet. |
| Min-entropy (measured) | = | bits per octet, |
then, it can be considered that this generator is correct using entropies. Note that the Shannon’s entropy value of
bits per octet fits close to the theoretical perfection of 8 bits per octet.
4. Lyapunov exponent
Lyapunov exponent measures the rate of divergence of nearby trajectories, which is a key component of chaotic dynamics. It is used as a quantitative measure for the sensitive dependence on initial conditions. It is desirable that two very close initial conditions (for instance, seeds or keys) provide very different trajectories (sequences). If Lyapunov exponent is greater than zero, the distance between two close initial conditions rapidly increases in the time, which means there exists an exponential divergence of the trajectories of a chaotic system. This value gives an idea of how different are the sequences generated by similar seeds, a very important feature to avoid attacks on the key of the generator. So, Lyapunov exponent is, in this case, a useful tool to evaluate the key space.
Next, a formal definition of Lyapunov exponent [
41] is given.
Definition 3. Consider the measure of the initial distance between two sequences and the measure of the distance between the same sequences but after t iterations. We define Lyapunov exponent as: If , the sequences decrease their distance, tend to join and confused in one. The system converges and it is not at all random. If , the distance increases, there is dependence sensitive to initial conditions, there is an exponential divergence of the orbit and randomness grows as higher is the value of .
Note that the Lyapunov exponent uses the natural logarithm of the Euclidean distance. Nevertheless, in information theory, other type of distances for measuring the distance between two sequences are used, for example Hamming distance, which indicates the number of bit positions in which both sequences differ.
If the Lyapunov exponent is modified simply by using the Hamming distance instead of the logarithm of the Euclidean distance, then it is called the Lyapunov Hamming exponent (LHE). If two numbers are identical, then its LHE value will be 0. Nevertheless, if all the bits of both numbers are different, then its LHE will be , where n is the number of bits with which the numbers are encoded.
Obtaining the Lyapunov Hamming exponent for the chosen sequence is done by calculating the average of the LHE between every two consecutive numbers of the sequence. The best value will be .
For this case, the best value is 4; we show the value obtained for our particular sequence analyzed:
| Lyapunov Hamming exponent, ideal | = | 4. |
| Lyapunov Hamming exponent, real | = | 4. |
| Absolute deviation from the ideal | = | |
hence, the proposed generator passes perfectly this test.
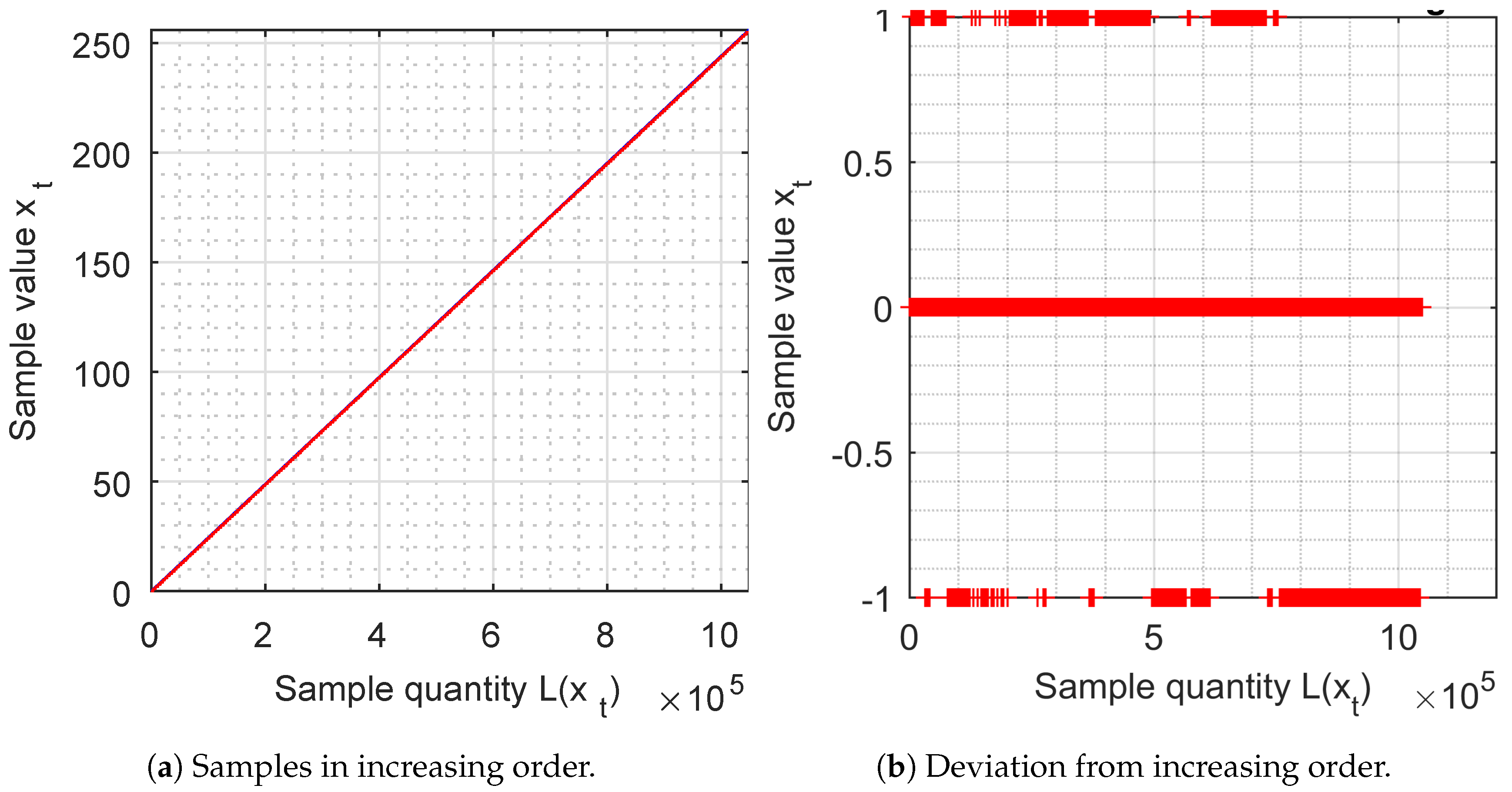
5. Samples in increasing order
The samples of 8 bits are ordered by increasing value and are represented by a graph. They should give a continuous straight line (red), with an inclination of 45 degrees, which must cover the blue reference line.
This representation means that all the numbers are generated (if it is continuous) and that the density is uniform (if its inclination is 45 degrees). In
Figure 5a, we observe that the samples are perfectly represented by a continuous straight line with the perfect inclination of 45 degrees.
From
Figure 5b, the deviation between the increasing samples is analysed and the values
or 1 are obtained.
6. Chaos game
Chaos game is a method that allows converting a one-dimensional sequence into a two dimensions sequence providing a very provocative visual representation, which reveals some of the statistical properties of the sequence under study. From this graphical technique is easy to look for, visually, patterns in the sequences generated by a random number generator. Furthermore, it allows us to find non-randomness within pseudo-random sequences.
Chaos game can be described mathematically by an Iterated Functions System (IFS) [
10,
42,
43] and through which the transition to chaos associated with fractals can be studied. The result of chaos game is called attractor and not always is a fractal, it may be any compact set. If the output is a graph with fractals or patterns, then it means that the sequence cannot be considered random.
In
Figure 6, it cannot be observe any pattern or fractal, it is a messy (or unordered) cloud of points, which does not provide any useful information for analysis, which implies good randomness.
In order to better understand this graphical test, we present in
Figure 7a,b two Chaos Game representations, which appeared in Reference [
10], which are not cryptographically secure. Their graphics are fractal which indicates that the design depends on a pattern (denoting the lack of randomness) and it is also worth mentioning that this pattern could be used to obtain important information for cryptanalysis.
7. Autocorrelation
The analysis of autocorrelation is a mathematical tool for finding repeating patterns analysing different sections of a message and compares them to find similarities. The autocorrelation function is defined as the crosscorrelation of the sequence with itself and allows measuring the linear relationship between random variables of processes separated a certain distance. It is very useful for finding periodic patterns within a signal.
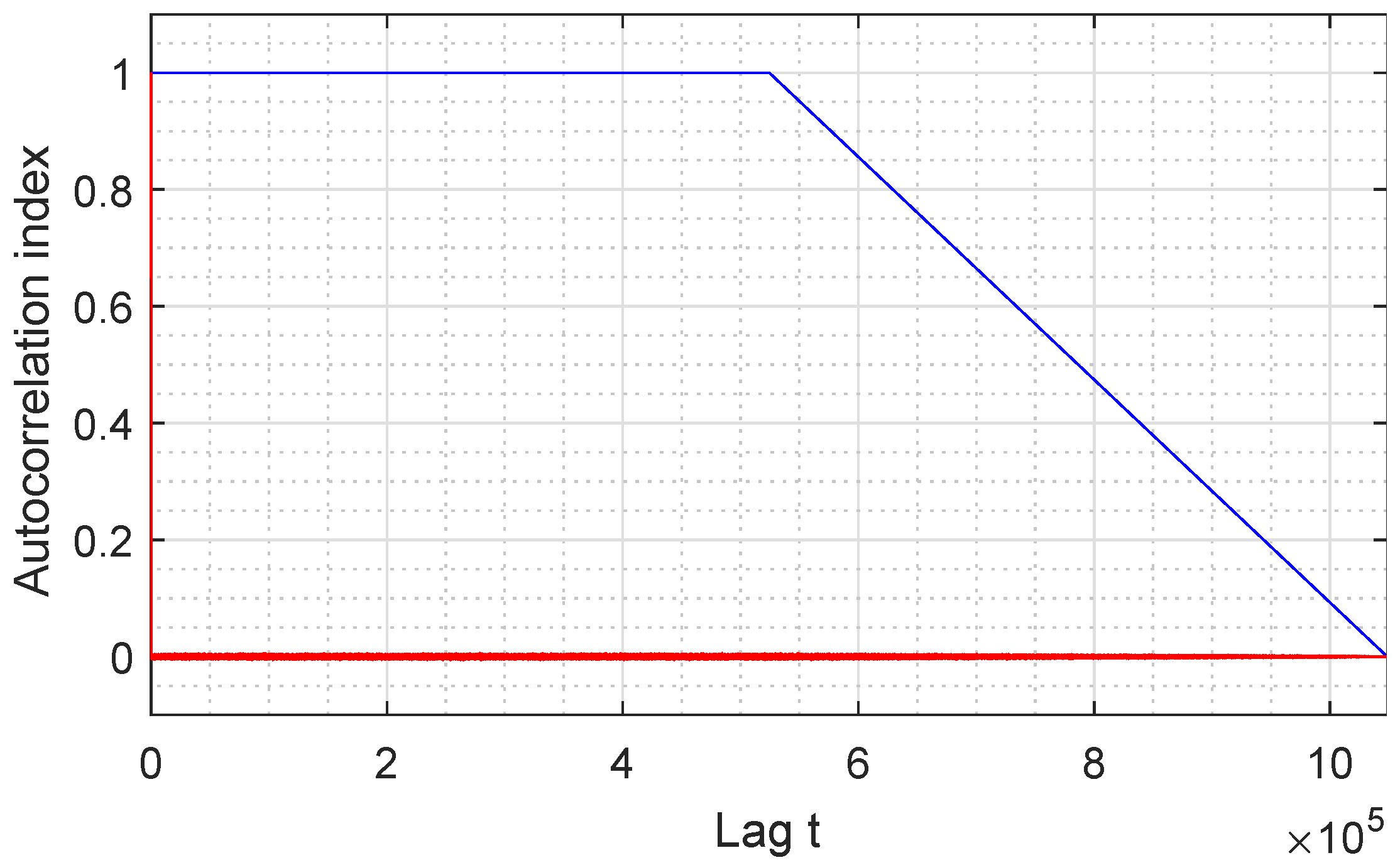
Figure 8 represents the autocorrelation index of our GSS-sequence, for all samples available. It can be seen that the sequence has a very long period, larger than the size of the sequence analyzed since the repetition frequency is not reached in the graph.
The first autocorrelation coefficient is always equal to 1, while the other coefficients must have the smallest possible amplitude so that the sequence can be considered random before finding the period in which it begins to repeat itself. In the case at hand, values close to 0 are obtained, which means that the proposed sequence can be considered random for this study.
8. Fast Fourier Transform
The goal of Fast Fourier Transform test is the peak heights in the discrete Fast Fourier Transform. It consists of detecting repetitive patterns in the sequence analysed which would indicate a deviation from the assumption of randomness [
8].
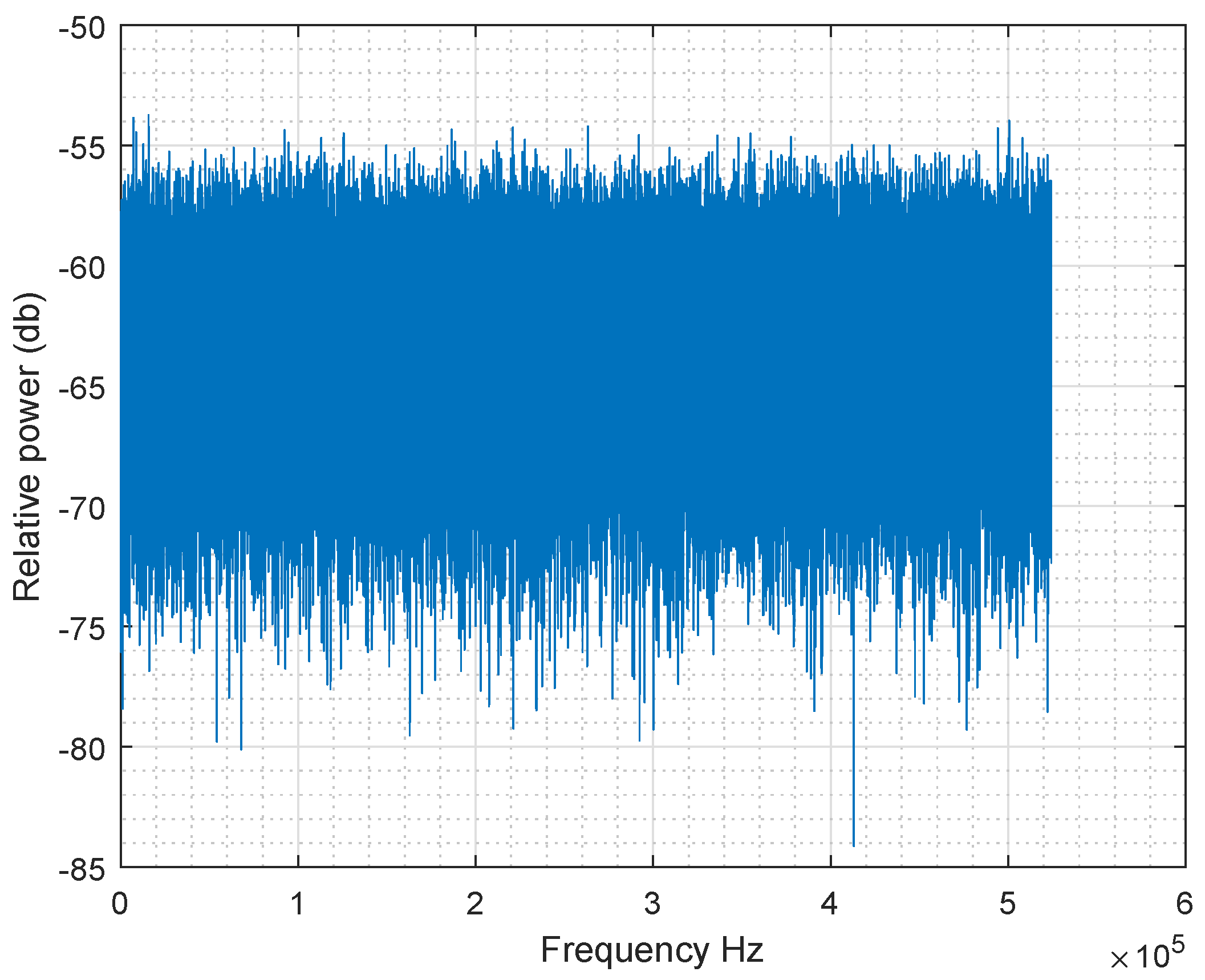
If the sequence is random, then all the maximum harmonics of Fast Fourier Transform have approximately the same horizontal level without an up or down trend.
Figure 9 shows that all amplitude values are included in the same range, which means that the test is passed.
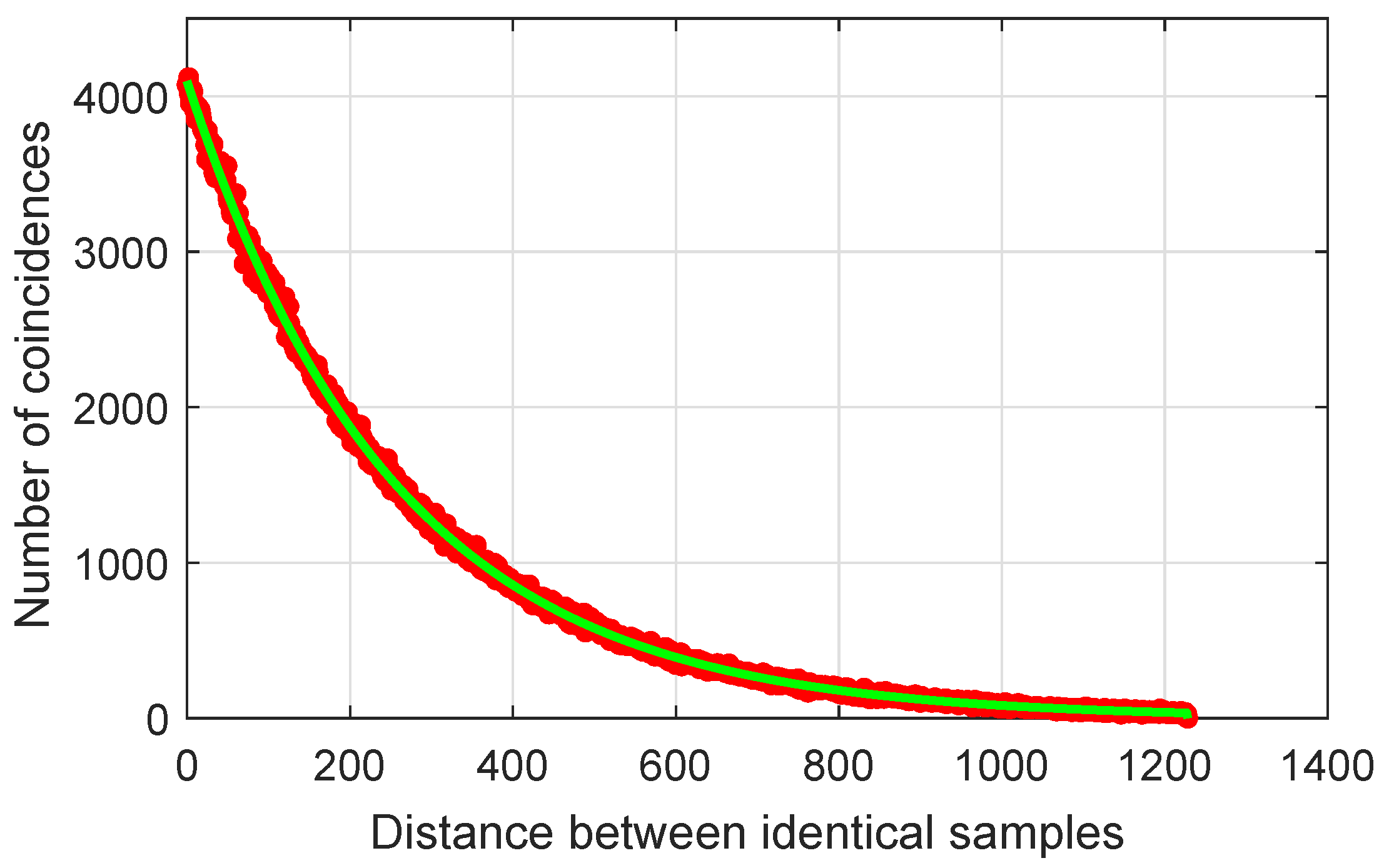
9. Distribution of identical samples
In this subsection, the distance of occurrence between samples of equal value is studied, because this measure is an important property of random sequences. The most probable distance between two identical samples of a perfect sequence is zero. If this distance increases, then the probability of coincidence between the two identical samples decreases following a Poisson distribution.
Figure 10 shows that the distribution of samples of the proposed sequence is close to the ideal.
10. Collisions of the sequence
Collisions are an intrinsic property of random sequences. If one has a sequence of integers module
m, the amount of different integer numbers will be
m. When a number appears repeated, we say that a collision has occurred. In Reference [
44] an analysis of the collisions problem is presented based on the
birthday paradox which states that in a group of
k people chosen at random, at least a pair of them will have the same birthday with probability:
where
m is the number of days of the year and
k is the number of people in the living room.
This paradox can be applied to hash functions. One of the desirable properties of cryptographic hash functions is that it is computationally impossible for a collision to occur; that is, given two different inputs, hash function does not produce the same output.
Suppose that we have a hash function of
n bits, so we have
output possible values. From this idea, it can be deduced the inequality:
which provides an estimated value of the quantity
k of rolls of a random sequence that must be extracted to have a probability of a first collision greater than or equal to
.
From Equation (
3) it can be deduced the collision probability density distribution
as a function of
k,
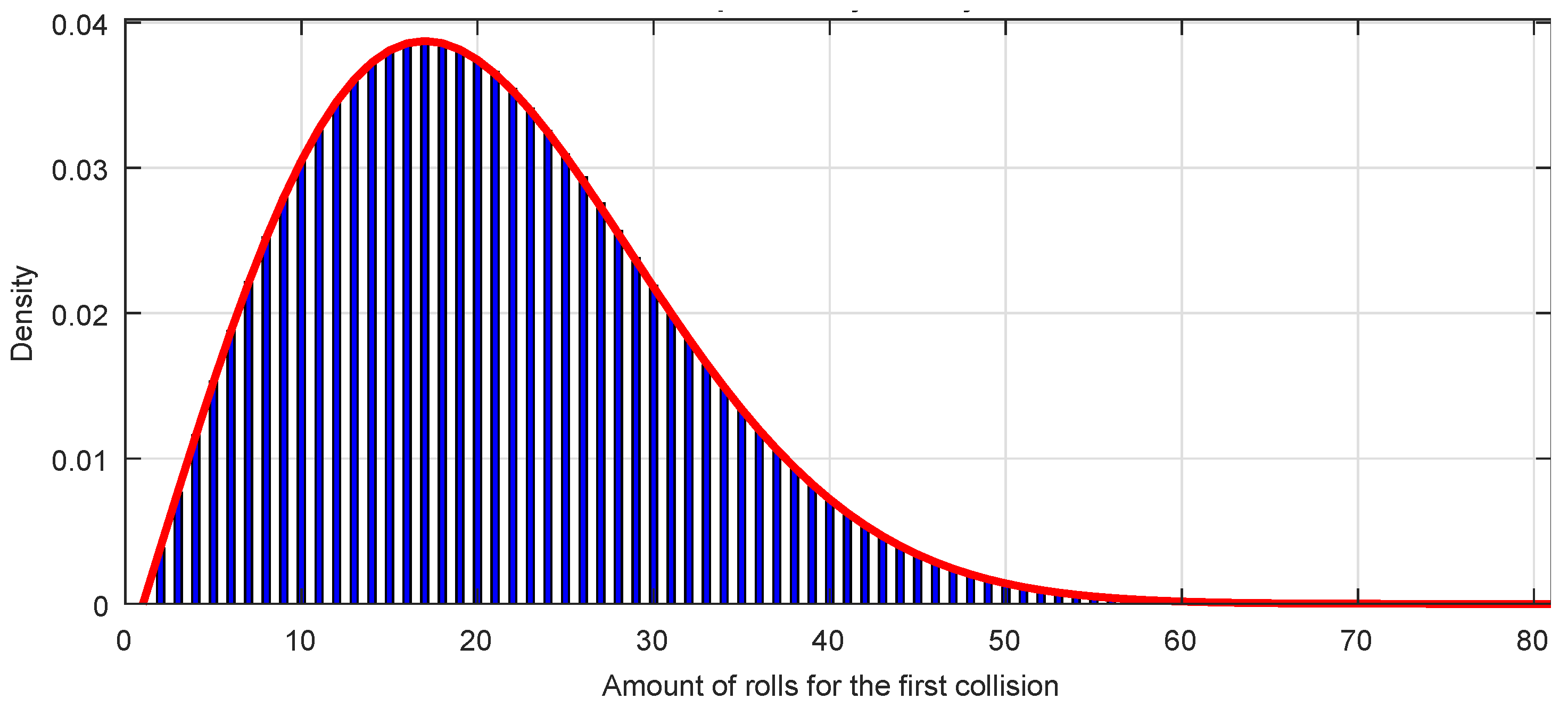
In
Figure 11 is represented the first collision probability density distribution function for a sequence of octets, that is,
,
as a red line. It can be seen that the mode of the distribution is
and for a quantity of rolls
the collision probability density is practically zero.
Any sequence with a perfect randomness must fit the first collision probability density distribution function corresponding to Equation (
4).
The
Figure 11 represents also a bar graph, with one bar for each value of
k, of a GSS-sequence of
octets. It can be seen the perfect fitting with the expected theoretical distribution.
As a curiosity, the first collision probability density distribution function coincides with a Weibull distribution function for the variable k, that is, the distribution which is most used to model data from reliability against catastrophes; in the present case, it models the amount of random number generation rolls needed for a first collision to appear, which is also a catastrophe for a hash function.