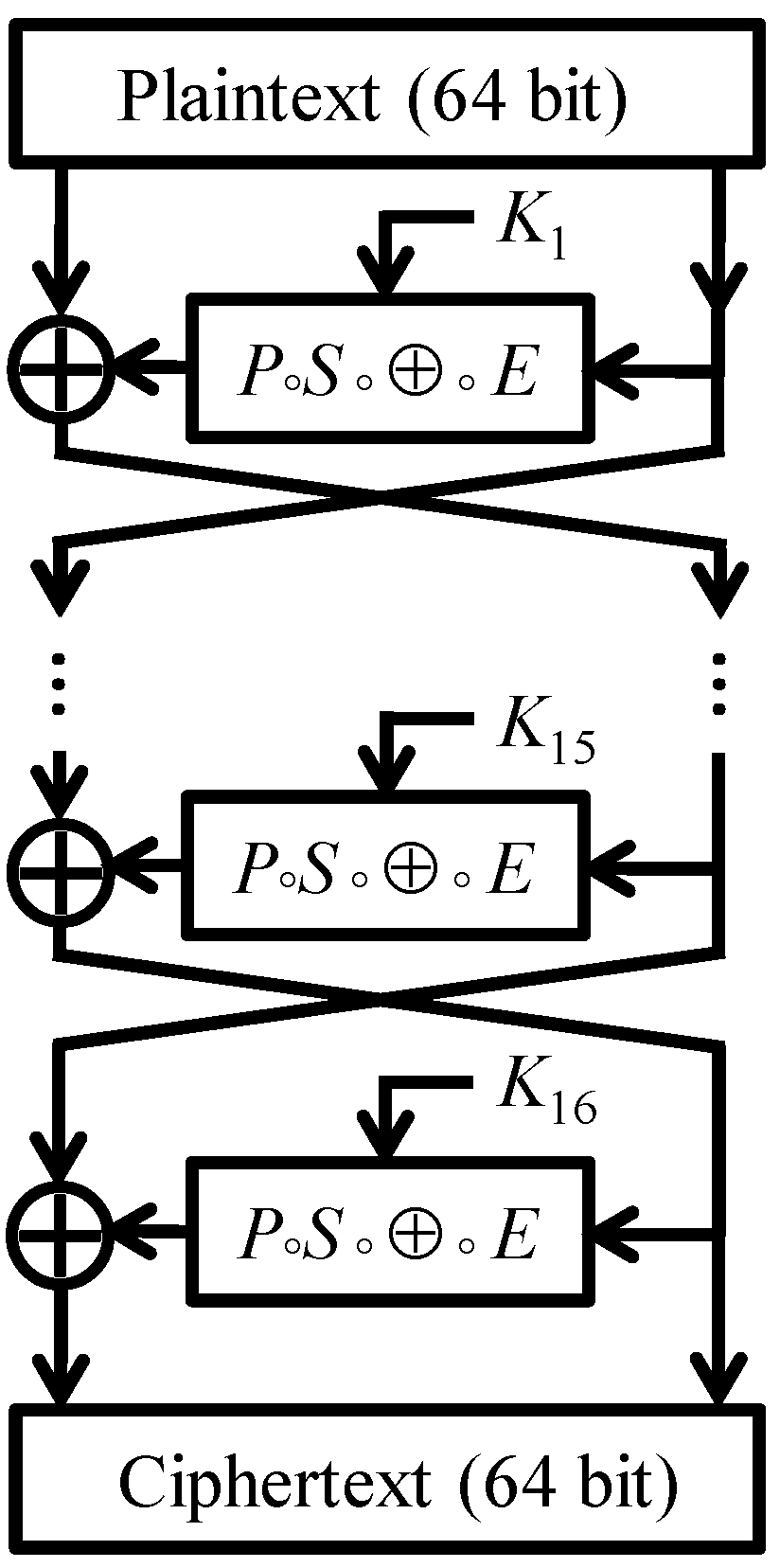
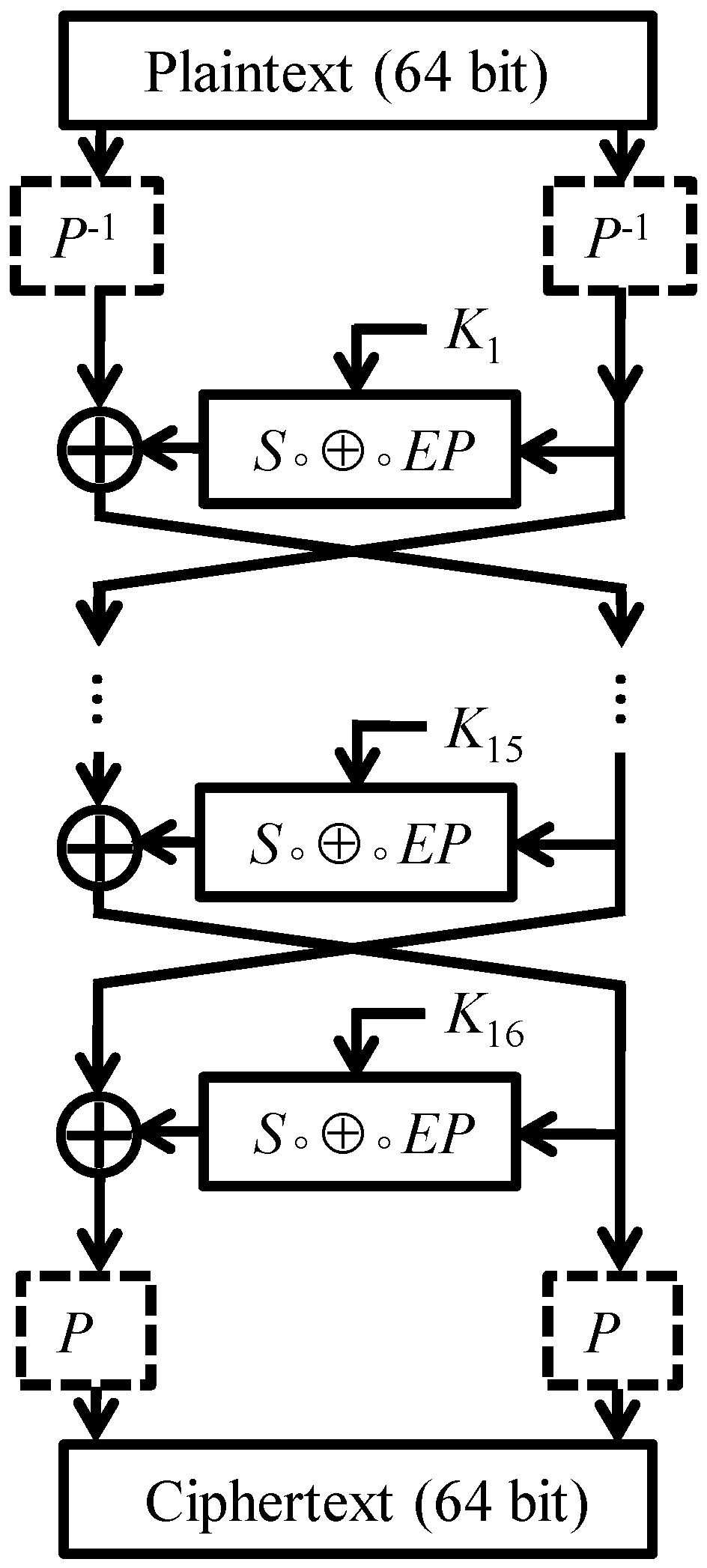
In this section we show that the round functions of DESL generate the same group as the round functions of DES. The main part of the argument is to establish 3-transitivity of the group generated by DESL’s round functions. To present the (somewhat technical) proof it will be convenient to introduce some notation.
3.2. Establishing 3-Transitivity of G
Before proving the main result, we will prove some previous lemmas.
Lemma 1. The round functions of DESL generate a subgroup of that acts transitively on .
Proof. Verifying the transitivity of
G is straightforward, and the work of Even and Goldreich [
15] ensures that
G is contained in the alternating group. ☐
As an intermediate step, we will show the transitivity of on and transitivity of on , where has a single non-zero entry at the 31st position.
Before doing so, let us have a closer look at and :
In view of the Feistel structure of DESL, it is perhaps not very surprising that we deal with pairs of round functions when exploring the transitivity of
and
. We define four sets of key pairs, where the last two depend on the auxiliary value
:
The elements in
G we are mainly interested in are of the form
or
with the key pair
being chosen from
. For input pairs
we have
In other words, when evaluating
, the right half of the input does not vary and its left half is XORed with the value
to the left half of the input.
For the situation is similar, with the left half of the input being stabilized.
The following proposition helps in understanding the effect of repeatedly applying a map of the form , respectively .
Proposition 1. The functions and defined above satisfy the following:
- (a)
and .
- (b)
and .
- (c)
Let . Then, for all and for all , the following hold:
and, analogously,
Proof. The proof is immediate from the definition of and . ☐
To understand better which values can be obtained in the left and right 32-bit halves of the output through repeated application of a map of the form (respectively ), given some 64-bit input, it is helpful to take a look at some -vector subspaces of :
Lemma 2. For letbe the -vector space spanned by . Similarly, denote by the -vector space Then, the following statements hold:
- (a)
.
- (b)
.
- (c)
.
- (d)
.
Proof. The proof is by direct computation, e.g., using a programming language like Python [
16]. ☐
Remark 1. Bringing the notation in Lemma 2 to use, from Proposition 1 we obtain the following statements which for the case (respectively ) may be regarded as “hinting at transitivity”:
For let be a bitstring. Then, there exist such that for all .
For let be a bitstring. Then, there exist such that for all .
For let be a bitstring and let . Then, there exist such that for all .
For let be a bitstring and let . Then there exist such that for all .
Therefore, if we know that the equality holds for some , then for each bitstring we can find a sequence of key pairs with For instance, we can choose pairs with corresponding to the linear combination of , and the rest of the positions being 0. This ensures that all are contained in , and if or , we can also ensure .
Similarly, in case contains all bitstrings of length 4, we can obtain a sequence of key pairs with The subsequent lemmata enable us to argue that acts transitively on . In other words, we prove that for all the equivalence holds, where . The proofs exploit in particular the transitivity of ∼.
Lemma 3. Let be the 32-bit vector which has a single 0-entry at the second position and 1-entries everywhere else, and let be arbitrary. Then .
Proof. Let
be arbitrary, but fixed. From
Table 2 we see that
Hence, by properties (a) and (c) of Lemma 2 we obtain for all as well as .
Therefore, because of Remark 1 for we get:
, since , for the corresponding , .
Analogously, since , we can obtain:
If we continue carrying out the same procedure, since all the subspaces considered are , we can finally see that . ☐
Lemma 4. .
Proof. If , then we obtain the lemma with .
Otherwise, we distinguish two cases:
If :
Then such that :
- –
If , then . Therefore, because of Remark 1, we can show such that for . Thus, .
- –
If , then . With an argument similar to the previous one, we can get an element , such that for . Therefore, .
If .
Since , then . Therefore, such that and, like before (but using “right-functions”) we prove that we can get an element , where , such that . Notice that in this case the pairs must be not only in , but in , so that (Proposition 1(b)).
- –
If
- ∗
If , then .
Therefore, because of Remark 1, we can have , where , with for some .
- ∗
If , then . With the same argument as before, we can get an element , such that for , where .
- –
If
: Since
, according to
Table 2,
. Therefore, we have
(Lemma 2(d)) and we can obtain, as in the previous cases, an element
, with
for some
.
Hence, this case is traced back to the case and the proof is complete. ☐
Lemma 5. .
Proof. If , then we immediately obtain the Lemma with .
Otherwise, we choose an index and we will prove that
, where the sets
are defined in
Figure 4.
We define , with . Therefore, , and we will see that if have been chosen appropriately, we can have .
For :
According to
Table 2,
and
, since the corresponding positions for
are 12 and 14, which are in blocks 2 and 3. Therefore, we have:
If , then . Hence, because of Remark 1, such that . Therefore, for all .
If , then . With a similar argument, such that . Therefore, for all .
Since , then and therefore such that . Therefore, for all .
Thus, considering the composition of the functions involved, we obtain such that .
A similar argument applies to the other values of .
Now, we will see that
, where the sets
are defined in
Figure 5.
We define , with . Therefore, , and we will see that choosing adequate elements , we can have .
For , :
According to
Table 2, let us see which positions
are in for the different values of
. We can see
is in position 18 (block 3) and 20 (block 4),
is in position 41 (block 7) and 43 (block 8),
is in position 3 (block 1),
is in position 35 and 37 (blocks 6 and 7),
is in position 23 and 25 (block 4 and 5),
is in position 45 (block 8), and
is in position 9 (block 2).
In all blocks j, for , we have and then . Therefore, as discussed in the previous proofs, such that . For block 3, we have , therefore such that .
Therefore, the only position we cannot assure is equal to e is , therefore .
For the rest of the indices j, we use similar arguments to compute sets .
If , the set has only one element. Therefore, as J(j),, so . Therefore, choosing appropriate we get , such that (Remark 1).
Therefore, we have , so . Now, choosing adequate , we can have , such that . Therefore, for we have the desired result.
Hence, we have seen that the lemma holds if for .
For indices , we have . Therefore, we are in the case where such that , and carrying out the same procedure as the one to get from , we get satisfying .
☐
Lemma 6. .
Proof. According to
Table 2,
corresponds to positions 26, 5, 18, 31, and 2. Since
, we know
. Therefore,
and because of Lemma 2 (c),
. Thus, considering appropriate
, we get
, for some
. ☐
Corollary 1. .
Proof. Considering the chain , where these elements are as described in the previous lemmata, the result follows. ☐
Corollary 2. is transitive on .
Proof. Let , by Lemma 6 and Corollary 1, ☐
Corollary 3. is transitive on .
Proof. Because of Corollary 1, it is enough to show that such that .
Note that since , then .
Let , then and . Therefore, , and . ☐
Lemma 7. If is transitive on and is transitive on , then G is 3-transitive on .
Proof. It follows immediately from [
17] (Theorem 9.1). ☐
Once we have shown that G is a 3-transitive subgroup of , it is not particularly difficult to verify that G is actually equal to the alternating group on points.
Theorem 1. The round functions of DESL generate the alternating group, i.e., .
Proof. We refer to the proof of Theorem 1 in [
7], since the same proof applies here. ☐