1. Introduction
There are various problems in the field of applied mathematics that can be reformulated by means of fixed point theory. Fixed point theorems provide us with sufficient conditions for the existence of a fixed point, and thus the existence of a solution for the original problem is ensured.
The first step in the direction of a fixed point theory on metric spaces was Banach contraction principle. Came out as an abstraction for Picard iteration, this principle not only ensures the existence and uniqueness of a fixed point for contraction mappings, but also provides us an iterative algorithm to approximate this point. Finding iterative ways to approximate fixed points of different kind of mappings becomes essential as many problems of nonlinear analysis can not be solved analytically. In this regard, Picard iteration was an important starting point for the development of other processes. Despite the success it had with contraction mappings, Krasnoselskii [
1] proved in 1955 that Picard iteration does not always converge to a fixed point when taking a larger class of mappings defined on Banach spaces, namely nonexpansive mappings (for
C being a nonempty closed convex subset of a Banach space
X over the real field
, a mapping
is said to be nonexpansive if it satisfies the inequality
, for all
x,
; moreover, if
, where
and
, for all
and
, then
T is called quasi-nonexpansive). The main reason for such a behavior is that, unlike contraction mappings, successive iteration for nonexpansive mappings needs not converge to a fixed point. From this moment onwards, many others iterative processes have been developed for numerical reckoning fixed points of nonexpansive mappings. For instance, one of the earliest would be Mann’s [
2] iteration process, defined as follows: for an arbitrary chosen
, the sequence of successive iterations is defined by
where
is a sequence of real numbers in the interval
, followed by Ishikawa [
3] iteration, a two step iteration process widely applied for numerical reckoning fixed points of nonexpansive mappings; for a starting point
, this iterative scheme is defined by
where
. Important to be mentioned would also be Agarwal et al. [
4]’s two step iteration process introduced in 2007: for an arbitrary
, define
with
and
sequences in
.
In 2000, Noor [
5] introduced a new three-step iteration scheme for approximation fixed points of nonexpansive mappings as follows: starting with
, define
iteratively by
where
,
,
are sequences of real numbers in
. This has pioneered a number of new three-step iteration techniques as, for example, Abbas and Nazir [
6]: for an arbitrary
, the sequence
is defined by
where
,
,
are real number sequences in
. In the sequel, we will consider the following iterative process defined by Thakur et al. in [
7] for numerical reckoning fixed points of nonexpansive mappings; see, also [
8]: for an arbitrary chosen element
, the sequence
is generated by
for all
, where
,
,
are sequences of real numbers in
. We shall refer to this iterative procedure as TTP.
As it can be seen, nonexpansive mappings are an intensely studied category of operators in terms of finding various conditions for the existence of their fixed points (see for example Browder [
9] and Kirk [
10]), in terms of defining iterative processes to approximate the fixed points whose existence has been established, or even in connection with hybrid methods in very recent research directions (see, for instance [
11]). However, in 2008, Suzuki [
12] introduced a new class of mappings on Banach spaces (herein referred as Suzuki-generalized nonexpansive mappings or Suzuki mappings), which properly includes the class of nonexpansive mappings; this came out by limiting the range of points satisfying the nonexpansive inequality. One simple example provided by Suzuki in order to emphasize the idea that the newly introduced class is larger than nonexpansiveness is the following
This new property, named condition
, caught the attention of many authors that searched different fixed point theorems for such mappings (see for example [
13,
14,
15,
16]). In particular, a consistent analysis in connection with condition
was performed in [
17], in a modular vectorial setting. An interesting extension of
-property is the class of generalized nonexpansive mappings that satisfy the so-called condition
introduced by Garcia-Falset et al. [
18]. Condition
is wider than Suzuki’s condition but stronger than quasi-nonexpansiveness. Another extension was subject to analysis in [
19]. However, these generalized properties will not be a topic to be approached in this survey.
In this paper, we will focus on extending the study of the above-mentioned TTP process to the more general class of Suzuki-generalized nonexpansive mappings. In this respect, we will provide an outcome regarding the existence of fixed points for Suzuki mappings in the framework of uniformly convex Banach spaces. In addition, some convergence theorems concerning this iterative process will be stated.
3. Convergence Theorems
Inspired by the results obtained in [
7] via the iteration procedure (
1), for nonexpansive mappings, we phrase and prove similar convergence outcomes regarding mappings satisfying condition
. Knowing that property
leads to a wider class of mappings than nonexpansiveness, the results provided next are expected to be more general than the outcomes in [
7].
Lemma 4. Let C be a nonempty, closed and convex subset of a Banach space X and a mapping satisfying condition (C) with . For an arbitrary chosen , let be the sequence generated by (1). Then exists for any . Proof. Let
. Since
T satisfies condition (C) and has at least a fixed point; it follows that
T is quasi-nonexpansive. Thus, from (
1), one has
The same reasoning applies to
, and one obtains
Now, using inequality (
2), one finds
In addition, the following inequality holds
and together with (
2) and (
3) becomes
We conclude from (
4) that
is bounded and nonincreasing for all
. Hence,
exists. □
Theorem 2. Let C be a nonempty, closed and convex subset of a uniformly convex Banach space X, and let be a mapping satisfying condition (C). For an arbitrary chosen , let the sequence be generated by (1) for all , where , , , bounded away from 0 and 1. Then if and only if is bounded and . Proof. Let us first prove the direct implication. Suppose
and let
. By Lemma 4 it follows that
exists and
is bounded. Let us denote
From (
2), it is known that
. Taking lim sup on both sides of the inequality and using (
5), one obtains
Again, since
T is quasi-nonexpansive, one has
Now, the following inequality holds true
and combined with (3) becomes
Dividing the above relation by
, conducts to
and it follows that
i.e.,
Applying lim sup to (
8) and using (
5) together with (
6), one obtains
which implies
Relation (
9) can be rewritten as
From (
5), (
7), (
9) and Lemma 1 one finds
.
Let us now prove the converse statement. Suppose
is bounded and
. Let
. By Proposition 1(iii) one has
The above relation implies that . As mentioned above, when dealing with closed bounded convex subsets of uniformly convex Banach spaces, the asymptotic center is a singleton. Therefore, i.e., , and the proof is complete. □
Theorem 3. Let C be a nonempty closed convex subset of a uniformly convex Banach space X with Opial’s property, T and be as in Theorem and . Then converges weakly to a fixed point of T.
Proof. The proof is identical with the proof of the Theorem 3.3. in [
15]. This is not surprising since the conclusions of Lemma 4 and Theorem 2 are the same as in Theorem 3.2. and Lemma 3.1. in [
15], via a distinct iterative process. We chose to display the proof just for the sake of making the paper self-contained.
Since
, let
. By Theorem 2,
is bounded and
and by Lemma 4,
exists. Since
X is uniformly convex, according to Milman–Pettis’s Theorem, it is reflexive. Therefore, by Eberlin’s Theorem, every bounded sequence of elements of
X contains a subsequence which converges weakly to an element of
X. Let
be the subsequence of
which converges weakly to an element
. Since
C is closed and convex, according to Mazur’s Theorem,
. By Lemma 2, we obtain
, consequently
. Further we will show that
itself converges weakly to
. Let us assume the contrary and suppose that there exists a subsequence
of
, such that
, where
. Again, using Lemma 2 we have
i.e.,
. Since
X is endowed with Opial’s property, we obtain
This leads to a contradiction, so and we conclude that converges weakly to a fixed point of T. □
Theorem 4. Let C be a nonempty, compact and convex subset of a uniformly convex Banach space X and let T and be as in Theorem. Then converges strongly to a fixed point of T.
Proof. Again, the proof does not differ at all from the proof of Theorem 3.4 in [
15].
By Lemma 3, we have
. Since
C is compact, there exists a subsequence
of
such that
converges strongly to an element
. Using Proposition 1 (iii), we have
Taking the limit of the above relation, we obtain
By Theorem 2, we have and , so the previous inequality gives that i.e., . But the limit is unique, so which implies . Furthermore, by Lemma 4, exists for any , thus p is the strong limit of the sequence itself. □
Theorem 5. Let C be a nonempty closed convex subset of a uniformly convex Banach space X, let T and be as in Theorem and . If T satisfies the condition (I), then converges strongly to a fixed point of T.
Proof. The proof runs as in [
15] (Theorem 3.5).
By Lemma 4,
exists for any
, therefore
exists. Suppose
, for some
. If
, then the desired result follows. Let
. By condition (I) in Definition 4, we obtain
From the hypothesis
so using Theorem 2,
which implies
Considering the properties of the function
f, we find
Let
be a subsequence of
and
such that
For
, it follows
therefore
is a Cauchy sequence. Since
is a closed set,
converges to a fixed point
p. Letting
in (
10) we have
. Since
exists, it leads to
which completes the proof. □
5. Example and Comparative Study
In order to emphasize the value of the analyzed TTP iteration procedure in connection with Suzuki-type mappings, by comparing it further with other iterative processes, we consider next an example.
Example 1. We shall further prove that T is a Suzuki but not a nonexpansive mapping. To develop the desired proof we chose to work with the Taxicab norm or 1-norm on , that is .
Proof. We start by proving that there exist and , such that, T mentioned above is not nonexpansive. Let us take for example , , and . Then , thus T is not a nonexpansive mapping.
To prove that T satisfies condition (C), the following cases need to be analyzed:
Case I: Let . If , then it can easily be seen that T is nonexpansive and condition is automatically satisfied. Further, if we take , then stands true only for . Moreover, evaluating the nonexpansiveness condition for and , one finds which is obviously true as , while . Therefore, T satisfies condition C for the case considered.
Case II: Let us now consider the rest of the interval i.e., . Similarly with Case I, if and belongs to the same interval, then T is a contraction and satisfies condition C since all contractions are included in the class of Suzuki mappings. On the other side, if then becomes , or, even more, , as . Further, this implies i.e., . For and , the nonexpansive condition is which is true as and , so T satisfies condition C for this case also.
Considering all the situations previously analyzed, we conclude that the above defined T is indeed an example of a Suzuki mapping, although it is not a nonexpansive one. □
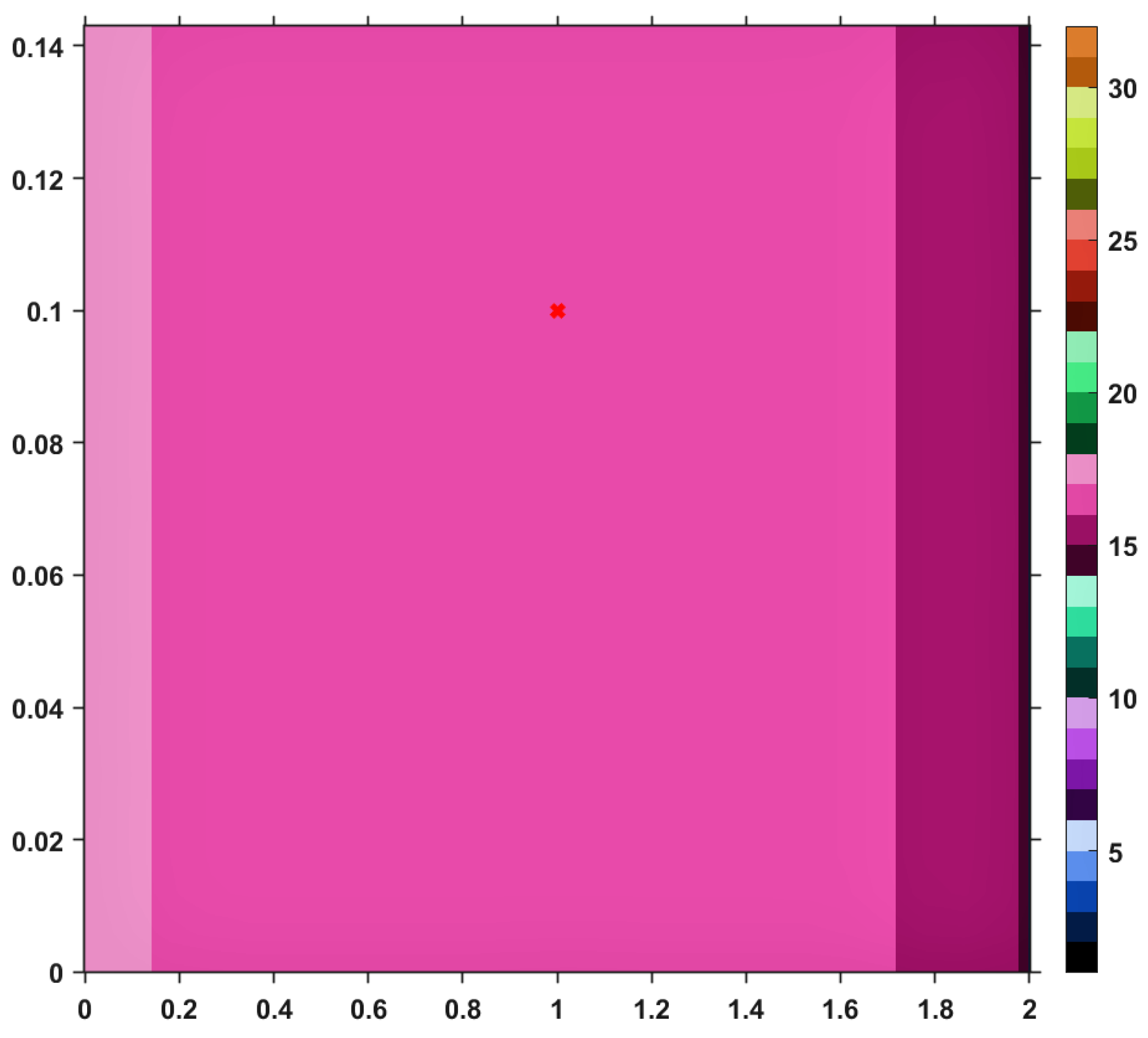
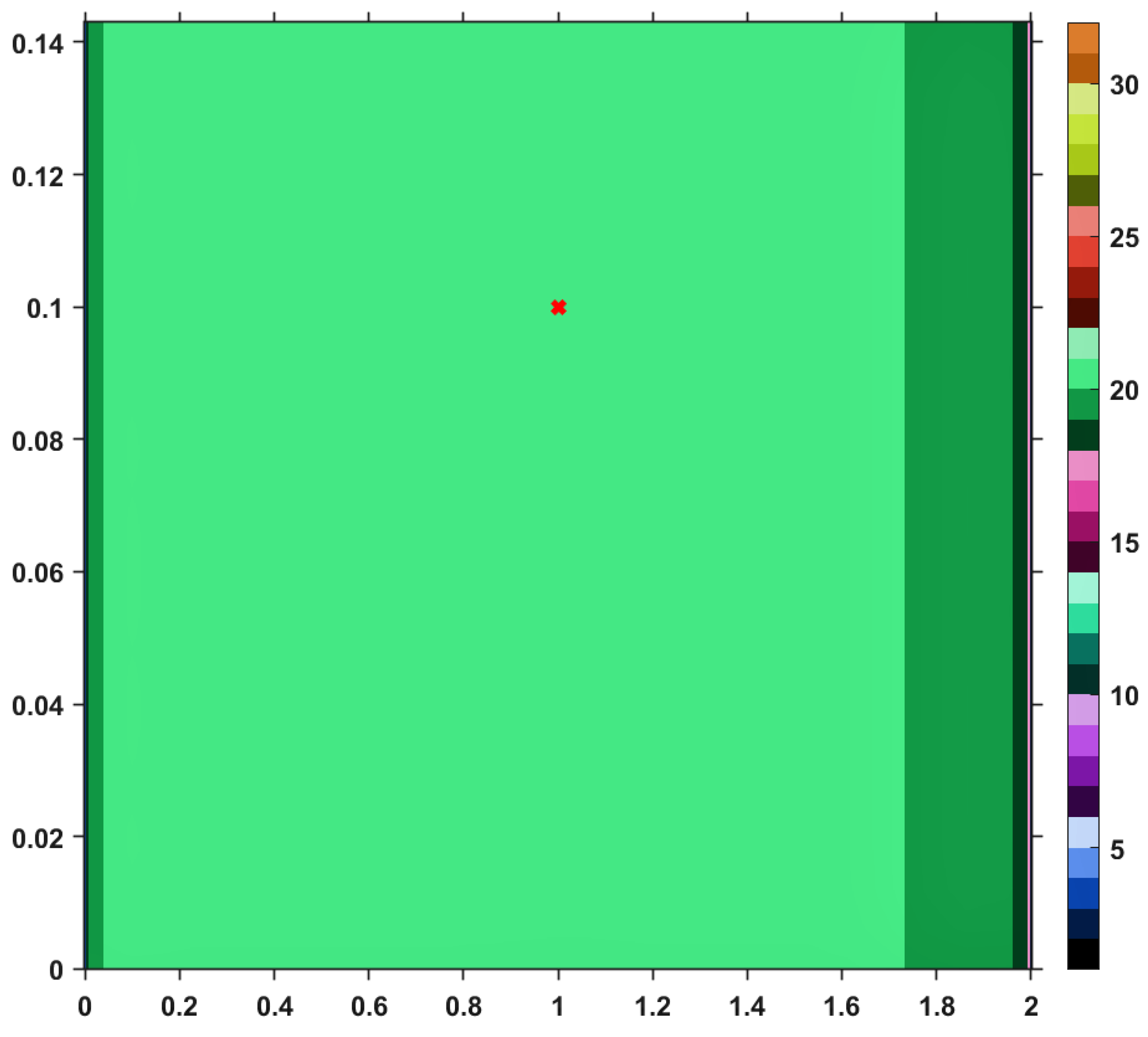
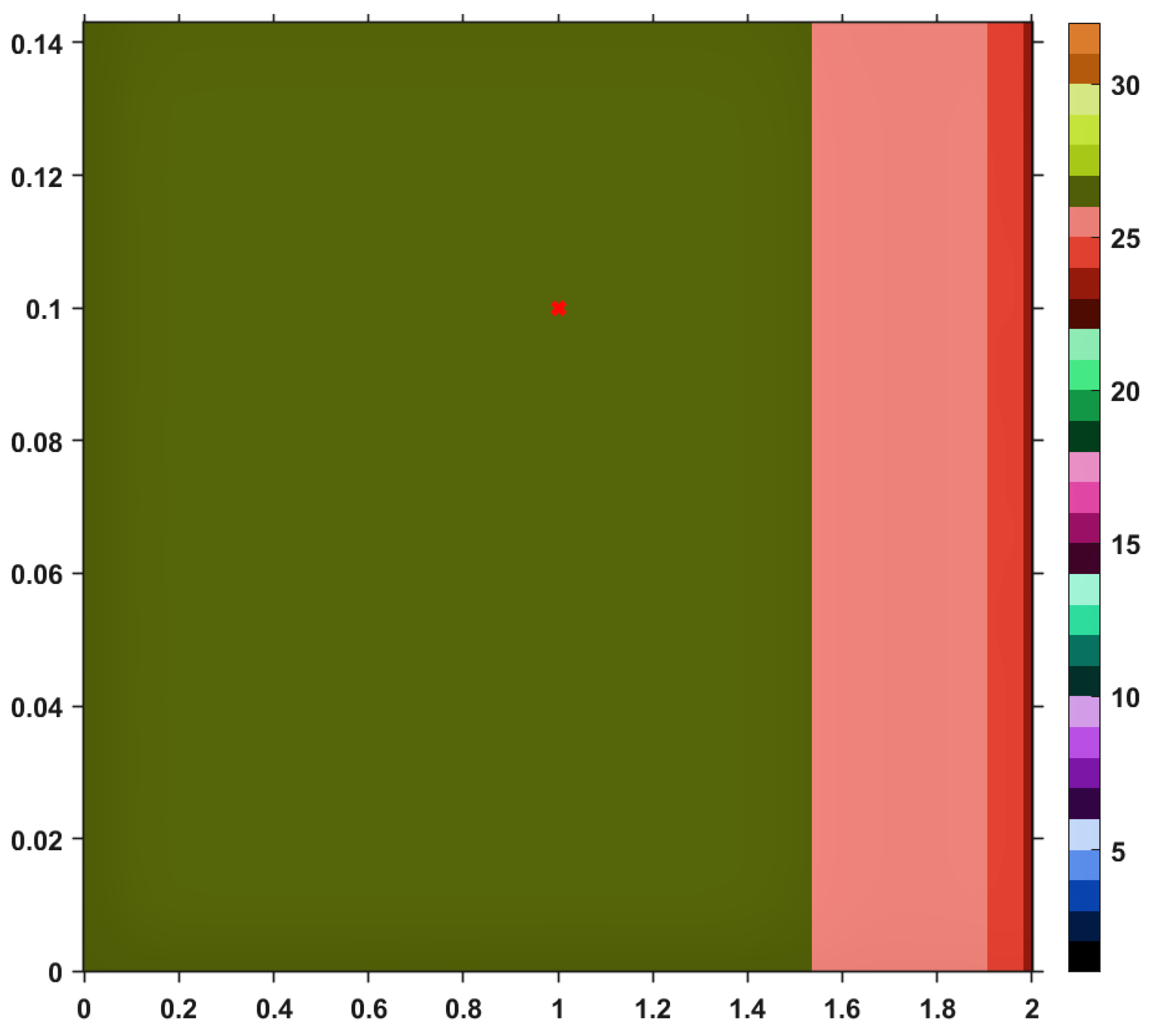
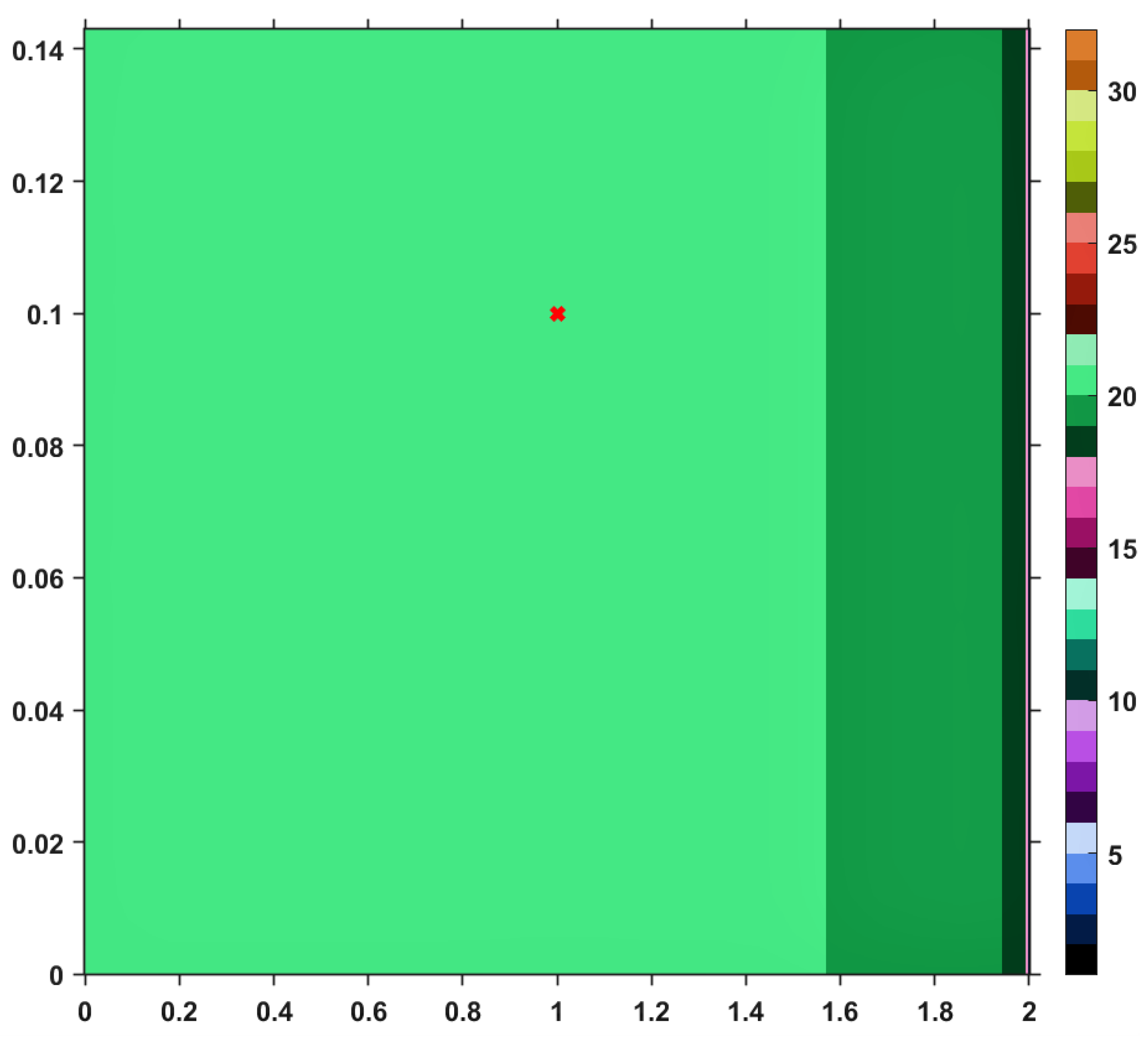
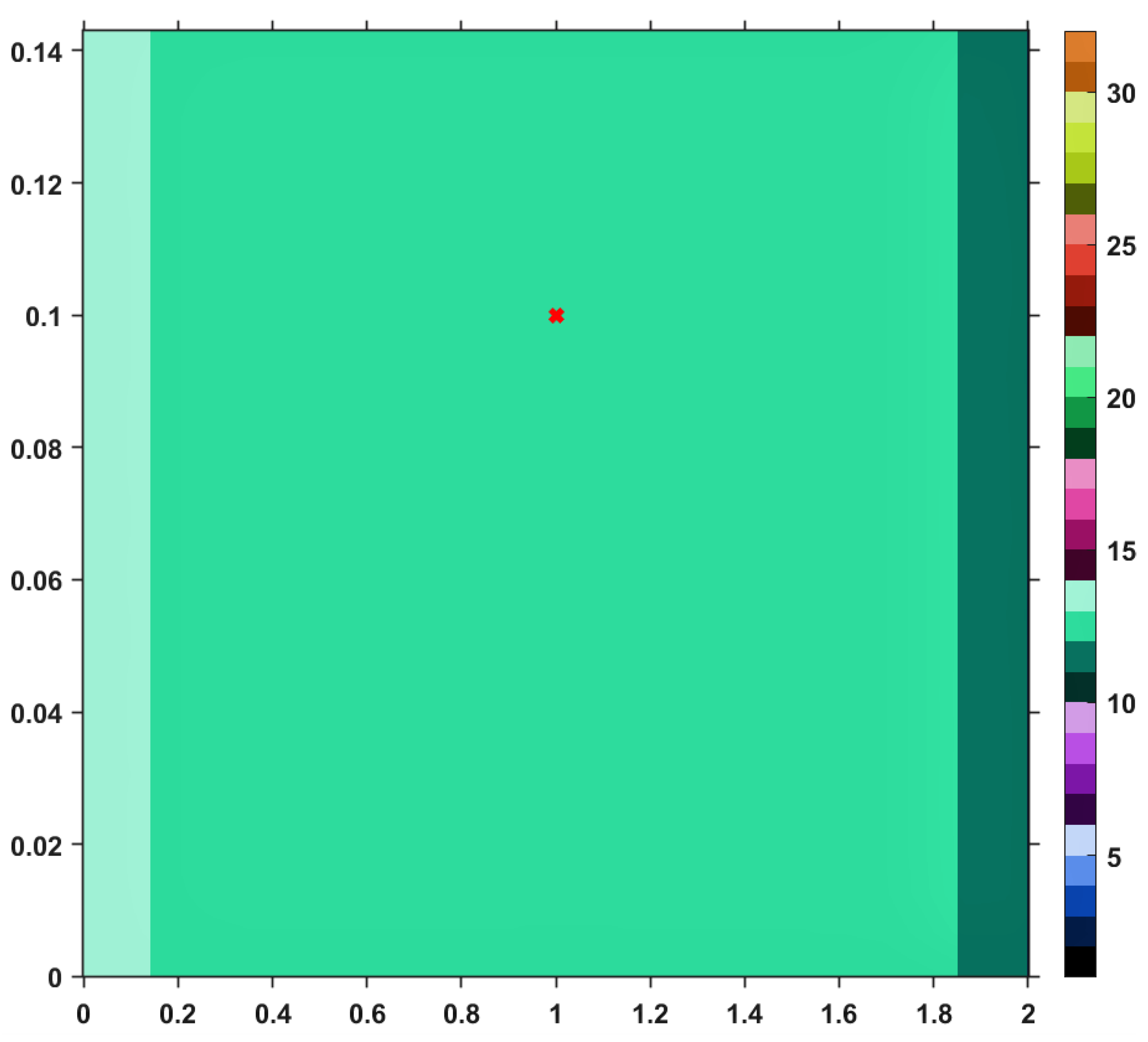
Using this Suzuki mapping and the TTP iteration procedure, along with other iterative schemes mentioned in the first section, let us visualize (and analyze) the convergence behaviors by performing a numerical simulation. The results are pictured in the images included in
Figure 1,
Figure 2,
Figure 3,
Figure 4,
Figure 5,
Figure 6 and
Figure 7. The maximum number of iterations to be performed until the algorithm stops is set to
and the exit parameter to
. The
rectangle is represented by an open window having the values of
on the horizontal axis and those of
on the vertical one. As a general feature of the obtained images, the first color (black) of the right-sided colorbar, corresponds to those pairs of points having long orbits, non-convergent for the maximum number of iterations imposed. Apart from black, each color in the range corresponds to a value between 1 and 30, in ascending order, signifying the number of iterations needed to reach the fixed point of
T with the error
. On what concerns the values of the involved parameters, we chose (purely arbitrary) the sequences
,
and
. The Algorithm 1 is used to generate these images and goes through the following steps: first, take a pair of starting points from the area
, then choose an iteration procedure and perform it until the maximum number of iteration
K is reached or the exit criterion is satisfied (for this case, as we have worked with the Taxicab norm, the exit criterion is
. When the loop terminates, the program will assign to every starting point from the specified area a pixel and a corresponding color, based on the number of iterations performed.
| Algorithm 1: Convergence visualization |
![Symmetry 11 01441 i001]() |
Let us take a closer look to the first image; namely,
Figure 1, the one corresponding to the TTP iterative process. One can see that, as the set of fixed points is approached, the color becomes darker, meaning that the number of iterations performed decreases. Moreover, the last line of the image takes a dark blue color. This is actually to be expected since that particular line is corresponding to the set of fixed points of
T and just one iteration is needed until the exit criterion is satisfied. Similar analyses regarding convergence speed can be realized for the images provided by others iterative processes, i.e., Picard, Mann, Agarwal and Abbas-Nazir. It is interesting to point out that the corresponding images for iterations like Ishikawa and Noor are entirely black, meaning that the procedures are very slowly convergent (they need more than 30 iterative steps) or they do not converge at all. The explanation for such a behavior is that
T defined above is a Suzuki-generalized nonexpansive mapping, but it is not nonexpansive. Nevertheless, it is clear that, among all iterative processes, TTP remains one of the fastest; it is only surpassed by he Abbas-Nazir procedure. This last statement is also emphasized on the
Table 1, by taking a random point from the domain of
T (
, also marked on each image with a red ’x’) and listing the number of iterations needed to approximate the fixed point
for each iteration procedure.
In the following, we provide a second example of a Suzuki mapping which is not nonexpansive, on a function space. This is meant to strengthen the assertion that mappings satisfying condition
C is indeed a wide class of operators, and examples for it can be provided both on
(see [
15]) and
, as well as on infinite dimensional spaces.
Example 2. Consider the Banach space of all essentially bounded Lebesgue measurable functions, endowed with the essential supremum norm Let and We shall further prove that T mentioned above is an example of a Suzuki-generalized nonexpansive mapping.
Proof. Suppose the inequality is satisfied. This is further equivalent with . Thus, two cases arise:
Case 1: Let us presume that . For T to satisfy condition , this must imply . Because of this last inequality, it is expected the problem to be divided again into two sub-cases. We will analyze just the nontrivial one i.e., implies , as the desired result follows easly from the other one. If and , or and , it can be easly noticed that T is nonexpansive, and therefore condition is automatically fulfilled. For and , T is nonexpansive just for , and again, condition is satisfied. For and , becomes which is not true as and . The same result is obtained if we take and . Considering all the situations analyzed, we conclude that T is a Suzuki-mapping for the current case.
Case 2: Suppose . The inequality must imply . If we consider that , it follows ; but as , it follows that too, so T is nonexpansive. If we suppose , kipping in mind that on one side, on the other side and considering all combinations that T could involve, we find that the assumption is absurd and could not be grater than . So, overall, T is a Suzuki mapping in Case 2 also. □
6. Conclusions
This paper analyzes a three-steps Thakur iterative procedure in connection with mappings satisfying Suzuki’s generalized nonexpansiveness condition, known as property . A necessary and sufficient condition regarding the existence of fixed points for Suzuki mappings is stated and proved via the TTP iterative process. Furthermore, convergence results are obtained when additional hypotheses related to Opial’s property, compactness or condition are assumed. Fresh examples of Suzuki mappings which are not nonexpansive are further provided; the settings for these examples are , with the Taxicab norm, and endowed with the essential supremum norm. But, the most interesting feature about the example in is a numerical simulation, resulting in a visual comparative analysis of the convergence behaviors of several iteration procedures. This numerical modeling uses similar techniques as the root-finding procedures for complex polynomials, which ultimately led to polynomiographic visualization.
Overall, the novelty of this paper is twofold. First, a new perspective on the TTP iteration procedure is provided; this iterative scheme was originally conceived as a tool in connection with nonexpansive mappings; now, it is proved to be an instrument as good as before for reaching the fixed points of Suzuki mappings too. Moreover, having in mind the computational dimension of an iteration procedure, a data dependency analysis is convenient, since errors can occur when using computer programs. Usually, this constrains us to actually use a perturbed mapping , instead of the theoretical one. We managed to prove that a small perturbation of the initial data does not significantly affect the computational process of the fixed point of a contractive operator.
Secondly, more complex examples of Suzuki mappings are provided. Picking as the setting, an interesting visual procedure is suggested as a possible new approach related to convergence analysis. In addition, another example proves that one could easily exceed the framework of finite dimensional normed spaces.