Symmetric Identities for Carlitz-Type Higher-Order Degenerate (p,q)-Euler Numbers and Polynomials

Abstract

The main goal of this paper is to investigate some interesting symmetric identities for Carlitz-type higher-order degenerate $(p,q)$-Euler numbers, and polynomials. At first, the Carlitz-type higher-order degenerate $(p,q)$-Euler numbers and polynomials are defined. We give few new symmetric identities for Carlitz-type higher-order degenerate $(p,q)$-Euler numbers and polynomials.

1. Introduction

Many $(p,q)$-extensions of some special functions such as the hypergeometric functions, the gamma and beta functions, special polynomials, the zeta and related functions, q-series, and series representations have been studied (see [1,2,3,4,5,6]). In our paper, we always make use of the following notations: ${\mathbb{Z}}_{+}=\mathbb{N}\cup \left\{0\right\}$ is the set of nonnegative integers, and the notation

$$\sum _{m_1,\cdots ,m_r=0}^{\infty }\mathrm{is}\mathrm{used}\mathrm{instead}\mathrm{of}\sum _{m_1=0}^{\infty }\cdots \sum _{m_r=0}^{\infty }.$$

The $(p,q)$-number is defined as

$${\left[n\right]}_{p,q}=\frac{p^n-q^n}{p-q}=p^{n-1}+p^{n-2}q+p^{n-3}{q}^2+\cdots +p^2{q}^{n-3}+p{q}^{n-2}+q^{n-1}.$$

Much research has been conducted in the area of special functions by using $(p,q)$-number (see [1,2,3,4,5,6]). The classical Stirling numbers of the first kind $S_1(n,k)$ and the second kind $S_2(n,k)$ are related to each other like this (see [7,8,9,10])

$${(x)}_n=\sum _{k=0}^n{S}_1(n,k)x^k\mathrm{and}{x}^n=\sum _{k=0}^n{S}_2(n,k){(x)}_k,$$

respectively, where ${(x)}_n=x(x-1)\cdots (x-n+1)$. The generalized $(p,q)$-falling factorial ${({\left[x\right]}_{p,q}|\lambda )}_n$ with increment $\lambda$ is defined by

$${({\left[x\right]}_{p,q}|\lambda )}_n=\prod _{k=0}^{n-1}({\left[x\right]}_{p,q}-\lambda k)$$

for positive integer n, with the convention ${({\left[x\right]}_{p,q}|\lambda )}_0=1$; we also write

$${({\left[x\right]}_{p,q}|\lambda )}_n=\sum _{k=0}^n{S}_1(n,k){\lambda }^{n-k}{\left[x\right]}_{p,q}^k.$$

Clearly, ${({\left[x\right]}_{p,q}|0)}_n={\left[x\right]}_{p,q}^n$. We also have the binomial theorem: for a variable x,

$${(1+\lambda t)}^{{\displaystyle \frac{{\left[x\right]}_{p,q}}{\lambda }}}=\sum _{n=0}^{\infty }{({\left[x\right]}_{p,q}|\lambda )}_n{\displaystyle \frac{t^n}{n!}}.$$

We introduced Carlitz-type degenerate Euler numbers ${\mathcal{E}}_n(\lambda )$ and Euler polynomials ${\mathcal{E}}_n(x,\lambda )$ using $(p,q)$-number (see [4]). For $0<q<p\le 1$, ${\mathcal{E}}_{n,p,q}(\lambda )$ and polynomials ${\mathcal{E}}_{n,p,q}(x,\lambda )$ are defined by the generating functions

$$\sum _{n=0}^{\infty }{\mathcal{E}}_{n,p,q}(\lambda )\frac{t^n}{n!}={\left[2\right]}_q\sum _{m=0}^{\infty }{(-1)}^m{q}^m{(1+\lambda t)}^{{\displaystyle \frac{{\left[m\right]}_{p,q}}{\lambda }}},$$

and

$$\sum _{n=0}^{\infty }{\mathcal{E}}_{n,p,q}(x,\lambda )\frac{t^n}{n!}={\left[2\right]}_q\sum _{m=0}^{\infty }{(-1)}^m{q}^m{(1+\lambda t)}^{{\displaystyle \frac{{[m+x]}_{p,q}}{\lambda }}},$$

respectively (see [4]).

Hwang and Ryoo [11] discussed some properties for Carlitz-type higher-order $(p,q)$-Euler numbers and polynomials. For $r\in \mathbb{N}$ and $0<q<p\le 1$, the Carlitz-type higher-order $(p,q)$-Euler polynomials $E_{n,p,q}^{(r)}(x)$ are defined by the generating function:

$$\sum _{n=0}^{\infty }{E}_{n,p,q}^{(r)}(x){\displaystyle \frac{t^n}{n!}}={\left[2\right]}_q^r\sum _{m_1,\cdots ,m_r=0}^{\infty }{(-1)}^{m_1+\cdots +m_r}{q}^{m_1+\cdots +m_r}{e}^{{[m_1+\cdots +m_r+x]}_{p,q}t}.$$

(1)

When $x=0,E_{n,p,q}^{(r)}=E_{n,p,q}^{(r)}(0)$ are called the Carlitz-type higher-order $(p,q)$-Euler numbers $E_{n,p,q}^{(r)}$ (see [11]). Furthermore, we obtain

$$E_{n,p,q}^{(r)}(x)={\left[2\right]}_q^r\sum _{m_1,\cdots ,m_r=0}^{\infty }{(-1)}^{m_1+\cdots +m_r}{q}^{m_1+\cdots +m_r}{[m_1+\cdots +m_r+x]}_{p,q}^n.$$

(2)

For $0<q<p\le 1$, $h\in \mathbb{Z}$, and $r\in \mathbb{N}$, Carlitz-type higher-order $(h,p,q)$-Euler polynomials $E_{n,p,q}^{(r,h)}(x)$ are defined using generating function

$$\sum _{n=0}^{\infty }{E}_{n,p,q}^{(r,h)}(x){\displaystyle \frac{t^n}{n!}}={\left[2\right]}_q^r\sum _{k_1,\cdots ,k_r=0}^{\infty }{(-1)}^{k_1+\cdots +k_r}{q}^{k_1+\cdots +k_r}{p}^{h(k_1+\cdots +k_r)}{e}^{{[k_1+\cdots +k_r+x]}_{p,q}t}.$$

When $x=0,E_{n,p,q}^{(r,h)}=E_{n,p,q}^{(r,h)}(0)$ are called the Carlitz-type higher-order $(h,p,q)$-Euler numbers $E_{n,p,q}^{(r,h)}$.

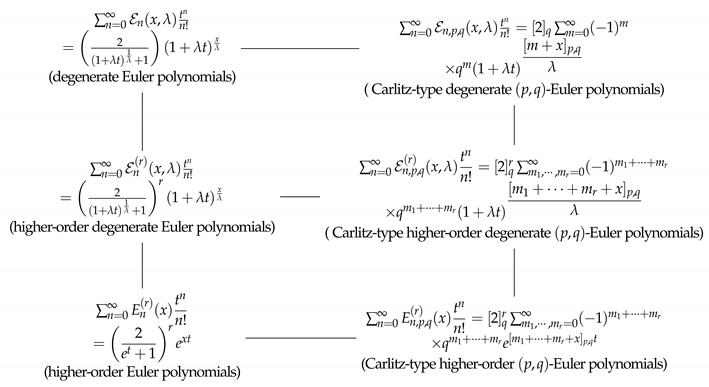
The following diagram shows the variations of the different types of degenerate Euler polynomials and Euler polynomials. Those polynomials in the first row and the third row of the diagram are studied by Hwang and Ryoo [4,11], Carlitz [7], Cenkci and Howard [9], Wu and Pan [12], Luo [13], and Srivastava [14], respectively. The study of these has produced beneficial results in combinatorics and number theory (see [4,7,9,12,13,14,15,16,17,18]). The motivation of this paper is to investigate some explicit identities and symmetric identities for Carlitz-type higher-order degenerate $(p,q)$-Euler polynomials in the second row of the diagram.

The goal of this paper is that new generalizations of the Carlitz-type degenerate $(p,q)$-Euler numbers and polynomials is introduced and studied. Each section has the following contents. In Section 2, Carlitz-type higher-order degenerate $(p,q)$-Euler numbers and polynomials are defined. We induce some of their properties involved distribution relation, explicit formula, and so on. In Section 3, we make several symmetric identities about Carlitz-type higher-order degenerate $(p,q)$-Euler numbers and polynomials.

2. Carlitz-Type Higher-Order Degenerate $(p,q)$-Euler Numbers and Polynomials

At first, the Carlitz-type higher-order degenerate $(p,q)$-Euler numbers and polynomials are defined like this:

Definition 1.

For positive integer n and $r\in \mathbb{N}$, the classical higher-order Euler numbers ${\mathcal{E}}_n^{(r)}(\lambda )$ and Euler polynomials ${\mathcal{E}}_n^{(r)}(x,\lambda )$ are defined by using generating functions

$${\left(\frac{2}{{(1+\lambda t)}^{\frac{1}{\lambda }}+1}\right)}^r=\sum _{n=0}^{\infty }{\mathcal{E}}_n^{(r)}(\lambda )\frac{t^n}{n!},$$

and

$${\left(\frac{2}{{(1+\lambda t)}^{\frac{1}{\lambda }}+1}\right)}^r{(1+\lambda t)}^{\frac{x}{\lambda }}=\sum _{n=0}^{\infty }{\mathcal{E}}_n^{(r)}(x,\lambda )\frac{t^n}{n!},$$

respectively (see [9,12]).

Now, new generalizations of the Carlitz-type degenerate $(p,q)$-Euler numbers and polynomials are introduced. As we have done so far, the Carlitz-type higher-order $(p,q)$-Euler polynomials can be defined as:

Definition 2.

For $r\in \mathbb{N}$, the Carlitz-type higher-order degenerate $(p,q)$-Euler numbers ${\mathcal{E}}_{n,p,q}^{(r)}(\lambda )$ and polynomials ${\mathcal{E}}_{n,p,q}^{(r)}(x,\lambda )$ are defined by using generating functions, where $0<q<p\le 1$.

$$\sum _{n=0}^{\infty }{\mathcal{E}}_{n,p,q}^{(r)}(\lambda ){\displaystyle \frac{t^n}{n!}}={\left[2\right]}_q^r\sum _{m_1,\cdots ,m_r=0}^{\infty }{(-1)}^{m_1+\cdots +m_r}{q}^{m_1+\cdots +m_r}{(1+\lambda t)}^{{\displaystyle \frac{{[m_1+\cdots +m_r]}_{p,q}}{\lambda }}},$$

and

$$\sum _{n=0}^{\infty }{\mathcal{E}}_{n,p,q}^{(r)}(x,\lambda ){\displaystyle \frac{t^n}{n!}}={\left[2\right]}_q^r\sum _{m_1,\cdots ,m_r=0}^{\infty }{(-1)}^{m_1+\cdots +m_r}{q}^{m_1+\cdots +m_r}{(1+\lambda t)}^{{\displaystyle \frac{{[m_1+\cdots +m_r+x]}_{p,q}}{\lambda }}},$$

respectively.

Observe that, if $p=1,q\to 1$, then ${\mathcal{E}}_{n,p,q}^{(r)}(\lambda )\to {\mathcal{E}}_n^{(r)}(\lambda )$ and ${\mathcal{E}}_{n,p,q}^{(r)}(x,\lambda )\to {\mathcal{E}}_n^{(r)}(x,\lambda )$. Note that, if $r=1$, then ${\mathcal{E}}_{n,p,q}^{(r)}(\lambda )={\mathcal{E}}_{n,p,q}(\lambda )$ and ${\mathcal{E}}_{n,p,q}^{(r)}(x)={\mathcal{E}}_{n,p,q}(x)$. If $\lambda =0$, we have the Carlitz-type higher-order $(p,q)$-Euler polynomials $E_{n,p,q}^{(r)}(x)$.

By binomial theorem, we note that

$$\begin{array}{l}{(1+\lambda t)}^{{\displaystyle \frac{{[m_1+\cdots +m_r+x]}_{p,q}}{\lambda }}}\\ ={\displaystyle \sum _{k=0}^{\infty }}\left(\genfrac{}{}{0pt}{}{{[m_1+\cdots +m_r+x]}_{p,q}}{k}\right){\lambda }^k{t}^k\\ ={\displaystyle \sum _{k=0}^{\infty }}{\left({\displaystyle \frac{1}{\lambda }}{[m_1+\cdots +m_r+x]}_{p,q}\right)}_k{\lambda }^k{\displaystyle \frac{t^k}{k!}}\\ ={\displaystyle \sum _{k=0}^{\infty }}\left({\displaystyle \frac{1}{\lambda }}{[m_1+\cdots +m_r+x]}_{p,q}\right)\left({\displaystyle \frac{1}{\lambda }}{[m_1+\cdots +m_r+x]}_{p,q}-1\right)\\ \cdots \left({\displaystyle \frac{1}{\lambda }}{[m_1+\cdots +m_r+x]}_{p,q}-(k-1)\right){\lambda }^k{\displaystyle \frac{t^k}{k!}}\\ ={\displaystyle \sum _{k=0}^{\infty }}\left({[m_1+\cdots +m_r+x]}_{p,q}\right)\left({[m_1+\cdots +m_r+x]}_{p,q}-\lambda \right)\\ \cdots \left({[m_1+\cdots +m_r+x]}_{p,q}-(k-1)\lambda \right){\displaystyle \frac{t^k}{k!}}\\ ={\displaystyle \sum _{k=0}^{\infty }}{\left({[m_1+\cdots +m_r+x]}_{p,q}|\lambda \right)}_k{\displaystyle \frac{t^k}{k!}},\end{array}$$

(3)

where generalized $(p,q)$-falling factorial ${\left({\left[x\right]}_{p,q}|\lambda \right)}_k={\left[x\right]}_{p,q}({\left[x\right]}_{p,q}-\lambda )\cdots ({\left[x\right]}_{p,q}-(k-1)\lambda )$. By Definition 2, we have the theorem below.

Theorem 1.

If $r\in \mathbb{N}$, we have

$${\mathcal{E}}_{n,p,q}^{(r)}(x,\lambda )={\left[2\right]}_q^r{\displaystyle \sum _{m_1,\cdots ,m_r=0}^{\infty }}{(-1)}^{m_1+\cdots +m_r}{q}^{m_1+\cdots +m_r}{\left({[m_1+\cdots +m_r+x]}_{p,q}|\lambda \right)}_n.$$

Proof. 

By (3), we have

$$\begin{array}{ll}{\displaystyle \sum _{l=0}^{\infty }}{\mathcal{E}}_{l,p,q}^{(r)}(x,\lambda ){\displaystyle \frac{t^l}{l!}}& ={\left[2\right]}_q^r{\displaystyle \sum _{m_1,\cdots ,m_r=0}^{\infty }}{(-1)}^{m_1+\cdots +m_r}{q}^{m_1+\cdots +m_r}{(1+\lambda t)}^{{\displaystyle \frac{{[m_1+\cdots +m_r+x]}_{p,q}}{\lambda }}}\\ & ={\displaystyle \sum _{l=0}^{\infty }}\left({\left[2\right]}_q^r{\displaystyle \sum _{m_1,\cdots ,m_r=0}^{\infty }}{(-1)}^{m_1+\cdots +m_r}{q}^{m_1+\cdots +m_r}{\left({[m_1+\cdots +m_r+x]}_{p,q}|\lambda \right)}_l\right){\displaystyle \frac{t^l}{l!}}.\end{array}$$

The first part of the theorem follows when we compare the coefficients of $\frac{t^l}{l!}$ in the above equation. We prove Theorem 1. □

Note that

$${\left({[m_1+\cdots +m_r+x]}_{p,q}|\lambda \right)}_n={\displaystyle \sum _{l=0}^n}{S}_1(n,l){\lambda }^{n-l}{[m_1+\cdots +m_r+x]}_{p,q}^l,$$

(4)

where $S_1(n,l)$ is the Stirling numbers of the first kind.

The relation between Carlitz-type high order degenerate $(p,q)$-Euler polynomials ${\mathcal{E}}_{n,p,q}^{(r)}(x,\lambda )$ and Carlitz-type high order $(p,q)$-Euler polynomials $E_{n,p,q}^{(r)}(x)$ is given by the below theorem.

Theorem 2.

For $r\in \mathbb{N}$ and $n\in {\mathbb{Z}}_{+}$, we have

$${\mathcal{E}}_{n,p,q}^{(r)}(x,\lambda )={\displaystyle \sum _{l=0}^n}{S}_1(n,l){\lambda }^{n-l}{E}_{l,p,q}^{(r)}(x),{\mathcal{E}}_{n,p,q}^{(r)}(\lambda )={\displaystyle \sum _{l=0}^n}{S}_1(n,l){\lambda }^{n-l}{E}_{l,p,q}^{(r)}.$$

Proof. 

By Theorem 1, (2), and (4), we get

$$\begin{array}{ll}{\mathcal{E}}_{n,p,q}^{(r)}(x,\lambda )& ={\displaystyle \sum _{l=0}^n}{S}_1(n,l){\lambda }^{n-l}{\left[2\right]}_q^r{\displaystyle \sum _{m_1,\cdots ,m_r=0}^{\infty }}{(-1)}^{m_1+\cdots +m_r}{q}^{m_1+\cdots +m_r}{[m_1+\cdots +m_r+x]}_{p,q}^l\\ & ={\displaystyle \sum _{l=0}^n}{S}_1(n,l){\lambda }^{n-l}{E}_{l,p,q}^{(r)}(x).\end{array}$$

One can obtain the desired result immediately. □

The Carlitz-type higher-order degenerate $(p,q)$-Euler number ${\mathcal{E}}_{n,p,q}(\lambda )$ can be determined explicitly. A few of them are

$$\begin{array}{l}{\mathcal{E}}_{0,p,q}^{(r)}(\lambda )=1,\\ {\mathcal{E}}_{1,p,q}^{(r)}(\lambda )={\displaystyle \frac{{\left[2\right]}_q^r}{p-q}}{\left({\displaystyle \frac{1}{1+pq}}\right)}^r-{\displaystyle \frac{{\left[2\right]}_q}{p-q}}{\left({\displaystyle \frac{1}{1+q^2}}\right)}^r,\\ {\mathcal{E}}_{2,p,q}^{(r)}(\lambda )=-{\displaystyle \frac{{\left[2\right]}_q^r\lambda }{p-q}}{\left({\displaystyle \frac{1}{1+pq}}\right)}^r+{\displaystyle \frac{{\left[2\right]}_q}{{(p-q)}^2}}{\left({\displaystyle \frac{1}{1+p^{2}q}}\right)}^r+{\displaystyle \frac{{\left[2\right]}_q^r\lambda }{p-q}}{\left({\displaystyle \frac{1}{1+q^2}}\right)}^r\\ -{\displaystyle \frac{2{\left[2\right]}_q^r}{{(p-q)}^2}}{\left({\displaystyle \frac{1}{1+p{q}^2}}\right)}^r+{\displaystyle \frac{{\left[2\right]}_q^r}{{(p-q)}^2}}{\left({\displaystyle \frac{1}{1+q^3}}\right)}^r,\\ {\mathcal{E}}_{3,p,q}^{(r)}(\lambda )={\displaystyle \frac{2{\left[2\right]}_q^r{\lambda }^2}{(p-q)}}{\left({\displaystyle \frac{1}{1+pq}}\right)}^r-{\displaystyle \frac{3{\left[2\right]}_q^r\lambda }{{(p-q)}^2}}{\left({\displaystyle \frac{1}{1+p^{2}q}}\right)}^r+{\displaystyle \frac{{\left[2\right]}_q^r}{{(p-q)}^3}}{\left({\displaystyle \frac{1}{1+p^{3}q}}\right)}^r\\ -{\displaystyle \frac{2{\left[2\right]}_q^r{\lambda }^2}{(p-q)}}{\left({\displaystyle \frac{1}{1+q^2}}\right)}^r+{\displaystyle \frac{6{\left[2\right]}_q^r\lambda }{{(p-q)}^2}}{\left({\displaystyle \frac{1}{1+p{q}^2}}\right)}^r-{\displaystyle \frac{3{\left[2\right]}_q^r}{{(p-q)}^3}}{\left({\displaystyle \frac{1}{1+p^2{q}^2}}\right)}^r\\ -{\displaystyle \frac{3{\left[2\right]}_q^r\lambda }{{(p-q)}^2}}{\left({\displaystyle \frac{1}{1+q^3}}\right)}^r+{\displaystyle \frac{3{\left[2\right]}_q^r}{{(p-q)}^3}}{\left({\displaystyle \frac{1}{1+p{q}^3}}\right)}^r-{\displaystyle \frac{{\left[2\right]}_q^r}{{(p-q)}^3}}{\left({\displaystyle \frac{1}{1+q^4}}\right)}^r.\end{array}$$

By using computer, Carlitz-type higher-order degenerate $(p,q)$-Euler number ${\mathcal{E}}_{n,p,q}^{(r)}(\lambda )$ can be determined explicitly. The first few ${\mathcal{E}}_{n,p,q}^{(r)}(\lambda )$ and $E_{n,p,q}^{(r)}$ are listed in

Table 1. The first few numbers ${\mathcal{E}}_{n,p,q}^{(r)}(\lambda )$ and $E_{n,p,q}^{(r)}$.

Degree n	${\mathcal{E}}_{\mathit{n},1/2,1/3}^{(2)}\left({\displaystyle \frac{9}{10}}\right)$	${\mathcal{E}}_{\mathit{n},1/2,1/3}^{(2)}\left({\displaystyle \frac{1}{10}}\right)$	${\mathcal{E}}_{\mathit{n},1/2,1/3}^{(2)}\left({\displaystyle \frac{1}{100}}\right)$	${\mathit{E}}_{\mathit{n},1/2,1/3}^{(2)}$
1	$-{\displaystyle \frac{984}{1225}}$	$-{\displaystyle \frac{984}{1225}}$	$-{\displaystyle \frac{984}{1225}}$	$-{\displaystyle \frac{984}{1225}}$
2	$-{\displaystyle \frac{6149664}{53382875}}$	$-{\displaystyle \frac{283179072}{373680125}}$	$-{\displaystyle \frac{1550969286}{1868400625}}$	$-{\displaystyle \frac{2505564}{2989441}}$
3	${\displaystyle \frac{43455323971646694}{520267306514580625}}$	$-{\displaystyle \frac{334418269722928746}{520267306514580625}}$	$-{\displaystyle \frac{11096966497657123158}{13006682662864515625}}$	$-{\displaystyle \frac{152830161504}{174034980625}}$

.

Note that the limit of ${\mathcal{E}}_{n,1/2,1/3}^{(2)}\left(\lambda \right)$ is $E_{n,1/2,1/3}^{(2)}$ as $\lambda$ approaches 0 (see Table 1).

Again, we give a relation between Carlitz-type higher-order $(p,q)$-Euler polynomials $E_{n,p,q}^{(r)}(x)$ and Carlitz-type higher-order degenerate $(p,q)$-Euler polynomials ${\mathcal{E}}_{n,p,q}^{(r)}(x,\lambda )$ in the theorem below.

Theorem 3.

For $m\in Z_{+}$, we have

$$E_{m,p,q}^{(r)}(x)={\displaystyle \sum _{n=0}^m}{\mathcal{E}}_{n,p,q}^{(r)}(x,\lambda ){\lambda }^{m-n}{S}_2(m,n).$$

Proof. 

We use t instead of ${\displaystyle \frac{e^{\lambda t}-1}{\lambda }}$ in Definition 2, we have

$$\begin{array}{ll}{\displaystyle \sum _{m=0}^{\infty }}{E}_{m,p,q}^{(r)}(x){\displaystyle \frac{t^m}{m!}}& ={\left[2\right]}_q^r{\displaystyle \sum _{m_1,\cdots ,m_r=0}^{\infty }}{(-1)}^{m_1+\cdots +m_r}{q}^{m_1+\cdots +m_r}{e}^{{[m_1+\cdots +m_r+x]}_{p,q}t}\\ & ={\displaystyle \sum _{n=0}^{\infty }}{\mathcal{E}}_{n,p,q}^{(r)}(x,\lambda ){\left({\displaystyle \frac{e^{\lambda t}-1}{\lambda }}\right)}^n{\displaystyle \frac{1}{n!}}\\ & ={\displaystyle \sum _{n=0}^{\infty }}{\mathcal{E}}_{n,p,q}^{(r)}(x,\lambda ){\lambda }^{-n}{\displaystyle \sum _{m=n}^{\infty }}{S}_2(m,n){\lambda }^m{\displaystyle \frac{t^m}{m!}}\\ & ={\displaystyle \sum _{m=0}^{\infty }}\left({\displaystyle \sum _{n=0}^m}{\mathcal{E}}_{n,p,q}^{(r)}(x,\lambda ){\lambda }^{m-n}{S}_2(m,n)\right){\displaystyle \frac{t^m}{m!}}.\end{array}$$

Use t instead of $log{(1+\lambda t)}^{1/\lambda }$ in (1), we have

$$\begin{array}{l}{\displaystyle \sum _{n=0}^{\infty }}{E}_{n,p,q}^{(r)}(x){\left(log{(1+\lambda t)}^{1/\lambda }\right)}^n{\displaystyle \frac{1}{n!}}\\ ={\left[2\right]}_q^r{\displaystyle \sum _{m_1,\cdots ,m_r=0}^{\infty }}{(-1)}^{m_1+\cdots +m_r}{q}^{m_1+\cdots +m_r}{(1+\lambda t)}^{{\displaystyle \frac{{[m_1+\cdots +m_r+x]}_{p,q}}{\lambda }}}\\ ={\displaystyle \sum _{m=0}^{\infty }}{\mathcal{E}}_{m,p,q}^{(r)}(x,\lambda ){\displaystyle \frac{t^m}{m!}},\end{array}$$

(5)

and

$${\displaystyle \sum _{n=0}^{\infty }}{E}_{n,p,q}^{(r)}(x){\left(log{(1+\lambda t)}^{1/\lambda }\right)}^n{\displaystyle \frac{1}{n!}}={\displaystyle \sum _{m=0}^{\infty }}\left({\displaystyle \sum _{n=0}^m}{E}_{n,p,q}^{(r)}(x){\lambda }^{m-n}{S}_1(m,n)\right){\displaystyle \frac{t^m}{m!}}.$$

(6)

Thus, we have the theorem below from $(5)$ and $(6)$. □

Theorem 4.

For $m\in Z_{+}$, we have

$${\mathcal{E}}_{m,p,q}^{(r)}(x,\lambda )={\displaystyle \sum _{n=0}^m}{E}_{n,p,q}^{(r)}(x){\lambda }^{m-n}{S}_1(m,n).$$

We note that

$$\begin{array}{l}{\left(1+\lambda t\right)}^{{\displaystyle \frac{{[m_1+\cdots +m_r+x]}_{p,q}}{\lambda }}}\\ ={(1+\lambda t)}^{{\displaystyle \frac{p^x{[m_1+\cdots +m_r]}_{p,q}}{\lambda }}}{(1+\lambda t)}^{{\displaystyle \frac{q^{m_1+\cdots +m_r}{\left[x\right]}_{p,q}}{\lambda }}}\\ ={\displaystyle \sum _{m=0}^{\infty }}{(p^x{[m_1+\cdots +m_r]}_{p,q}|\lambda )}_m{\displaystyle \frac{t^m}{m!}}{e}^{log{(1+\lambda t)}^{{\displaystyle \frac{q^{m_1+\cdots +m_r}{\left[x\right]}_{p,q}}{\lambda }}}}\\ ={\displaystyle \sum _{m=0}^{\infty }}{(p^x{[m_1+\cdots +m_r]}_{p,q}|\lambda )}_m{\displaystyle \frac{t^m}{m!}}{\displaystyle \sum _{l=0}^{\infty }}{\left({\displaystyle \frac{q^{m_1+\cdots +m_r}{\left[x\right]}_{p,q}}{\lambda }}\right)}^l{\displaystyle \frac{log{(1+\lambda t)}^l}{l!}}\\ ={\displaystyle \sum _{m=0}^{\infty }}{(p^x{[m_1+\cdots +m_r]}_{p,q}|\lambda )}_m{\displaystyle \frac{t^m}{m!}}{\displaystyle \sum _{l=0}^{\infty }}{\left({\displaystyle \frac{q^{m_1+\cdots +m_r}{\left[x\right]}_{p,q}}{\lambda }}\right)}^l{\displaystyle \sum _{k=l}^{\infty }}{S}_1(k,l){\lambda }^k{\displaystyle \frac{t^k}{k!}}\\ ={\displaystyle \sum _{n=0}^{\infty }}\left({\displaystyle \sum _{k=0}^n}{\displaystyle \sum _{l=0}^k}\left(\genfrac{}{}{0pt}{}{n}{k}\right){(p^x{[m_1+\cdots +m_r]}_{p,q}|\lambda )}_{n-k}{\lambda }^{k-l}{q}^{(m_1+\cdots +m_r)l}{\left[x\right]}_{p,q}^l{S}_1(k,l)\right){\displaystyle \frac{t^n}{n!}}.\end{array}$$

(7)

By Definition 2 and (7), we get

$$\begin{array}{l}{\displaystyle \sum _{n=0}^{\infty }}{\mathcal{E}}_{n,p,q\zeta }^{(r)}(x,\lambda )\frac{t^n}{n!}\\ ={\left[2\right]}_q^r{\displaystyle \sum _{m_1,\cdots ,m_r=0}^{\infty }}{(-1)}^{m_1+\cdots +m_r}{q}^{m_1+\cdots +m_r}{\left(1+\lambda t\right)}^{{\displaystyle \frac{{[m_1+\cdots +m_r+x]}_{p,q}}{\lambda }}}\\ ={\left[2\right]}_q^r{\displaystyle \sum _{m_1,\cdots ,m_r=0}^{\infty }}{(-1)}^{m_1+\cdots +m_r}{q}^{m_1+\cdots +m_r}\\ \times {\displaystyle \sum _{n=0}^{\infty }}\left({\displaystyle \sum _{k=0}^n}{\displaystyle \sum _{l=0}^k}\left(\genfrac{}{}{0pt}{}{n}{k}\right){(p^x{[m_1+\cdots +m_r]}_{p,q}|\lambda )}_{n-k}{\lambda }^{k-l}{q}^{(m_1+\cdots +m_r)l}{\left[x\right]}_{p,q}^l{S}_1(k,l)\right){\displaystyle \frac{t^n}{n!}}.\end{array}$$

When we compare the coefficients of $\frac{t^n}{n!}$ in the above equation, we have the theorem below.

Theorem 5.

For $0<q<p\le 1$, $r\in \mathbb{N}$, and $n\in Z_{+}$,

$$\begin{array}{l}{\mathcal{E}}_{n,p,q}^{(r)}(x,\lambda )={\left[2\right]}_q^r{\displaystyle \sum _{m_1,\cdots ,m_r=0}^{\infty }}{\displaystyle \sum _{k=0}^n}{\displaystyle \sum _{l=0}^k}\left(\genfrac{}{}{0pt}{}{n}{k}\right){(-1)}^{m_1+\cdots +m_r}{q}^{m_1+\cdots +m_r}\\ \times {(p^x{[m_1+\cdots +m_r]}_{p,q}|\lambda )}_{n-k}{\lambda }^{k-l}{q}^{(m_1+\cdots +m_r)l}{\left[x\right]}_{p,q}^l{S}_1(k,l).\end{array}$$

From (4) and Theorem 2, we get this:

$$\begin{array}{l}{\displaystyle \sum _{n=0}^{\infty }}{\mathcal{E}}_{n,p,q}^{(r)}(x,\lambda )\frac{t^n}{n!}\\ ={\left[2\right]}_q^r{\displaystyle \sum _{m_1,\cdots ,m_r=0}^{\infty }}{(-1)}^{m_1+\cdots +m_r}{q}^{m_1+\cdots +m_r}{\left(1+\lambda t\right)}^{{\displaystyle \frac{{[m_1+\cdots +m_r+x]}_{p,q}}{\lambda }}}\\ ={\left[2\right]}_q^r{\displaystyle \sum _{m_1,\cdots ,m_r=0}^{\infty }}{(-1)}^{m_1+\cdots +m_r}{q}^{m_1+\cdots +m_r}\\ \times {\displaystyle \sum _{n=0}^{\infty }}{\displaystyle \sum _{l=0}^n}{S}_1(n,l){\lambda }^{n-l}{\displaystyle \frac{{\sum }_{j=0}^l\left(\genfrac{}{}{0pt}{}{l}{j}\right){(-1)}^j{p}^{x(l-j)}{q}^{xj}}{{(p-q)}^l}}{p}^{(l-j)(m_1+\cdots +m_r)}{q}^{j(m_1+\cdots +m_r)}\frac{t^n}{n!}\\ ={\displaystyle \sum _{n=0}^{\infty }}\left({\left[2\right]}_q^r{\displaystyle \sum _{l=0}^n}{\displaystyle \sum _{j=0}^l}{\displaystyle \frac{S_1(n,l){\lambda }^{n-l}\left(\genfrac{}{}{0pt}{}{l}{j}\right){(-1)}^j{q}^{xj}{p}^{x(l-j)}}{{(p-q)}^l}}{\left({\displaystyle \frac{1}{1+q^{j+1}{p}^{l-j}}}\right)}^r\right)\frac{t^n}{n!}.\end{array}$$

When we compare the coefficients $\frac{t^n}{n!}$ in the above equation, we get the theorem.

Theorem 6.

For $r\in \mathbb{N}$ and $n\in Z_{+}$,

$$\begin{array}{l}{\mathcal{E}}_{n,p,q}^{(r)}(x,\lambda )={\left[2\right]}_q^r{\displaystyle \sum _{l=0}^n}{\displaystyle \sum _{j=0}^l}{\displaystyle \frac{S_1(n,l){\lambda }^{n-l}\left(\genfrac{}{}{0pt}{}{l}{j}\right){(-1)}^j{q}^{xj}{p}^{x(l-j)}}{{(p-q)}^l}}{\left({\displaystyle \frac{1}{1+q^{j+1}{p}^{l-j}}}\right)}^r,\\ {\mathcal{E}}_{n,p,q}^{(r)}(\lambda )={\left[2\right]}_q^r{\displaystyle \sum _{l=0}^n}{\displaystyle \sum _{j=0}^l}{\displaystyle \frac{S_1(n,l){\lambda }^{n-l}\left(\genfrac{}{}{0pt}{}{l}{j}\right){(-1)}^j}{{(p-q)}^l}}{\left({\displaystyle \frac{1}{1+q^{j+1}{p}^{l-j}}}\right)}^r.\end{array}$$

The Carlitz-type high order degenerate $(p,q)$-Euler polynomials ${\mathcal{E}}_{n,p,q}(x,\lambda )$ can be determined explicitly. Here are a few of them:

$$\begin{array}{l}{\mathcal{E}}_{0,p,q}^{(r)}(x,\lambda )=1,\\ {\mathcal{E}}_{1,p,q}^{(r)}(x,\lambda )={\displaystyle \frac{{\left[2\right]}_q^r{p}^x}{p-q}}{\left({\displaystyle \frac{1}{1+pq}}\right)}^r-{\displaystyle \frac{{\left[2\right]}_q^r{q}^x}{p-q}}{\left({\displaystyle \frac{1}{1+q^2}}\right)}^r,\\ {\mathcal{E}}_{2,p,q}^{(r)}(x,\lambda )=-{\displaystyle \frac{{\left[2\right]}_q^r\lambda p^x}{p-q}}{\left({\displaystyle \frac{1}{1+pq}}\right)}^r+{\displaystyle \frac{{\left[2\right]}_q^r{p}^{2x}}{{(p-q)}^2}}{\left({\displaystyle \frac{1}{1+p^{2}q}}\right)}^r+{\displaystyle \frac{{\left[2\right]}_q^r\lambda q^x}{p-q}}{\left({\displaystyle \frac{1}{1+q^2}}\right)}^r\\ -{\displaystyle \frac{2{\left[2\right]}_q^r{p}^x{q}^x}{{(p-q)}^2}}{\left({\displaystyle \frac{1}{1+p{q}^2}}\right)}^r+{\displaystyle \frac{{\left[2\right]}_q^r{q}^{2x}}{{(p-q)}^2}}{\left({\displaystyle \frac{1}{1+q^3}}\right)}^r,\\ {\mathcal{E}}_{3,p,q}^{(r)}(x,\lambda )={\displaystyle \frac{2{\left[2\right]}_q^r{\lambda }^2{p}^x}{p-q}}{\left({\displaystyle \frac{1}{1+pq}}\right)}^r-{\displaystyle \frac{3{\left[2\right]}_q^r\lambda p^{2x}}{{(p-q)}^2}}{\left({\displaystyle \frac{1}{1+p^{2}q}}\right)}^r+{\displaystyle \frac{{\left[2\right]}_q^r{p}^{3x}}{{(p-q)}^3}}{\left({\displaystyle \frac{1}{1+p^{3}q}}\right)}^r\\ -{\displaystyle \frac{2{\left[2\right]}_q^r{\lambda }^2{q}^x}{p-q}}{\left({\displaystyle \frac{1}{1+q^2}}\right)}^r+{\displaystyle \frac{6{\left[2\right]}_q^r\lambda p^x{q}^x}{{(p-q)}^2}}{\left({\displaystyle \frac{1}{1+p{q}^2}}\right)}^r-{\displaystyle \frac{3{\left[2\right]}_q^r{p}^{2x}{q}^x}{{(p-q)}^3}}{\left({\displaystyle \frac{1}{1+p^2{q}^2}}\right)}^r\\ -{\displaystyle \frac{3{\left[2\right]}_q^r\lambda q^{2x}}{{(p-q)}^2}}{\left({\displaystyle \frac{1}{1+q^3}}\right)}^r+{\displaystyle \frac{3{\left[2\right]}_q^r{p}^x{q}^{2x}}{{(p-q)}^3}}{\left({\displaystyle \frac{1}{1+p{q}^3}}\right)}^r-{\displaystyle \frac{{\left[2\right]}_q^r{q}^{3x}}{{(p-q)}^3}}{\left({\displaystyle \frac{1}{1+q^4}}\right)}^r.\end{array}$$

3. Some Symmetric Identities for Carlitz-Type Higher-Order Degenerate $(p,q)$-Euler Numbers and Polynomials

Let $w_1\equiv 1(\mathrm{mod}2)$, $w_2\equiv 1(\mathrm{mod}2)$ for $w_1,w_2\in N$. For $r\in N$ and $n\in Z_{+}$, we obtain certain symmetry identities for Carlitz-type higher-order degenerate $(p,q)$-Euler numbers and polynomials.

Theorem 7.

Let $w_1\equiv 1(\mathrm{mod}2)$, $w_2\equiv 1(\mathrm{mod}2)$ for $w_1,w_2\in N$. Then, we obtain

$$\begin{array}{l}{\left[w_1\right]}_{p,q}^n{\left[2\right]}_{q^{w_2}}^r{\displaystyle \sum _{j_1,\cdots ,j_r=0}^{w_1-1}}{(-1)}^{j_1+\cdots +j_r}{q}^{w_2(j_1+\cdots +j_r)}\\ \times {\mathcal{E}}_{n,p^{w_1}{q}^{w_1}}^{(r)}\left(w_{2}x+{\displaystyle \frac{w_2}{w_1}}(j_1+\cdots +j_r),{\displaystyle \frac{\lambda }{{\left[w_1\right]}_{p,q}}}\right)\\ ={\left[w_2\right]}_{p,q}^n{\left[2\right]}_{q^{w_1}}^r{\displaystyle \sum _{j_1,\cdots ,j_r=0}^{w_2-1}}{(-1)}^{j_1+\cdots +j_r}{q}^{w_1(j_1+\cdots +j_r)}\\ \times {\mathcal{E}}_{n,p^{w_2},q^{w_2}}^{(r)}\left(w_{1}x+{\displaystyle \frac{w_1}{w_2}}(j_1+\cdots +j_r),{\displaystyle \frac{\lambda }{{\left[w_2\right]}_{p,q}}}\right).\end{array}$$

(8)

Proof. 

Note that ${\left[xy\right]}_{p,q}={\left[x\right]}_{p^y,q^y}{\left[y\right]}_{p,q}$ for any $x,y\in \mathbb{C}$. In Definition 2, we induce the next result by substituting $w_{1}x+{\displaystyle \frac{w_1}{w_2}}(j_1+\cdots +j_r)$ instead of x and replace q, p, and $\lambda$ by $q^{w_2}$, $p^{w_2}$, and ${\displaystyle \frac{\lambda }{{\left[w_2\right]}_{p,q}}}$, respectively:

$$\begin{array}{l}{\displaystyle \sum _{n=0}^{\infty }}\left({\left[w_2\right]}_{p,q}^n{\left[2\right]}_{q^{w_1}}^r{\displaystyle \sum _{j_1,\cdots ,j_r=0}^{w_2-1}}{(-1)}^{{\sum }_{l=1}^r{j}_l}{q}^{w_1({\sum }_{l=1}^r{j}_l)}{\mathcal{E}}_{n,p^{w_2},q^{w_2}}^{(r)}\left(w_{1}x+{\displaystyle \frac{w_1}{w_2}}({\displaystyle \sum _{l=1}^r}{j}_l),{\displaystyle \frac{\lambda }{{\left[w_2\right]}_{p,q}}}\right)\right){\displaystyle \frac{t^n}{n!}}\\ ={\left[2\right]}_{q^{w_1}}^r{\displaystyle \sum _{j_1,\cdots ,j_r=0}^{w_2-1}}{(-1)}^{{\sum }_{l=1}^r{j}_l}{q}^{w_1({\sum }_{l=1}^r{j}_l)}{\displaystyle \sum _{n=0}^{\infty }}{\mathcal{E}}_{n,p^{w_2},q^{w_2}}^{(r)}\left(w_{1}x+{\displaystyle \frac{w_1}{w_2}}({\displaystyle \sum _{l=1}^r}{j}_l),{\displaystyle \frac{\lambda }{{\left[w_2\right]}_{p,q}}}\right){\displaystyle \frac{{({\left[w_2\right]}_{p,q}t)}^n}{n!}}\\ ={\left[2\right]}_{q^{w_1}}^r{\displaystyle \sum _{j_1,\cdots ,j_r=0}^{w_2-1}}{(-1)}^{{\sum }_{l=1}^r{j}_l}{q}^{w_1({\sum }_{l=1}^r{j}_l)}{\left[2\right]}_{q^{w_2}}^r{\displaystyle \sum _{m_1,\cdots ,m_r=0}^{\infty }}{(-1)}^{m_1+\cdots +m_r}{q}^{w_2(m_1+\cdots +m_r)}\\ \times {\left(1+{\displaystyle \frac{\lambda }{{\left[w_2\right]}_{p,q}}}{\left[w_2\right]}_{p,q}t\right)}^{{\displaystyle \frac{{\left[w_{1}x+w_{1}x+{\displaystyle \frac{w_1}{w_2}}(j_1+\cdots +j_r)+m_1+\cdots +m_r\right]}_{p^{w_2},q^{w_2}}}{\frac{\lambda }{{\left[w_2\right]}_{p,q}}}}}\\ ={\left[2\right]}_{q^{w_1}}^r{\displaystyle \sum _{j_1,\cdots ,j_r=0}^{w_2-1}}{(-1)}^{{\sum }_{l=1}^r{j}_l}{q}^{w_1({\sum }_{l=1}^r{j}_l)}{\left[2\right]}_{q^{w_2}}^r{\displaystyle \sum _{m_1,\cdots ,m_r=0}^{\infty }}{(-1)}^{m_1+\cdots +m_r}{q}^{w_2(m_1+\cdots +m_r)}\\ \times {\left(1+\lambda t\right)}^{{\displaystyle \frac{{[w_1{w}_{2}x+w_1(j_1+\cdots +j_r)+w_2(m_1+\cdots m_r)]}_{p,q}}{\lambda }}}.\end{array}$$

Since there exists the unique non-negative integer n such that $m=wn+i$ with $0\le i\le w-1$ for any non-negative integer m and odd positive integer w, this can be written

$$\begin{array}{l}{\left[2\right]}_{q^{w_1}}^r{\left[2\right]}_{q^{w_2}}^r{\displaystyle \sum _{j_1,\cdots ,j_r=0}^{w_2-1}}{(-1)}^{{\sum }_{l=1}^r{j}_l}{q}^{w_1({\sum }_{l=1}^r{j}_l)}{\displaystyle \sum _{m_1,\cdots ,m_r=0}^{\infty }}{(-1)}^{m_1+\cdots +m_r}{q}^{w_2(m_1+\cdots +m_r)}\\ \times {\left(1+\lambda t\right)}^{{\displaystyle \frac{{[w_1{w}_{2}x+w_1(j_1+\cdots +j_r)+w_2(m_1+\cdots m_r)]}_{p,q}}{\lambda }}}\\ ={\left[2\right]}_{q^{w_1}}^r{\left[2\right]}_{q^{w_2}}^r{\displaystyle \sum _{j_1,\cdots ,j_r=0}^{w_2-1}}{(-1)}^{{\sum }_{l=1}^r{j}_l}{q}^{w_1({\sum }_{l=1}^r{j}_l)}\\ \times {\displaystyle \sum _{\begin{array}{c}{w}_1{n}_1+i_1,\cdots ,w_1{n}_r+i_r=0\\ 0\le i_k\le w_1-1\\ 1\le k\le r\end{array}}^{\infty }}{(-1)}^{w_1{n}_1+i_1+\cdots +w_1{n}_r+i_r}{q}^{w_2(w_1{n}_1+i_1+\cdots +w_1{n}_r+i_r)}\\ \times {\left(1+\lambda t\right)}^{{\displaystyle \frac{{[w_1{w}_{2}x+w_1(j_1+\cdots +j_r)+w_2{w}_1(n_1+\cdots +n_r)+w_2(i_1+\cdots +i_r)]}_{p,q}}{\lambda }}}\\ ={\left[2\right]}_{q^{w_1}}^r{\left[2\right]}_{q^{w_2}}^r{\displaystyle \sum _{j_1,\cdots ,j_r=0}^{w_2-1}}{(-1)}^{{\sum }_{l=1}^r{j}_l}{q}^{w_1({\sum }_{l=1}^r{j}_l)}\\ \times {\displaystyle \sum _{i_1,\cdots ,i_r=0}^{w_1-1}}{\displaystyle \sum _{n_1,\cdots ,n_r=0}^{\infty }}{(-1)}^{{\sum }_{l=1}^r{n}_l}{(-1)}^{{\sum }_{l=1}^r{i}_l}{q}^{w_2({\sum }_{l=1}^r{i}_l)}{q}^{w_1{w}_2({\sum }_{l=1}^r{n}_l)}\\ \times {\left(1+\lambda t\right)}^{{\displaystyle \frac{{[w_1{w}_{2}x+w_1(j_1+\cdots +j_r)+w_2{w}_1(n_1+\cdots +n_r)+w_2(i_1+\cdots +i_r)]}_{p,q}}{\lambda }}}.\end{array}$$

We obtain the following formula using the formula above:

$$\begin{array}{l}{\displaystyle \sum _{n=0}^{\infty }}\left({\left[w_2\right]}_{p,q}^n{\left[2\right]}_{q^{w_1}}^r{\displaystyle \sum _{j_1,\cdots ,j_r=0}^{w_2-1}}{(-1)}^{{\sum }_{l=1}^r{j}_l}{q}^{w_1({\sum }_{l=1}^r{j}_l)}{\mathcal{E}}_{n,p^{w_2},q^{w_2}}^{(r)}\left(w_{1}x+{\displaystyle \frac{w_1}{w_2}}({\displaystyle \sum _{l=1}^r}{j}_l),{\displaystyle \frac{\lambda }{{\left[w_2\right]}_{p,q}}}\right)\right){\displaystyle \frac{t^n}{n!}}\\ ={\left[2\right]}_{q^{w_1}}^r{\left[2\right]}_{q^{w_2}}^r{\displaystyle \sum _{n_1,\cdots ,n_r=0}^{\infty }}{\displaystyle \sum _{j_1,\cdots ,j_r=0}^{w_2-1}}{\displaystyle \sum _{i_1,\cdots ,i_r=0}^{w_1-1}}{(-1)}^{{\sum }_{l=1}^r{j}_l}{(-1)}^{{\sum }_{l=1}^r{n}_l}{(-1)}^{{\sum }_{l=1}^r{i}_l}\\ \times q^{w_1({\sum }_{l=1}^r{j}_l)}{q}^{w_2({\sum }_{l=1}^r{i}_l)}{q}^{w_1{w}_2({\sum }_{l=1}^r{n}_l)}\\ \times {\left(1+\lambda t\right)}^{{\displaystyle \frac{{[w_1{w}_{2}x+w_1(j_1+\cdots +j_r)+w_2{w}_1(n_1+\cdots +n_r)+w_2(i_1+\cdots +i_r)]}_{p,q}}{\lambda }}}.\end{array}$$

(9)

From a similar approach, we also have that

$$\begin{array}{l}{\displaystyle \sum _{n=0}^{\infty }}\left({\left[w_1\right]}_{p,q}^n{\left[2\right]}_{q^{w_2}}^r{\displaystyle \sum _{j_1,\cdots ,j_r=0}^{w_1-1}}{(-1)}^{{\sum }_{l=1}^r{j}_l}{q}^{w_2({\sum }_{l=1}^r{j}_l)}{\mathcal{E}}_{n,p^{w_1},q^{w_1}}^{(r)}\left(w_{2}x+{\displaystyle \frac{w_2}{w_1}}({\displaystyle \sum _{l=1}^r}{j}_l),{\displaystyle \frac{\lambda }{{\left[w_1\right]}_{p,q}}}\right)\right){\displaystyle \frac{t^n}{n!}}\\ ={\left[2\right]}_{q^{w_2}}^r{\left[2\right]}_{q^{w_1}}^r{\displaystyle \sum _{n_1,\cdots ,n_r=0}^{\infty }}{\displaystyle \sum _{j_1,\cdots ,j_r=0}^{w_1-1}}{\displaystyle \sum _{i_1,\cdots ,i_r=0}^{w_2-1}}{(-1)}^{{\sum }_{l=1}^r{j}_l}{(-1)}^{{\sum }_{l=1}^r{n}_l}{(-1)}^{{\sum }_{l=1}^r{i}_l}\\ \times q^{w_2({\sum }_{l=1}^r{j}_l)}{q}^{w_1({\sum }_{l=1}^r{i}_l)}{q}^{w_1{w}_2({\sum }_{l=1}^r{n}_l)}\\ \times {\left(1+\lambda t\right)}^{{\displaystyle \frac{{[w_1{w}_{2}x+w_2(j_1+\cdots +j_r)+w_2{w}_1(n_1+\cdots +n_r)+w_1(i_1+\cdots +i_r)]}_{p,q}}{\lambda }}}.\end{array}$$

(10)

Therefore, by (9) and (10), we can obtain the desired result. □

Taking $w_2=1$ in Theorem 7, we obtain the following multiplication theorem for Carlitz-type higher-order degenerate $(p,q)$-Euler polynomials.

Theorem 8.

Let $w_1\equiv 1(\mathrm{mod}2)$ for $w_1\in N$. For $r\in N$ and $n\in Z_{+}$, we obtain

$$\begin{array}{l}{\mathcal{E}}_{n,p,q}^{(r)}\left(w_{1}x,\lambda \right)={\displaystyle \frac{{\left[2\right]}_q^r}{{\left[2\right]}_{q^{w_1}}^r}}{\left[w_1\right]}_{p,q}^n{\displaystyle \sum _{j_1,\cdots ,j_r=0}^{w_1-1}}{(-1)}^{j_1+\cdots +j_r}{q}^{j_1+\cdots +j_r}\\ \times {\mathcal{E}}_{n,p^{w_1},q^{w_1}}^{(r)}\left(x+{\displaystyle \frac{j_1+\cdots +j_r}{w_1}},{\displaystyle \frac{\lambda }{{\left[w_1\right]}_{p,q}}}\right).\end{array}$$

(11)

Taking $\lambda =0$ in (11), we get the multiplication theorem for Carlitz-type high order $(p,q)$-Euler polynomials (see [11]).

Corollary 1.

Let $w_1\equiv 1(\mathrm{mod}2)$ for $w_1\in N$. For $n\in Z_{+}$ and $r\in N$, we get

$$\begin{array}{l}{E}_{n,p,q}^{(r)}(w_{1}x)={\displaystyle \frac{{\left[2\right]}_q^r}{{\left[2\right]}_{q^{w_1}}^r}}{\left[w_1\right]}_{p,q}^n{\displaystyle \sum _{j_1,\cdots ,j_r=0}^{w_1-1}}{(-1)}^{j_1+\cdots +j_r}{q}^{j_1+\cdots +j_r}\\ \times E_{n,p^{w_1},q^{w_1}}^{(r)}\left(x+{\displaystyle \frac{j_1+\cdots +j_r}{w_1}}\right).\end{array}$$

For $r=1$ in (10), we have the multiplication theorem for Carlitz-type degenerate $(p,q)$-Euler polynomials (see [4]).

Corollary 2.

Let $w_1\equiv 1(\mathrm{mod}2)$ for $w_1\in N$. For $n\in Z_{+}$,

$${\mathcal{E}}_{n,p,q}(w_{1}x,\lambda )={\displaystyle \frac{{\left[2\right]}_q}{{\left[2\right]}_{q^{w_1}}}}{\left[w_1\right]}_{p,q}^n{\displaystyle \sum _{j=0}^{w_1-1}}{(-1)}^j{q}^j{\mathcal{E}}_{n,p^{w_1},q^{w_1}}\left(x+{\displaystyle \frac{j}{w_1}},{\displaystyle \frac{\lambda }{{\left[w_1\right]}_{p,q}}}\right).$$

If $p=1,q\to 1$ in Corollary 2, then we get the corollary.

Corollary 3.

Let $m\equiv 1(\mathrm{mod}2)$ for $m\in N$. For $n\in Z_{+}$,

$${\mathcal{E}}_n(x,\lambda )=m^n{\displaystyle \sum _{j=0}^{m-1}}{(-1)}^j{q}^j{\mathcal{E}}_n\left({\displaystyle \frac{x+j}{m}},{\displaystyle \frac{\lambda }{m}}\right).$$

(12)

If $\lambda$ approaches to 0 in (12), this leads to the distribution relation for Euler polynomials

$$E_n(x)=m^n{\displaystyle \sum _{j=0}^{m-1}}{(-1)}^j{E}_n\left({\displaystyle \frac{x+i}{m}}\right).$$

By Theorem 2 and Theorem 7, it follows the theorem below.

Theorem 9.

Let $w_1$ and $w_2$ be odd positive integers. Then, it has

$$\begin{array}{l}{\displaystyle \sum _{l=0}^n}{S}_1(n,l){\lambda }^{n-l}{\left[w_1\right]}_{p,q}^l{\left[2\right]}_{q^{w_2}}^r\\ \times {\displaystyle \sum _{j_1,\cdots ,j_r=0}^{w_1-1}}{(-1)}^{j_1+\cdots +j_r}{q}^{w_2(j_1+\cdots +j_r)}{E}_{l,p^{w_1},q^{w_1}}^{(r)}\left(w_{2}x+{\displaystyle \frac{w_2}{w_1}}(j_1+\cdots +j_r)\right)\\ ={\displaystyle \sum _{l=0}^n}{S}_1(n,l){\lambda }^{n-l}{\left[w_2\right]}_{p,q}^l{\left[2\right]}_{q^{w_1}}^r\\ \times {\displaystyle \sum _{j_1,\cdots ,j_r=0}^{w_2-1}}{(-1)}^{j_1+\cdots +j_r}{q}^{w_1(j_1+\cdots +j_r)}{E}_{l,p^{w_2},q^{w_2}}^{(r)}\left(w_{1}x+{\displaystyle \frac{w_1}{w_2}}(j_1+\cdots +j_r)\right).\end{array}$$

We get another symmetry identity by using the addition theorem about the Carlitz-type higher-order degenerate $(p,q)$-Euler polynomials ${\mathcal{E}}_{n,p,q}^{(r)}(x)$. Let

$${\mathcal{A}}_{n,k,p,q}^{(r)}(w)={\displaystyle \sum _{j_1,\cdots ,j_r=0}^{w-1}}{(-1)}^{{\sum }_{i=1}^r{j}_i}{q}^{(n-k+1)({\sum }_{i=1}^r{j}_i)}{[j_1\cdots +j_k]}_{p,q}^k$$

for each integer $n\ge 0$. The ${\mathcal{A}}_{n,k,p,q}^{(k)}(w)$ is called as the alternating $(p,q)$-sums of powers.

Theorem 10.

Let $w_1,w_2\in N$ with $w_1\equiv 1(\mathrm{mod}2)$, $w_2\equiv 1(\mathrm{mod}2)$. For $r\in N$ and $n\in Z_{+}$, we obtain

$$\begin{gathered} {\displaystyle \sum _{l=0}^n}{\displaystyle \sum _{k=0}^l}\left(\genfrac{}{}{0pt}{}{l}{k}\right)S_1(n,l){\lambda }^{n-l}{p}^{w_1{w}_{2}xk}{\left[2\right]}_{q^{w_1}}{\left[w_1\right]}_{p,q}^k{\left[w_2\right]}_{p,q}^{l-k}{E}_{l-k,p^{w_2},q^{w_2}}^{(r,k)}(w_{1}x){\mathcal{A}}_{l,k,p^{w_1},q^{w_1}}^{(r)}(w_2) \\ ={\displaystyle \sum _{l=0}^n}{\displaystyle \sum _{k=0}^l}\left(\genfrac{}{}{0pt}{}{l}{k}\right)S_1(n,l){\lambda }^{n-l}{p}^{w_1{w}_{2}xk}{\left[2\right]}_{q^{w_2}}{\left[w_2\right]}_{p,q}^k{\left[w_1\right]}_{p,q}^{l-k}{E}_{l-k,p^{w_1},q^{w_1}}^{(r,k)}(w_{2}x){\mathcal{A}}_{l,k,p^{w_2},q^{w_2}}^{(r)}(w_1). \end{gathered}$$

Proof. 

Now, we use the addition theorem about the Carlitz-type higher-order degenerate $(p,q)$-Euler polynomials (see [10]). We derive

$$\begin{array}{l}{\displaystyle \sum _{j_1,\cdots ,j_r=0}^{w_1-1}}{(-1)}^{{\sum }_{i=1}^r{j}_i}{q}^{w_2({\sum }_{i=1}^r{j}_i)}{E}_{l,p^{w_1},q^{w_1}}^{(r)}\left(w_{2}x+{\displaystyle \frac{w_2}{w_1}}(j_1+\cdots +j_k)\right)\\ ={\displaystyle \sum _{j_1,\cdots ,j_r=0}^{w_1-1}}{(-1)}^{{\sum }_{i=1}^r{j}_i}{q}^{w_2({\sum }_{i=1}^r{j}_i)}\\ \times {\displaystyle \sum _{k=0}^l}\left(\genfrac{}{}{0pt}{}{l}{k}\right)q^{w_2(l-k)({\sum }_{i=1}^r{j}_i)}{p}^{w_1{w}_{2}xk}{E}_{l-k,p^{w_1},q^{w_1}}^{(r,k)}(w_{2}x){\left[{\displaystyle \frac{w_2}{w_1}}(j_1+\cdots +j_r)\right]}_{p^{w_1},q^{w_1}}^k\\ ={\displaystyle \sum _{j_1,\cdots ,j_r=0}^{w_1-1}}{(-1)}^{{\sum }_{i=1}^r{j}_i}{q}^{w_2({\sum }_{i=1}^r{j}_i)}\\ \times {\displaystyle \sum _{k=0}^l}\left(\genfrac{}{}{0pt}{}{l}{k}\right)q^{w_2(l-k)({\sum }_{i=1}^r{j}_i)}{p}^{w_1{w}_{2}xk}{E}_{l-k,p^{w_1},q^{w_1}}^{(r,k)}(w_{2}x){\left({\displaystyle \frac{{\left[w_2\right]}_{p,q}}{{\left[w_1\right]}_{p,q}}}\right)}^k{\left[j_1+\cdots +j_r\right]}_{p^{w_2},q^{w_2}}^k.\end{array}$$

By Theorem 12, then we have

$$\begin{array}{l}{\displaystyle \sum _{l=0}^n}{S}_1(n,l){\lambda }^{n-l}{\left[w_1\right]}_{p,q}^l{\left[2\right]}_{q^{w_2}}^r\\ \times {\displaystyle \sum _{j_1,\cdots ,j_r=0}^{w_1-1}}{(-1)}^{j_1+\cdots +j_r}{q}^{w_2(j_1+\cdots +j_r)}{E}_{l,p^{w_1},q^{w_1}}^{(r)}\left(w_{2}x+{\displaystyle \frac{w_2}{w_1}}(j_1+\cdots +j_r)\right)\\ ={\displaystyle \sum _{l=0}^n}{\displaystyle \sum _{k=0}^l}\left(\genfrac{}{}{0pt}{}{l}{k}\right)S_1(n,l){\lambda }^{n-l}{\left[w_1\right]}_{p,q}^{l-k}{\left[w_2\right]}_{p,q}^k{\left[2\right]}_{q^{w_2}}^r{p}^{w_1{w}_{2}xk}{E}_{l-k,p^{w_1},q^{w_1}}^{(r,k)}(w_{2}x)\\ \times {\displaystyle \sum _{j_1,\cdots ,j_r=0}^{w_1-1}}{(-1)}^{{\sum }_{i=1}^r{j}_i}{q}^{w_2(l-k+1)({\sum }_{i=1}^r{j}_i)}{\left[j_1+\cdots +j_r\right]}_{p^{w_2},q^{w_2}}^k\\ ={\displaystyle \sum _{l=0}^n}{\displaystyle \sum _{k=0}^l}\left(\genfrac{}{}{0pt}{}{l}{k}\right)S_1(n,l){\lambda }^{n-l}{\left[w_1\right]}_{p,q}^{l-k}{\left[w_2\right]}_{p,q}^k{\left[2\right]}_{q^{w_2}}^r{p}^{w_1{w}_{2}xk}{E}_{l-k,p^{w_1},q^{w_1}}^{(r,k)}(w_{2}x){\mathcal{A}}_{l,k,p^{w_2},q^{w_2}}^{(k)}(w_2).\end{array}$$

(13)

Similarly, we have

$$\begin{array}{l}{\displaystyle \sum _{l=0}^n}{S}_1(n,l){\lambda }^{n-l}{\left[w_2\right]}_{p,q}^l{\left[2\right]}_{q^{w_1}}^r\\ \times {\displaystyle \sum _{j_1,\cdots ,j_r=0}^{w_2-1}}{(-1)}^{j_1+\cdots +j_r}{q}^{w_1(j_1+\cdots +j_r)}{E}_{l,p^{w_2},q^{w_2}}^{(r)}\left(w_{1}x+{\displaystyle \frac{w_1}{w_2}}(j_1+\cdots +j_r)\right)\\ ={\displaystyle \sum _{l=0}^n}{\displaystyle \sum _{k=0}^l}\left(\genfrac{}{}{0pt}{}{l}{k}\right)S_1(n,l){\lambda }^{n-l}{\left[w_2\right]}_{p,q}^{l-k}{\left[w_1\right]}_{p,q}^k{\left[2\right]}_{q^{w_1}}^r{p}^{w_1{w}_{2}xk}{E}_{l-k,p^{w_2},q^{w_2}}^{(r,k)}(w_{1}x)\\ \times {\displaystyle \sum _{j_1,\cdots ,j_r=0}^{w_2-1}}{(-1)}^{{\sum }_{i=1}^r{j}_i}{q}^{w_1(l-k+1)({\sum }_{i=1}^r{j}_i)}{\left[j_1+\cdots +j_r\right]}_{p^{w_1},q^{w_1}}^k\\ ={\displaystyle \sum _{l=0}^n}{\displaystyle \sum _{k=0}^l}\left(\genfrac{}{}{0pt}{}{l}{k}\right)S_1(n,l){\lambda }^{n-l}{\left[w_2\right]}_{p,q}^{l-k}{\left[w_1\right]}_{p,q}^k{\left[2\right]}_{q^{w_1}}^r{p}^{w_1{w}_{2}xk}{E}_{l-k,p^{w_2},q^{w_2}}^{(r,k)}(w_{1}x){\mathcal{A}}_{l,k,p^{w_1},q^{w_1}}^{(k)}(w_2).\end{array}$$

(14)

By (13) and (14), we make the desired symmetric identity. □

By Theorem 10, we have the symmetric identity for the Carlitz-type high order $(h,p,q)$-Euler numbers $E_{n,p,q}^{(r,h)}$ in complex field.

Corollary 4.

Let $w_1\equiv 1(\mathrm{mod}2)$, $w_2\equiv 1(\mathrm{mod}2)$, where $w_1,w_2\in N$. For $r\in N$ and $n\in Z_{+}$, we obtain

$$\begin{array}{l}{\displaystyle \sum _{l=0}^n}{\displaystyle \sum _{k=0}^l}\left(\genfrac{}{}{0pt}{}{l}{k}\right)S_1(n,l){\lambda }^{n-l}{\left[2\right]}_{q^{w_1}}{\left[w_1\right]}_{p,q}^k{\left[w_2\right]}_{p,q}^{l-k}{\mathcal{A}}_{l,k,p^{w_1},q^{w_1}}^{(r)}(w_2)E_{l-k,p^{w_2},q^{w_2}}^{(r,k)}\\ ={\displaystyle \sum _{l=0}^n}{\displaystyle \sum _{k=0}^l}\left(\genfrac{}{}{0pt}{}{l}{k}\right)S_1(n,l){\lambda }^{n-l}{\left[2\right]}_{q^{w_2}}{\left[w_2\right]}_{p,q}^k{\left[w_1\right]}_{p,q}^{l-k}{\mathcal{A}}_{l,k,p^{w_2},q^{w_2}}^{(r)}(w_1)E_{l-k,p^{w_1},q^{w_1}}^{(r,k)}.\end{array}$$

4. Conclusions

In our previous paper [4], we studied some identities of symmetry on the Carlitz-type degenerate $(p,q)$-Euler polynomials. The motivation of this paper is to investigate some explicit identities for the Carlitz-type higher-order degenerate $(p,q)$-Euler polynomials in the second row of the diagram at page 3. Thus, we defined the Carlitz-type higher-order degenerate $(p,q)$-Euler polynomials in Definition 2 and obtained the formulas (explicit formula (Theorem 6), multiplication theorem (Theorem 8), and distribution relation (Corollary 2, Corollary 3)). In Theorem 7, we gave some symmetry identities for the Carlitz-type higher-order degenerate $(p,q)$-Euler polynomials. We also obtained the explicit identities related to the Carlitz-type higher-order $(p,q)$-Euler polynomials, the alternating $(p,q)$-sums of powers, and Stirling numbers (see Theorem 10 and Corollary 4). In particular, these results generalized some well-known properties relating degenerate Euler numbers and polynomials, degenerate Stirling numbers, alternating sums of powers, multiplication theorem, distribution relation, falling factorial, symmetry properties of the degenerate Euler numbers and polynomials (see [7,8,9,10,11,12,13,14,15,16,17,18]). In addition, in this paper, if we take $r=1$, then [4] is the special case of this paper.