Application of Fractional Residual Power Series Algorithm to Solve Newell–Whitehead–Segel Equation of Fractional Order
Abstract
1. Introduction
2. Preliminaries and Notations
- , .
- , .
- , that is, is a linear, .
3. Solution Methodology of the FRPS Algorithm
- Step 1: Assume that the solution of FNWSEs (1) and (2) has the MFPS about :where , , , and such that is continuous on , for .
- Step 2: Define the th truncated series of such that
- Step 3: Consider the initial condition , then the zeroth MFPS approximate solution of is .
- Step 4: Define the th residual function such that
- Step 5: Substitute the th truncated series into the th residual function such that
- Step 6: Set in Step 5, then by using , the first unknown coefficient is obtained. Therefore, the first approximate PS solution is also obtained.
- Step 7: For , do the following subroutine:
- (A)
- Apply the operator , () times, on both sides of the th residual function in Step 4 such that .
- (B)
- Compute the resulting equation at with equality to zero such that , with the help of for at .
- (C)
- Find the th unknown coefficient and do Step 7 for until the arbitrary .
- Step 8: Collect the obtained coefficients for each in terms of expanded MFPS and try to find a general pattern with the term of infinite series so that the exact solution of FNWSEs (1) and (2) is obtained; otherwise, the pattern obtained in the sense of the series coefficients will be the th approximate MFPS solution of FNWSEs (1) and (2).
- Step 9: Stop.
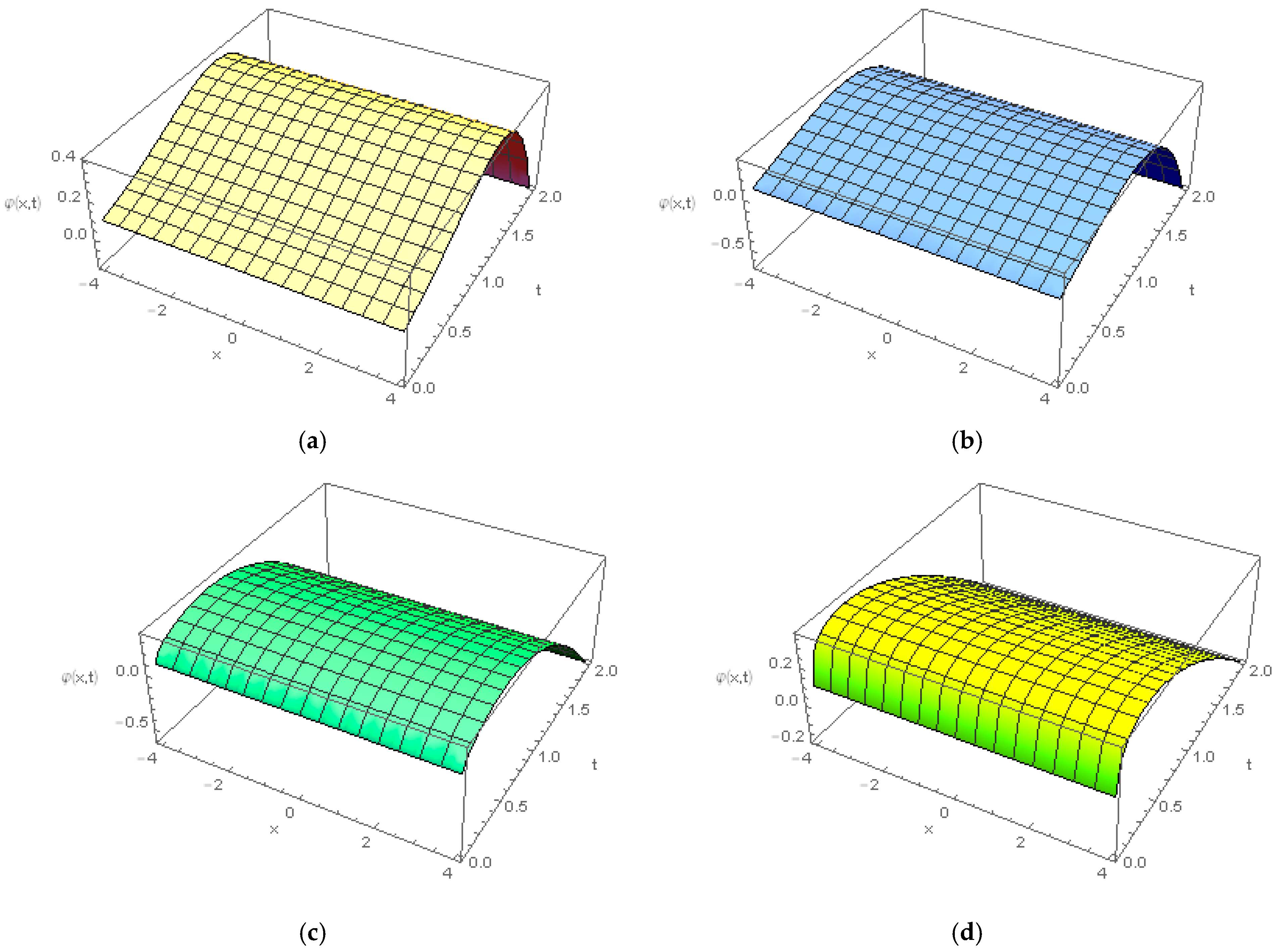
4. Numerical Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Baleanu, D.; Machado, J.A.T.; Luo, A.C. Fractional Dynamics and Control; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2010; p. 523. ISBN 0444518320. [Google Scholar]
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- El-Ajou, A.; Abu Arqub, O.; Momani, S. Approximate analytical solution of the nonlinear fractional KdV-Burgers equation: A new iterative algorithm. J. Comput. Phys. 2015, 293, 81–95. [Google Scholar] [CrossRef]
- Al-Smadi, M. Simplified iterative reproducing kernel method for handling time-fractional BVPs with error estimation. Ain Shams Eng. J. 2018, 9, 2517–2525. [Google Scholar] [CrossRef]
- Rosu, H.C.; Cornejo-Perez, O. Super symmetric pairing of kinks for polynomial nonlinearities. Phys. Rev. E 2005, 4, 1–13. [Google Scholar]
- He, J.M. Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- Kumar, D.; Prakash, R. Numerical approximation of Newell Whitehead-Segel equation of fractional order. Nonlin Eng. 2016, 5, 81–86. [Google Scholar] [CrossRef]
- Prakash, A.; Goyal, M.; Gupta, S. Fractional variational iteration method for solving time-fractional Newell-Whitehead- Segel equation. Nonlin Eng. 2019, 8, 164–171. [Google Scholar] [CrossRef]
- Prakash, A.; Verma, V. Numerical Method for Fractional Model of Newell-Whitehead-Segel Equation. Frontiers in Physics 2019, 7, 15. [Google Scholar] [CrossRef]
- Edeki, S.O.; Ogundile, O.P.; Osoba, B.; Adeyemi, G.A.; Egara, F.O.; Ejoh, A.S. Coupled FCT-HP for Analytical Solutions of the Generalized Time-fractional Newell-Whitehead-Segel Equation. WSEAS Trans. Syst. Control 2018, 13, 266–274. [Google Scholar]
- Al-Smadi, M.; Freihat, A.; Khalil, H.; Momani, S.; Khan, R.A. Numerical multistep approach for solving fractional partial differential equations. Int. J. Comput. Methods 2017, 14, 1750029. [Google Scholar] [CrossRef]
- Altawallbeh, Z.; Al-Smadi, M.; Komashynska, I.; Ateiwi, A. Numerical solutions of fractional systems of two-point BVPs by using the iterative reproducing kernel algorithm. Ukrainian Math. J. 2018, 70, 687–701. [Google Scholar] [CrossRef]
- Al-Smadi, M.; Abu Arqub, O. Computational algorithm for solving fredholm time-fractional partial integrodifferential equations of dirichlet functions type with error estimates. Appl. Math. Comput. 2019, 342, 280–294. [Google Scholar] [CrossRef]
- Al-Smadi, M. Solving fractional system of partial differential equations with parameters derivative by combining the GDTM and RDTM. Nonlinear Stud. 2019, 26, 587–601. [Google Scholar]
- Momani, S.; Abu Arqub, O.; Freihat, A.; Al-Smadi, M. Analytical approximations for Fokker-Planck equations of fractional order in multistep schemes. Appl. Comput. Math. 2016, 15, 319–330. [Google Scholar]
- Alshammari, S.; Al-Smadi, M.; Hashim, I.; Alias, M.A. Applications of fractional power series approach in solving fractional Volterra integro-differential equations. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2019; Volume 2111, p. 020003. [Google Scholar]
- Kumar, A.; Kumar, S.; Yan, S.P. Residual power series method for fractional diffusion equations. Fundam. Inform. 2017, 151, 213–230. [Google Scholar] [CrossRef]
- Zhang, Y.; Kumar, A.; Kumar, S.; Baleanu, D.; Yang, X.J. Residual power series method for time fractional Schrödinger equations. J. Nonlinear Sci. 2016, 9, 5821–5829. [Google Scholar] [CrossRef]
- Alaroud, M.; Al-Smadi, M.; Ahmad, R.R.; Din, S.K.U. Numerical computation of fractional Fredholm integro-differential equation of order 2b arising in natural sciences. J. Phys. Conf. Ser. 1212, 2019, 012022. [Google Scholar]
- Freihet, A.; Hasan, S.; Al-Smadi, M.; Gaith, M.; Momani, S. Construction of fractional power series solutions to fractional stiff system using residual functions algorithm. Adv. Differ. Equ. 2019, 2019, 95. [Google Scholar] [CrossRef]
- Al Shammari, M.; Al-Smadi, M.; Abu Arqub, O.; Hashim, I.; Alias, M.A. Adaptation of residual power series method to solve Fredholm fuzzy integro-differential equations. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2019; Volume 2111, p. 020002. [Google Scholar]
- Alaroud, M.; Al-Smadi, M.; Ahmad, R.R.; Din, S.K.U. Computational optimization of residual power series algorithm for certain classes of fuzzy fractional differential equations. Int. J. Differ. Equ. 2018, 2018, 8686502. [Google Scholar] [CrossRef]
- Alshammari, S.; Al-Smadi, M.; Al Shammari, M.; Hashim, I.; Alias, M.A. Advanced analytical treatment of fractional logistic equations based on residual error functions. Int. J. Differ. Equ. 2019, 2019, 7609879. [Google Scholar] [CrossRef]
- Alaroud, M.; Al-Smadi, M.; Ahmad, R.R.; Din, S.K.U. An Analytical Numerical Method for Solving Fuzzy Fractional Volterra Integro-Differential Equations. Symmetry 2019, 11, 205. [Google Scholar] [CrossRef]
- Freihet, A.; Hasan, S.; Alaroud, M.; Al-Smadi, M.; Ahmad, R.R.; Din, S.K.U. Toward computational algorithm for time-fractional Fokker-Planck models. Adv. Mech. Eng. 2019, 11, 1–11. [Google Scholar] [CrossRef]
- Hasan, S.; Al-Smadi, M.; Freihet, A.; Momani, S. Two computational approaches for solving a fractional obstacle system in Hilbert space. Adv. Differ. Equ. 2019, 2019, 55. [Google Scholar] [CrossRef]
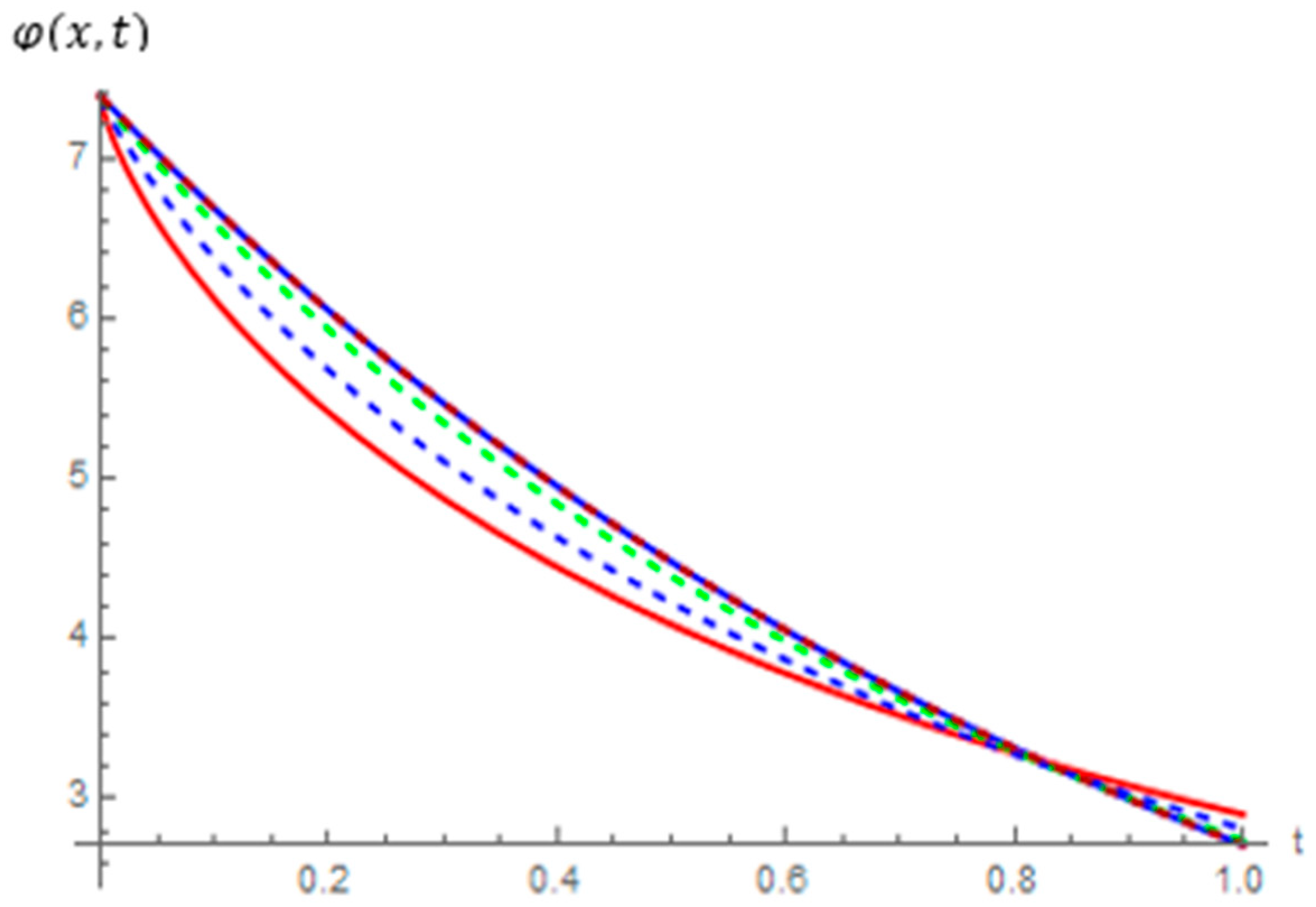
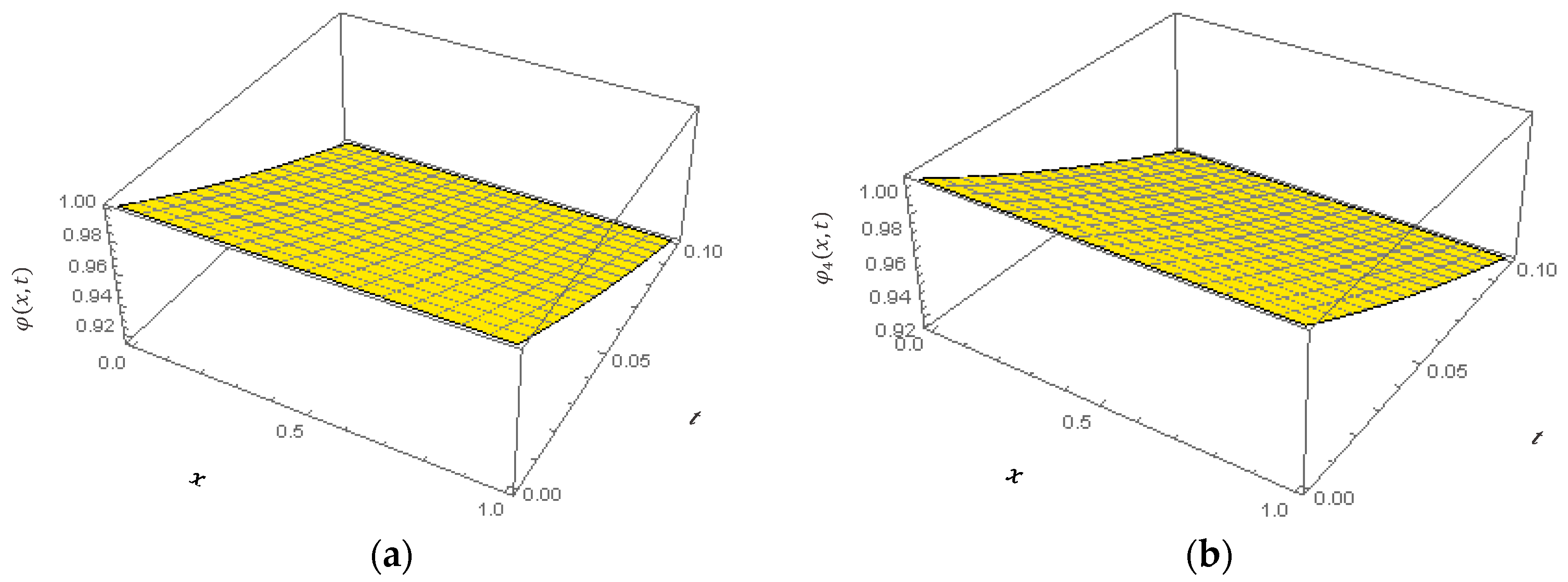
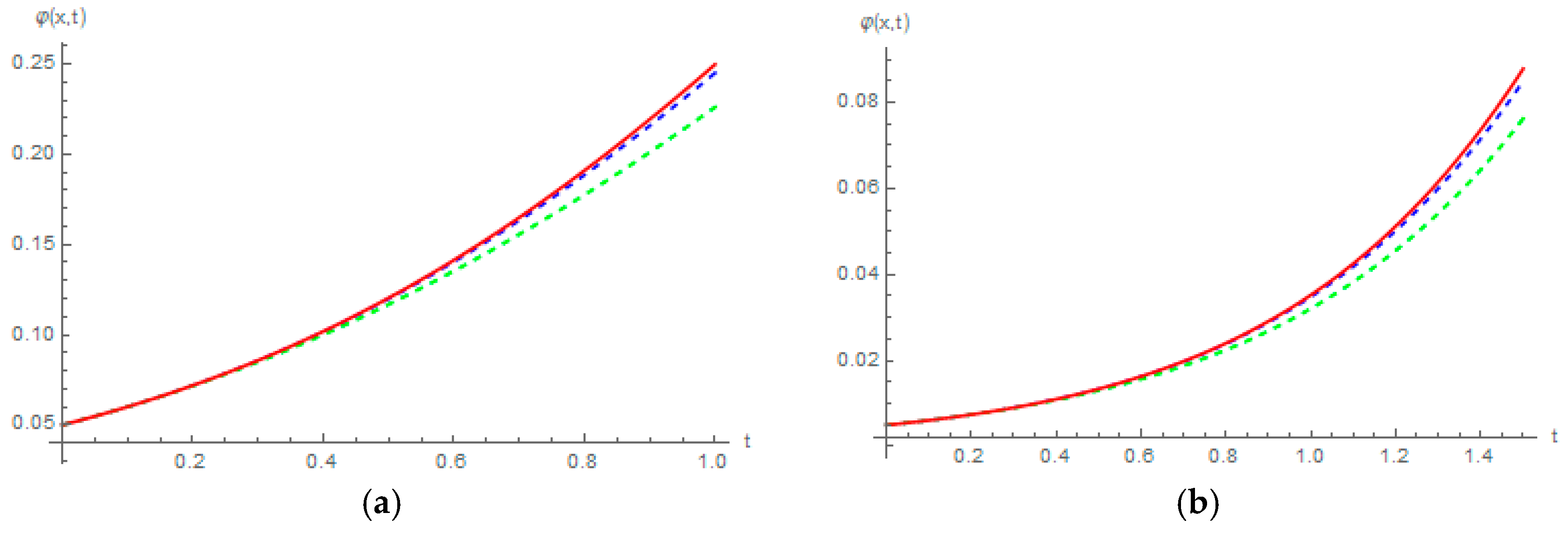
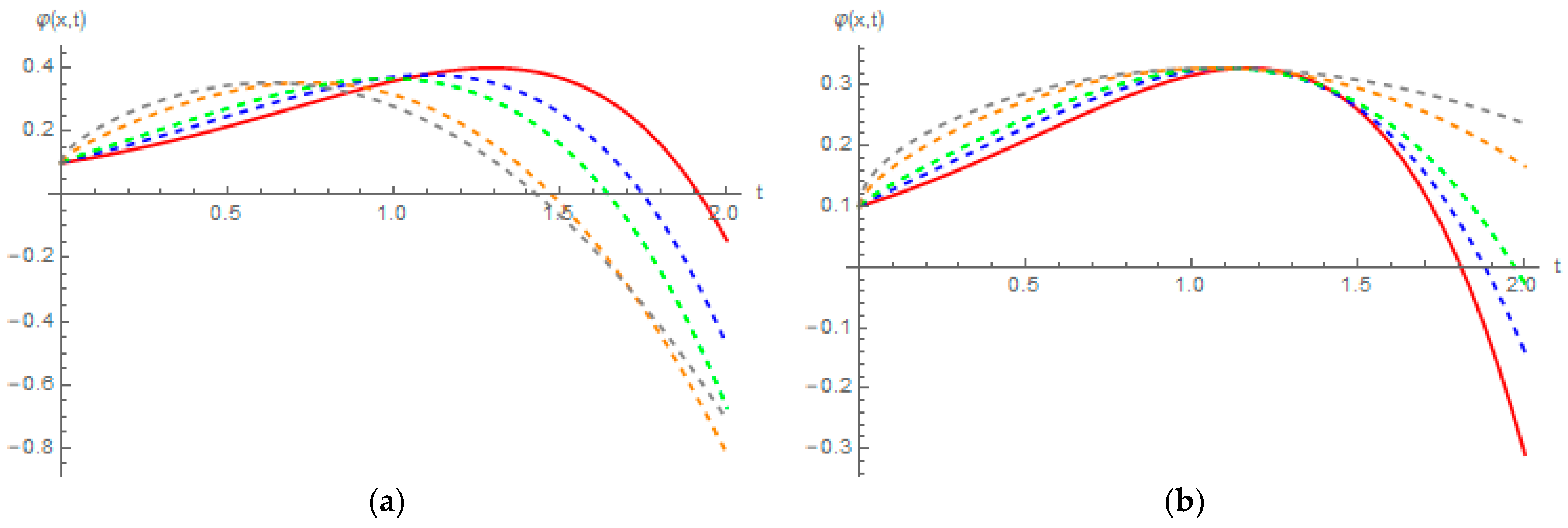
| Exact Solution | Approximation | Absolute Error | ||
|---|---|---|---|---|
| Iteration | Errors | ||||
|---|---|---|---|---|---|
| Absolute | |||||
| Relative | |||||
| Absolute | |||||
| Relative | |||||
| Absolute | |||||
| Relative | |||||
| Absolute | |||||
| Relative |
| Exact | FPS Method | FCT-HP Method [12] | |||
|---|---|---|---|---|---|
| Fifth Appr. Sol. | Absolute Error | Fifth Appr. Sol. | Absolute Error | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saadeh, R.; Alaroud, M.; Al-Smadi, M.; Ahmad, R.R.; Salma Din, U.K. Application of Fractional Residual Power Series Algorithm to Solve Newell–Whitehead–Segel Equation of Fractional Order. Symmetry 2019, 11, 1431. https://doi.org/10.3390/sym11121431
Saadeh R, Alaroud M, Al-Smadi M, Ahmad RR, Salma Din UK. Application of Fractional Residual Power Series Algorithm to Solve Newell–Whitehead–Segel Equation of Fractional Order. Symmetry. 2019; 11(12):1431. https://doi.org/10.3390/sym11121431
Chicago/Turabian StyleSaadeh, Rania, Mohammad Alaroud, Mohammed Al-Smadi, Rokiah Rozita Ahmad, and Ummul Khair Salma Din. 2019. "Application of Fractional Residual Power Series Algorithm to Solve Newell–Whitehead–Segel Equation of Fractional Order" Symmetry 11, no. 12: 1431. https://doi.org/10.3390/sym11121431
APA StyleSaadeh, R., Alaroud, M., Al-Smadi, M., Ahmad, R. R., & Salma Din, U. K. (2019). Application of Fractional Residual Power Series Algorithm to Solve Newell–Whitehead–Segel Equation of Fractional Order. Symmetry, 11(12), 1431. https://doi.org/10.3390/sym11121431






