Robust Hybrid Beamforming Scheme for Millimeter-Wave Massive-MIMO 5G Wireless Networks
Abstract
:1. Introduction
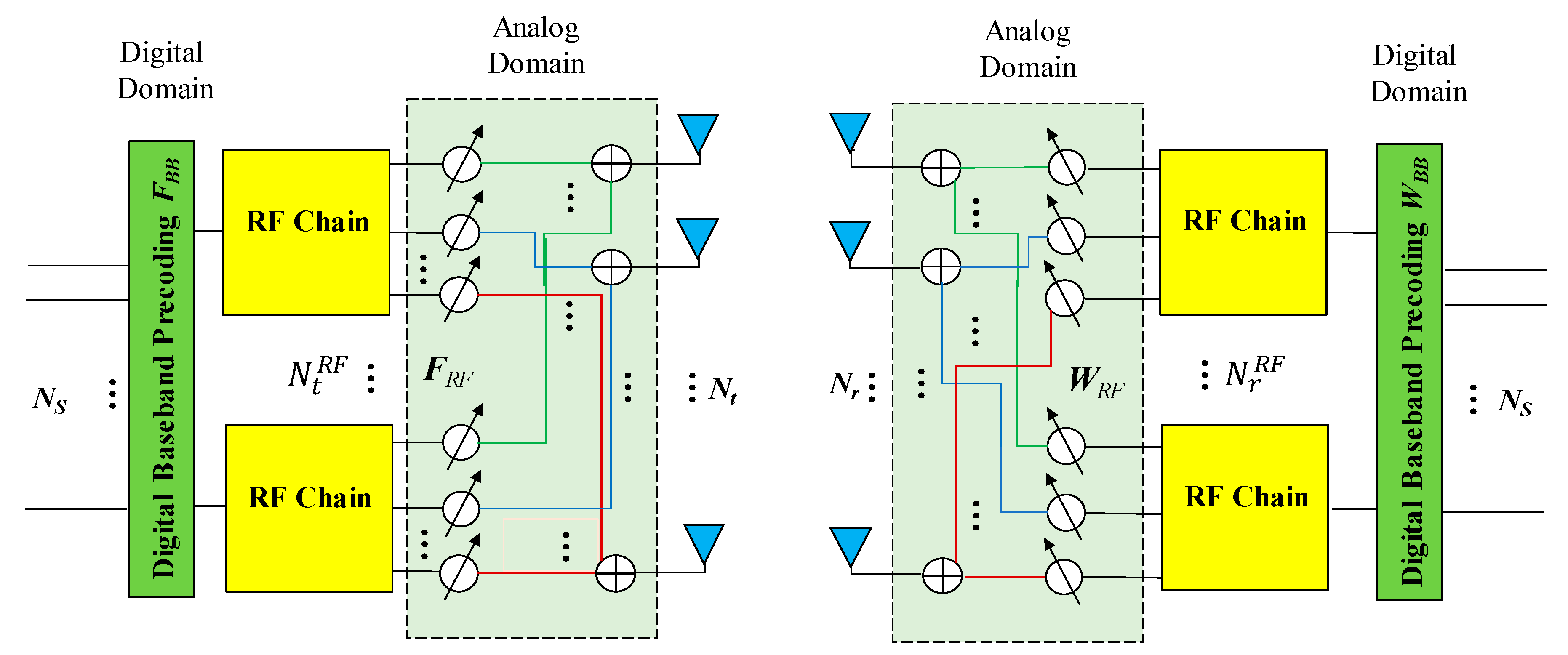
2. System Model
2.1. System Specifications
2.2. Channel Model
2.3. Objective Function
3. Proposed Algorithm
3.1. Initial Digital Beamforming Matrix Design
3.2. Algorithm Design
| Algorithm 1 Alt-MMSE Algorithm. |
| Input: , , 1: Determine 2: Calculate the SVD of according to Equations (11) and (19) 3: Determine according to Equations (12) and (13) 4: 5: 6: Calculate according to Equation (16) 7: Obtain the SVD of 8: Determine according to Equation (19) 9: Obtain the argument of using Equation (15) 10: Calculate 11: Calculate the SVD of 12: Determine using the method of Equation (19) 13: Obtain the argument of using the method of Equation (15) 14: 15: end 16: Determine , 17: return ,, , |
4. Simulation Results
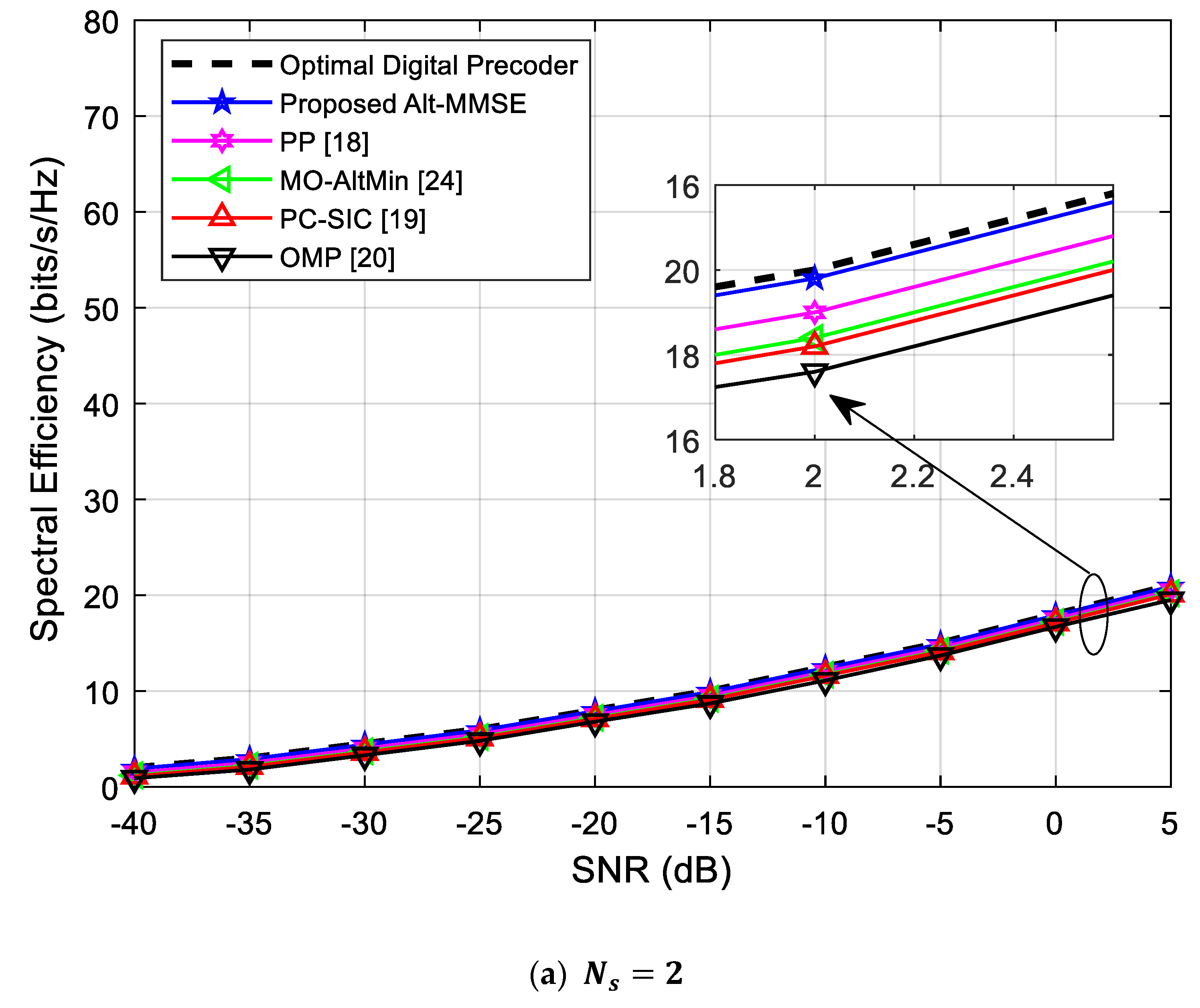
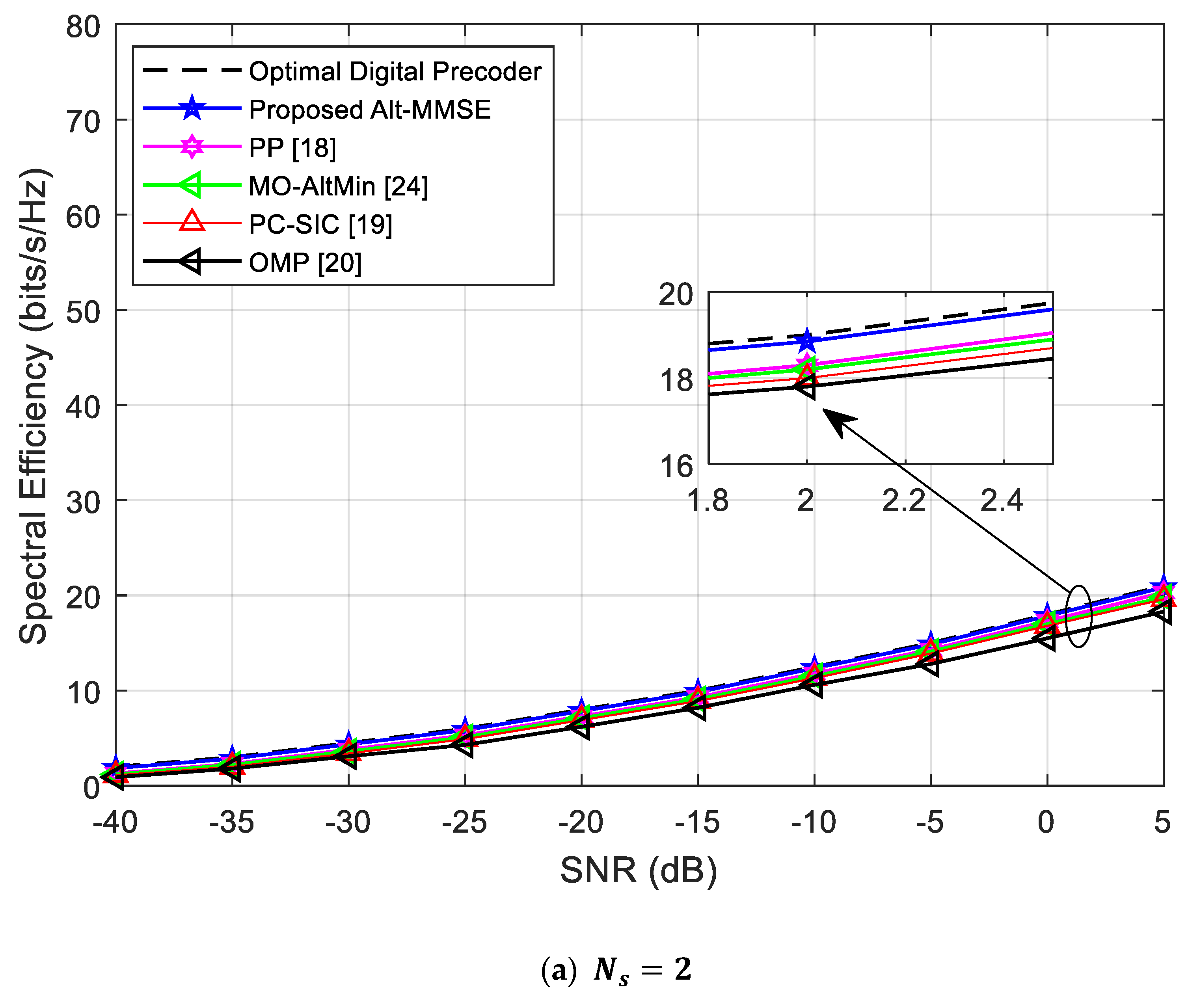
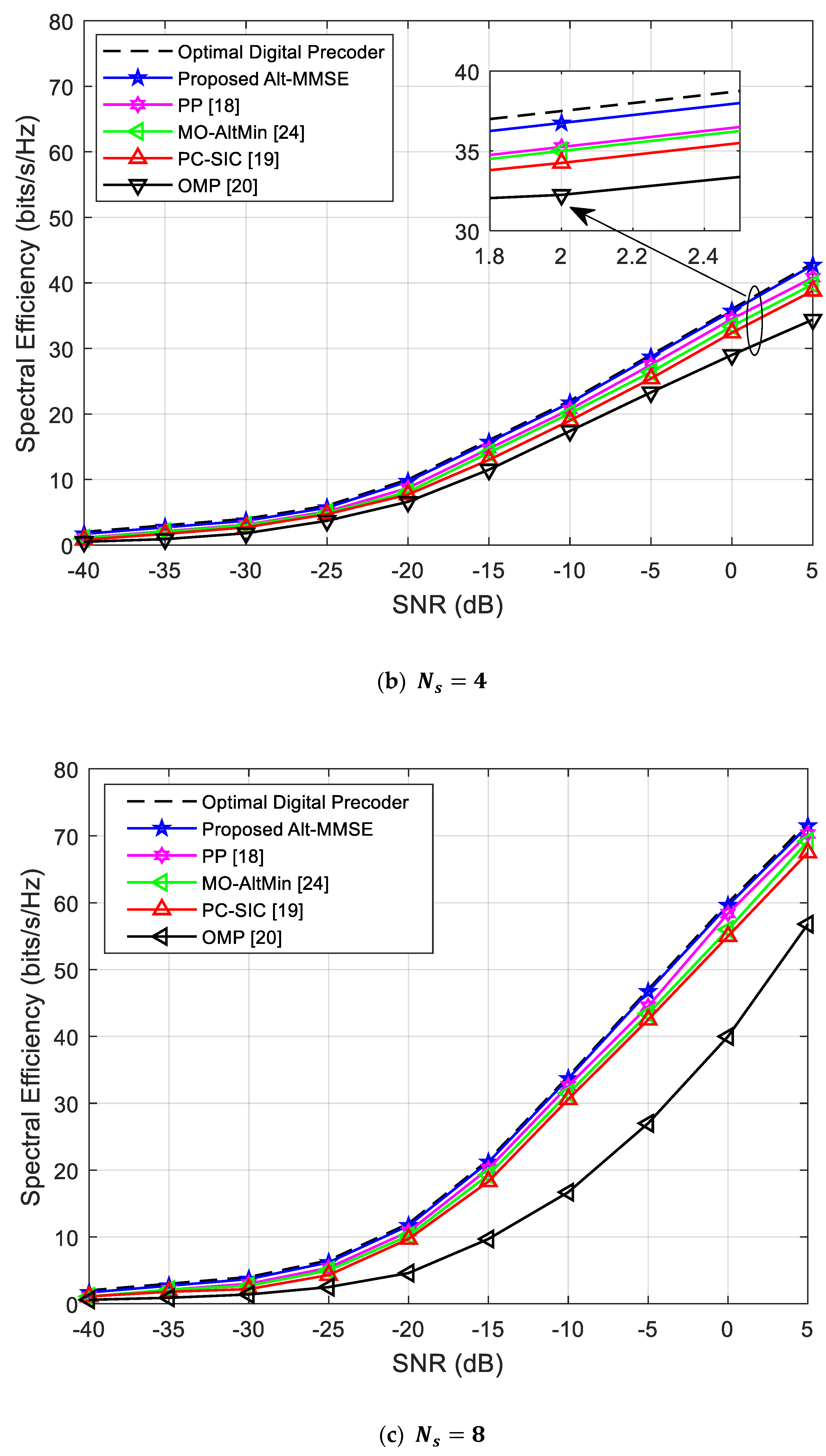
4.1. Spectral Efficiency Analysis when
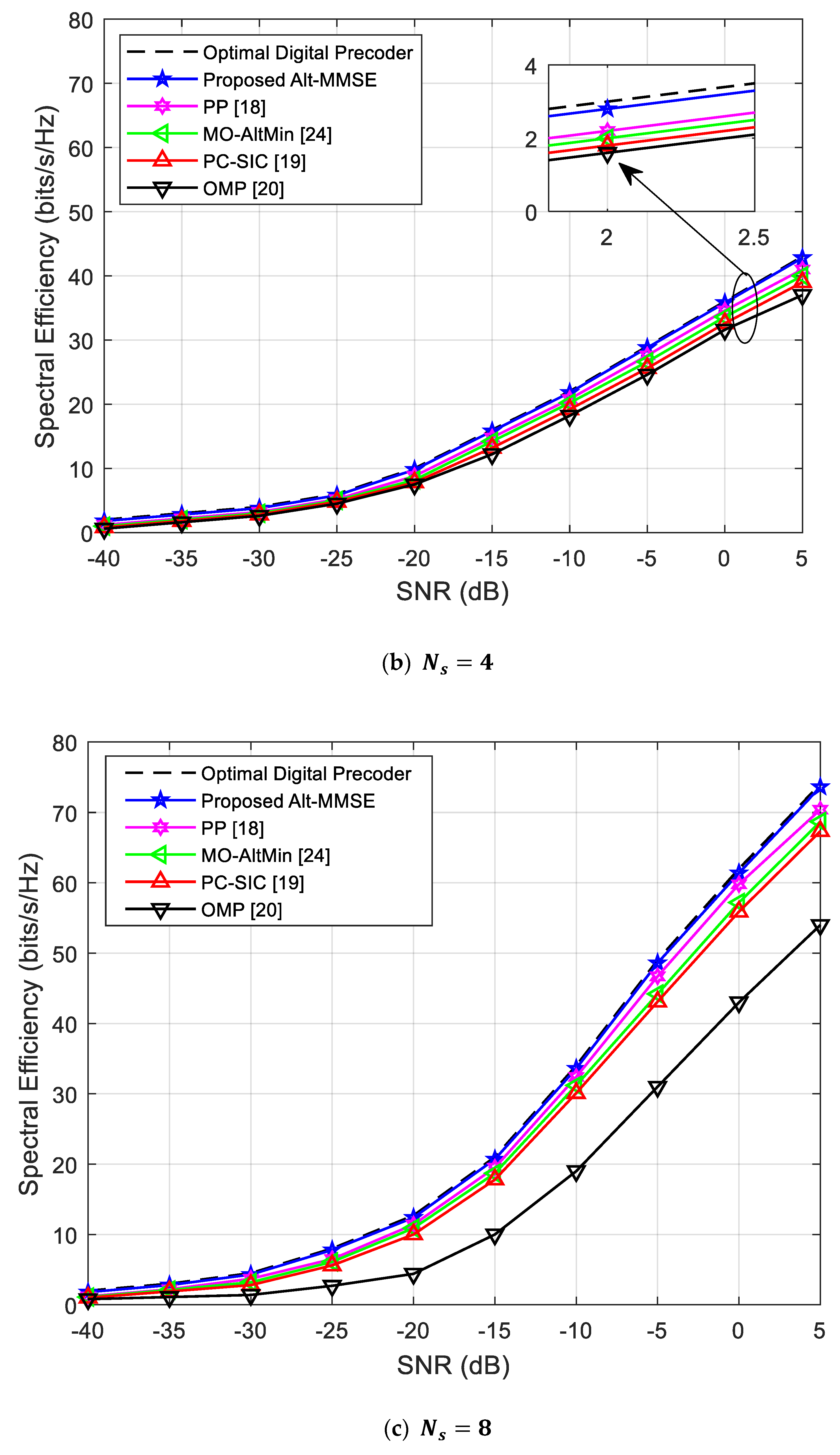
4.2. Spectral Efficiency Analysis when
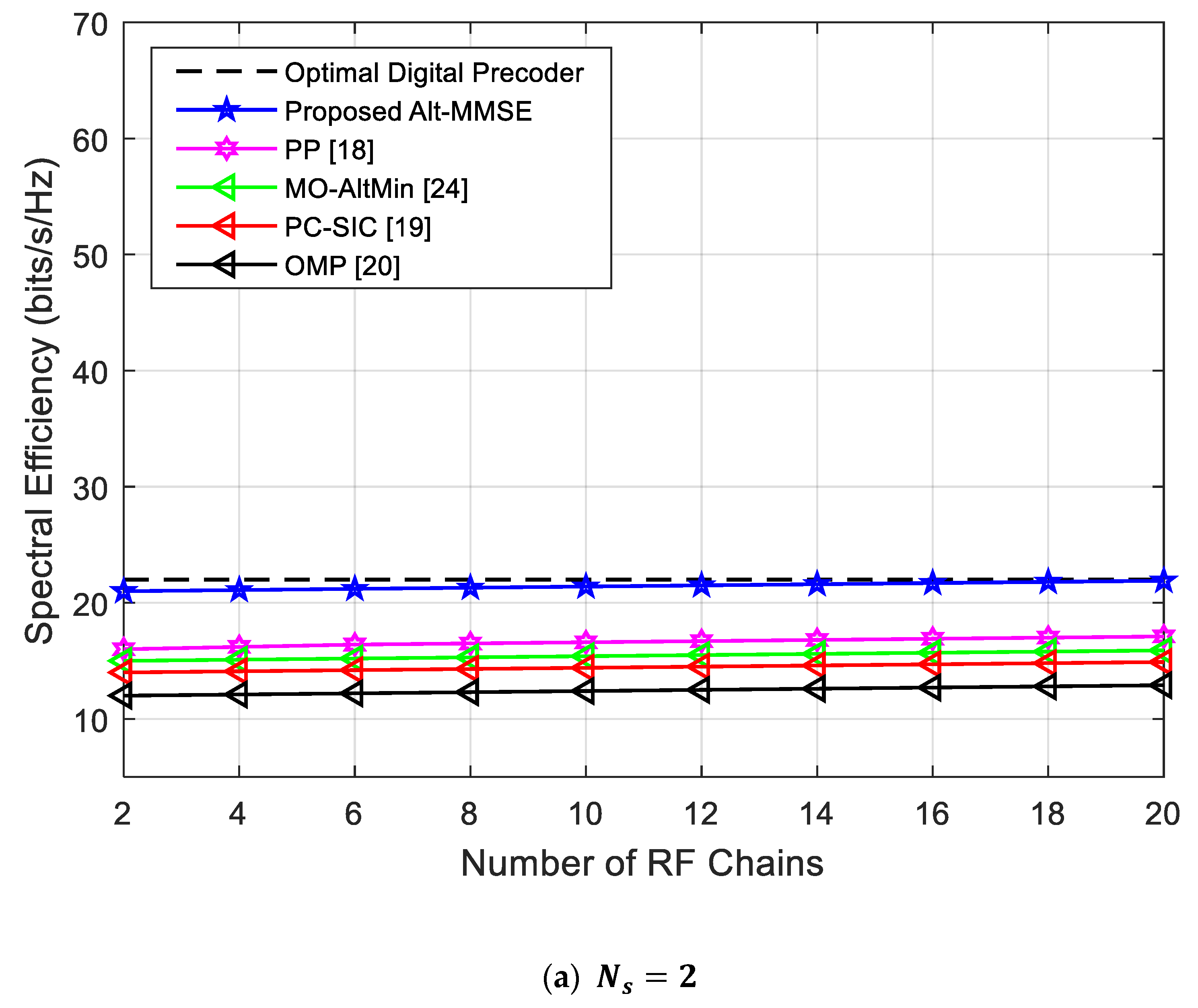
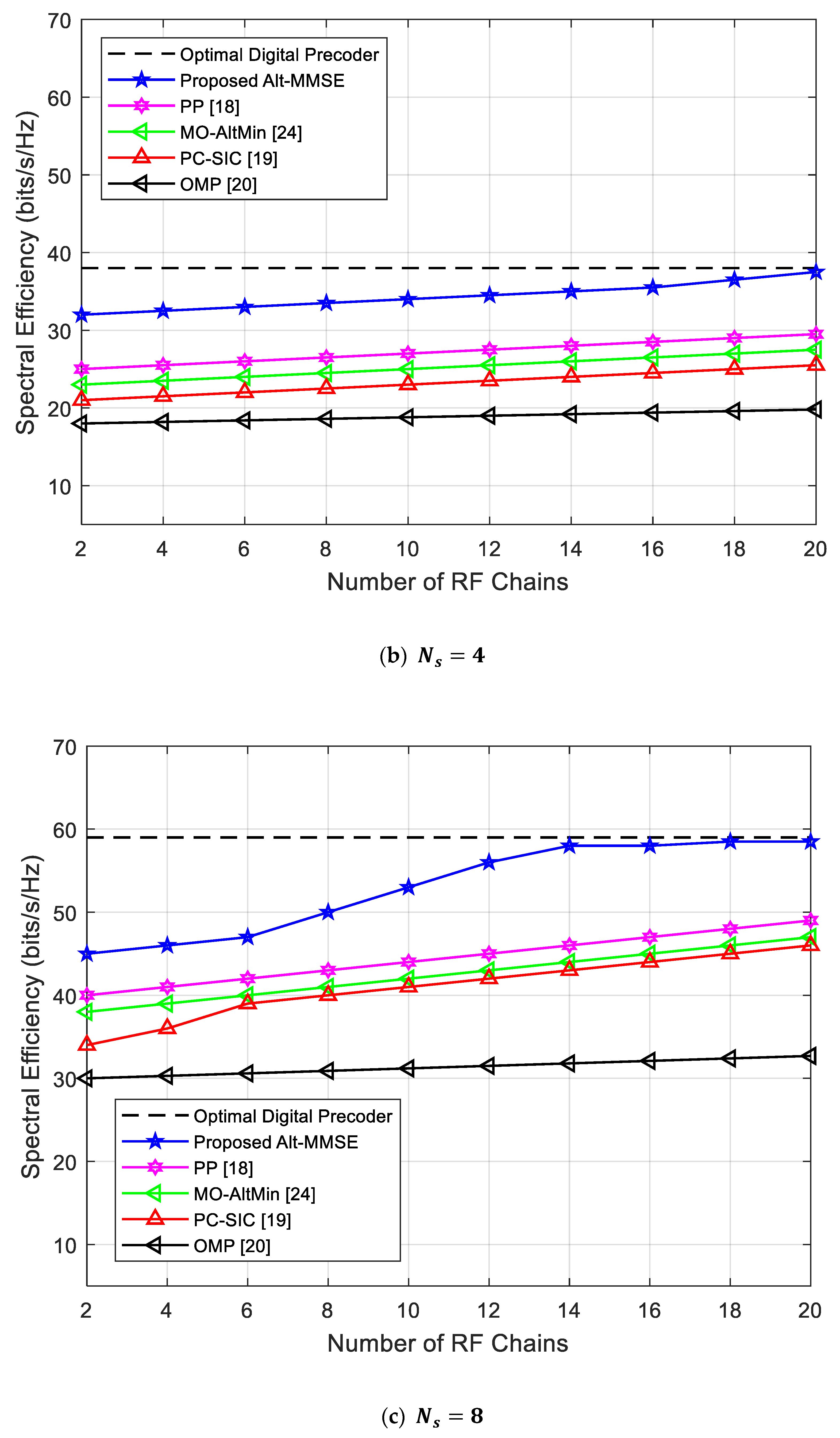
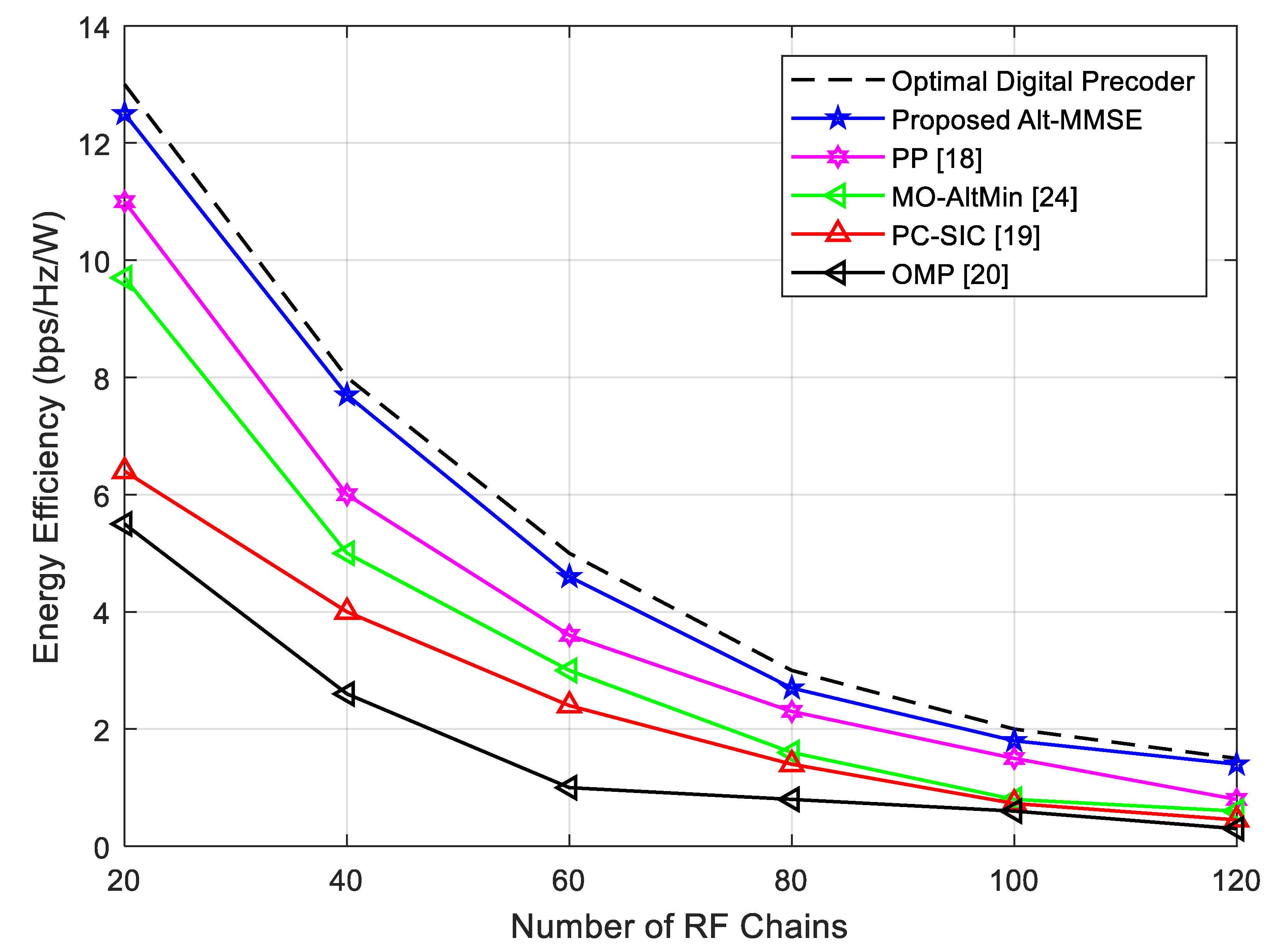
4.3. Impact of RF Chains
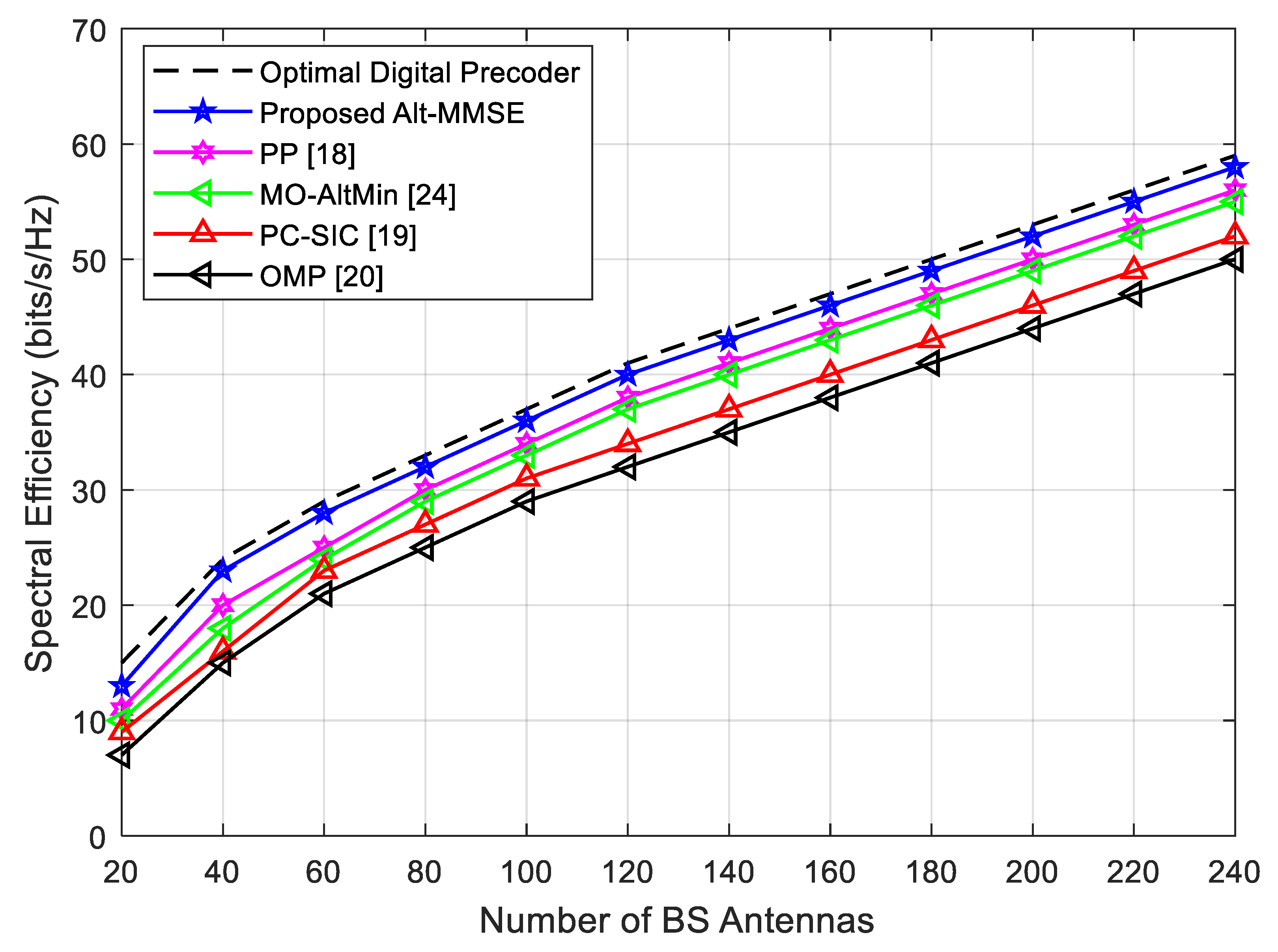
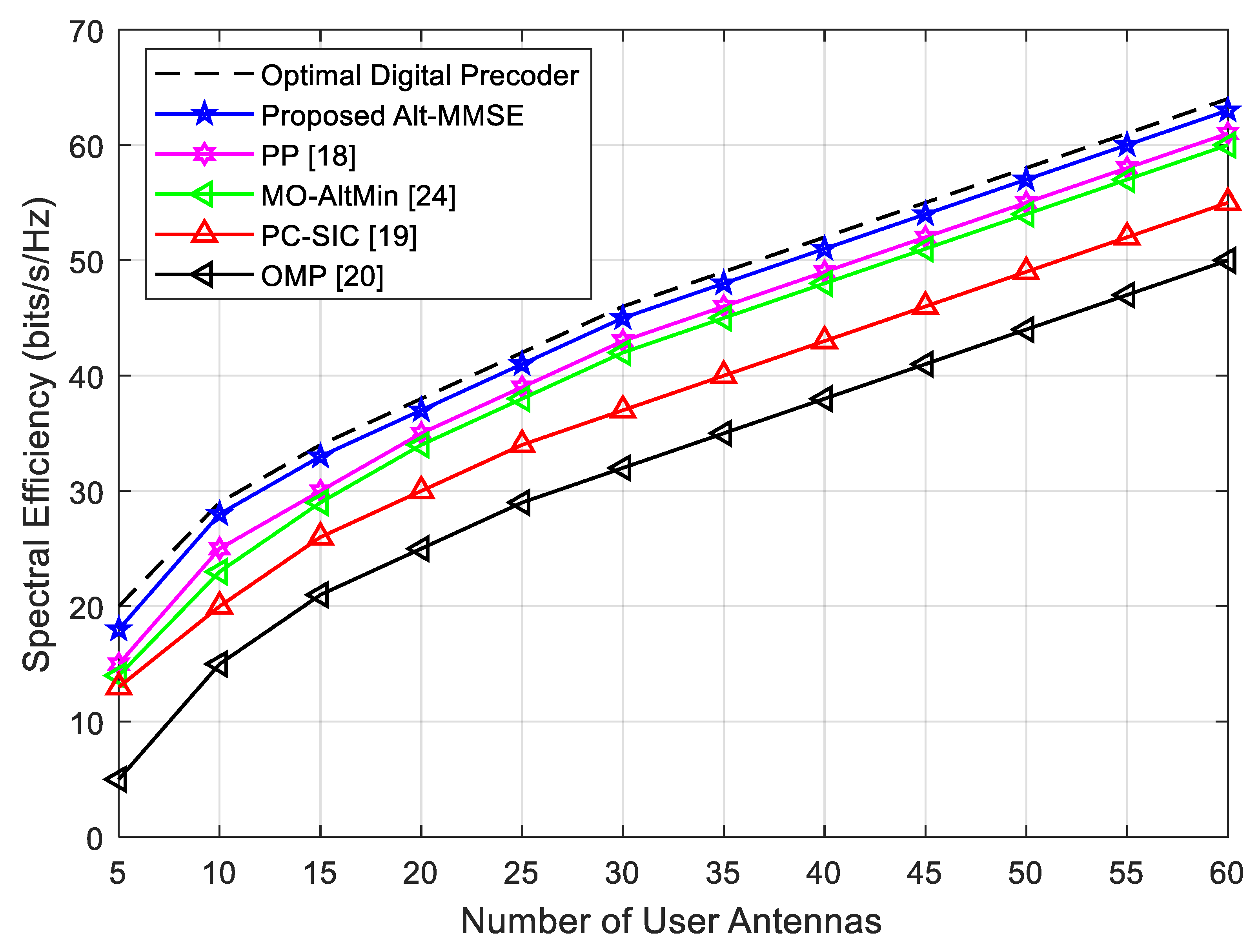
4.4. Impact of Antennas
4.5. Energy Efficiency Analysis
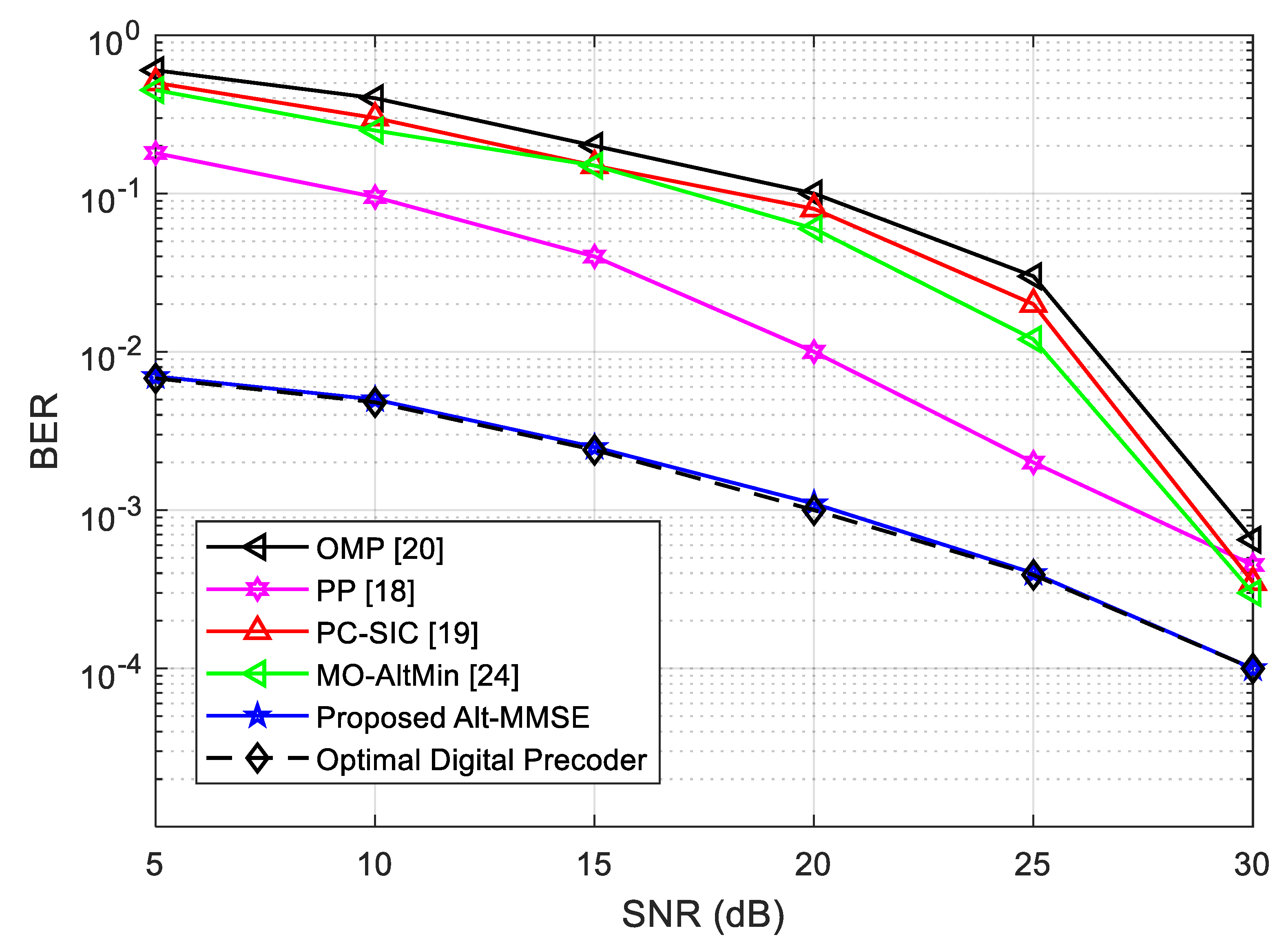
4.6. Bit Error Rate (BER) Analysis
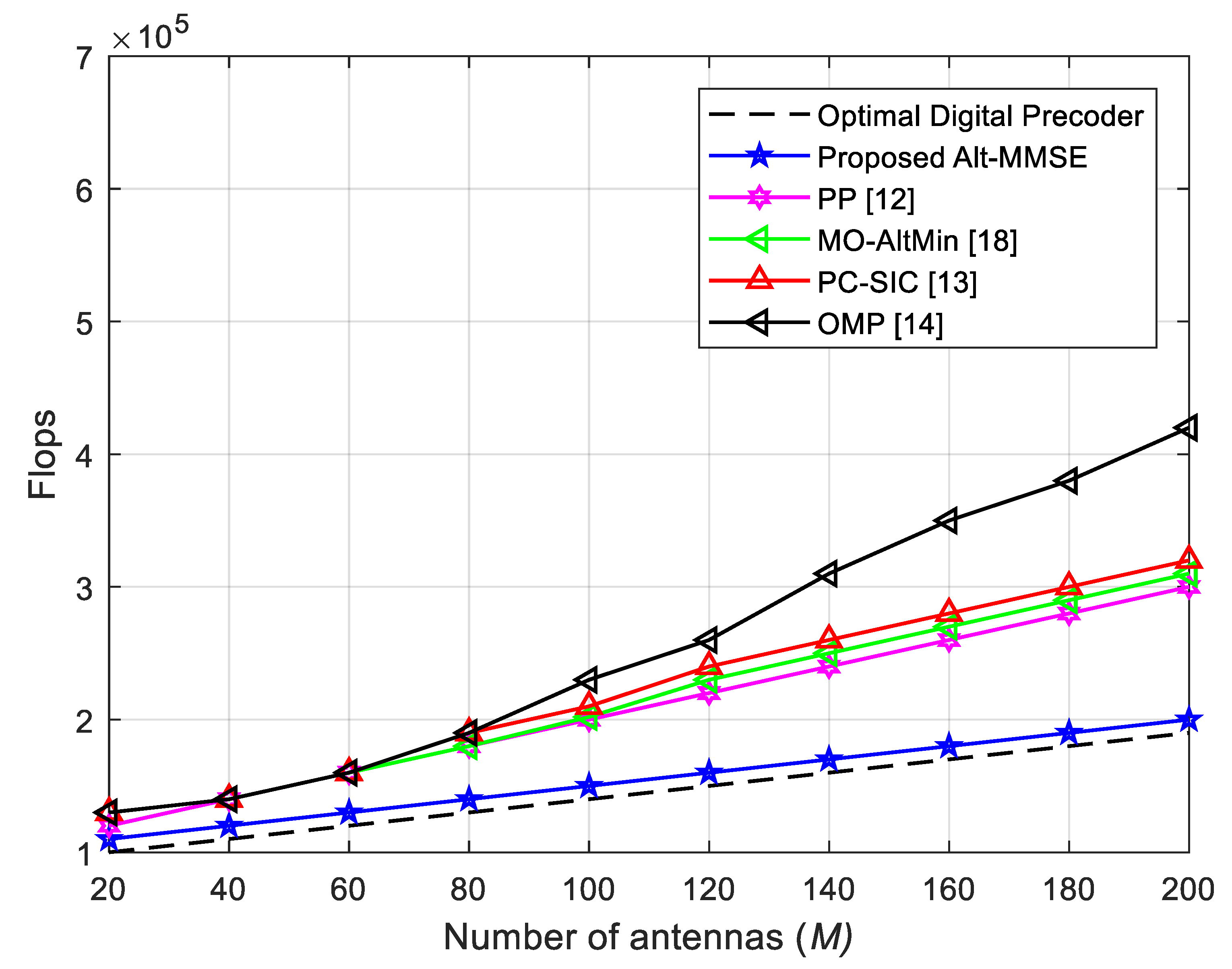
5. Complexity Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhou, B.; Liu, A.; Lau, V. Successive localization and beamforming in 5G mmWave MIMO communication systems. IEEE Trans. Signal Process. 2019, 67, 1620–1635. [Google Scholar] [CrossRef]
- Busari, S.A.; Huq, K.M.S.; Mumtaz, S.; Dai, L.; Rodriguez, J. Millimeter-wave massive MIMO communications for future wireless systems: A survey. IEEE Commun. Surv. Tutorials 2018, 20, 836–869. [Google Scholar] [CrossRef]
- Bjornson, E.; Perre, L.V.D.; Buzzi, S.; Larsson, E.G. Massive MIMO in sub-6 GHz and mmWave: Physical, practical, and use-case differences. IEEE Wirel. Commun. 2019, 26, 100–108. [Google Scholar] [CrossRef]
- Ahmed, I.; Khammari, H.; Shahid, A.; Musa, A. A Survey on Hybrid Beamforming Techniques in 5G: Architecture and System Model Perspectives. IEEE Comm. Sur. & Tut. 2018, 20, 3060–3097. [Google Scholar]
- Alsharif, M.H.; Nordin, R. A evolution towards fifth generation (5G) wireless networks: Current trends and challenges in the deployment of millimetre wave, massive MIMO, and small cells. Telecommun. Syst. 2017, 64, 617–637. [Google Scholar] [CrossRef]
- Alemaishat, S.; Saraereh, A.O.; Khan, I.; Affes, S.H.; Li, X.; Lee, J.W. An efficient precoding scheme for millimeter-wave massive MIMO systems. Electronics 2019, 8, 927. [Google Scholar] [CrossRef]
- Cacciapuoti, S.A.; Sankhe, K.; Caleffi, M.; Chowdhury, K.R. Beyond 5G: THz-based medium access protocol for mobile heterogeneous networks. IEEE Commun. Mag. 2018, 56, 110–115. [Google Scholar] [CrossRef]
- Andrews, J.G.; Bai, T.; Kulkarni, M.N.; Alkhateeb, A.; Gupta, A.K.; Heath, R.W. Modeling and anayalzing millimeter wave cellular systems. IEEE Trans. Commun. 2017, 65, 403–430. [Google Scholar]
- Alsharif, M.H.; Nordin, R.; Shakir, M.M.; Ramly, A.M. Small cells integration with the macro-cell LTE cellular networks and potential extension for 5G. J. Electr. Eng. Technol. 2019, 14, 2455–2465. [Google Scholar] [CrossRef]
- Cacciapioti, A.S. Mobility-aware user association for 5G mmWave networks. IEEE Access 2017, 5, 21497–21507. [Google Scholar] [CrossRef]
- Alsharif, M.H.; Nordin, R.; Abdullah, N.F.; Kelechi, A.H. How to make key 5G wireless technologies environmental friendly: A review. Trans. Emerg. Telecommun. Technol. 2018, 29, e3254. [Google Scholar] [CrossRef]
- Psomas, C.; Krikidis, I. Low-complexity base station selection scheme in mmWave cellular networks. IEEE Trans. Commun. 2017, 65, 4049–4064. [Google Scholar]
- Yang, B.; Yu, Z.; Lan, J.; Zhang, R.; Zhou, J.; Hong, W. Digital beamforming-based massive MIMO transceiver for 5G millimeter-wave communications. IEEE Trans. Microw. Theory Tech. 2018, 66, 3403–3418. [Google Scholar] [CrossRef]
- Bangash, K.; Khan, I.; Lloret, J.; Leon, A. A joint approach for low-complexity channel estimation in 5G massive MIMO systems. Electronics 2018, 7, 218. [Google Scholar] [CrossRef]
- Eltayeb, M.E.; Al-Naffouri, T.Y.; Heath, R.W. Compressive sensing for millimeter-wave antenna array diagnosis. IEEE Trans. Commun. 2018, 66, 2708–2721. [Google Scholar] [CrossRef]
- Khan, I.; Zafar, M.H.; Ashraf, M.; Kim, S. Computationally efficient channel estimation in 5G massive multiple-input multiple-output systems. Electronics 2018, 7, 382. [Google Scholar] [CrossRef]
- Andrews, J.G.; Buzzi, S.; Wan, C.; Hanly, S.V.; Lozano, A.; Soong, A.C.K.; Zhang, J.C. What will 5G be? IEEE J. Sel. Areas Commun. 2014, 32, 1065–1082. [Google Scholar] [CrossRef]
- Wang, Y.; Zou, W. Low complexity hybrid precoder design for millimeter wave MIMO systems. IEEE Commun. Lett. 2019, 23, 1259–1262. [Google Scholar] [CrossRef]
- Liu, Y.; Feng, Q.; Wu, Q.; Zhang, Y.; Jin, M.; Qiu, T. Energy-efficient hybrid precoding with low complexity for mmWave massive MIMO systems. IEEE Access 2019, 7, 95021–95032. [Google Scholar] [CrossRef]
- El, A.O.; Rajagopal, S.; Abu-Aurra, S.; Pi, Z.; Heath, R.W. Spatially sparse precoding in millimeter-wave MIMO systems. IEEE Trans. Wirel. Commun. 2013, 130, 1499–1513. [Google Scholar]
- Jiang, J.; Lei, M.; Hou, H. Downlink Multiuser Hybrid Beamforming for mmWave Massive MIMO-NOMA System with Imperfect CSI. Int. J. Antennas Propag. 2019, 9764958, 1–10. [Google Scholar] [CrossRef]
- TSANG, Y.M.; Poon, A.S.Y.; Addepalli, S. Coding the BEAMS: Improving beamforming training in mmWave communication system. In Proceedings of the IEEE Global Telecommunications Conference, Houston, TX, USA, 5–9 December 2011; pp. 1–6. [Google Scholar]
- Sohrabi, F.; Yu, W. Hybrid digital and analog beamforming design for large-scale antenna arrays. IEEE J. Sel. Top. Signal Process. 2016, 10, 501–513. [Google Scholar] [CrossRef]
- Yu, X.; Shen, J.C.; Zhang, J.; Letaief, K.B. Alternating minimization algorithms for hybrid precoding in millimeter wave MIMO systems. IEEE J. Sel. Top. Signal Process. 2016, 10, 485–500. [Google Scholar] [CrossRef]
- Singh, J.; Ramakrishna, S. On the feasibility of codebook-based beamforming in millimeter wave systems with multiple antenna arrays. IEEE Trans. Wirel. Commun. 2014, 14, 2670–2683. [Google Scholar] [CrossRef]
- Dai, L.; Gao, X.; Quanl, J.; Han, S.; I, C.-L. Near-optimal hybrid analog and digital precoding for downlink mmwave massive MIMO systems. In Proceedings of the IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 1334–1339. [Google Scholar]
- Verma, R.; Mahajan, S.; Rohita, V. Classification of MIMO channel models. In Proceedings of the 16th IEEE International Conference on Networks, New Delhi, India, 12–14 December 2008; pp. 1–4. [Google Scholar]
- Vitanyi, P. Analysis of sorting algorithms by kolmogorov complexity (a survey). Entropy Search Complex. 2007, 16, 209–232. [Google Scholar]
- Hanif, M.; Yang, H.C.; Boudrea, G.; Sich, E.; Seyedmehdi, H. Low-complexity hybrid precoding for multi-user massive MIMO systems: A hybrid EGT/ZF approach. IET Commun. 2017, 11, 765–771. [Google Scholar] [CrossRef]
| Parameter | Value |
|---|---|
| Number of transmitting antennas | 256 |
| Number of receiving antennas | 64 |
| Antenna arrangement | UPA |
| Antenna spacing (mm) | λ/2 |
| Number of clusters | 5 |
| Number of scatterers ray | 10 |
| Angle of Arrival (AoA), Angle of Departure (AoD) distribution | Laplacian |
| Number of data streams | 8 |
| Signal-to-noise ratio (SNR) | 30 dB |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammed, S.L.; Alsharif, M.H.; Gharghan, S.K.; Khan, I.; Albreem, M. Robust Hybrid Beamforming Scheme for Millimeter-Wave Massive-MIMO 5G Wireless Networks. Symmetry 2019, 11, 1424. https://doi.org/10.3390/sym11111424
Mohammed SL, Alsharif MH, Gharghan SK, Khan I, Albreem M. Robust Hybrid Beamforming Scheme for Millimeter-Wave Massive-MIMO 5G Wireless Networks. Symmetry. 2019; 11(11):1424. https://doi.org/10.3390/sym11111424
Chicago/Turabian StyleMohammed, Saleem Latteef, Mohammed H. Alsharif, Sadik Kamel Gharghan, Imran Khan, and Mahmoud Albreem. 2019. "Robust Hybrid Beamforming Scheme for Millimeter-Wave Massive-MIMO 5G Wireless Networks" Symmetry 11, no. 11: 1424. https://doi.org/10.3390/sym11111424
APA StyleMohammed, S. L., Alsharif, M. H., Gharghan, S. K., Khan, I., & Albreem, M. (2019). Robust Hybrid Beamforming Scheme for Millimeter-Wave Massive-MIMO 5G Wireless Networks. Symmetry, 11(11), 1424. https://doi.org/10.3390/sym11111424






