Automatic Registration of Multi-Projector Based on Coded Structured Light
Abstract
:1. Introduction
2. Geometric Registration Principle
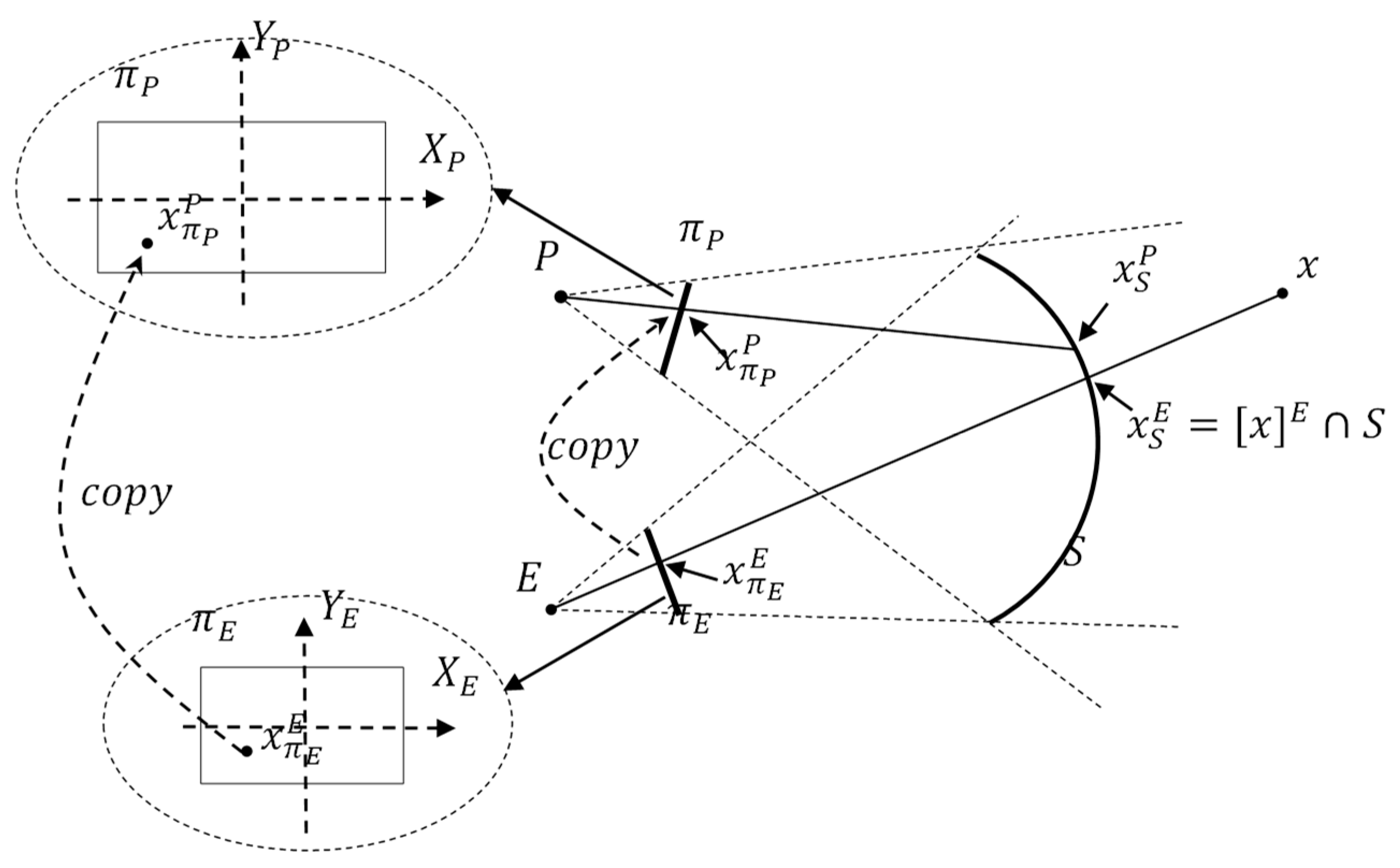
2.1. Coordinate System
2.2. Consistency of Geometric Correction
- When remains unchanged, for each point on the screen and on the image plane , the geometric error is determined and only related to the structural parameters of the multi-projector system, not to the virtual scene (consistency of geometric correction).
3. Geometric Correction
3.1. Geometric Distortion Correction
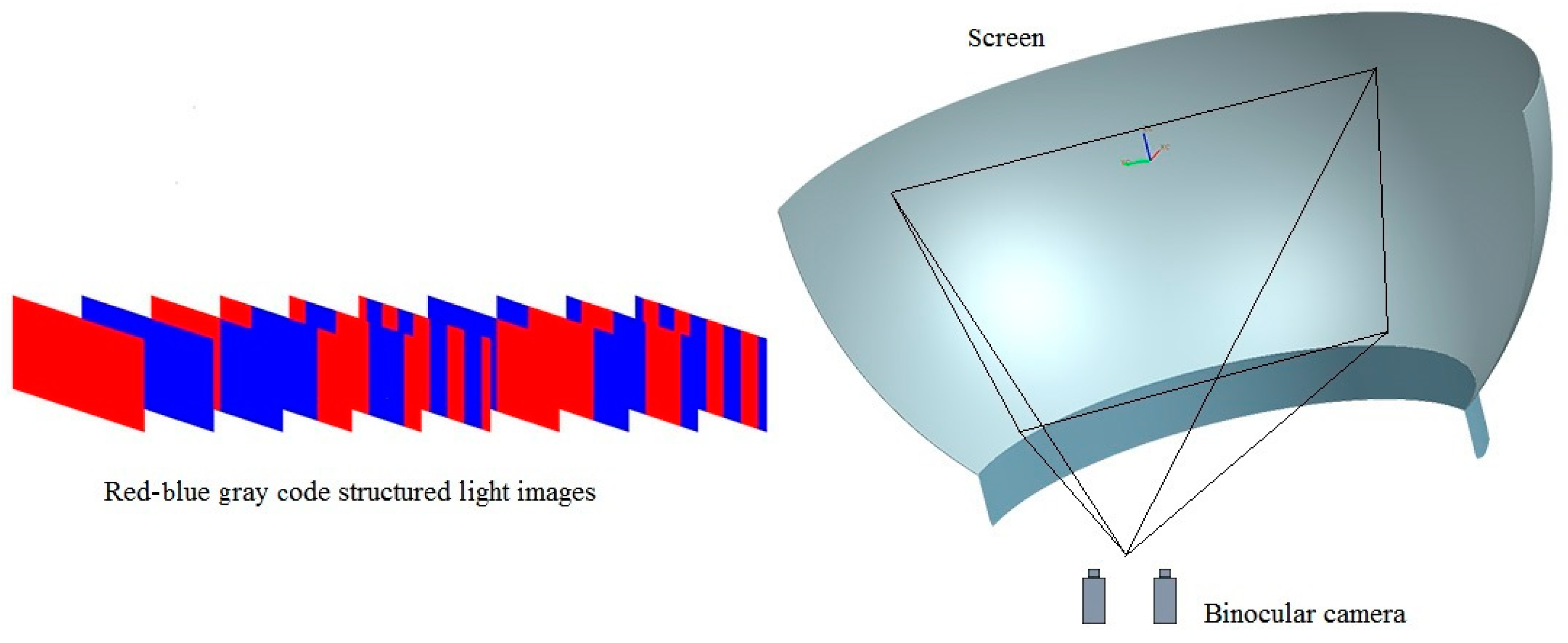
3.2. Geometric Description of Screen
3.2.1. Feature Points
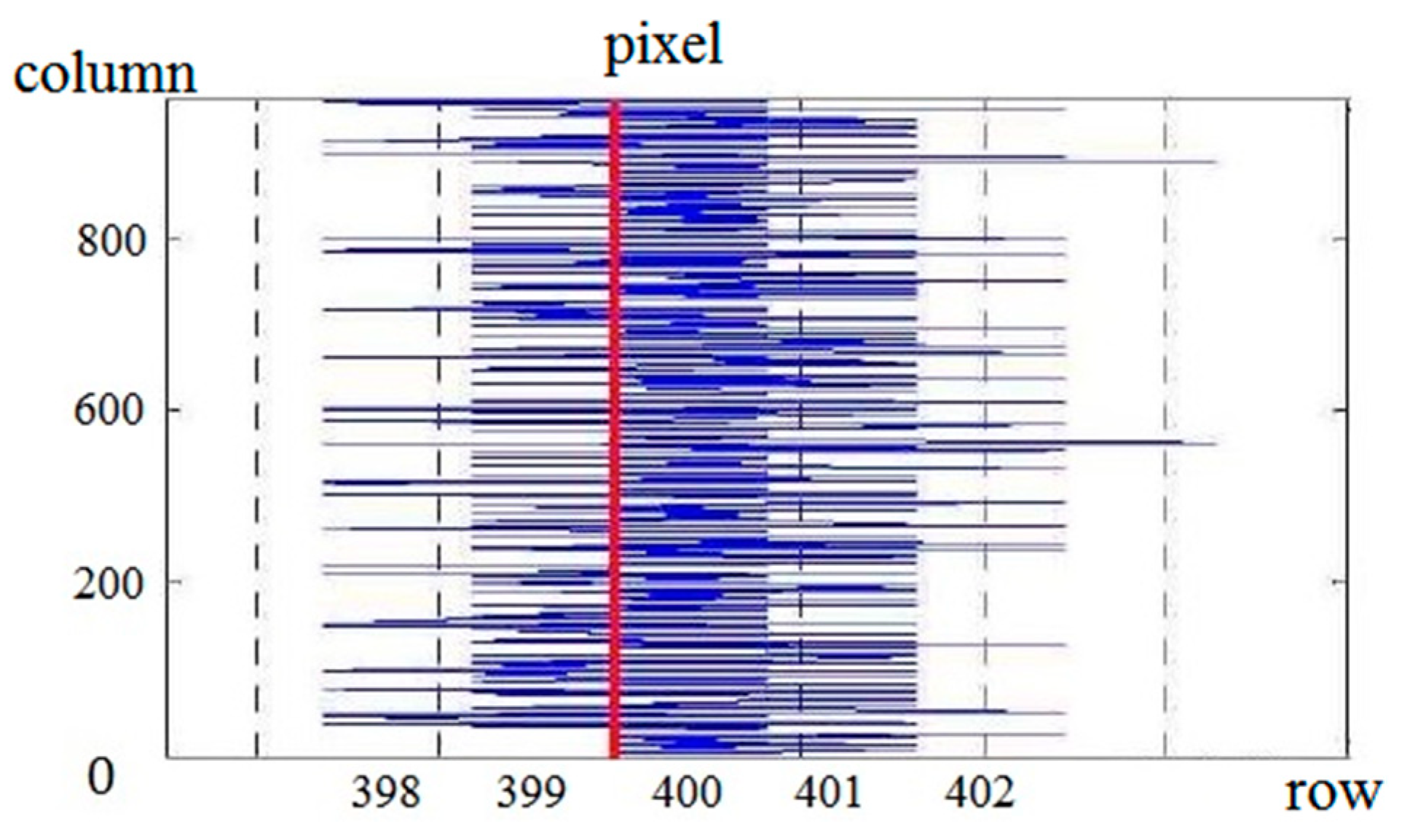
3.2.2. Edge Detection for RBGC
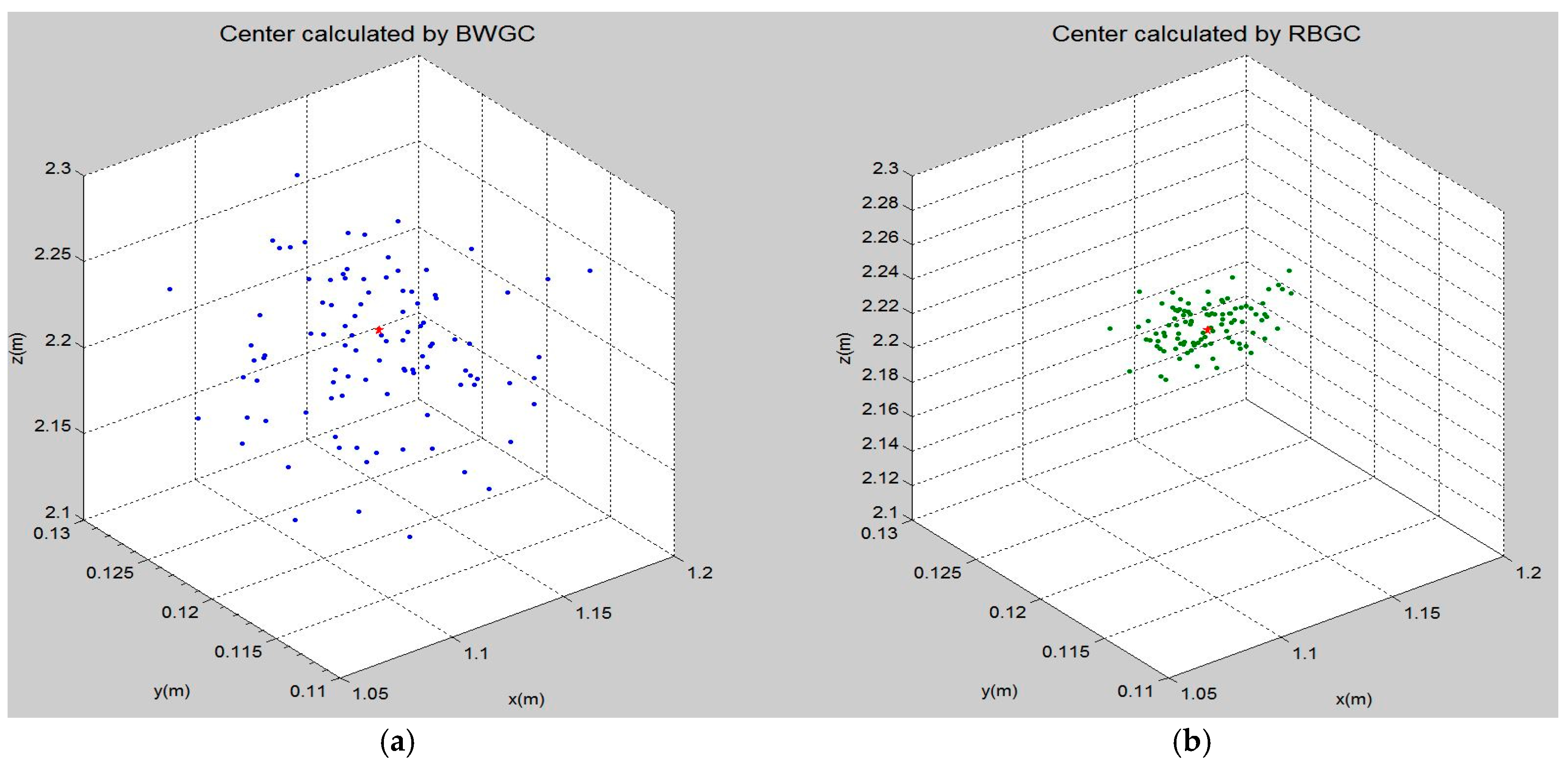
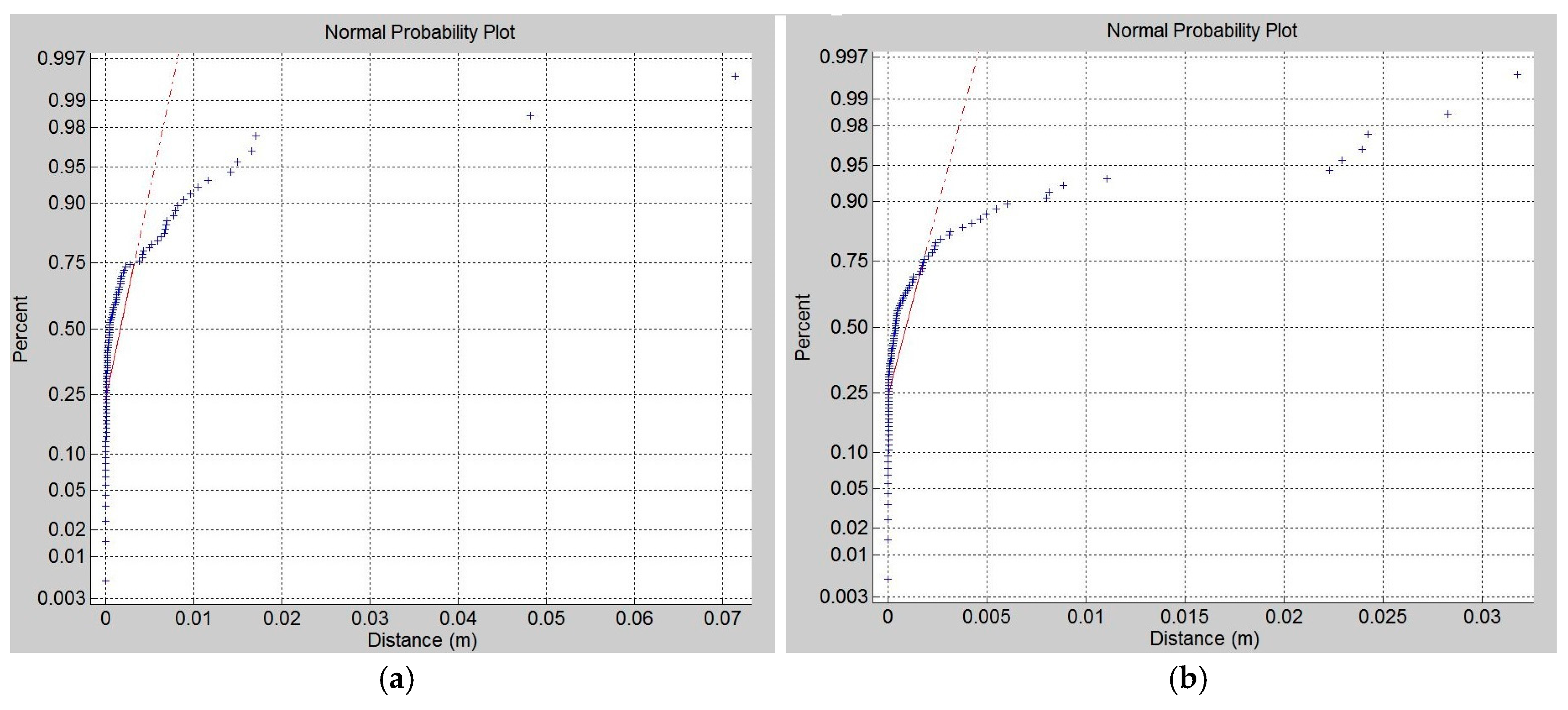
3.2.3. Three-Dimensional Reconstruction
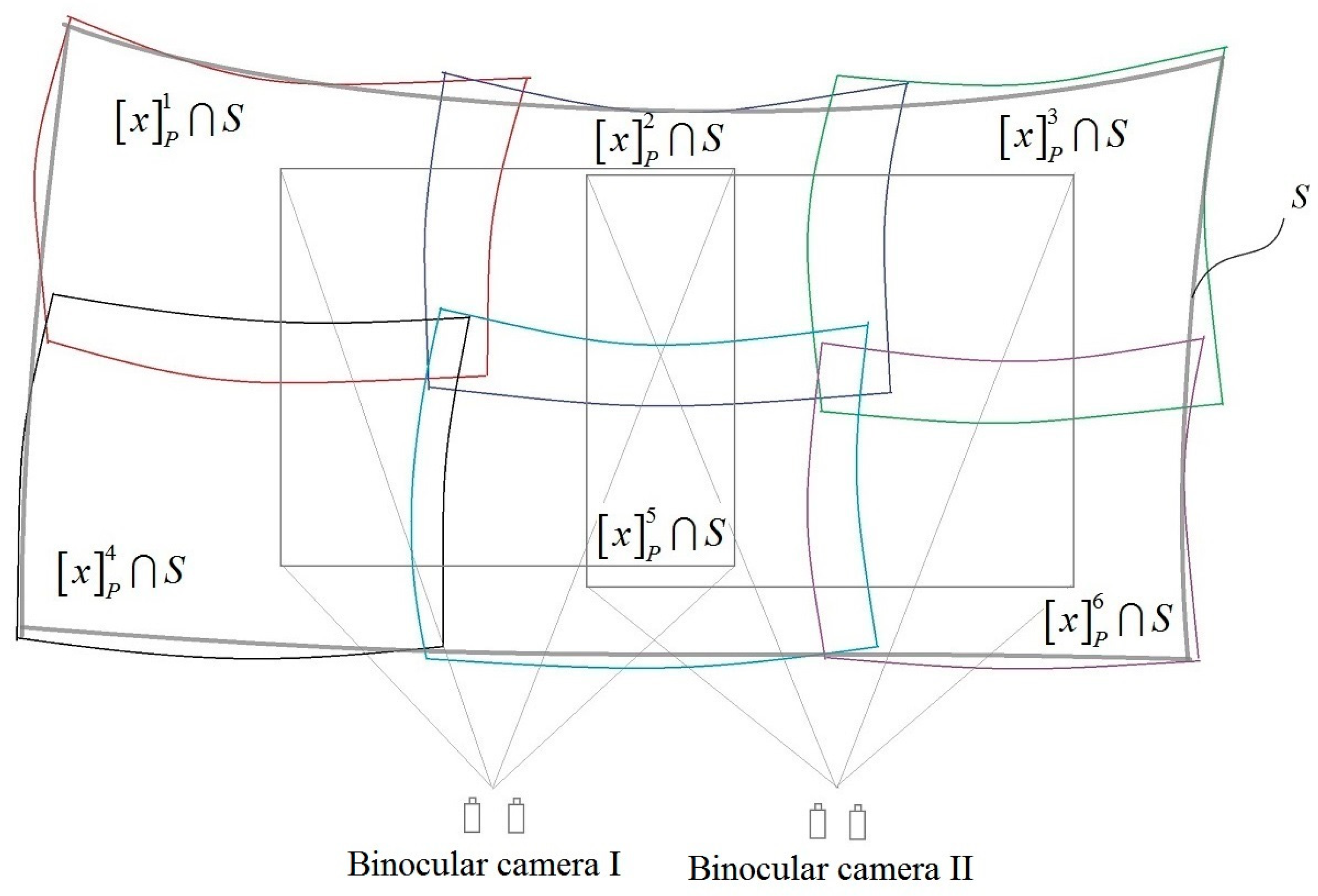
3.3. Geometric Description of Projector
4. Results
4.1. Feature Points Identification Result
4.2. Geometric Registration Result
5. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Allard, J.; Gouranton, V.; Lecointre, L.; Limet, S.; Melin, E.; Raffin, B.; Robert, S. FlowVR: A Middleware for Large Scale Virtual Reality Applications; Springer: Berlin, Germany, 2003; Volume 12, pp. 497–505. [Google Scholar]
- Raffin, B.; Soares, L. PC clusters for virtual reality. In Proceedings of the IEEE Virtual Reality Conference, Alexandria, VA, USA, 25–29 March 2006. [Google Scholar]
- Mine, M.R.; Rose, D.; Yang, B.; van Baar, J.; Grundhofer, A. Projection-based augmented reality in Disney theme parks. Computer 2012, 45, 32–40. [Google Scholar] [CrossRef]
- Sun, W.; Sobel, I.; Culbertson, B.; Gelb, D.; Robinson, I. Calibrating multi-projector cylindrically curved displays for “wallpaper” projection. In Proceedings of the PROCAMS 2008, Marina del Rey, CA, USA, 10 August 2008. [Google Scholar]
- Allen, W.; Ulichney, R. Doubling the addressed resolution of projection displays. SID Symp. Dig. Tech. Papers 2005, 36, 1514–1517. [Google Scholar] [CrossRef]
- Damera, V.N.; Chang, N.L. Realizing super-resolution with superimposed projection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar]
- Raskar, R.; Van, B.J.; Beardsley, P.; Willwacher, T.; Rao, S.; Forlines, C. iLamps: Geometrically aware and self-configuring projectors. In Proceedings of the ACM Transactions on Graphics, San Diego, CA, USA, 27–31 July 2003; pp. 809–819. [Google Scholar]
- Park, J.; Lee, B.U. Defocus and geometric distortion correction for projected images on a curved surface. Appl. Opt. 2016, 55, 896. [Google Scholar] [CrossRef] [PubMed]
- Yang, R.; Gotz, D.; Hensley, J.; Towles, H. Pixel Flex: A reconfigurable multi-projector display system. Visualization 2001. In Proceedings of the IEEE Computer Society, San Diego, CA, USA, 8–12 January 2001; pp. 167–554. [Google Scholar]
- Raij, A.; Gill, G.; Majumder, A.; Towles, H.; Fuchs, H. A comprehensive, automatic, casually-aligned multi-projector display. In Proceedings of the IEEE International Workshop on Projector-Camera Systems, Nice, France, 13–16 October 2003; pp. 203–211. [Google Scholar]
- Raij, A.; Pollefeys, M. Auto-calibration of multi-projector display walls. In Proceedings of the International Conference on Pattern Recognition, Cambridge, UK, 23–26 August 2004; pp. 14–17. [Google Scholar]
- Brown, M.; Majumder, A.; Yang, R. Camera-based calibration techniques for seamless multi-projector displays. IEEE Trans. Vis. Comput. Graph. 2005, 11, 193–206. [Google Scholar] [CrossRef] [PubMed]
- Chufan, J.; Beatrice, L.; Song, Z. Three-dimensional shape measurement using a structured light system with dual projectors. Appl. Opt. 2018, 57, 3983. [Google Scholar]
- Hongyu, W.; Chengdong, W.; Tong, J.; Xiaosheng, Y. Projector calibration algorithm in omnidirectional structured light. In Proceedings of the LIDAR Imaging Detection and Target Recognition, Changchun, China, 23–25 July 2017; p. 11. [Google Scholar]
- Xiao, C.; Yang, H.; Su, X. Image alignment algorithm for multi-projector display system based on structured light. J. Southwest Jiaotong Univ. 2012, 10, 790–796. [Google Scholar]
- Robert, W.D. The gray code. J. Univers. Comput. Sci. 2007, 13, 1573–1597. [Google Scholar]
- Yi, S. Auto-Calibrated Multi-Projector Tiled Display System. Ph.D. Thesis, Beihang University, Beijing, China, December 2012. [Google Scholar]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, S.; Zhao, M.; Dai, S. Automatic Registration of Multi-Projector Based on Coded Structured Light. Symmetry 2019, 11, 1397. https://doi.org/10.3390/sym11111397
Zhao S, Zhao M, Dai S. Automatic Registration of Multi-Projector Based on Coded Structured Light. Symmetry. 2019; 11(11):1397. https://doi.org/10.3390/sym11111397
Chicago/Turabian StyleZhao, Shuaihe, Mengyi Zhao, and Shuling Dai. 2019. "Automatic Registration of Multi-Projector Based on Coded Structured Light" Symmetry 11, no. 11: 1397. https://doi.org/10.3390/sym11111397
APA StyleZhao, S., Zhao, M., & Dai, S. (2019). Automatic Registration of Multi-Projector Based on Coded Structured Light. Symmetry, 11(11), 1397. https://doi.org/10.3390/sym11111397




