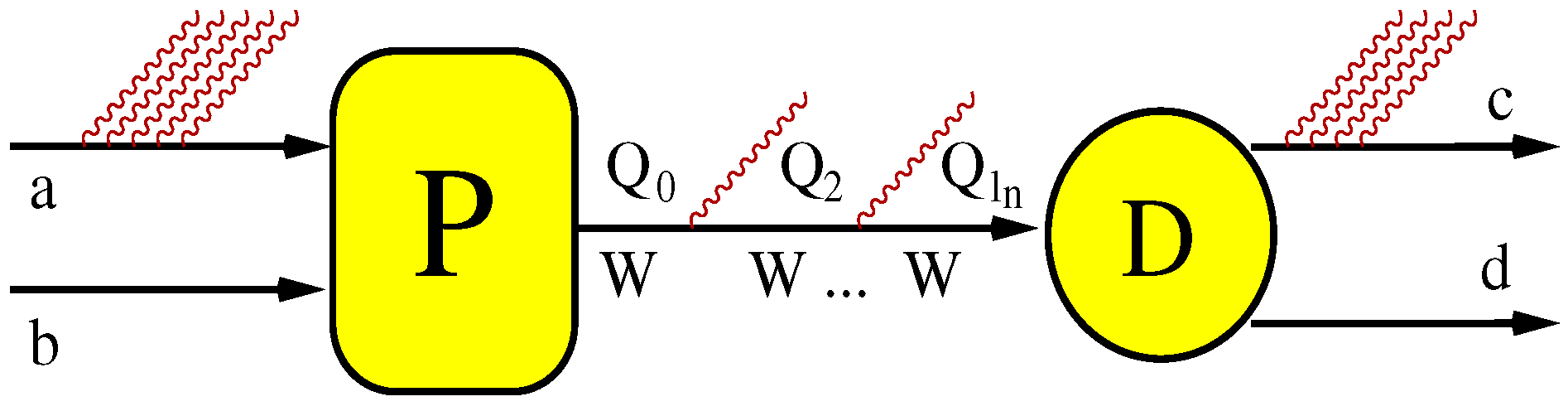1. Introduction
Emission of soft photons accompany every process with charged particles. Therefore proper treatment of such emission is mandatory. These emissions happen from the external particles, decouple from the process itself and can be resummed and exponentiated in an universal way [
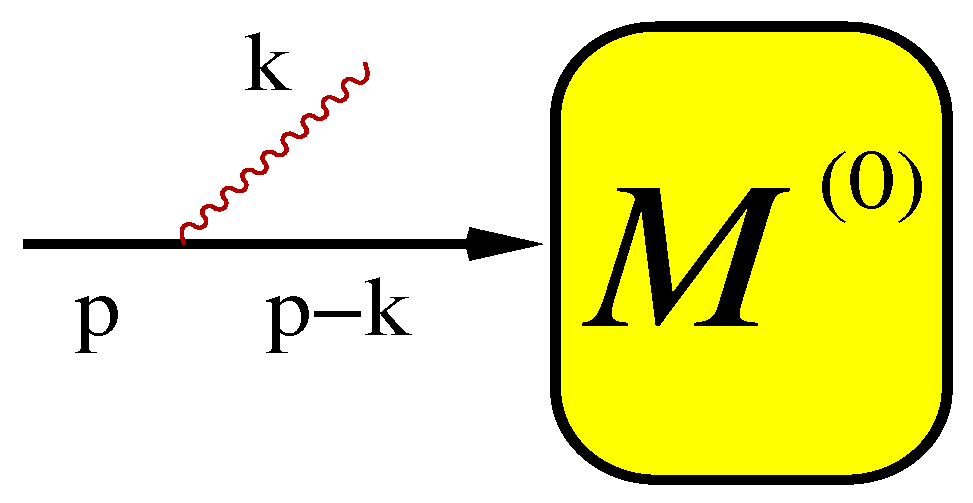
1]. In such an approach the information on the photonic emission is not transmitted to the process itself. This can pose a problem if the process includes resonant particles in the intermediate state, because any energy loss due to photonic emission, larger compared to the width of the resonance can shift the process off resonance and the Γ/
M suppression should be visible. We will refer to it as the recoil effect. This effect for the case of neutral resonance has been resolved with the help of coherent states in References [
2,
3], and then at the level of spin amplitudes in Reference [
4].
In the case of charged resonances another complication appears: the resonance is a source of the soft photons as well. Of course, strictly speaking, the internal particles do not radiate soft photons (do not have singularities due to such radiation), as demonstrated by Yennie, Frautschi and Suura (YFS61) in the classical Reference [
1]. However, the resonances are special – they are quasi-stable and there is a clear separation between their production and decay. One can illustrate it with the case of lepton
for which the lifetime is longer than the time-scale of the production by an astronomical factor of
. Resummation (exponentiation) of such emissions is the subject of this note. We will present a solution that smoothly interpolates between two situations: for
we have the normal YFS61 behaviour, i.e. internal radiation is suppressed, whereas for
the recoil effect is properly accounted for. More details can be found in a recent paper [
5].
We analyse two processes: the simplest toy model, , on which we demonstrate the methodology; and with an eye on future collider, the full-scale process, . The latter process is one of a few gold-plated processes of the projected FCCee machine. In its second phase, at the -threshold, the FCCee would provide about events. That number corresponds to a statistical error on the total cross section of 0.02%, or equivalently MeV (measured from the threshold scan). The current state of the art, inherited from the LEP2 era, is 0.5–2% for the total cross section. That means, an increase of the precision by factor of 100 is needed. The most important part of that challenge is to calculate the corrections to the signal process . Exponentiation of soft radiation from Ws, which is equivalent to resummation (exact in the soft limit) of photon interferences between production and decay stages as well as between decays of the two Ws would encapsulate an important part of these corrections, not only to the second order but to all orders!
There is also another, practical, and perhaps even most important, application of the soft YFS-based exponentiation—the Monte Carlo event generators. The whole familly of such generators has emerged from the never published note of S. Jadach [
6]. All of them generate multiple sof-photon emissions based on the classical YFS61 exponentiation. Among them one should list
BHLUMI [
7] and
KORALZ [
8]. The latter one has been then replaced by a next-generation-code
KKMC [
9] which includes recoil in production-decay interferences of the
Z-resonance. The partial solutions related to the charged
W bosons have been implemented in the
YFSWW3 program [
10] where exponentiation of the emission in the
pair production (
) with the recoil has been done and in
WINHAC [
11] in which exponentiation of radiation in the
W decay (
) is implemented for the single-
W process.
At last, let us only touch upon the issue of QED deconvolution. The YFS approach provides for a very convenient scheme of such a deconvolution also in higher orders. When supplied with the treatment of resonances, it would form a complete and well defined deconvolution system.
The paper is organized as follows. In
Section 2 we present the standard YFS scheme and its new extension on the example of the simple “toy model”
. In
Section 3 we discuss the exponentiation in the process of
W-pair production and decay. In particular we show how to introduce virtual soft-photon interferences and how to exponentiate them. The last section contains conclusions and summary.
3. W-Pair Production and Decay
Having explained in very detail the resummation of the real emission in the toy model, we now proceed briefly to the resummation in the
W-pair production and decay process. Let us include virtual photons into the formulae. In the case of YFS61, shown on LHS of
Figure 5, their resummation goes in complete analogy to the real photons, and the appropriate formula for
m real photons and an arbitrary number of virtual ones, for 6 external particles, reads:
where
The real soft-photon emissions have the familiar form of a product of the currents , and the similar virtual soft-photon currents are resummed.
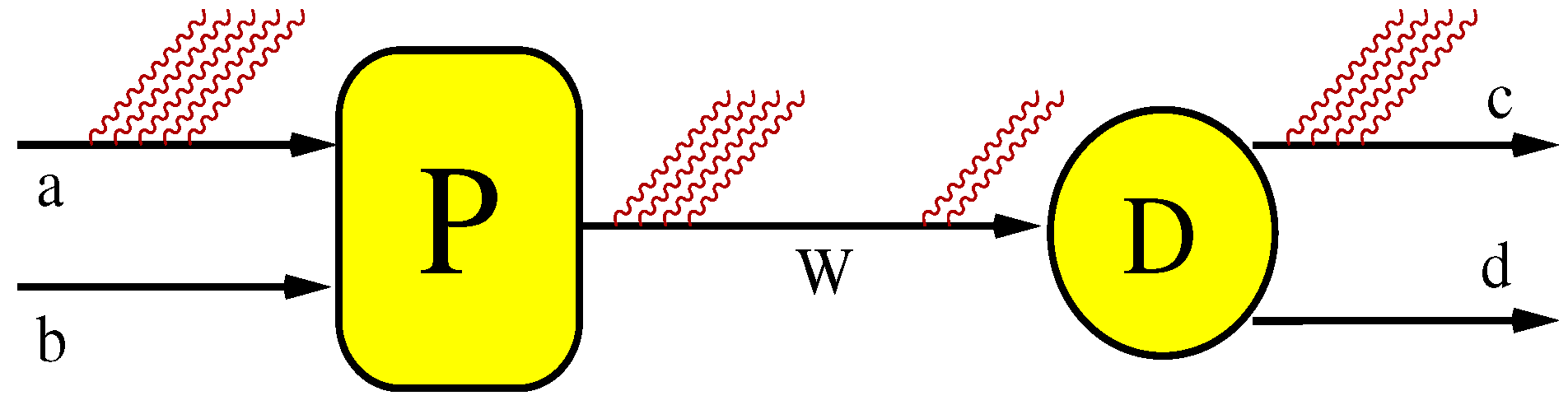
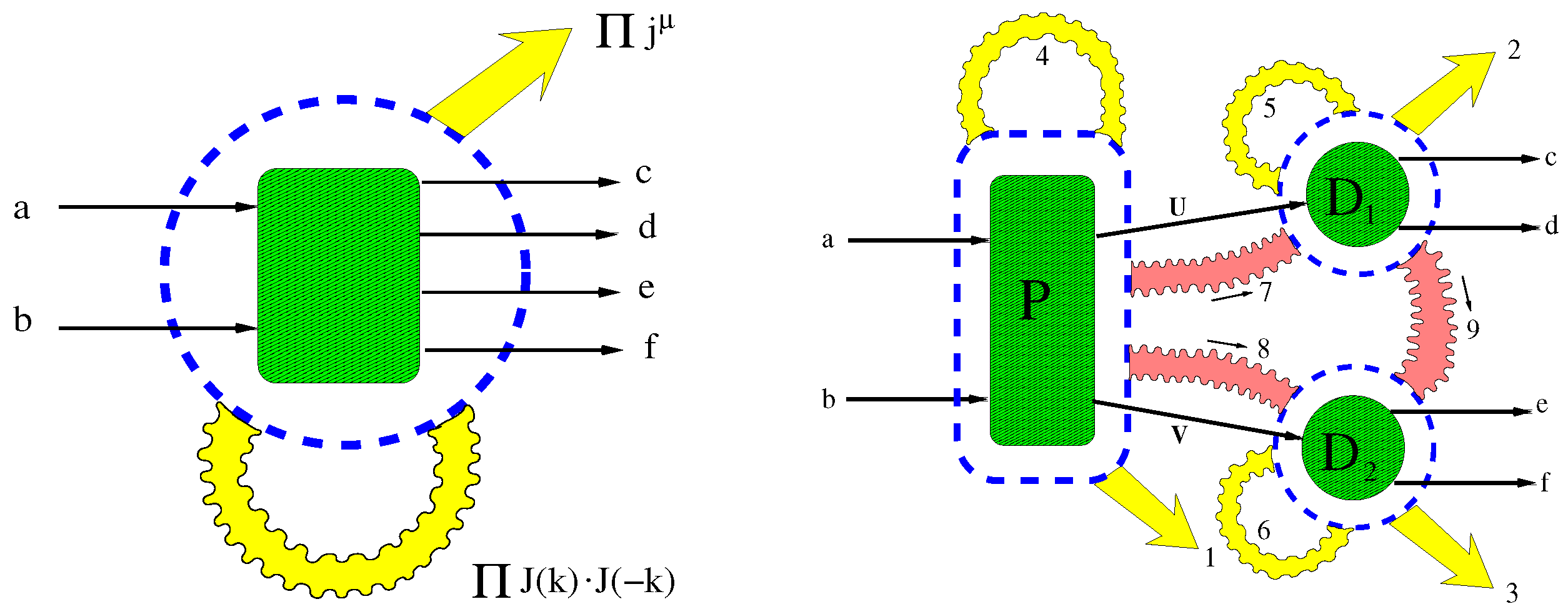
Let us now proceed to a new, extended scheme. That scheme is illustrated on RHS of
Figure 5. We have additional real soft-photon emissions from
Ws as well as all virtual soft-photon interferences between the production and two decays. The resummation of real emissions proceeds exactly as in the toy example as a product of currents. The virtual soft-photon emissions follow the same logics and formulae as the real ones. The only exceptions are the issues related to the definition of the mass and width of the resonance and the UV renormalisation. Analysis of these issues is beyond the scope of this paper. Here we make an educated guess based on the solid principle of the cancellation of soft-photon singularities in QED and propose the following formula for a given partition of real momenta
is the sum of appropriate photon momenta as depicted on the RHS of
Figure 5. The recoiled
W propagators do not depend on
and
, i.e. on the interferences
and
, so the corresponding sums can be folded into the exponential form. For example:
In order to fold the virtual sums 7, 8 and 9 we have to rearrange the
W propagators which depend on
and
. That can be done in the soft-photon approximation, i.e., dropping all bilinear products of the type
. With the help of formulae such as
we can write for one of the
Ws
where
. That way we have rewritten the recoiled
W propagator in a factorized form suitable for the resummation and we can write down the final formula
, .
The
function is defined as
Equations (26) and (27) are the principal new result presented in this note. Equation (26) has an identical, exponential form as the original YFS61 formula of Equation (20). The only difference is that the B functions responsible for the virtual interferences include now ratios of W propagators, see Equation (27). That way the recoil effect is incorporated into the scheme.