Numerical Analysis with Keller-Box Scheme for Stagnation Point Effect on Flow of Micropolar Nanofluid over an Inclined Surface
Abstract
:1. Introduction
2. Mathematical Formulation
3. Results and Discussion
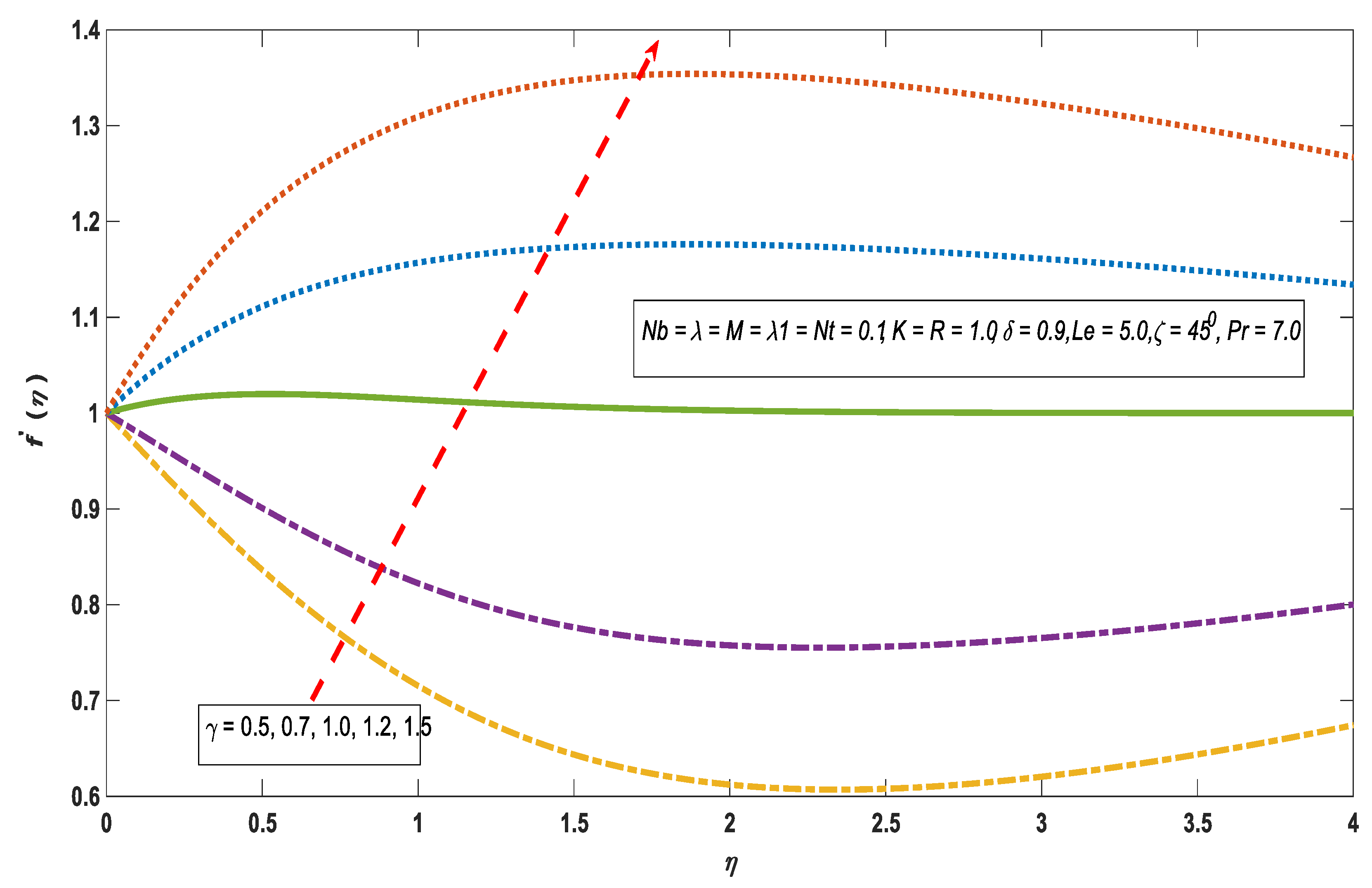
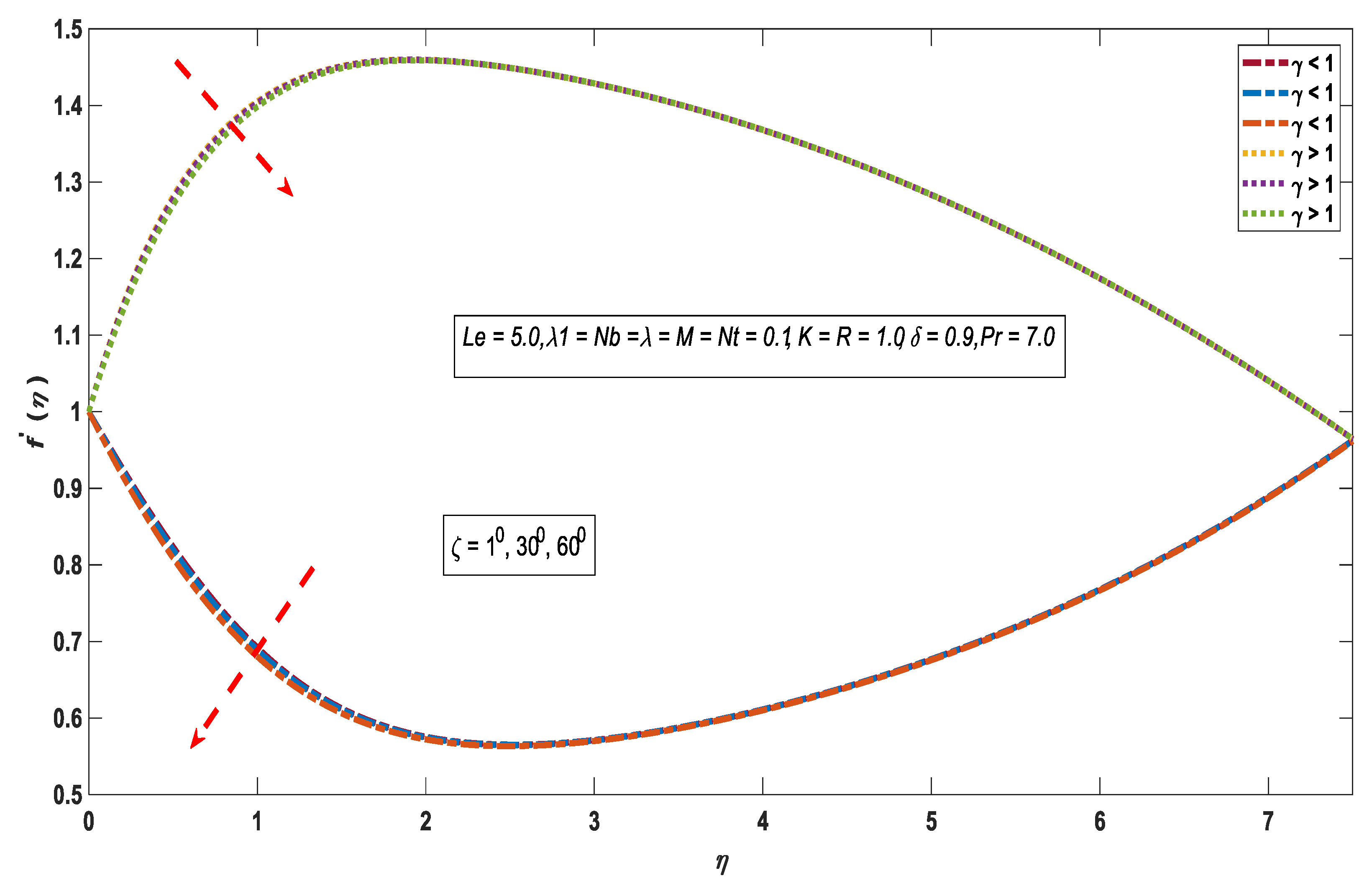
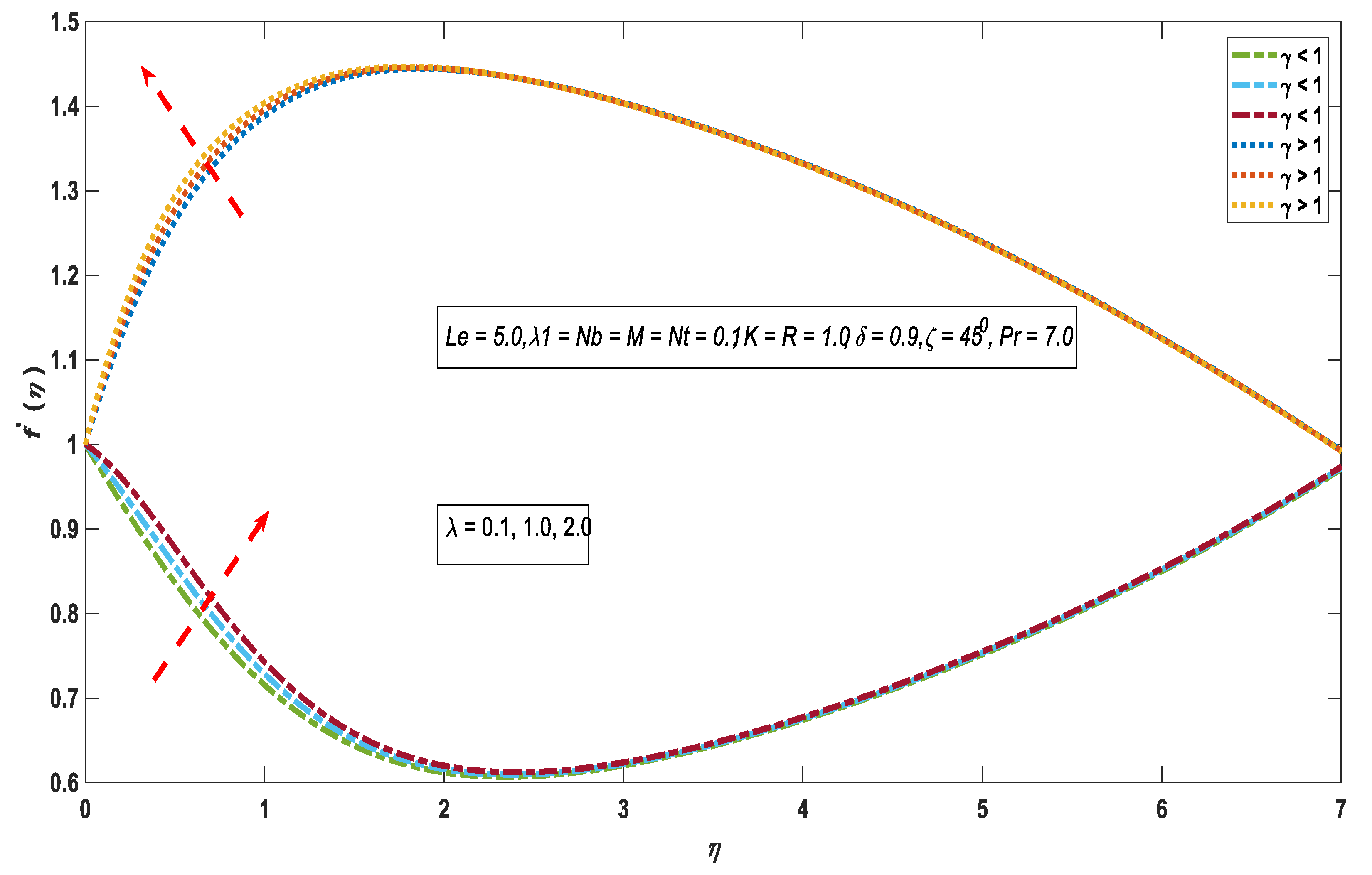
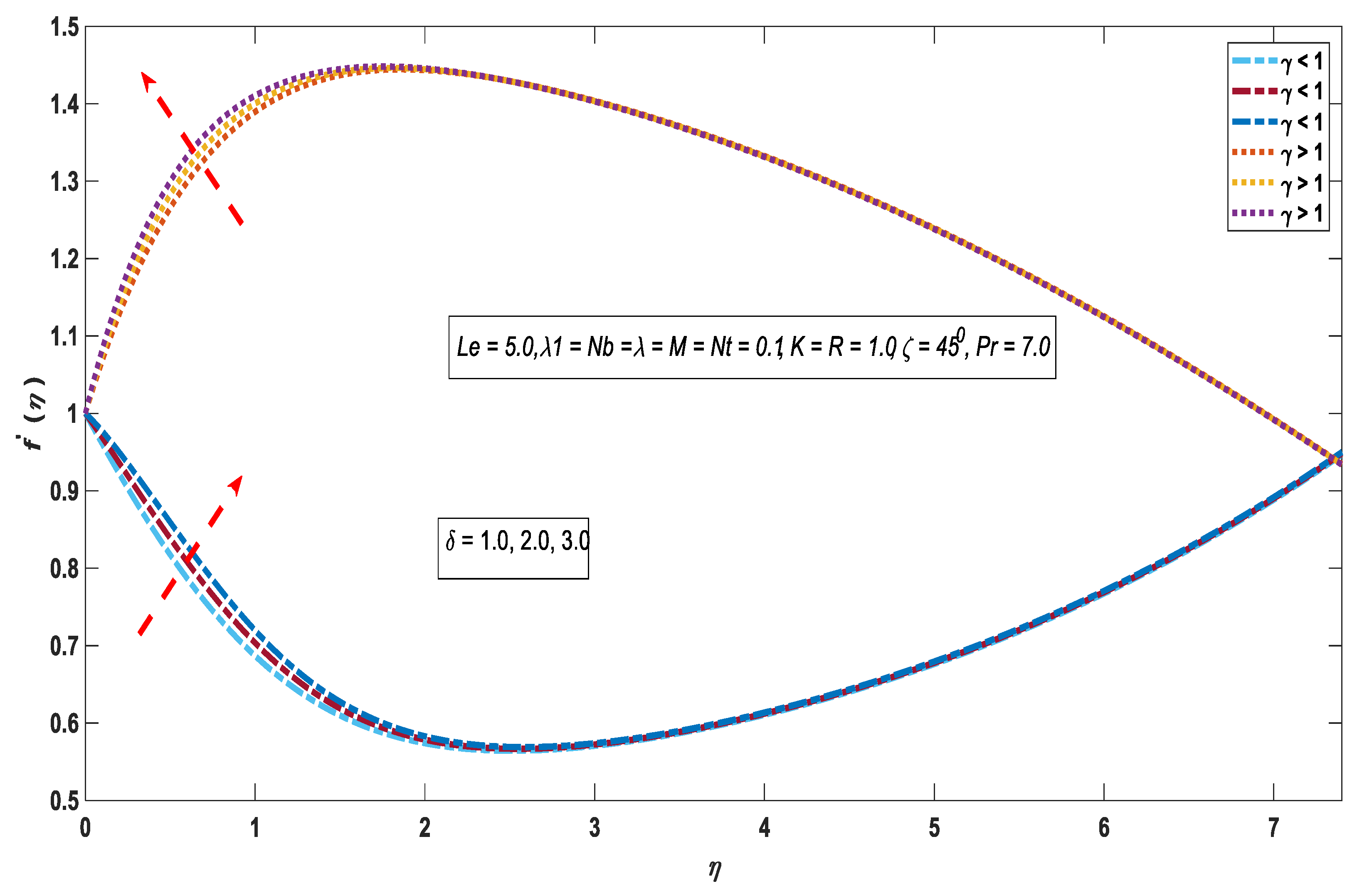
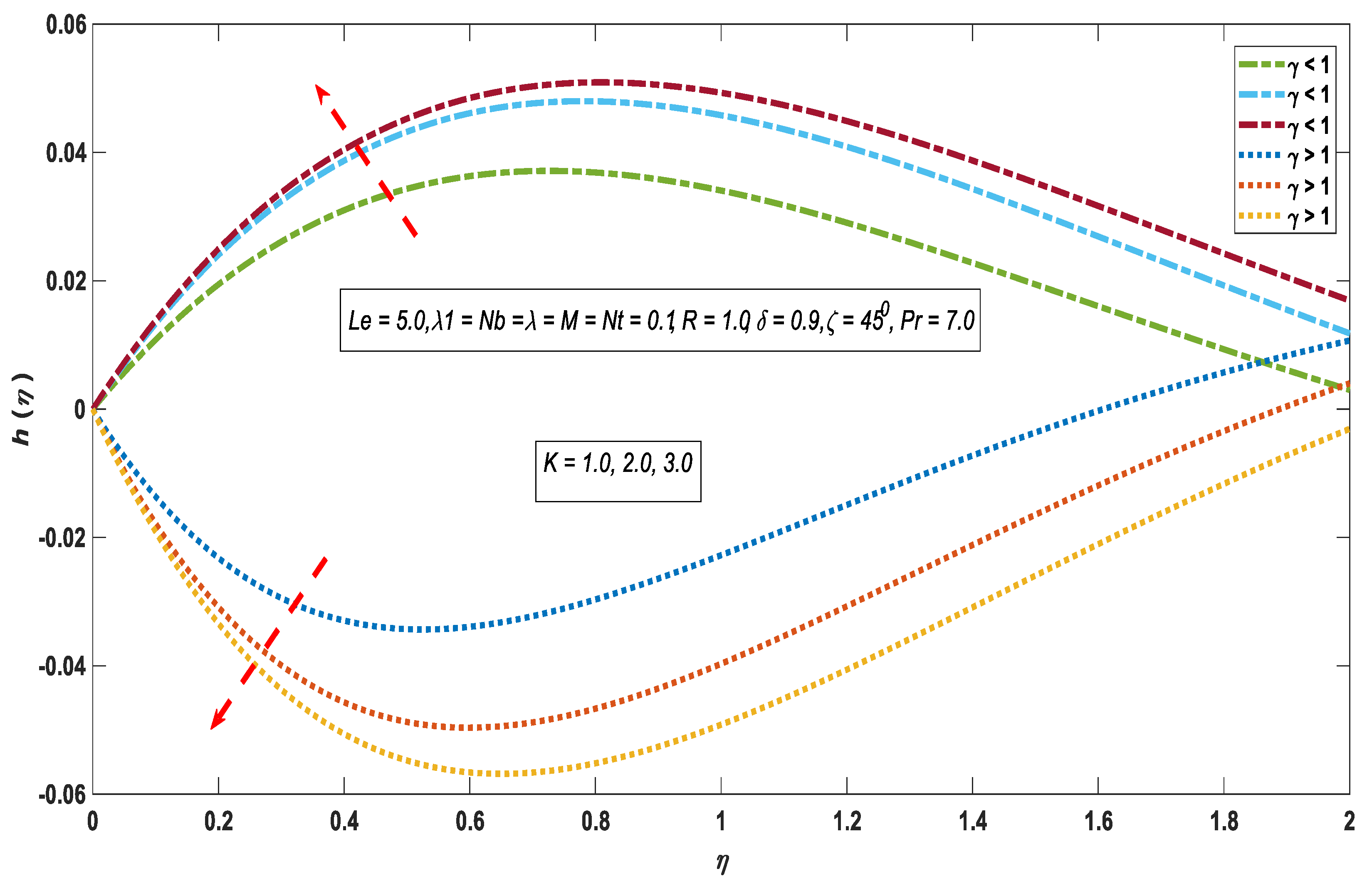
3.1. Velocity Profile
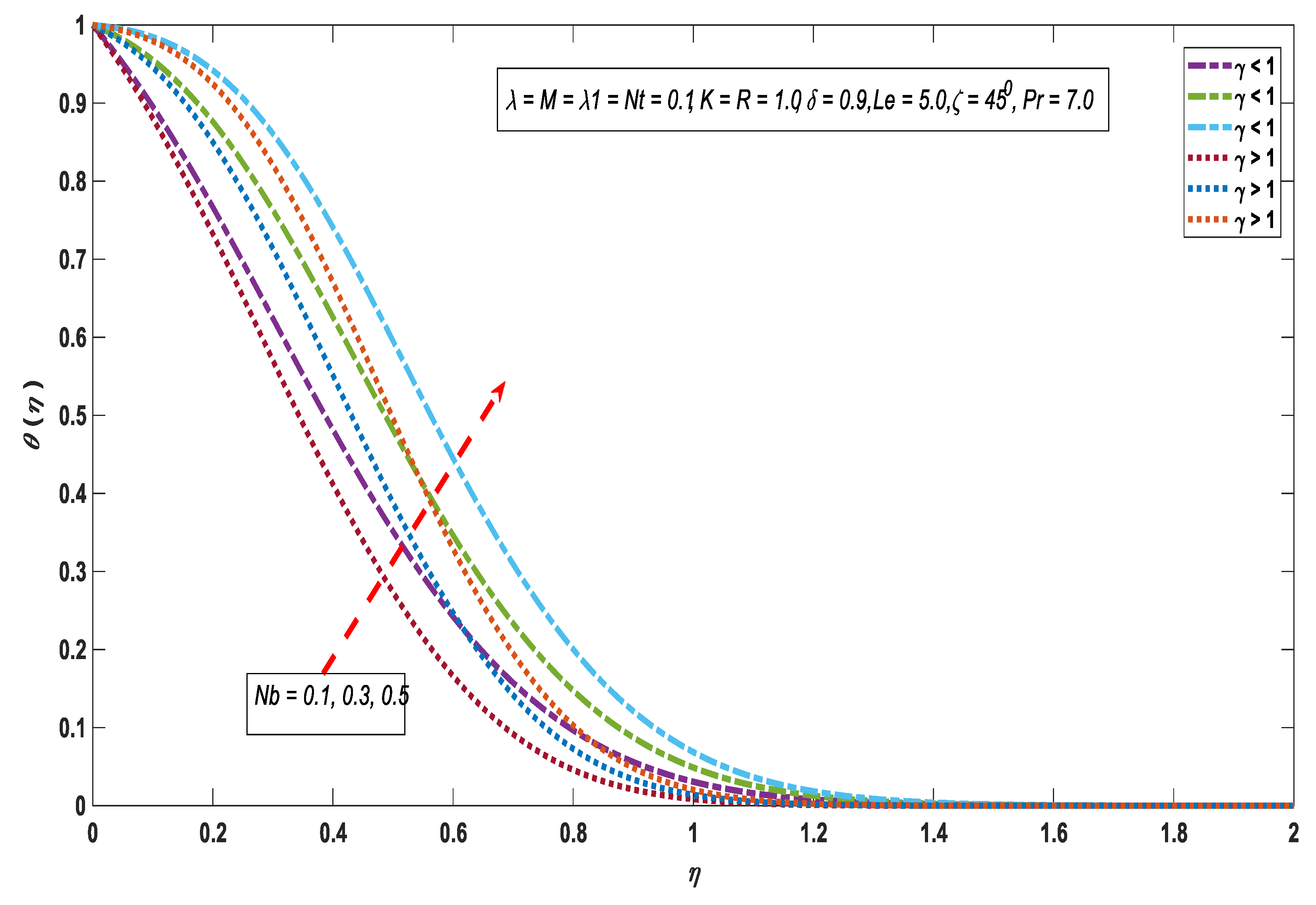
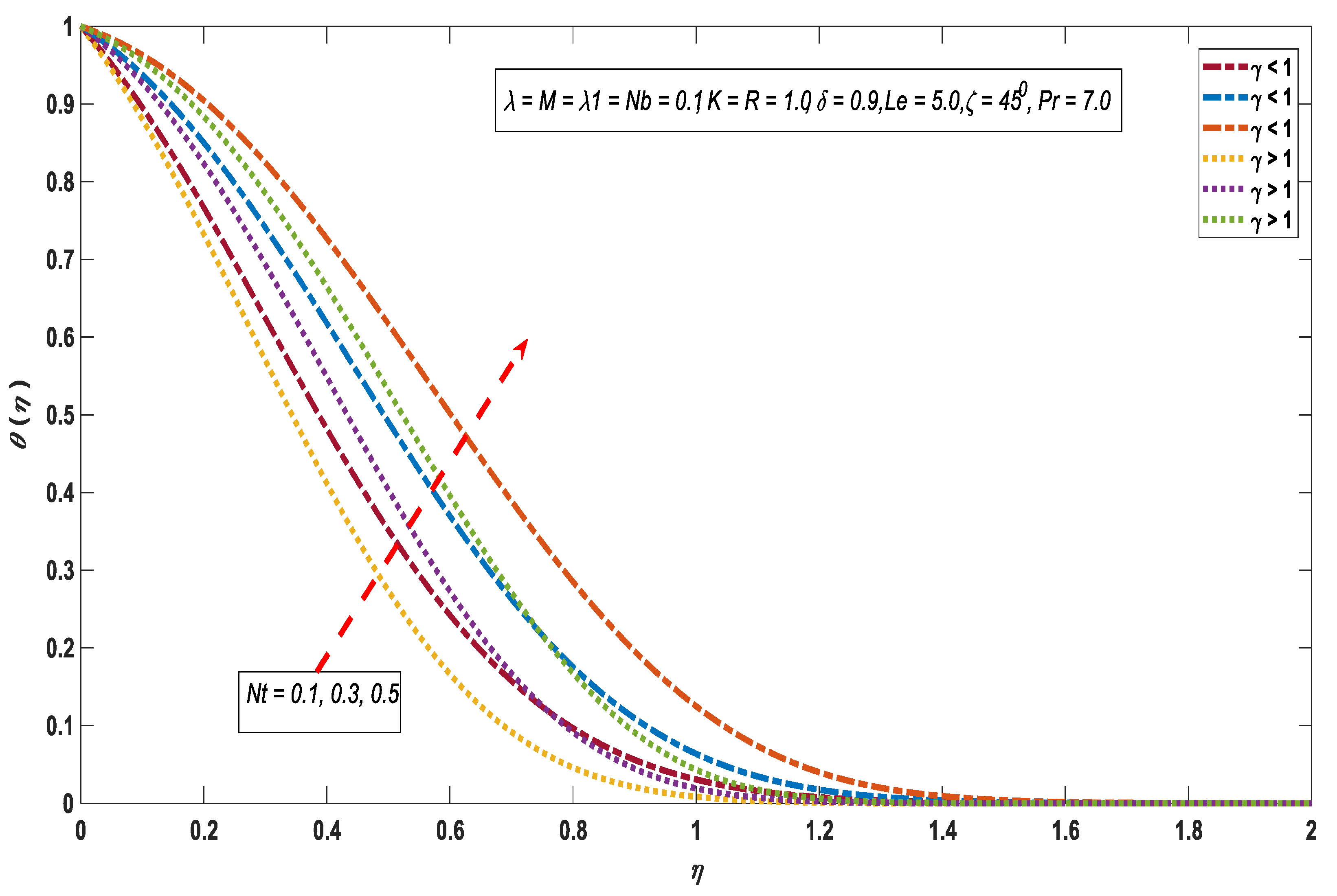
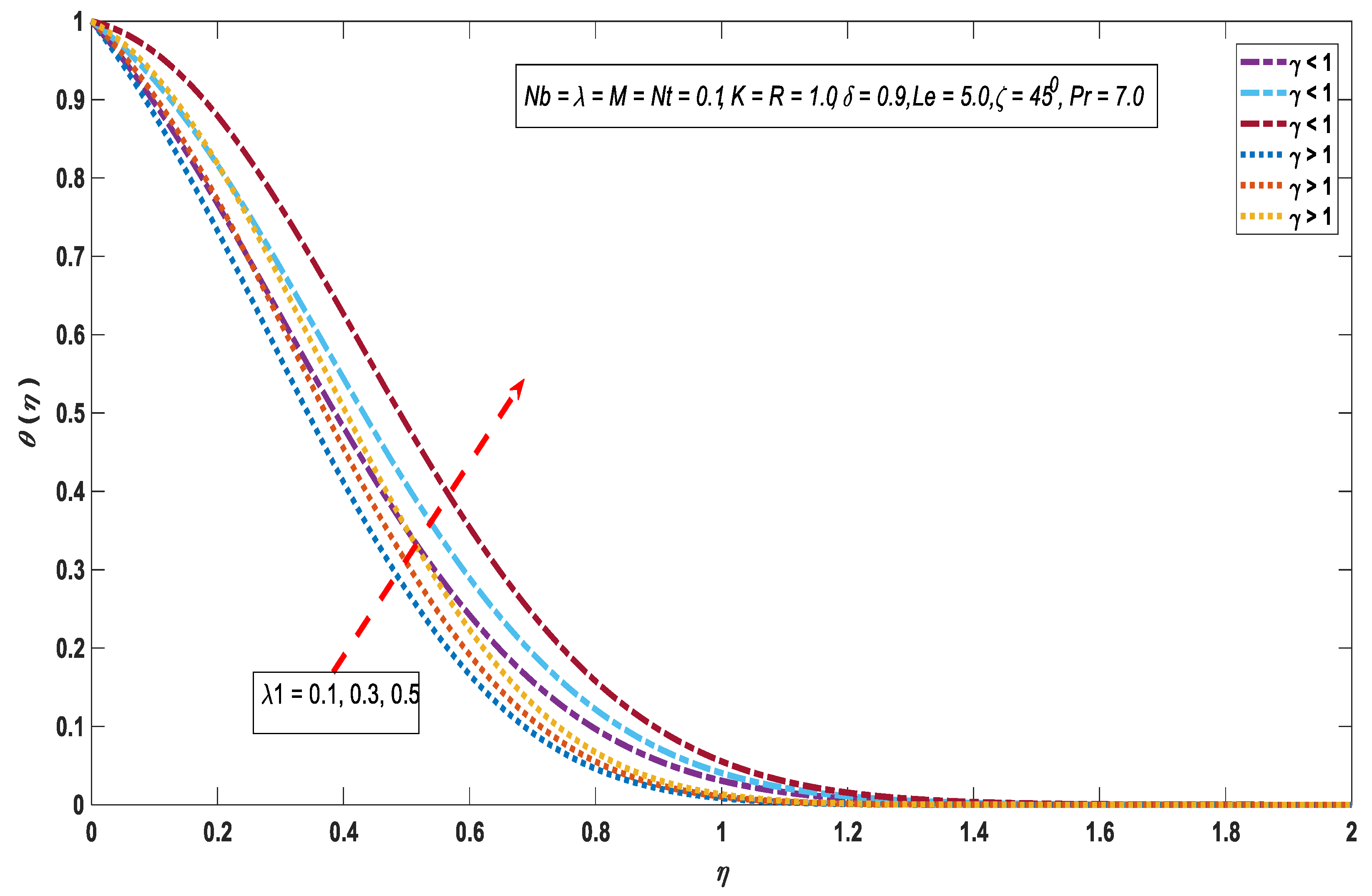
3.2. Temperature Profile
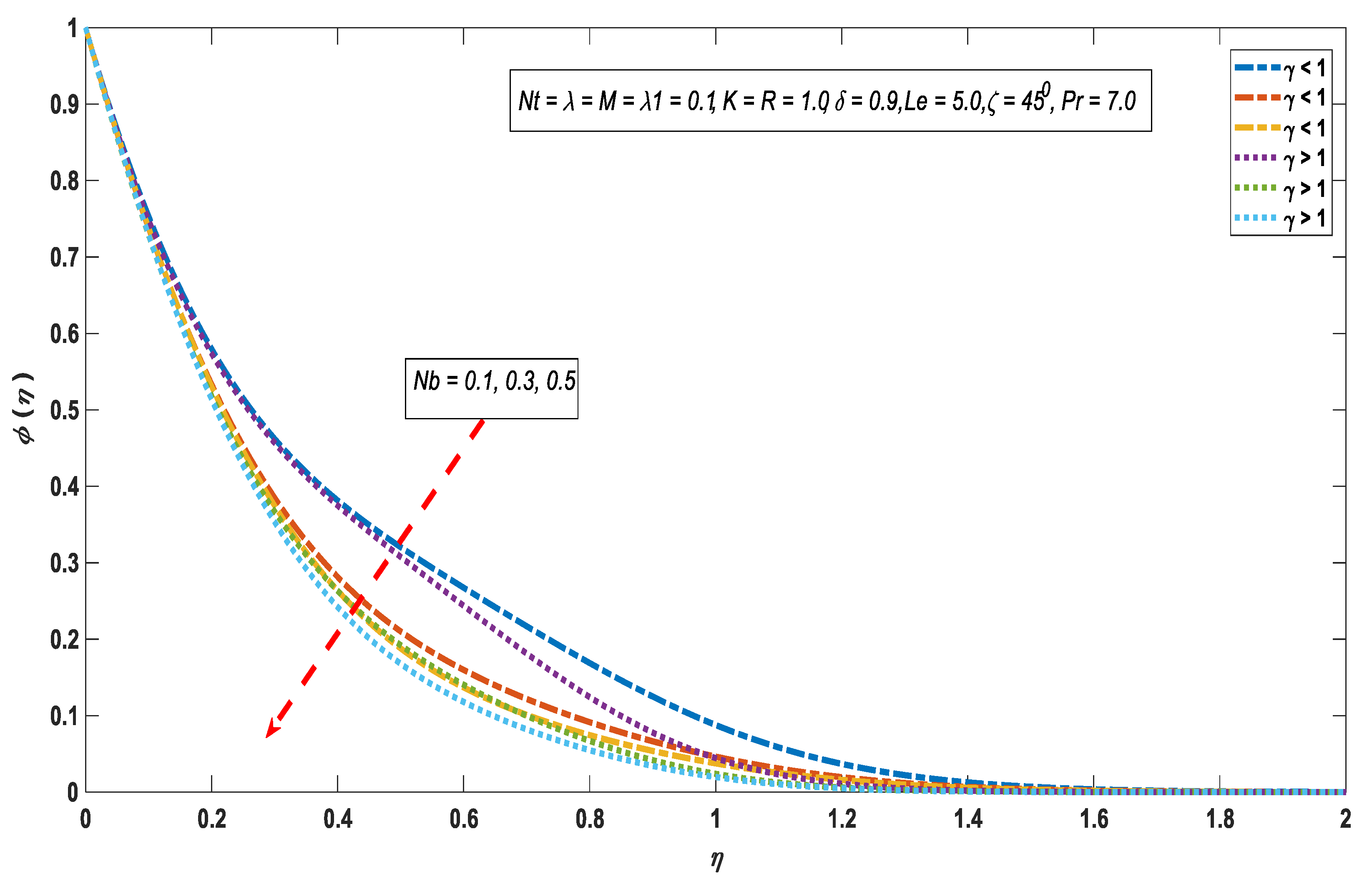
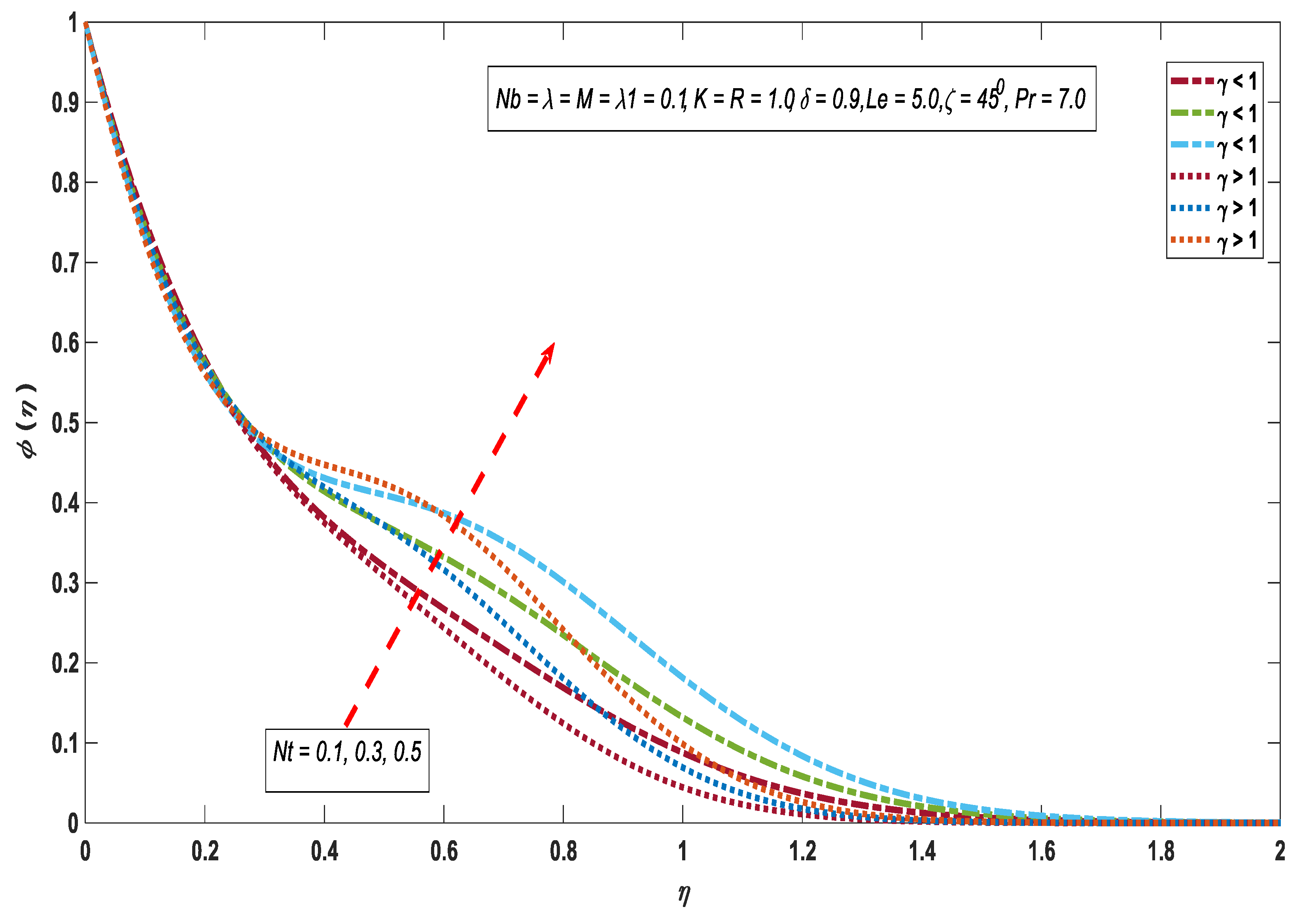
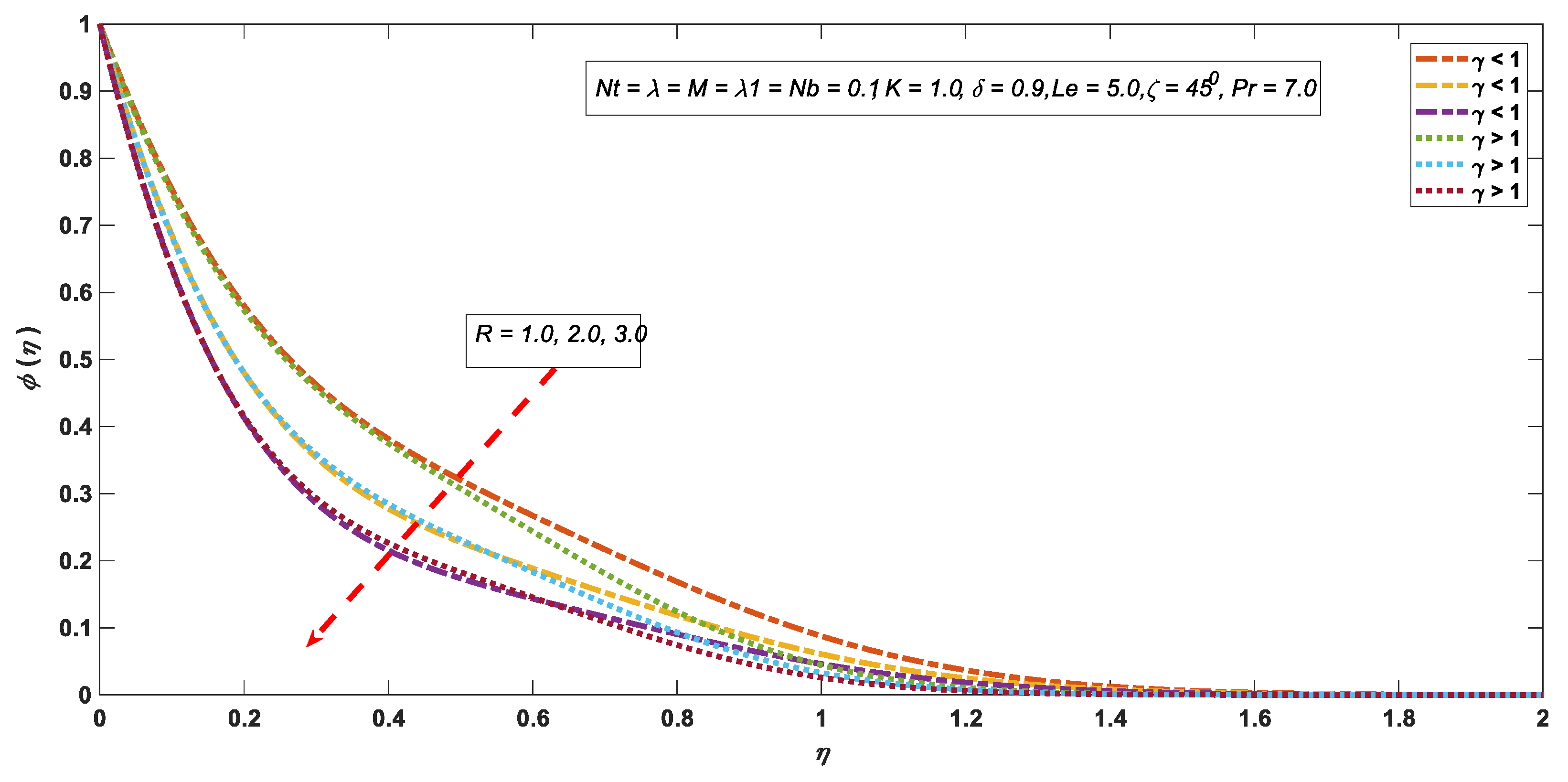
3.3. Concentration Profile
4. Conclusions
- ➢
- Energy and mass exchange enhance with the growth of the stagnation parameter.
- ➢
- The chemical reaction diminishes the concentration field with higher values.
- ➢
- The stagnation parameter shows direct correspondence with the velocity profile.
- ➢
- The heat generation or absorption factor declines the energy transport rate, whereas it improves the mass flux rate.
- ➢
- The velocity profile shows an opposite behavior for , and .
- ➢
- The velocity profile shows direct relation against growing magnitudes of bouncy impacts for , and .
- ➢
- This study can be utilized in the building envelop applications because of the heat transfer.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations Table
| Fluid Concentration | Dimensionless Reaction Rate | Heat Generation Parameter | |||
| Skin friction coefficient | Chemical reaction parameter | Reynolds number | |||
| Ambient nanoparticle volume fraction | Lewis number | Sherwood number | |||
| Surface volume fraction | Brownian motion parameter | Fluid temperature | |||
| Specific heat at constant pressure | Thermophoretic parameter | Wall temperature | |||
| Brownian diffusion coefficient | Nusselt number | Ambient temperature | |||
| Thermophoretic diffusion coefficient | Prandtle number | Composite velocity | |||
| Similarity function for velocity | Dimensionless heat generation | Wall velocity | |||
| Volume heat capacity | Kinematic viscosity | Dynamic viscosity | |||
| Dimensionless solid volume fraction | Condition at the wall | Ambient condition | |||
| Solutal buoyancy parameter | Thermal expansion coefficient | Concentration expansion coefficient | |||
| Electric conductivity | Spin gradient viscosity | Vertex viscosity | |||
| Micro inertia per unit mass | Inclination parameter | Differentiation with respect to | |||
| Velocity in direction | Velocity in direction | Cartesian coordinate | |||
| Dimensionless temperature | Velocity ratio parameter | Thermal conductivity | |||
| Fluid density | Bouncy parameter | Uniform magnetic field strength | |||
| Material parameter | Similarity independent variable | Thermal diffusivity | |||
| Non-dimensional angular velocity | Gravitational acceleration | Reduced Nusselt number | |||
| Reduced Sherwood number |
References
- Mishra, S.; Khan, I.; Al-Mdallal, Q.; Asifa, T. Free convective micropolar fluid flow and heat transfer over a shrinking sheet with heat source. Case Stud. Therm. Eng. 2018, 11, 113–119. [Google Scholar] [CrossRef]
- Salleh, M.Z.; Rohni, A.M.; Amin, N. Boundary Layer Flow Due to a Moving Flat Plate in Micropolar Fluid. J. Teknol. 2005, 43, 67–83. [Google Scholar] [CrossRef]
- Eringen, A.C. Simple microfluids. Int. J. Eng. Sci. 1964, 2, 205–217. [Google Scholar] [CrossRef]
- Rahman, M.M.; Aziz, A.; Al-Lawatia, M.A. Heat transfer in micropolar fluid along an inclined permeable plate with variable fluid properties. Int. J. Therm. Sci. 2010, 49, 993–1002. [Google Scholar] [CrossRef]
- Uddin, M.J. Convective Flow of Micropolar Fluids along an Inclined Flat Plate with Variable Electric Conductivity and Uniform Surface Heat Flux. Daffodil Int. Univ. J. Sci. Technol. 2011, 6, 69–79. [Google Scholar] [CrossRef]
- Md, S.; Thumma, T.; Shamshuddin, M. Numerical study of a dissipative micropolar fluid flow past an inclined porous plate with heat source/sink. Propuls. Power Res. 2019, 8, 56–68. [Google Scholar] [CrossRef]
- Rafique, K.; Anwar, M.I.; Misiran, M. Numerical Study on Micropolar Nanofluid Flow over an Inclined Surface by Means of Keller-Box. Asian J. Probab. Stat. 2019, 4, 1–21. [Google Scholar] [CrossRef]
- Ali, V.; Gul, T.; Afridi, S.; Ali, F.; Alharbi, S.O.; Khan, I. Thin Film Flow of Micropolar Fluid in a Permeable Medium. Coatings 2019, 9, 98. [Google Scholar] [CrossRef]
- Matta, A.; Gajjela, N. Order of chemical reaction and convective boundary condition effects on micropolar fluid flow over a stretching sheet. AIP Adv. 2018, 8, 115212. [Google Scholar] [CrossRef] [Green Version]
- Jaiswal, S.; Yadav, P.K. A micropolar-Newtonian blood flow model through a porous layered artery in the presence of a magnetic field. Phys. Fluids 2019, 31, 071901. [Google Scholar] [CrossRef]
- Rauf, A.; Shehzad, S.A.; Abbas, Z.; Hayat, T. Unsteady three-dimensional MHD flow of the micropolar fluid over an oscillatory disk with Cattaneo-Christov double diffusion. Appl. Math. Mech. 2019, 40, 1471–1486. [Google Scholar] [CrossRef]
- Soid, S.K.; Ishak, A.; Pop, I. MHD Stagnation-Point Flow over a Stretching/Shrinking Sheet in a Micropolar Fluid with a Slip Boundary. Sains Malays. 2018, 47, 2907–2916. [Google Scholar] [CrossRef]
- Xiao, B.; Wang, W.; Zhang, X.; Long, G.; Fan, J.; Chen, H.; Deng, L. A novel fractal solution for permeability and Kozeny-Carman constant of fibrous porous media made up of solid particles and porous fibers. Powder Technol. 2019, 349, 92–98. [Google Scholar] [CrossRef]
- Duncan, T.V. Applications of nanotechnology in food packaging and food safety: Barrier materials, antimicrobials and sensors. J. Colloid Interface Sci. 2011, 363, 1–24. [Google Scholar] [CrossRef]
- Qu, X.; Alvarez, P.J.; Li, Q. Applications of nanotechnology in water and wastewater treatment. Water Res. 2013, 47, 3931–3946. [Google Scholar] [CrossRef]
- Krajnik, P.; Pusavec, F.; Rashid, A. Nanofluids: Properties, Applications and Sustainability Aspects in Materials Processing Technologies. In Advances in Sustainable Manufacturing; Springer Science and Business Media LLC: Berlin, Germany, 2011; pp. 107–113. [Google Scholar]
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; No. ANL/MSD/CP-84938; CONF-951135-29; Argonne National Lab.: DuPage, IL, USA, 1995. [Google Scholar]
- Abbas, Z.; Hasnain, J.; Sajid, M. Effects of Slip on MHD Flow of a Dusty Fluid over a Stretching Sheet through Porous Space. J. Eng. Thermophys. 2019, 28, 84–102. [Google Scholar] [CrossRef]
- Sakiadis, B.C. Boundary-layer behavior on continuous solid surfaces: I. Boundary-layer equations for two-dimensional and axisymmetric flow. AIChE J. 1961, 7, 26–28. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. Z. Angew. Math. Phys. ZAMP 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Ali, M.; Alim, M.A.; Alam, M.S. Heat transfer boundary layer flow past an inclined stretching sheet in the presence of magnetic field. Int. J. Adv. Res. Technol. 2014, 3, 34–40. [Google Scholar]
- Khan, I.; Shafquatullah; Malik, M.; Hussain, A.; Khan, M. Magnetohydrodynamics Carreau nanofluid flow over an inclined convective heated stretching cylinder with Joule heating. Results Phys. 2017, 7, 4001–4012. [Google Scholar] [CrossRef]
- Rashad, A.M. Unsteady nanofluid flow over an inclined stretching surface with convective boundary condition and anisotropic slip impact. Int. J. Heat Technol. 2017, 35, 82–90. [Google Scholar] [CrossRef]
- Reddy, P.B.A.; Bareddy, P. Magnetohydrodynamic flow of a Casson fluid over an exponentially inclined permeable stretching surface with thermal radiation and chemical reaction. Ain Shams Eng. J. 2016, 7, 593–602. [Google Scholar] [CrossRef] [Green Version]
- Samanta, A. Effect of electric field on an oscillatory film flow. Phys. Fluids 2019, 31, 034109. [Google Scholar] [CrossRef]
- Ramreddy, C.; Naveen, P.; Srinivasacharya, D. Department of Mathematics National Institute of Technology Warangal-; India Quadratic Convective Flow of a Micropolar Fluid along an Inclined Plate in a Non-Darcy Porous Medium with Convective Boundary Condition. Nonlinear Eng. 2017, 6, 139–151. [Google Scholar] [CrossRef]
- Hayat, T.; Asad, S.; Mustafa, M.; Alsaedi, A. Radiation Effects on the Flow of Powell-Eyring Fluid Past an Unsteady Inclined Stretching Sheet with Non-Uniform Heat Source/Sink. PLoS ONE 2014, 9, e103214. [Google Scholar] [CrossRef]
- Hiemenz, K. Die Grenzschicht an einem in den gleichformigen Flussigkeitsstrom eingetauchten geraden Kreiszylinder. Dinglers Polytech. J. 1911, 326, 321–324. [Google Scholar]
- Gupta, S.; Kumar, D.; Singh, J. MHD mixed convective stagnation point flow and heat transfer of an incompressible nanofluid over an inclined stretching sheet with chemical reaction and radiation. Int. J. Heat Mass Transf. 2018, 118, 378–387. [Google Scholar] [CrossRef]
- Rehman, F.U.; Nadeem, S.; Rehman, H.U.; Haq, R.U. Thermophysical analysis for three-dimensional MHD stagnation-point flow of nano-material influenced by an exponential stretching surface. Results Phys. 2018, 8, 316–323. [Google Scholar] [CrossRef]
- Anwar, M.I.; Shafie, S.; Hayat, T.; Shehzad, S.A.; Salleh, M.Z. Numerical study for MHD stagnation-point flow of a micropolar nanofluid towards a stretching sheet. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 89–100. [Google Scholar] [CrossRef]
- Dholey, S. Unsteady separated stagnation-point flow over a permeable surface. Z. Angew. Math. Phys. 2019, 70, 10. [Google Scholar] [CrossRef]
- Kamal, F.; Zaimi, K.; Ishak, A.; Pop, I. Stability Analysis of MHD Stagnation-point Flow towards a Permeable Stretching/Shrinking Sheet in a Nanofluid with Chemical Reactions Effect. Sains Malays. 2019, 48, 243–250. [Google Scholar] [CrossRef]
- Ghasemian, A.; Dinarvand, S.; Adamian, A.; Sheremet, M.A. Unsteady General Three-Dimensional Stagnation Point Flow of a Maxwell/Buongiorno Non-Newtonian Nanofluid. J. Nanofluids 2019, 8, 1544–1559. [Google Scholar] [CrossRef]
- Nadeem, S.; Khan, M.R.; Khan, A.U. MHD oblique stagnation point flow of nanofluid over an oscillatory stretching/shrinking sheet: Existence of dual solutions. Phys. Scr. 2019, 94, 075204. [Google Scholar] [CrossRef]
- Vasanthakumari, R.; Pondy, P. Mixed convection of silver and titanium dioxide nanofluids along inclined stretching sheet in presence of MHD with heat generation and suction effect. Math. Model. Eng. Probl. 2018, 5, 123–129. [Google Scholar] [CrossRef]
- Saeed, A.; Shah, Z.; Islam, S.; Jawad, M.; Ullah, A.; Gul, T.; Kumam, P. Three-Dimensional Casson Nanofluid Thin Film Flow over an Inclined Rotating Disk with the Impact of Heat Generation/Consumption and Thermal Radiation. Coatings 2019, 9, 248. [Google Scholar] [CrossRef]
- Elgazery, N.S. Nanofluids flow over a permeable unsteady stretching surface with non-uniform heat source/sink in the presence of inclined magnetic field. J. Egypt. Math. Soc. 2019, 27, 9. [Google Scholar]
- Mjankwi, M.A.; Masanja, V.G.; Mureithi, E.W.; James, M.N. Unsteady MHD Flow of Nanofluid with Variable Properties over a Stretching Sheet in the Presence of Thermal Radiation and Chemical Reaction. Int. J. Math. Math. Sci. 2019, 2019, 1–14. [Google Scholar] [CrossRef]
- Rafique, K.; Anwar, M.I.; Misiran, M. Keller-box Study on Casson Nano Fluid Flow over a Slanted Permeable Surface with Chemical Reaction. Asian Res. J. Math. 2019, 14, 1–17. [Google Scholar] [CrossRef]
- Mishra, A.; Kumar, M. Ohmic–Viscous Dissipation and Heat Generation/Absorption Effects on MHD Nanofluid Flow Over a Stretching Cylinder with Suction/Injection. In Advanced Computing and Communication Technologies; Springer: Singapore, 2019; pp. 45–55. [Google Scholar]
- Khan, W.; Pop, I.; Khan, W. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]


| Khan and Pop [42] | Present Results | ||||
|---|---|---|---|---|---|
| 0.1 | 0.1 | 0.9524 | 2.1294 | 0.9524 | 2.1294 |
| 0.2 | 0.2 | 0.3654 | 2.5152 | 0.3654 | 2.5152 |
| 0.3 | 0.3 | 0.1355 | 2.6088 | 0.1355 | 2.6088 |
| 0.4 | 0.4 | 0.0495 | 2.6038 | 0.0495 | 2.6038 |
| 0.5 | 0.5 | 0.0179 | 2.5731 | 0.0179 | 2.5731 |
| 0.1 | 0.1 | 7.0 | 5.0 | 0.1 | 1.0 | 1.0 | 0.1 | 0.1 | 0.9 | 0.5 | 450 | 0.8966 | 2.8563 | 0.6967 |
| 0.5 | 0.1 | 7.0 | 5.0 | 0.1 | 1.0 | 1.0 | 0.1 | 0.1 | 0.9 | 0.5 | 450 | 0.0640 | 2.8806 | 0.7234 |
| 0.1 | 0.3 | 7.0 | 5.0 | 0.1 | 1.0 | 1.0 | 0.1 | 0.1 | 0.9 | 0.5 | 450 | 0.4931 | 3.6809 | 0.6509 |
| 0.1 | 0.1 | 10.0 | 5.0 | 0.1 | 1.0 | 1.0 | 0.1 | 0.1 | 0.9 | 0.5 | 450 | 0.8322 | 2.9741 | 0.6955 |
| 0.1 | 0.1 | 7.0 | 10.0 | 0.1 | 1.0 | 1.0 | 0.1 | 0.1 | 0.9 | 0.5 | 450 | 0.8100 | 4.1661 | 0.7506 |
| 0.1 | 0.1 | 7.0 | 5.0 | 0.5 | 1.0 | 1.0 | 0.1 | 0.1 | 0.9 | 0.5 | 450 | 0.8885 | 2.8524 | 0.8200 |
| 0.1 | 0.1 | 7.0 | 5.0 | 0.1 | 3.0 | 1.0 | 0.1 | 0.1 | 0.9 | 0.5 | 450 | 0.9120 | 2.8642 | 0.9514 |
| 0.1 | 0.1 | 7.0 | 5.0 | 0.1 | 1.0 | 3.0 | 0.1 | 0.1 | 0.9 | 0.5 | 450 | 0.8122 | 4.4944 | 0.7482 |
| 0.1 | 0.1 | 7.0 | 5.0 | 0.1 | 1.0 | 1.0 | 0.5 | 0.1 | 0.9 | 0.5 | 450 | 0.1890 | 3.3436 | 0.7051 |
| 0.1 | 0.1 | 7.0 | 5.0 | 0.1 | 1.0 | 1.0 | 0.1 | 0.5 | 0.9 | 0.5 | 450 | 0.9007 | 2.8579 | 0.6064 |
| 0.1 | 0.1 | 7.0 | 5.0 | 0.1 | 1.0 | 1.0 | 0.1 | 0.1 | 2.0 | 0.5 | 450 | 0.9071 | 2.8607 | 0.4742 |
| 0.1 | 0.1 | 7.0 | 5.0 | 0.1 | 1.0 | 1.0 | 0.1 | 0.1 | 0.9 | 1.5 | 450 | 1.0243 | 2.9339 | −1.4412 |
| 0.1 | 0.1 | 7.0 | 5.0 | 0.1 | 1.0 | 1.0 | 0.1 | 0.1 | 0.9 | 0.5 | 600 | 0.8937 | 2.8552 | 0.7570 |
| 0.1 | 0.1 | 7.0 | 5.0 | 0.1 | 1.0 | 1.0 | 0.1 | 0.1 | 0.9 | 0.5 | 900 | 0.8867 | 2.8523 | 0.9033 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rafique, K.; Anwar, M.I.; Misiran, M.; Khan, I.; Seikh, A.H.; Sherif, E.-S.M.; Nisar, K.S. Numerical Analysis with Keller-Box Scheme for Stagnation Point Effect on Flow of Micropolar Nanofluid over an Inclined Surface. Symmetry 2019, 11, 1379. https://doi.org/10.3390/sym11111379
Rafique K, Anwar MI, Misiran M, Khan I, Seikh AH, Sherif E-SM, Nisar KS. Numerical Analysis with Keller-Box Scheme for Stagnation Point Effect on Flow of Micropolar Nanofluid over an Inclined Surface. Symmetry. 2019; 11(11):1379. https://doi.org/10.3390/sym11111379
Chicago/Turabian StyleRafique, Khuram, Muhammad Imran Anwar, Masnita Misiran, Ilyas Khan, Asiful H. Seikh, El-Sayed M. Sherif, and Kottakkaran Sooppy Nisar. 2019. "Numerical Analysis with Keller-Box Scheme for Stagnation Point Effect on Flow of Micropolar Nanofluid over an Inclined Surface" Symmetry 11, no. 11: 1379. https://doi.org/10.3390/sym11111379
APA StyleRafique, K., Anwar, M. I., Misiran, M., Khan, I., Seikh, A. H., Sherif, E.-S. M., & Nisar, K. S. (2019). Numerical Analysis with Keller-Box Scheme for Stagnation Point Effect on Flow of Micropolar Nanofluid over an Inclined Surface. Symmetry, 11(11), 1379. https://doi.org/10.3390/sym11111379







