A Robust and High Capacity Data Hiding Method for H.265/HEVC Compressed Videos with Block Roughness Measure and Error Correcting Techniques
Abstract
1. Introduction
2. Related Works and Motivation
3. Overview of H.265/HEVC Video Coding Standard
3.1. Improvements in H.265/HEVC over H.264/AVC
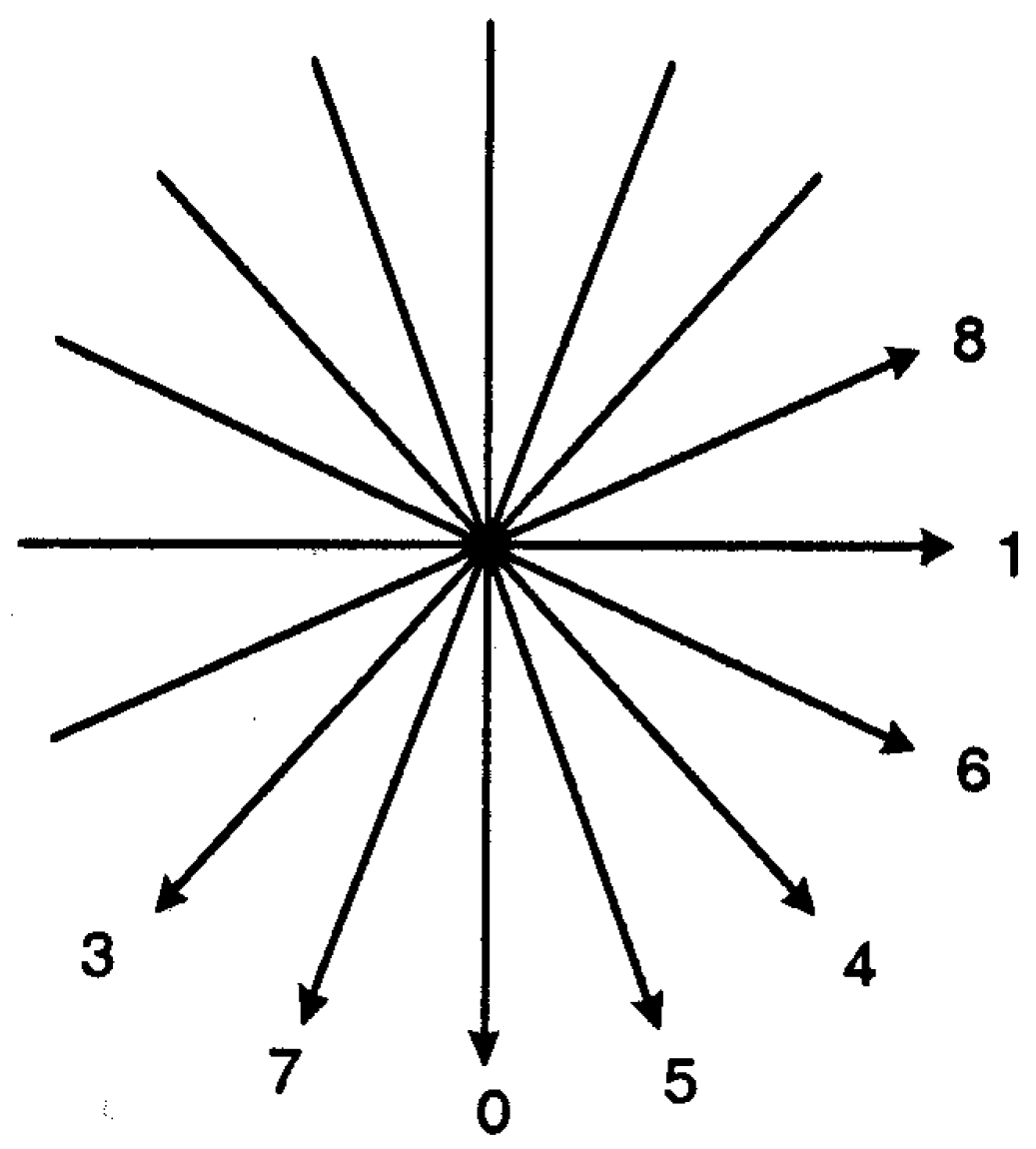
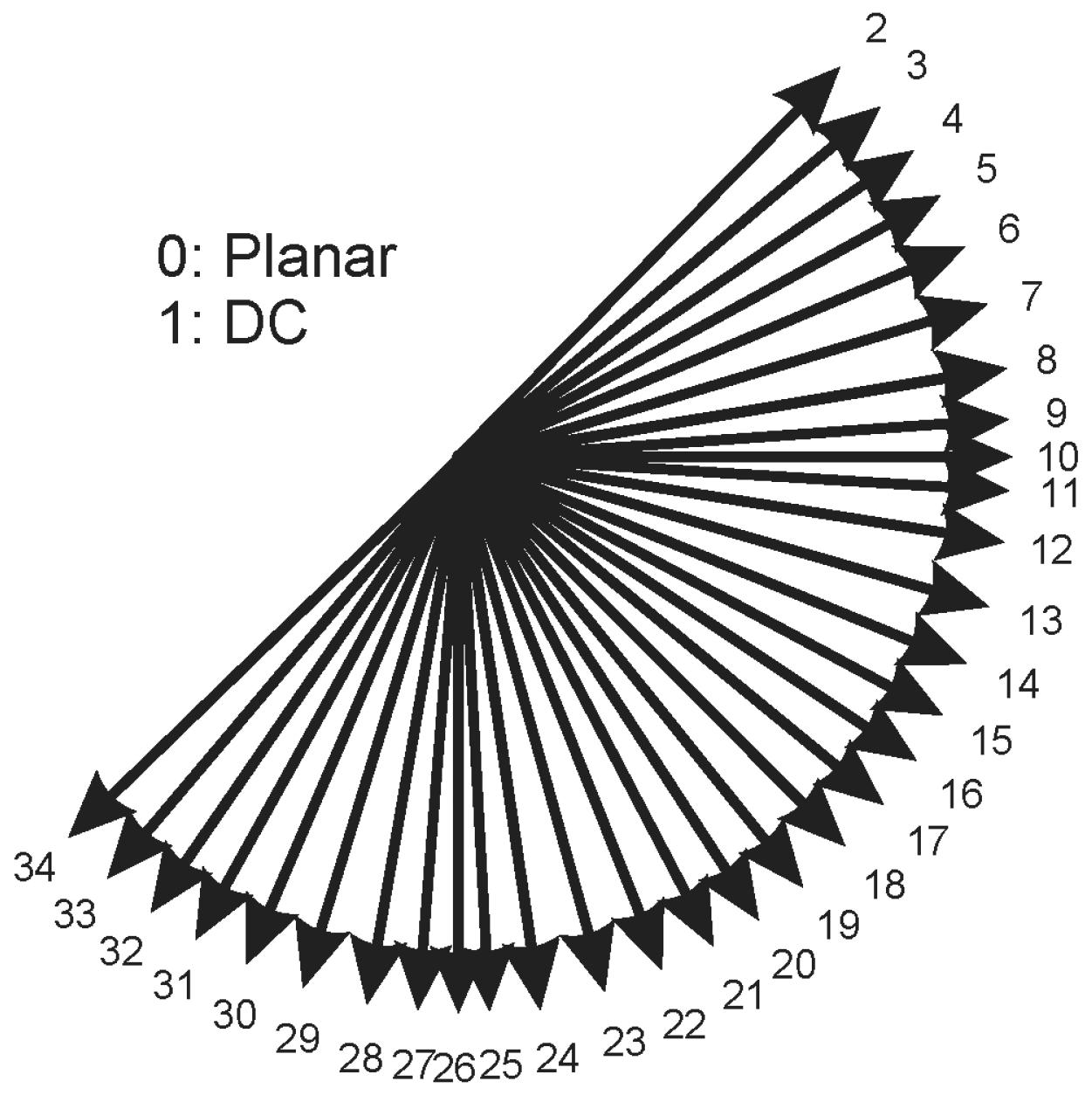
3.1.1. Coding Unit
3.1.2. Motion Estimation
3.1.3. Transform Coding and Quantisation
3.1.4. Entropy Coding
4. Overview of Error Correcting Techniques
4.1. BCH Syndrome Error Correcting Codes
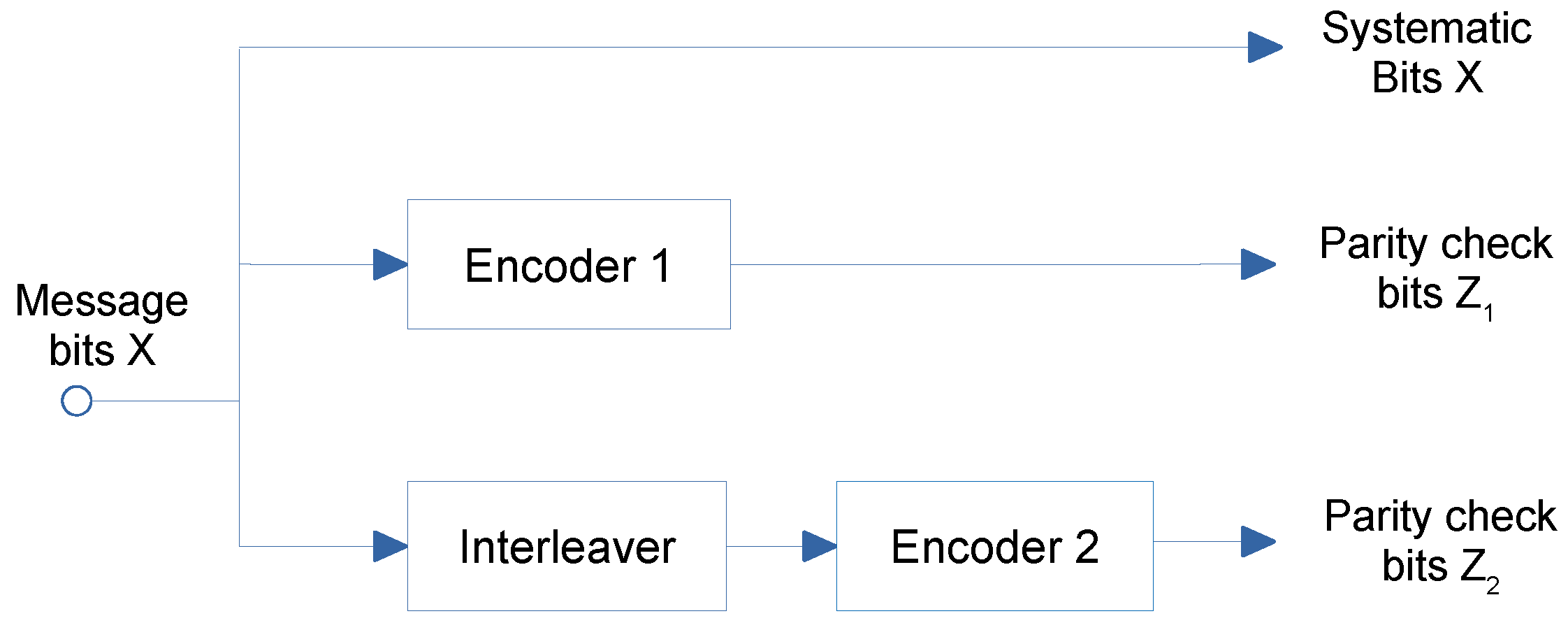
4.2. Turbo Codes
5. Proposed Method of Data Hiding
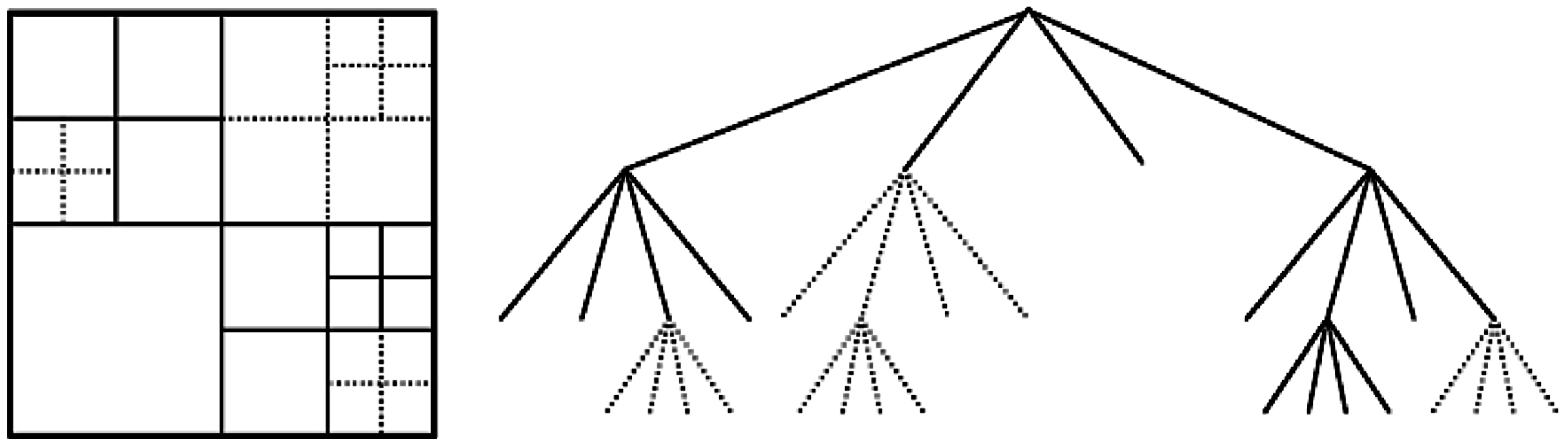
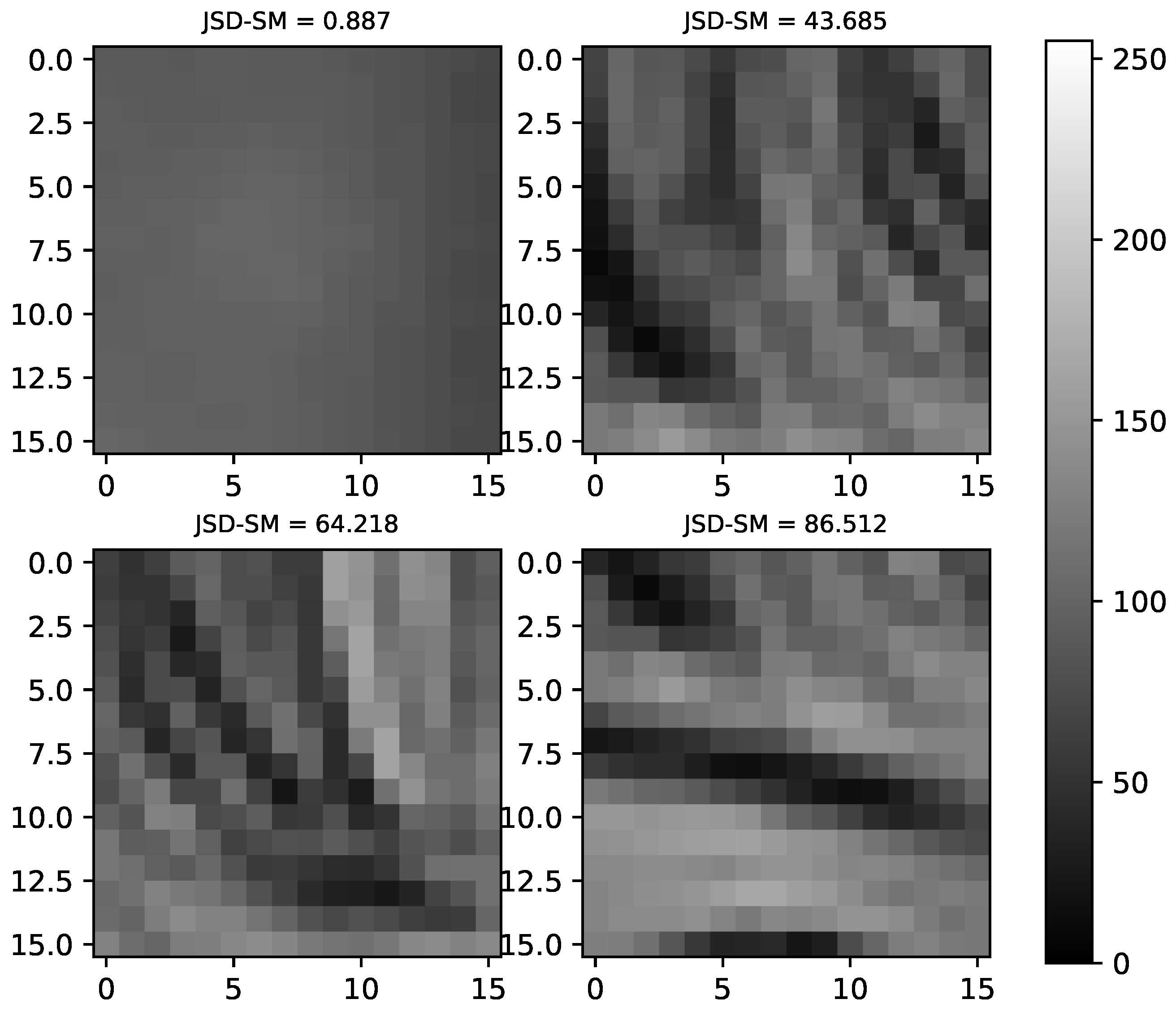
5.1. Block Selection Using JSD-SM Coarseness Measure
| Algorithm 1: JSD-SM block coarseness algorithm |
 |
5.2. Data Embedding and Extraction
- Let a 3-bit message block be and the destination block of seven QTCs is . Only one of the s is modified to encode the message block in QTC block.
- Define three parity values and as follows.
- To encode binary message bits , modify the QTC values according to the following rules:
- Case 1. If , modify no QTC
- Case 2. If , modify as follows. If , . Else,
- Case 3. If , modify as follows. If , . Else,
- Case 4. If , modify as follows. If , . Else,
- Case 5. If , modify as follows. If , . Else,
- Case 6. If , modify as follows. If , . Else,
- Case 7. If , modify as follows. If , . Else,
- Case 8. If , modify as follows. If , . Else,
- Let a modified block of QTCs be .
- Three message bits are extracted from as follows.
Illustration
5.3. Design of the BCH and Turbo Error Correcting Codes
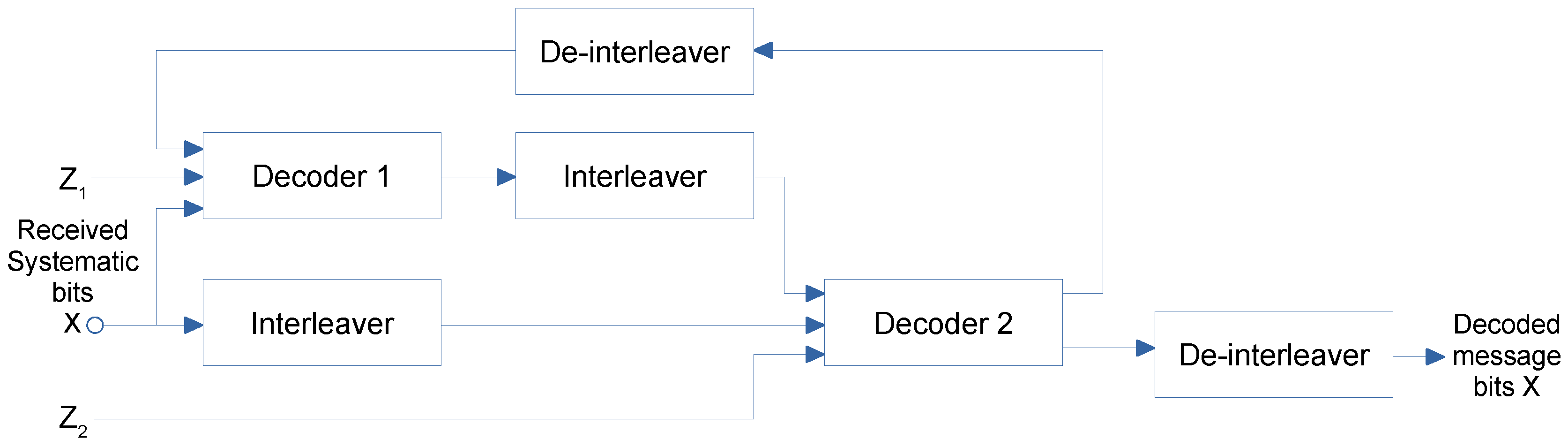
5.4. Overall Architecture of the Proposed Method
| Algorithm 2: Embedding | |
| Data: Video sequence, input message, parameter | |
| Result: HEVC/H.265 compressed video with embedded message | |
| 1 | Convert input message to binary data matrix D (e.g., using ASCII values if it is text); |
| 2 | Encode data matrix D with either BCH (Table 1) or Turbo coding scheme (Table 2). Let encoded data be ; |
| 3 | Start encoding YUV video to H.265/HEVC; |
| 4 | For each I-frame select the , and TU blocks; |
| 5 | Evaluate coarseness of each and blocks using Algorithm 1; |
| 6 | Sort two groups of and blocks based on their values; |
| 7 | Select top % most coarse blocks in each group of and TUs; |
| 8 | Embed encoded data sequentially in quantised DST coefficients of all TUs using embedding technique as described in Section 5.2; |
| 9 | Embed rest of the data in quantised DCT coefficients of selected and blocks using embedding technique as described in Section 5.2; |
| 10 | Continue HEVC compression process and the modified TU blocks are entropy coded (CABAC); |
| 11 | HEVC/H.265 compressed video stream with embedded payload data is output for storage or transmission; |
| 12 | Output the key , if BCH error correcting code is used, where are parameters of BCH coding OR if Turbo coding is used, output key , where or (See Section 5.3); |
| Algorithm 3: Extraction | |
| Data: H.265/HEVC compressed video with embedded data, key | |
| Result: Extracted payload data | |
| 1 | Begin entropy decoding of the compressed video; |
| 2 | Extract all , and luma TUs from I-frames; |
| 3 | Measure JSD-SM block coarseness of all and luma blocks using Algorithm 1 in spatial domain; |
| 4 | Sort the two groups of and blocks on the basis of value; |
| 5 | Select % most coarse blocks in each group of and luma TUs; |
| 6 | Extract embedded bits from all and selected and luma TU blocks using SME(1,3,7) extraction process as described in Section 5.2; |
| 7 | Combine all data to get the BCH or Turbo encoded data that possibly contains some errors due to unreliable transmission or re-compression attack; |
| 8 | If is BCH encoded, decode using Berelkamp’s iterative algorithm [44]; |
| 9 | If is Turbo encoded, decode with Soft-Output Viterbi algorithm (SOVA) [45]; |
| 10 | Decoded data is output as the extracted data; |
6. Experimental Results and Discussion
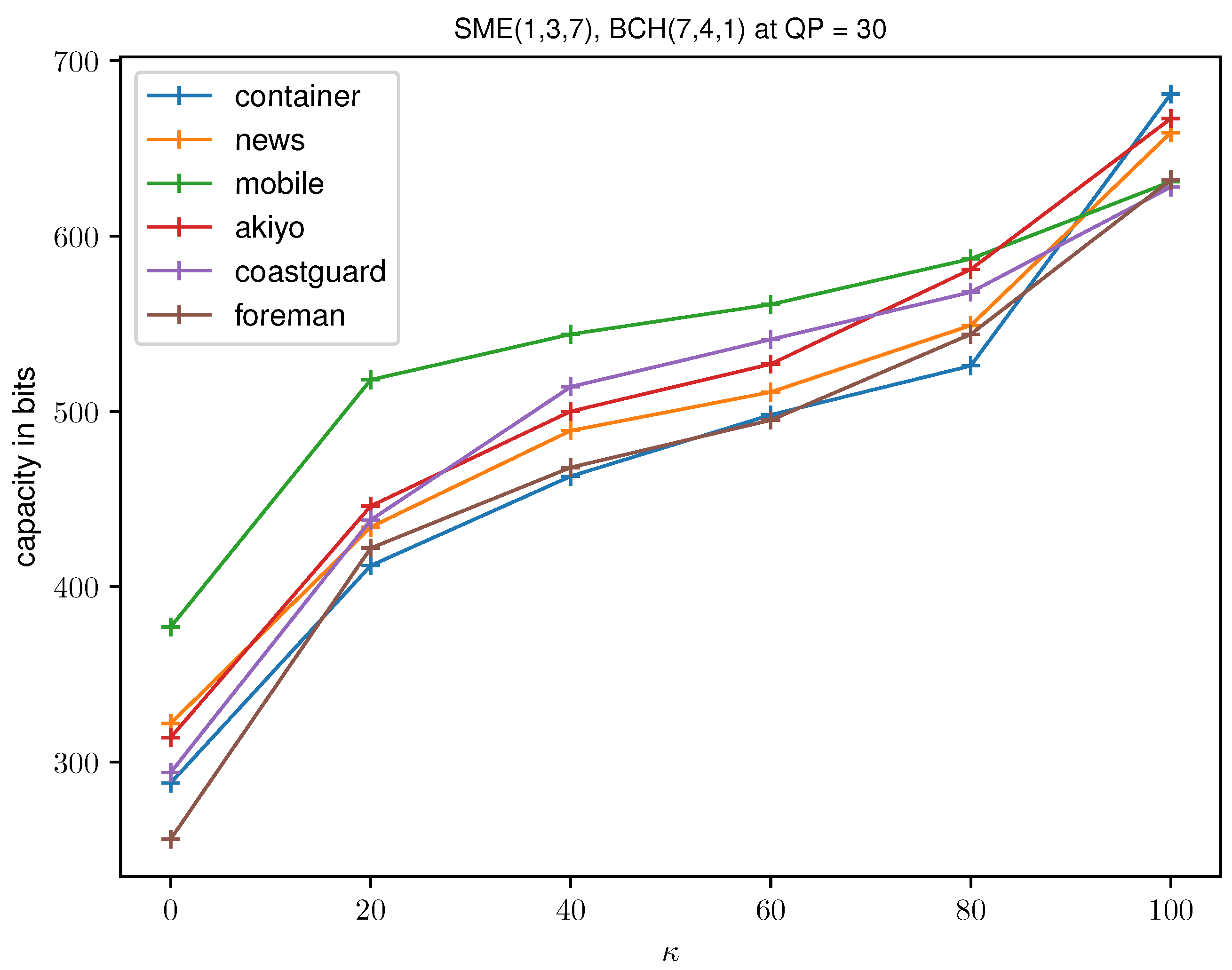
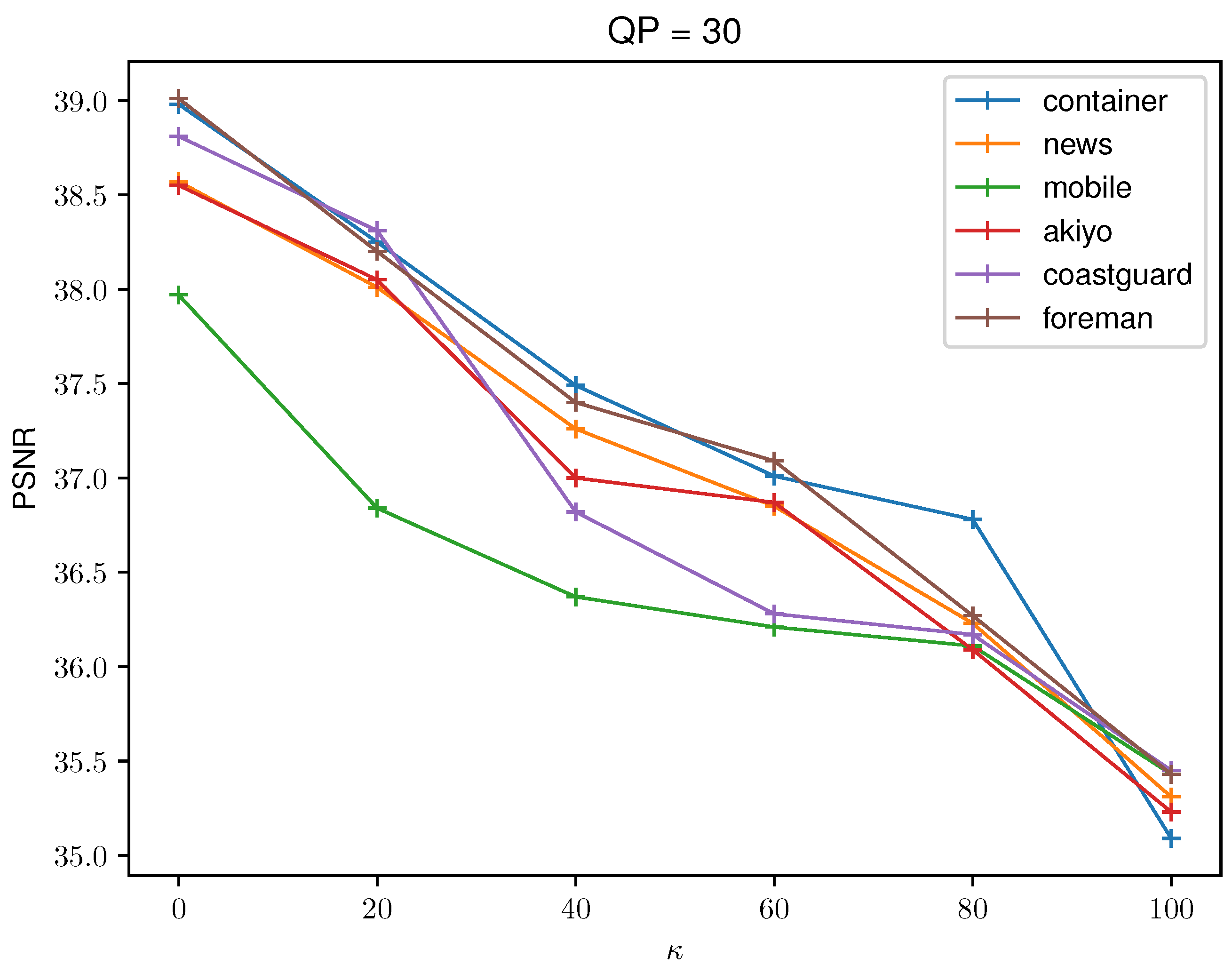
6.1. Visual Quality and Payload Capacity
6.2. Robustness Performance
6.3. Bit-Rate Increase
6.4. JSD-SM Coarness Measure Analysis
6.5. Computation Time
- A.
- Average data pre-processing and data encoding time: in this step, the data to be embedded are first converted to binary bit-stream from its original format. Then, they are encoded in one of the schemes of BCH or Turbo coding described in Section 5.3. Different schemes of BCH and Turbo encoding take slightly different time. The average time taken by all the proposed schemes is considered.
- B.
- block selection using proposed JSD-SM technique as described in Section 5.1
- C.
- data embedding using SME(1,3,7) technique as described in Section 5.2
- D.
- total time: The total time taken to complete the whole embedding process. This includes A, B, C and rest of the usual HEVC process such as motion vector analysis, quantisation, entropy coding, etc.
- M.
- Block selection using the proposed JSD-SM technique
- N.
- Data extraction using SME(1,3,7) technique
- O.
- Data decoding using one of the proposed schemes of Turbo/BCH coding and post processing
- P.
- Total time that includes M, N, O and rest of the HEVC decoding steps, e.g., inverse DST/DCT, quantisation, etc.
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ohm, J.R.; Sullivan, G.J.; Schwarz, H.; Tan, T.K.; Wiegand, T. Comparison of the coding efficiency of video coding standards—Including high efficiency video coding (HEVC). IEEE Trans. Circuits Syst. Video Technol. 2012, 22, 1669–1684. [Google Scholar] [CrossRef]
- Chang, P.C.; Chung, K.L.; Chen, J.J.; Lin, C.H.; Lin, T.J. A DCT/DST-based error propagation-free data hiding algorithm for HEVC intra-coded frames. J. Vis. Commun. Image Represent. 2014, 25, 239–253. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Z.; Ma, X.; Liu, J. A robust data hiding algorithm for H.264/AVC video streams. J. Syst. Softw. 2013, 86, 2174–2183. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, M.; Ma, X.; Zhao, H. A new robust data hiding method for H.264/AVC without intra-frame distortion drift. Neurocomputing 2015, 151, 1076–1085. [Google Scholar] [CrossRef]
- Ma, X.; Li, Z.; Tu, H.; Zhang, B. A data hiding algorithm for H. 264/AVC video streams without intra-frame distortion drift. IEEE Trans. Circuits Syst. Video Technol. 2010, 20, 1320–1330. [Google Scholar] [CrossRef]
- Xu, D.; Wang, R.; Shi, Y.Q. Data hiding in encrypted H. 264/AVC video streams by codeword substitution. IEEE Trans. Inf. Forensics Secur. 2014, 9, 596–606. [Google Scholar] [CrossRef]
- Niu, K.; Yang, X.; Zhang, Y. A novel video reversible data hiding algorithm using motion vector for H. 264/AVC. Tsinghua Sci. Technol. 2017, 22, 489–498. [Google Scholar] [CrossRef]
- Ma, Z.; Huang, J.; Jiang, M.; Niu, X. A video watermarking DRM method based on H. 264 compressed domain with low bit-rate increasement. Chin. J. Electron. 2016, 25, 641–647. [Google Scholar] [CrossRef]
- Lin, T.J.; Chung, K.L.; Chang, P.C.; Huang, Y.H.; Liao, H.Y.M.; Fang, C.Y. An improved DCT-based perturbation scheme for high capacity data hiding in H.264/AVC intra frames. J. Syst. Softw. 2013, 86, 604–614. [Google Scholar] [CrossRef]
- Stutz, T.; Autrusseau, F.; Uhl, A. Non-blind structure-preserving substitution watermarking of H. 264/CAVLC inter-frames. IEEE Trans. Multimed. 2014, 16, 1337–1349. [Google Scholar] [CrossRef]
- Ogawa, K.; Ohtake, G. Watermarking for HEVC/H.265 stream. In Proceedings of the 2015 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 9–12 January 2015; pp. 102–103. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, S.; Zhao, H.; Liu, S. A new data hiding method for H.265/HEVC video streams without intra-frame distortion drift. Multimed. Tools Appl. 2018. [Google Scholar] [CrossRef]
- Dutta, T.; Gupta, H.P. A robust watermarking framework for High Efficiency Video Coding (HEVC)—Encoded video with blind extraction process. J. Vis. Commun. Image Represent. 2016, 38, 29–44. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, L.; Hu, M.; Jia, Z.; Jia, S.; Zhao, H. A reversible data hiding method for H. 264 with Shamir’s (t, n)-threshold secret sharing. Neurocomputing 2016, 188, 63–70. [Google Scholar] [CrossRef]
- Swati, S.; Hayat, K.; Shahid, Z. A watermarking scheme for high efficiency video coding (HEVC). PLoS ONE 2014, 9, e105613. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, H.; Liu, S.; Feng, C.; Liu, S. A robust and improved visual quality data hiding method for HEVC. IEEE Access 2018, 6, 53984–53997. [Google Scholar] [CrossRef]
- Gaj, S.; Sur, A.; Bora, P.K. A robust watermarking scheme against re-compression attack for H. 265/HEVC. In Proceedings of the 2015 Fifth National Conference on Computer Vision, Pattern Recognition, Image Processing and Graphics (NCVPRIPG), Patna, India, 16–19 December 2015; pp. 1–4. [Google Scholar]
- Tew, Y.; Wong, K. Information hiding in HEVC standard using adaptive coding block size decision. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 5502–5506. [Google Scholar]
- Yang, Y.; Li, Z.; Xie, W.; Zhang, Z. High capacity and multilevel information hiding algorithm based on pu partition modes for HEVC videos. Multimed. Tools Appl. 2019, 78, 8423–8446. [Google Scholar] [CrossRef]
- Bo, P.; Jie, Y. A Reversible Information Hiding Method Based on HEVC. IFAC-PapersOnLine 2018, 51, 238–243. [Google Scholar] [CrossRef]
- Thiesse, J.M.; Jung, J.; Antonini, M. Rate distortion data hiding of motion vector competition information in chroma and luma samples for video compression. IEEE Trans. Circuits Syst. Video Technol. 2011, 21, 729–741. [Google Scholar] [CrossRef]
- Aly, H.A. Data hiding in motion vectors of compressed video based on their associated prediction error. IEEE Trans. Inf. Forensics Secur. 2010, 6, 14–18. [Google Scholar] [CrossRef]
- Sullivan, G.J.; Ohm, J.R.; Han, W.J.; Wiegand, T. Overview of the high efficiency video coding (HEVC) standard. IEEE Trans. Circuits Syst. Video Technol. 2012, 22, 1649–1668. [Google Scholar] [CrossRef]
- Sole, J.; Joshi, R.; Nguyen, N.; Ji, T.; Karczewicz, M.; Clare, G.; Henry, F.; Duenas, A. Transform coefficient coding in HEVC. IEEE Trans. Circuits Syst. Video Technol. 2012, 22, 1765–1777. [Google Scholar] [CrossRef]
- Sze, V.; Budagavi, M.; Sullivan, G.J. High efficiency video coding (HEVC). Integr. Circuit Syst. Algorithms Archit. Springer 2014, 39, 40. [Google Scholar]
- Pastuszak, G. Flexible architecture design for H. 265/HEVC inverse transform. Circuits Syst. Signal Process. 2015, 34, 1931–1945. [Google Scholar] [CrossRef][Green Version]
- Wiegand, T.; Sullivan, G.J.; Bjontegaard, G.; Luthra, A. Overview of the H. 264/AVC video coding standard. IEEE Trans. Circuits Syst. Video Technol. 2003, 13, 560–576. [Google Scholar] [CrossRef]
- Marpe, D.; Schwarz, H.; Wiegand, T. Context-based adaptive binary arithmetic coding in the H. 264/AVC video compression standard. IEEE Trans. Circuits Syst. Video Technol. 2003, 13, 620–636. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Z.; Ma, X.; Liu, J. A robust without intra-frame distortion drift data hiding algorithm based on H. 264/AVC. Multimed. Tools Appl. 2014, 72, 613–636. [Google Scholar] [CrossRef]
- Mstafa, R.J.; Elleithy, K.M. A high payload video steganography algorithm in DWT domain based on BCH codes (15, 11). In Proceedings of the 2015 Wireless Telecommunications Symposium (WTS), New York, NY, USA, 15–17 April 2015; pp. 1–8. [Google Scholar]
- Mstafa, R.J.; Elleithy, K.M. A DCT-based robust video steganographic method using BCH error correcting codes. In Proceedings of the 2016 IEEE Long Island Systems, Applications and Technology Conference (LISAT), Farmingdale, NY, USA, 29 April 2016; pp. 1–6. [Google Scholar]
- Yoo, H.; Jung, J.; Jo, J.; Park, I.C. Area-efficient multimode encoding architecture for long BCH codes. IEEE Trans. Circuits Syst. II Express Briefs 2013, 60, 872–876. [Google Scholar] [CrossRef]
- Hagenauer, J.; Offer, E.; Papke, L. Iterative decoding of binary block and convolutional codes. IEEE Trans. Inf. Theory 1996, 42, 429–445. [Google Scholar] [CrossRef]
- Massey, J. Shift-register synthesis and BCH decoding. IEEE Trans. Inf. Theory 1969, 15, 122–127. [Google Scholar] [CrossRef]
- Berrou, C.; Glavieux, A.; Thitimajshima, P. Near Shannon limit error-correcting coding and decoding: Turbo-codes. 1. In Proceedings of the ICC’93—IEEE International Conference on Communications, Geneva, Switzerland, 23–26 May 1993; Volume 2, pp. 1064–1070. [Google Scholar] [CrossRef]
- Endres, D.M.; Schindelin, J.E. A new metric for probability distributions. IEEE Trans. Inf. Theory 2003, 49, 1858–1860. [Google Scholar] [CrossRef]
- Chan, C.K.; Cheng, L. Hiding data in images by simple {LSB} substitution. Pattern Recognit. 2004, 37, 469–474. [Google Scholar] [CrossRef]
- Li, B.; He, J.; Huang, J.; Shi, Y.Q. A survey on image steganography and steganalysis. J. Inf. Hiding Multimed. Signal Process. 2011, 2, 142–172. [Google Scholar]
- Wang, R.Z.; Lin, C.F.; Lin, J.C. Image hiding by optimal LSB substitution and genetic algorithm. Pattern Recognit. 2001, 34, 671–683. [Google Scholar] [CrossRef]
- Roque, J.J.; Minguet, J.M. SLSB: Improving the Steganographic Algorithm LSB. In Proceedings of the Workshop on Security in Information Systems (WOSIS 2009), Milan, Italy, 6–7 May 2009; pp. 57–66. [Google Scholar]
- Gutub, A.A.A. Pixel indicator technique for RGB image steganography. J. Emerg. Technol. Web Intell. 2010, 2, 56–64. [Google Scholar] [CrossRef]
- Fridrich, J.; Lisoněk, P.; Soukal, D. On steganographic embedding efficiency. In Proceedings of the International Workshop on Information Hiding, Alexandria, VA, USA, 10–12 July 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 282–296. [Google Scholar]
- Fridrich, J.; Soukal, D. Matrix embedding for large payloads. IEEE Trans. Inf. Forensics Secur. 2006, 1, 390–395. [Google Scholar] [CrossRef]
- Berlekamp, E.R. Non-Binary BCH Decoding; Technical Report; Department of Statistics, North Carolina State University: Raleigh, NC, USA, 1966. [Google Scholar]
- Hagenauer, J.; Hoeher, P. A Viterbi algorithm with soft-decision outputs and its applications. In Proceedings of the 1989 IEEE Global Telecommunications Conference and Exhibition‘Communications Technology for the 1990s and Beyond’, Dallas, TX, USA, 27–30 November 1989; pp. 1680–1686. [Google Scholar]
- University of Hannover. High Resolution Video Datasets. 2013. Available online: http://ftp.tnt.uni-hannover.de/testsequences (accessed on 7 July 2019).
- Li, Z.; Meng, L.; Jiang, X.; Li, Z. High Capacity HEVC Video Hiding Algorithm Based on EMD Coded PU Partition Modes. Symmetry 2019, 11, 1015. [Google Scholar] [CrossRef]
- Richardson, I.E. H. 264 and MPEG-4 Video Compression: Video Coding for Next-Generation Multimedia; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]









| Name | n | k | t | Generator Polynomial |
|---|---|---|---|---|
| BCH | 7 | 4 | 1 | 1 011 |
| BCH | 31 | 16 | 3 | 1 000 111 110 101 111 |
| BCH | 31 | 11 | 5 | 101 100 010 011 011 010 101 |
| Name | Seed | m | a | c | Sequence | Constraint Length |
|---|---|---|---|---|---|---|
| Turbo-16 | 3 | 5 | 3 | 2 | 16 | |
| Turbo-24 | 2 | 7 | 3 | 0 | 24 |
| Name | Resolution | RAW Format | HEVC GOP Length | GOP Conguration |
|---|---|---|---|---|
| Container | YUV | 10 | IBPBPBPBPB | |
| News | YUV | 10 | IBPBPBPBPB | |
| Mobile | YUV | 10 | IBPBPBPBPB | |
| Akiyo | YUV | 10 | IBPBPBPBPB | |
| Coastguard | YUV | 10 | IBPBPBPBPB | |
| Foreman | YUV | 10 | IBPBPBPBPB |
| Video | PSNR | PSNR and SME and Following Error Codes | ||||
|---|---|---|---|---|---|---|
| B(7,4,1) | B(31,16,3) | B(31,11,5) | T | T | ||
| Container | 39.41 | 38.25 | 38.37 | 38.28 | 38.06 | 38.22 |
| News | 38.96 | 38.00 | 37.81 | 37.93 | 37.90 | 37.94 |
| Mobile | 39.82 | 38.99 | 38.98 | 38.76 | 38.53 | 38.71 |
| Akiyo | 39.75 | 38.05 | 37.99 | 38.20 | 38.02 | 38.18 |
| Coastguard | 39.83 | 38.31 | 38.26 | 38.33 | 37.97 | 38.01 |
| Foreman | 39.47 | 38.73 | 38.28 | 38.36 | 38.53 | 38.24 |
| Video | Liu et al. [4] | Liu et al. [14] | SME(1,3,7) + BCH(7,4,1) | SME(1,3,7) + Turbo | ||||
|---|---|---|---|---|---|---|---|---|
| PSNR | Capacity | PSNR | Capacity | PSNR | Capacity | PSNR | Capacity | |
| Container | 36.50 | 171 | 36.44 | 120 | 38.25 | 412 | 38.22 | 338 |
| News | 36.50 | 171 | 36.95 | 132 | 38.00 | 434 | 37.94 | 346 |
| Mobile | 36.50 | 171 | 34.24 | 172 | 38.99 | 518 | 38.71 | 392 |
| Akiyo | 36.50 | 171 | 38.63 | 124 | 38.05 | 446 | 38.18 | 354 |
| Coastguard | 36.50 | 171 | – | – | 38.31 | 438 | 39.01 | 348 |
| Foreman | 36.50 | 171 | – | – | 38.73 | 422 | 38.24 | 336 |
| Video | QP | BCH(7,4,1) | BCH(31,16,3) | BCH(31,11,5) | Turbo | Turbo | ||
|---|---|---|---|---|---|---|---|---|
| Container | 29 | 63% | 61% | 74.22% | 81.01% | 95.10% | 96.00% | 96.10% |
| 30 | 65% | 78% | 89.04% | 97.07% | 99.02% | 98.56% | 99.72% | |
| 31 | 78% | 80% | 91.17% | 98.99% | 100% | 100% | 100% | |
| 32 | 87% | 83% | 92.50% | 100% | 100% | 100% | 100% | |
| 33 | 61% | 85% | 94.50% | 99% | 100% | 100% | 100% | |
| 34 | 61% | 54% | 76.66% | 88.45% | 94.05% | 95.44% | 98.29% | |
| 35 | 42% | 22% | 64.53% | 79.10% | 83.87% | 89.39% | 91.44% | |
| News | 29 | 60% | 59% | 82.41% | 92.15% | 94.61% | 96.20% | 96.35% |
| 30 | 63% | 82% | 88.23% | 97.82% | 99.98% | 99.99% | 99.99% | |
| 31 | 56% | 80% | 90.84% | 99.95% | 100% | 100% | 100% | |
| 32 | 70% | 81% | 89.90% | 100% | 100% | 100% | 100% | |
| 33 | 46% | 85% | 91.92% | 99.98% | 100% | 100% | 100% | |
| 34 | 44% | 38% | 76.61% | 91.40% | 93.00% | 95.16% | 96.60% | |
| 35 | 42% | 31% | 63.96% | 84.35% | 88.55% | 91.25% | 92.91% | |
| Mobile | 29 | 59% | 60% | 80.95% | 92.18% | 94.61% | 97.01% | 98.77% |
| 30 | 63% | 77% | 85.77% | 97.83% | 99.24% | 99.89% | 99.98% | |
| 31 | 65% | 82% | 90.50% | 98.59% | 100% | 100% | 100% | |
| 32 | 71% | 85% | 92.94% | 100% | 100% | 100% | 100% | |
| 33 | 67% | 68% | 91.97% | 98.00% | 100% | 100% | 100% | |
| 34 | 59% | 59% | 77.90% | 92.49% | 93.28% | 95.10% | 96.62% | |
| 35 | 51% | 44% | 69.09% | 87.35% | 88.94% | 92.56% | 92.99% |
| Attack Type | Liu et al. [16] | Swati et al. [15] | Liu et al. [14] | Proposed (avg) | |||||
|---|---|---|---|---|---|---|---|---|---|
| SIM | BER | SIM | BER | SIM | BER | SIM | BER | ||
| No attack | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | |
| Re-quantisation attack | QP = 30 | 0.94 | 6 | 0.62 | 38.35 | 0.80 | 22.40 | 0.98 | 2 |
| QP = 31 | 1 | 0 | 0.80 | 22.34 | 0.81 | 20.70 | 1 | 0 | |
| QP = 32 | 1 | 0 | 0.86 | 15.60 | 0.85 | 17.20 | 1 | 0 | |
| Qp = 33 | 0.96 | 4 | 0.58 | 42.50 | 0.85 | 16.30 | 0.98 | 2 | |
| QP = 34 | 0.80 | 22 | 0.58 | 42.20 | 0.50 | 45.98 | 0.88 | 11 | |
| Video | Liu et al. [14] | Proposed Method (SME with Following Error Codes) | ||||
|---|---|---|---|---|---|---|
| BCH(7,4,1) | BCH(31,16,3) | BCH(31,11,5) | Turbo(16) | Turbo(24) | ||
| Container | 2.7 | 0.01 | 0.02 | 0.02 | 0.03 | 0.04 |
| News | 2.8 | 0.02 | 0.02 | 0.03 | 0.03 | 0.05 |
| Mobile | 4.0 | 0.02 | 0.03 | 0.02 | 0.04 | 0.05 |
| Akiyo | 1.4 | 0.02 | 0.03 | 0.02 | 0.04 | 0.05 |
| Coastguard | - | 0.02 | 0.03 | 0.03 | 0.04 | 0.06 |
| Foreman | - | 0.01 | 0.03 | 0.04 | 0.04 | 0.06 |
| Technique | Video Dataset | Bit Rate Increase (avg.) |
|---|---|---|
| Liu et al. [16] | ParkScene (), FourPeople (), KirstenAndSara (), etc. PartyScene (), BQMall (), RaceHorses () | 0.785% |
| Li et al. [47] | BasketBallDrive (), ParkScene (), BQTerrace (), Kimono (), ChinaSpeed (), Keiba (), etc. | 0.014% |
| Proposed | Container (), News (), Mobile (), Akiyo (), Coastguard () and Foreman () | 0.031% |
| Name | A | B | C | D |
|---|---|---|---|---|
| Container | 0.6 | 32.6 | 11.8 | 221.2 |
| News | 0.6 | 31.4 | 12.3 | 224.7 |
| Mobile | 0.6 | 33.8 | 11.9 | 229.0 |
| Akiyo | 0.6 | 33.7 | 12.1 | 219.8 |
| Coastguard | 0.6 | 32.2 | 12.3 | 224.2 |
| Foreman | 0.6 | 33.0 | 11.9 | 232.3 |
| Name | M | N | O | P |
|---|---|---|---|---|
| Container | 31.4 | 13.2 | 1.3 | 102.8 |
| News | 32.6 | 12.8 | 1.4 | 105.1 |
| Mobile | 33.1 | 13.1 | 1.6 | 110.7 |
| Akiyo | 32.7 | 14.0 | 1.4 | 108.5 |
| Coastguard | 31.4 | 13.5 | 1.5 | 111.8 |
| Foreman | 32.3 | 13.2 | 1.6 | 118.0 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Biswas, K. A Robust and High Capacity Data Hiding Method for H.265/HEVC Compressed Videos with Block Roughness Measure and Error Correcting Techniques. Symmetry 2019, 11, 1360. https://doi.org/10.3390/sym11111360
Biswas K. A Robust and High Capacity Data Hiding Method for H.265/HEVC Compressed Videos with Block Roughness Measure and Error Correcting Techniques. Symmetry. 2019; 11(11):1360. https://doi.org/10.3390/sym11111360
Chicago/Turabian StyleBiswas, Kusan. 2019. "A Robust and High Capacity Data Hiding Method for H.265/HEVC Compressed Videos with Block Roughness Measure and Error Correcting Techniques" Symmetry 11, no. 11: 1360. https://doi.org/10.3390/sym11111360
APA StyleBiswas, K. (2019). A Robust and High Capacity Data Hiding Method for H.265/HEVC Compressed Videos with Block Roughness Measure and Error Correcting Techniques. Symmetry, 11(11), 1360. https://doi.org/10.3390/sym11111360






