Abstract
We demonstrate that the evolution of superflows in interacting persistent currents of ultracold gases is strongly affected by symmetry breaking of the quantum vortex dynamics. We study counter-propagating superflows in a system of two parallel rings in regimes of weak (a Josephson junction with tunneling through the barrier) and strong (rings merging across a reduced barrier) interactions. For the weakly interacting toroidal Bose–Einstein condensates, formation of rotational fluxons (Josephson vortices) is associated with spontaneous breaking of the rotational symmetry of the tunneling superflows. The influence of a controllable symmetry breaking on the final state of the merging counter-propagating superflows is investigated in the framework of a weakly dissipative mean-field model. It is demonstrated that the population imbalance between the merging flows and the breaking of the underlying rotational symmetry can drive the double-ring system to final states with different angular momenta.
1. Introduction
Interacting Bose–Einstein condensates (BECs) suggest intriguing possibilities for the investigation of spontaneous symmetry breaking in quantum systems at the macroscopic level. In particular, coupled persistent currents of ultracold atomic gases provide a possibility to investigate the interaction of the superflows in a tunable and controllable environment. Using accessible experimental techniques, it is possible to consider a variety of physical phenomena in this setting: from Josephson’s effects in the regime of weak interactions to quantum Kelvin–Helmholtz instability for merging rings.
Here we consider two parallel toroidal atomic BECs with opposite vorticities in a three-dimensional (3D) trap. Previous theoretical investigations [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16] have drawn considerable interest to systems of coupled circular BECs. In this vein, two parallel coaxial BEC rings, separated in the axial direction by a potential barrier, were considered in the context of the spontaneous generation of vortex lines [17] and defects by means of the Kibble-Zurek mechanism [3]. It is worth to mention that binary systems with incoherent nonlinear interaction between their components conserve the norms in each component separately. Unlike the present setting, such systems readily admit stationary states with different vorticities and different chemical potentials in the components. In particular, systems of this type give rise to stable states with “hidden vorticity”, i.e., ones with opposite vorticities and equal norms in the two components, the corresponding total angular moment being zero, as predicted in BEC [18,19,20,21,22,23,24,25] and optics [26,27,28].
Tunneling of atoms through the potential barrier which separates two weakly coupled ring-shaped condensates with different angular momenta leads to the formation of Josephson vortices (rotational fluxons) in the low-density area between the rings [29]. This effect is characterized by zero total tunneling flow between the rings. In the case of non-zero particle-number (population) imbalance between the rings, the Josephson vortices rotate and bend. Splitting of Josephson vortices in the course of barrier reducing in the system with weak dissipation makes it possible to reach states with different final values of the total angular momenta of the merging rings, depending on the initial population imbalance between them [30].
The main objective of the present work is investigation of the impact of symmetries on interacting counter-propagating superflows in double-ring systems. The analysis reveals three noteworthy effects: (i) The axial symmetry of the superflows is spontaneously broken due to tunneling flow across the potential barrier and formation of Josephson vortices in the low-density region between the rings. (ii) When two axially-symmetric rings with the counter-propagating superflows merge, the final state of the toroidal condensate is never a ground state with zero angular momentum, as might appear at the first sight. (iii) The ring-merging process and topological charge of the final state can be controlled by the perturbation of the trapping potential, specially adapted for the initiation of symmetry-breaking of the system, and by tuning of the initial population imbalance.
2. The Model
In modeling nonequilibrium phenomenology, such as quantum turbulence [31] or nucleation of vortices [32], dissipative effects are of crucial importance for providing relaxation to equilibrium states. In particular, the dissipation drives the drift of the vortex core to the edge of the BEC cloud. Such effects naturally arise in a trapped inhomogeneous condensate due to its interaction with a thermal component, and can be captured phenomenologically by the dissipative GPE derived by Choi et al. [33,34]. Close to the thermodynamic equilibrium, the weakly dissipative GPE is written as
where is the nonlinearity strength, M is the atomic mass ( kg for Na atoms), is the s-wave scattering length (positive nm, corresponding to the repulsion of sodium atoms, is used below), is the chemical potential of the equilibrium state, and is a dimensionless phenomenological dissipative parameter. This form of the dissipative GPE has been used extensively in previous studies of vortex dynamics (see, e.g., [31,32,35,36]). It is based on the phenomenological approach, which correctly reproduces experimental observations in inhomogeneous BEC at finite temperature provided that . As is well known (see, e.g. [37]), the results of damped GPE for vortex dynamics are essentially the same as produced by more general (and much more cumbersome) dissipative extensions of GPE. In what follows below, we assume to be spatially uniform, and set , as in Refs. [31,32]. We have verified that results reported below do not essentially depend on a specific value of .
To elucidate the physical nature of the parameters and , it is instructive to follow a simple derivation of the damped GPE (1) presented in Ref. [31]. It is assumed that the condensate, described by wave function , exchanges energy and particles with a thermal cloud (reservoir) of non-condensed atoms. The interaction with the cloud is accounted for by an imaginary term on the right-hand side of the GPE:
which arises from the chemical-potential difference of the condensate and thermal reservoir: , where is the chemical potential of the reservoir. Applying the simplest approximation that and , the gauge transformation of the wave function, leads to dissipative GPE in the form of Equation (1).
We consider a toroidal condensate, split by a narrow blue-detuned sheet beam in upper and lower weakly coupled rings-shaped components. The respective total trapping potential is
where , and the sheet (barrier) potential is
with the time-dependent strength,
An experimentally relevant switching time is chosen as s, being a possible shift of the barrier along the z-axis. The initial barrier amplitude is well above the chemical potential , so that at two rings appear to be weakly coupled through the long Josephson junction. To address effects of the symmetry breaking on the dynamics of the vortices in the course of the merger, in Equation (4) we introduce, in addition to time modulation (5), uniform rotation of the sheet beam around the x-axis:
Note that trapping potential (3)–(6) with (i.e., in Equation (6)) is symmetric with respect to rotation about the vertical (z) axis. Angular velocity in our simulations lies in the range from (horizontal sheet beam) to Hz. Thus the final slope of the sheet beam with respect to the horizontal plane, , at (when the barrier’s amplitude vanishes, as per Equation (5)), is small enough, to prevent full rotation of the sheet around the x-axis.
For numerical simulations of the 3D GPE we rescale time, , length, , the chemical potential, , the external potential, , and the wave function, , which casts GPE (1) in the following form:
where the scaled positive nonlinearity strength is , and the scaled trapping potential is
with the aspect ratio of the toroidal trap,
It turns out that dynamics of quantum vortices, observed after the merger of the rings, crucially depends on A [30], while the variation of other parameters of condensate does not change our main conclusions qualitatively. In this work we concentrate on the pancake-shaped trapping potential with typical values of the trapping frequencies [38,39]: Hz and Hz, hence , the oscillator length of the radial trapping potential is m, m, and . Scaled parameters of the potentials in Equations (4) and (5) are fixed to be , which make it possible to produce generic results. Below, we use the same notation for the scaled wave function , spatial coordinates , and time t as above, as it will produce no confusion.
3. Symmetry Breaking in Coupled Condensate Rings
3.1. Spontaneous Symmetry Breaking in a Stationary Hybrid Vortex Structure
First, we use the imaginary-time-propagation (ITP) numerical method to obtain a steady-state solution of Equation (7) with . “Hybrid” states, with coupled rings carrying different vorticities [40], are produced by this method, starting from the following initial state:
where is the azimuthal angle, for and for . The ITP converges to steady states with required accuracy for an arbitrary input in Equation (10) with a fixed norm:
where and are scaled populations in the bottom and top rings, respectively:
with integration areas corresponding to half-space for lower ring, and for the upper one, respectively.
We note that, by shifting center of the splitting barrier (4), it is easy to prepare an initial state with a dominant population in the ring with topological charge ( for ) or ( for ), the respective asymmetry parameter being
Here we consider stationary hybrid states with hidden vorticities: . Figure 1 shows three different states produced by the ITP method for and with high accuracy. Different directions of the flow in the top and bottom rings inevitably lead to the appearance of Josephson vortices (fluxons), with the number of fluxon cores , as pointed out in our previous work [30]. To produce additional description of the vortices, we need to consider the flow in both parts of the condensate.
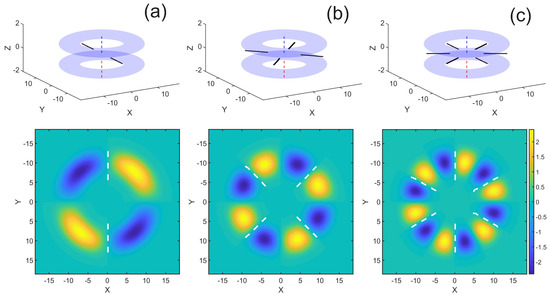
Figure 1.
(Color online) Hybrid vortex stationary states with hidden vorticity and zero population imbalance, (see Equation (13)): (a) , (b) , (c) . Shown are density isosurfaces (the top row) and the z-component of the corresponding tunnel-flow density distribution through the barrier, (the bottom row). The cores of the Josephson vortices are indicated by black lines in the top row, and by white dashed lines in the bottom one. Vertical red and blue dashed lines designate cores of the counter-propagating persistent currents in the two rings.
The density of the superflow in scaled units is defined by the usual expression:
As it was shown in [29], in the case of BEC loaded in parallel-coupled ring-shaped traps, azimuthal distribution of the component of the flow can be accurately described in the Galerkin (finite-mode) approximation. This approach yields the following azimuthal distribution for the flow tunneling across the potential barrier:
where the scaled angular velocity of the fluxon,
is defined by chemical potential difference, and is a constant phase difference between the upper and lower rings.
The position of fluxon cores is determined by the flow distribution, given by Equation (14), and rotation of this distribution around the z-axis will cause a similar rotation around the same axis of the radially-oriented Josephson vortices without changing their relative position. The initial vertical position of the fluxons is imposed by , meanwhile their angular positions may be arbitrary, being defined by the value of . It is remarkable that the spatial structure of the tunneling flows and formation of the Josephson vortices spontaneously breaks the azimuthal symmetry of the stationary hybrid vortex states with hidden vorticity, even in a fully symmetric trapping potential, cf. Ref. [40]. It also follows from Equation (15) that, in the case of the population imbalance ( with nonzero chemical potential difference, and, accordingly, , see Equation (16)), vortices perform rotational motion with angular velocity . Here and in the next section we consider the case of . The corresponding flow distribution and positions of the vortices for are shown in Figure 1. Further we consider evolution of the stationary hybrid states with a reduced barrier for different values of imbalance P in the range from to 1.
We stress that the outlined mechanism of the rotational symmetry breaking in atomic BECs is not related directly to the spontaneous symmetry breaking in the quantum field theory, or BCS theory of superconductivity. However, in a certain sense, Josephson vortices play a similar role in the present setting as the Nambu-Goldstone bosons in the above-mentioned contexts [41,42,43,44]. In particular, the dispersion law of the vortices is quadratic, for a straightforward reason: if the vortex is slowly moving, its kinetic energy is proportional to the square of the velocity.
It noteworthy that the hybrid stationary states, which also play the role of the initial conditions for dynamical simulations, feature the symmetry under the rotation around the z-axis by an angle of (discrete rotational symmetry), where k is integer and is the even number of radially-oriented Josephson vortices located in the junction between the counter-propagating superflows. In the next section, we investigate the influence of this symmetry on the evolution of the merging persistent currents.
3.2. Influence of the Symmetry on Dynamics of the Merging Rings
We concentrate here on simulations of dynamics of the merging rings with single-charged counter-propagating persistent currents, , in a pancake-shaped toroidal trap. Note that a similar double-ring system, but loaded in a trap elongated in the z-direction, was investigated in [30]. As pointed out in that work, vortex dynamics and the relaxation process are strongly affected by the value of aspect ratio A, see Equation (9). Our analysis in the present work demonstrates that the evolution of the merging rings is substantially affected by the symmetry of the pancake-shaped trap. Detailed analysis of the impact of the symmetry breaking on the evolution of the merging persistent currents is the main objective of this subsection.
We used the split-step fast-Fourier-transform method for numerical simulations of the dissipative GPE (7) in real time. The total number of atoms (12), z-component of the angular momentum
and energy
are not conserved in the dissipative setting described by GPE (7) with . For the time-independent trapping potential, the wave function evolves towards the steady state corresponding to the chemical potential . However, for the time-dependent external potential and constant chemical potential , the temporal evolution of the number of atoms is inconsistent with typical experimental observations, where the number of particles exponentially reduces with time: exp , where s is a characteristic lifetime of the BEC in the experiment [45]. To reproduce correctly the time evolution of the number of atoms we use a method similar to the approach suggested in Ref. [31] for quantum hydrodynamics. Namely, an appropriate decay rate of N is forced by adjustment of chemical potential of the equilibrium state at each time step in the course of the simulations. The initial total number of atoms is .
Figure 2a summarizes our findings. It shows, by means of black lines with circles, the final value of the angular momentum per particle, , as a function of population imbalance P. The integer values of are obtained after completion of the merger of the rings separated by the horizontal sheet beam ( in Equation (6)) and subsequent relaxation process towards a stationary persistent current in the toroidal trap. Two remarkable features are seen: (i) The final non-rotating ground state, with , is not produced by the simulations even for practically symmetric states with (so that the initial total angular momentum is close to zero). Instead, the merging rings evolve into an overall-vortex () or antivortex () state. (ii) For the initial states with the imbalance below a well-defined critical value,
the final angular momentum is, counterintuitively, determined by the less populated ring, while for the more populated ring imposes its angular-momentum state onto the whole condensate. This unexpected conclusion is explained below.
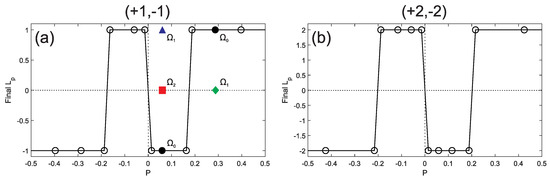
Figure 2.
(Color online) The final value of the total angular momentum per particle, , for the merging rings with initial vorticities , as a function of initial imbalance P: (a) , (b) . Solid black lines with circles represent the final states for the axially symmetric trapping potential (the horizontal sheet beam, which corresponds to in Equation (6)). Surprisingly, merging counter-rotating flows in the axially-symmetric trap never evolve towards the non-rotating ground state, with , even for small imbalances, . The vorticity of the final state is imposed by the less populated component if (see Equation (19)) for initial vorticities , and for (this counter-intuitive result is explained in the main text), and by the stronger component if . The impact of the symmetry breaking of the trapping potential is illustrated for the setup with initial vorticities by examples of the final states for two values of the imbalance, and . For , the filled black circle corresponds to the nonrotating (horizontal) barrier (with in Equation (6), see Figure 3), while the blue triangle and red square correspond to the barrier rotating around the x-axis barrier with angular velocity Hz (see Figure 4) and Hz (see Figure 5), respectively. For , the filled black circle corresponds to the , and the green diamond corresponds to Hz. Note that, above the threshold imbalance, , the final state with is never observed even for the system with broken symmetry.
We have performed similar analysis for double-charged counter-propagating persistent currents, with . As is seen from Figure 2b, final states solely with and are observed for the symmetric trapping potential with the horizontal sheet beam. The critical value of the imbalance appears to be .
Note that the merging rings with vorticities , which we investigated in Ref. [30], also evolve into the final state with the total angular momentum or , while the single-charged state, with , was not realized even when the angular momentum per particle of the initial state was . A more populated component with imposes its angular momentum onto the final state, provided that the initial imbalance takes values above some critical value . However, the values of found in [30] for the set are different from those for the set of the merging rings with , given by Equation (19). These differences are not surprising, as the set of features an obvious symmetry with respect to the two components.
Typical vortex dynamics for the system with the horizontal sheet beam (without the discrete rotational symmetry breaking, i.e., with in Equation (6)), for imbalance parameter , is shown in Figure 3. The initial pair of the Josephson vortices are bending in the course of the merger of the rings. The horizontal orientation of the Josephson vortices is not energetically preferable in the pancake-shaped setup: vortex lines tend to change the orientation and to be directed along the z-axis (see also [30]). As is seen in Figure 3b, the initial central antivortex (shown by the dashed blue line in the upper, less populated, ring in Figure 3a) splits into two antivortex lines (blue curves at the end of the Josephson vortices) and the vortex one (the red dashed line) immediately when the separating barrier vanishes. This process allows the central vortex, which is initially located only in the bottom, more populated, ring to occupy also the top, less populated, area of the eventual state. Figure 3d shows the state when the splitting and reorientation of the initial Josephson vortices is completed. Vertically oriented vortices and antivortices move from high-density to a low-density area due to the dissipation, hence the system relaxes to the available state with the lower energy. This process is illustrated in Figure 3d–f: both vortices (red lines) shown in Figure 3d disappear at the periphery of the condensate, while both antivortices (blue lines) move to the inner edge of the toroidal condensate, and one of these antivortex annihilates with the central initial vortex (the red dashed line). Thus, the final state is determined by the less populated subsystem carrying the antivortex (see Figure 3f).
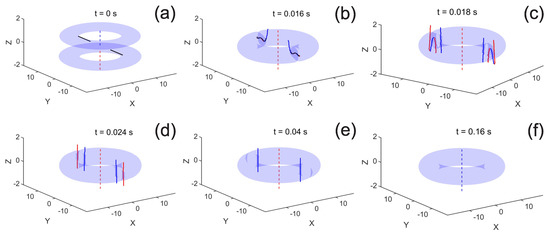
Figure 3.
(Color online) The evolution of the merging rings without symmetry breaking ( in Equation (6)). The barrier separating two rings is switched off at s. Red (blue) lines indicates positions of the vortex (antivortex) core. The population of the bottom ring, with , is slightly larger than in the top one, with (imbalance parameter (13) is ). The final state has , as shown in Figure 2a by the filled black circle. Note that, in the course of the evolution of the merging counter-rotating flows in the axially symmetric trap, the discrete rotational symmetry is observed for the positions of the vortex cores with respect to the rotation around the z-axis by an angle of . The symmetric drift of two diametrically opposite antivortices towards the central hole leads to subsequent annihilation of the central vortex and relaxation of the toroidal condensate into a final antivortex state.
As said above, this result seems counter-intuitive, because in the initial state vorticity of the bottom ring was more populated than its top-ring counterpart with . Nevertheless, it is reasonable to expect that the subsystem with imposes its vorticity onto the final state when the population in the bottom ring substantially dominates (at least in the limit of ). Indeed, at values of the initial imbalance exceeding the threshold value given by Equation (19), the final state is the single-charged persistent current with (see Figure 2a).
Analysis of the symmetry in the vortex dynamics provides insight into unusual properties of the merging persistent currents. The dynamics of the vortices maintains the discrete rotational symmetry imposed by the symmetry of the external trapping potential. In particular, it is seen in Figure 3 that the dynamics of the vortex cores obeys the symmetry under the rotation around the z-axis by , for both groups of vortices, which appear after decay of two Josephson vortices (see Figure 3b–e). Thus, in addition to the vortex line originated from the stronger component, either none or even number of vortices (antivortices) can be simultaneously trapped in the central hole of the toroidal condensate after the merger of the double-ring set with counter-rotating flows . For example, at the symmetric drift of two diametrically opposite antivortices towards the central hole (as seen in Figure 3e) leads to subsequent annihilation of the central vortex, and the relaxation of the toroidal condensate into the final antivortex state with (see Figure 3f). At , after the merger of the rings, the split vortices and antivortices (similar to those shown in Figure 3d) are located close to the external edge of the condensate, in comparison to the case of considered above. Thus all these vortices tend to decay at the external periphery, and the final state is determined by the vorticity of the initially more populated ring with .
This is why the final topological charge appears to be imposed by the stronger component (with ) at , and by weaker one, with , at , while the ground state with is forbidden as an outcome of the relaxation of the merging rings in the axially-symmetric trapping potential. These properties may be expected for any setting with two counter-rotating superflows and an even number of Josephson vortices in the initial state, as illustrated for double-charged persistent currents in Figure 2b. When the superlflows merge, the symmetric dynamics of the relaxation process, outlined above, excludes the final state , and explains why, for , the final angular momentum of the merged system is determined by the less populated ring. Note that these properties are not affected by the dissipative effects, since they are completely determined by the symmetry of the system.
It is well known that the toroidal condensate carrying a persistent current is a remarkable example of quantum multistable systems with local minima of the energy for a given integer value of the per-particle angular momentum (see, e.g., [46]). Thus, as the result of the merger of the double-ring set, the final states with different topological charges can be realized. However, the above results also demonstrate that some values of the angular momentum (vorticity) cannot be produced by the merger in the symmetric system. This raises the question as to whether the final states inaccessible for the symmetric system can be observed if the rotational symmetry of the trapping potential is broken.
Certainly, there are many ways to break the symmetry of the trapping potential. In this work we break the symmetry of the setup in a controllable way by the slow rotation of the barrier around the horizontal axis in the course of the merger, see Equation (6). The rotation is a simple perturbation, which can be easily realized experimentally. The breaking of the azimuthal symmetry of the potential, induced by the rotation, leads to redistribution of the condensate density in the course of the merger, which strongly affects subsequent dynamics of the vortices, when the barrier is switched off.
Obviously, an atomic cloud is never purely symmetric in a real experiment, due to imperfections of the trapping potential and irregular time-dependent fluctuations of the system’s parameters. Then, the question arises if unusual manifestations of the symmetry of the merging persistent currents, predicted above, are experimentally observable, or maybe any non-negligible symmetry-breaking perturbation essentially affects the final vorticity state. To address this issue, we have performed extensive simulations, including stronger or weaker symmetry-breaking perturbations. It turns out that, when the sheet beam rotates very slowly ( Hz in Equation (6)), the symmetry breaking does not produce any visible effect on the dynamics of the vortices, with the vorticity of the final state being the same as for the horizontal sheet beam (with ). The impact of the symmetry breaking becomes essential as the angular velocity of the rotating sheet beam increases.
Typical examples of the relaxation dynamics for small imbalance and broken symmetry are shown in Figure 4 for Hz (the final topological charge is ) and in Figure 5 for Hz (the system relaxes to the non-rotating ground state, with ). Note that, for the same imbalance but without the rotation of the barrier (), the final state is (see Figure 2a and Figure 3).
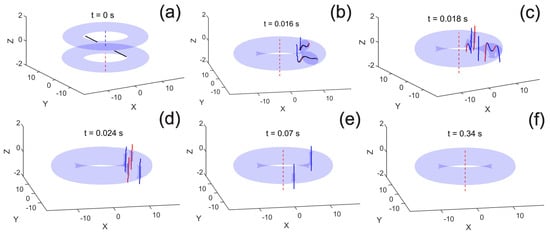
Figure 4.
(Color online) The evolution of the merging rings affected by symmetry breaking which is induced by slow rotation of the sheet beam (6) around the x-axis, with angular velocity Hz. Note that the system with the broken symmetry evolves towards the final topological charge (vorticity) , while, for the same value of imbalance (13), (the population of the bottom ring with slightly dominates over the top one, with ), the final state of the axially-symmetric system has (see Figure 3).
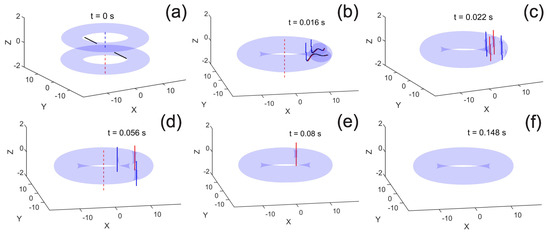
Figure 5.
(Color online) The evolution of the merging rings affected by stronger, than in the case of Figure 4, symmetry breaking, imposed by rotation (6) with angular velocity Hz. The population in the bottom ring with slightly dominates over the top one, with (the respective imbalance parameter (13) is , as well as in Figure 3 and Figure 4). Being controlled by the barrier’s angular velocity, , the symmetry breaking drives the merging rings to final states with different topological charges (vorticities). In this case, when the axial symmetry is strongly broken, the final nonrotating state is established, with vorticity . Surprisingly, merging counter-rotating persistent currents evolve into a nonrotating final state neither for the symmetric system (see Figure 3, where and the final topological charge is ), nor for a weakly asymmetric trapping potential (see Figure 4, where Hz and the final topological charge is ).
Remarkably, when the barrier is switched off, the positions of the split vortices are not diametrically opposite, as it was observed in the absence of the symmetry breaking (). In the course of the merger, if , the initial Josephson vortices move toward each other until they break, bend and split (see Figure 4b,c and Figure 5b,c).
Recall that the initial hybrid state has different vorticities, and , in their two axially separated parts (see Figure 4a). Both vorticities share a common vertically oriented axis threading the separated double-ring system, and radially oriented rotational fluxons inside the separating barrier. The remarkable moment of the evolution of the merging persistent currents is illustrated in Figure 4b: as soon as the barrier vanishes, the central vortex line (the dashed red line in Figure 4a), which originates from the dominating bottom ring, still exists at (see Figure 4b), while the antivortex from the upper ring (the dashed blue line in Figure 4a) splits into one vortex and two antivortices, which are shown by solid blue lines attached to the bending Josephson vortices in Figure 4b. As the result, the central hole contains a single vortex line (the dashed red line in Figure 4b) threading the whole toroidal condensate. Thus, similar transformations are observed for the axisymmetric trap (Figure 3b) and in the case of broken symmetry (Figure 4b and Figure 5b). However, for the system with the horizontal barrier (, Figure 3b) two connected fluxon-antivortex topological excitations appear to be diametrically opposed. In contrast to that, the greater is the angular velocity of the sheet beam, the closer to each other these two groups of vortices are located at the same moment of time, see Figure 4b and Figure 5b.
Finally, for the case of slowly rotating barrier ( Hz) the antivortex, which is closest to the axis, moves towards the central hole and annihilates with the central vortex (the red dashed line), as seen in Figure 4c. Then, one of the vortices (the red line nearest to the axis of the ring in Figure 4d) finally drifts towards the central hole of the torus (Figure 4e), while other vortices and antivortices move to the outer (low-density) region and eventually decay there. As the result, the vorticity of the system tends to be (Figure 4d–f).
When angular velocity in Equation (6) increases, the symmetry of the trapping potential breaks even stronger, which can drive the evolution of the system towards a nonrotating ground state with (zero vorticity), which is never observed not only for the axially-symmetric potential, but also in the case of weak symmetry breaking. As one can see in Figure 5a–c, for Hz the dynamics generally resembles that in Figure 4; nevertheless, the subsequent evolution leads to the nullification of the final vorticity. The point is that the vortex and antivortex which are nearest to the inner edge (Figure 5c) drift towards the center and annihilate with each other (Figure 5c–e). Other vortices and antivortices leave the system, moving to the external periphery and disappearing there (Figure 5d–f).
4. Conclusions
We have investigated dynamics of quantum vortices associated with the symmetry-breaking instability of superflows in interacting ring-shaped BECs. We demonstrate that the tunneling across the Bose Josephson junction in the double-ring system is associated with the spontaneous breaking of the rotational symmetry due to the formation of rotational fluxons (Josephson vortices). We demonstrate that dynamics of the merging contour-rotating persistent currents is determined by the discrete rotational symmetry of the system. We have studied in detail the relaxation process of the merging counter-propagating persistent currents with vorticities and in the framework of the weakly dissipative mean-field model. It turns out that, when the population in one of the rings slightly dominates (i.e., the respective imbalance parameter does not reach a threshold (critical) value, ), the final state of the system is imposed by the less populated ring. For instance, in the case of , so that the population with vorticity dominates over its counterpart with , the final state produced by the merger has vorticity . On the other hand, it is found that the system with broken discrete rotational symmetry and the imbalance taking values below the critical level, , can be driven into a final state with any vorticity, , depending on the symmetry-breaking perturbation of the barrier potential which separates the initial rings. For values of the imbalance above the critical level, , only two final values of the vorticity ( or 0 for , and or 0 for ) are observed as a result of the merger.
These results may stimulate further investigation of the fundamental role of the symmetry breaking in the evolution of quantum systems at the macroscopic level in the ongoing experiments with matter-wave settings and atomtronic circuits.
Author Contributions
A.Y. and B.M. suggested the idea and supervised the work. A.O. and I.Y. developed and performed the simulations. All authors were involved in analysis and discussions of the results, and contributed to writing the manuscript.
Funding
The work of B.M. on this topic is supported, in part, by the Israel Science Foundation through grant No. 1287/17.
Acknowledgments
We wish to thank O.G. Chelpanova for useful discussions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Brand, J.; Haigh, T.J.; Zülicke, U. Sign of coupling in barrier-separated Bose-Einstein condensates and stability of double-ring systems. Phys. Rev. A 2010, 81, 025602. [Google Scholar] [CrossRef]
- Brand, J.; Haigh, T.J.; Zulicke, U. Rotational fluxons of Bose-Einstein condensates in coplanar double-ring traps. Phys. Rev. A 2009, 80, 011602(R). [Google Scholar] [CrossRef]
- Su, S.W.; Gou, S.C.; Bradley, A.; Fialko, O.; Brand, J. Kibble-Zurek Scaling and its Breakdown for Spontaneous Generation of Josephson Vortices in Bose-Einstein Condensates. Phys. Rev. Lett. 2013, 110, 215302. [Google Scholar] [CrossRef]
- Baals, C.; Ott, H.; Brand, J.; Mateo, A.M. Nonlinear standing waves in an array of coherently coupled Bose-Einstein condensates. Phys. Rev. A 2018, 98, 053603. [Google Scholar] [CrossRef]
- Lesanovsky, I.; von Klitzing, W. Spontaneous Emergence of Angular Momentum Josephson Oscillations in Coupled Annular Bose-Einstein Condensates. Phys. Rev. Lett. 2007, 98, 050401. [Google Scholar] [CrossRef]
- Amico, L.; Aghamalyan, D.; Crepaz, H.; Auksztol, F.; Dumke, R.; Kwek, L.C. Superfluid qubit systems with ring shaped optical lattices. Sci. Rep. 2014, 4, 4298. [Google Scholar] [CrossRef]
- Aghamalyan, D.; Amico, L.; Kwek, L.C. Effective dynamics of cold atoms flowing in two ring shaped optical potentials with tunable tunneling. Phys. Rev. A 2013, 88, 063627. [Google Scholar] [CrossRef]
- Zhang, X.F.; Li, B.; Zhang, S.G. Rotating spin–orbit coupled Bose-Einstein condensates in concentrically coupled annular traps. Laser Phys. 2013, 23, 105501. [Google Scholar] [CrossRef]
- Polo, J.; Benseny, A.; Busch, T.; Ahufinger, V.; Mompart, J. Transport of ultracold atoms between concentric traps via spatial adiabatic passage. New J. Phys. 2016, 18, 015010. [Google Scholar] [CrossRef]
- Haug, T.; Amico, L.; Dumke, R.; Kwek, L.C. Mesoscopic Vortex-Meissner currents in ring ladders. Quantum Sci. Technol. 2018, 3, 035006. [Google Scholar] [CrossRef]
- Richaud, A.; Penna, V. Quantum dynamics of bosons in a two-ring ladder: Dynamical algebra, vortexlike excitations, and currents. Phys. Rev. A 2017, 96, 013620. [Google Scholar] [CrossRef]
- Gallemí, A.; Mateo, A.M.; Mayol, R.; Guilleumas, M. Coherent quantum phase slip in two-component bosonic atomtronic circuits. New J. Phys. 2016, 18, 015003. [Google Scholar] [CrossRef]
- Baggaley, A.W.; Parker, N.G. Kelvin-Helmholtz instability in a single-component atomic superfluid. Phys. Rev. A 2018, 97, 053608. [Google Scholar] [CrossRef]
- Kanai, T.; Guo, W.; Tsubota, M. Merging of Rotating Bose-Einstein Condensates. J. Low Temp. Phys. 2019, 195, 37–50. [Google Scholar] [CrossRef]
- Takeuchi, H.; Suzuki, N.; Kasamatsu, K.; Saito, H.; Tsubota, M. Quantum Kelvin-Helmholtz instability in phase-separated two-component Bose-Einstein condensates. Phys. Rev. B 2010, 81, 094517. [Google Scholar] [CrossRef]
- Suzuki, N.; Takeuchi, H.; Kasamatsu, K.; Tsubota, M.; Saito, H. Crossover between Kelvin-Helmholtz and counter-superflow instabilities in two-component Bose-Einstein condensates. Phys. Rev. A 2010, 82, 063604. [Google Scholar] [CrossRef]
- Montgomery, T.W.A.; Scott, R.G.; Lesanovsky, I.; Fromhold, T.M. Spontaneous creation of nonzero-angular-momentum modes in tunnel-coupled two-dimensional degenerate Bose gases. Phys. Rev. A 2010, 81, 063611. [Google Scholar] [CrossRef]
- Brtka, M.; Gammal, A.; Malomed, B.A. Hidden vorticity in binary Bose-Einstein condensates. Phys. Rev. A 2010, 82, 053610. [Google Scholar] [CrossRef]
- Wen, L.; Qiao, Y.; Xu, Y.; Mao, L. Structure of two-component Bose-Einstein condensates with respective vortex-antivortex superposition states. Phys. Rev. A 2013, 87, 033604. [Google Scholar] [CrossRef]
- Yakimenko, A.I.; Isaieva, K.O.; Vilchinskii, S.I.; Weyrauch, M. Stability of persistent currents in spinor Bose-Einstein condensates. Phys. Rev. A 2013, 88, 051602. [Google Scholar] [CrossRef]
- Ishino, S.; Tsubota, M.; Takeuchi, H. Counter-rotating vortices in miscible two-component Bose-Einstein condensates. Phys. Rev. A 2013, 88, 063617. [Google Scholar] [CrossRef]
- Ishino, S.; Tsubota, M.; Takeuchi, H. Matter-wave interactions in two-component Bose-Einstein condensates. EPL 2015, 111, 30005. [Google Scholar]
- Hoashi, M.; Nakamura, Y.; Yamanaka, Y. Analytical study of parameter regions of dynamical instability for two-component Bose-Einstein condensates with coaxial quantized vortices. Phys. Rev. A 2016, 93, 043622. [Google Scholar] [CrossRef]
- Xu, S.-L.; Wang, Z.-Q.; He, J.-R.; Xue, L.; Belic, M.R. Vector vortex solitons in two-component Bose-Einstein condensates with modulated nonlinearities and a harmonic trap. J. Mod. Opt. 2018, 65, 1542–1548. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Z.; Luo, Z.; Huang, C.; Tan, H.; Pang, W.; Malomed, B.A. Two-dimensional vortex quantum droplets. Phys. Rev. A 2018, 98, 063602. [Google Scholar] [CrossRef]
- Leykam, D.; Malomed, B.; Desyatnikov, A.S. Composite vortices in nonlinear circular waveguide arrays. J. Opt. 2013, 82, 053610. [Google Scholar] [CrossRef]
- Salgueiro, J.R. Vector-vortex solitons in nonlinear photonic crystal fibers. J. Opt. 2016, 18, 074004. [Google Scholar] [CrossRef]
- Mayteevarunyoo, T.; Malomed, B.; Skryabin, D. Vortex modes supported by spin-orbit coupling in a laser with saturable absorption. New J. Phys. 2018, 20, 113019. [Google Scholar] [CrossRef]
- Oliinyk, A.; Yakimenko, A.; Malomed, B. Tunneling of persistent currents in coupled ring-shaped Bose-Einstein condensate. arXiv 2019, arXiv:1901.06502. [Google Scholar]
- Oliinyk, A.; Malomed, B.; Yakimenko. Nonlinear dynamics of Josephson vortices in merging superfluid ring. arXiv 2019, arXiv:1908.02468. [Google Scholar]
- Tsubota, M.; Kobayashi, M.; Takeuchi, H. Quantum hydrodynamics. Phys. Rep. 2013, 522, 191. [Google Scholar] [CrossRef]
- Yakimenko, A.I.; Bidasyuk, Y.M.; Prikhodko, O.O.; Vilchinskii, S.I.; Ostrovskaya, E.A.; Kivshar, Y.S. Optical tweezers for vortex rings in Bose-Einstein condensates. Phys. Rev. A 2013, 88, 043637. [Google Scholar] [CrossRef]
- Choi, S.; Morgan, S.A.; Burnett, K. Phenomenological damping in trapped atomic Bose-Einstein condensates. Phys. Rev. A 1998, 57, 4057. [Google Scholar] [CrossRef]
- Proukakis, N.P.; Jackson, B. Finite-temperature models of Bose-Einstein condensation. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 203002. [Google Scholar] [CrossRef]
- Carretero-González, R.; Whitaker, N.; Kevrekidis, P.G.; Frantzeskakis, D.J. Vortex structures formed by the interference of sliced condensates. Phys. Rev. A 2008, 77, 023605. [Google Scholar] [CrossRef]
- Kasamatsu, K.; Tsubota, M.; Ueda, M. Vortex lattice formation in a rotating Bose-Einstein condensate. Phys. Rev. A 2003, 67, 033610. [Google Scholar] [CrossRef]
- Rooney, S.J.; Bradley, A.S.; Blakie, P.B. Decay of a quantum vortex: Test of nonequilibrium theories for warm Bose-Einstein condensates. Phys. Rev. A 2010, 81, 023630. [Google Scholar] [CrossRef]
- Wright, K.C.; Blakestad, R.B.; Lobb, C.J.; Phillips, W.D.; Campbell, G.K. Driving Phase Slips in a Superfluid Atom Circuit with a Rotating Weak Link. Phys. Rev. Lett. 2013, 110, 025302. [Google Scholar] [CrossRef]
- Jendrzejewski, F.; Eckel, S.; Murray, N.; Lanier, C.; Edwards, M.; Lobb, C.J.; Campbell, G.K. Resistive flow in a weakly interacting Bose-Einstein condensate. Phys. Rev. Lett. 2014, 113, 045305. [Google Scholar] [CrossRef]
- Driben, R.; Kartashov, Y.; Malomed, B.A.; Meier, T.; Torner, L. Three-dimensional hybrid vortex solitons. New J. Phys. 2014, 16, 063035. [Google Scholar] [CrossRef][Green Version]
- Arrautf, I. The Quantum Yang-Baxter Conditions: The Fundamental Relations behind the Nambu-Goldstone Theorem. Symmetry 2019, 11, 803. [Google Scholar] [CrossRef]
- Nambu, Y. Spontaneous Breaking of Lie and Current Algebras. J. Stat. Phys. 2004, 115, 7–17. [Google Scholar] [CrossRef]
- Brauner, T. Spontaneous Symmetry Breaking and Nambu–Goldstone Bosons in Quantum Many-Body Systems. Symmetry 2010, 2, 609–657. [Google Scholar] [CrossRef]
- Nielsen, H.B.; Chadha, S. On how to count Goldstone bosons. Nucl. Phys. B 1976, 105, 445–453. [Google Scholar] [CrossRef]
- Beattie, S.; Moulder, S.; Fletcher, R.J.; Hadzibabic, Z. Persistent Currents in Spinor Condensates. Phys. Rev. Lett. 2013, 110, 025301. [Google Scholar] [CrossRef] [PubMed]
- Yakimenko, A.I.; Vilchinskii, S.I.; Bidasyuk, Y.M.; Kuriatnikov, Y.I.; Isaieva, K.O.; Weyrauch, M. Generation and decay of persistent current in a toroidal Bose-Einstein condensate. Rom. Rep. Phys. 2015, 67, 249–272. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).