Structure Learning of Gaussian Markov Random Fields with False Discovery Rate Control
Abstract
:1. Introduction
LASSO and SLOPE
2. nsSLOPE (Neighborhood Selection Sorted L-One Penalized Estimation)
2.1. Sub-Problems
2.2. Connection to Inverse Covariance Matrix Estimation
3. Algorithm
| Algorithm 1: The nsSLOPE Algorithm |
| Input: with zero-centered columns Input: Input: The target level of FDR q Set according to Section 3.2;  |
3.1. Sub-Problem Solver
3.2. Choice of
3.3. Estimation of
3.4. Stopping Criterion of the External Loop
3.5. Uniqueness of Sub-Problem Solutions
4. Analysis
4.1. Estimation Error Analysis
4.1.1. Off-Diagonal Entries
- The true signal satisfies for some (this condition is satisfied for example, if and is s-sparse, that is, it has at most s nonzero elements).
- The noise satisfies the condition This will allow us to say that the true signal is feasible with respect to the constraint in (6).
4.1.2. Diagonal Entries
4.1.3. Discussion on Asymptotic Behaviors
4.2. Neighborhood FDR Control under Group Assumptions
5. Numerical Results
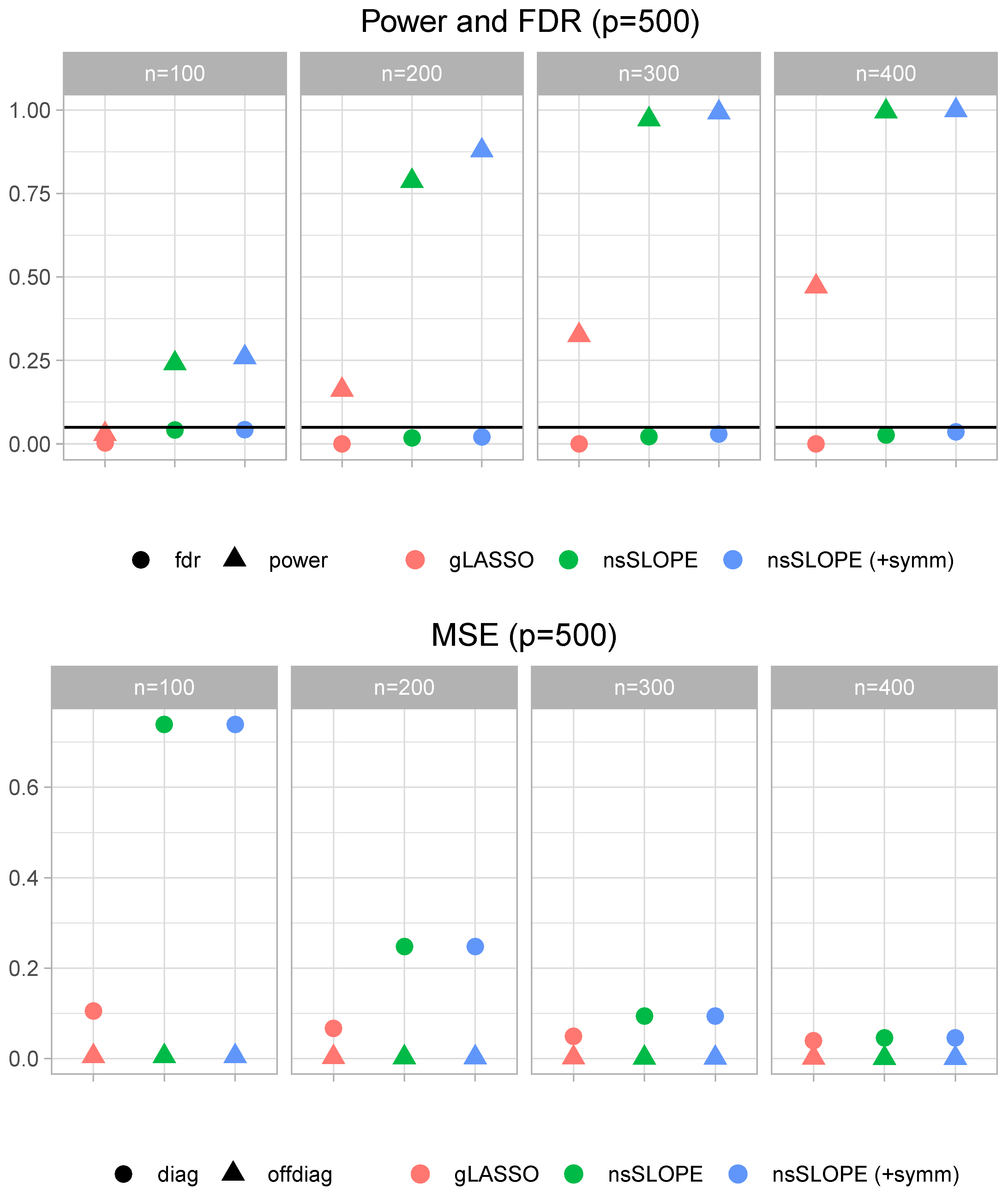
5.1. Quality of Estimation
5.1.1. Mean Square Estimation Error
5.1.2. FDR Control
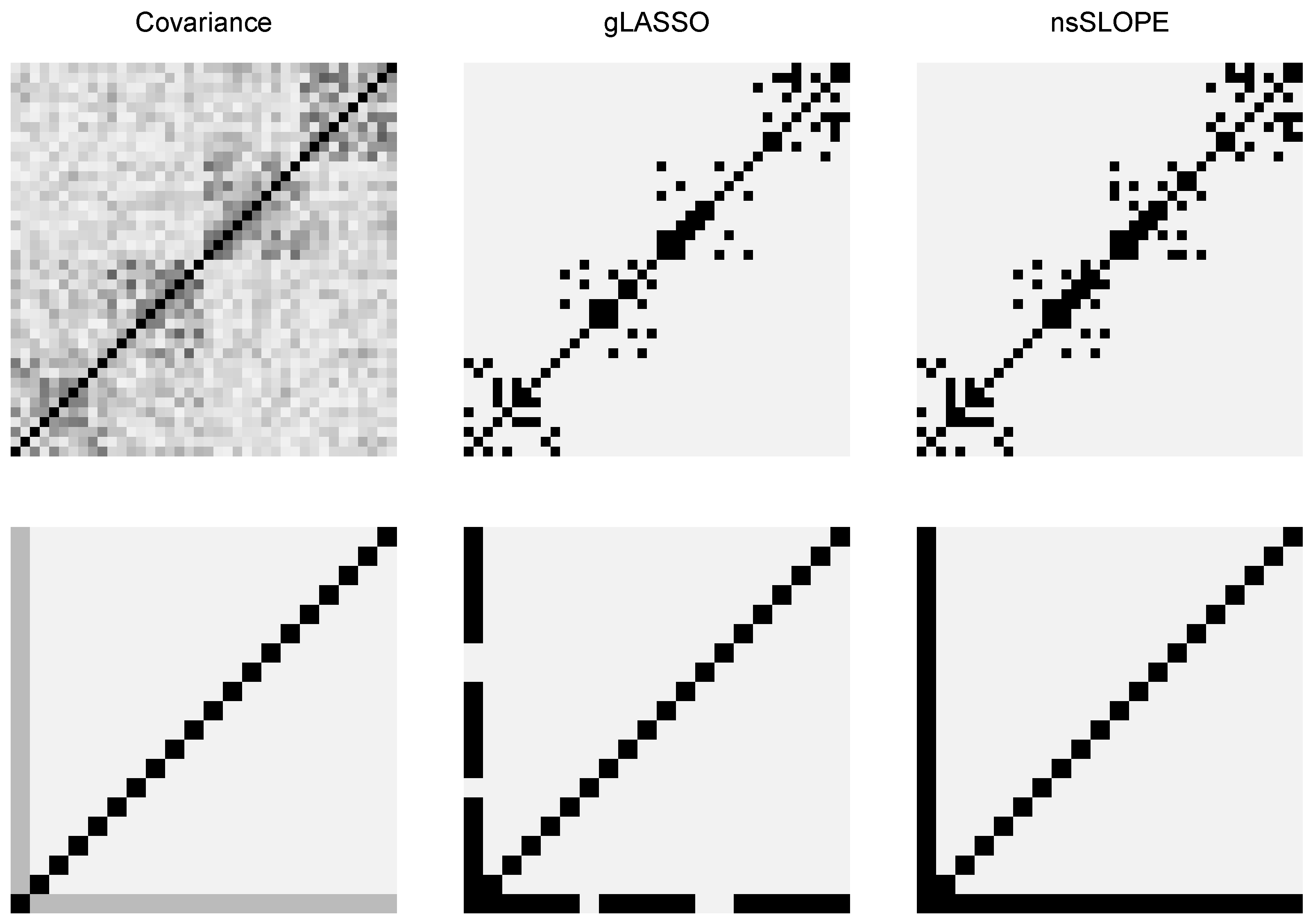
5.2. Structure Discovery
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yuan, M.; Lin, Y. Model selection and estimation in the Gaussian graphical model. Biometrika 2007, 94, 19–35. [Google Scholar] [CrossRef] [Green Version]
- D’Aspremont, A.; Banerjee, O.; El Ghaoui, L. First-Order Methods for Sparse Covariance Selection. SIAM J. Matrix Anal. Appl. 2008, 30, 56–66. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, O.; Ghaoui, L.E.; d’Aspremont, A. Model Selection Through Sparse Maximum Likelihood Estimation for Multivariate Gaussian or Binary Data. J. Mach. Learn. Res. 2008, 9, 485–516. [Google Scholar]
- Friedman, J.; Hastie, T.; Tibshirani, R. Sparse inverse covariance estimation with the graphical lasso. Biostatistics 2008, 9, 432–441. [Google Scholar] [CrossRef] [PubMed]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. (Ser. B) 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Oztoprak, F.; Nocedal, J.; Rennie, S.; Olsen, P.A. Newton-Like Methods for Sparse Inverse Covariance Estimation. In Advances in Neural Information Processing Systems 25; MIT Press: Cambridge, MA, USA, 2012; pp. 764–772. [Google Scholar]
- Rolfs, B.; Rajaratnam, B.; Guillot, D.; Wong, I.; Maleki, A. Iterative Thresholding Algorithm for Sparse Inverse Covariance Estimation. In Advances in Neural Information Processing Systems 25; MIT Press: Cambridge, MA, USA, 2012; pp. 1574–1582. [Google Scholar]
- Hsieh, C.J.; Dhillon, I.S.; Ravikumar, P.K.; Sustik, M.A. Sparse Inverse Covariance Matrix Estimation Using Quadratic Approximation. In Advances in Neural Information Processing Systems 24; MIT Press: Cambridge, MA, USA, 2011; pp. 2330–2338. [Google Scholar]
- Hsieh, C.J.; Banerjee, A.; Dhillon, I.S.; Ravikumar, P.K. A Divide-and-Conquer Method for Sparse Inverse Covariance Estimation. In Advances in Neural Information Processing Systems 25; MIT Press: Cambridge, MA, USA, 2012; pp. 2330–2338. [Google Scholar]
- Hsieh, C.J.; Sustik, M.A.; Dhillon, I.; Ravikumar, P.; Poldrack, R. BIG & QUIC: Sparse Inverse Covariance Estimation for a Million Variables. In Advances in Neural Information Processing Systems 26; MIT Press: Cambridge, MA, USA, 2013; pp. 3165–3173. [Google Scholar]
- Mazumder, R.; Hastie, T. Exact Covariance Thresholding into Connected Components for Large-scale Graphical Lasso. J. Mach. Learn. Res. 2012, 13, 781–794. [Google Scholar]
- Treister, E.; Turek, J.S. A Block-Coordinate Descent Approach for Large-scale Sparse Inverse Covariance Estimation. In Advances in Neural Information Processing Systems 27; MIT Press: Cambridge, MA, USA, 2014; pp. 927–935. [Google Scholar]
- Zhang, R.; Fattahi, S.; Sojoudi, S. Large-Scale Sparse Inverse Covariance Estimation via Thresholding and Max-Det Matrix Completion; International Conference on Machine Learning, PMLR: Stockholm, Sweden, 2018. [Google Scholar]
- Meinshausen, N.; Bühlmann, P. High-dimensional graphs and variable selection with the Lasso. Ann. Stat. 2006, 34, 1436–1462. [Google Scholar] [CrossRef] [Green Version]
- Meinshausen, N.; Bühlmann, P. Stability selection. J. R. Stat. Soc. (Ser. B) 2010, 72, 417–473. [Google Scholar] [CrossRef]
- Rothman, A.J.; Bickel, P.J.; Levina, E.; Zhu, J. Sparse permutation invariant covariance estimation. Electron. J. Stat. 2008, 2, 494–515. [Google Scholar] [CrossRef]
- Lam, C.; Fan, J. Sparsistency and rates of convergence in large covariance matrix estimation. Ann. Stat. 2009, 37, 4254–4278. [Google Scholar] [CrossRef]
- Raskutti, G.; Yu, B.; Wainwright, M.J.; Ravikumar, P.K. Model Selection in Gaussian Graphical Models: High-Dimensional Consistency of ℓ1-regularized MLE. In Advances in Neural Information Processing Systems 21; MIT Press: Cambridge, MA, USA, 2009; pp. 1329–1336. [Google Scholar]
- Yuan, M. High Dimensional Inverse Covariance Matrix Estimation via Linear Programming. J. Mach. Learn. Res. 2010, 11, 2261–2286. [Google Scholar]
- Fattahi, S.; Zhang, R.Y.; Sojoudi, S. Sparse Inverse Covariance Estimation for Chordal Structures. In Proceedings of the 2018 European Control Conference (ECC), Limassol, Cyprus, 12–15 June 2018; pp. 837–844. [Google Scholar]
- Bogdan, M.; van den Berg, E.; Sabatti, C.; Su, W.; Candes, E.J. SLOPE—Adaptive Variable Selection via Convex Optimization. Ann. Appl. Stat. 2015, 9, 1103–1140. [Google Scholar] [CrossRef] [PubMed]
- Brzyski, D.; Su, W.; Bogdan, M. Group SLOPE—Adaptive selection of groups of predictors. arXiv 2015, arXiv:1511.09078. [Google Scholar] [CrossRef] [PubMed]
- Su, W.; Candès, E. SLOPE is adaptive to unknown sparsity and asymptotically minimax. Ann. Stat. 2016, 44, 1038–1068. [Google Scholar] [CrossRef]
- Bondell, H.D.; Reich, B.J. Simultaneous Regression Shrinkage, Variable Selection, and Supervised Clustering of Predictors with OSCAR. Biometrics 2008, 64, 115–123. [Google Scholar] [CrossRef]
- Figueiredo, M.A.T.; Nowak, R.D. Ordered Weighted L1 Regularized Regression with Strongly Correlated Covariates: Theoretical Aspects. In Proceedings of the 19th International Conference on Artificial Intelligence and Statistics, AISTATS 2016, Cadiz, Spain, 9–11 May 2016; pp. 930–938. [Google Scholar]
- Lee, S.; Brzyski, D.; Bogdan, M. Fast Saddle-Point Algorithm for Generalized Dantzig Selector and FDR Control with the Ordered l1-Norm. In Proceedings of the 19th International Conference on Artificial Intelligence and Statistics (AISTATS), Cadiz, Spain, 9–11 May 2016; Volume 51, pp. 780–789. [Google Scholar]
- Chen, S.; Banerjee, A. Structured Matrix Recovery via the Generalized Dantzig Selector. In Advances in Neural Information Processing Systems 29; Lee, D.D., Sugiyama, M., Luxburg, U.V., Guyon, I., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2016; pp. 3252–3260. [Google Scholar]
- Bellec, P.C.; Lecué, G.; Tsybakov, A.B. Slope meets Lasso: Improved oracle bounds and optimality. arXiv 2017, arXiv:1605.08651v3. [Google Scholar] [CrossRef]
- Derumigny, A. Improved bounds for Square-Root Lasso and Square-Root Slope. Electron. J. Stat. 2018, 12, 741–766. [Google Scholar] [CrossRef]
- Anderson, T.W. An Introduction to Multivariate Statistical Analysis; Wiley-Interscience: London, UK, 2003. [Google Scholar]
- Beck, A.; Tetruashvili, L. On the Convergence of Block Coordinate Descent Type Methods. SIAM J. Optim. 2013, 23, 2037–2060. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef] [Green Version]
- Nesterov, Y. A Method of Solving a Convex Programming Problem with Convergence Rate O(1/k2). Soviet Math. Dokl. 1983, 27, 372–376. [Google Scholar]
- Razaviyayn, M.; Hong, M.; Luo, Z.Q. A Unified Convergence Analysis of Block Successive Minimization Methods for Nonsmooth Optimization. SIAM J. Optim. 2013, 23, 1126–1153. [Google Scholar] [CrossRef] [Green Version]
- Figueiredo, M.; Nowak, R. Sparse estimation with strongly correlated variables using ordered weighted ℓ1 regularization. arXiv 2014, arXiv:1409.4005. [Google Scholar]
- Johnstone, I.M. Chi-square oracle inequalities. Lect. Notes-Monogr. Ser. 2001, 36, 399–418. [Google Scholar]
- Park, T.; Casella, G. The Bayesian Lasso. J. Am. Stat. Assoc. 2008, 103, 681–686. [Google Scholar] [CrossRef]
- Mallick, H.; Yi, N. A New Bayesian Lasso. Stat. Its Interface 2014, 7, 571–582. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.; Sobczyk, P.; Bogdan, M. Structure Learning of Gaussian Markov Random Fields with False Discovery Rate Control. Symmetry 2019, 11, 1311. https://doi.org/10.3390/sym11101311
Lee S, Sobczyk P, Bogdan M. Structure Learning of Gaussian Markov Random Fields with False Discovery Rate Control. Symmetry. 2019; 11(10):1311. https://doi.org/10.3390/sym11101311
Chicago/Turabian StyleLee, Sangkyun, Piotr Sobczyk, and Malgorzata Bogdan. 2019. "Structure Learning of Gaussian Markov Random Fields with False Discovery Rate Control" Symmetry 11, no. 10: 1311. https://doi.org/10.3390/sym11101311
APA StyleLee, S., Sobczyk, P., & Bogdan, M. (2019). Structure Learning of Gaussian Markov Random Fields with False Discovery Rate Control. Symmetry, 11(10), 1311. https://doi.org/10.3390/sym11101311




