Braids, 3-Manifolds, Elementary Particles: Number Theory and Symmetry in Particle Physics
Abstract
1. Introduction
2. Preliminaries: Branched Coverings of 3- and 4-Manifolds
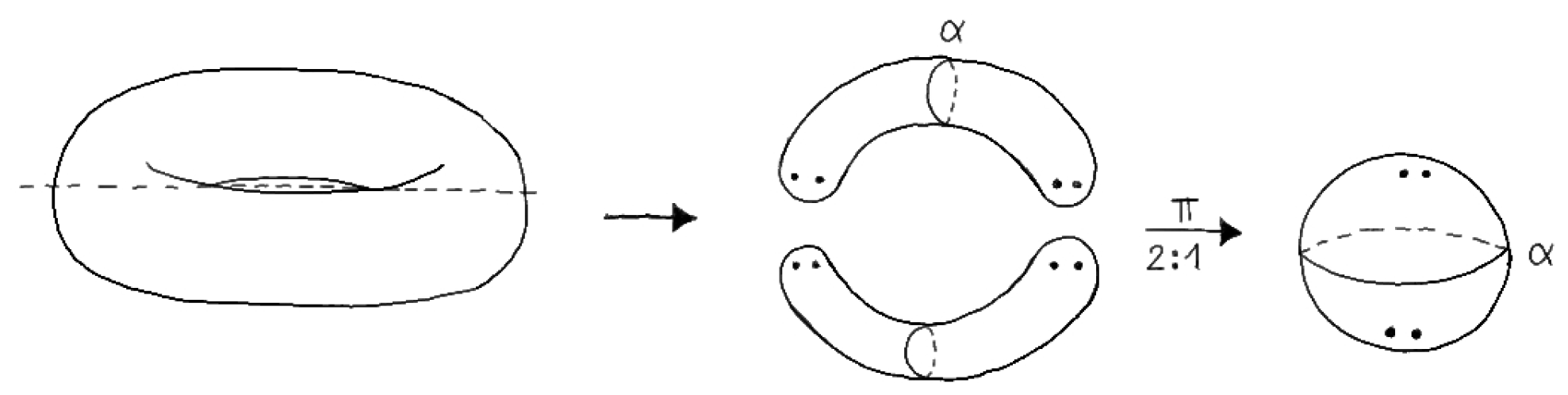
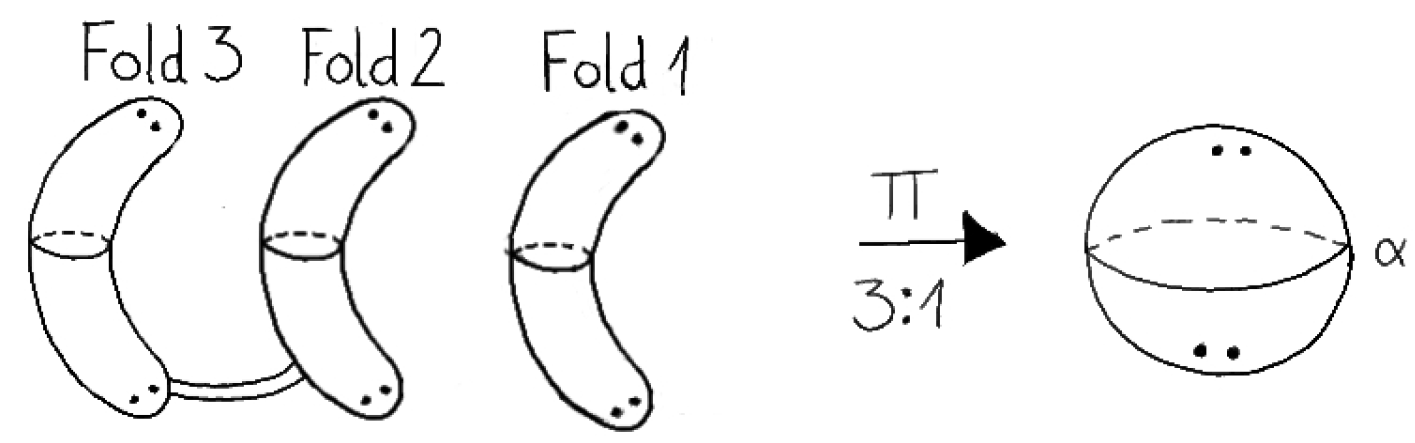
2.1. As Warmup: Branched Coverings of 2-Manifolds
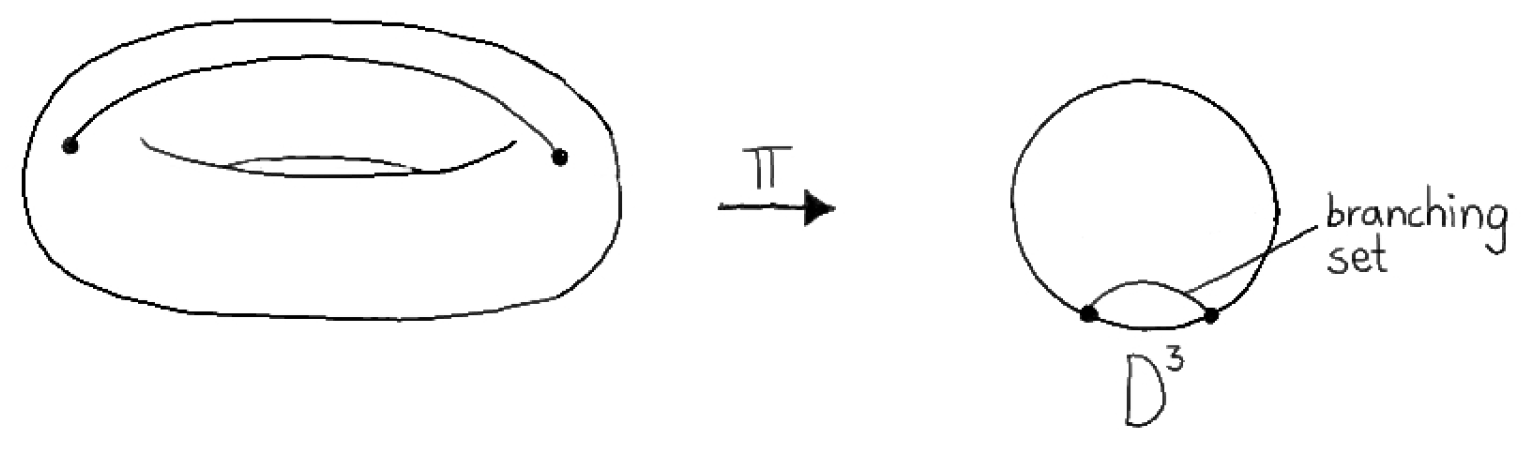
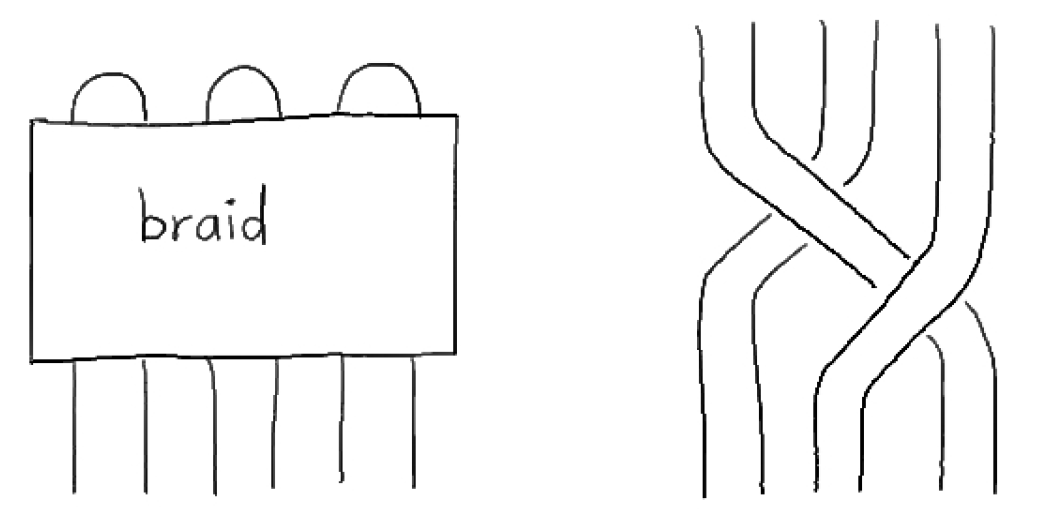
2.2. Branched Coverings of 3-Manifolds
2.3. Branched Covering of 4-Manifolds
2.4. Branched Coverings of Knot Complements
3. Reconstructing a Spacetime: The K3 Surface and Particle Physics
- is a smooth 4-manifold,
- any sequence of spacetime event has to converge to a spacetime event and
- any loop (time-like or not) must be contracted.
- has to admit a smoothness structure with Ricci-flat metric representing the vacuum.
- there is a compact, contactable submanifold (called Akbulut cork) so that cutting out Aand reglue it (by an involution) will produce a new smoothness structure,
- splits topologically intotwo copies of the manifold and three copies of and
- the 3-sphere is a submanifold of A.
4. From K3 Surfaces to Octonions, 3-Braids and Particles
4.1. K3 Surfaces and Octonions
4.2. From Immersed Surfaces in K3 Surfaces to Fermions and Knot Complements
4.3. Fermions as Knot Complements
4.4. Torus Bundle as Gauge Fields
- finite order (orders ): the tangent bundle is three-dimensional,
- Dehn-twist (left/right twist): the tangent bundle is a sum of a two-dimensional and a one-dimensional bundle,
- Anosov: the tangent bundle is a sum of three one-dimensional bundles.
- finite order: 2 isotopy classes (= no/even twist or odd twist),
- Dehn-twist: 2 isotopy classes (= left or right Dehn twists),
- Anosov: 8 isotopy classes (= all possible orientations of the three line bundles forming the tangent bundle).
- torus bundle with no/even twists: one isotopy class,
- torus bundle with twist (Dehn twist or odd finite twist): three isotopy classes,
- torus bundle with Anosov map: eight isotopy classes.
- torus bundle with no twists: one isotopy class with ,
- torus bundle with twist: three isotopy classes with ,
- torus bundle with Anosov map: eight isotopy classes with .
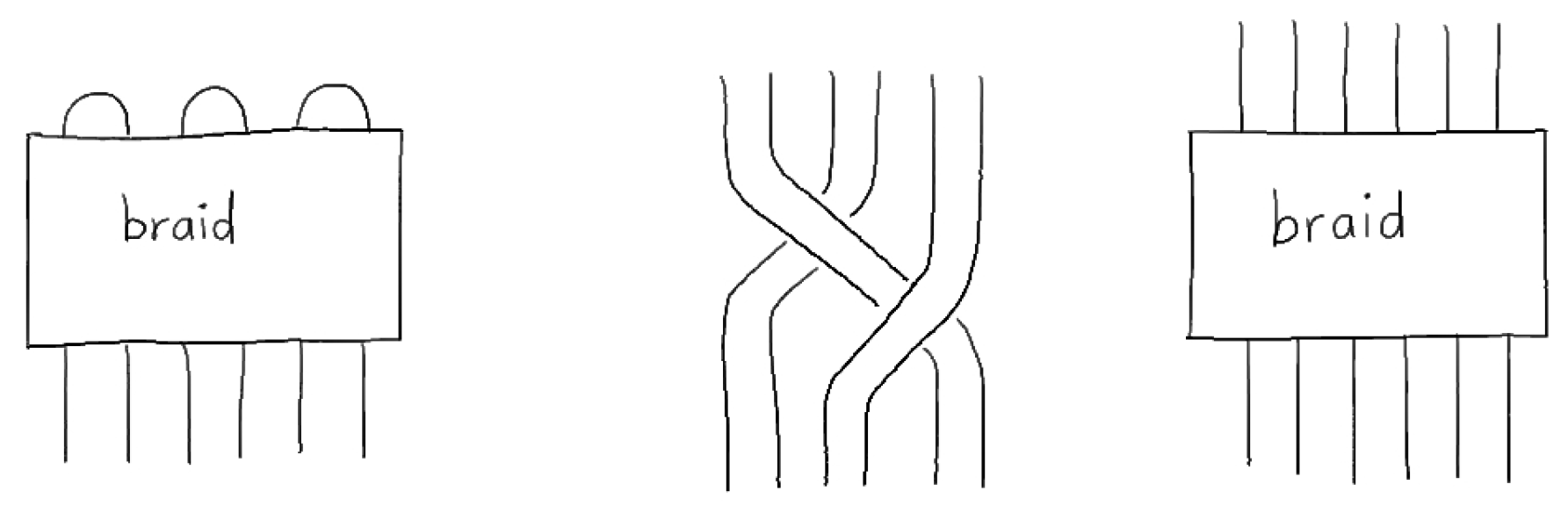
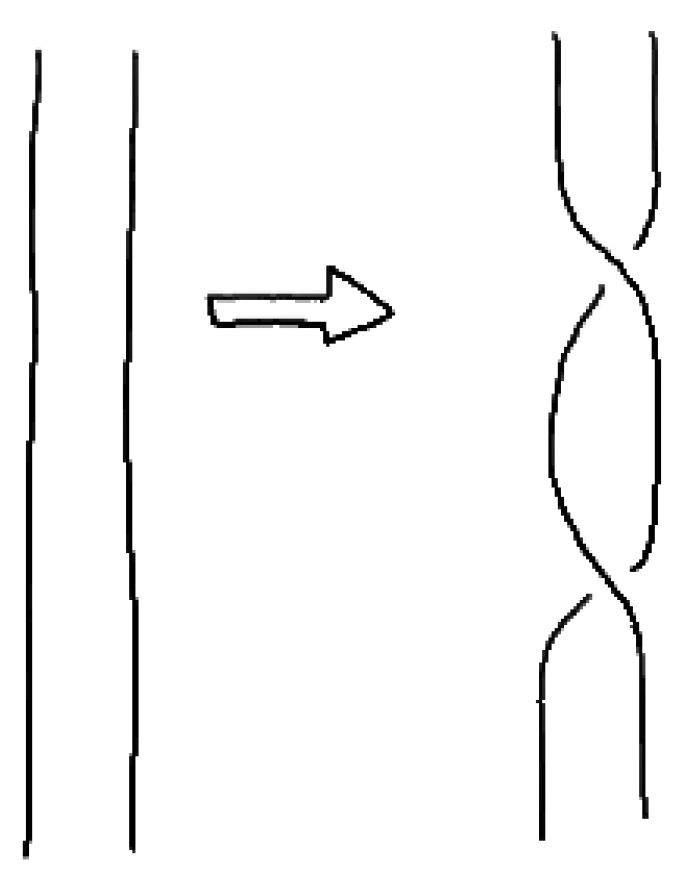
4.5. Fermions, Bosons and 3-Braids
5. Electric Charge and Quasimodularity
5.1. Electric Charge as Dehn Twist of the Boundary
5.2. Electric Charge as a Frame of the Knot Complement
5.3. The Charge Spectrum
5.4. Vanishing of the Magnetic Charge and Quasimodularity
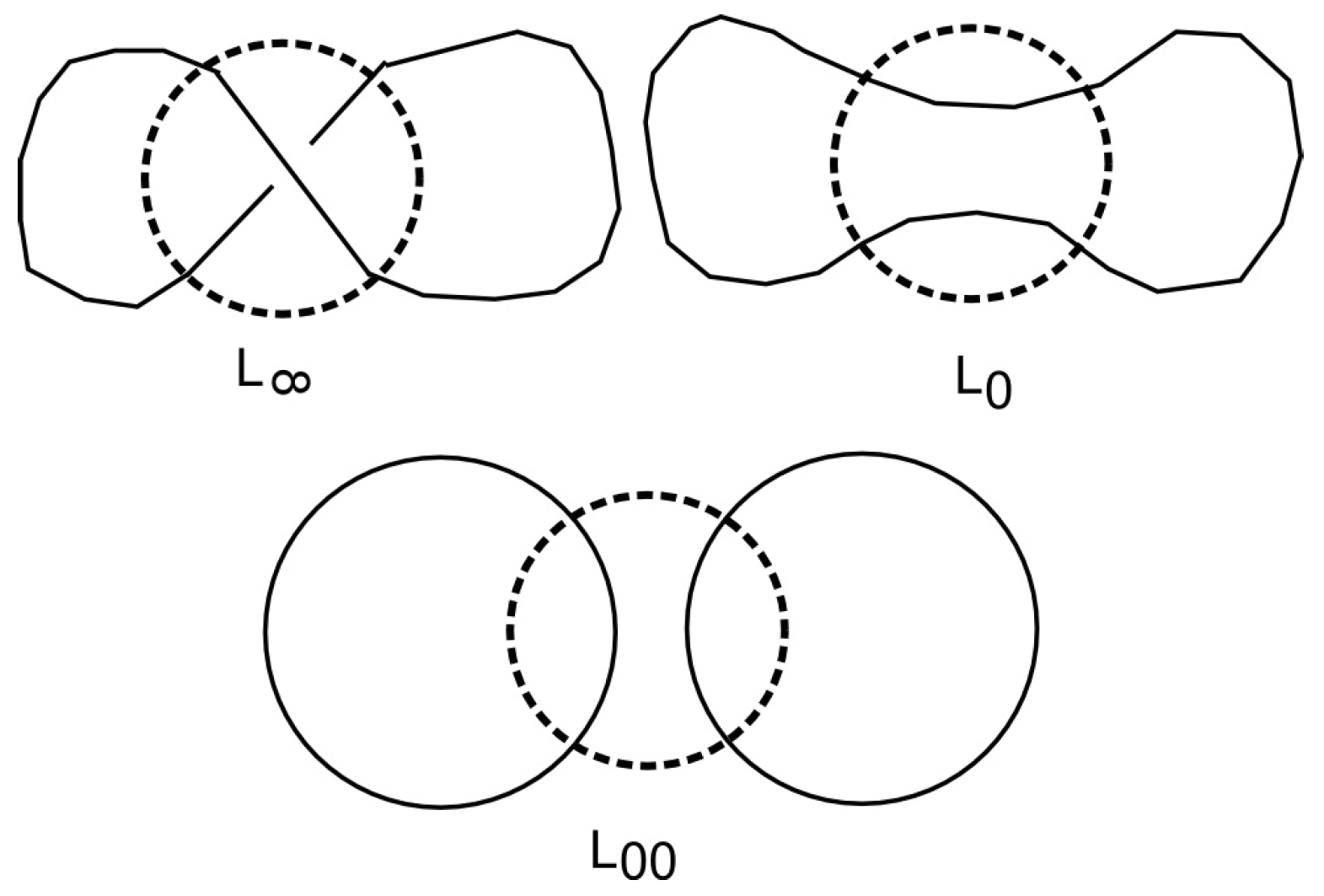
6. Drinfeld–Turaev Quantization and Quantum States
- The surface S (branching set of ) is inducing a representation .
- The space of all representations has a natural Poisson structure (induced by the bilinear on the group) and the Poisson algebra of complex functions over them is the algebra of observables.
- The skein algebra is the quantization of the Poisson algebra with the deformation parameter (see also [69]) .
- The module for is a commutative algebra.
- Let S be a surface. Then, carries the structure of an algebra.
7. Fermions and Number Theory
8. The K3 Surface and the Number of Generations
9. Conclusions and Outlook
- We constructed a spacetime, the K3 surface and derive some numbers like the cosmological constant or some energy scales and neutrino masses agreeing with experimental data.
- We derived from a representation of K3 surfaces by branched covering a simple picture: fermions are hyperbolic knot complements, whereas bosons are link complements (torus bundles).
- We obtained the gauge group from this picture (at least in principle).
- We derived the correct charge spectrum and obtained one generation.
- We conjectured about the number of generations and global symmetry (the ) to get the mixing between the generations.
Funding
Acknowledgments
Conflicts of Interest
References
- Collaborations, F.G. Testing Einstein’s Special Relativity with Fermi’s Short Hard Gamma-Ray Burst GRB090510. Nature 2009, 462, 331–334. [Google Scholar]
- Furey, C. Towards a Unified Theory of Ideals. Phys. Rev. D 2012, 86, 025024. [Google Scholar] [CrossRef]
- Furey, C. Generations: Three Prints, in Colour. JHEP 2014, 10, 046. [Google Scholar] [CrossRef]
- Furey, C. Charge Quantization from a Number Operator. Phys. Lett. B 2015, 742, 195–199. [Google Scholar] [CrossRef]
- Furey, C. Standard Model Physics from an Algebra? Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 2015. Available online: https://arxiv.org/abs/1611 (accessed on 1 October 2019).
- Gresnigt, N. Braids, Normed Division Algebras, and Standard Model Symmetries. Phys. Lett. B 2018, 783, 212–221. [Google Scholar] [CrossRef]
- Gresnigt, N. Braided Fermions from Hurwitz Algebras. J. Phys. Conf. Ser. 2019, 1194, 012040. [Google Scholar] [CrossRef]
- Gillard, A.; Gresnigt, N. Three Fermion Generations with Two Unbroken Gauge Symmetries from the Complex Sedenions. Eur. Phys. J. C 2019, 79, 446. [Google Scholar] [CrossRef]
- Stoica, O. Leptons, Quarks, and Gauge from the Complex Clifford Algebra Cℓ6. Adv. Appl. Cliff. Alg. 2018, 28, 52. [Google Scholar] [CrossRef]
- Thomson, W. On Vortex Motion. Trans. R. Soc. Ed. 1869, 25, 217–260. [Google Scholar] [CrossRef]
- Misner, C.; Thorne, K.; Wheeler, J. Gravitation; Freeman: San Francisco, CA, USA, 1973. [Google Scholar]
- Mielke, E. Knot Wormholes in Geometrodynamics? Gen. Relat. Grav. 1977, 8, 175–196. [Google Scholar] [CrossRef]
- Giulini, D. Matter from Space. Based on a talk delivered at the conference “Beyond Einstein: Historical Perspectives on Geometry, Gravitation, and Cosmology in the Twentieth Century”, September 2008 at the University of Mainz in Germany. To appear in the Einstein-Studies Series, Birkhaeuser, Boston. arXiv 2008, arXiv:0910.2574. [Google Scholar]
- Jehle, H. Topological characterization of leptons, quarks and hadrons. Phys. Lett. B 1981, 104, 207–211. [Google Scholar] [CrossRef]
- Gavrilik, A.M. Quantum algebras in phenomenological description of particle properties. Nucl. Phys. B (Proc. Suppl.) 2001, 102/103, 298–305. [Google Scholar] [CrossRef]
- Finkelstein, R. Knots and Preons. Int. J. Mod. Phys. A 2009, 24, 2307–2316. [Google Scholar] [CrossRef]
- Bilson-Thompson, S. A Topological Model of Composite Preons. arXiv 2005, arXiv:0503213v2. [Google Scholar]
- Bilson-Thompson, S.; Markopoulou, F.; Smolin, L. Quantum Gravity and the Standard Model. Class. Quant. Grav. 2007, 24, 3975–3994. [Google Scholar] [CrossRef]
- Duston, C. Exotic Smoothness in 4 Dimensions and Semiclassical Euclidean Quantum Gravity. Int. J. Geom. Meth. Mod. Phys. 2010, 8, 459–484. [Google Scholar] [CrossRef]
- Duston, C.L. Topspin Networks in Loop Quantum Gravity. Class. Quant. Grav. 2012, 29, 205015. [Google Scholar] [CrossRef][Green Version]
- Duston, C.L. The Fundamental Group of a Spatial Section Represented by a Topspin Network. Based on Work Presented at the LOOPS 13 Conference at the Perimeter Institute. arXiv 2013, arXiv:1308.2934. [Google Scholar]
- Denicola, D.; Marcolli, M.; al Yasry, A. Spin Foams and Noncommutative Geometry. Class. Quant. Grav. 2010, 27, 205025. [Google Scholar] [CrossRef]
- Asselmeyer-Maluga, T. Smooth Quantum Gravity: Exotic Smoothness and Quantum Gravity. In At the Frontiers of Spacetime: Scalar-Tensor Theory, Bell’s Inequality, Mach’s Principle, Exotic Smoothness; Asselmeyer-Maluga, T., Ed.; Springer: Basel, Switzerland, 2016. [Google Scholar]
- Rolfson, D. Knots and Links; Publish or Prish: Berkeley, CA, USA, 1976. [Google Scholar]
- Hilden, H. Every Closed Orientable 3-Manifold is a 3-Fold Branched Covering Space of S3. Bull. Am. Math. Soc. 1974, 80, 1243–1244. [Google Scholar] [CrossRef]
- Hirsch, U. Über Offene Abbildungen Auf Die 3-Sphäre. Math. Z. 1974, 140, 203–230. [Google Scholar] [CrossRef]
- Montesinos, J. A Representation of Closed, Orientable 3-Manifolds as 3-Fold Branched Coverings of S3. Bull. Am. Math. Soc. 1974, 80, 845–846. [Google Scholar] [CrossRef]
- Piergallini, R. Four-Manifolds as 4-Fold Branched Covers of S4. Topology 1995, 34, 497–508. [Google Scholar] [CrossRef]
- Iori, M.; Piergallini, R. 4-Manifolds as Covers of S4 Branched over Non-Singular Surfaces. Geom. Topol. 2002, 6, 393–401. [Google Scholar] [CrossRef]
- Piergallini, R.; Zuddas, D. On Branched Covering Representation of 4-Manifolds. J. Lond. Math. Soc. 2018, 99. in press. [Google Scholar] [CrossRef]
- Asselmeyer-Maluga, T.; Brans, C. How to Include Fermions Into General Relativity by Exotic Smoothness. Gen. Relat. Grav. 2015, 47, 30. [Google Scholar] [CrossRef][Green Version]
- Asselmeyer-Maluga, T.; Rosé, H. On the Geometrization of Matter by Exotic Smoothness. Gen. Relat. Grav. 2012, 44, 2825–2856. [Google Scholar] [CrossRef][Green Version]
- Brans, C. Localized exotic smoothness. Class. Quant. Grav. 1994, 11, 1785–1792. [Google Scholar] [CrossRef]
- Brans, C. Exotic smoothness and physics. J. Math. Phys. 1994, 35, 5494–5506. [Google Scholar] [CrossRef][Green Version]
- Yau, S.T. On the Ricci Curvature of a Compact Kähler Manifold and the Complex Monge-Ampère Equation. Commun. Pure Appl. Math. 1978, 31, 339–411. [Google Scholar] [CrossRef]
- LeBrun, C. Four-Manifolds Without Einstein Metrics. Math. Res. Lett. 1996, 3, 133–147. [Google Scholar] [CrossRef]
- Asselmeyer-Maluga, T.; Król, J. On Topological Restrictions of the Spacetime in Cosmology. Mod. Phys. Lett. A 2012, 27, 1250135. [Google Scholar] [CrossRef]
- Donaldson, S. An Application of Gauge Theory to the Topology of 4-Manifolds. J. Diff. Geom. 1983, 18, 269–316. [Google Scholar] [CrossRef]
- Asselmeyer-Maluga, T.; Krol, J. How to Obtain a Cosmological Constant from Small Exotic R4. Phys. Dark Universe 2018, 19, 66–77. [Google Scholar] [CrossRef]
- Asselmeyer-Maluga, T.; Krol, J. A Topological Approach to Neutrino Masses by Using Exotic Smoothness. Mod. Phys. Lett. A 2019, 34, 1950097. [Google Scholar] [CrossRef]
- Asselmeyer-Maluga, T.; Krol, J. A Topological Model for Inflation. arXiv 2018, arXiv:1812.08158. [Google Scholar]
- Whitt, B. Fourth Order Gravity as General Relativity Plus Matter. Phys. Lett. 1984, 145B, 176–178. [Google Scholar] [CrossRef]
- Starobinski, A. A New Type of Isotropic Cosmological Models Without Singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Gompf, R.; Stipsicz, A. 4-Manifolds and Kirby Calculus; American Mathematical Society: Providence, RI, USA, 1999. [Google Scholar]
- Ade, P.A.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2013 Results. XVI. Cosmological Parameters. Astron. Astrophys. 2013, 571, A16. [Google Scholar]
- Ade, P.C.P.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N. Planck 2015 Results. XIII Cosmological Parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar]
- Bonvin, V.; Courbin, F.; Suyu, S.H.E.A. H0LiCOW-V. New COSMOGRAIL Time Delays of HE 0435-1223: H0 to 3.8 Per Cent Precision from Strong Lensing in a Flat ΛCDM Model. Mon. Not. R. Astron. Soc. 2016, 465, 4914–4930. [Google Scholar] [CrossRef]
- Asselmeyer-Maluga, T.; Król, J. Inflation and Topological Phase Transition Driven by Exotic Smoothness. Adv. HEP 2014, 14. [Google Scholar] [CrossRef]
- Freedman, M. The topology of four-dimensional manifolds. J. Diff. Geom. 1982, 17, 357–454. [Google Scholar] [CrossRef]
- Coxeter, H. Integral Caleay Numbers. Duke Math. J. 1946, 13, 561–578. [Google Scholar] [CrossRef]
- Friedrich, T. On the Spinor Representation of Surfaces in Euclidean 3-Space. J. Geom. Phys. 1998, 28, 143–157. [Google Scholar] [CrossRef]
- Ashtekar, A.; Engle, J.; Sloan, D. Asymptotics and Hamiltonians in a First, Order Formalism. Class. Quant. Grav. 2008, 25, 095020. [Google Scholar] [CrossRef][Green Version]
- Ashtekar, A.; Sloan, D. Action and Hamiltonians in Higher Dimensional General Relativity: First, Order Framework. Class. Quant. Grav. 2008, 25, 225025. [Google Scholar] [CrossRef]
- Floer, A. An instanton Invariant for 3-manifolds. Commun. Math. Phys. 1988, 118, 215–240. [Google Scholar] [CrossRef]
- Calegari, D. Foliations and the Geometry of 3-Manifolds; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Thurston, W. Three-Dimensional Geometry and Topology, 1st ed.; Princeton University Press: Princeton, NJ, USA, 1997. [Google Scholar]
- Giulini, D. Properties of 3-Manifolds for Relativists. Int. J. Theor. Phys. 1994, 33, 913–930. [Google Scholar] [CrossRef]
- Kalliongis, J.; McCullough, D. Isotopies of 3-Manifolds. Top. Appl. 1996, 71, 227–263. [Google Scholar] [CrossRef][Green Version]
- Hatcher, A.; McCullough, D. Finiteness of Classifying Spaces of Relative Diffeomorphism Groups of 3-Manifolds. Geom. Top. 1997, 1, 91–109. Available online: http://www.math.cornell.edu/~hatcher/Papers/bdiffrel.pdf (accessed on 1 October 2019). [CrossRef]
- Giveon, A.; Kutasov, D. Brane Dynamics and Gauge Theory. Rev. Mod. Phys. 1999, 71, 983–1084. [Google Scholar] [CrossRef]
- Hong, S.; McCullough, D. Mapping Class Groups of 3-Manifolds, Then and Now. In Geometry and Topology Down Under; Hodgson, C.D., Jaco, W.H., Scharlemann, M.G., Tillmann, S., Eds.; AMS: Providence, RI, USA, 2013; Volume 597. [Google Scholar]
- Asselmeyer-Maluga, T.; Król, J. Abelian Gerbes, Generalized Geometries and Foliations of Small Exotic R4. arXiv 2014, arXiv:0904.1276v5. [Google Scholar]
- Atiyah, M. On Framings of 3-Manifolds. Topology 1990, 29, 1–7. [Google Scholar] [CrossRef]
- Hirzebruch, F. Topological Methods in Algebraic Geometry; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1973. [Google Scholar]
- Freed, D.; Gompf, R. Computer calculation of Witten’s 3-manifold invariant. Commun. Math. Phys. 1991, 141, 79–117. [Google Scholar] [CrossRef]
- Asselmeyer-Maluga, T.; Król, J. Quantum Geometry and Wild Embeddings as Quantum States. arXiv 2013, arXiv:1211.3012. [Google Scholar] [CrossRef]
- Asselmeyer-Maluga, T. Hyperbolic Groups, 4-Manifolds and Quantum Gravity. J. Phys. Conf. Ser. 2019, 1194, 012009. [Google Scholar] [CrossRef]
- Piergallini, R.; Zuddas, D. A Universal Ribbon Surface in B4. Proc. Lond. Math. Soc. 2005, 90, 763–782. [Google Scholar] [CrossRef]
- Bullock, D.; Przytycki, J. Multiplicative Structure of Kauffman Bracket Skein Module Quantization. Proc. AMS 1999, 128, 923–931. [Google Scholar] [CrossRef]
- Bullock, D. A Finite Set of Generators for the Kauffman Bracket Skein Algebra. Math. Z. 1999, 231, 91–101. [Google Scholar] [CrossRef]
- Prasolov, V.; Sossinisky, A. Knots, Links, Braids and 3-Manifolds; AMS: Providence, RI, USA, 1997. [Google Scholar]
- Asselmeyer-Maluga, T.; Mader, R. Exotic R4 and Quantum Field Theory. In Proceedings of the 7th International Conference on Quantum Theory and Symmetries (QTS7), Prague, Czech Republic, 7–13 August 2011; Al, C.B.E., Ed.; IOP Publishing: Bristol, UK, 2012; p. 012011. [Google Scholar] [CrossRef]
- Maclachlan, C.; Reid, A.W. The Arithmetic of Hyperbolic 3-Manifolds; Springer Publisher: New York, NY, USA, 2003; Volume 219. [Google Scholar]
- Casson, A. Three Lectures on New Infinite Constructions in 4-Dimensional Manifolds, Progress in Mathematics ed.; Notes by Lucian Guillou; Birkhauser Boston: Boston, MA, USA, 1986; Volume 62. First Published 1973. [Google Scholar]
- Cheng, M.; Duncan, J.; Harvey, J. Umbral Moonshine and the Niemeier Lattices. Res. Math. Sci. 2014, 1, 3. [Google Scholar] [CrossRef]
- Asselmeyer-Maluga, T.; Król, J. Higgs Potential and Confinement in Yang-Mills Theory on Exotic R4. arXiv 2013, arXiv:1303.1632. [Google Scholar]


© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asselmeyer-Maluga, T. Braids, 3-Manifolds, Elementary Particles: Number Theory and Symmetry in Particle Physics. Symmetry 2019, 11, 1298. https://doi.org/10.3390/sym11101298
Asselmeyer-Maluga T. Braids, 3-Manifolds, Elementary Particles: Number Theory and Symmetry in Particle Physics. Symmetry. 2019; 11(10):1298. https://doi.org/10.3390/sym11101298
Chicago/Turabian StyleAsselmeyer-Maluga, Torsten. 2019. "Braids, 3-Manifolds, Elementary Particles: Number Theory and Symmetry in Particle Physics" Symmetry 11, no. 10: 1298. https://doi.org/10.3390/sym11101298
APA StyleAsselmeyer-Maluga, T. (2019). Braids, 3-Manifolds, Elementary Particles: Number Theory and Symmetry in Particle Physics. Symmetry, 11(10), 1298. https://doi.org/10.3390/sym11101298



