A Novel Two-Stage Heuristic for Solving Storage Space Allocation Problems in Rail–Water Intermodal Container Terminals
Abstract
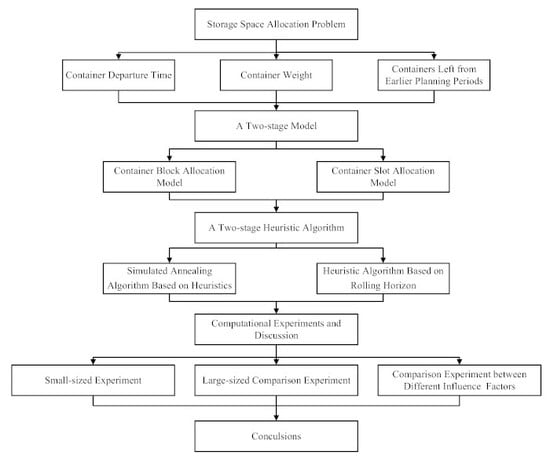
:1. Introduction
2. Literature Review
3. Problem Description
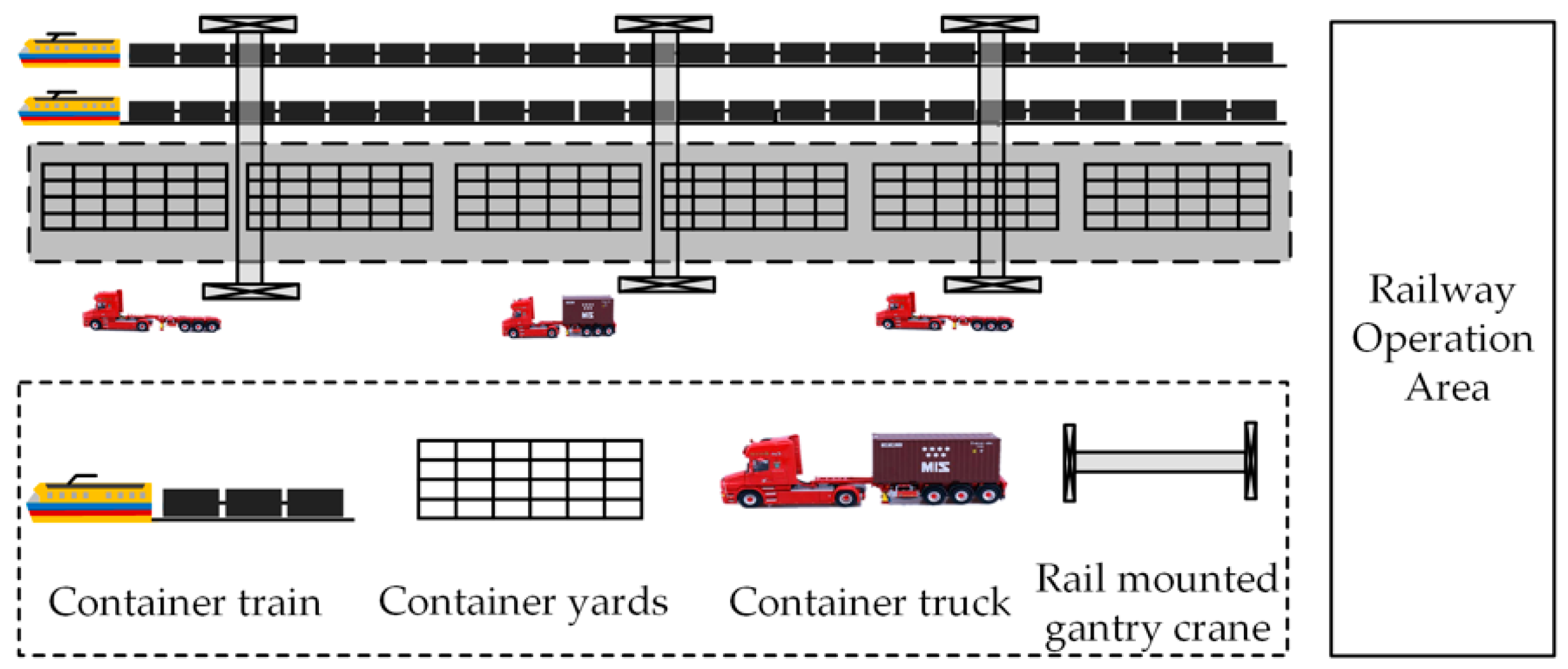
3.1. Related Descriptions
- ICs on vessels or inner trucks waiting for discharging and assigning to the railway container yard, called VDs;
- ICs have been already stored in the railway container yard, waiting for loading onto trains, called TPs;
3.2. Overlapping Amount
- Since heavier containers are stored below lighter containers in the containership, the lighter containers are loaded before the heavier containers. Therefore, in the railway container yards the lighter containers should be stored below the heavier containers to ensure the safety and stability of the storage.
- In order to ensure containers with an early departure time can be put onto trains early, containers with an earlier departure time need to be stacked on containers with later departure times.
- Height difference between two neighboring stacks in the same bay should not exceed three.
4. Problem Formulation
4.1. Assumptions
- All the containers were assumed to have the same size and meanwhile special containers, such as refrigerated containers and hazardous containers, were not considered in our paper;
- The positions and information of the containers left from earlier planning horizons were known before;
- The information of the new arrival containers, such as weight and departure time, were known before;
- There was enough handling equipment to handle and store containers in the railway operation area.
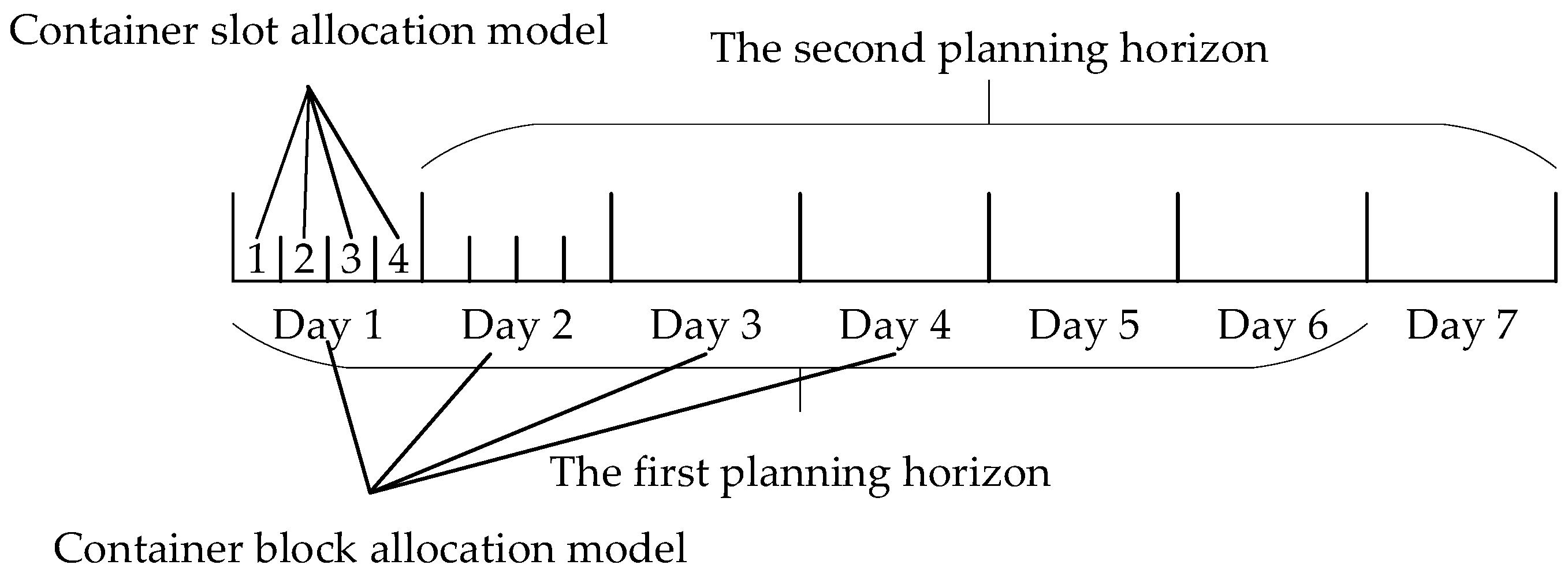
4.2. Container Block Allocation Model
4.2.1. Notations and Variables
4.2.2. Objective
4.2.3. Constraints
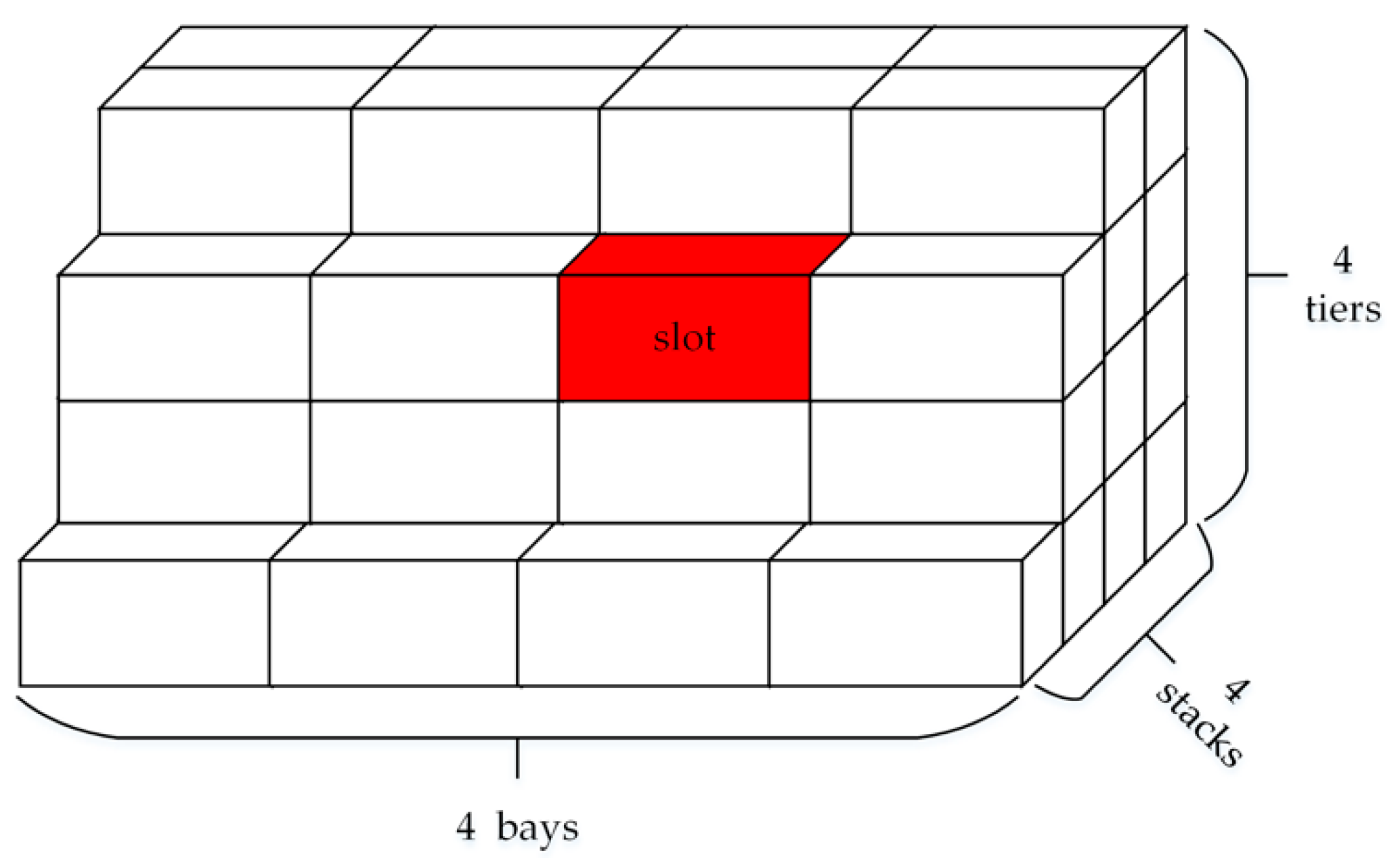
4.3. Container Slot Allocation Model
4.3.1. Notations and Variables
4.3.2. Objective
4.3.3. Constraints
5. Solution Algorithms
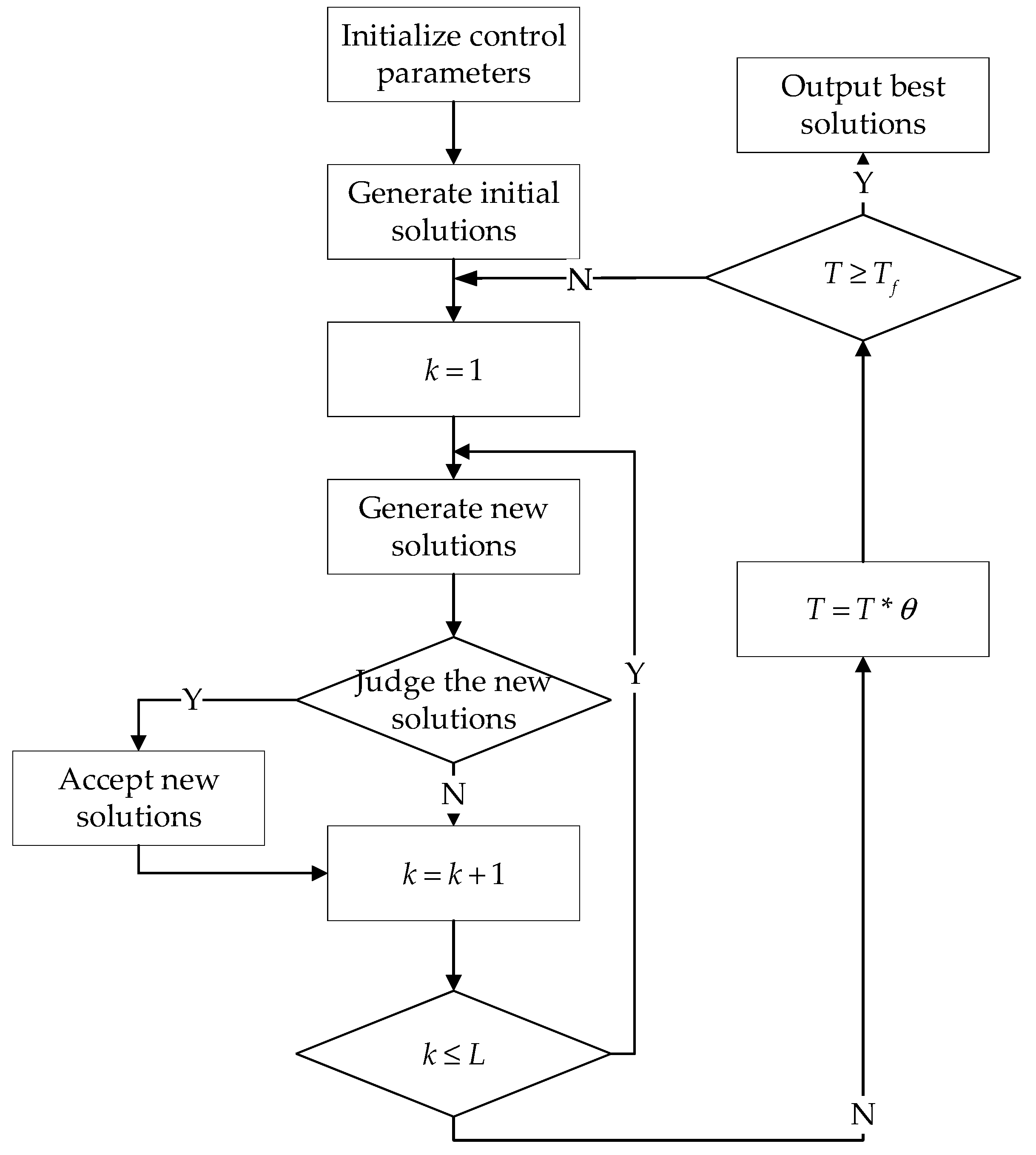
5.1. Simulated Annealing Algorithm Based on Heuristics
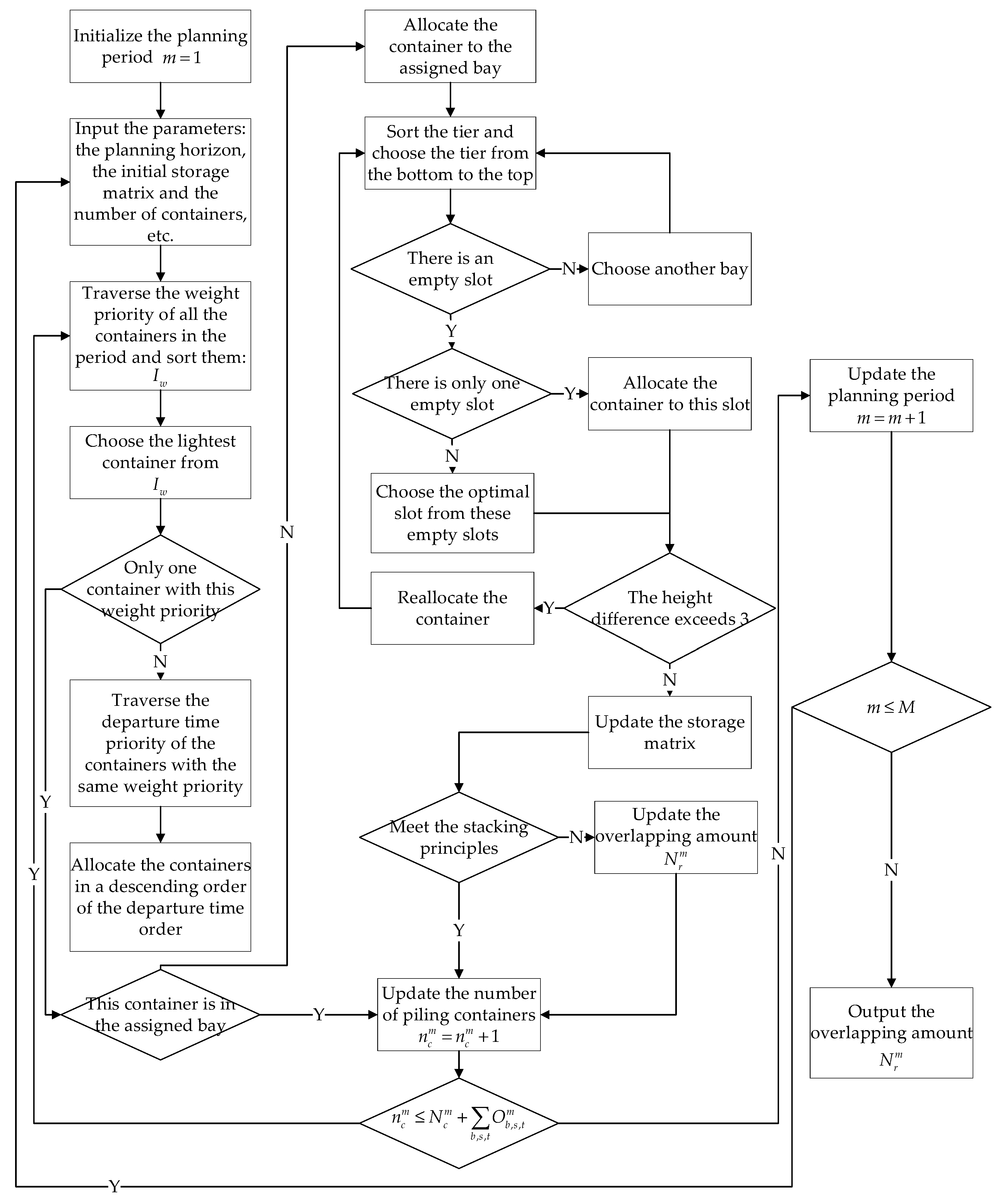
5.2. Heuristic Algorithm Based on Rolling Horizon
6. Computational Experiments
6.1. Initial Setting
- In all the experiments, we set a planning horizon to be three, a planning epoch to be one and a planning period to be six hours. Thus, one planning epoch had four planning periods, while one planning horizon had 12 planning periods.
- Following surveys made on some famous Chinese container terminals, railway container terminals and RWICTs, such as Dalian RWICT, Chengdu Railway Container Terminal, there were always three RMGCs traveling on the same railway track, which were responsible for the fixed container blocks.
- In our experiments, in order to guarantee safe and feasible stacking operations, we selected 12 blocks of ICs in the railway container yards based on the survey data and the IC blocks were equally divided by three RMGCs.
- There were five bays in each block, which had four tiers and five stacks. As a result of re-handling operations, when one bay had four tiers, it was essential to leave three empty slots in the bay. Therefore, one bay could store 17 containers at most. Therefore, the storage capacity of a block () was 100 and storage coefficient () was 0.85.
- According to the pre-experiments, when the parameter of the algorithm was: T0 = 99, Tf = 1, = 0.9, and L = 1200, SAAH had better effect in solving CBAP.
- All computational experiments were carried out based on a personal computer with Intel Core i7-8650U at 4.20 GHz processors and 16 GB RAM.
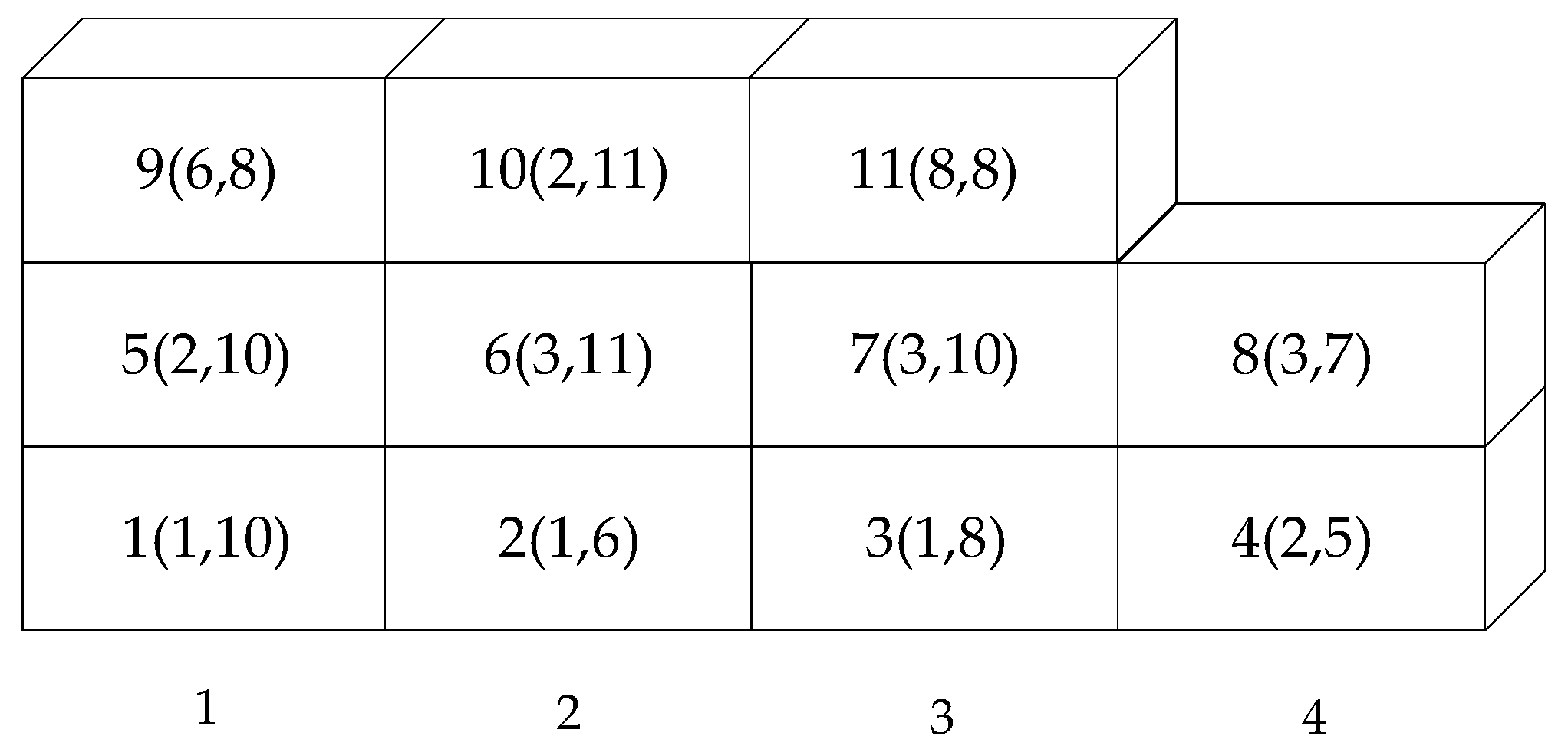
6.2. Small-Sized Experiments
6.3. Large-Sized Comparison Experiments
6.4. Comparison Experiments between Different Influence Factors
7. Conclusion
Author Contributions
Funding
Conflicts of Interest
References
- Chang, Y.M.; Zhu, X.N.; Haghani, A. The outbound container slot allocation based on the stowage plan in rail–water intermodal container terminals. Meas. Control 2019. [Google Scholar] [CrossRef]
- Carlo, H.J.; Vis, I.F.A.; Roodbergen, K.J. Storage Yard Operations in Container Terminals: Literature Overview, Trends, and Research Directions. Flex. Serv. Manuf. J. 2015, 27, 224–262. [Google Scholar] [CrossRef]
- Wiese, J.; Kliewer, N.; Suhl, L. A Survey of Container Terminal Characteristics and Equipment Types. Working Paper. University of Paderborn. 2009. Available online: wiwi.unipaderborn.de/fileadmin/lehrstuehle/department-3/wiwi-dep-3-ls-5/Forschung/Publikationen/wiese_et_al_a_survey_of_container_terminal_characteristics_and_equipment_types_2009.pdf (accessed on 1 May 2012).
- Wiese, J.; Suhl, L.; Kliewer, N. Mathematical Models and Solution Methods for Optimal Container Terminal Yard Layouts. OR Spectr. 2010, 32, 427–452. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, J.; Wan, Y.W.; Murty, K.G.; Linn, R.J. Storage Space Allocation in Container Terminals. Transp. Res. B-Meth. 2003, 37, 883–903. [Google Scholar] [CrossRef]
- Casey, B.; Kozan, E. Optimizing Container Storage Processes at Multimodal Terminals. J. Oper. Res. Soc. 2012, 63, 1126–1142. [Google Scholar] [CrossRef]
- Kim, K.Y.; Kim, K.H. A Routing Algorithm for A Single Transfer Crane to Load Export Containers onto A Containership. Comput. Ind. Eng. 1997, 33, 673–676. [Google Scholar] [CrossRef]
- Guo, X.; Huang, S.Y. Dynamic Space and Time Partitioning for Gantry Crane Workload Management in Container Terminals. Transp. Sci. 2012, 46, 134–148. [Google Scholar] [CrossRef]
- Lee, Y.; Lee, Y.J. A Heuristic for Retrieving Container from A Yard. Comput. Oper. Res. 2010, 37, 1139–1147. [Google Scholar] [CrossRef]
- Huang, S.H.; Lin, T.H. Heuristic Algorithms for Container Pre-marshalling Problems. Comput. Ind. Eng. 2012, 62, 13–20. [Google Scholar] [CrossRef]
- Kim, K.H.; Park, Y.M.; Ryu, K.R. Deriving Decision Rules to Locate Export Containers in Container Yards. Eur. J. Oper. Res. 2000, 124, 89–101. [Google Scholar] [CrossRef]
- Kim, K.H.; Kang, T.P. A Note on a Dynamic Space-allocation Method for Outbound Containers. Eur. J. Oper. Res. 2003, 148, 92–101. [Google Scholar] [CrossRef]
- Yan, X.; Zhao, N.; Bian, Z.; Mi, C. An Intelligent Storage Determining Method for Inbound Containers in Container Terminals. J. Coast. Res. 2005, 73, 197–204. [Google Scholar]
- Lee, L.H.; Chew, E.P.; Tan, K.C.; Han, Y. An Optimization Model for Storage Yard Management in Transshipment Hubs. OR Spectr. 2006, 28, 107–129. [Google Scholar] [CrossRef]
- Mckendall, A.R.; Jaramillo, J.R. A Tabu Search Heuristic for the Dynamic Space Allocation Problem. Comput. Oper. Res. 2006, 33, 768–789. [Google Scholar] [CrossRef]
- Mckendall, A.R. Improved Tabu Search Heuristics for the Dynamic Space Allocation Problem. Comput. Oper. Res. 2008, 35, 3347–3359. [Google Scholar] [CrossRef]
- Bazzazi, M.; Safaei, N.; Javadian, N. A Genetic Algorithm to Solve the Storage Space Allocation Problem in A Container Terminal. Comput. Ind. Eng. 2009, 56, 44–52. [Google Scholar] [CrossRef]
- Choe, R.; Park, T.; Oh, M.S.; Kang, J.; Ryu, K.R. Generating A Rehandling-free Intra-block Remarshaling Plan for An Automated Container Yard. J. Intell. Manuf. 2011, 22, 201–217. [Google Scholar] [CrossRef]
- Yu, M.; Qi, X. Storage Space Allocation Models for Inbound Containers in An Automatic Container Terminal. Eur. J. Oper. Res. 2013, 226, 32–45. [Google Scholar] [CrossRef]
- Sharif, O.; Huynh, N. Storage Space Allocation at Marine Container Terminals Using Ant-based Control. Expert Syst. Appl. 2013, 40, 2323–2330. [Google Scholar] [CrossRef]
- Jiang, X.; Chew, E.P.; Lee, L.H.; Tan, K.C. Short-term Space Allocation for Storage Yard Management in A Transshipment Hub Port. OR Spectr. 2014, 36, 879–901. [Google Scholar] [CrossRef]
- Zheng, H.X.; Du, L.; Dong, J. Optimization Model on Container Slot Allocation in Container Yard with Mixed Storage Mode. J. Transp. Syst. Eng. Inf. Technol. 2012, 12, 153–159. [Google Scholar]
- Wang, L.; Zhu, X.N.; Yan, W.; Xie, Z.Y.; Li, Q.B. Optimization Model of Mixed Storage in Railway Container Terminal Yard. J. Transp. Syst. Eng. Inf. Technol. 2013, 13, 172–178. [Google Scholar]
- Wang, L.; Zhu, X.N.; Xie, Z.Y. Storage Space Allocation of Inbound Container in Railway Container Terminal. Math. Probl. Eng. 2014, 2014. [Google Scholar] [CrossRef]
- Liu, C.J.; Hu, Z.H. Space Allocation Optimization Model and Algorithm for Outbound Containers in the Yard. J. Jiangsu Univ. Sci. Technol. (Nat. Sci. Ed.) 2016, 30, 490–497. [Google Scholar]
- Ji, M.J.; Huang, S.J.; Guo, W.W. Container Allocation Optimization of the Center Terminal Yard under Rail-sea Intermodal Transportation. Syst. Eng. Theory Pract. 2016, 36, 1555–1567. [Google Scholar]
- Li, Y.J.; Zhu, X.N.; Wang, L.; Chen, X. Stowage Plan Based Slot Optimal Allocation in Rail-Water Container Terminal. J. Control Sci. Eng. 2017, 2017. [Google Scholar] [CrossRef]
| Tiers | Empty Slots |
|---|---|
| 3 | 2 |
| 4 | 3 |
| 5 | 4 |
| Container Type | m = 1 | m = 2 | m = 3 | m = 4 |
|---|---|---|---|---|
| 240 | 225 | 236 | 221 | |
| 440 | 458 | 436 | 448 |
| Container Type | n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | n = 7 | n = 8 | n = 9 | n = 10 | n = 11 | n = 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 50 | 54 | 45 | 56 | 55 | 48 | 57 | 43 | 46 | 51 | 42 | 49 | ||
| m = 1 | 10 | 11 | 15 | 10 | 12 | 9 | 12 | 11 | 8 | 7 | 9 | 10 | |
| m = 2 | 12 | 13 | 11 | 13 | 14 | 11 | 10 | 8 | 9 | 11 | 10 | 11 | |
| m = 3 | 13 | 7 | 9 | 12 | 11 | 10 | 9 | 9 | 11 | 12 | 13 | 7 | |
| m = 4 | 9 | 11 | 12 | 11 | 10 | 5 | 11 | 10 | 10 | 8 | 9 | 10 | |
| Container Type | n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | n = 7 | n = 8 | n = 9 | n = 10 | n = 11 | n = 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| m = 1 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | |
| m = 2 | 19 | 19 | 19 | 19 | 19 | 19 | 19 | 19 | 19 | 19 | 19 | 16 | |
| m = 3 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 16 | |
| m = 4 | 18 | 18 | 18 | 18 | 18 | 18 | 18 | 18 | 18 | 18 | 18 | 23 | |
| m = 1 | 37 | 37 | 37 | 37 | 37 | 37 | 37 | 37 | 37 | 37 | 37 | 33 | |
| m = 2 | 38 | 38 | 38 | 38 | 38 | 38 | 38 | 38 | 38 | 38 | 38 | 40 | |
| m = 3 | 36 | 36 | 36 | 36 | 36 | 36 | 36 | 36 | 36 | 36 | 36 | 40 | |
| m = 4 | 37 | 37 | 37 | 37 | 37 | 37 | 37 | 37 | 37 | 37 | 37 | 41 | |
| Planning Period | ||||||
|---|---|---|---|---|---|---|
| m = 1 | 38 | 7 | 483 | 26 | 92.1% | 73.0% |
| m = 2 | 11 | 28 | 60.7% | |||
| m = 3 | 10 | 27 | 63.0% | |||
| m = 4 | 16 | 34 | 52.9% |
| Planning Period | ||||||
|---|---|---|---|---|---|---|
| m = 1 | 169 | 7 | 1,219 | 26 | 86.1% | 73.0% |
| m = 2 | 11 | 28 | 60.7% | |||
| m = 3 | 10 | 27 | 63.0% | |||
| m = 4 | 16 | 34 | 52.9% | |||
| m = 5 | 12 | 27 | 55.6% | |||
| m = 6 | 15 | 37 | 59.4% | |||
| m = 7 | 12 | 34 | 64.7% | |||
| m = 8 | 11 | 33 | 66.7% | |||
| m = 9 | 20 | 50 | 60.0% | |||
| m = 10 | 16 | 46 | 65.2% | |||
| m = 11 | 15 | 38 | 60.5% | |||
| m = 12 | 23 | 58 | 60.3% | |||
| m = 13 | 19 | 53 | 64.2% | |||
| m = 14 | 9 | 33 | 72.7% | |||
| m = 15 | 8 | 25 | 68.0% | |||
| m = 16 | 10 | 33 | 69.7% | |||
| m = 17 | 13 | 34 | 61.8% | |||
| m = 18 | 10 | 30 | 66.7% | |||
| m = 19 | 9 | 28 | 67.8% | |||
| m = 20 | 8 | 26 | 69.2% |
| Planning Period | |||
|---|---|---|---|
| m = 1 | 7 | 9 | 22.2% |
| m = 2 | 11 | 14 | 21.4% |
| m = 3 | 10 | 12 | 16.7% |
| m = 4 | 16 | 23 | 30.4% |
| m = 5 | 12 | 17 | 29.4% |
| m = 6 | 15 | 20 | 25.0% |
| m = 7 | 12 | 19 | 36.8% |
| m = 8 | 11 | 15 | 26.7% |
| m = 9 | 20 | 26 | 23.0% |
| m = 10 | 16 | 21 | 23.8% |
| m = 11 | 15 | 20 | 25.0% |
| m = 12 | 23 | 32 | 28.1% |
| m = 13 | 19 | 28 | 32.1% |
| m = 14 | 9 | 13 | 30.8% |
| m = 15 | 8 | 13 | 38.5% |
| m = 16 | 10 | 14 | 28.6% |
| m = 17 | 13 | 19 | 31.6% |
| m = 18 | 10 | 14 | 28.6% |
| m = 19 | 9 | 12 | 25.0% |
| m = 20 | 8 | 13 | 38.5% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, Y.; Zhu, X. A Novel Two-Stage Heuristic for Solving Storage Space Allocation Problems in Rail–Water Intermodal Container Terminals. Symmetry 2019, 11, 1229. https://doi.org/10.3390/sym11101229
Chang Y, Zhu X. A Novel Two-Stage Heuristic for Solving Storage Space Allocation Problems in Rail–Water Intermodal Container Terminals. Symmetry. 2019; 11(10):1229. https://doi.org/10.3390/sym11101229
Chicago/Turabian StyleChang, Yimei, and Xiaoning Zhu. 2019. "A Novel Two-Stage Heuristic for Solving Storage Space Allocation Problems in Rail–Water Intermodal Container Terminals" Symmetry 11, no. 10: 1229. https://doi.org/10.3390/sym11101229
APA StyleChang, Y., & Zhu, X. (2019). A Novel Two-Stage Heuristic for Solving Storage Space Allocation Problems in Rail–Water Intermodal Container Terminals. Symmetry, 11(10), 1229. https://doi.org/10.3390/sym11101229