Abstract
The symmetry of hyperoperation is expressed by hypergroup, more extensive hyperalgebraic structures than hypergroups are studied in this paper. The new concepts of neutrosophic extended triplet semihypergroup (NET- semihypergroup) and neutrosophic extended triplet hypergroup (NET-hypergroup) are firstly introduced, some basic properties are obtained, and the relationships among NET- semihypergroups, regular semihypergroups, NET-hypergroups and regular hypergroups are systematically are investigated. Moreover, pure NET-semihypergroup and pure NET-hypergroup are investigated, and a strucuture theorem of commutative pure NET-semihypergroup is established. Finally, a new notion of weak commutative NET-semihypergroup is proposed, some important examples are obtained by software MATLAB, and the following important result is proved: every pure and weak commutative NET-semihypergroup is a disjoint union of some regular hypergroups which are its subhypergroups.
1. Introduction and Preliminaries
As a generalization of traditional algebraic structures, hyper algebraic structures (or hypercompositional structures) have been extensively studied and applied [1,2,3,4,5,6,7]. Especially, hypergroups and semihypergroups are basic hyper structures which are extensions of groups and semigroups [8]. In fact, hypergroups characterize the symmetry of hyperoperations.
On the other hand, as an extension of fuzzy set and intuitionistic fuzzy set, the concept of neutrosophic set firstly proposed by F. Smarandache in [9], has been applied to many fields [10,11,12]. Moreover, as an application of the ideal of neutrosphic sets, a new notion of neutrosophic triplet group (NTG) was proposed by F. Smarandache and Ali in [13], while the new notion of neutrosophic extended group (NETG) was proposed by Smarandache in [14]. Furthermore, the basic properties and structural characteristics of neutrosophic extended groups (NETGs) are studied in [15,16]; the closed connection between between NETG and regular semigroup investigated, and the new notion of neutrosophic extended triplet Abel-Grassmann’s Groupoid is proposed in [17]; the decomposition theorem of NETG is poved in [18]; the generalized neutrosophic extended groups are presented in [19]; the relationship and difference between NETGs and generalized groups are systematically studied in [20]. From these research results, we know that NETG is a typical algebraic system with important research value.
In this paper, we combine the two directions mentioned above to study the hyperalgebraic structures related to neutrosophic extended triplet groups (NETGs), which can be regarded as a further development of the research ideas in [21].
At first, we recall some concepts and results on hypergroups, semigroups and NETGs.
Let H be a non-empty set and P*(H) the set of all non-empty subsets of H. A map ◦: H × H→P*(H) is called (binary) hyperoperation (or hypercomposition), and (H, ◦) is called a hypergroupoid. If A, B∊P*(H), x∊H, then
Definition 1.
([1,2,3,4]) Let (H, ◦) be a hypergroupoid. If (∀x,y,z∊H) (x◦y)◦z=x◦(y◦z), then (H, ◦) is called a semihypergroup. That is,
For a semihypergroup (H, ◦), if (∀x,y∊H) x◦y=y◦x, then we call that H is commutative.
Note that, if (H, ◦) is a semihypergroup, then (A◦B)◦C = A◦(B◦C), ∀A, B, C∊P*(H).
Definition 2.
([1,2,3,4]) Assume that (H, ◦) is a semihypergroup. (1) If a∊H satisfies (∀x∊H) |a◦x| = |x◦a|=1, then a is called to be scalar. (2) If e∊H satisfies (∀x∊H) x◦e = e◦x = {x}, then e is called scalar identity. (3) If e∊H satisfies (∀x∊H) x∊(e◦x)∩(x◦e), then e is called identity. (4) Let a, b∊H. If there exists an identity e∊H satisfies e∊ (a◦b)∩(b◦a), then b is called an inverse of a. (5) If 0∊H satisfies (∀x∊H) x◦0 = 0◦x = {0}, then 0 is called zero element.
Definition 3.
([1,2,3,4]) Let (H, ◦) be a semihypergroup. (1) If (∀x∊H) a◦H = H◦a = H (reproductive axiom), then (H, ◦) is called a hypergroup. (2) If (H, ◦) is a hypergroup and (H, ◦) has at least one identity and each element has at least one inverse, then (H, ◦) is called to be regular.
Definition 4.
([1,2,3,4]) Let (H, ◦) be a semihypergroup. If x∊H satisfies x∊x◦H◦x, i.e., there exists an element y∊H, x∊x◦y◦x, then x is said to be regular. If (∀x∊H) x is regular, then (H, ◦) is called to be regular.
Note that, Every regular semigroup is a regular semihypergroup, and every hypergroup is a regular semihypergroup.
Definition 5.
([14]) Let N be a non-empty set, and * a binary operation on N. If (∀a∊N) there exist neut(a)∊N, anti(a)∊N satisfy
Then N is called a neutrosophic extended triplet set (NETS). Moreover, for a∊N, (a, neut(a), anti(a)) is called a neutrosophic extend triplet, neut(a) is called an extend neutral of “a”, and anti(a) is called an opposite of “a”.
neut(a)*a = a*neut(a) = a, and
anti(a)*a = a*anti(a) = neut(a).
anti(a)*a = a*anti(a) = neut(a).
For a neutrosophic extended triplet set N, a∊N, the set of neut(a) is denoted by {neut(a)}, and the set of anti(a) is denoted by {anti(a)}.
Definition 6.
([13,14]) Let (N, *) be a NETS. If (N,*) is a semigroup, then (N, *) is called to be a neutrosophic extended triplet group (NETG).
About some basic properties of neutrosophic extended triplet groups, plesse see [15,17,20].
2. Neutrosophic Extended Triplet Semihypergroups (NET-Semihypergroups) and Neutrosophic Extended Triplet Hypergroups (NET-Hypergroups)
In this section, we propose the new concepts of neutrosophic extended triplet semihypergroup (NET-semihypergroup) and neutrosophic extended triplet hypergroup (NET-hypergroup), and give some typical examples to illustrate their wide representativeness.
Definition 7.
Let (H,*) be a semihypergroup (i.e., * be a binary hyperoperation on nonempty set H such that (x*y)*z = x*(y*z), for all x, y, z∊H). (H,*) is called a neutrosophic extended triplet semihypergroup (shortened form, NET-semihypergroup), if for every x∊H, there exist neut(x) and anti(x) such that
x∊(neut(x)*x)∩(x*neut(x)), and
neut(x)∊(anti(x)*x)∩(x*anti(x)).
Here, we call that (x, neut(x), anti(x)) to be a hyper-neutrosophic-triplet.
Example 1.

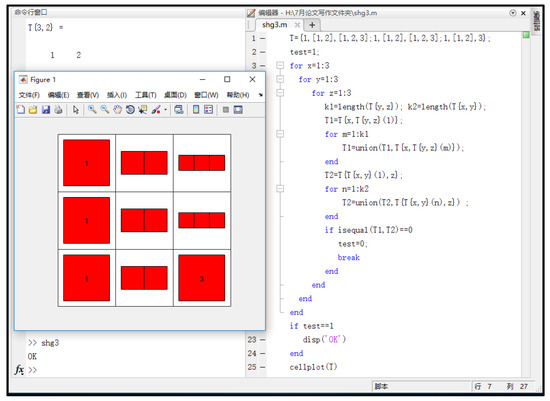
Denote H = {a, b, c}, define hyperoperations * on H as shown in Table 1. We can verify that (H, *) is semihypergroup by software MATLAB (see Figure 1).

Table 1.
The hyperoperation * on H.

Figure 1.
A program by Matlab to verify hyperoperation.
Moreover,
a∊(a*a)∩(a*a);
b∊(b*b)∩(b*b);
c∊(c*c)∩(c*c).
b∊(b*b)∩(b*b);
c∊(c*c)∩(c*c).
This means that (H, *) is neutrosophic extended triplet semihypergroup (NET-semihypergroup) and (a, a, a), (b, b, b), (c, c, c) are hyper-neutrosophic-triplets.
Example 2.

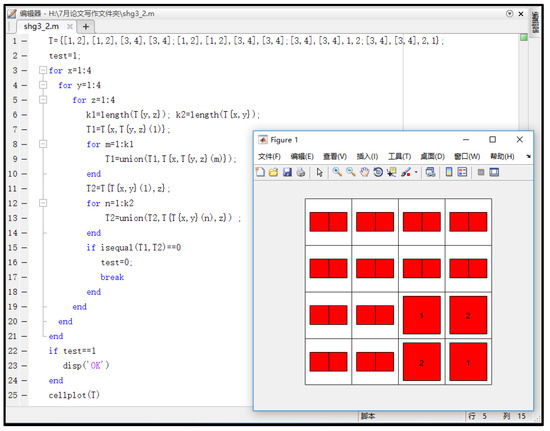
Denote H = {a, b, c, d}, define hyperoperations * on H as shown in Table 2. We can verify that (H, *) is semihypergroup by software MATLAB (see Figure 2).

Table 2.
The hyperoperation * on H.

Figure 2.
Verify hyperoperation by Matlab.
Moreover,
A∊(a*a)∩(a*a); a∊(b*a)∩(a*b), b∊(b*a)∩(a*b).
b∊(b*b)∩(b*b).
c∊(a*c)∩(c*a), a∊(c*c)∩(c*c); c∊(b*c)∩(c*b), b∊(d*c)∩(c*d).
d∊(a*d)∩(d*a), a∊(d*d)∩(d*d); d∊(b*d)∩(d*b), b∊(c*d)∩(d*c).
This means that (H, *) is neutrosophic extended triplet semihypergroup (NET-semihypergroup) and (a, a, a), (a, b, b), (b, b, b), (c, a, c), (c, b, d), (d, a, d), (d, b, c) are hyper-neutrosophic-triplets.
Remark 1.
From Example 2 we know that neut(x) may be not unique for an element x in a neutrosophic extended triplet semihypergroup (NET-semihypergroup). In fact, in Example 2, we have
{neut(a)} = {a, b}, neut(b) = b, {neut(c)} = {a, b}, {neut(d)} = {a, b}.
Example 3.
Let H be the set of all nonnegative integers, and define a hyperoperation * on H as following:
x*y = {z∊H | z≥max{x,y}}.
For examples,
3*5 = {5, 6, 7, 8, …}; 9*9 = {9, 10, 11, 12, …}; 2019*0 = {2019, 2020, 2021,2022, …}.
Then (H, *) is a commutative semihypergroup. Moreove, for any x∊H, we have
x∊ (x*x)∩(x*x); x∊ (x*x)∩(x*x).
This means that (H, *) is a neutrosophic extended triplet semihypergroup (NET-semihypergroup). In fact, we have
neut(0)=0; {neut(1)}={0,1}; {neut(2)}={0, 1, 2}; {neut(3)}={0, 1, 2, 3}…
Example 4.
Let R be the set of all real numbers, and Z the set of integers. We use the modulo of real numbers (that we denote by modR) in the following way:
∀ a, b∊R, then a = b (modR 6), if and only if a - b = 6n, where n is an integer.
For examples, 14.73 = 2.73 (modR 6), since 14.73 – 2.73 = 12 = 6 × 2; but 18≠15 (modR 6), since 18 - 15 = 3 ≠ 6n with n integer. Now, we define a hyperoperation # on R as following:
a#b = {x∊R | x=4ab (modR 6)}.
Then (R, #) is a commutative semihypergroup, since a#b = b#a = 4ab (modR 6), and associative because:
(a#b)#c = (4ab)#c = 4(4ab)c = 16abc (modR 6), and
a#(b#c) = a#(4bc) = 4a(4bc) = 16abc (modR 6).
a#(b#c) = a#(4bc) = 4a(4bc) = 16abc (modR 6).
Moreove, for any a∊R, we have
- (1)
- when a=0, (a, 6m, r) are hyper-triplets for any integer number m and real number r;
- (2)
- when a≠ 0, are hyper-neutrosophic-triplets for any integer numbers m, n.
This means that (R, #) is a neutrosophic extended triplet semihypergroup (NET-semihypergroup), and infinitely many neut(a) and infinitely many anti(a) for any element a in R.
Remark 2.
The following example shows that a sub-semihypergroup of a NET-semihypergroup may be not a NET-semihypergroup.
Example 5.

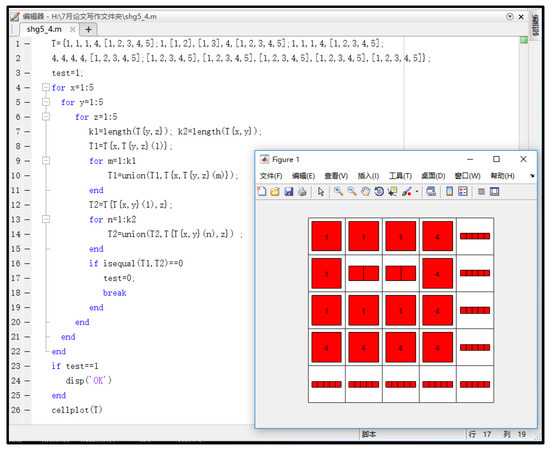
Denote H = {a, b, c, d, e}, define hyperoperations * on H as shown in Table 3. We can verify that (H, *) is semihypergroup by software MATLAB (see Figure 3).

Table 3.
The hyperoperation * on H.

Figure 3.
Verify the hyperoperation by Matlab.
Moreover, (a, a, a), (a, e, e), (b, b, b), (b, e, e), (c, e, e), (d, d, d), (d, e, e), (e, e, e), (e, a, e), (e, b, e), (e, c, e), (e, d, e) are hyper-neutrosophic-triplets.This means that (H, *) is a NET-semihypergroup. For S={a, b, c }⊆H, (S, *) is sub-semihypergroup of (H, *). But, (S, *) is not a NET-semihypergroup.
Remark 3.
For the traditional algebraic structures, we have the conclusion that any group must be a neutrosophic extended triplet group (NETG). For hyper algebraic structures, we know from Example 1 that a NET-semihypergroup is not necessarily a hypergroup (since a*H≠H in Example 1). Moreover, the following example shows that a hypergroup may be not a NET-semihypergroup. Therefore, hypergroup and NET-semihypergroup are two non-inclusion hyperalgebraic systems.
Example 6.

Denote H = {1, 2, 3}, define hyperoperations * on H as shown in Table 4. We can verify that (H, *) is semihypergroup by software MATLAB.

Table 4.
The hyperoperation * on H.
Moreover,
1*H = H*1 = H, 2*H = H*2 = H, 3*H = H*3 = H.
This means that (H, *) is a hypergroup. But, for 1∊H, we cannot find x,y∊H such that 1∊(x*1)∩(1*x), and x∊(y*1)∩(1*y). That is, (H, *) is not a NET- semihypergroup.
Definition 8.
Let (H,*) be a semihypergroup. (H,*) is called a neutrosophic extended triplet hypergroup (shortened form, NET-hypergroup), if (H,*) is both a NET-semihypergroup and a hypergroup.
Obviously, the NET-semihypergroups in Example 2 and Example 5 are all NET-hypergroups. And, the following propostion is true (the proof is omitted).
Proposition 1.
Every regular hypergroup is a NET-hypergroup.
The NET-hypergroup in Example 2 is not a regular hypergroup, it shows that the inverse of Proposition 1 is not true.
Proposition 2.
Let (H,*) be a NET-semihypergroup (or a NET-hypergroup). Then (H,*) is a regular semihypergroup.
Proof.
Assume that (H,*) is a NET-semihypergroup. For any x∊H, by Definition 7 we get that there exist neut(x) and anti(x) such that
x∊(neut(x)*x)∩(x*neut(x)), and neut(x)∊(anti(x)*x)∩(x*anti(x)).
Then,
x∊neut(x)*x ⊆ (x*anti(x))*x.
That is, x∊x*anti(x)*x. From this, by Definition 4, we know that (H,*) is a regular semihypergroup.
If (H,*) is a NET-hypergroup, by Definition 8, it follows that (H,*) is a NET-semihypergroup. Then, by the proof above, (H,*) is a regular semihypergroup. □
The following example shows that the inverse of Proposition 2 is not true. Moreover, it also shows that a regular semihypergroup may be not a hypergroup.
Example 7.

Denote H = {a, b, c}, define hyperoperations * on H as shown in Table 5. We can verify that (H, *) is semihypergroup.

Table 5.
The hyperoperation * on H.
Moreover, a ∊ a*a*a; b ∊ b*b*b; c ∊ c*a*c.This means that (H, *) is a regular semihypergroup. But it is not a NET-semihypergroup, since there is not any x ∊ H such that c ∊ x*c and c ∊ c*x.Obviously, (H, *) is not a hypergroup.
Therefore, the relationships among semihypergroup, NET-semihypergroup, NET-hypergroup, (regular) hypergroup and regular semihypergroup can be expressed by Figure 4.
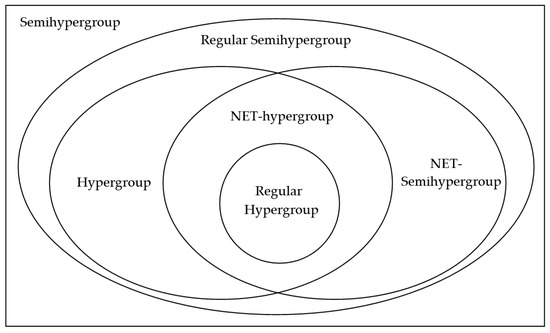
Figure 4.
The relationships among some kinds of semihypergroups.
For basic properties of NET-semihypergroups and NET-hypergroups, we can get following results.
Theorem 1.
Let (H,*) be a semihypergroup. Then
- (1)
- if (H,*) is commutative NET-semihypergroup, then for any x∊H and hyper-neutrosophic-triplet (x, neut(x), anti(x)), there exists p∊neut(x)*neut(x) and q∊anti(x)*neut(x) such that (x, p, q) is also a hyper-neutrosophic-triplet.
- (2)
- if (H,*) is commutative NET-semihypergroup, then for any x∊H and neut(x)∊{neut(x)}, there exists p∊neut(x)*neut(x) such that p∊{neut(x)}.
- (3)
- if (H,*) is NET-semihypergroup and x∊H is scalar, then |{neut(x)}|=1, that is, the neutral element of x is unique; Moreover, if x is scalar, then neut(x)*neut(x)=neut(x).
- (4)
- if (H,*) is commutative hypergroup, then (H,*) is NET-hypergroup.
Proof.
(1) Assume that x∊H and (x, neut(x), anti(x)) is a hyper-neutrosophic-triplet. By Definition 7:
Since (H, *) is commutative, then:
x∊(neut(x)*x)∩(x*neut(x)), and neut(x)∊(anti(x)*x)∩(x*anti(x)).
x∊neut(x)*x ⊆ neut(x)*(neut(x)*x) = (neut(x)*neut(x))*x = x*(neut(x)*neut(x)).
This means that there exists p∊neut(x)*neut(x) such that x∊p*x = x*p. Moreover:
p∊neut(x)*neut(x) ⊆ (x*anti(x))*neut(x) = x*(anti(x)*neut(x)) = (anti(x)*neut(x))*x.
It follows that there exists q∊anti(x)*neut(x) such that p∊q*x = x*q. By Definition 7 we know that (x, p, q) is also a hyper-neutrosophic-triplet.
(2) It follows from (1).
(3) Suppose that x∊H and x is scalar. Using Definition 2, |x*a|=|a*x|=1 for any a∊H. From this, for a hyper-neutrosophic-triplet (x, neut(x), anti(x)), applying Definition 7, we have:
x = neut(x)*x = x*neut(x), and neut(x) = anti(x)*x = x*anti(x).
Assume p1, p2∊{neut(x)}, then there exists q1, q2∊H such that:
x = p1*x = x*p1, p1 = q1*x = x*q1; x = p2*x = x*p2, p2 = q2*x = x*q2.
Then:
It follows that p1 = p2 and p1 = p1*p1. That is, |{neut(x)}|=1 and neut(x)*neut(x) = neut(x).
p1 = q1*x = q1*(x*p2) = (q1*x)*p2 = p1*p2;
p2 = x*q2 = (x*p1)*q2 = (x*(q1*x))*q2 = (x*q1)*(x*q2) = p1*p2.
p2 = x*q2 = (x*p1)*q2 = (x*(q1*x))*q2 = (x*q1)*(x*q2) = p1*p2.
(4) Let (H, *) be a commutative hypergroup. By Definition 3, for any x∊H, x*H = H*x = H. Then, for any x∊H, there exists h∊H such that x = h*x = x*h. Moreover, for h∊H, there exists u∊H such that h = u*x = x*u. Thus, (x, h, u) is a hyper-neutrosophic-triplet, and it means that (H, *) is a NET-semihypergroup by Definition 7. On the other hand, since (H, *) is a hypergroup, so (H, *) is a NET-hypergroup by Definition 8.
3. Pure NET-semihypergroups and Regular hypergroups
In this section, we discuss some properties of NET-semihypergroups. We’ll propose the new notion of pure NET-semihypergroup, investigate the structure of pure NET-semihypergroups.
Definition 9.
Let (H,*) be a NET-semihypergroup. (H,*) is called a pure NET-semihypergroup, if for every x∊H, there exist neut(x) and anti(x) such that
x = (neut(x)*x)∩(x*neut(x)), and neut(x) = (anti(x)*x)∩(x*anti(x)).
Obviously, the following proposition is true and the proof is omitted.
Proposition 3.
(1) Every neutrosophic extended triplet group (NETG) is pure NET-semihypergroup. (2) If (H,*) is a pure NET-semihypergroup and the hyper operation * is commutative, then for every x∊H, there exists y, z∊H such that
x = y*x = x*y, and y = z*x = x*z.
Example 8.

Denote H = {a, b, c}, define hyperoperations * on H as shown in Table 6. We can verify that (H, *) is semihypergroup.

Table 6.
The hyperoperation * on H.
Moreover,
a=(a*a)∩(a*a); b=(c*b)∩(b*c), c=(b*b)∩(b*b); c=(c*c)∩(c*c).
This means that (H, *) is a pure NET-semihypergroup.
Example 9.

Denote H = {a, b, c, d, e}, define hyperoperations * on H as shown in Table 7. We can verify that (H, *) is semihypergroup.

Table 7.
The hyperoperation * on H.
Moreover:
a=(a*a)∩(a*a); b=(b*b)∩(b*b); c=(b*c)∩(c*b), b=(c*c)∩(c*c); d=(d*d)∩(d*d); e=(e*e)∩(e*e).
This means that (H, *) is a pure NET-semihypergroup.
Remark 4.
From Example 8 and Example 9, we have:
a=(a*a)∩(a*a);
a∊(b*a)∩(a*b), b∊(b*a)∩(a*b); a∊(c*a)∩(a*c), c∊(c*a)∩(a*c).
a∊(b*a)∩(a*b), b∊(b*a)∩(a*b); a∊(c*a)∩(a*c), c∊(c*a)∩(a*c).
This means that {neut(a)} = {a, b, c}. But, b∊{neut(a)} and c∊{neut(a)} are different to a∊{neut(a)}, since one is “∊“ and the other is “=“. In order to clearly express the difference between the two kinds of neutral elements, we introduce a new concept: pure neutral element.
Definition 10.
Let (H,*) be a NET-semihypergroup and x∊H. An element y∊H is called a pure neutral element of the element x, if there exist z∊H such that:
x = y*x = x*y, and y = z*x = x*z.
Here, we denote y by pneut(x).
Proposition 4.
Let (H,*) be a NET-semihypergroup and x∊H. If there exists a pure neutral element of x, then the pure neutral element of x, that is, pneut(x), is unique.
Proof.
Assume that there exists two pure neutral elements y1, y2 for x∊H. Then there exists z1, z2 ∊ H such that:
x = y1*x = x*y1, and y1 = z1*x = x*z1;
x = y2*x = x*y2, and y2 = z2*x = x*z2.
x = y2*x = x*y2, and y2 = z2*x = x*z2.
Therefore,
y1 = z1*x = z1*(x*y2) = (z1*x)*y2 = y1*y2;
y2 = x*z2 = (x*y1)*z2 = (x*(z1*x))*z2 = (x*z1)* (x*z2) = y1*y2.
y2 = x*z2 = (x*y1)*z2 = (x*(z1*x))*z2 = (x*z1)* (x*z2) = y1*y2.
Hence, y1 = y2. That is, pneut(x) is unique. □
By the proof of Proposition 4, we know that y1 = y2= y1*y2, it follows that y1 = y1*y1. Therefore, we have the following corollary.
Corollary 1.
Let (H,*) be a NET-semihypergroup and x∊H. If there exists a pure neutral element of x, then the pure neutral element of x is idempotent, that is, pneut(x)*pneut(x)= pneut(x).
Remark 5.
From Proposition 4, we know that the pure neutral element of an elemetn x is unique when there exists one pure neutral element of x. Particularly, for commutative pure NET- semihypergroups, applying Proposition 3 (2), we get following Proposition 5 (the proof is omitted).
Proposition 5.
Let (H,*) be a commutative pure NET-semihypergroup. Then for any x∊H, pneut(x) is unique.
Proposition 6.
Let (H,*) be a commutative pure NET-semihypergroup. Then for any x, y∊H, pneut(x*y)= pneut(x)*pneut(y) when | x*y|=1. Moreover, if pneut(x) = z1*x = x*z1 and pneut(y) = z2*y = y*z2, z1, z2∊H, then:
pneut(x*y) = (z1*z2)*(x*y) = (x*y)*(z1*z2).
Proof.
Assume that x, y∊H and | x*y|=1. Since (H, *) be a commutative pure NET-semihypergroup, then:
(x*y)*(pneut(x)*pneut(y)) = (x*y)*(pneut(y)*pneut(x))
= x*(y*pneut(y))*pneut(x)
= x*y*pneut(x)
= (x*pneut(x))*y
= x*y;
(pneut(x)*pneut(y))*(x*y) = (pneut(y)*pneut(x))*(x*y)
= pneut(y)*(pneut(x)*x)* y
= pneut(y)*x*y
= x*(pneut(y)*y)
= x*y.
= x*(y*pneut(y))*pneut(x)
= x*y*pneut(x)
= (x*pneut(x))*y
= x*y;
(pneut(x)*pneut(y))*(x*y) = (pneut(y)*pneut(x))*(x*y)
= pneut(y)*(pneut(x)*x)* y
= pneut(y)*x*y
= x*(pneut(y)*y)
= x*y.
On the other hand, assume that (x, pneut(x), anti(x)) and (y, pneut(y), anti(y)) are hyper-neutrosophic-triplets, then:
(x*y)*(anti(x)*anti(y)) = (x*y)*(anti(y)*anti(x))
= x*(y*anti(y))*anti(x)
= x*pneut(y)*anti(x)
= (x*anti(x))*pneut(y)
= pneut(x)*pneut(y);
(anti(x)*anti(y))*(x*y) = (anti(x)*anti(y))*(y*x)
= anti(x)*(anti(y)*y)*x
= anti(x)*pneut(y)*x
= (anti(x)*x)*pneut(y)
= pneut(x)*pneut(y).
= x*(y*anti(y))*anti(x)
= x*pneut(y)*anti(x)
= (x*anti(x))*pneut(y)
= pneut(x)*pneut(y);
(anti(x)*anti(y))*(x*y) = (anti(x)*anti(y))*(y*x)
= anti(x)*(anti(y)*y)*x
= anti(x)*pneut(y)*x
= (anti(x)*x)*pneut(y)
= pneut(x)*pneut(y).
Applying Proposition 5 we get that pneut(x*y)= pneut(x)*pneut(y).
Moroeover, assume pneut(x) = z1*x = x*z1, pneut(y) = z2*y = y*z2. Then, by commutativity of the hyper operation *:
(z1*z2)*(x*y) = (z1*x)*(z2*y)
= pneut(x)*pneut(y)
= pneut(x*y);
(x*y)*(z1*z2) =(x*z1)*(y*z2)
= pneut(x)*pneut(y)
= pneut(x*y).
= pneut(x)*pneut(y)
= pneut(x*y);
(x*y)*(z1*z2) =(x*z1)*(y*z2)
= pneut(x)*pneut(y)
= pneut(x*y).
Therefore, the proof is completed. □
Theorem 2.
Let (H,*) be a commutative pure NET-semihypergroup and H satisfies:
Define a binary relation ≈ on H as following:
∀x, y∊H, pneut(x)=pneut(y)⇒ | x*y|=1.
∀x, y∊H, x≈y if and only if pneut(x)=pneut(y).
Then:
- (1)
- The binary relation is a equivalent relation on H;
- (2)
- For any x∊H, [x]≈ is a sub-NET-semihypergroup of H, where [x]≈ is the equivalent class of x based on equivalent relation ≈;
- (3)
- For any x∊H, [x]≈ is a regular hypergroupe.
Proof.
(1) It is obviously.
(2) Assume a, b∊[x]≈, then pneut(a)= pneut(b)=pneut(x). Applying Proposition 6 and Corollary 1, we have
pneut(a*b) = pneut(a)*pneut(b)
= pneut(x)*pneut(x)
= pneut(x).
= pneut(x)*pneut(x)
= pneut(x).
This means that [x]≈ is closed on the hyper operation *.
Moreover, by Corollary 1, we have pneut(x)*pneut(x) = pneut(x). From this and using Proposition 5, we get that pneut(pneut(x)) = pneut(x). It follows that pneut(a) ∊[x]≈ for any a∊[x]≈. Moreover, assume that a∊[x]≈, by the definition of commutative pure NET-semihypergroup, there exists r∊H such that:
pneut(a) = r*a = a*r.
It follows that:
pneut(a) = (r*pneut(a))*a = a*(r*pneut(a)).
Applying Proposition 6 and Corollary 1:
pneut(r*pneut(a))
= pneut(r)* pneut(pneut(a))
= pneut(r)* pneut(a)
= pneut(r*a)
= pneut(pneut(a)
= pneut(a).
= pneut(r)* pneut(pneut(a))
= pneut(r)* pneut(a)
= pneut(r*a)
= pneut(pneut(a)
= pneut(a).
That is, pneut(r*pneut(a)) = pneut(a) = pneut(x). This means that r*pneut(a) ∊[x]≈. Therefore, by (C2), there exists anti(a) (see Definition 7), it is in [x]≈. This means that [x]≈ is a sub-NET-semihypergroup of H.
(3) For any x∊H, from (2) we know that [x]≈ is a sub-NET-semihypergroup of H. By the definition of ≈, for any a∊[x]≈, pneut(a) = pneut(x). Then, a*[x]≈*a =[x]≈, and pneut(x) is a (local) identity in [x]≈. By Definition 3, we get that [x]≈ is a regular hypergroup. □
From Theorem 2 we know that for a commutative pure NET-semihypergroup (it satisfies the condition in Theorem 2), it is a union of some regular hypergroups. The following picture (Figure 5) shows this special structure.
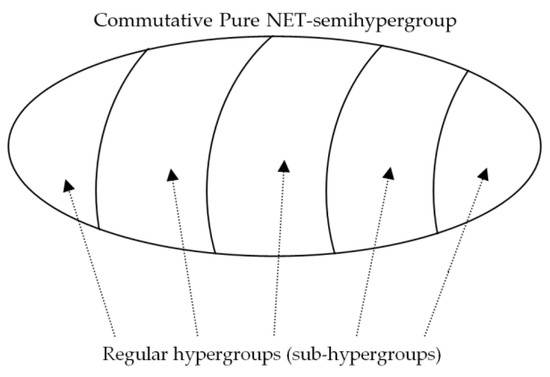
Figure 5.
The structure of a commutative pure NET-semihypergroups.
Example 10.

Denote H = {a, b, c, d, e}, define hyperoperations * on H as shown in Table 8. We can verify that (H, *) is commutative pure NET-semihypergroup.

Table 8.
The hyperoperation * on H.
Moreover:
and H= H1∪H2∪H3∪H4, where, Hi (i=1, 2, 3, 4) are regular hypergroups.
H1={a}=[a]≈;
H2={b, c}=[b]≈ =[c]≈;
H3={d}=[d]≈;
H4={e}=[e]≈;
H2={b, c}=[b]≈ =[c]≈;
H3={d}=[d]≈;
H4={e}=[e]≈;
Remark 6.
The above example shows that a commutative pure NET-semihypergroup may be not a hypergroup (since d*H≠H in Example 10).
4. Weak Commutative NET-Semihypergroups and Their Structures
In this section, we discuss generalized commutativity in NET-semihypergroups. We propose a new notion of weak commutative NET-semihypergroup, and prove the structure theorem of weak commutative pure NET-semihypergroup (WCP-NET-semihypergroup), which can be regarded as a generalization of Cliffod Theorem in semigroup theory.
Definition 11.
Let (H,*) be a NET-semihypergroup. (H,*) is called a weak commutative NET- semihypergroup, if for every x∊H, every hyper-neutrosophic-triplet (x, neut(x), anti(x)), the following conditions are satisfied:
(H,*) is called a weak commutative pure NET-semihypergroup (shortly, WCP-NET-semihypergroup), if it both weak commutative and pure.
Obviously, the following proposition is true and the proof is omitted.
Proposition 7.
Every commutative NET-semihypergroup is weak commutative.
The following examples show that there exists some weak commutative NET- semihypergroups which are not commutative.
Example 11.

Denote H = {1, 2, 3, 4, 5, 6, 7, 8}, define hyperoperations * on H as shown in Table 9. We can verify that (H, *) is NET-semihypergroup.

Table 9.
The hyperoperation * on H.
Moreover, (1, 1, 1), (2, 2, 2), (3, 3, 3), (4, 3, 4), (5, 3, 5), (6, 3, 6), (7, 3, 8) and (8, 3, 7) are hyper-neutrosophic-triplets, and (∀x∊H) 1*x = x*1, 2*x = x*2 and 3*x = x*3, 7*8 = 8*7. This means that (H, *) is a weak commutative NET-semihypergroup. Since 4*5 ≠ 5*4, (H, *) is not commutative.
Remark 7.
The above example shows that there exists WCP-NET-semihypergroup (by Definition 9, we know that the NET-semihypergroup in Example 11 is pure).
Example 12.

Denote H = {1, 2, 3, 4, 5, 6, 7, 8, 9}, define hyperoperations * on H as shown in Table 10. We can verify that (H, *) is NET-semihypergroup.

Table 10.
The hyperoperation * on H.
Moreover, (1, 2, 1), (2, 2, 2), (3, 1, 3), (4, 4, 4), (5, 4, 5), (6, 4, 6), (7, 4, 7), (8, 4, 9) and (9, 4, 8) are hyper-neutrosophic-triplets, and (∀x∊H) 2*x = x*2, 1*x = x*1 and 4*x = x*4, 8*9 = 9*8. This means that (H, *) is a weak commutative NET-semihypergroup. Since 5*6 ≠ 6*5, (H, *) is not commutative.
Proposition 8.
Let (H,*) be a weak commutative pure NET-semihypergroup (WCP-NET-semihypergroup). Then for any x∊H, there exists a pure neutral element of x, and pneut(x) is unique, pneut(x)*pneut(x)= pneut(x).
Proof.
For any x∊H. Since (H, *) is pure, by Definition 9, there exists hyper-neutrosophic-triplet (x, neut(x), anti(x)) such that
x = (neut(x)*x)∩(x*neut(x)), and neut(x) = (anti(x)*x)∩(x*anti(x)).
Moreover, since (H, *) is weak commutative, by Definition 11, neut(x)*x = x*neut(x), and anti(x)*x = x*anti(x). Thus
x = neut(x)*x = x*neut(x), and neut(x) = anti(x)*x = x*anti(x).
Therefore, by Definition 10, neut(x) is a pure neutral element of x. Applying Proposition 4 we know that pure neutral element of x is unique. Moreover, using Corollary 1, pneut(x)*pneut(x)= pneut(x). □
Proposition 9.
Let (H,*) be a weak commutative pure NET-semihypergroup (WCP-NET-semihypergroup). Then for any x, y∊H, pneut(x*y)= pneut(x)*pneut(y) when | x*y |=1. Moreover, if pneut(x) = z1*x = x*z1 and pneut(y) = z2*y = y*z2, z1, z2 ∊ H, then
pneut(x*y) = (z2*z1)*(x*y) = (x*y)*(z2*z1).
Proof.
Since (H, *) be a WCP-NET-semihypergroup, then for any x, y∊H and | x*y |=1, pneut(x)*y = y*pneut(x) by Definition 11. Then
x*y)*(pneut(x)*pneut(y)) = (x*y)*(pneut(y)*pneut(x)) = x*y*pneut(x) = (x*pneut(x))*y = x*y;
(pneut(x)*pneut(y))*(x*y) = (pneut(y)*pneut(x))*(x*y) = pneut(y)*x*y = x*(pneut(y)*y) = x*y.
(pneut(x)*pneut(y))*(x*y) = (pneut(y)*pneut(x))*(x*y) = pneut(y)*x*y = x*(pneut(y)*y) = x*y.
On the other hand, let (x, pneut(x), anti(x)) and (y, pneut(y), anti(y)) are hyper-neutrosophic-triplets, then
xx*y)*(anti(y)*anti(x))
= x*(y*anti(y))*anti(x)
= x*pneut(y)*anti(x)
= pneut(y)*x*anti(x)
= pneut(y)*pneut(x)
= pneut(x)*pneut(y);
(anti(y)*anti(x))*(x*y) = anti(y)*(anti(x)*x)*y = anti(y)*pneut(x)*y = pneut(x)*anti(y)*y = pneut(x)*pneut(y).
= x*(y*anti(y))*anti(x)
= x*pneut(y)*anti(x)
= pneut(y)*x*anti(x)
= pneut(y)*pneut(x)
= pneut(x)*pneut(y);
(anti(y)*anti(x))*(x*y) = anti(y)*(anti(x)*x)*y = anti(y)*pneut(x)*y = pneut(x)*anti(y)*y = pneut(x)*pneut(y).
Thus, pneut(x)*pneut(y) is a pure neutral element of x*y by Definition 7 and Definition 10. Applying Proposition 8 we get that pneut(x*y)= pneut(x)*pneut(y).
Moroeover, assume pneut(x) = z1*x = x*z1, pneut(y) = z2*y = y*z2. Then, by weak commutativity (Definition 11) we have
(z2*z1)*(x*y) = z2*(z1*x)*y = z2*pneut(x)*y = pneut(x)*(z2*y) = pneut(x)*pneut(y) = pneut(x*y);
(x*y)*(z2*z1) = x*(y*z2)*z1 = x*pneut(y)*z1 = (x*z1)*pneut(y) = pneut(x)*pneut(y) = pneut(x*y).
(x*y)*(z2*z1) = x*(y*z2)*z1 = x*pneut(y)*z1 = (x*z1)*pneut(y) = pneut(x)*pneut(y) = pneut(x*y).
Therefore, the proof is completed. □
Theorem 3.
Let (H,*) be a WCP-NET-semihypergroup and H satisfies
(∀x, y∊H, pneut(x)=pneut(y)⇒ | x*y|=1.
Define a binary relation ≈ on H as following:
∀x, y∊H, x≈y if and only if pneut(x)=pneut(y).
Then
- (1)
- The binary relation≈ is a equivalent relation on H;
- (2)
- For any x∊H, [x]≈ is a sub-NET-semihypergroup of H, where [x]≈ is the equivalent class of x based on equivalent relation≈;
- (3)
- For any x∊H, [x]≈ is a regular hypergroupe.
Proof.
(1) From the definition of ≈, by Proposition 8 and Proposition 9, we know that the binary relation ≈ is a equivalent relation.
(2) Suppose a, b∊[x]≈. By the definition of ≈, pneut(a) = pneut(b) = pneut(x). Using Proposition 8 and Proposition 9, we have
pneut(a*b) = pneut(a)*pneut(b) = pneut(x)*pneut(x) = pneut(x).
It follows that [x]≈ is closed on the hyper operation *.
And, applying Proposition 8, we have pneut(x)*pneut(x) = pneut(x). From this and using Proposition 8, we get that pneut(pneut(x)) = pneut(x). It follows that pneut(a)∊[x]≈ for any a∊[x]≈. Moreover, assume that a∊[x]≈, by the definition of WCP-NET-semihypergroup, there exists r∊H such that pneut(a) = r*a = a*r. Thus (by Proposition 9)
pneut(a) = (r*pneut(a))*a = a*(r*pneut(a))
⇒ r*pneut(a) ∊{anti(a)}.
pneut(r*pneut(a))
= pneut(r)* pneut(pneut(a))
= pneut(r)* pneut(a)
= pneut(r*a)
= pneut(pneut(a))
= pneut(a).
⇒ r*pneut(a) ∊{anti(a)}.
pneut(r*pneut(a))
= pneut(r)* pneut(pneut(a))
= pneut(r)* pneut(a)
= pneut(r*a)
= pneut(pneut(a))
= pneut(a).
That is, pneut(r*pneut(a)) = pneut(a) = pneut(x). This means that r*pneut(a) ∊[x]≈. Combining this and r*pneut(a)∊{anti(a)}, we know that there exists anti(a) which is in [x]≈. This means that [x]≈ is a sub-NET- semihypergroup of H.
(3) Assume x∊H, from (2) we know that [x]≈ is a sub-NET-semihypergroup of H. By the definition of ≈, for any a∊[x]≈, pneut(a) = pneut(x). From the proof of (2), there exists anti(a)∊{anti(a)} and anti(a)∊[x]≈. Then, [x]≈ ⊆ a*[x]≈*a. Obviously, a*[x]≈*a ⊆ [x]≈. Thus, a*[x]≈*a=[x]≈.
On the other hand, pneut(x) is a (local) identity in [x]≈. Therefore, by Definition 3, we get that [x]≈ is a regular hypergroup. □
Example 13.

Denote H = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}, define hyperoperations * on H as shown in Table 11. We can verify that (H, *) is WCP-NET-semihypergroup, and not commutative.

Table 11.
The hyperoperation * on H.
Moreover,
H1 = {1} = [1]≈;
H2 = {2, 3} = [2]≈ = [3]≈;
H3 = {4, 5} = [4]≈ =[5]≈;
H4 = {6, 7, 8, 9, 10, 11} = [6]≈ = [7]≈ = [8]≈ = [9]≈ = [10]≈ = [11]≈;
and H= H1∪H2∪H3∪H4, where, Hi (i=1, 2, 3, 4) are regular hypergroups.
H2 = {2, 3} = [2]≈ = [3]≈;
H3 = {4, 5} = [4]≈ =[5]≈;
H4 = {6, 7, 8, 9, 10, 11} = [6]≈ = [7]≈ = [8]≈ = [9]≈ = [10]≈ = [11]≈;
and H= H1∪H2∪H3∪H4, where, Hi (i=1, 2, 3, 4) are regular hypergroups.
5. Conclusions
In this paper, we propose some new notions of neutrosophic extended triplet semihypergroup (NET-semihypergroup), neutrosophic extended triplet hypergroup (NET-hypergroup), pure NET- semihypergroup and weak commutative NET-semihypergroup, investigate some basic properties and the relationships among them (see Figure 6), study their close connections with regular hypergroups and regular semihypergroups. Particularly, we prove two structure theorems of commutative pure NET-semihypergroup (CP-NET-semihypergroup) and weak commutative pure NET-semihypergroup (WCP-NET-semihypergroup) under the condition (C1) (see Theorem 2 and Theorem 3). From these results, we know that NET-semihypergroup is a hyperalgebraic structure independent of hypergroup, and NET-semihypergroup is also a generalization of group concept in hyperstructures. The research results in this paper show that NET-semihypergroups and NET- hypergroups have important theoretical research value, which greatly enriches the traditional theory of hyperalgebraic structures.
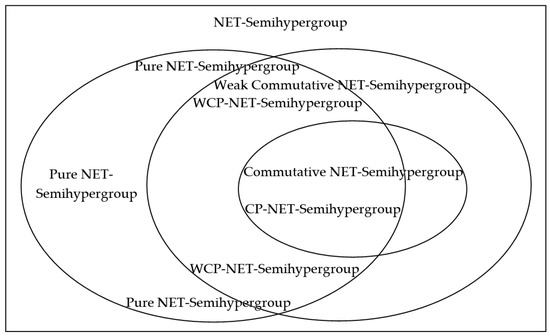
Figure 6.
The relationships among some kinds of NET-semihypergroups.
In the future, we will investigate the combinations of NET-semihypergroups and related algebraic systems ([22,23,24]).
Author Contributions
F.S. and X.Z. proposed the idea of the research, X.Z. and Y.M. wrote the paper.
Funding
This research was funded by National Natural Science Foundation of China (Grant Nos. 61573240 and 61976130).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Corsini, P.; Leoreanu, V. Applications of Hyperstructure Theory; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Wall, H.S. Hypergroups. Am. J. Math. 1937, 59, 77–98. [Google Scholar] [CrossRef]
- Freni, D. A new characterization of the derived hypergroup via strongly regular equivalences. Commun. Algebra 2002, 30, 3977–3989. [Google Scholar] [CrossRef]
- Davvaz, B. Semihypergroup Theory; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Jafarabadi, H.M.; Sarmin, N.H.; Molaei, M.R. Simple semihypergroups. Aust. J. Basic Appl. Sci. 2011, 5, 51–55. [Google Scholar]
- Salvo, M.D.; Freni, D.; Faro, G.L. Fully simple semihypergroups. J. Algebra 2014, 399, 358–377. [Google Scholar] [CrossRef]
- Jafarabadi, H.M.; Sarmin, N.H.; Molaei, M.R. Completely simple and regular semihypergroups. Bull. Malays. Math. Sci. Soc. 2012, 35, 335–343. [Google Scholar]
- Howie, J.M. Fundamentals of Semigroup Theory; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Smarandache, F. Neutrosophic set—A generialization of the intuituionistics fuzzy sets. Int. J. Pure Appl. Math. 2005, 3, 287–297. [Google Scholar]
- Zhang, X.H.; Bo, C.X.; Smarandache, F.; Dai, J.H. New inclusion relation of neutrosophic sets with applications and related lattice structure. Int. J. Mach. Learn. Cybern. 2018, 9, 1753–1783. [Google Scholar] [CrossRef]
- Zhang, X.H.; Bo, C.X.; Smarandache, F.; Park, C. New operations of totally dependent-neutrosophic sets and totally dependent-neutrosophic soft sets. Symmetry 2018, 10, 187. [Google Scholar] [CrossRef]
- Zhang, X.H.; Mao, X.Y.; Wu, Y.T.; Zhai, X.H. Neutrosophic filters in pseudo-BCI algebras. Int. J. Uncertain. Quantif. 2018, 8, 511–526. [Google Scholar] [CrossRef]
- Smarandache, F.; Ali, M. Neutrosophic triplet group. Neural Comput. Appl. 2018, 29, 595–601. [Google Scholar] [CrossRef]
- Smarandache, F. Neutrosophic Perspectives: Triplets, Duplets, Multisets, Hybrid Operators, Modal Logic, Hedge Algebras. And Applications; Pons Publishing House: Brussels, Belgium, 2017. [Google Scholar]
- Zhang, X.H.; Hu, Q.Q.; Smarandache, F.; An, X.G. On neutrosophic triplet groups: Basic properties, NT-subgroups, and some notes. Symmetry 2018, 10, 289. [Google Scholar] [CrossRef]
- Jaíyéolá, T.G.; Smarandache, F. Some sesults on neutrosophic triplet group and their applications. Symmetry 2018, 10, 202. [Google Scholar] [CrossRef]
- Zhang, X.H.; Wu, X.Y.; Mao, X.Y.; Smarandache, F.; Park, C. On neutrosophic extended triplet groups (Loops) and Abel-Grassmann’s Groupoids (AG-Groupoids). J. Intell. Fuzzy Syst. 2019. [Google Scholar] [CrossRef]
- Wu, X.Y.; Zhang, X.H. The decomposition theorems of AG-neutrosophic extended triplet loops and strong AG-(l, l)-loops. Mathematics 2019, 7, 268. [Google Scholar] [CrossRef]
- Ma, Y.C.; Zhang, X.H.; Yang, X.F.; Zhou, X. Generalized neutrosophic extended triplet group. Symmetry 2019, 11, 327. [Google Scholar] [CrossRef]
- Zhang, X.H.; Wang, X.J.; Smarandache, F.; Jaíyéolá, T.G.; Lian, T.Y. Singular neutrosophic extended triplet groups and generalized groups. Cogn. Syst. Res. 2019, 57, 32–40. [Google Scholar] [CrossRef]
- Gulistan, M.; Nawaz, S.; Hassan, N. Neutrosophic triplet non-associative semihypergroups with application. Symmetry 2018, 10, 613. [Google Scholar] [CrossRef]
- Zhang, X.H.; Borzooei, R.A.; Jun, Y.B. Q-filters of quantum B-algebras and basic implication algebras. Symmetry 2018, 10, 573. [Google Scholar] [CrossRef]
- Omidi, S.; Davvaz, B.; Zhan, J.M. An investigation on ordered algebraic hyperstructures. Acta Math. Sin. Engl. Ser. 2017, 33, 1107–1124. [Google Scholar] [CrossRef]
- Zhang, X.H.; Mao, X.Y.; Smarandache, F.; Park, C. On homomorphism theorem for perfect neutrosophic extended triplet groups. Information 2018, 9, 237. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).