Volumes of Hyperbolic Three-Manifolds Associated with Modular Links
Abstract
:1. Introduction
1.1. Knots Associated with Closed Geodesics
1.2. Modular Links and Their Volumes
1.3. Results and Structure of This Paper
2. Modular Links and Quadratic Fields
2.1. Periodic Geodesics on the Modular Surface
2.2. Quadratic Forms and Geodesics
3. Coding of Geodesics
3.1. Conjugacy Classes in and Words in Two Generators
3.2. From Matrices to Words
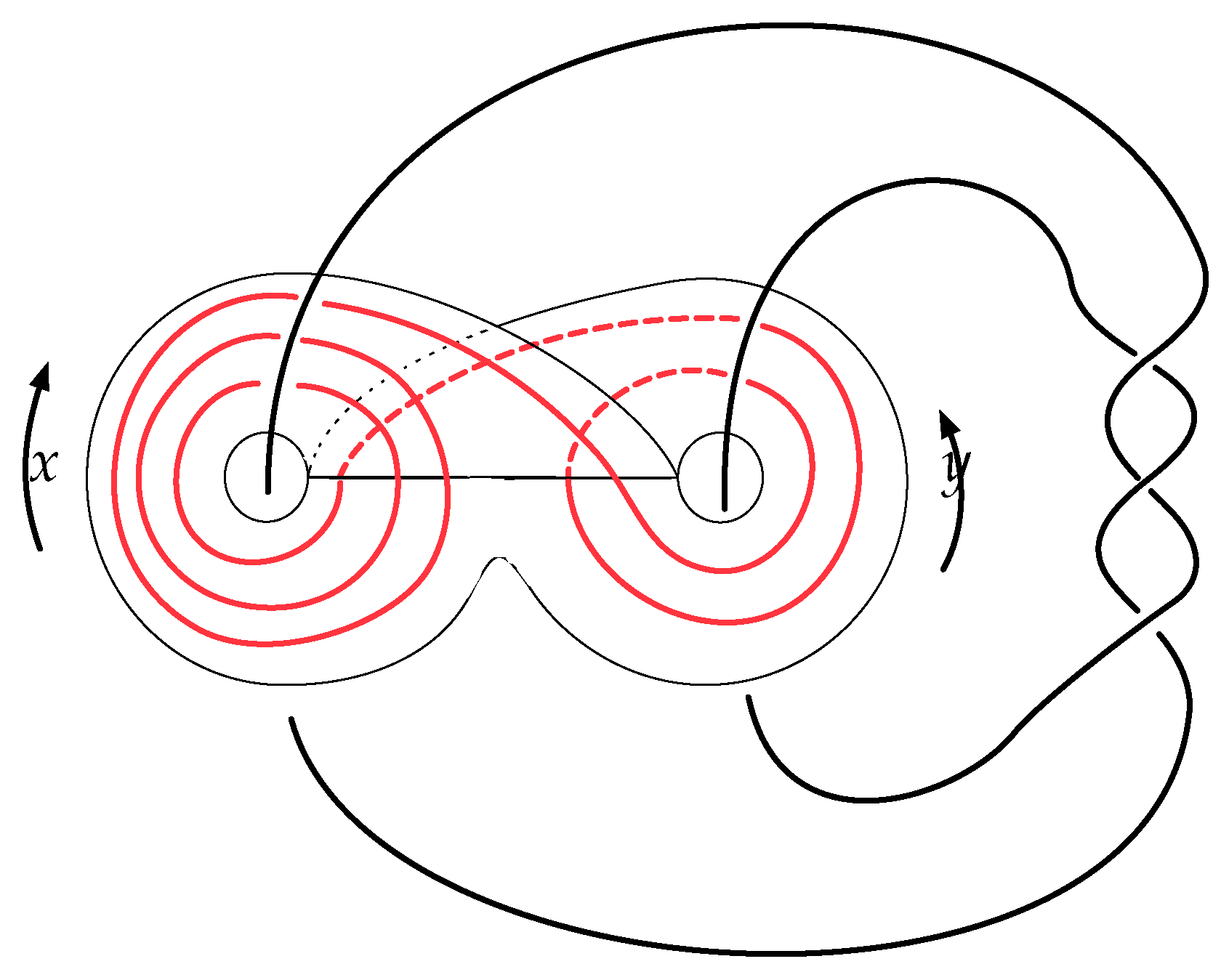
3.3. Curves from Words and the Template
4. Computational Method
- The fundamental unit has norm . In this case, is the regulator and the narrow class number is twice the class number. Thus, the sum of the geometric lengths is given by .
- The fundamental unit has norm . In this case, the unit we use is not the fundamental unit, but . i.e., its log is twice the regulator. On the other hand, the narrow class number is in this case the same as the class number, and thus the sum of the geometric lengths is given by in this case as well.
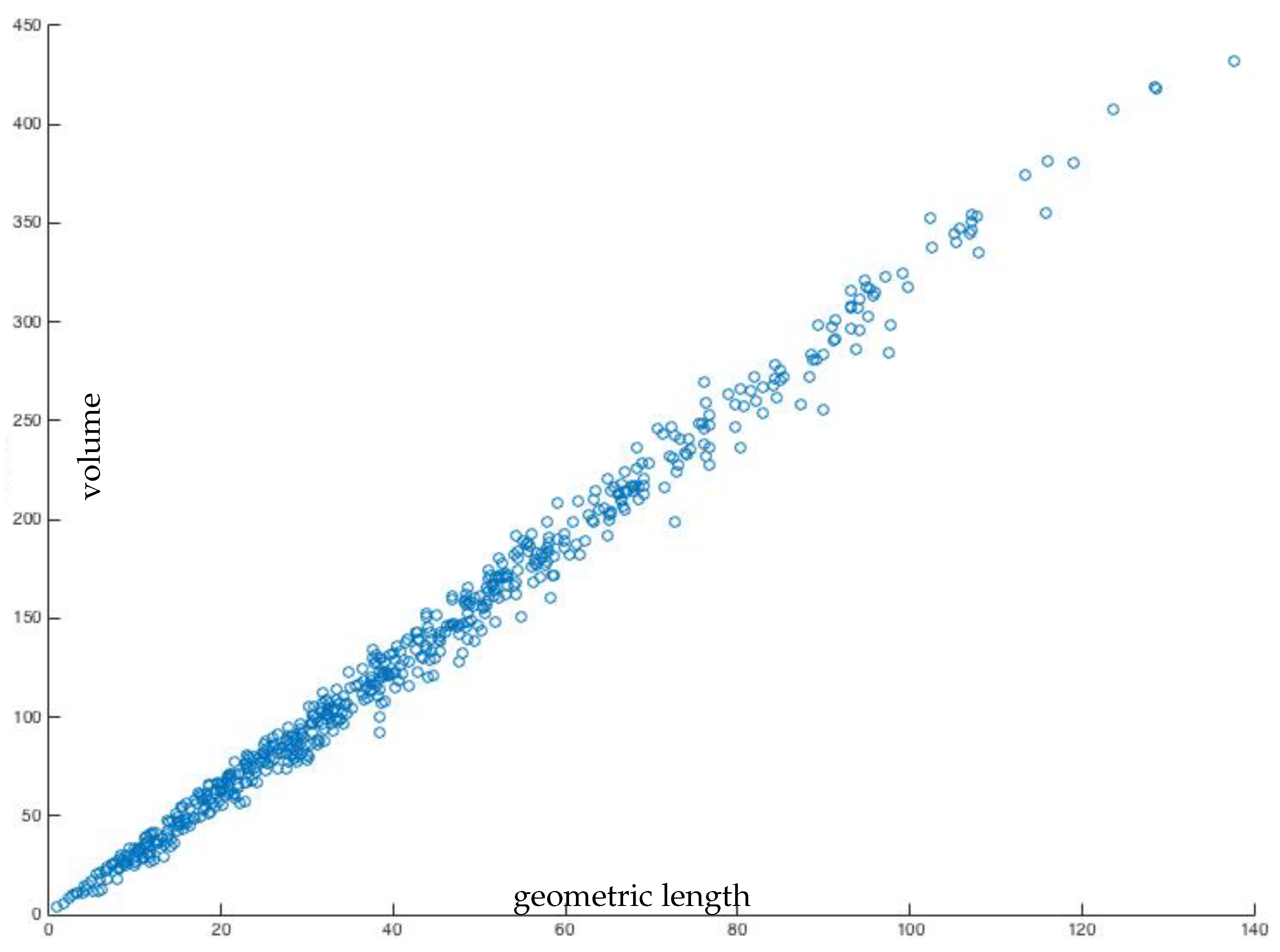
5. Results and Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Katok, S. Fuchsian Groups; Chicago Lectures in Mathematics; University of Chicago Press: Chicago, IL, USA, 1992. [Google Scholar]
- Ghys, É. Knots and dynamics. In International Congress of Mathematicians, Vol. I; European Mathematical Society: Zürich, Switzerland, 2007; pp. 247–277. [Google Scholar] [CrossRef]
- Sarnak, P. Linking numbers of modular knots. Commun. Math. Anal. 2010, 8, 136–144. [Google Scholar]
- Foulon, P.; Hasselblatt, B. Contact Anosov flows on hyperbolic 3-manifolds. Geom. Topol. 2013, 17, 1225–1252. [Google Scholar] [CrossRef]
- Bergeron, M.; Pinsky, T.; Silberman, L. An upper bound for the volumes of complements of periodic geodesics. Int. Math. Res. Not. IMRN 2014, 2019, 4707–4729. [Google Scholar] [CrossRef]
- Duke, W. Hyperbolic distribution problems and half-integral weight Maass forms. Invent. Math. 1988, 92, 73–90. [Google Scholar] [CrossRef]
- Developers, T.S. SageMath, the Sage Mathematics Software System (Version 7.4). Available online: http://www.sagemath.org (accessed on 15 August 2016).
- Culler, M.; Dunfield, N.M.; Goerner, M.; Weeks, J.R. SnapPy, a Computer Program for Studying the Geometry and Topology of 3-Manifolds, Version 2.5.1. Available online: http://snappy.computop.org (accessed on 26 April 2017).
- Dehornoy, P. Les noeuds de Lorenz. L’Enseign. Math. 2011, 57, 211–280. [Google Scholar] [CrossRef]
- Cohn, H. Advanced Number Theory; Dover Publications, Inc.: New York, NY, USA, 1980. [Google Scholar]
- Birman, J.S.; Williams, R.F. Knotted periodic orbits in dynamical systems. II. Knot holders for fibered knots. In Contemporary Mathematics—Low-Dimensional Topology (San Francisco, Calif., 1981); American Mathematical Society: Providence, RI, USA, 1983; Volume 20, pp. 1–60. [Google Scholar] [CrossRef]
- Williams, R.F. The structure of Lorenz attractors. Inst. Hautes Études Sci. Publ. Math. 1979, 50, 73–99. [Google Scholar] [CrossRef]
- Adams, C.C. Thrice-punctured spheres in hyperbolic 3-manifolds. Trans. Am. Math. Soc. 1985, 287, 645–656. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brandts, A.; Pinsky, T.; Silberman, L. Volumes of Hyperbolic Three-Manifolds Associated with Modular Links. Symmetry 2019, 11, 1206. https://doi.org/10.3390/sym11101206
Brandts A, Pinsky T, Silberman L. Volumes of Hyperbolic Three-Manifolds Associated with Modular Links. Symmetry. 2019; 11(10):1206. https://doi.org/10.3390/sym11101206
Chicago/Turabian StyleBrandts, Alex, Tali Pinsky, and Lior Silberman. 2019. "Volumes of Hyperbolic Three-Manifolds Associated with Modular Links" Symmetry 11, no. 10: 1206. https://doi.org/10.3390/sym11101206
APA StyleBrandts, A., Pinsky, T., & Silberman, L. (2019). Volumes of Hyperbolic Three-Manifolds Associated with Modular Links. Symmetry, 11(10), 1206. https://doi.org/10.3390/sym11101206




