MADM Based on Generalized Interval Neutrosophic Schweizer-Sklar Prioritized Aggregation Operators
Abstract
:1. Introduction
2. Literature Review
- (1)
- INNs are superior in depicting tentative information by identifying the interval TMD, interval IMD, and interval FMD than FSs and IFSs in dealing with MADM problems.
- (2)
- The Sh-Sk operations are too flexible and better than the former operations by a variable parameter;
- (3)
- Conveniently, several MADM problems exist in which the attributes have a priority relationship, and a number of existing AGOs can moderate these circumstances only when the attributes take the form of real numbers. So far, there are no such AGOs to handle MADM problems under IN information established on Sh-Sktn and Sh-Sktcn. In response to this limitation, we merged the ordinary generalized PA operator with Sh-Sk operations to handle MADM problems with the IN information.
- (1)
- Anticipating a generalized IN Sh-Sk prioritized weighted averaging (GIN Sh-Sk PWA) operator and generalized IN Sh-Sk prioritized weighted geometric (GIN Sh-Sk PWG) operator.
- (2)
- Examining properties and precise cases of these anticipated AGOs.
- (3)
- Put forward two novel MADM approaches based on the anticipated AGOs.
- (4)
- Confirming the efficacy and realism of the anticipated approaches.
3. Preliminaries
4. Sh-Sk Operations for INNs
5. Some Generalized Prioritized Aggregation Operators for INNs
5.1. Generalized Interval Neutrosophic Schweizer-Sklar Prioritized Aggregation (GINSh-SkPA) Operator
- (1)
- If , then the GINSh–SkPWA operator reduces into an INSS prioritized weighted average (PWA) operator:
- (2)
- If and , then the GINSh-SkPWA operator reduces to an IN prioritized weighted average operator based on algebraic operation. That is:
5.2. Some Generalized Interval Neutrosophic Schweizer-Sklar Power Geometric Aggregation Operators
- (1)
- If , then the GINSh-SkPWGA operator reduces to an INSS prioritized weighted geometric average (INPWGA) operator:
- (2)
- If and , then the GINSSPWGA operator reduces to an IN prioritized weighted geometric average operator based on algebraic operation. That is:
6. Models for Multiple-Attribute Decision Making Established on Proposed Aggregation Operators
6.1. The Model Established on GINSh-SkPWA Operator
6.2. The Model Established on GINSh–SkPWGA Operator
7. Numerical Example
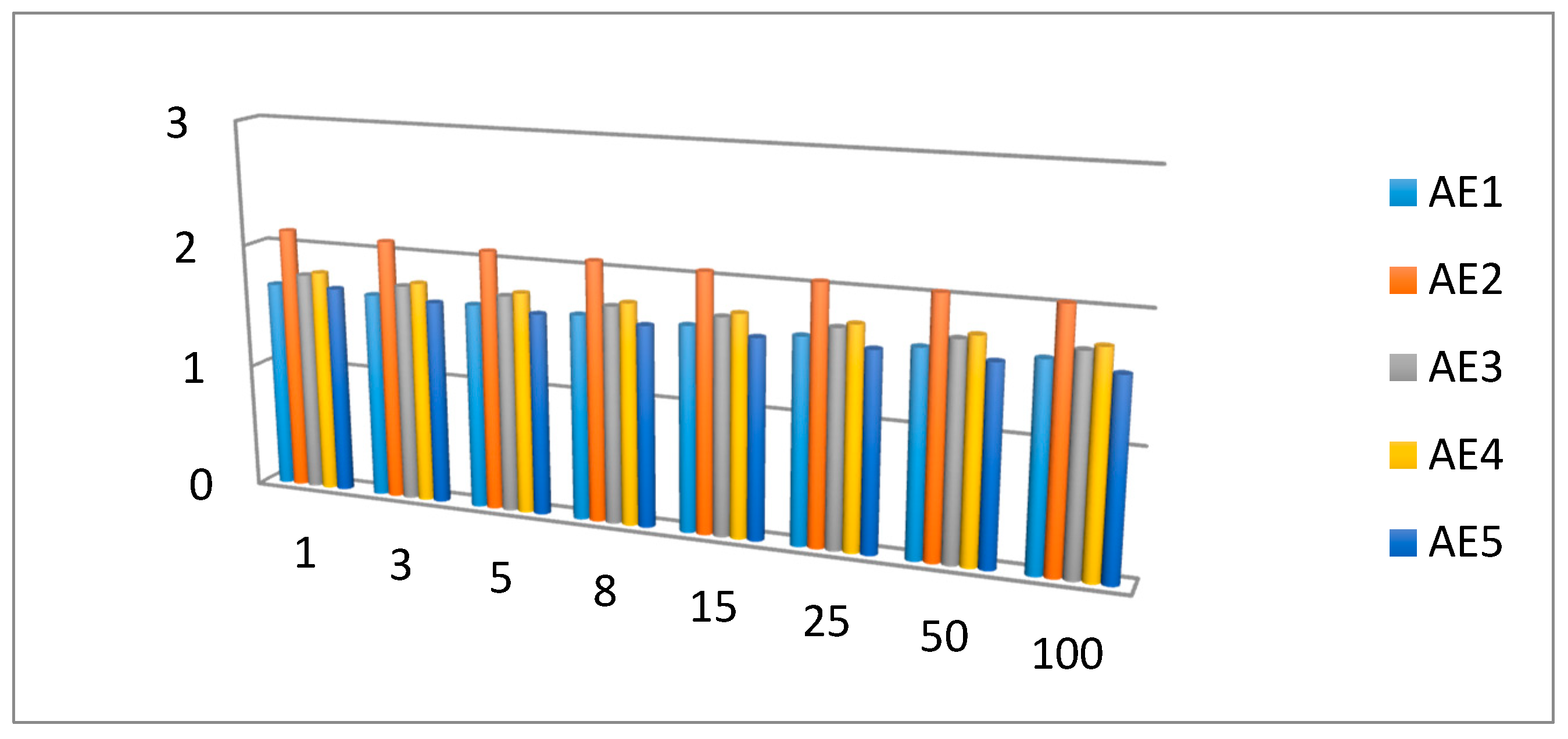
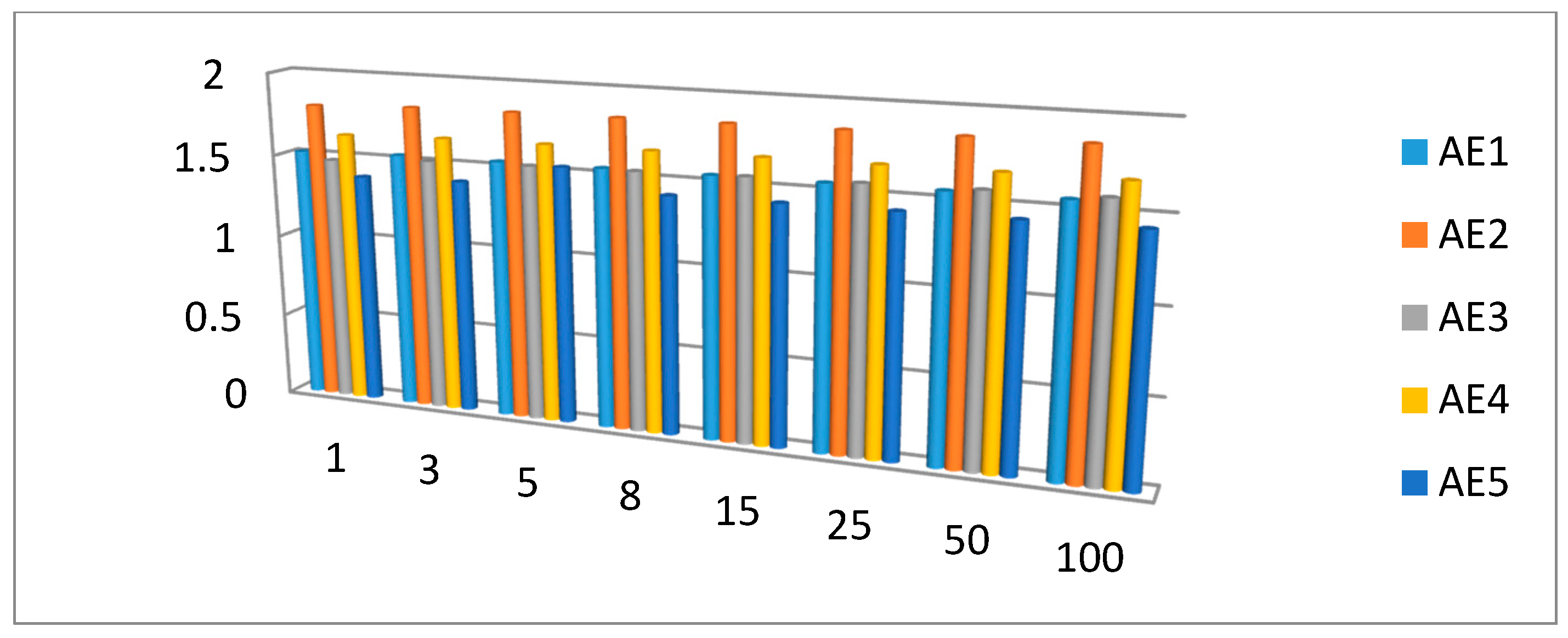
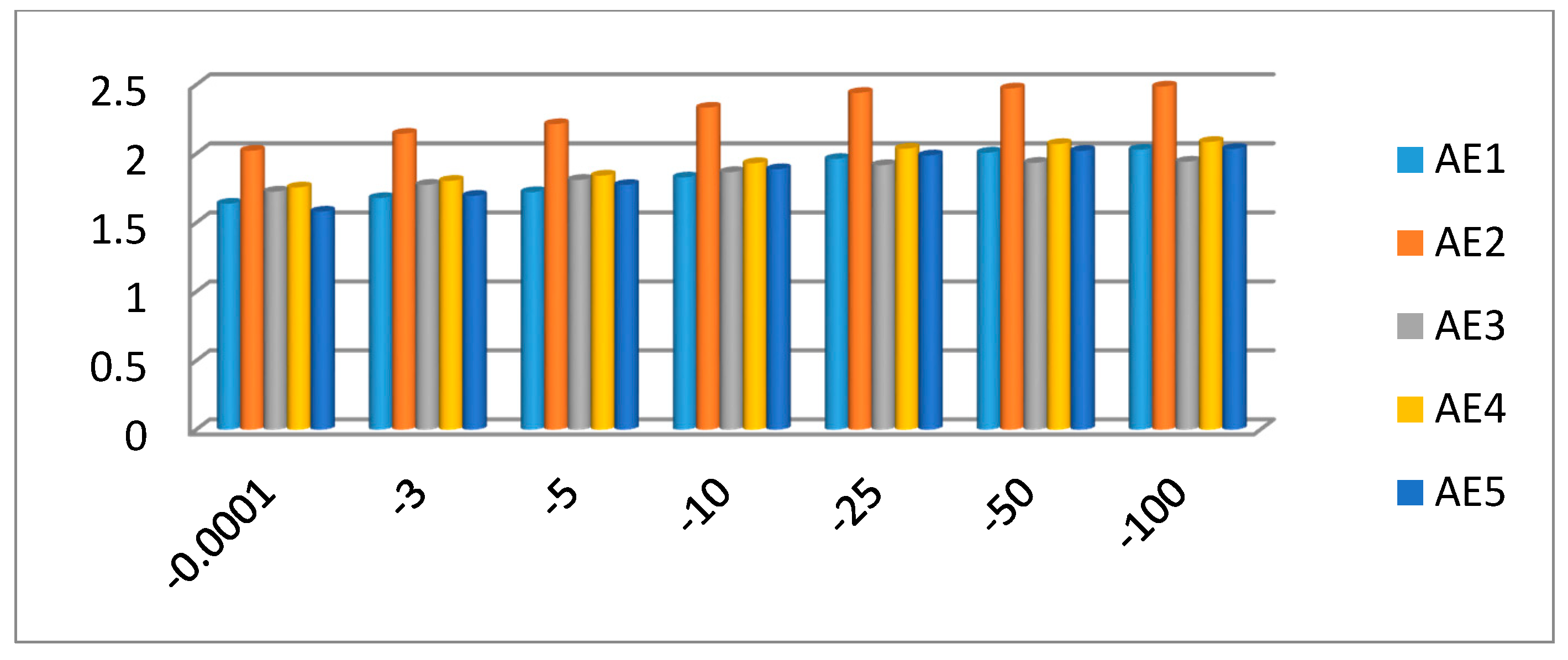
7.1. Effect of the Parameters and on Decision Result
7.2. Comparison with Existing Approaches
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Some Concepts about INS
- (1)
- Ifthenis better thanand denoted by
- (2)
- Ifandthenis better thanand denoted by
- (3)
- Ifandthenis equal toand denoted by
Appendix B
Prioritized Average (PA) Operator
Appendix C
| Author Years | Interval Neutrosophic MADM Methods Based on Different Aggregation operators | Generalized Parameter | Schweizer-Sklar Operational Laws | Consider Priority Relationship among the Attributes |
|---|---|---|---|---|
| Zhang et al. [12] (2014) | IN weighted averaging and geometric operators | No | No | No |
| Ye and Du [54] (2019) | Similarity Measures | No | No | No |
| Zhang et al. [53] (2016) | An outranking approach | No | No | No |
| Tain et al. [51] (2016) | Cross entropy | No | No | No |
| Liu and Wang [32] (2016) | Prioritized OWA operators | No | No | Yes |
| Liu and Tang [27] (2016) | Power generalized aggregation operators | Yes | No | No |
| Peng and Dia [52] (2017) | MABAC and EDAS methods | No | No | No |
| Huang et al. [49] and Hu et al. [50] (2017) | VIKOR methods | No | No | No |
| Liu and You [36] (2017) | Muirhead Mean Operators | No | No | No |
| Khan et al. [19] (2018) | Dombi Power Bonferroni Mean operators | Yes | No | No |
| Liu et al. [22] | Power Hamy mean operators | Yes | No | No |
| Wei et al. [16] (2019) | Generalized Bonferroni mean Operators | No | No | No |
| Proposed Method | Generalized Schweitzer-Sklar prioritized Operators | Yes | Yes | Yes |
References
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Xu, Z.; Yager, R.R. Some geometric aggregation operators based on intuitionistic fuzzy sets. Int. J. Gen. Syst. 2006, 35, 417–433. [Google Scholar] [CrossRef]
- Xu, Z. Intuitionistic Fuzzy Aggregation Operators. IEEE Trans. Fuzzy Syst. 2007, 15, 1179–1187. [Google Scholar]
- Liu, P.; Mahmood, T.; Khan, Q. Multi-attribute decision-making based on prioritized aggregation operator under hesitant intuitionistic fuzzy linguistic environment. Symmetry 2007, 9, 270. [Google Scholar] [CrossRef]
- Smarandache, F. A Unifying Field in Logics: Neutrosophic Logic. In Philosophy; American Research Press: Santa Fe, NM, USA, 1999; pp. 1–141. [Google Scholar]
- Wang, H.; Smarandache, F.; Zhang, Y.Q.; Sunderraman, R. Single valued neutrosophic sets. Multispace Multistructure 2010, 4, 410–413. [Google Scholar]
- Wang, H.; Smarandache, F.; Sunderraman, R.; Zhang, Y.Q. Interval Neutrosophic Sets and Logic: Theory and Applications in Computing: Theory and Applications in Computing; Hexis: Phoenix, AZ, USA, 2005. [Google Scholar]
- Ye, J. A multicriteria decision-making method using aggregation operators for simplified neutrosophic sets. J. Intell. Fuzzy Syst. 2014, 26, 2459–2466. [Google Scholar]
- Peng, J.J.; Wang, J.Q.; Wang, J.; Zhang, H.Y.; Chen, X.H. Simplified neutrosophic sets and their applications in multi-criteria group decision-making problems. Int. J. Syst. Sci. 2016, 47, 2342–2358. [Google Scholar] [CrossRef]
- Lu, Z.; Ye, J. Single-Valued Neutrosophic Hybrid Arithmetic and Geometric Aggregation Operators and Their Decision-Making Method. Information 2017, 8, 84. [Google Scholar] [CrossRef]
- Zhang, H.-Y.; Wang, J.-Q.; Chen, X.-H. Interval Neutrosophic Sets and Their Application in Multicriteria Decision Making Problems. Sci. World J. 2014. [Google Scholar] [CrossRef]
- Ye, J. Multiple attribute decision-making method based on the possibility degree ranking method and ordered weighted aggregation operators of interval neutrosophic numbers. J. Intell. Fuzzy Syst. 2015, 28, 1307–1317. [Google Scholar]
- Sun, H.-X.; Yang, H.-X.; Wu, J.-Z.; Ouyang, Y. Interval neutrosophic numbers Choquet integral operator for multi-criteria decision making. J. Intell. Fuzzy Syst. 2015, 28, 2443–2455. [Google Scholar] [CrossRef] [Green Version]
- Garg, H. Non-linear programming method for multi-criteria decision making problems under interval neutrosophic set environment. Appl. Intell. 2018, 48, 2199–2213. [Google Scholar] [CrossRef]
- Wei, G.; Wang, R.; Wang, J.; Wei, C.; Zhang, Y. Methods for Evaluating the Technological Innovation Capability for the High-Tech Enterprises With Generalized Interval Neutrosophic Number Bonferroni Mean Operators. IEEE Access 2019, 7, 86473–86492. [Google Scholar] [CrossRef]
- Tan, R.; Zhang, W.; Chen, S. Exponential Aggregation Operator of Interval Neutrosophic Numbers and Its Application in Typhoon Disaster Evaluation. Symmetry 2018, 10, 196. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.-Q.; Wang, T.-L. Fuzzy stochastic multi-criteria decision-making methods with interval neutrosophic probability based on regret theory. J. Intell. Fuzzy Syst. 2018, 35, 2309–2322. [Google Scholar] [CrossRef]
- Khan, Q.; Liu, P.; Mahmood, T.; Smarandache, F.; Ullah, K. Some Interval Neutrosophic Dombi Power Bonferroni Mean Operators and Their Application in Multi–Attribute Decision–Making. Symmetry 2018, 10, 459. [Google Scholar] [CrossRef]
- Zhou, L.-P.; Dong, J.-Y.; Wan, S.-P. Two New Approaches for Multi-Attribute Group Decision-Making with Interval-Valued Neutrosophic Frank Aggregation Operators and Incomplete Weights. IEEE Access 2019, 7, 102727–102750. [Google Scholar] [CrossRef]
- Rani, D.; Garg, H. Some modified results of the subtraction and division operations on interval neutrosophic sets. J. Exp. Theor. Artif. Intell. 2019, 31, 677–698. [Google Scholar] [CrossRef]
- Liu, P.; Khan, Q.; Mahmood, T. Application of Interval Neutrosophic Power Hamy Mean Operators in MAGDM. Informatica 2019, 30, 293–325. [Google Scholar] [CrossRef]
- Yang, H.; Wang, X.; Qin, K. New Similarity and Entropy Measures of Interval Neutrosophic Sets with Applications in Multi-Attribute Decision-Making. Symmetry 2019, 11, 370. [Google Scholar] [CrossRef]
- Meng, F.; Wang, N.; Xu, Y. Interval neutrosophic preference relations and their application in virtual enterprise partner selection. J. Ambient. Intell. Hum. Comput. 2019, 1–30. [Google Scholar] [CrossRef]
- Kakati, P.; Borkotokey, S.; Rahman, S.; Davvaz, B. Interval neutrosophic hesitant fuzzy Einstein Choquet integral operator for multicriteria decision making. Artif. Intell. Rev. 2019, 1–36. [Google Scholar] [CrossRef]
- Liu, P.; Chu, Y.; Li, Y.; Chen, Y. Some Generalized Neutrosophic Number Hamacher Aggregation Operators and Their Application to Group Decision Making. Int. J. Fuzzy Syst. 2016, 16, 242–255. [Google Scholar]
- Liu, P.; Tang, G. Some power generalized aggregation operators based on the interval neutrosophic sets and their application to decision making. J. Intell. Fuzzy Syst. 2016, 30, 2517–2528. [Google Scholar] [CrossRef]
- Yang, L.; Li, B.; Xu, H. Novel Power Aggregation Operators Based on Einstein Operations for Interval Neutrosophic Linguistic Sets. IAENG Int. J. Appl. Math 2018, 48, 475–484. [Google Scholar]
- Yager, R.R. Prioritized aggregation operators. Int. J. Approx. Reason. 2008, 48, 263–274. [Google Scholar] [CrossRef] [Green Version]
- Wei, C.; Tang, X. Generalized prioritized aggregation operators. Int. J. Intell. Syst. 2012, 27, 578–589. [Google Scholar] [CrossRef]
- Wu, X.-H.; Wang, J.-Q.; Peng, J.-J.; Chen, X.-H. Cross-Entropy and Prioritized Aggregation Operator with Simplified Neutrosophic Sets and Their Application in Multi-Criteria Decision-Making Problems. Int. J. Fuzzy Syst. 2016, 18, 1104–1116. [Google Scholar] [CrossRef] [Green Version]
- Liu, P.; Wang, Y. Interval neutrosophic prioritized OWA operator and its application to multiple attribute decision making. J. Syst. Sci. Complex. 2016, 29, 681–697. [Google Scholar] [CrossRef]
- Ji, P.; Wang, J.Q.; Zhang, H. Frank prioritized Bonferroni mean operator with single-valued neutrosophic sets and its application in selecting third-party logistics providers. Neural Comput. Appl. 2018, 30, 799–823. [Google Scholar] [CrossRef]
- Wei, G.; Wei, Y. Some single-valued neutrosophic dombi prioritized weighted aggregation operators in multiple attribute decision making. J. Intell. Fuzzy Syst. 2018, 35, 1–13. [Google Scholar] [CrossRef]
- Şahin, R. Normal neutrosophic multiple attribute decision making based on generalized prioritized aggregation operators. Neural Comput. Appl. 2018, 30, 3095–3115. [Google Scholar] [CrossRef]
- Liu, P.; You, X. Interval neutrosophic muirhead mean operators and their application in multiple attribute group decision-making. Int. J. Uncertain. Quantif. 2017, 7, 303–334. [Google Scholar] [CrossRef]
- Sarkar, B.; Mondal, S.P.; Hur, S.; Ahmadian, A.; Salahshour, S.; Guchhait, R.; Iqbal, M.W. An optimization technique for national income determination model with stability analysis of differential equation in discrete and continuous process under the uncertain environment. Rairo Oper. Res. 2018. [Google Scholar] [CrossRef]
- Liu, P. The Aggregation Operators Based on Archimedean t-Conorm and t-Norm for Single-Valued Neutrosophic Numbers and their Application to Decision Making. Int. J. Fuzzy Syst. 2016, 18, 849–863. [Google Scholar] [CrossRef]
- Deschrijver, G.; Kerre, E.E. A generalization of operators on intuitionistic fuzzy sets using triangular norms and conorms. Notes Intuit. Fuzzy Sets 2002, 8, 19–27. [Google Scholar]
- Deschrijver, G. Generalized arithmetic operators and their relationship to t-norms in interval-valued fuzzy set theory. Fuzzy Sets Syst. 2009, 160, 3080–3102. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; He, H.; Xu, Y. A fuzzy logic system based on Schweizer-Sklar t-norm. Sci. China Ser. F Inf. Sci. 2006, 49, 175–188. [Google Scholar] [CrossRef]
- Liu, P.; Wang, P. Some interval-valued intuitionistic fuzzy Schweizer–Sklar power aggregation operators and their application to supplier selection. Int. J. Syst. Sci. 2018, 49, 1188–1211. [Google Scholar] [CrossRef]
- Zhang, L. Intuitionistic fuzzy averaging Schweizer-Sklar operators based on interval-valued intuitionistic fuzzy numbers and its applications. In Proceedings of the 2018 Chinese Control and Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 2194–2197. [Google Scholar]
- Wang, P.; Liu, P. Some Maclaurin symmetric mean aggregation operators based on Schweizer-Sklar operations for intuitionistic fuzzy numbers and their application to decision making. J. Intell. Fuzzy Syst. 2019, 36, 3801–3824. [Google Scholar] [CrossRef]
- Liu, P.; Khan, Q.; Mahmood, T. Multiple-attribute decision making based on single-valued neutrosophic Schweizer-Sklar prioritized aggregation operator. Cogn. Syst. Res. 2019, 57, 175–196. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, F.; Geng, Y. Multi-Criteria Decision-Making Method Based on Single-Valued Neutrosophic Schweizer–Sklar Muirhead Mean Aggregation Operators. Symmetry 2019, 11, 152. [Google Scholar] [CrossRef]
- Nagarajan, D.; LathaMaheswari, M.; Broumi, S.; Kavikumar, J. A new perspective on traffic control management using triangular interval type-2 fuzzy sets and interval neutrosophic sets. Oper. Res. Perspect. 2019, 6, 100099. [Google Scholar] [CrossRef]
- Guan, H.; Zhao, A.; Du, J. Enterprise Green Technology Innovation Behaviour; Economic Science Press: Beijing, China, 2017. [Google Scholar]
- Huang, Y.-H.; Wei, G.-W.; Wei, C. VIKOR Method for Interval Neutrosophic Multiple Attribute Group Decision-Making. Information 2017, 8, 144. [Google Scholar] [CrossRef]
- Hu, J.; Pan, L.; Chen, X. An Interval Neutrosophic Projection-Based VIKOR Method for Selecting Doctors. Cogn. Comput. 2017, 9, 801–816. [Google Scholar] [CrossRef]
- Tian, Z.P.; Zhang, H.Y.; Wang, J.; Wang, J.Q.; Chen, X.H. Multi-criteria decision-making method based on a cross-entropy with interval neutrosophic sets. Int. J. Syst. Sci. 2016, 47, 3598–3608. [Google Scholar] [CrossRef]
- Peng, X.; Dai, J. Algorithms for interval neutrosophic multiple attribute decision-making based on mabac, similarity measure, and edas. Int. J. Uncertain. Quantif. 2017, 7, 395–421. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, J.; Chen, X. An outranking approach for multi-criteria decision-making problems with interval-valued neutrosophic sets. Neural Comput. Appl. 2016, 27, 615–627. [Google Scholar] [CrossRef]
- Ye, J.; Du, S. Some distances, similarity and entropy measures for interval-valued neutrosophic sets and their relationship. Int. J. Mach. Learn. Cybern. 2019, 10, 347–355. [Google Scholar] [CrossRef]
- Chi, P.; Liu, P. An extended TOPSIS method for the multiple attribute decision making problems based on interval neutrosophic set. Neutrosophic Sets Syst. 2013, 1, 63–70. [Google Scholar]
- Kretzschmar, H.; Spies, M.; Sprunk, C.; Burgard, W. Socially compliant mobile robot navigation via inverse reinforcement learning. Int. J. Robot. Res. 2016, 35, 1289–1307. [Google Scholar] [CrossRef]
- Omrane, H.; Masmoudi, M.S.; Masmoudi, M. Fuzzy Logic Based Control for Autonomous Mobile Robot Navigation. Comput. Intell. Neurosci. 2016. [Google Scholar] [CrossRef] [PubMed]

| Author | Interval Neutrosophic MADM Methods Based on Different Aggregation Operators |
|---|---|
| Zhang et al. [12] (2014) | IN weighted averaging and geometric operators |
| Wei et al [16] (2019) | Generalized Bonferroni mean Operators |
| Khan et al. [19] (2018) | Dombi Power Bonferroni Mean operators |
| Liu et al. [22] | Power Hamy mean operator |
| Liu and Tang [27] | Power generalized aggregation operators |
| Liu and Wang [32] | Prioritized OWA aggregation operators |
| Liu and You [36] | Muirhead mean operator |
| Huang et al. [49] and Hu et al. [50] (2017) | VIKOR methods |
| Tain et al. [51] (2016) | Cross entropy |
| Peng and Dia [52] (2017) | MABAC and EDAS methods |
| Zhang et al. [53] (2016) | An outranking approach |
| Ye and Du [54] (2019) | Similarity Measures |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, Q.; Abdullah, L.; Mahmood, T.; Naeem, M.; Rashid, S. MADM Based on Generalized Interval Neutrosophic Schweizer-Sklar Prioritized Aggregation Operators. Symmetry 2019, 11, 1187. https://doi.org/10.3390/sym11101187
Khan Q, Abdullah L, Mahmood T, Naeem M, Rashid S. MADM Based on Generalized Interval Neutrosophic Schweizer-Sklar Prioritized Aggregation Operators. Symmetry. 2019; 11(10):1187. https://doi.org/10.3390/sym11101187
Chicago/Turabian StyleKhan, Qaisar, Lazim Abdullah, Tahir Mahmood, Muhammad Naeem, and Saima Rashid. 2019. "MADM Based on Generalized Interval Neutrosophic Schweizer-Sklar Prioritized Aggregation Operators" Symmetry 11, no. 10: 1187. https://doi.org/10.3390/sym11101187
APA StyleKhan, Q., Abdullah, L., Mahmood, T., Naeem, M., & Rashid, S. (2019). MADM Based on Generalized Interval Neutrosophic Schweizer-Sklar Prioritized Aggregation Operators. Symmetry, 11(10), 1187. https://doi.org/10.3390/sym11101187






