A Novel 2D—Grid of Scroll Chaotic Attractor Generated by CNN
Abstract
1. Introduction
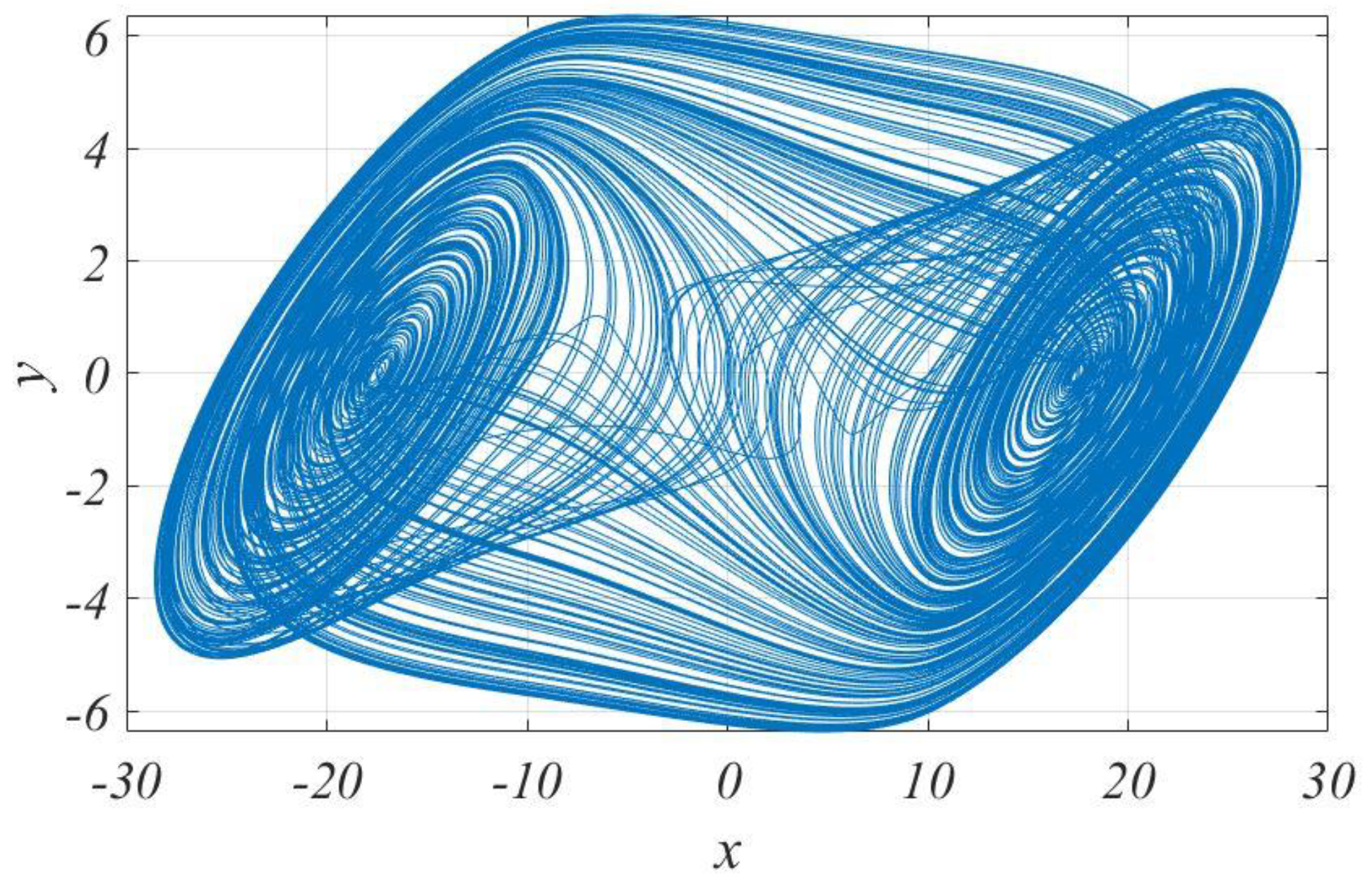
2. The Generation of 2D-Grid of Scroll from a Modified Chua Model
- (1)
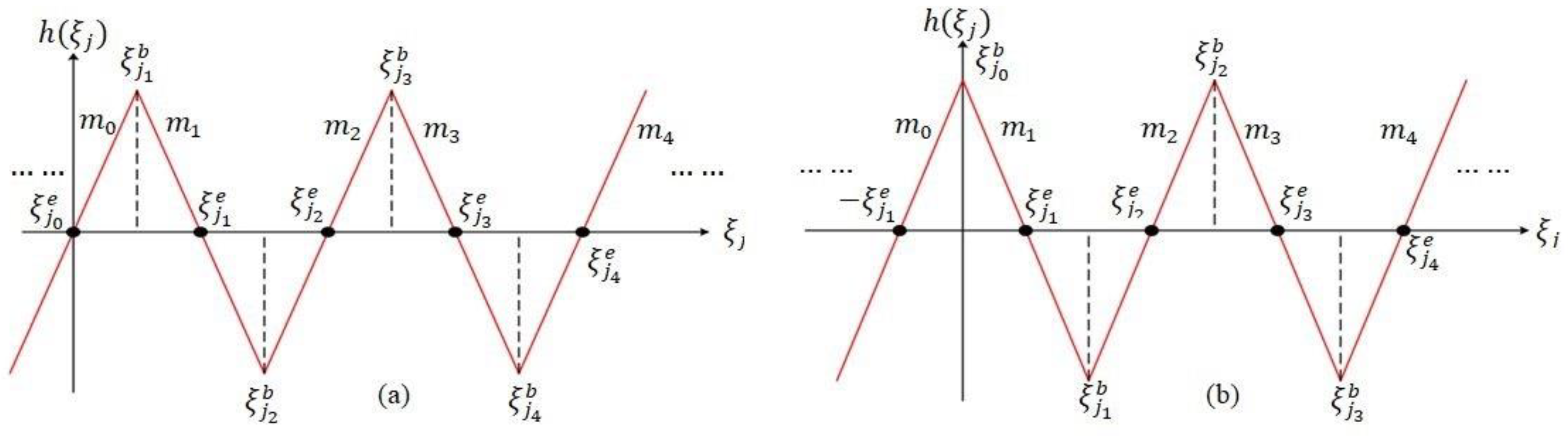
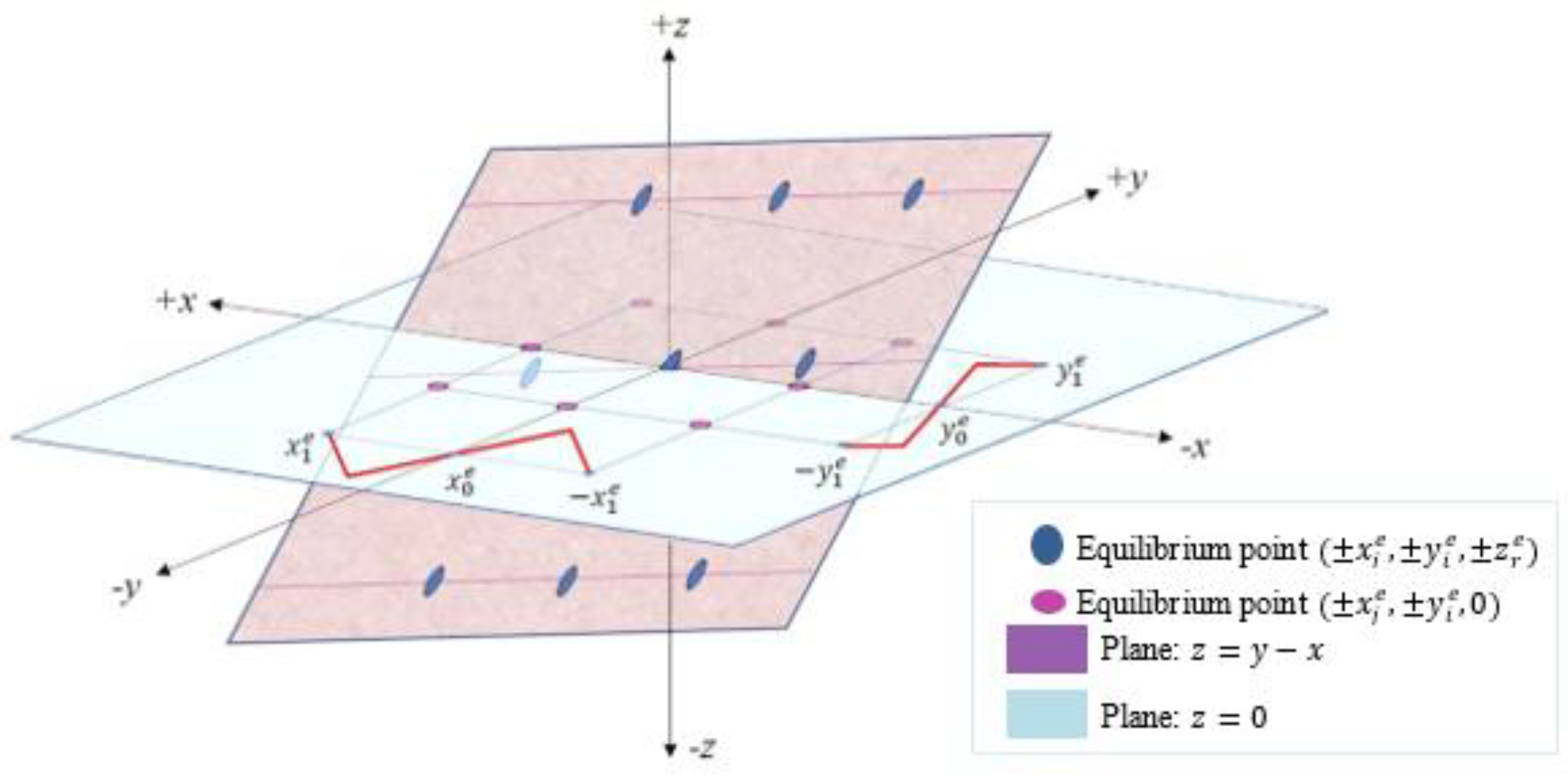
- Equilibrium points: As mentioned earlier, the distribution of saddle index-2 equilibrium points over the -plane to get a grid of scroll chaotic attractor. By setting , the equilibrium points can be discussed as follows:
- The equilibrium points are located on the -direction in the state space.One can deduce all positive equilibrium points by using the recursive formula which is given by
- For the equilibrium points which are located on the -direction in the state space. The positive equilibrium points:
- For the equilibrium points which are located on the z-direction in the state space. The positive equilibrium points:
- (2)
- Bifurcation diagram: To confirm the existence of chaos in the new system (3) with (4), assume that the case of . Then, . The bifurcation diagram of the parameter of system (3) with (4) can be obtained as illustrated in Figure 4.
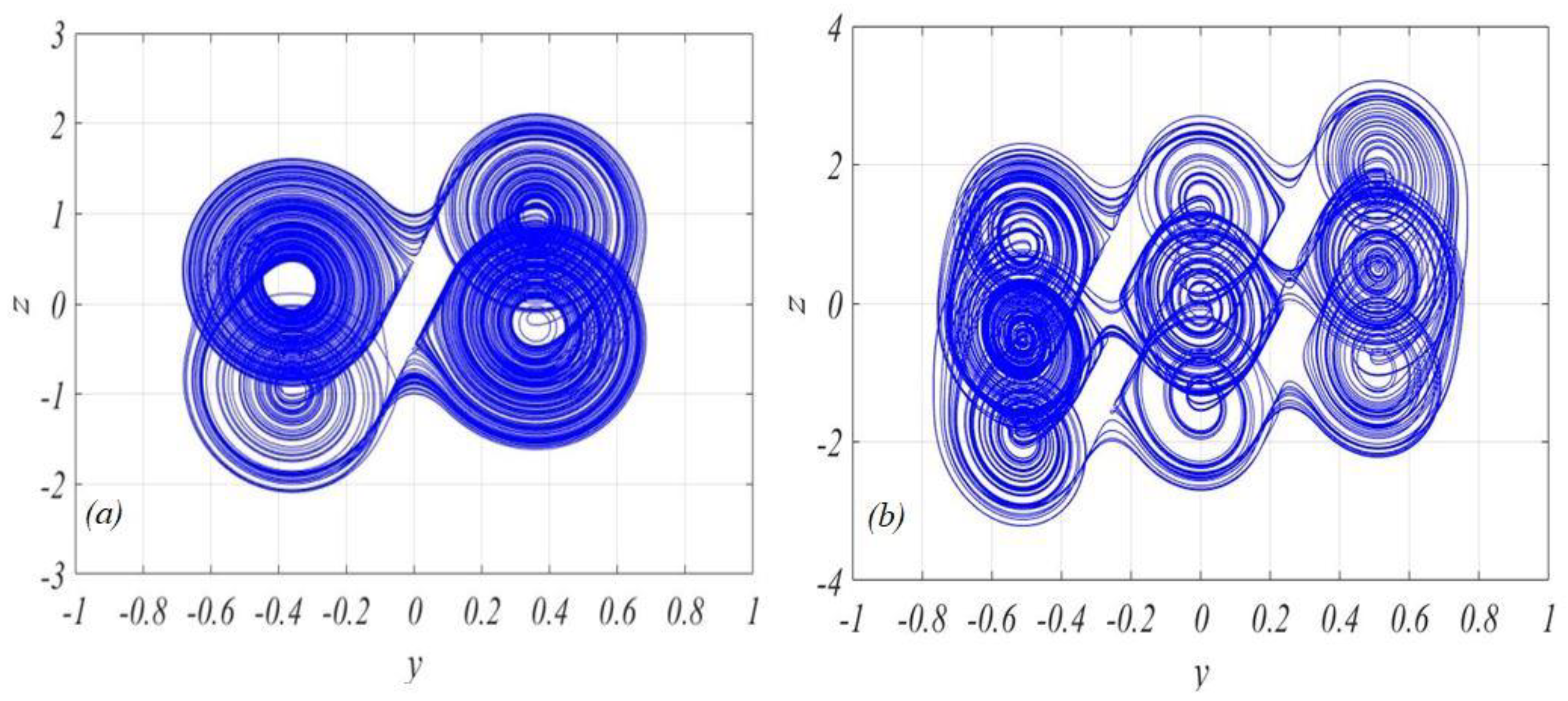
3. Design of CNN—Based New Chaotic System
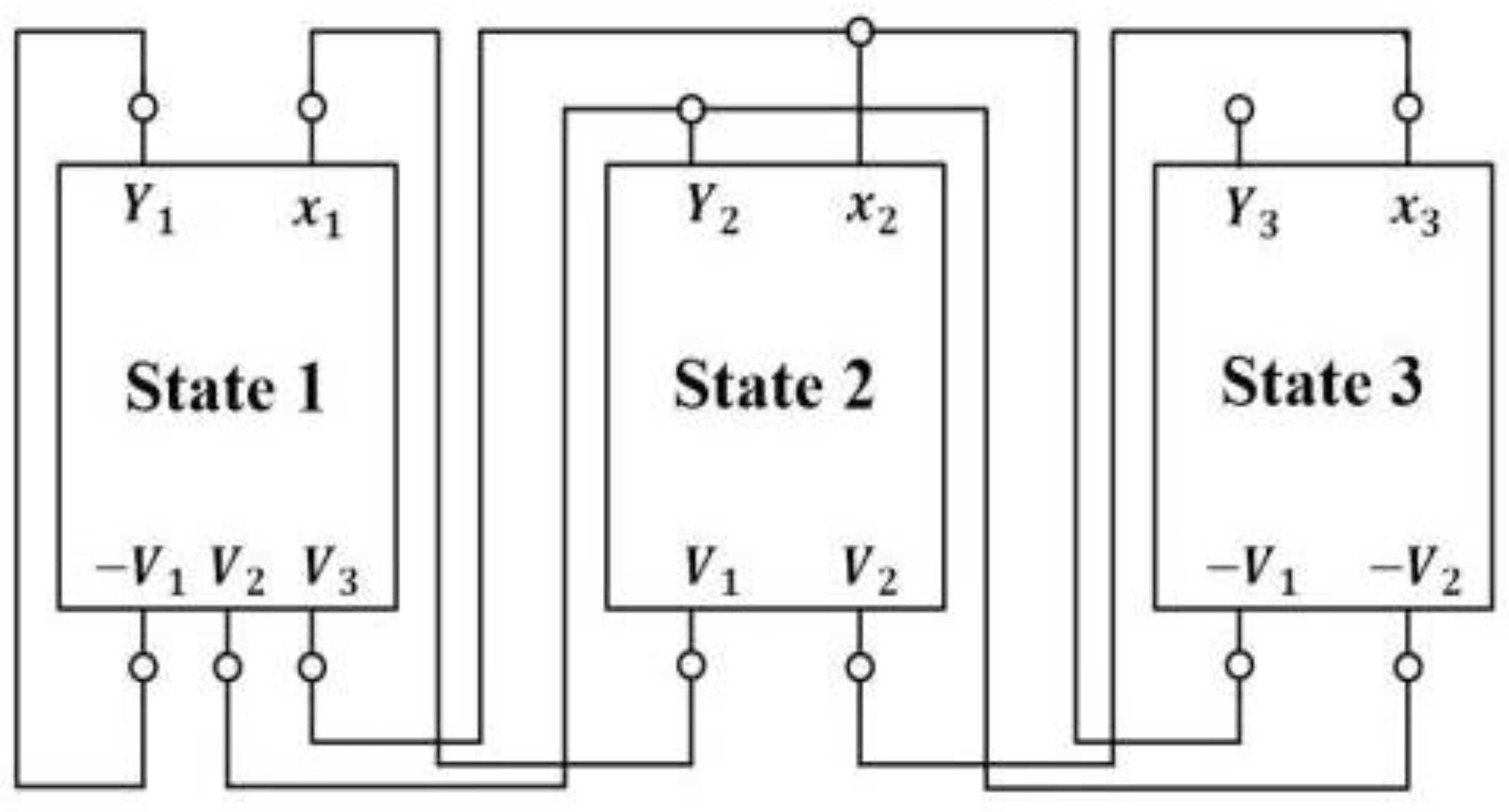
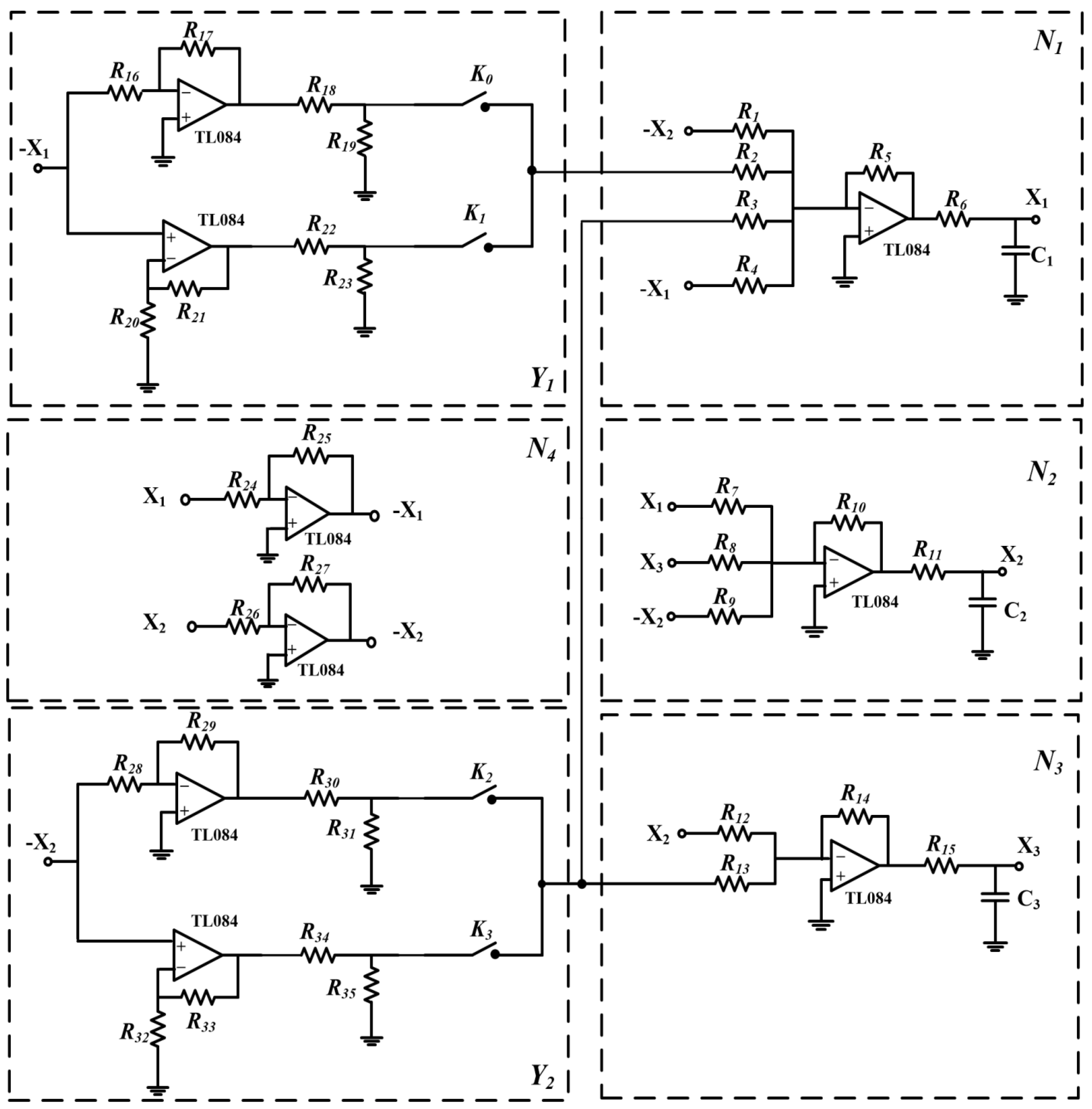
4. CNN Circuit Implementation
- N1 is the first state variable generator; , , , .
- N2 is the second state variable generator; , .
- N3 is the third state variable generator; , .
- N4 is an inverting amplifier block with unity gain.
- Both are the nonlinearities of the CNN.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chua, L.; Komuro, M.; Matsumoto, T. The double scroll family: Part I: Rigorous Proof of chaos. IEEE Trans. Circuits Syst. 1986, 33, 1072–1118. [Google Scholar] [CrossRef]
- Matsumoto, T.; Chua, L.O.; Komuro, M. Birth and death of the double scroll. Phys. D Nonlinear Phenomena 1987, 24, 97–124. [Google Scholar] [CrossRef]
- Transaction, I.; Circuits, O.N. Canonical Realization of Chua’s. IEEE Trans. Circuits Syst. 1990, 37, 885–902. [Google Scholar]
- Chua, L.O.; Wu, C.W.; Huang, A.S.; Zhon, G.Q. A Universal Circuit for Studying and Generating Chaos 2. Strange Attractors. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1993, 40, 745–761. [Google Scholar] [CrossRef]
- Zhong, G. Implementation of Chua’s Circuit with a Cubic Nonlinearity. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1994, 41, 934–941. [Google Scholar] [CrossRef]
- Wang, X.F.; Chen, G. Chaotification via arbitrarily small feedback controls: Theory, method, and applications. Int. J. Bifurcation Chaos 2000, 10, 549–570. [Google Scholar] [CrossRef]
- Chen, G. On a generalized Lorenze canonical form of chaotic systems. Int. J. Bifurc. Chaos Appl. Sci. Eng. 2002, 12, 1789–1812. [Google Scholar]
- Kong, H. A new chaotic attractor coined. Int. J. Bifurc. Chaos 2002, 12, 659–661. [Google Scholar]
- Wang, L. Yet another 3D quadratic autonomous system generating three-wing and four-wing chaotic attractors. Chaos 2014, 19, 013107. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, W. A novel bounded 4D chaotic system. Nonlinear Dyn. 2012, 67, 2455–2465. [Google Scholar] [CrossRef]
- Cicek, S.; UYAROĞLU, Y.; Pehlivan, I. Simulation and circuit implementation of sprott case H chaotic system and its synchronization application for secure communication systems. J. Circuits Syst. Comput. 2013, 22, 1350022. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Vandewalle, J. Experimental Confirmation of 3- and 5-Scroll Attractors from a Generalized Chua’s Circuit. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2000, 47, 425–429. [Google Scholar]
- Ozo, S. Families of scroll grid attractors. Int. J. Bifurc. Chaos 2002, 12, 23–41. [Google Scholar]
- Deng, W. Design of multidirectional multiscroll chaotic attractors based on fractional differential systems via switching control. Chaos 2006, 16, 043120. [Google Scholar] [CrossRef] [PubMed]
- Lü, J.; Chen, G. Generating multiscroll chaotic attractors: Theories, methods. Int. J. Bifurc. Chaos 2006, 16, 775–858. [Google Scholar] [CrossRef]
- Yu, S.; Lü, J.; Chen, G. Theoretical design and circuit implementation of multidirectional multi-torus chaotic attractors. IEEE Trans. Circuits Syst. I Regul. Pap. 2007, 54, 2087–2098. [Google Scholar] [CrossRef]
- Lü, J.; Murali, K.; Sinha, S.; Leung, H.; Aziz-Alaoui, M.A. Generating multi-scroll chaotic attractors by thresholding. Phys. Lett. Sect. A Gen. Atomic Solid State Phys. 2008, 372, 3234–3239. [Google Scholar] [CrossRef]
- Xu, F.; Yu, P. Chaos control and chaos synchronization for multi-scroll chaotic attractors generated using hyperbolic functions. J. Math. Anal. Appl. 2010, 362, 252–274. [Google Scholar] [CrossRef][Green Version]
- Liu, C.; Yi, J.; Xi, X.; An, L.; Qian, Y.; Fu, Y. Research on the Multi-Scroll Chaos Generation Based on Jerk Mode. Procedia Eng. 2012, 29, 957–961. [Google Scholar]
- Zuo, T.; Sun, K.; Ai, X.; Wang, H. High-order grid multiscroll chaotic attractors generated by the second-generation current conveyor circuit. IEEE Trans. Circuits Syst. II Express Briefs 2014, 61, 818–822. [Google Scholar] [CrossRef]
- Choo, L.C.; Ling, C. Superposition lattice coding for Gaussian broadcast channel with confidential message. In Proceedings of the 2014 IEEE Information Theory Workshop, Hobart, TAS, Australia, 2–5 November 2014; pp. 311–315. [Google Scholar]
- Yu, S.; Tang, W.K.S.; Lü, J.; Member, S.; Chen, G. Generation of n × m-Wing Lorenz-Like Attractors from a Modified Shimizu–Morioka Model. IEEE Trans. Circ. Syst. II Express Briefs 2008, 55, 1168–1172. [Google Scholar] [CrossRef]
- Wang, F.-Q.; Liu, C.X. Generation of multi-scroll chaotic attractors via the saw-tooth function. Int. J. Modern Phys. B 2008, 22, 2399–2405. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, C.H.; Yin, J.W.; Hu, Y. A Simple Grid Multiscroll Chaotic Electronic Oscillator Employing CFOAs. Int. J. Bifurc. Chaos 2014, 24. [Google Scholar] [CrossRef]
- Hu, X.; Liu, C.; Liu, L.; Yao, Y.; Zheng, G. Multi-scroll hidden attractors and multi-wing hidden attractors in a 5-dimensional memristive system. Chin. Phys. B 2017, 26. [Google Scholar] [CrossRef]
- Tahir, F.R.; Ali, R.S.; Pham, V.T.; Buscarino, A.; Frasca, M.; Fortuna, L. A novel 4D autonomous 2n-butterfly wing chaotic attractor. Nonlinear Dyn. 2016, 85, 2665–2671. [Google Scholar] [CrossRef]
- Schultz, A.; Rekeczky, C.; Szatmari, I.; Roska, T.; Chua, L.O. Spatio-temporal CNN algorithm for object segmentation and object recognition. In Proceedings of the 1998 Fifth IEEE International Workshop on Cellular Neural Networks and Their Applications, London, UK, 14–17 April 1998; pp. 347–352. [Google Scholar]
- Arena, P.; Baglio, S.; Fortuna, L.; Manganaro, G. Chua’s Circuit Can Be generalized by CNN Cells. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1995, 42, 123–125. [Google Scholar] [CrossRef]
- Rahma, F.; Fortuna, L.; Frasca, M. New Attractors and New Behaviors in the Photo-Controlled Chua’s Circuit. Int. J. Bifurc. Chaos 2009, 19, 329. [Google Scholar] [CrossRef]
- Huang, X.; Zhao, Z.; Wang, Z.; Li, Y. Chaos and hyperchaos in fractional-order cellular neural networks. Neurocomputing 2012, 94, 13–21. [Google Scholar] [CrossRef]
- Günay, E.; Altun, K. Multi-Scroll Chaotic Attractors in SC-CNN via Hyperbolic Tangent Function. Symmetry 2018, 7, 67. [Google Scholar] [CrossRef]
- Günay, E.; Altun, K. Switched State Controlled-CNN: An Alternative Approach in Generating Complex Systems with Multivariable Nonlinearities Using CNN. Int. J. Bifurc. Chaos 2018, 28, 1830019. [Google Scholar] [CrossRef]
- Arena, P.; Baglio, S.; Fortuna, L.; Manganaro, G. SC-CNN Based systems to realize a class of autonomous and coupled chaotic circuits. In Proceedings of the 1997 IEEE International Symposium on Circuits and Systems, Hong Kong, China, 9–12 June 1997. [Google Scholar]
- Chua, L.O.; Yang, L. Cellular Neural Network: Theory. IEEE Trans. Circ. Syst. 1988, 35, 1257–1272. [Google Scholar] [CrossRef]
- Chua, L.O.; Yang, L. Cellular Neural Networks: Applications. IEEE Trans. Circuits Syst. 1988, 35, 1273–1290. [Google Scholar] [CrossRef]
- Chua, L.O.; Roska, T. Cellular Neural Networks and Visual Computing: Foundations and Applications; Cambridge University Press: Cambridge, England, 2002. [Google Scholar]
- Deregel, P. Chua’s Oscillator: Azoo of attractors. J. Circuits Syst. Comput. 1993, 3, 309–359. [Google Scholar] [CrossRef]
- Kevorkian, P. Snapshots of Dynamical Evolution of Attractors from Chua’s Oscillator. IEEE Trans. Circ. Syst. 1993, 40, 762–780. [Google Scholar] [CrossRef]

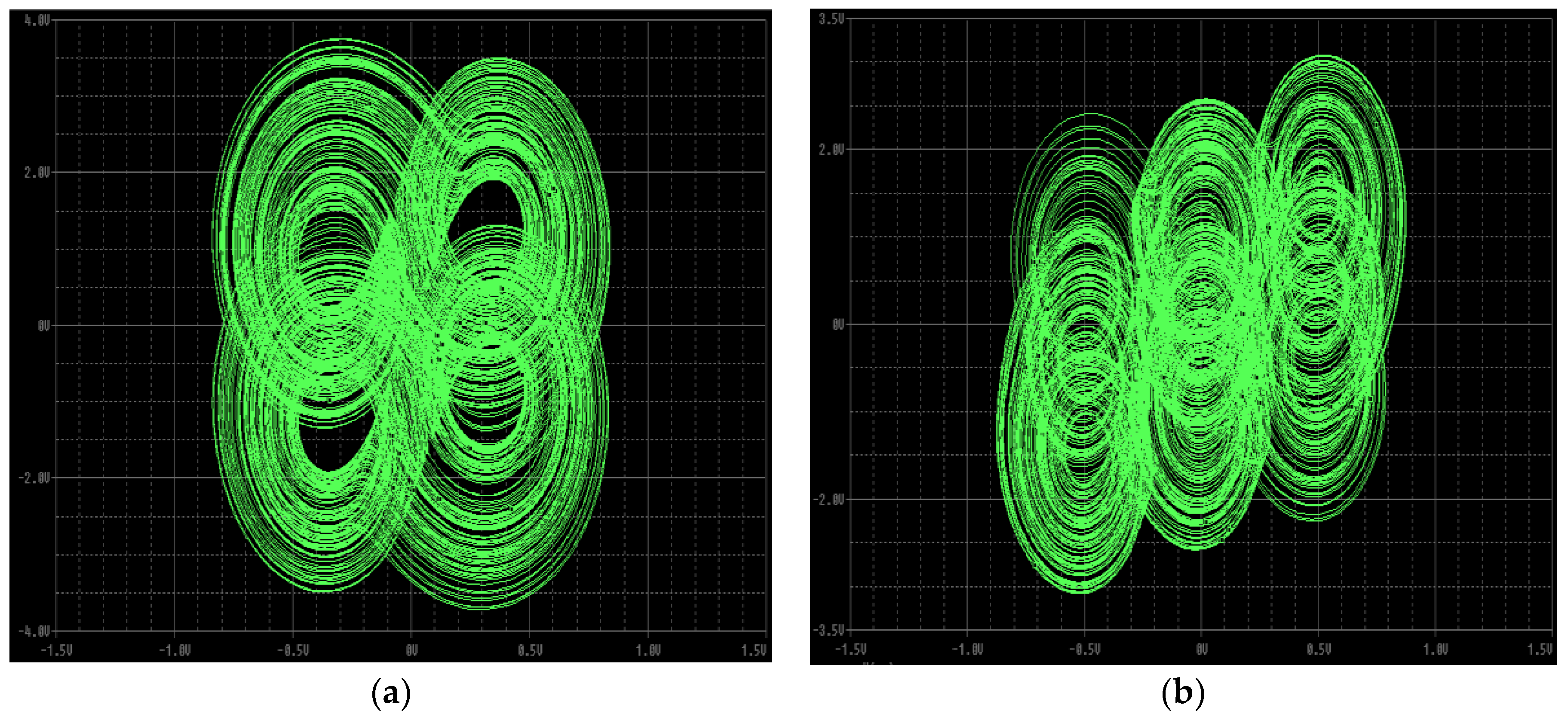
| Parameters | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Grid | ||||||||||
| 2 × 2-scroll | 15.0 | −25.2 | 36.0 | −1.5 | 7.0 | 1.0 | 1.0 | −10.0 | 1.0 | |
| 3 × 3-scroll | −7.5 | 46.2 | −66.0 | −1.625 | 15.4 | 1.0 | 1.0 | −22.0 | 1.0 | |
| Switch | |||||
|---|---|---|---|---|---|
| Grids | |||||
| 2 × 2-scroll | ON | OFF | ON | OFF | |
| 3 × 3-scroll | ON | ON | ON | ON | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, A.M.; Ramadhan, S.M.; Tahir, F.R. A Novel 2D—Grid of Scroll Chaotic Attractor Generated by CNN. Symmetry 2019, 11, 99. https://doi.org/10.3390/sym11010099
Ali AM, Ramadhan SM, Tahir FR. A Novel 2D—Grid of Scroll Chaotic Attractor Generated by CNN. Symmetry. 2019; 11(1):99. https://doi.org/10.3390/sym11010099
Chicago/Turabian StyleAli, Ahmed M., Saif M. Ramadhan, and Fadhil R. Tahir. 2019. "A Novel 2D—Grid of Scroll Chaotic Attractor Generated by CNN" Symmetry 11, no. 1: 99. https://doi.org/10.3390/sym11010099
APA StyleAli, A. M., Ramadhan, S. M., & Tahir, F. R. (2019). A Novel 2D—Grid of Scroll Chaotic Attractor Generated by CNN. Symmetry, 11(1), 99. https://doi.org/10.3390/sym11010099




