Abstract
The objective of this paper is to propose a mathematical interpretation of the continuous geometric proportion (Timaeus, 32a) with which Plato accomplishes the goal to unify, harmonically and symmetrically, the Two Opposite Elements of Timaeus Cosmos—Fire and Earth—through the Mean Ratio. As we know, from the algebraic point of view, it is possible to compose a continuous geometric proportion just starting from two different quantities a (Fire) and b (Earth); their sum would be the third term, so that we would obtain the continuous geometric proportion par excellence, which carries out the agreement of opposites most perfectly: (a + b)/a = a/b. This equal proportion, applied to linear geometry, corresponds to what Euclid called the Division into Extreme and Mean Ratio (DEMR) or The Golden Proportion. In fact, according to my mathematical interpretation, in the Timaeus 32b and in the Epinomis 991 a–b, Plato uses Pingala’s Mātrāmeru or The First Analogy of the Double to mould the body of the Cosmos as a whole, to the pint of identifying the two supreme principles of the Cosmos—the One (1) and the Indefinite Dyad (Φ and1/Φ)—with the DEMR. In effect, Fire and Earth are joined not by a single Mean Ratio but by two (namely, Air and Water). Moreover, using the Platonic approach to analyse the geometric properties of the shape of the Cosmos as a whole, I think that Timaeus constructed the 12 pentagonal faces of Dodecahedron by means of elementary Golden Triangles (a/b = Φ) and the Mātrāmeru sequence. And, this would prove that my mathematical interpretation of the platonic texts is at least plausible.
1. Introduction: The Idea of Justice and the Paradigm of the Line of the Horizon
In my recent research [Salamone, 2017: 27–30] I proposed a cosmological interpretation of the term díkē in ancient Greek, in agreement with Aristotle, which establishes the synonymy between justice and equality, through the use of the paradigm of the Divided Line. I analysed the etymological origin of the Greek word díkē which derives from the Sanskrit root word * diś-(dik) whose meaning refers to the «cosmological concept of the Line of the Horizon, that is to say, the apparent boundary line that divides the Cosmos into two equal parts: the Earth and the Sky». Furthermore, I tried to demonstrate the philosophical relationship between the idea of cosmic justice and the paradigm of the Line of the Horizon from the point of view of the founders of Greek scientific thought. In my opinion, the «original conception representing justice as a divine division of the Cosmos into two equal parts, or cosmic dasmós, turns out to be both spatial (the Sky is separated from the Earth) and temporal (Day is split from Night), and has its roots in ancient cosmogony not only of Greek origin, but also Indo-Iranian, Hindu, Old Persian, Egyptian, Babylonian and Chinese (…). The representation is as follows: the Cosmos began as an undifferentiated mass, without any internal boundaries or limits (Anaximander’s boundless universe). This mass separated into two parts, Earth and Sky, which were opposed or contrary, male and female. Finally, the male and the female were united by Eros, the contraries were combined, and gave birth to the individual existence of Gods, or of things» [1]. It is probable that Plato refers to the paradigm of the Line of the Horizon in his Republic when he speaks of the Divided Line to explain his cosmological doctrine of ideas [2]. In this way, political and moral questions intertwine with cosmological and metaphysical ones, as prescribed at the beginning of the Book of the Timaeus with reference to The Republic.
2. Plato’s Cosmology and the Division into Extreme and Mean Ratio (DEMR)
Against the innumerable coexisting universes of the Atomists, and the succession of single universes which had figured in some Ionian systems and in Empedocles, Plato contemplated the Cosmos as a single and unique living creature: «Heaven has come to be and is and shall be hereafter one and unique» [3]. According to the philosopher’s views, the creator made only one copy in order that the Cosmos should resemble its model in respect of its uniqueness. Uniqueness is perfection, and the Cosmos is marvellous for possessing it. In fact, if it were not unique, there would be body left outside it, whose strong powers might impair its life and even destroy it. That is why the Cosmos must be (1) whole and complete, consisting of parts each of which is whole and complete; (2) single or unique (not one of many coexistent worlds); (3) everlasting (not destroyed and superseded by another world), which it could hardly be if it were exposed to assaults from outside. Also, Aristotle explained that there is no body, place, or void or time outside the Cosmos [4].
Furthermore, Plato reduced the four material Elements of Empedocles to two from start—as did Parmenides, who postulated Fire and Earth—and made “the middle” a blend of these.
In fact, for Empedocles, who postulated four elements:
Fire and Earth, moreover, are extremes and purest: Water and Air, on the contrary, are intermediates and more like blends. The same course is followed by those who advocate three (we may compare what Plato does in the Divisions: for he makes “the middle” a blend). Indeed there is practically no difference between those who postulate two and those who postulate three, except that the former split the middle element into two, while the latter treat it as only one.[De Generatione et Corruptione, 330b] [5]
Plato deduces the need of two Primary Elements by the following argument. (1) There must be two (not one primary form of matter, as the Ionian monists had held) because Fire is needed to make the world’s body visible, and Earth to make it tangible. Fire and Earth had been commonly regarded as the two extreme and contrary elements (or end elements), since Fire belongs to the Sky in opposition to the Earth; (2) But, two cannot hold together without a middle element which serves as bond, because the Cosmos is a three-dimensional space. Also, the three terms must be in proportion, and the most perfect bond is that proportion which makes the most perfect unity between the middle and extreme elements. Actually, according to Euclid, in order to construct a proportion, at least three terms are necessary; (3) The most perfect type of proportion is the geometrical continued proportion [6], which Plato next proceeds to define, as follows:
Hence the god, when he began to put together the body of the Universe, set about making it on Fire and Earth. But two things alone cannot be satisfactorily united without a third; for there must be some bond between them drawing them together. And of all bonds the best is that which makes itself and the terms it connects a unity in the fullest sense; and it is the nature of a continued proportion to effect this most perfectly (τοῦτο δὲ πέφυκεν ἀναλογία κάλλιστα ἀποτελεῖν).[Timaeus, 31b]
In fact, according to Huffman: «At Timaeus 31c–32c it is clear that the term ἀναλογία means the continuous geometric ἀναλογία what we would call a continuous geometric proportion, or just a continuous proportion (Cornford, 1937: 45ff). When Plato discusses the arithmetic and harmonic means at Timaeus 36a ff, he does not use the term ἀναλογία. Similarly at EN 1131 a31, Aristotle defines ἀναλογία as “equality of ratio”, and, a few lines later, he tells us that “the mathematicians call this sort of ἀναλογία geometrical ἀναλογία” (Καλοῦσι δὲ τὴν τοιαύτην ἀναλογίαν γεωμετρικὴν οἱ μαθηματικοί, 1131 b13)» [7].
To tell the truth, here, as in many other places, Plato is compressing his statement of technical matters to such a point that only expert readers could fully appreciate its meaning. Therefore, I am trying to explain my interpretative hypothesis in accordance with the newer Tübingen paradigm, which gives greatest importance to Plato’s so-called Agrapha Dogmata (Unwritten Lectures) or Lectures On the Good [8]. The question, actually, is as follows: what kind of continuous geometric proportion can accomplish the goal to unify harmonically the two opposite Elements, Fire and Earth? As we know, from the algebraic point of view, it is possible to compose a continuous geometric proportion just starting from two different quantities A (Fire) and B (Earth); their sum would be the third term A + B (Fire + Earth), so that we would obtain the continuous geometric proportion par excellence, which carries out the agreement of opposites most perfectly:
(A + B):A = A:B
This equal proportion, applied to linear geometry, corresponds to what Euclid called the Division in Extreme and Mean Ratio (DEMR) or the Golden Proportion (Figure 1): «A straight line is said to have been divided in extreme and mean ratio, when the ratio of the whole line to the larger segment is the same as the ratio of the larger segment to the smaller segment» [9]. The Golden Proportion, also known as the Divine Proportion, is the irrational number 1.618 which is represented by the Greek Letter Phi (Φ).

Figure 1.
The Division of a straight Line into Extreme and Mean Ratio.
In agreement with many scholars like Brunes [10], Neufert [11], Michel [12], Herz-Fischler and, more recently, Gaiser [13], Krämer [14] and Olsen [15], in Timaeus 32a, Plato may allude to the Division of a line into Extreme and Mean Ratio to explain the unity and harmony of opposite Elements (Fire and Earth), obtained thanks to “the middle one”: the Golden Ratio.
This is my mathematical interpretation of Plato’s well-known fragment:
For whenever, of three numbers, the middle one [1] between any two [1.618 and 0.618] that are either solids or planes (squares) is such that as the first is to it, so is it to the last [1.618:1 = 1:0.618], and conversely as the last is to the middle, so is the middle to the first [0.618:1 = 1:1.618], then since the middle becomes first and last [1:1.618=0.618:1], and again the last and first become middle [1:0.618 = 1.618:1], in that way all will necessarily come to play the same part towards one another, and by so doing they will all make a unity.[Timaeus, 32a]
In fact, the intelligible form of the Golden Proportion is that all terms are interchangeable and, being interchangeable, all form a harmonious unity. Moreover, the numbers of this geometrical proportion «are either solids or planes», which means that they apply not only to linear geometry but also to plane geometry and solid geometry, as we shall see in a moment.
Golden Proportion: 1.618:1 = 1:0.618 = Φ
Conversely: 0.618:1 = 1:1.618 = 1/Φ
Alternately: 1:0.618 = 1.618:1 = Φ
Alternately: 1:1.618 = 0.618:1 = 1/Φ
In cosmological terms, this indicates that the Cosmos is a multiplicity deriving from a unity of opposites (Fire and Earth), according to the old cosmogony. Actually, and in accordance with the Pythagorean Philolaus of Croton—who said that «Harmony in every way arises out of opposites. For harmony is the unification of what is a mixture of many ingredients and the agreement of the disagreeing» [16], the cause of harmony is the agreement of the Elements, and the reason for this agreement is their equal proportion (isomoiria) and the fact that no one of them is more powerful than any other (isonomia). Plato’s Cosmos is characterized precisely by this superior harmony which derives from the conjunction/unification of opposite Elements through «the middle intelligible one» [17]. In my opinion, it is also impossible to solve this geometric theorem of Plato if we do not consider Aristotle’s arguments, which explain not only that the divisibility and continuity of magnitudes depend on the number of dimensions—one sort being continuous in one dimension (longitude/linear geometry), another in two (longitude and altitude/plan geometry), and another in three or all dimensions (longitude, altitude and depth/solid geometry)—but also that the triad is the divine number of the whole Cosmos. The Cosmos, in fact, is completely perfect because it is a three-dimensional space, which is divisible into all dimensions.
The Mātrāmeru Sequence and the Construction of the Body of the Timaeus Cosmos
If the Cosmos is completely perfect due to the fact that it is a three-dimensional space, it consequently follows that (as Parmenides said) beyond the Cosmos, there is no other magnitude, since the three dimensions are all there is, and what is divisible into three dimensions (longitude, altitude and depth) is divisible into all. Cosmologically, this implies that the Timaeus Cosmos is one and unique, and not one of the innumerable coexisting worlds of the Atomists. Once again, the Cosmos is perfect because of its uniqueness, that is because it is based on a unique model (the Form of living being). Moreover, this is the reason why Plato says that the shape of the Cosmos must be solid in its form, that is, Fire and Earth are joined not by a single geometric mean but by two (namely, Air and Water):
Now, if it had been required that the body of the Universe should be a plane surface with no depth, a single mean would have been enough to connect its companions and itself; but in fact the world was to be solid in form, and solids are always conjoined, not by one mean, but by two. Accordingly the god set water and air between fire and earth, and made them, so far as was possible, proportional to one another, so that as fire [A] is to air [B], so is air [B] to water [C] and as air [B] is to water [C], so is water [C] to earth [D], and thus he bound together the frame of a world visible and tangible.[Timaeus, 32b]
According to Bury, “two mean terms are required for a continuous proportion of ‘solid’ (or cubic) numbers” [18]. Mathematically, four quantities A, B, C and D are said to be divided into Golden Proportion, if the ratio of the first term and the second term is equal to the ratio of the second term and the third term, which is equal to the ratio of the third term and the fourth term (A/B = B/C = C/D = Φ). For example, in Pingala’s Mātrāmeru, which was discovered around 400–300 B.C. (?) [19], the consecutive numbers 1, 2, 3, 5, 8, 13 are in Golden Proportion because 1/1, 2/1, 3/2, 5/3, 8/5, 13/8 = approximately equal to Φ (as well 1/1, 1/2 2/3, 3/5, 5/8, 8/13 = approximately equal to 1/Φ). In fact, the ratio of any two sequential Mātrāmeru numbers approximates to the value of Φ. The larger the consecutive numbers in the sequence, the more accurate the approximation of Φ (Table 1). Let me try a few:

Table 1.
Pingala’s Mātrāmeru.
The Mātrāmeru, or the Fibonacci sequence, is itself simple to follow. In this sequence (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …, ∞), each number is the sum of the two preceding numbers (for instance, 1 + 1 = 2, 2 + 3 = 5, 3 + 5 = 8). As you go farther and farther to the right in this sequence, the ratio of a term to the one before it will get closer and closer to Φ. Furthering this observation, shapes can be created based upon length measurements of the Mātrāmeru numbers in sequence. For example, creating a rectangle with the values of any of the two successive Mātrāmeru numbers forms what is known as the “Golden Rectangle”. You can start with a square and add a square of the same size to form a new rectangle (Figure 2). Continue adding squares whose sides are the length of the longer side of the rectangle; the longer side will always be a successive Mātrāmeru number. Eventually, the large rectangle formed will look like a Golden Rectangle—the longer you continue, the closer it will be.
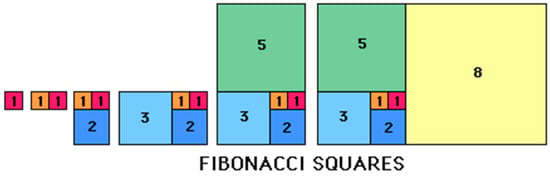
Figure 2.
Mātrāmeru Squares.
In my opinion, it is possible that, in the book Epinomis, Plato refers precisely to the Golden Proportion and to Mātrāmeru numbers, when he explains the difference between geometric, arithmetic and harmonic sequences of numbers. In fact, in The First Analogy of the Double, that is, in the Mātrāmeru sequence in which the new number is the previous two added together (ἡ μὲν δὴ πρώτη τοῦ διπλασίου κατ᾿ ἀριθμὸν ἓν πρὸς δύο κατὰ λόγον φερομένη), the first two sequential numbers are 1 and 1, and the scale proceeds up to number 8. This is my mathematical interpretation of Plato’s problematic fragment:
And therefore there will be need of studies: the most important and first is, in fact, of numbers in themselves; not of those which are corporeal, but of the whole origin of the odd and the even, and the greatness of their influence on the nature of reality. When he has learnt these things, there comes next after these what they call by the very ridiculous name of geometry, when it proves to be a manifest likening of numbers not like one another by nature by reference to the province of planes; and this will be clearly seen by him who is able to understand it to be a marvel not of human, but of divine origin. And then, after that, the numbers thrice increased and like to the solid nature, and those again which have been made unlike, he likens by another art, namely, that which its adepts called stereometry; and a divine and marvellous thing it is to those who envisage it and reflect how the whole of nature moulds off species and class, as power [the One: 1] and its opposite [the Indefinite Dyad: Φ and1/Φ] continually turn upon the double according to each analogy. Thus the first analogy is of the double [in point of number: 1, 1], passing by numerical scale in the proportion of one to two [1 + 1 = 2], and that which is according to power is double; that which passes to the solid and tangible is likewise again double having proceeded from one to eight [1,1,2,3,5,8]. But, that passing to a mean of the double, as much more than the less as it is less than the greater, [in fact, in the geometric sequence of Mātrāmeru, between 3 and 8 the geometric mean is 5, which is 2 more than 3 and 3 less than 8] while the other mean exceeds and is exceeded by the same portion of the extremes themselves—between six (6) and twelve (12) comes the whole-and-a-half [in the arithmetic sequence, between 6 and 12 the arithmetic mean is 9, which is 3 more than 6 and 3 less than 12] and whole-and-a-third [in the harmonic sequence, between 6 and 12 the harmonic mean is 8, which is 6 plus 1/3 of 6 and 12 minus 1/3 of 12]—turning between these very two, to one side or the other, this analogy assigned to men an accordant and proportioned use for the purpose of rhythm and harmony in their pastimes, and has been bestowed by the blessed dance of the Muses.[Epinomis, 990e-991b] [20]
In order to better understand the implication of Mātrāmeru consecutive numbers in Platonic cosmology, we have to consider Plato’s chaos, which is the body of the Cosmos as existing before the Cosmos was made or the Demiurge designed the geometrical figures of the Primary Bodies [21]. In fact, at this point, Plato clarifies the existence of the Receptacle of all Becoming (Timaeus, 48e-49) which is compared to a Mother (Timaeus, 50d) of what has come to be visible and otherwise sensible (Timaeus, 51b). The Receptacle is an intermediate order among the world of Being which «always is real and has no becoming» and the world of Becoming, which «becomes and passes away, but never has real being». The point is that all that becomes «must needs become by the agency of some cause: for without a cause nothing can come to be» (Timaeus, 28a-9). Plato finally identifies the Receptacle with Space «which is everlasting, not admitting destruction; providing a situation for all things that come into being, but itself apprehended without the senses by a sort of bastard reasoning, and hardly an object of belief» (Timaeus, 51–52b). In accordance with Aristotle, Space is, for Plato, the place, the medium or substratum—formless and unshapen—in which the Elements are conceived as a material for composing things, or in which all becoming takes place. Before the creation of the Cosmos, the elements are present in indefinite form; their motion is disorderly. There is no substance yet, but a flux of shifting qualities—Fire is hot, Air is cold, Water is wet and Earth is dry—appearing and vanishing in permanent Space.
3. The Two Material Elements of Timaeus Cosmos, and the Shapes of the Four Primary Bodies of the Universe
Plato rejected the old Milesian doctrine of a single fundamental form of matter (the monism), which was to serve both as the original Element of the cosmos and as the permanent ground underlying change. As we know, Thales of Miletus had held Water to be a component of all things. Xenophanes of Colophon had posited that all things came to be from Earth. Heraclitus of Ephesus had considered Fire as the most fundamental Element, and Anaximenes of Miletus had believed that Air was underlying all other things. Plato only partially accepted the belief of the Pythagorean pluralists, like Parmenides of Elea, who had postulated that the material Elements of the cosmos were two: Fire and Earth; or Empedocles of Akragas, who had suggested that everything in the world was created from the four Elements: Fire, Earth, Air and Water. However, and in contrast to them, Plato admitted the possibility of the transmutation of Elements. In fact, Parmenides’ cosmic space consisted of being, which did not change, did not become, did not move, always remained the same and was everlasting; whereas Empedocles had assumed that although the four Elements could be mixed together in various proportions, and the Elements themselves were unbreakable and could never be changed. In contrast, Plato did not hold material Elements to be really primary, permanent and with a constant nature, and worked hard to prove it. In fact, Plato’s theory allowed primary Elements to be transmuted and recombined into different types of bodies:
We must, in fact, consider in itself the nature of fire and water, air and earth, before the generation of the Heaven and their conditions before the Heaven was. For to this day no one has explained their generation, but we speak as if men knew what fire and each of the others is, positing them as original principles, elements (as it were, letters) of the universe; whereas one who has ever so little intelligence should not rank them in this analogy even so low as syllables.[Timaeus, 48 b3]
The unexplained existence of the four Elements had been taken as the starting point for cosmogony, their properties and behaviour had been assumed as if men really knew what Fire and Earth were. Plato now denies them the status of «Primary Elements» (from this moment, Timaeus will call them the «Primary Bodies of the Cosmos») and tries to consider their intelligible form. How do Primary Bodies come into being? What are they made of? What are their original forms? Plato’s answer is that Primary Bodies actually derive from the two Elementary Triangles that are now taken as the two irreducible Elements for the geometrical construction of the Four Primary Bodies/Solids of the Cosmos (Timaeus, 53c–d). That is to say, the faces of the Four Solids are decomposed into “fundamental” Triangles (we must remember Aristotle’s statement about the triad being the divine number of the whole Cosmos) which Plato considers as the real Primary Elements («as it were, letters») of the Universe (Figure 3). The two fundamental Triangles are considered in such a way as to explain how the change and the transmutation of Elements is possible. The first Element is the scalene triangle (30°/60°/90°)—«the half-equilateral»—by which the Demiurge generated the first three Primary Bodies of the Universe, the particles of Fire, Air and Water. The half-equilateral is obtained by dropping a perpendicular from any angle of the equilateral to the opposite side. The sides of the half-equilateral have lengths corresponding to the numbers 1, 2, √3. This is accordingly described below (54b) as «having the greater side (of the two containing the right angle) triple in square of the lesser». The second Element is the isosceles triangle (45°/45°/90°), whose sides correspond to the numbers 1, 1, √2—«the half-square»—by which the Demiurge generated the fourth Primary Body, the particle of Earth.
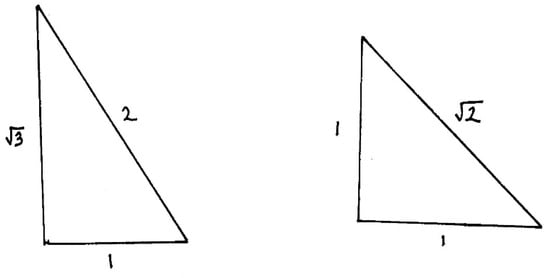
Figure 3.
The Two Material Elements of the Timaeus Cosmos.
In this sense, we have to pick up Plato’ statement:
Here one of the two elements, having generated these bodies, had done it. But the isosceles triangle went on to generate the fourth body, being together in sets of four, with their right angles meeting at the centre, thus forming a single equilateral quadrangle. Six such quadrangles, joined together, produced eight solid angles, each composed by a set of three plane right angles. The shape of the resulting body was cubical, having six quadrangular equilateral planes as its faces.[Timaeus, 55b]
Consequently, we will be able to understand Platonic physics if we know the proprieties of the two Primary Elements by which the Demiurge first constructed geometrically, and then harmoniously joined the four Primary Bodies of the Cosmos (Figure 4) through the Golden Proportion [22]. Specifically, the Primary Body of Fire is a Pyramid or a Tetrahedron (“the simplest and smallest figure”) made of 4 equilateral triangles consisting of 24 scalene right triangles altogether; the Primary Body of Air is an Octahedron made of 8 equilateral triangles consisting of 48 scalene right triangles altogether; the Primary Body of Water is an Icosahedron made of 20 equilateral triangles consisting of 120 scalene right triangles altogether; and the Primary Body of Earth is a Cube made of 6 squares consisting of 24 isosceles right triangles altogether.
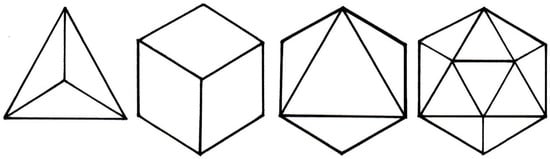
Figure 4.
The Four Primary Bodies of the Timaeus Cosmos.
The platonic belief is that Tetrahedron, Octahedron and Icosahedron are composed of elementary scalene triangles, which means that transformations and transmutations into different kinds of solids are possible only among the particles of Fire, Air and Water; while the Cube is composed of elementary isosceles triangles, which means that particles of Earth cannot be transformed by any of others (Timaeus, 54b–55c). The exclusion of Earth from the cycle of transformation was severely criticized by Aristotle.
From a modern scientific perspective, of course, Plato’s mapping from mathematical ideals to physical reality looks hopelessly wrong. Nevertheless, Plato’s cosmology anticipated the spirit of modern theoretical physics. His program of describing the material world by analysing («reducing») it to a few atomic substances (the two irreducible elements), each with simple properties, existing in great numbers of identical copies, coincides with modern understanding.
The Rational Element of the Timaeus Cosmos, and the Shape of the Universe as a Whole: The Dodecahedron
For a deeper understanding of the cosmic body generation, transformation and unification, we have finally to consider the ultimate principles of Plato’s Cosmos with reference to the Unwritten Doctrines, which are «very hard to apprehend». It means that—in accordance to Cornford’s suggestion—the supreme principles (the intelligible forms) known to mathematicians are «Lines» and «Numbers»: indeed, if Primary Bodies are made up of Planes, and Planes are made up of Triangles, Triangles themselves can be constructed with Lines and Lines can be expressed as Numbers. And, all of this is consistent with my interpretation. Essentially, for me, the myth of the Demiurge moulding all sorts of triangles and figures out of gold (Timaeus, 50a–c) explains, in clearer terms, the dualism between «the Power and its Opposite», that is between the permanent nature of the rational principle of the Cosmos (The One)—which Plato now calls «Matrix», almost certainly in reference to a specific sequence of numbers and structures («By nature it is there as a matrix for everything»)—and the shifting qualities of the four Primary Bodies of the Cosmos (The Indefinite Dyad). The result is the construction of the Dodecahedron, the fifth regular solid, which is the shape of the cosmic body as a whole:
There still remained one construction, the fifth, and the god used it for the whole, making a pattern of animal figures thereon.[Timaeus, 55c]
But what about the Dodecahedron and its decomposition into triangles? Taylor observes that «Timaeus does not describe its construction (Is it just a touch of Pythagorean ‘reserve’?») [23]. Along the same lines, Olsen states that «Plato gives us the √2 triangle for the construction of the Cube, and the √3 triangle for the construction of the Tetrahedron, Octahedron and Icosahedron. But, the triangle (or the root numbers embedded in it) necessary for the construction of the Dodecahedron is most conspicuously absent. Regarding the √2 and √3 primitive triangles, however, Plato states cryptically (and yet very revealingly for the astute student)»:
Now all triangles are derived from two, each having one right angle and the other angle acute. Of these triangles, one has on either side the half of a right angle, the division of which is determined by equal sides (the right-angled isosceles); the other has unequal parts of a right angle allotted to unequal sides (the right-angled scalene). This we assume as the first beginning of fire and the other bodies, following the account which combines likelihood with necessity; the principles yet more remote than these are known to Heaven and such men as Heaven favours. (…) Now, of the two triangles, the isosceles is of one type only; the scalene, of an endless number. Of this unlimited multitude we must choose the best, if we are to make a beginning on our own principles. Accordingly, if anyone can tell us of a better kind that he has chosen for the construction of these bodies, his will be the victory, not of an enemy, but of a friend. For ourselves, however, we postulate as the best of these many triangles one kind, passing over all the rest; that, namely, a pair of which compose the equilateral triangle. The reason is too long a story; but if anyone should put matter to the test and discover that it is not so, the prize is his with all good will.[Timaeus, 53c–54b]
However, in line with Heath, who considers that Timaeus is an exposition of Pythagorean ideas («There seems to be therefore no room for doubt that the construction of a pentagon by means of an isosceles triangle having each of its base angles double of the vertical angle was due to the Pythagoreans») [24], I think that the Timaeus Dodecahedron is composed by 12 pentagonal faces consisting of 60 Golden Triangles (5 Golden Triangles per face) having each of its base angles double of the vertical angle (36°/72/72°). That is, using the Platonic approach also to analyse the geometric properties of the shape of the cosmic body as a whole, I discover that the Primary Element of the Dodecahedron is the Golden Triangle, which could confirm the validity of my hermeneutical hypothesis (Figure 5). In fact, the Golden Triangle is an isosceles triangle «such that the ratio of the hypotenuse (a) to base (b) is equal to the Golden Ratio, a/b = Φ» [25].
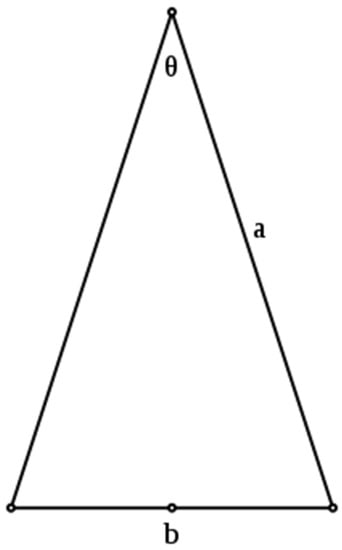
Figure 5.
The Rational Element of the Timaeus Cosmos.
For this reason, the Pentagon naturally contains the Divisions into Extreme and Mean Ratio. The Pentagon could actually be defined as a regular polygon of five sides whose diagonals are in a Golden Proportion with its sides. Furthermore, each Pentagon contains a Pentagram, also called the five-point star, pentacle or pentangle, (obtained by connecting all the vertices of the Pentagon through the diagonals), that is a star polygon in which we find a second Pentagon, and so on. The fact of being able to generate an indefinite series of Pentagons and Pentagrams inserted into one another can be used to show that the diagonal and the side of the Pentagon are incommensurable, that is, the ratio of their lengths, Φ, cannot be expressed as a ratio between integers. Also, since the ratio of a pair of consecutive Mātrāmeru numbers is approximately equal to Φ, we can obtain an approximate Pentagon and Pentagram using Mātrāmeru numbers as line lengths.
In the figure below (Figure 6), there are Mātrāmeru numbers 5, 8, 13. The ratio of these three pairs of consecutive Mātrāmeru numbers is approximately equal to Φ, so that the Pentagram symbolism can be directly related to the Golden Proportion. As we know, the Pentagram became one of the symbols of the Pythagorean School and was called “five alpha” because it represented the five Bodies of the Cosmos: Air, Water, Earth, Fire (already validated by Empedocles) and Spirit (added by Pythagoras). And, this would mathematically prove that my research hypothesis is at least plausible.
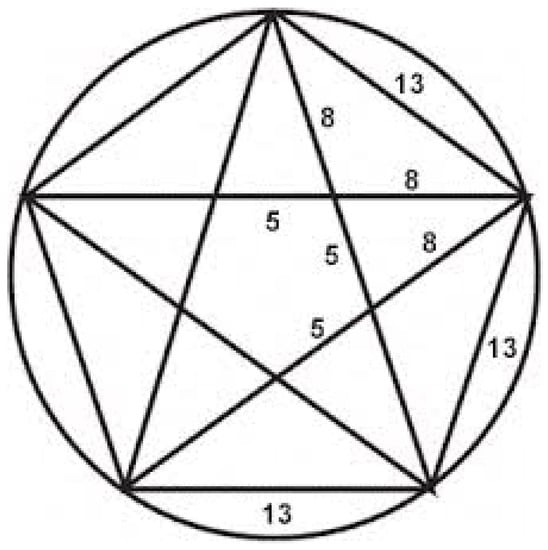
Figure 6.
The construction of the pentagonal faces of Dodecahedron by means of Mātrāmeru sequence.
But what does the Dodecahedron represent? The Dodecahedron is the fifth Body of the Cosmos, Ether (the Soul), and represents the shape of the Universe as a whole, which is realized when the four Primary Bodies of the Cosmos unite, harmoniously and symmetrically, through the matrix for everything, that is the rational and permanent principle of the Cosmos—The One or the Golden Ratio—and The First Analogy of the Double or the Pingala’s Mātrāmeru (Figure 7).
Ath. Athenian. On the most likely account there are to be reckoned five solid bodies, from which one might fashion things fairest and best; but all the rest of creation has a single shape, for there is nothing that could come to be without a body and never possessing any colour at all, except only that really most divine creature, the soul. And this alone, one may say, has the business of fashioning and manufacturing, whereas the body, as we call it, has that of being fashioned and created and seen. But the other—let us repeat it, for not once only be it said—has the properties of being unseen, of knowing and being thought, and of being endowed with memory and reckoning by alternations of odd and even.The bodies, then, being five, we must name them as fire, water, and thirdly air, earth fourth, and ether fifth; and by predominance of these are each of the many varieties of creatures perfected.[Epinomis, 981 b–d]
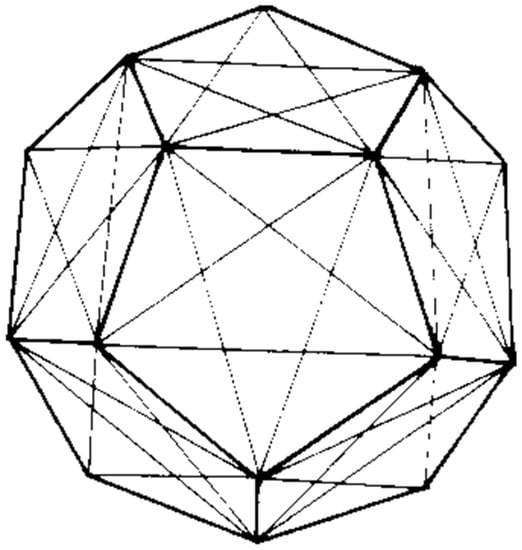
Figure 7.
The Shape of the Timaeus Cosmos as a whole.
4. Conclusions
As a result, the Two Ontological, Epistemological, and Ethical Principles of Plato’s Cosmos, the One and the Indefinite Dyad, in my view, refer to the Division of a straight Line into Extreme and Mean Ratio (Φ:1 = 1:1/Φ):
- (1)
- The Rational Principle of the Universe: The Being (Soul)The Golden Ratio (1)—The Good
- Ontological Principle: The One (1)
- Epistemological Principle: Identity
- Ethical Principle: Justice
- (2)
- The Two Material Principles of the Universe: The Becoming (Fire and Earth)The Greater and the Lesser (Φ and 1/Φ)—The Evil
- Ontological Principles: The Indefinite Dyad (1.618 and 0.618)
- Epistemological Principles: Sameness and Difference
- Ethical Principles: Excess and Deficiency
In point of fact, and in agreement with Aristotle:
In reality this doctrine that ‘the one’ and ‘excess and defect’ are the principles of all that is turns out to have been in possession of men’s minds from of old; but not always in the same way, for the earlier thinkers made the ‘one’ the receptive subject and the contrasted ‘two’ the active agents, whereas more recently (Plato) the ‘two’ have sometimes been regarded as the subject passively acted upon and the ‘one’ as the agent.[The Physics, 189 b 10–20] [26]
Funding
This research received no external funding.
Acknowledgments
I would like to thank two anonymous reviewers for their valuable and stimulating comments, and my dear friend Masi Ribaudo for having meticulously corrected the text in English, greatly improving the mathematical interpretation of the Platonic quotations contained therein. Without his critical support and his linguistic advice, this work would probably not have been completed.
Conflicts of Interest
The author declares no conflict of interest.
References
- Salamone, M.A. Equality and Justice in Early Greek Cosmologies: The Paradigm of the Line of the Horizon. Philos. Cosmol. 2017, 18, 22–31. [Google Scholar]
- Plato. The Republic; Shorey, P., Translator; Harvard University Press: London, UK, 1946; Volume 2, Books VI-X. [Google Scholar]
- Cornford, F.M. Plato’s Cosmology; Routledge & Kegan Paul: London, UK, 1937; reprinted in Hackett Publishing Co.: Indianapolis, USA, 1997, 31 b. [Google Scholar]
- Aristotle. The Works of Aristotle. De Caelo; Stocks, J.L., Joachim, H.H., Eds.; Oxford University Press: New York, NY, USA, 1922; Book 1. [Google Scholar]
- Aristotle. The Works of Aristotle. De Generatione et Corruptione; Stocks, J.L., Joachim, H.H., Eds.; Oxford University Press: New York, NY, USA, 1922; 330b. [Google Scholar]
- Herz-Fischler, R. A Mathematical History of the Golden Ratio; Dover Publications: New York, NY, USA, 1977; the expression ‘continuous proportion’ probably came from V, Def. 10. [Google Scholar]
- Huffman, C.A. Archytas of Tarentum: Pythagorean, Philosopher, and Mathematician King; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Reale, G. Per una nuova interpretazione di Platone alla luce delle «Dottrine non scritte»; Vita e Pensiero: Milano, Italy, 1990. [Google Scholar]
- Euclid. The First Six Books of the Elements of Euclid in Which Coloured Diagrams and Symbols Are Used Instead of Letters for the Greater Ease of Learners by Oliver Byrne; William Pickering: London, UK, 1847; Book VI, Theorem VI, Definition 3. [Google Scholar]
- Brunes, T. The Secrets of Ancient Geometry and Its Use; 2 vols.; Rhodos: Copenhagen, Denmark, 1967. [Google Scholar]
- Neufert, E. Bauordnungslehre; Bauverlag GMBH: Wiesbaden, Germany; Berlin, Germany, 1967. [Google Scholar]
- Michel, P. De Pythagore à Euclide; Contribution à l’Histoire des Mathématiques Préeuclidienne; Les Belles Lettres: Paris, France, 1950. [Google Scholar]
- Gaiser, K. La dottrina non scritta di Platone. Studi sulla fondazione sistematica e storica delle scienze nella scuola platonica; Vita e Pensiero: Milan, Italy, 1944. [Google Scholar]
- Krämer, H.J. Plato and the Foundations of Metaphysics. A Work on the Theory of the Principles and Unwritten Doctrines of Plato with a Collection of the Fundamental Documents; State University of New York Press: Albany, NY, USA, 1990. [Google Scholar]
- Olsen, S.A. The Indefinite Dyad and the Golden Section: Uncovering Plato’s Second Principle. Nexus Netw. J. 2002, 4, 97–110. [Google Scholar] [CrossRef]
- Huffman, C.A. Philolaus of Croton: Pythagorean and Presocratic: A Commentary on the Fragments and Testimonia with Interpretive Essays, 1st ed.; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Aristotle. On Sophistical Refutations. On Coming-to-be and Passing Away. On the Cosmos; Forster, E.S.; Furley, D.J., Translators; Loeb Classical Library 400; Harvard University Press: Cambridge, MA, USA, 1955. [Google Scholar]
- Plato. Timaeus. Critias. Cleitophon. Menexenus. Epistles; Bury, R.G., Translator; Loeb Classical Library 234; Harvard University Press: Cambridge, MA, USA, 1929; p. 59. [Google Scholar]
- Singh, P. Acharya Hemachandra and the (So Called) Fibonacci Numbers. Math. Ed. Siwan 1986, 20, 28–30. [Google Scholar]
- Plato. Charmides. Alcibiades I and II. Hipparchus. The Lovers. Theages. Minos. Epinomis; Lamb, W.R.M., Translator; Loeb Classical Library 201; Harvard University Press: Cambridge, MA, USA, 1927. [Google Scholar]
- Plato. Gorgias; Lamb, W.R.M., Translator; Harvard University Press: London, UK, 1925. [Google Scholar]
- Persaud-Sharma, D.; O’Leary, J.P. Fibonacci Series, Golden Proportions, and the Human Biology. Austin J. Surg. 2015, 2, 1066. [Google Scholar]
- Taylor, A.E. A Commentary on Plato’s Timaeus; Clarendon Press: Oxford, UK, 1967; reprinted in Garland: New York, NY, USA, 1929, p. 377. [Google Scholar]
- Euclid-Heath. The Thirteen Books of Euclid’s Elements, 2nd ed.; Heath, T., Ed.; Cambridge Univ. Press: Cambridge, UK; New York, NY, USA; Dover, UK, 1956; Volume II, p. 99. [Google Scholar]
- Weisstein, E.W. “Golden Triangle.” From MathWorld—A Wolfram Web Resource. Available online: http://mathworld.wolfram.com/GoldenTriangle.html (accessed on 15 June 2018).
- Aristotle. The Physics; Wicksteed, P.H.; Cornford, F.M., Translators; in Two Volumes; W. Heinemann: London, UK, 1957; Volume I, VI. [Google Scholar]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).