The Two Supreme Principles of Plato’s Cosmos—the One and the Indefinite Dyad—the Division of a Straight Line into Extreme and Mean Ratio, and Pingala’s Mātrāmeru
Abstract
:1. Introduction: The Idea of Justice and the Paradigm of the Line of the Horizon
2. Plato’s Cosmology and the Division into Extreme and Mean Ratio (DEMR)
Fire and Earth, moreover, are extremes and purest: Water and Air, on the contrary, are intermediates and more like blends. The same course is followed by those who advocate three (we may compare what Plato does in the Divisions: for he makes “the middle” a blend). Indeed there is practically no difference between those who postulate two and those who postulate three, except that the former split the middle element into two, while the latter treat it as only one.[De Generatione et Corruptione, 330b] [5]
Hence the god, when he began to put together the body of the Universe, set about making it on Fire and Earth. But two things alone cannot be satisfactorily united without a third; for there must be some bond between them drawing them together. And of all bonds the best is that which makes itself and the terms it connects a unity in the fullest sense; and it is the nature of a continued proportion to effect this most perfectly (τοῦτο δὲ πέφυκεν ἀναλογία κάλλιστα ἀποτελεῖν).[Timaeus, 31b]
For whenever, of three numbers, the middle one [1] between any two [1.618 and 0.618] that are either solids or planes (squares) is such that as the first is to it, so is it to the last [1.618:1 = 1:0.618], and conversely as the last is to the middle, so is the middle to the first [0.618:1 = 1:1.618], then since the middle becomes first and last [1:1.618=0.618:1], and again the last and first become middle [1:0.618 = 1.618:1], in that way all will necessarily come to play the same part towards one another, and by so doing they will all make a unity.[Timaeus, 32a]
The Mātrāmeru Sequence and the Construction of the Body of the Timaeus Cosmos
Now, if it had been required that the body of the Universe should be a plane surface with no depth, a single mean would have been enough to connect its companions and itself; but in fact the world was to be solid in form, and solids are always conjoined, not by one mean, but by two. Accordingly the god set water and air between fire and earth, and made them, so far as was possible, proportional to one another, so that as fire [A] is to air [B], so is air [B] to water [C] and as air [B] is to water [C], so is water [C] to earth [D], and thus he bound together the frame of a world visible and tangible.[Timaeus, 32b]
And therefore there will be need of studies: the most important and first is, in fact, of numbers in themselves; not of those which are corporeal, but of the whole origin of the odd and the even, and the greatness of their influence on the nature of reality. When he has learnt these things, there comes next after these what they call by the very ridiculous name of geometry, when it proves to be a manifest likening of numbers not like one another by nature by reference to the province of planes; and this will be clearly seen by him who is able to understand it to be a marvel not of human, but of divine origin. And then, after that, the numbers thrice increased and like to the solid nature, and those again which have been made unlike, he likens by another art, namely, that which its adepts called stereometry; and a divine and marvellous thing it is to those who envisage it and reflect how the whole of nature moulds off species and class, as power [the One: 1] and its opposite [the Indefinite Dyad: Φ and1/Φ] continually turn upon the double according to each analogy. Thus the first analogy is of the double [in point of number: 1, 1], passing by numerical scale in the proportion of one to two [1 + 1 = 2], and that which is according to power is double; that which passes to the solid and tangible is likewise again double having proceeded from one to eight [1,1,2,3,5,8]. But, that passing to a mean of the double, as much more than the less as it is less than the greater, [in fact, in the geometric sequence of Mātrāmeru, between 3 and 8 the geometric mean is 5, which is 2 more than 3 and 3 less than 8] while the other mean exceeds and is exceeded by the same portion of the extremes themselves—between six (6) and twelve (12) comes the whole-and-a-half [in the arithmetic sequence, between 6 and 12 the arithmetic mean is 9, which is 3 more than 6 and 3 less than 12] and whole-and-a-third [in the harmonic sequence, between 6 and 12 the harmonic mean is 8, which is 6 plus 1/3 of 6 and 12 minus 1/3 of 12]—turning between these very two, to one side or the other, this analogy assigned to men an accordant and proportioned use for the purpose of rhythm and harmony in their pastimes, and has been bestowed by the blessed dance of the Muses.[Epinomis, 990e-991b] [20]
3. The Two Material Elements of Timaeus Cosmos, and the Shapes of the Four Primary Bodies of the Universe
We must, in fact, consider in itself the nature of fire and water, air and earth, before the generation of the Heaven and their conditions before the Heaven was. For to this day no one has explained their generation, but we speak as if men knew what fire and each of the others is, positing them as original principles, elements (as it were, letters) of the universe; whereas one who has ever so little intelligence should not rank them in this analogy even so low as syllables.[Timaeus, 48 b3]
Here one of the two elements, having generated these bodies, had done it. But the isosceles triangle went on to generate the fourth body, being together in sets of four, with their right angles meeting at the centre, thus forming a single equilateral quadrangle. Six such quadrangles, joined together, produced eight solid angles, each composed by a set of three plane right angles. The shape of the resulting body was cubical, having six quadrangular equilateral planes as its faces.[Timaeus, 55b]
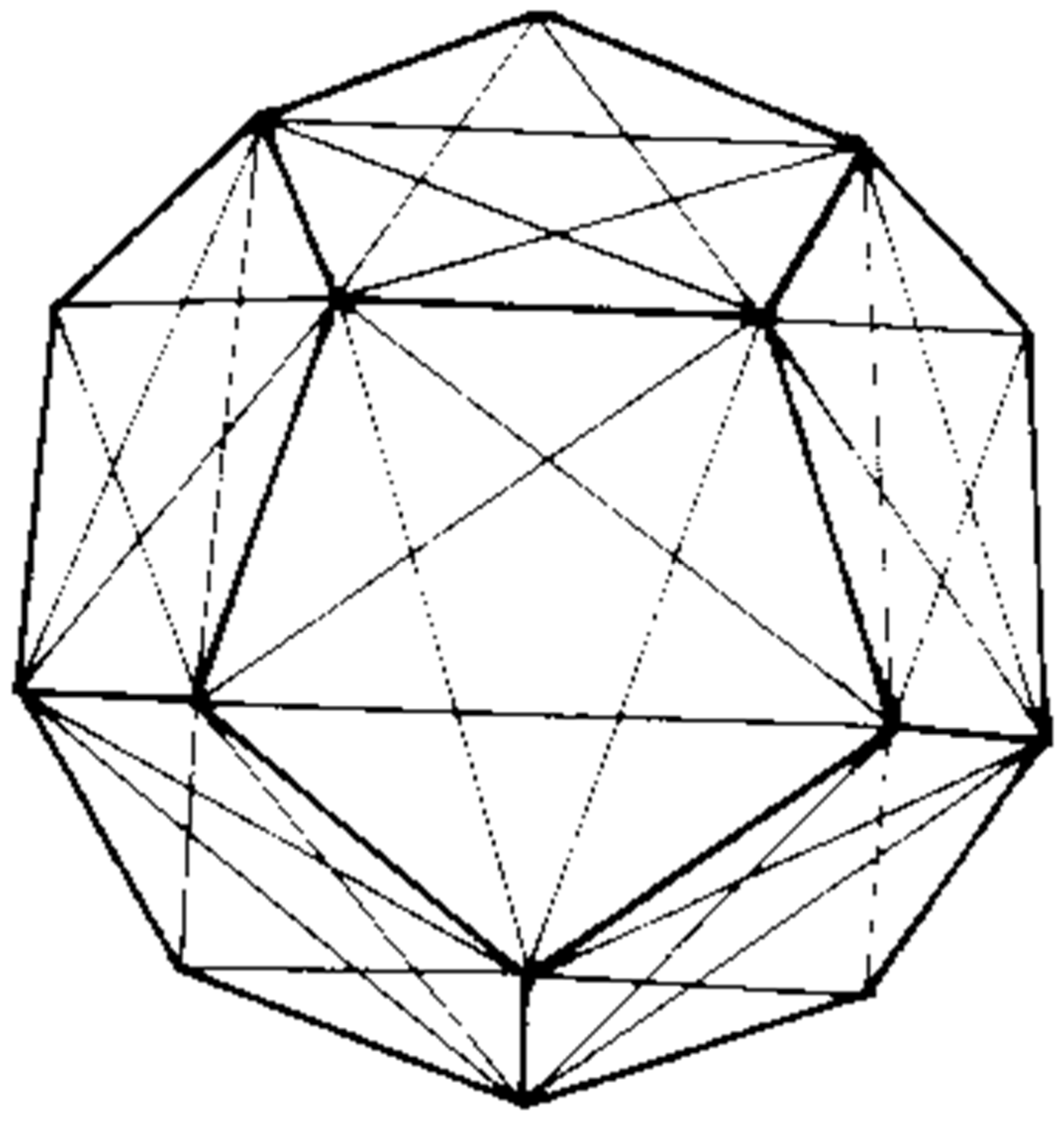
The Rational Element of the Timaeus Cosmos, and the Shape of the Universe as a Whole: The Dodecahedron
There still remained one construction, the fifth, and the god used it for the whole, making a pattern of animal figures thereon.[Timaeus, 55c]
Now all triangles are derived from two, each having one right angle and the other angle acute. Of these triangles, one has on either side the half of a right angle, the division of which is determined by equal sides (the right-angled isosceles); the other has unequal parts of a right angle allotted to unequal sides (the right-angled scalene). This we assume as the first beginning of fire and the other bodies, following the account which combines likelihood with necessity; the principles yet more remote than these are known to Heaven and such men as Heaven favours. (…) Now, of the two triangles, the isosceles is of one type only; the scalene, of an endless number. Of this unlimited multitude we must choose the best, if we are to make a beginning on our own principles. Accordingly, if anyone can tell us of a better kind that he has chosen for the construction of these bodies, his will be the victory, not of an enemy, but of a friend. For ourselves, however, we postulate as the best of these many triangles one kind, passing over all the rest; that, namely, a pair of which compose the equilateral triangle. The reason is too long a story; but if anyone should put matter to the test and discover that it is not so, the prize is his with all good will.[Timaeus, 53c–54b]
Ath. Athenian. On the most likely account there are to be reckoned five solid bodies, from which one might fashion things fairest and best; but all the rest of creation has a single shape, for there is nothing that could come to be without a body and never possessing any colour at all, except only that really most divine creature, the soul. And this alone, one may say, has the business of fashioning and manufacturing, whereas the body, as we call it, has that of being fashioned and created and seen. But the other—let us repeat it, for not once only be it said—has the properties of being unseen, of knowing and being thought, and of being endowed with memory and reckoning by alternations of odd and even.The bodies, then, being five, we must name them as fire, water, and thirdly air, earth fourth, and ether fifth; and by predominance of these are each of the many varieties of creatures perfected.[Epinomis, 981 b–d]
4. Conclusions
- (1)
- The Rational Principle of the Universe: The Being (Soul)The Golden Ratio (1)—The Good
- Ontological Principle: The One (1)
- Epistemological Principle: Identity
- Ethical Principle: Justice
- (2)
- The Two Material Principles of the Universe: The Becoming (Fire and Earth)The Greater and the Lesser (Φ and 1/Φ)—The Evil
- Ontological Principles: The Indefinite Dyad (1.618 and 0.618)
- Epistemological Principles: Sameness and Difference
- Ethical Principles: Excess and Deficiency
In reality this doctrine that ‘the one’ and ‘excess and defect’ are the principles of all that is turns out to have been in possession of men’s minds from of old; but not always in the same way, for the earlier thinkers made the ‘one’ the receptive subject and the contrasted ‘two’ the active agents, whereas more recently (Plato) the ‘two’ have sometimes been regarded as the subject passively acted upon and the ‘one’ as the agent.[The Physics, 189 b 10–20] [26]
Funding
Acknowledgments
Conflicts of Interest
References
- Salamone, M.A. Equality and Justice in Early Greek Cosmologies: The Paradigm of the Line of the Horizon. Philos. Cosmol. 2017, 18, 22–31. [Google Scholar]
- Plato. The Republic; Shorey, P., Translator; Harvard University Press: London, UK, 1946; Volume 2, Books VI-X. [Google Scholar]
- Cornford, F.M. Plato’s Cosmology; Routledge & Kegan Paul: London, UK, 1937; reprinted in Hackett Publishing Co.: Indianapolis, USA, 1997, 31 b. [Google Scholar]
- Aristotle. The Works of Aristotle. De Caelo; Stocks, J.L., Joachim, H.H., Eds.; Oxford University Press: New York, NY, USA, 1922; Book 1. [Google Scholar]
- Aristotle. The Works of Aristotle. De Generatione et Corruptione; Stocks, J.L., Joachim, H.H., Eds.; Oxford University Press: New York, NY, USA, 1922; 330b. [Google Scholar]
- Herz-Fischler, R. A Mathematical History of the Golden Ratio; Dover Publications: New York, NY, USA, 1977; the expression ‘continuous proportion’ probably came from V, Def. 10. [Google Scholar]
- Huffman, C.A. Archytas of Tarentum: Pythagorean, Philosopher, and Mathematician King; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Reale, G. Per una nuova interpretazione di Platone alla luce delle «Dottrine non scritte»; Vita e Pensiero: Milano, Italy, 1990. [Google Scholar]
- Euclid. The First Six Books of the Elements of Euclid in Which Coloured Diagrams and Symbols Are Used Instead of Letters for the Greater Ease of Learners by Oliver Byrne; William Pickering: London, UK, 1847; Book VI, Theorem VI, Definition 3. [Google Scholar]
- Brunes, T. The Secrets of Ancient Geometry and Its Use; 2 vols.; Rhodos: Copenhagen, Denmark, 1967. [Google Scholar]
- Neufert, E. Bauordnungslehre; Bauverlag GMBH: Wiesbaden, Germany; Berlin, Germany, 1967. [Google Scholar]
- Michel, P. De Pythagore à Euclide; Contribution à l’Histoire des Mathématiques Préeuclidienne; Les Belles Lettres: Paris, France, 1950. [Google Scholar]
- Gaiser, K. La dottrina non scritta di Platone. Studi sulla fondazione sistematica e storica delle scienze nella scuola platonica; Vita e Pensiero: Milan, Italy, 1944. [Google Scholar]
- Krämer, H.J. Plato and the Foundations of Metaphysics. A Work on the Theory of the Principles and Unwritten Doctrines of Plato with a Collection of the Fundamental Documents; State University of New York Press: Albany, NY, USA, 1990. [Google Scholar]
- Olsen, S.A. The Indefinite Dyad and the Golden Section: Uncovering Plato’s Second Principle. Nexus Netw. J. 2002, 4, 97–110. [Google Scholar] [CrossRef]
- Huffman, C.A. Philolaus of Croton: Pythagorean and Presocratic: A Commentary on the Fragments and Testimonia with Interpretive Essays, 1st ed.; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Aristotle. On Sophistical Refutations. On Coming-to-be and Passing Away. On the Cosmos; Forster, E.S.; Furley, D.J., Translators; Loeb Classical Library 400; Harvard University Press: Cambridge, MA, USA, 1955. [Google Scholar]
- Plato. Timaeus. Critias. Cleitophon. Menexenus. Epistles; Bury, R.G., Translator; Loeb Classical Library 234; Harvard University Press: Cambridge, MA, USA, 1929; p. 59. [Google Scholar]
- Singh, P. Acharya Hemachandra and the (So Called) Fibonacci Numbers. Math. Ed. Siwan 1986, 20, 28–30. [Google Scholar]
- Plato. Charmides. Alcibiades I and II. Hipparchus. The Lovers. Theages. Minos. Epinomis; Lamb, W.R.M., Translator; Loeb Classical Library 201; Harvard University Press: Cambridge, MA, USA, 1927. [Google Scholar]
- Plato. Gorgias; Lamb, W.R.M., Translator; Harvard University Press: London, UK, 1925. [Google Scholar]
- Persaud-Sharma, D.; O’Leary, J.P. Fibonacci Series, Golden Proportions, and the Human Biology. Austin J. Surg. 2015, 2, 1066. [Google Scholar]
- Taylor, A.E. A Commentary on Plato’s Timaeus; Clarendon Press: Oxford, UK, 1967; reprinted in Garland: New York, NY, USA, 1929, p. 377. [Google Scholar]
- Euclid-Heath. The Thirteen Books of Euclid’s Elements, 2nd ed.; Heath, T., Ed.; Cambridge Univ. Press: Cambridge, UK; New York, NY, USA; Dover, UK, 1956; Volume II, p. 99. [Google Scholar]
- Weisstein, E.W. “Golden Triangle.” From MathWorld—A Wolfram Web Resource. Available online: http://mathworld.wolfram.com/GoldenTriangle.html (accessed on 15 June 2018).
- Aristotle. The Physics; Wicksteed, P.H.; Cornford, F.M., Translators; in Two Volumes; W. Heinemann: London, UK, 1957; Volume I, VI. [Google Scholar]


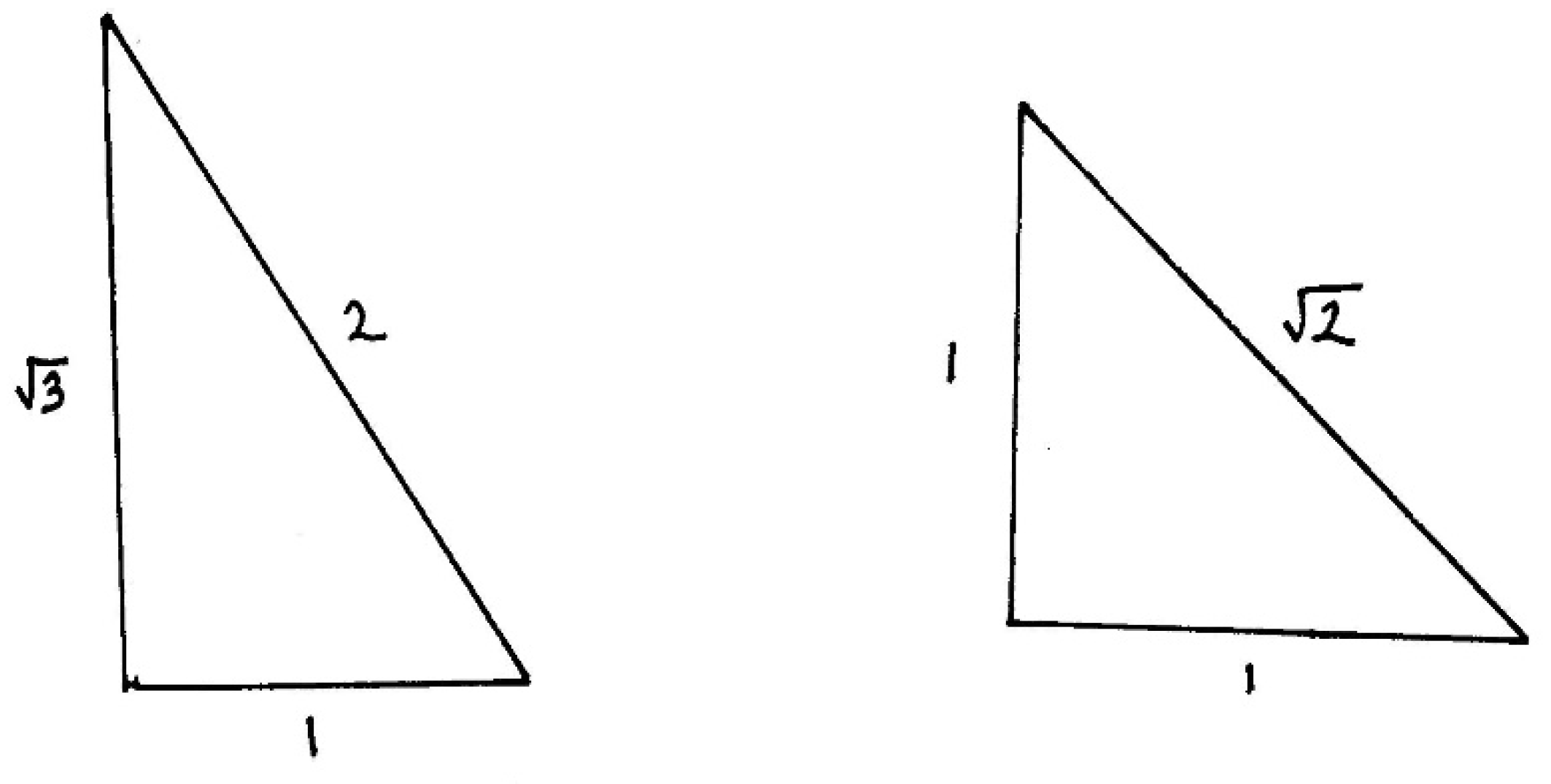
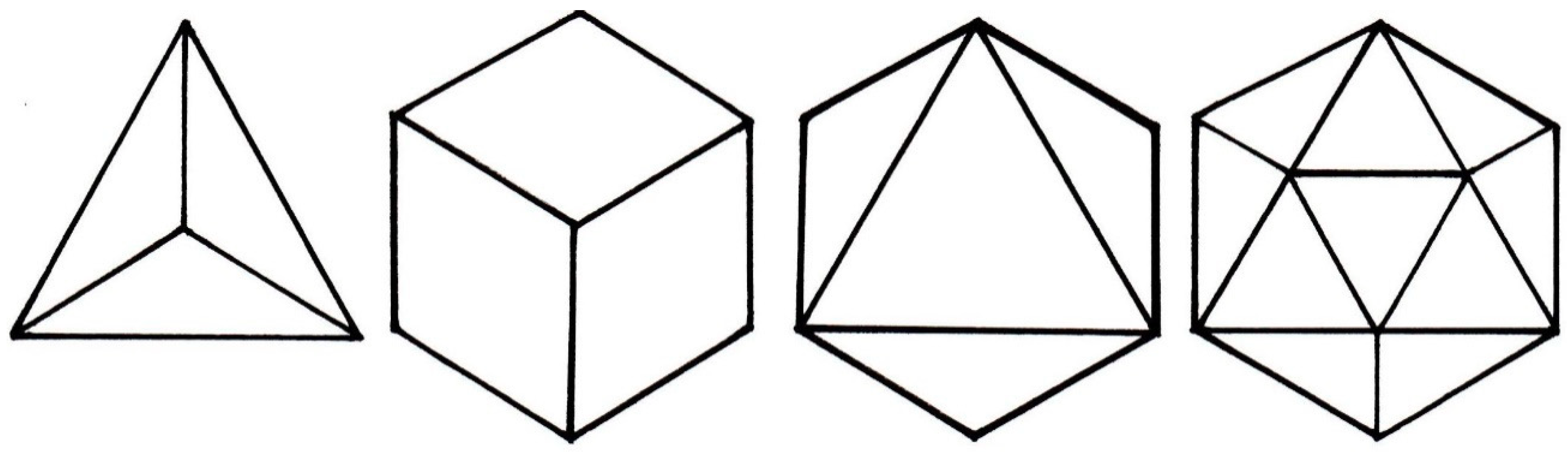
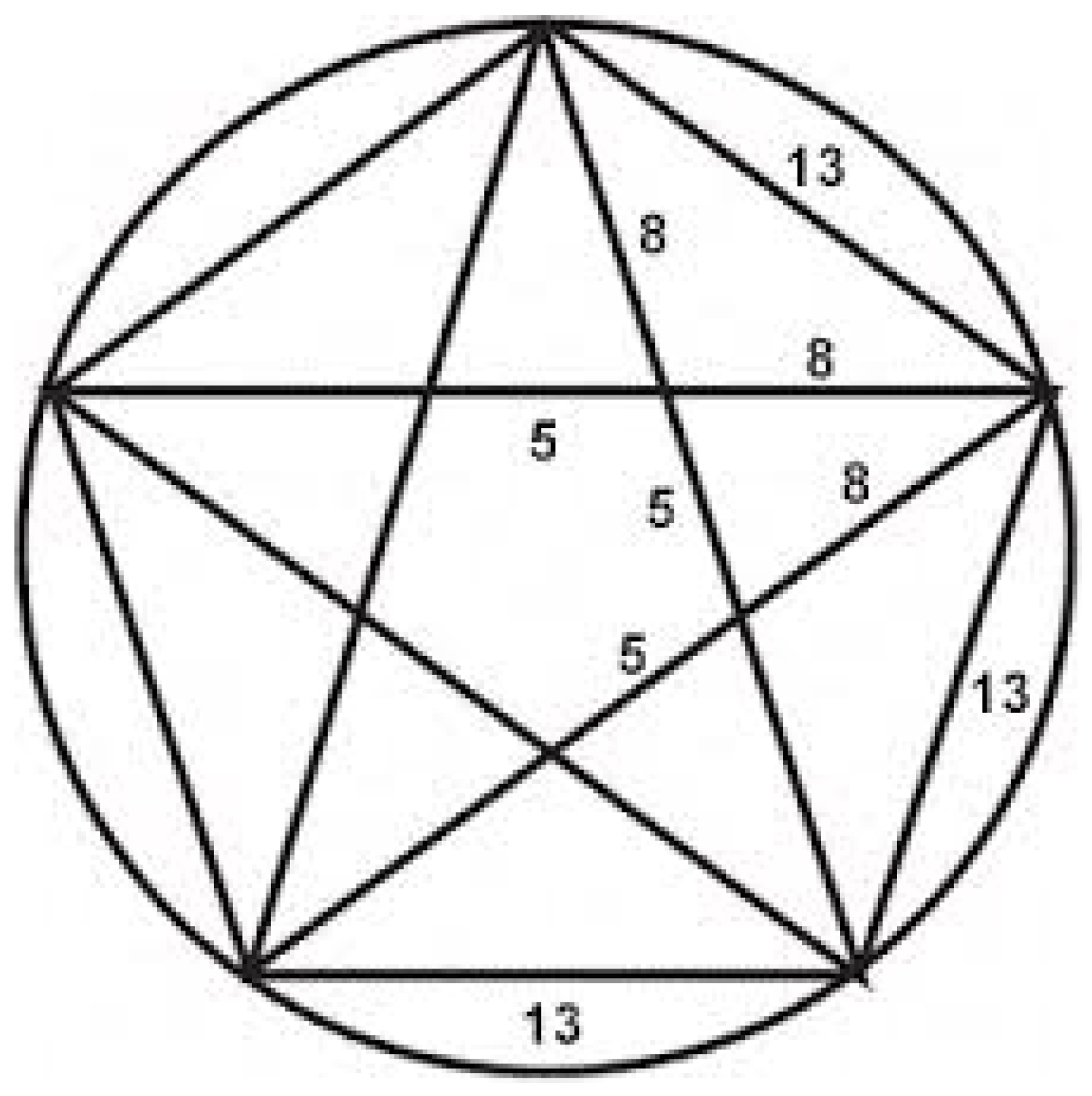
| A | B | B/A |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 2 | 2 |
| 2 | 3 | 1.5 |
| 3 | 5 | 1.666666666 … |
| 5 | 8 | 1.6 |
| 8 | 13 | 1.625 |
| … | … | … |
| 144 | 233 | 1.618055556 … |
| 233 | 377 | 1.618025751 … |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salamone, M.A. The Two Supreme Principles of Plato’s Cosmos—the One and the Indefinite Dyad—the Division of a Straight Line into Extreme and Mean Ratio, and Pingala’s Mātrāmeru. Symmetry 2019, 11, 98. https://doi.org/10.3390/sym11010098
Salamone MA. The Two Supreme Principles of Plato’s Cosmos—the One and the Indefinite Dyad—the Division of a Straight Line into Extreme and Mean Ratio, and Pingala’s Mātrāmeru. Symmetry. 2019; 11(1):98. https://doi.org/10.3390/sym11010098
Chicago/Turabian StyleSalamone, Maria Antonietta. 2019. "The Two Supreme Principles of Plato’s Cosmos—the One and the Indefinite Dyad—the Division of a Straight Line into Extreme and Mean Ratio, and Pingala’s Mātrāmeru" Symmetry 11, no. 1: 98. https://doi.org/10.3390/sym11010098
APA StyleSalamone, M. A. (2019). The Two Supreme Principles of Plato’s Cosmos—the One and the Indefinite Dyad—the Division of a Straight Line into Extreme and Mean Ratio, and Pingala’s Mātrāmeru. Symmetry, 11(1), 98. https://doi.org/10.3390/sym11010098





