Tsallis Holographic Dark Energy in f(G,T) Gravity

Abstract

In this paper, we study the reconstruction paradigm for Tsallis holographic dark energy model using generalized Tsallis entropy conjecture with Hubble horizon in the framework of $f(G,T)$ gravity (G and T represent the Gauss-Bonnet invariant and trace of the energy-momentum tensor). We take the flat Friedmann-Robertson-Walker universe model with dust fluid configuration. The cosmological evolution of reconstructed models is examined through cosmic diagnostic parameters and phase planes. The equation of the state parameter indicates phantom phase while the deceleration parameter demonstrates accelerated cosmic epoch for both conserved as well as non-conserved energy-momentum tensor. The squared speed of the sound parameter shows instability of the conserved model while stable non-conserved model for the entire cosmic evolutionary paradigm. The trajectories of the ${\omega }_{GT}-{\omega }_{GT}^{\prime }$ plane correspond to freezing as well as thawing regimes for the conserved and non-conserved scenario, respectively. The $r-s$ plane gives phantom and quintessence dark energy epochs for conserved while Chaplygin gas model regime for the non-conserved case. We conclude that, upon the appropriate choice of the free parameters involved, the derived models demonstrate a self-consistent phantom universe behavior.

1. Introduction

The current cosmic accelerated expansion manifests the spectacular development in modern cosmology. It has been suggested through numerous cosmological observational schemes that the phenomenon behind this marvelous cosmic expanding paradigm is the rapid accelerated scenario referred to exotic force. This type of force accommodates repulsive nature with large negative pressure, dubbed as dark energy (DE). This exotic energy is assumed to determine the ultimate fate of the cosmos but its enigmatic traits are still not settled. There are mainly two approaches to justify perplexing source causing this cosmic accelerating expansion. One approach is to modify the matter part yielding dynamical DE models and another choice is to modify the geometric part of the Einstein-Hilbert (EH) action leading to modified theories of gravity (see for review [1]).

The holographic dark energy (HDE) model has been found to be a promising candidate to resolve the perplexing DE puzzle. This is based on a holographic principle underlying the quantum features of the black hole (BH) [2]. Cohen et al. [3] used this idea to establish a relationship between UV and IR-cutoffs for analyzing the speculation of BH formation. The energy density of HDE is defined as [4]

$${\rho }_{hde}=3c^2{m}_p^2{L}^{-2},$$

(1)

where $m_p$ and L represent reduced Planck mass and IR-cutoff, respectively. Karami and Khaledian [5] explored HDE as well as new agegraphic DE in the context of $f\left(R\right)$ gravity and observed a transition from quintessence to phantom phase for entropy corrected reconstructed models. Houndjo and Piattella [6] reconstructed the HDE $f(R,T)$ model to analyze the current cosmic evolution. Daouda et al. [7] examined the HDE model for unifying outcomes of DE and dark matter in the framework of teleparallel theory. Jawad et al. [8] studied the stability of HDE $f\left(G\right)$ model for emergent, logamediate and intermediate scale factors using Granda-Oliveros cutoff and found the stability for intermediate scale factor only. Sharif and Zubair [9] reconstructed HDE as well as agegraphic DE $f(R,T)$ model which gives phantom and quintessence epochs of the derived model. Fayaz et al. [10] investigated phantom and quintessence phases of cosmic evolution for reconstructed $f(R,T)$ gravity using Bianchi type-I universe model in the context of HDE as well as new agegraphic DE.

The HDE model (primary model) was developed by using Bekenstein entropy with IR-cutoff as Hubble horizon but it fails to provide essential description for the evolutionary history of flat Friedmann-Robertson-Walker (FRW) universe model [11,12,13,14]. To resolve this issue, numerous physicists attempted to incorporate other cutoff values, probable interaction between cosmic regime, different entropy versions or through manipulation of all the above choices [15,16]. A variety of generalized entropy formalisms have also been developed in literature to interpret consequences of gravitational as well as cosmological phenomenon [17,18,19]. Recently, two new versions of stable HDE model has been introduced in connection with generalized entropy conjecture [20,21].

The cornerstone behind these models underlies for the implementation of Tsallis statistics to the horizon structure [22,23]. More precisely, the Tsallis entropy [24] is useful for understanding strongly correlated system of elements (gravitational and cosmological system) in the context of generalized statistical mechanics [25,26,27]. Tsallis and Citro established the fact that Bekenstein entropy is not the only sequel of Tsallis statistics execution for the system. More recently, Tavayef and his collaborators [28] proposed Tsallis HDE (THDE) based on Tsallis entropy as well as holographic speculation for describing the late-time cosmic expansion paradigm. They also observed the evolutionary history of the FRW universe as well as its approximate age and examined the instability of the model based on Bekenstein entropy.

Harko et al. [29] introduced curvature-matter coupling known as $f(R,T)$ gravity (R denotes Ricci scalar) to study the evolutionary paradigm of the cosmos. Recently, Sharif and Ikram [30] proposed such curvature-matter coupling in $f\left(G\right)$ gravity dubbed as $f(G,T)$ gravity. This coupling offers an extra force due to non-zero covariant divergence of the energy-momentum tensor (EMT). Consequently, the dust particle moves on non-geodesic trajectories contrarily to massive test particles. They explored energy conditions and also reconstructed $f(G,T)$ models as well as examined their stability [31]. Bhatti et al. [32] explored the role of physically viable $f(G,T)$ models in the evolutionary paradigm of relativistic compact stars. Shamir and Ahmad [33] reconstructed cosmologically viable $f(G,T)$ models using Noether symmetric approach to discuss cosmic expansion.

In reconstruction scenario, one compares relative energy densities of known cosmic solution (i.e, DE model) and modified gravity to find reconstructed Lagrangian which reproduces the entire cosmic history. Jamil and Saridakis [34] made correspondence between new agegraphic DE model and Horava-Lifshitz gravity exhibiting consistent regime with observations for accelerating expansion of the universe. Jawad and Chattopadhyay [35] analyzed the implications of pilgrim DE model in the framework of Horava-Lifshitz $f\left(R\right)$ gravity with Hubble horizon. Sharif and Nazir [36] investigated generalized ghost pilgrim DE in $f\left(\mathcal{T}\right)$ gravity ($\mathcal{T}$ denotes torsion scalar) to prevent BH formulation. They also explored cosmic evolutionary regime of reconstructed $f(\mathcal{T},{\mathcal{T}}_{\mathcal{G}})$ models (${\mathcal{T}}_{\mathcal{G}}$ indicates teleparallel equivalent to GB invariant) using different forms of scale factors [37]. Kleidis and Oikonomou [38] investigated entire cosmic evolutionary paradigm using scalar-tensor theory, specifically for single and two scalar theories. Recently, Ghaffari and his collaborator [39] analyzed THDE using Tsallis generalized entropy, holographic conjecture with IR-cutoff as Hubble horizon in the framework of Brans-Dicke (BD) theory.

In this paper, we establish reconstruction scenario for THDE model in the context of $f(G,T)$ gravity with Hubble horizon and generalized Tsallis entropy conjecture using power-law solution of the scale factor. The paper is organized in the following format. In the next section, we present basic terminologies of $f\left(G\right)$ gravity and THDE model and establish reconstruction paradigm between the corresponding physical entities. Section 3 is devoted to analyze cosmic evolutionary regime using cosmological diagnostics and phase planes. Finally, we conclude our results in the last section.

2. Reconstruction of THDE $\mathit{f}(\mathit{G},\mathit{T})$ Models

In this section, we develop the reconstruction paradigm for Tsallis holographic DE in the framework of $f(G,T)$ gravity. This theory is a more intriguing approach to study cosmic evolutionary regime as it incorporates curvature-matter coupling in modified Gauss-Bonnet gravity. The motivation behind this theory comes from string theory which can effectively elaborate late-time cosmic phase transitions. There appears an extra force due to non-conserved behavior of matter configuration which deviates the motion of test particles on the geodesic/non-geodesic path as compared to $f\left(R\right)$ or $f\left(T\right)$ models. The action of $f(G,T)$ gravity is given by [30]

$$\mathcal{S}=\int d^{4}x\sqrt{-g}\left(\frac{R+f(G,T)}{2{\kappa }^2}+{\mathcal{L}}_m\right),$$

(2)

where coupling constant ${\kappa }^2=1$ and ${\mathcal{L}}_m$ denote matter Lagrangian density. The corresponding field equations are

$$\begin{array}{ccc}\hfill R_{\alpha \rho }-\frac{1}{2}R{g}_{\alpha \rho }& =& {\kappa }^2{T}_{\alpha \rho }+\frac{1}{2}{g}_{\alpha \rho }f(G,T)-(T_{\alpha \rho }+{\mathsf{\Theta }}_{\alpha \rho })f_T(G,T)\hfill \\ & +& (4R_{\chi \rho }{R}_{\alpha }^{\chi }-2R{R}_{\alpha \rho }+4R_{\alpha \chi \rho \eta }{R}^{\chi \eta }-2R_{\alpha }^{\chi \eta \mathrm{\gamma }}{R}_{\rho \chi \eta \mathrm{\gamma }})f_G(G,T)\hfill \\ & +& (4R_{\alpha \rho }-2R{g}_{\alpha \rho })\square f_G(G,T)+2R{\nabla }_{\alpha }{\nabla }_{\rho }{f}_G(G,T)\hfill \\ & -& 4R_{\rho }^{\chi }{\nabla }_{\alpha }{\nabla }_{\chi }{f}_G(G,T)-4R_{\alpha }^{\chi }{\nabla }_{\rho }{\nabla }_{\chi }{f}_G(G,T)\hfill \\ & +& 4g_{\alpha \rho }{R}^{\chi \eta }{\nabla }_{\chi }{\nabla }_{\eta }{f}_G(G,T)-4R_{\alpha \chi \rho \eta }{\nabla }^{\chi }{\nabla }^{\eta }{f}_G(G,T),\hfill \end{array}$$

(3)

where ${\mathsf{\Theta }}_{\alpha \rho }=g^{\alpha \xi }(\frac{\delta T_{\alpha \xi }}{\delta g^{\alpha \rho }})$ and $\square ={\nabla }^2={\nabla }_{\eta }{\nabla }^{\eta }$ represents d’Alembert operator whereas ${\nabla }_{\eta }$, $f_G(G,T)$ and $f_T(G,T)$ denote covariant derivative, derivative of generic function with respect to G and T, respectively. The covariant divergence of the above equation gives

$$\begin{array}{c}\hfill {\nabla }^{\alpha }{T}_{\alpha \rho }=\frac{f_T(G,T)}{1-f_T(G,T)}[({\mathsf{\Theta }}_{\alpha \rho }+T_{\alpha \rho }){\nabla }^{\alpha }ln{f}_T(G,T)-\frac{1}{2}{g}_{\alpha \rho }{\nabla }^{\alpha }T+{\nabla }^{\alpha }{\mathsf{\Theta }}_{\alpha \rho }].\end{array}$$

(4)

The corresponding field equations for perfect fluid configuration using flat FRW universe yield

$$\begin{array}{c}\hfill 3H^2={\rho }_{eff}=\rho +{\rho }_{GT},-(2\dot{H}+3H^2)=P_{eff}=P+P_{GT},\end{array}$$

(5)

where

$$\begin{array}{ccc}\hfill {\rho }_{GT}& =& \frac{1}{2}f(G,T)+(\rho +P)f_T(G,T)-\frac{1}{2}G{f}_G(G,T)+12H^3\dot{G}{f}_{GG}(G,T)\hfill \\ & +& 12H^3\dot{T}{f}_{GT}(G,T),\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill P_{GT}& =& -\frac{1}{2}f(G,T)+\frac{1}{2}G{f}_G(G,T)-8H(\dot{H}+H^2)(\dot{G}{f}_{GG}(G,T)\hfill \\ & +& \dot{T}{f}_{GT}(G,T))-4H^2({\dot{G}}^2{f}_{GGG}(G,T)+2\dot{G}\dot{T}{f}_{GGT}(G,T)\hfill \\ & +& {\ddot{T}}^2{f}_{GTT}(G,T)+\ddot{G}{f}_{GG}(G,T)+\ddot{T}{f}_{GT}(G,T)),\hfill \end{array}$$

(7)

dot indicates derivative with respect to cosmic time t while $G=24H^2(H^2+\dot{H})$ and $T=\rho -3P$. The conservation Equation (4) for perfect fluid configuration turns out to be

$$\begin{array}{c}\hfill \dot{\rho }+3H(\rho +P)=\frac{-1}{1-f_T(G,T)}[(\dot{P}+\frac{1}{2}\dot{T})f_T(G,T)+(\rho +P){\partial }_t{f}_T(G,T)].\end{array}$$

(8)

The energy density of HDE (1) depends on the entropy-area relation $A\sim S\sim L^2$, while $A=4\pi L^2$ denotes the area of horizon. Motivated by holographic principle, Cohen et al. [3] established a relationship between the entropy of system (S), IR-cuttoff (L) and UV-cutoff ($\mathrm{\Lambda }$) as

$$L^3{\mathrm{\Lambda }}^3\le S^{\frac{3}{4}}.$$

(9)

Tsallis and Citro [25] suggested that the HDE can be redefined through the modification in horizon entropy of BH using quantum phenomenology as

$$S_{\mu }=\mathrm{\gamma }{A}_{\mu },$$

(10)

here $\mathrm{\gamma }$ and $\mu$ denote arbitrary constant and non-additivity parameter, respectively. Combining inequality (9) with (10), one gets

$${\mathrm{\Lambda }}^4\le \left(\mathrm{\gamma }{\left(4\pi \right)}^{\mu }\right)L^{2\mu -4},$$

(11)

where ${\mathrm{\Lambda }}^4$ is the vacuum energy density in the context of HDE hypothesis [40]. Using the above inequality, the energy density of THDE is defined as

$${\rho }_{thde}=B{L}^{2\mu -4},$$

(12)

here B is unknown parameter [40]. By choosing the simplest IR-cutoff as Hubble horizon ($L=H^{-1}$), the corresponding energy density becomes

$${\rho }_{thde}=B{H}^{4-2\mu },$$

(13)

Consequently, the equation of state (EoS) parameter for THDE density in the context of DE dominated universe becomes

$${\omega }_{thde}=-1+\frac{(2\mu -4)\dot{H}}{3H^2}.$$

(14)

It is observed that $\dot{H}<0$ for the entire cosmic history. Therefore, the universe may behave phantom-like for $\mu >2$ and non-phantom elsewhere.

Now, we reconstruct THDE $f(G,T)$ model using correspondence scheme in the framework of perfect fluid configuration with dust case ($P=0$). For the sake of simplicity, we take specific form of the generic function [41]

• $f(G,T)=f_1\left(G\right)+f_2\left(T\right)$,
• $f(G,T)=F\left(G\right)+\eta T$,

corresponding to conserved as well as non-conserved EMT paradigm.

2.1. Conserved EMT Based Reconstruction

We consider the generic function of the following form

$$f(G,T)=f_1\left(G\right)+f_2\left(T\right),$$

(15)

which involves minimal coupling of curvature and matter contents with some modification to $f\left(G\right)$ gravity. This specific form of generic function indicates that the interaction (coupling) is purely gravitational. This form of generic function can easily be handled and elaborate more effectively the current cosmic expansion. Moreover, the reconstruction framework demonstrated the posteriori that such developed models are physically viable [41,42,43,44]. The field equations corresponding to Lagrangian (15) for dust fluid yields

$$\begin{array}{c}\hfill 3H^2={\rho }_{eff}=\rho +{\rho }_{GT},-(2\dot{H}+3H^2)=P_{eff}=P_{GT},\end{array}$$

(16)

where

$$\begin{array}{ccc}\hfill {\rho }_{GT}& =& \frac{1}{2}{f}_1\left(G\right)+\frac{1}{2}{f}_2\left(T\right)+\rho f_{2T}\left(T\right)-\frac{1}{2}G{f}_{1G}\left(G\right)+12H^3\dot{G}{f}_{1GG}\left(G\right),\hfill \end{array}$$

(17)

$$\begin{array}{ccc}\hfill P_{GT}& =& -\frac{1}{2}{f}_1\left(G\right)-\frac{1}{2}{f}_2\left(T\right)+\frac{1}{2}G{f}_{1G}\left(G\right)-4H[2(\dot{H}+H^2)\dot{G}+H\ddot{G}]\hfill \\ & \times & f_{1GG}\left(G\right)-4H^2{\dot{G}}^2{f}_{1GGG}\left(G\right).\hfill \end{array}$$

(18)

The associated conservation Equation (8) reduces to

$$\dot{\rho }+3H\rho =\frac{-1}{1-f_{2T}\left(T\right)}[\frac{1}{2}\dot{T}{f}_{2T}\left(T\right)+T{\partial }_t{f}_{2T}\left(T\right)].$$

(19)

The Lagrangian (15) shows consistency with standard continuity equation if one takes the right hand side of Equation (19) to be zero

$$\dot{\rho }+3H\rho =0⟹\rho ={\rho }_0{(\tau -t)}^{-3m},$$

(20)

with constraint

$$f_{2T}\left(T\right)+2T{f}_{2TT}\left(T\right)=0,$$

(21)

which yields $f_2\left(T\right)$ as

$$f_2\left(T\right)={\eta }_1{T}^{\frac{1}{2}}+{\eta }_2,$$

(22)

where ${\eta }_1$ and ${\eta }_2$ are integration constants.

To establish reconstruction paradigm through correspondence scheme, we equate Equations (13) and (17) using constraint on $f_2\left(T\right)$ given in (22). The resulting differential equation in $f_1\left(G\right)$ is given as follows

$$\frac{1}{2}{f}_1\left(G\right)-\frac{1}{2}G{f}_{1G}\left(G\right)+12H^3\dot{G}{f}_{1GG}\left(G\right)+{\eta }_1{T}^{\frac{1}{2}}+\frac{1}{2}{\eta }_2=B{H}^{4-2\mu }.$$

(23)

To solve this differential equation, we consider the power-law solution for the scale factor as

$$a\left(t\right)=a_0{(\tau -t)}^m,\tau >t,m>0,$$

(24)

where $a_0$ and $\tau$ denote present day value of the scale factor and finite future singularity time. This scale factor is incredibly perceptible to categorize diverse phase of the evolving universe. It indicates accelerated epoch for $m>1$ whereas decelerated era for $0<m<1$ incorporating dust for $m=\frac{2}{3}$ and radiation dominated phase for $m=\frac{1}{2}$. Using relation (24), the expressions for Hubble parameter, its derivative, GB invariant, energy density and pressure in terms of cosmic time t are

$$\begin{array}{ccc}\hfill H& =& \frac{-m}{\tau -t},\dot{H}=\frac{-m}{{(\tau -t)}^2},G=\frac{24m^3(m-1)}{{(\tau -t)}^4},\hfill \\ \hfill {\rho }_{GT}& =& B{(\frac{-m}{\tau -t})}^{4-2\mu },P_{GT}=\frac{m(2-3m)}{{(\tau -t)}^2}.\hfill \end{array}$$

(25)

Since $\dot{H}<0$, the solution (24) indicates quintessence phase of cosmos. Moreover, the above relations of energy density and pressure represent that the cosmic evolutionary regime bears finite-time future singularity of type III as $t\to \tau$, i.e., both energy density and pressure diverge whereas the scale factor remains finite as $t\to \tau$. Using Equations (24) in (23), we obtain

$$\begin{array}{cc}& G^2{f}_{1GG}\left(G\right)+\frac{(m-1)G}{4}{f}_{1G}\left(G\right)-\frac{m-1}{4}{f}_1\left(G\right)-\frac{m-1}{2}{\eta }_{1}d\hfill \\ \times & {\left(\frac{G}{24m^3\left(m-1\right)}\right)}^{\frac{3m}{8}}-\frac{m-1}{4}{\eta }_2+B(\frac{m-1}{2})\hfill \\ \times & {\left(\frac{-m{G}^{\frac{1}{4}}}{{24m^3\left(m-1\right)}^{\frac{1}{4}}}\right)}^{4-2\mu }=0,\hfill \end{array}$$

(26)

where $d=\sqrt{{\rho }_0}$ (${\rho }_0$ is the integration constant), leading to the solution

$$\begin{array}{ccc}\hfill f_1\left(G\right)& =& c_{1}G+c_2{G}^{\frac{-1}{4}m+\frac{1}{4}}+\frac{1}{12(m+3)}[3^{-\mu }Bm{6}^{\frac{-\mu }{2}}{\left(\frac{-m}{6{\left(m^3(m-1)\right)}^{\frac{1}{4}}}\right)}^{-2\mu }\hfill \\ & \times & \left({\left(\frac{\mu }{2}\right)}^{-1}+{(\frac{-\mu }{2}+\frac{m}{4}+\frac{3}{4})}^{-1}\right)G^{1-\frac{\mu }{2}}+24d{\eta }_1(m-1)6^{\frac{m}{8}}{3}^{\frac{-m}{4}}\hfill \\ & \times & {\left(m^3(m-1)\right)}^{\frac{-3m}{8}}\left(2^{-m}{(\frac{3m}{8}-1)}^{-1}-{76}^{\frac{-m}{4}}{(\frac{5m}{8}-\frac{1}{4})}^{-1}\right)G^{\frac{3m}{8}}\hfill \\ & -& 12(m-1){\eta }_2\left(1-{(\frac{m}{4}-\frac{1}{4})}^{-1}\right)],\hfill \end{array}$$

(27)

where $c_1$ and $c_2$ are integration constants. Consequently, the reconstructed THDE $f(G,T)$ model is obtained by substituting Equations (22) and (27) in (15)

$$\begin{array}{ccc}\hfill f(G,T)& =& c_{1}G+c_2{G}^{\frac{-1}{4}m+\frac{1}{4}}+\frac{1}{12(m+3)}[3^{-\mu }Bm{6}^{\frac{-\mu }{2}}{\left(\frac{-m}{6{\left(m^3(m-1)\right)}^{\frac{1}{4}}}\right)}^{-2\mu }\hfill \\ & \times & \left({(\frac{\mu }{2})}^{-1}+{(\frac{-\mu }{2}+\frac{m}{4}+\frac{3}{4})}^{-1}\right)G^{1-\frac{\mu }{2}}+24d{\eta }_1(m-1)6^{\frac{m}{8}}{3}^{\frac{-m}{4}}\hfill \\ & \times & {\left(m^3(m-1)\right)}^{\frac{-3m}{8}}\left(2^{-m}{(\frac{3m}{8}-1)}^{-1}-{76}^{\frac{-m}{4}}{(\frac{5m}{8}-\frac{1}{4})}^{-1}\right)G^{\frac{3m}{8}}\hfill \\ & -& 12(m-1){\eta }_2\left(1-{(\frac{m}{4}-\frac{1}{4})}^{-1}\right)]+{\eta }_1{T}^{\frac{1}{2}}+{\eta }_2.\hfill \end{array}$$

(28)

The graphical behavior of the reconstructed THDE $f(G,T)$ model against red-shift parameter $z=(1-a)a^{-1}$ is shown in Figure 1. We have chosen free parameters as $c_1=0.25$, $c_2=-1.5$, $d=-3.125$, $B=-3.5$, $\mu =2.5$, ${\eta }_1=-1.5$ and ${\eta }_2=3.2$ for three particular choices of $m=1.7,1.8,1.9$ throughout the graphical analysis for this model in the context of conservative EMT. It is noted that our gravity theory restricts the choice of Tsallis parameter as $\mu =n+\frac{1}{2}$; $n\in N$ (set of natural numbers). It is observed that the reconstructed THDE $f(G,T)$ model elapses gradually with red-shift parameter. Moreover,

$$\underset{z\to 0}{lim}f(G,T)=0.$$

(29)

which ultimately gives a realistic model.

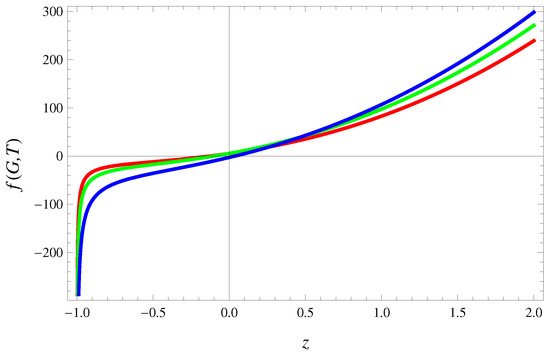
Figure 1. Plot of THDE $f(G,T)$ model against z for $m_1=1.7$ (red), $m_2=1.8$ (green) and $m_3=1.9$ (blue) for conserved EMT. The model shows gradual increase with convergence to zero from both sides, indicates realistic one.

2.2. Non-Conserved EMT Based Reconstruction

Here, we take specific form of Lagrangian as

$$f(G,T)=F\left(G\right)+\eta T,$$

(30)

where $\eta$ is an arbitrary constant. This particular form of generic function does not imply the non-minimal curvature-matter coupling and can recover the $\mathrm{\Lambda }$CDM model. Moreover, for $\eta =0$, our developed a model corresponds to $f\left(G\right)$ gravity. The resulting field equations give

$$\begin{array}{c}\hfill 3H^2={\rho }_{eff}=\rho +{\rho }_{GT},-(2\dot{H}+3H^2)=P_{eff}=P_{GT},\end{array}$$

(31)

where

$$\begin{array}{ccc}\hfill {\rho }_{GT}& =& \frac{3}{2}\eta T+\frac{1}{2}F\left(G\right)-\frac{1}{2}G{F}_G\left(G\right)+12H^3\dot{G}{F}_{GG}\left(G\right),\hfill \end{array}$$

(32)

$$\begin{array}{ccc}\hfill P_{GT}& =& -\frac{1}{2}\eta T-\frac{1}{2}F\left(G\right)+\frac{1}{2}G{F}_G\left(G\right)-4H[2(\dot{H}+H^2)\dot{G}+H\ddot{G}]\hfill \\ & \times & F_{GG}\left(G\right)-4H^2{\dot{G}}^2{F}_{GGG}\left(G\right).\hfill \end{array}$$

(33)

Consequently, the conservation Equation (8) reduces to

$$\dot{\rho }+3H\rho =(\frac{-\eta }{2-2\eta })\dot{T},$$

(34)

which yields

$$\rho ={\rho }_0{\left(\tau -t\right)}^{\frac{-6m\left(-1+\eta \right)}{-2+\eta }}.$$

(35)

Equating Equations (13) and (32), it follows that

$$\frac{3}{2}\eta T+\frac{1}{2}F\left(G\right)-\frac{1}{2}G{F}_G\left(G\right)+12H^3\dot{G}{F}_{GG}\left(G\right)=B{H}^{4-2\mu }.$$

(36)

Substituting Equations (24) and (35) in (36), we obtain

$$\begin{array}{cc}& G^2{F}_{GG}\left(G\right)+\frac{(m-1)G}{4}{F}_G\left(G\right)-\frac{m-1}{4}F\left(G\right)-{\left(\frac{G}{24m^3\left(m-1\right)}\right)}^{\frac{3m\left(\eta -1\right)}{2\eta -4}}\hfill \\ \times & \frac{3(m-1)}{4}\eta {\rho }_0+B(\frac{m-1}{2}){\left(\frac{-m{G}^{\frac{1}{4}}}{{24m^3\left(m-1\right)}^{\frac{1}{4}}}\right)}^{4-2\mu }=0,\hfill \end{array}$$

(37)

which yields the solution as

$$\begin{array}{ccc}\hfill F\left(G\right)& =& c_{1}G+c_2{G}^{\frac{-1}{4}m+\frac{1}{4}}+\frac{1}{252}(-mB{G}^{1-\frac{\mu }{2}}{\left(\frac{-m^{\frac{1}{4}}}{12{(m-1)}^{\frac{1}{4}}}\right)}^{-2\mu }\hfill \\ & \times & \left(\right(m{\eta }^2(21m-17)+\eta (-45m^2+53m-8)+(24m^2-38m\hfill \\ & +& 8\left)\right)2^{-\mu }{6}^{\frac{-3\mu }{2}}+2{\eta }^2{864}^{-\frac{\mu }{2}})+36\left(m-1\right)6^{-\frac{m\left(\eta -1\right)}{2\eta -4}}\left(2\mu -m-3\right)\hfill \\ & \times & {\left(\frac{1}{m^3\left(m-1\right)}\right)}^{\frac{3m\left(\eta -1\right)}{2\eta -4}}\eta {\rho }_0{G}^{\frac{3m\left(\eta -1\right)}{2\eta -4}}{48}^{\frac{-m\left(\eta -1\right)}{\eta -2}}{\left(\eta -2\right)}^2\mu )\hfill \\ & \times & {\left(\frac{-m}{2}+\mu -\frac{3}{2}\right)}^{-1}{\left((m-\frac{1}{7})\eta -\frac{8}{7}m+\frac{2}{7}\right)}^{-1}{\mu }^{-1}\hfill \\ & \times & {\left(\left(m-\frac{2}{3}\right)\eta -m+\frac{4}{3}\right)}^{-1}.\hfill \end{array}$$

The corresponding reconstructed THDE $f(G,T)$ model becomes

$$\begin{array}{ccc}\hfill f(G,T)& =& c_{1}G+c_2{G}^{\frac{-1}{4}m+\frac{1}{4}}+\frac{1}{252}(-mB{G}^{1-\frac{\mu }{2}}{\left(\frac{-m^{\frac{1}{4}}}{12{(m-1)}^{\frac{1}{4}}}\right)}^{-2\mu }\hfill \\ & \times & \left(\right(m{\eta }^2(21m-17)+\eta (-45m^2+53m-8)+(24m^2-38m\hfill \\ & +& 8\left)\right)2^{-\mu }{6}^{\frac{-3\mu }{2}}+2{\eta }^2{864}^{-\frac{\mu }{2}})+36\left(m-1\right)6^{-\frac{m\left(\eta -1\right)}{2\eta -4}}\left(2\mu -m-3\right)\hfill \\ & \times & {\left(\frac{1}{m^3\left(m-1\right)}\right)}^{\frac{3m\left(\eta -1\right)}{2\eta -4}}\eta {\rho }_0{G}^{\frac{3m\left(\eta -1\right)}{2\eta -4}}{48}^{\frac{-m\left(\eta -1\right)}{\eta -2}}{\left(\eta -2\right)}^2\mu )\hfill \\ & \times & {\left(\frac{-m}{2}+\mu -\frac{3}{2}\right)}^{-1}{\left((m-\frac{1}{7})\eta -\frac{8}{7}m+\frac{2}{7}\right)}^{-1}{\mu }^{-1}\hfill \\ & \times & {\left(\left(m-\frac{2}{3}\right)\eta -m+\frac{4}{3}\right)}^{-1}+\eta T.\hfill \end{array}$$

The plot of this model against z is shown in Figure 2. We have taken free parameters as $c_1=-1.5$, $c_2=-0.5$, ${\rho }_0=-0.125$, $B=-1.5$, $\mu =2.5$ and $\eta =-1.5$ for three specific values of $m=1.8, 2.1, 2.4$ giving red, green and blue curves throughout the analysis for non-conserved EMT regime. This model demonstrates gradual decline as z elapses. Also, $f(G,T)\to 0$ as $z\to 0$ which specifies the realistic phenomenon of the desired model.

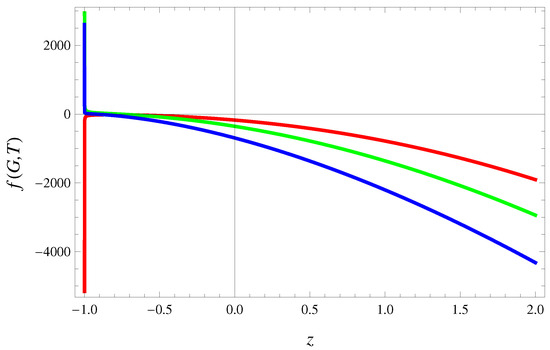
Figure 2. Plot of THDE $f(G,T)$ model against z for $m_1=1.8$ (red), $m_2=2.1$ (green) and $m_3=2.4$ (blue) for non-conserved EMT. In this case, the developed model shows reverse behavior as compared to conserved one which coincides with it for late-time phase of redshift parameter.

3. Cosmological Analysis

In this section, we analyze cosmic accelerated expansion paradigm using cosmological diagnostics and phase planes for conserved as well as non-conserved EMT-based reconstructed THDE $f(G,T)$ models.

3.1. Cosmic Diagnostics Parameters for Conserved EMT

The EoS parameter is defined as

$${\omega }_{GT}=\frac{P_{GT}}{{\rho }_{GT}}=\frac{P_{GT}}{{\rho }_{thde}}.$$

(38)

Using Equations (17), (18) and (28) in (38), this parameter for reconstructed model is given as

$$\begin{array}{ccc}\hfill {\omega }_{GT}& =& \frac{-1}{3GmB(m+3)}[{\eta }_{1}d{\left(24m^4-24m^3\right)}^{\frac{-3m}{8}}{6}^{\frac{m}{4}+\frac{\mu }{2}}{G}^{\frac{3m}{8}}{3}^{\mu }(-90m^2\hfill \\ & +& 126m-36)+{\eta }_{1}d{3}^{\mu +\frac{m}{4}}{19}^{\frac{m}{8}}{G}^{\frac{3m}{8}}{6}^{\frac{1}{2}\mu }{\left(114m^4-114m^3\right)}^{-\frac{3m}{8}}(54m^2\hfill \\ & -& 198m+144)+3^{-\mu }B{G}^{1-\frac{\mu }{2}}{\left(-\frac{m}{144\sqrt[4]{m^3\left(m-1\right)}}\right)}^{-2\mu }{192}^{-\mu }(3m^2\hfill \\ & +& 2\mu m+6\mu )+{\eta }_{1}d{24}^{\frac{-3m}{8}}{\left(\frac{G}{m^3\left(m-1\right)}\right)}^{\frac{3m}{8}}{3}^{\mu }{6}^{\frac{\mu }{2}}(36m^2+72m-108)\hfill \\ & +& 288{\eta }_2(m-1)3^{\mu }{6}^{\frac{\mu }{2}}+B{G}^{1-\frac{\mu }{2}}{2}^{-\mu }{\left(\frac{-m}{48\sqrt[4]{m^3\left(m-1\right)}}\right)}^{-2\mu }{32}^{-\mu }\hfill \\ & \times & (5m-12)]{\left(\frac{-m\sqrt[4]{G}}{6\sqrt[4]{m^3\left(m-1\right)}}\right)}^{2\mu }.\hfill \end{array}$$

(39)

Figure 3 gives the behavior of EoS parameter against z which indicates phantom epoch for current as well as late-time cosmic evolution. Moreover, large negative EoS parameter leads to phantom-like fate of the universe which may end up with a big-rip or remains consistent with the same current accelerating status.

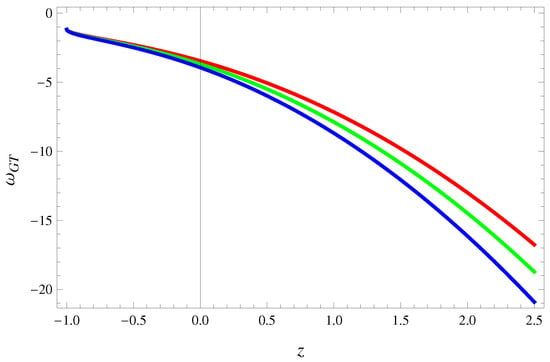
Figure 3. Plot of EoS parameter against z for $m_1=1.7$ (red), $m_2=1.8$ (green) and $m_3=1.9$ (blue) for conserved EMT shows phantom regime of the universe.

The corresponding deceleration parameter is

$$\begin{array}{ccc}\hfill q& =& \frac{1}{2}-\frac{1}{2GmB(m+3)}[{\eta }_{1}d{\left(24m^4-24m^3\right)}^{\frac{-3m}{8}}{6}^{\frac{m}{4}+\frac{\mu }{2}}{G}^{\frac{3m}{8}}{3}^{\mu }(-90m^2\hfill \\ & +& 126m-36)+{\eta }_{1}d{3}^{\mu +\frac{m}{4}}{19}^{\frac{m}{8}}{G}^{\frac{3m}{8}}{6}^{\frac{1}{2}\mu }{\left(114m^4-114m^3\right)}^{-\frac{3m}{8}}(54m^2\hfill \\ & -& 198m+144)+3^{-\mu }B{G}^{1-\frac{\mu }{2}}{\left(-\frac{m}{144\sqrt[4]{m^3\left(m-1\right)}}\right)}^{-2\mu }{192}^{-\mu }(3m^2\hfill \\ & +& 2\mu m+6\mu )+{\eta }_{1}d{24}^{\frac{-3m}{8}}{\left(\frac{G}{m^3\left(m-1\right)}\right)}^{\frac{3m}{8}}{3}^{\mu }{6}^{\frac{\mu }{2}}(36m^2+72m-108)\hfill \\ & +& 288{\eta }_2(m-1)3^{\mu }{6}^{\frac{\mu }{2}}+B{G}^{1-\frac{\mu }{2}}{2}^{-\mu }{\left(\frac{-m}{48\sqrt[4]{m^3\left(m-1\right)}}\right)}^{-2\mu }{32}^{-\mu }\hfill \\ & \times & (5m-12)]{\left(\frac{-m\sqrt[4]{G}}{6\sqrt[4]{m^3\left(m-1\right)}}\right)}^{2\mu }.\hfill \end{array}$$

Figure 4 indicates negative value for deceleration parameter throughout evolutionary regime of the universe. This shows that our non-conserved model ultimately exhibits accelerating phase of the expanding cosmos.

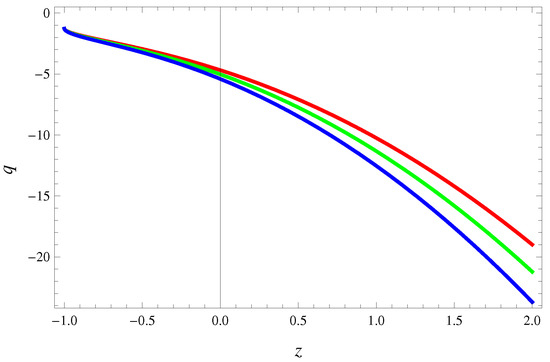
Figure 4. Plot of deceleration parameter versus z for $m_1=1.7$ (red), $m_2=1.8$ (green) and $m_3=1.9$ (blue) predicts accelerating phase for conserved EMT.

The squared speed of sound parameter is given as

$${\nu }_s^2=\frac{{\dot{P}}_{GT}}{{\dot{\rho }}_{GT}}=\frac{{\dot{P}}_{GT}}{{\dot{\rho }}_{thde}}.$$

(40)

Its positive sign shows the stability whereas its negative measure confers instability of the corresponding model. Substituting Equations (17), (18), (20) and (28) in (40), we obtain

$$\begin{array}{ccc}\hfill {\nu }_s^2& =& \frac{-1}{6mG\left(-2+\mu \right)B\left(m+3\right)}({\eta }_{1}d{3}^{\frac{m}{4}+\mu }{19}^{\frac{m}{8}}{G}^{\frac{3m}{8}}{6}^{\frac{\mu }{2}}{\left(114m^4-114m^3\right)}^{\frac{-3m}{8}}\hfill \\ & \times & (-81m^3+297m^2-216m)+{\eta }_{1}d{3}^{\mu }{6}^{\frac{\mu }{2}}{24}^{\frac{-3m}{8}}{\left(\frac{G}{m^3\left(m-1\right)}\right)}^{\frac{3m}{8}}(-54m^3\hfill \\ & -& 108m^2+162m)+{\eta }_{1}d{\left(24m^4-24m^3\right)}^{\frac{-3m}{8}}{6}^{\frac{m}{4}+\frac{\mu }{2}}{G}^{\frac{3m}{8}}{3}^{\mu }(135m^3-189m^2\hfill \\ & +& 54m)+G^{1-\frac{\mu }{2}}{3}^{-\mu }{\left(-\frac{m}{144\sqrt[4]{m^3\left(m-1\right)}}\right)}^{-2\mu }{192}^{-\mu }(6B{m}^2(\mu -2)\hfill \\ & +& 2B\mu (m-24))+G^{1-\frac{\mu }{2}}{\left(\frac{-m}{48\sqrt[4]{m^3\left(m-1\right)}}\right)}^{-2\mu }{32}^{-\mu }\left(6^{-\mu }{3}^{\mu }{\mu }^2\right(4m\hfill \\ & +& 12)+2^{-\mu }(-20m+48)\left)\right){\left(\frac{-m\sqrt[4]{G}}{6\sqrt[4]{m^3\left(m-1\right)}}\right)}^{2\mu }.\hfill \end{array}$$

Figure 5 demonstrates unstable reconstructed THDE $f(G,T)$ model for the entire cosmic evolution.

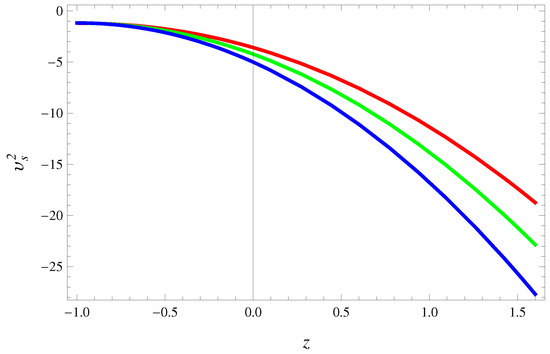
Figure 5. Plot of ${\nu }_s^2$ against z for conserved EMT for $m_1=1.7$ (red), $m_2=1.8$ (green) and $m_3=1.9$ (blue) illustrates instability of the model.

Now, we analyze ${\omega }_{GT}-{\omega }_{GT}^{\prime }$ phase plane whereas ${\omega }_{GT}^{\prime }$ gives evolutionary mode of ${\omega }_{GT}$ and prime indicates derivative with respect to $lna$. Caldwell and Linder [45] introduced this cosmological plane to examine the quintessence DE models and subdivided it into thawing (${\omega }_{GT}<0,{\omega }_{GT}^{\prime }>0$) and freezing (${\omega }_{GT}<0,{\omega }_{GT}^{\prime }<0$) regions. It is also observed that the freezing region demonstrates more accelerating phase as compared to thawing for describing current cosmic expansion paradigm. The cosmic trajectories of ${\omega }_{GT}-{\omega }_{GT}^{\prime }$ plane for particular choices of m are shown in Figure 6 which gives freezing region supporting phantom regime of the universe.

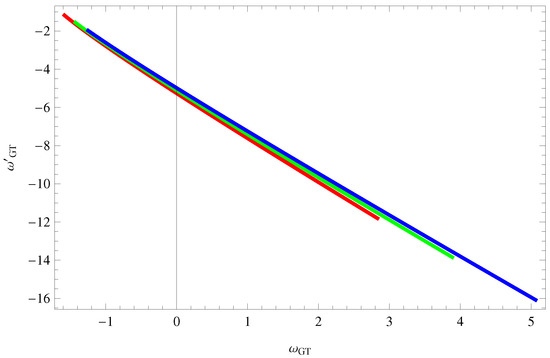
Figure 6. Trajectories of ${\omega }_{GT}-{\omega }_{GT}^{\prime }$ against z for conserved EMT for $m_1=1.7$ (red), $m_2=1.8$ (green) and $m_3=1.9$ (blue) shows freezing region which is more accelerating era of cosmos.

Sahni et al. [46] introduced two dimensionless parameters known as statefinders for eliminating viable choice of DE models as

$$r=\frac{\stackrel{⃛}{a}}{a{H}^3},s=\frac{r-1}{3(q-\frac{1}{2})}.$$

(41)

This plane is dubbed as $r-s$ plane and describes different cosmic regimes such as it indicates CDM limit for $(r,s)=(1,0)$ and $\mathrm{\Lambda }$CDM regime for $(r,s)=(1,1)$. Furthermore, phantom and quintessence DE eras are occupied by ($r<1,s>0$) phase while Chaplygin gas model through ($r>1$, $s<0$) region. Figure 7 exhibits the graphical behavior of statefinders diagnostic pair that indicates phantom and quintessence phases of the universe.

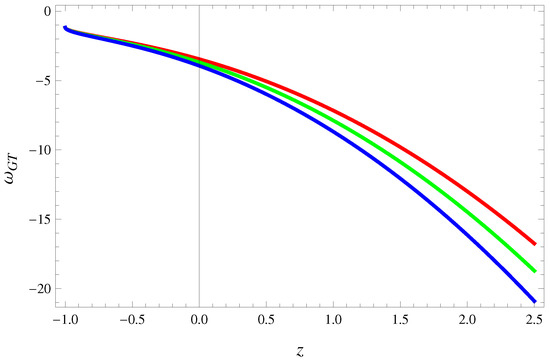
Figure 7. Trajectories of $r-s$ plan against z for $m_1=1.7$ (red), $m_2=1.8$ (green) and $m_3=1.9$ (blue) shows phantom and quintessence phase of the universe for conserved EMT.

3.2. Cosmic Diagnostics Parameters for Non-Conserved EMT

The corresponding EoS parameter is given as

$$\begin{array}{ccc}\hfill {\omega }_{GT}& =& \frac{-1}{3\left(m-1\right)\left(3\eta m-2\eta -3m+4\right)\left(7\eta m-\eta -8m+2\right)\left(\eta -2\right)BmG}\hfill \\ & \times & [3^{\mu }{\left(-\frac{1}{6}\frac{m\sqrt[4]{G}}{\sqrt[4]{m^3\left(m-1\right)}}\right)}^{2\mu }({\rho }_0{48}^{-\frac{m\left(\eta -1\right)}{\eta -2}}{\left(\frac{G}{m^3\left(m-1\right)}\right)}^{\frac{3m\left(\eta -1\right)}{2(\eta -2)}}\hfill \\ & \times & 6^{\frac{\eta \mu -\eta m-2\mu +m}{2(\eta -2)}}(-576\eta -432{\eta }^3+72{\eta }^4+864{\eta }^2+3996m{\eta }^3-13392m^3\hfill \\ & \times & {\eta }^2+15336m^2{\eta }^2-9828m^2{\eta }^3+9396m^3{\eta }^3+3888m\eta -756m{\eta }^4\hfill \\ & -& 17172{\eta }^3{m}^2+2052m^2{\eta }^4+6192m^3\eta -2124m^3{\eta }^4-7776m^2\eta \hfill \\ & +& 4104m^4{\eta }^2-3132m^4{\eta }^3-1728m^4\eta +756m^4{\eta }^4-6912m{\eta }^2)\hfill \\ & +& {\rho }_0{6}^{\frac{1}{2}\frac{\eta \mu -\eta m-2\mu +m}{\eta -2}}{\left(\frac{1}{m^3\left(m-1\right)}\right)}^{\frac{3}{2}\frac{m\left(\eta -1\right)}{\eta -2}}{G}^{\frac{3}{2}\frac{m\left(\eta -1\right)}{\eta -2}}{48}^{-\frac{m\left(\eta -1\right)}{\eta -2}}(216{\eta }^4\hfill \\ & +& 864{\eta }^2-864{\eta }^3+7452m{\eta }^3-5832m{\eta }^2-2268m{\eta }^4-4860m^4{\eta }^3\hfill \\ & +& 2268m^4{\eta }^4+11664m^2{\eta }^2-6696m^3{\eta }^2+15444m^3{\eta }^3-6372m^3{\eta }^4\hfill \\ & +& 6156m^2{\eta }^4)+B{G}^{1-\frac{\mu }{2}}{\left(\frac{-m^{\frac{1}{4}}}{12{(m-1)}^{\frac{1}{4}}}\right)}^{-2\mu }{2}^{-\mu }{6}^{-\mu }(564m^3-772m^2\hfill \\ & -& 144m^4+32-32{\eta }^2+96\eta -184m\mu +203m^2{\eta }^3+342m^4\eta -48\eta \mu \hfill \\ & -& 1230m^3\eta -198m^3{\eta }^3-261m^4{\eta }^2-744m\eta +63m^4{\eta }^3-68m{\eta }^3\hfill \\ & +& 288m^3\mu \eta +34m\mu {\eta }^3-190m\mu {\eta }^2+336m\mu \eta +42m^3\mu {\eta }^3-76m^2\mu {\eta }^3\hfill \\ & -& 516m^2\mu \eta -174m^3\mu {\eta }^2+248m^2\mu -981m^2{\eta }^2-96m^3\mu +16{\eta }^2\mu \hfill \\ & +& 870m^3{\eta }^2+1536m^2\eta +404m{\eta }^2+348m^2{\eta }^2-64)+B{\eta }^{3}m{G}^{1-\frac{\mu }{2}}\hfill \\ & \times & {864}^{-\frac{\mu }{2}}{6}^{\frac{-3\mu }{2}}{\left(\frac{-m^{\frac{1}{4}}}{72{(m-1)}^{\frac{1}{4}}}\right)}^{-2\mu }(-14m{\eta }^3+8\mu {\eta }^2-4\mu {\eta }^3+28m{\eta }^2\hfill \\ & -& 12m^2{\eta }^2-16{\eta }^2+8{\eta }^3+4m\mu {\eta }^3-8m\mu {\eta }^2+6m^2{\eta }^3)+54{\rho }_0{48}^{-\frac{\eta m-\eta -m}{\eta -2}}\hfill \\ & \times & {2304}^{-{\left(\eta -2\right)}^{-1}}{6}^{\frac{\eta \mu -\eta m-2\mu +m}{2(\eta -2)}}{\left(\frac{1}{m^3\left(m-1\right)}\right)}^{\frac{3m\left(\eta -1\right)}{2(\eta -2)}}{\eta }^2{G}^{\frac{3m\left(\eta -1\right)}{2(\eta -2)}}{m}^3\left)\right].\hfill \end{array}$$

Figure 8 shows phantom paradigm for the entire evolutionary mode of the universe which leads to big-rip or current accelerating phenomenology.

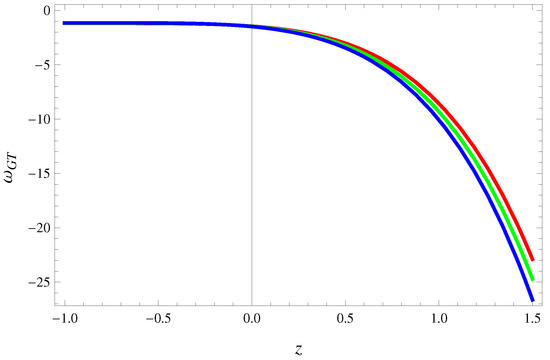
Figure 8. Plot of ${\omega }_{GT}$ parameter against z for $m_1=1.8$ (red), $m_2=2.1$ (green) and $m_3=2.4$ (blue) shows phantom expansion for entire cosmic evolutionary regime in case of non-conserved EMT.

The associated deceleration parameter turns out to be

$$\begin{array}{ccc}\hfill q& =& \frac{1}{2}-\frac{{\left(BmG\right)}^{-1}}{\left(m-1\right)\left(3\eta m-2\eta -3m+4\right)\left(7\eta m-\eta -8m+2\right)\left(\eta -2\right)}\hfill \\ & \times & [3^{\mu }{\left(-\frac{1}{6}\frac{m\sqrt[4]{G}}{\sqrt[4]{m^3\left(m-1\right)}}\right)}^{2\mu }({\rho }_0{48}^{-\frac{m\left(\eta -1\right)}{\eta -2}}{\left(\frac{G}{m^3\left(m-1\right)}\right)}^{\frac{3m\left(\eta -1\right)}{2(\eta -2)}}\hfill \\ & \times & 6^{\frac{\eta \mu -\eta m-2\mu +m}{2(\eta -2)}}(-576\eta -432{\eta }^3+72{\eta }^4+864{\eta }^2+3996m{\eta }^3-13392m^3\hfill \\ & \times & {\eta }^2+15336m^2{\eta }^2-9828m^2{\eta }^3+9396m^3{\eta }^3+3888m\eta -756m{\eta }^4\hfill \\ & -& 17172{\eta }^3{m}^2+2052m^2{\eta }^4+6192m^3\eta -2124m^3{\eta }^4-7776m^2\eta \hfill \\ & +& 4104m^4{\eta }^2-3132m^4{\eta }^3-1728m^4\eta +756m^4{\eta }^4-6912m{\eta }^2)\hfill \\ & +& {\rho }_0{6}^{\frac{1}{2}\frac{\eta \mu -\eta m-2\mu +m}{\eta -2}}{\left(\frac{1}{m^3\left(m-1\right)}\right)}^{\frac{3}{2}\frac{m\left(\eta -1\right)}{\eta -2}}{G}^{\frac{3}{2}\frac{m\left(\eta -1\right)}{\eta -2}}{48}^{-\frac{m\left(\eta -1\right)}{\eta -2}}(216{\eta }^4\hfill \\ & +& 864{\eta }^2-864{\eta }^3+7452m{\eta }^3-5832m{\eta }^2-2268m{\eta }^4-4860m^4{\eta }^3\hfill \\ & +& 2268m^4{\eta }^4+11664m^2{\eta }^2-6696m^3{\eta }^2+15444m^3{\eta }^3-6372m^3{\eta }^4\hfill \\ & +& 6156m^2{\eta }^4)+B{G}^{1-\frac{\mu }{2}}{\left(\frac{-m^{\frac{1}{4}}}{12{(m-1)}^{\frac{1}{4}}}\right)}^{-2\mu }{2}^{-\mu }{6}^{-\mu }(564m^3-772m^2\hfill \\ & -& 144m^4+32-32{\eta }^2+96\eta -184m\mu +203m^2{\eta }^3+342m^4\eta -48\eta \mu \hfill \\ & -& 1230m^3\eta -198m^3{\eta }^3-261m^4{\eta }^2-744m\eta +63m^4{\eta }^3-68m{\eta }^3\hfill \\ & +& 288m^3\mu \eta +34m\mu {\eta }^3-190m\mu {\eta }^2+336m\mu \eta +42m^3\mu {\eta }^3-76m^2\mu {\eta }^3\hfill \\ & -& 516m^2\mu \eta -174m^3\mu {\eta }^2+248m^2\mu -981m^2{\eta }^2-96m^3\mu +16{\eta }^2\mu \hfill \\ & +& 870m^3{\eta }^2+1536m^2\eta +404m{\eta }^2+348m^2{\eta }^2-64)+B{\eta }^{3}m{G}^{1-\frac{\mu }{2}}\hfill \\ & \times & {864}^{-\frac{\mu }{2}}{6}^{\frac{-3\mu }{2}}{\left(\frac{-m^{\frac{1}{4}}}{72{(m-1)}^{\frac{1}{4}}}\right)}^{-2\mu }(-14m{\eta }^3+8\mu {\eta }^2-4\mu {\eta }^3+28m{\eta }^2\hfill \\ & -& 12m^2{\eta }^2-16{\eta }^2+8{\eta }^3+4m\mu {\eta }^3-8m\mu {\eta }^2+6m^2{\eta }^3)+54{\rho }_0{48}^{-\frac{\eta m-\eta -m}{\eta -2}}\hfill \\ & \times & {2304}^{-{\left(\eta -2\right)}^{-1}}{6}^{\frac{\eta \mu -\eta m-2\mu +m}{2(\eta -2)}}{\left(\frac{1}{m^3\left(m-1\right)}\right)}^{\frac{3m\left(\eta -1\right)}{2(\eta -2)}}{\eta }^2{G}^{\frac{3m\left(\eta -1\right)}{2(\eta -2)}}{m}^3\left)\right].\hfill \end{array}$$

Figure 9 indicates that $q<0$ leading to accelerating phase of cosmic expansion. The squared speed of sound parameter in Figure 10 demonstrates that THDE $f(G,T)$ model remains stable throughout cosmic evolutionary regime. The evolutionary curves of ${\omega }_{GT}-{\omega }_{GT}^{\prime }$ phase plane in Figure 11 gives thawing region which favors the phantom conjecture for the universe. Figure 12 presents the graphical analysis of $r-s$ phase plane indicating Chaplygin gas model regime. Through reconstruction scenario using correspondence approach, we have developed viable $f(G,T)$ models in the vicinity of THDE which are capable to effectively describe current as well as late-time cosmic expansion. Moreover, in principle, there is no need to fix a priori a flat universe, since both open and closed cosmos seem to develop entire evolutionary cosmic phases with compatibility for observational data, for at least small redshift domain.

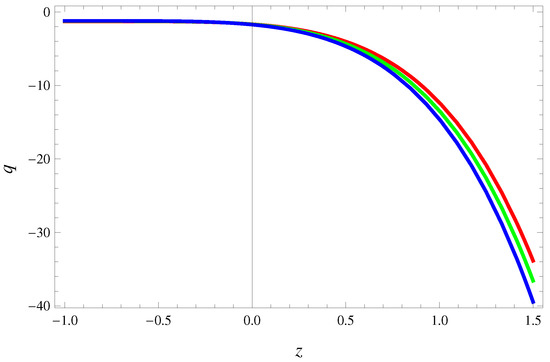
Figure 9. Plot of deceleration parameter against z for $m_1=1.8$ (red), $m_2=2.1$ (green) and $m_3=2.4$ (blue) indicates accelerating cosmic era for non-conserved matter distributions.

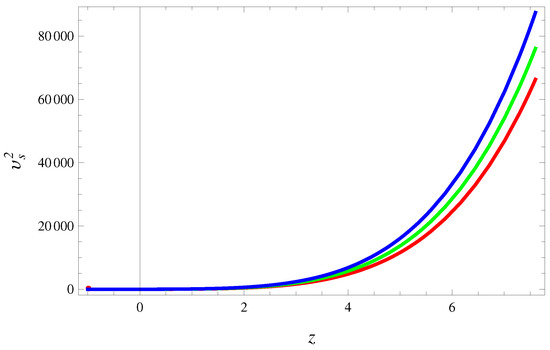
Figure 10. Squared speed of sound parameter against z for $m_1=1.8$ (red), $m_2=2.1$ (green) and $m_3=2.4$ (blue) shows stability of the model for current cosmic evolution while becomes unphysical for late-time cosmic regime in case of non-conserved EMT.

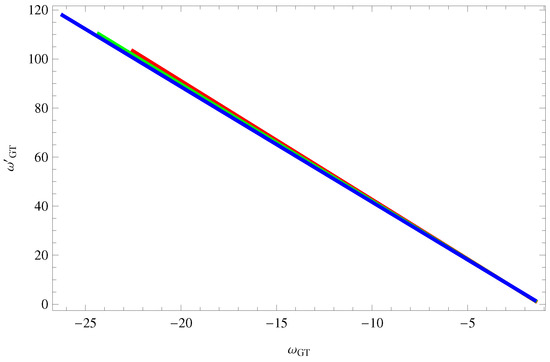
Figure 11. Trajectories of ${\omega }_{GT}-{\omega }_{GT}^{\prime }$ for $m_1=1.8$ (red), $m_2=2.1$ (green) and $m_3=2.4$ (blue) indicates more accelerating (freezing) phase as compared with thawing for non-conserved EMT.

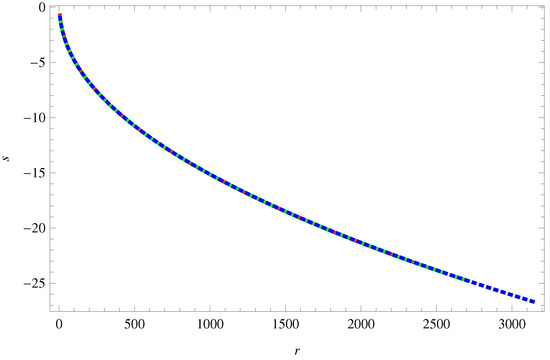
Figure 12. Trajectories of $r-s$ phase plane for $m_1=1.8$ (red), $m_2=2.1$ (green) and $m_3=2.4$ (blue) performs Chaplygin gas model regime for non-conserved EMT.

4. Concluding Remarks

In this paper, we have analyzed some features of THDE model in the context of $f(G,T)$ theory of gravity. For this purpose, we have established reconstruction paradigm through correspondence scenario for flat FRW universe using power-law scale factor. We have examined cosmic diagnostic parameters and phase planes for our derived model. The results are summarized as follows.

• The reconstructed THDE $f(G,T)$ model (Figure 1) exhibits increasing trend for conserved EMT while inverse behavior for non-conserved EMT (Figure 2).
• The EoS parameter (Figure 3 and Figure 8) demonstrates aggressive phantom regime of the universe which might predict phantom universe to preclude the chance of BH formation. Hence, THDE $f(G,T)$ model supports DE phenomenon of cosmic expansion.
• The deceleration parameter represents accelerated phase for both conserved as well as non-conserved EMT (Figure 4 and Figure 9).
• The squared speed of sound parameter gives unstable model for the entire cosmological evolutionary paradigm (Figure 5) while stability corresponds to non-conserved case (Figure 10).
• The trajectories of ${\omega }_{GT}-{\omega }_{GT}^{\prime }$ plane (Figure 6 and Figure 11) indicate freezing (thawing) region for conserved (non-conserved) EMT-based reconstruction.
• The curvatures of $r-s$ plane illustrate phantom and quintessence epoch for conserved case whereas Chaplygin gas model for the non-conserved EMT scenario (Figure 7 and Figure 12).

We conclude that our reconstructed THDE $f(G,T)$ models demonstrate consistency with accelerated expanding phenomenon of the universe for appropriate choice of free parameters. It is observed that both conserved as well as non-conserved EMT-based reconstructed models incline towards the phantom-like universe (caused by aggressive phantom features which seize the BH formation) to manifest its ultimate fate as big-rip or might be current accelerating phase. The EoS parameter exhibits consistent mode with the current observational data [47] given as

$$\begin{array}{cc}\hfill \omega =-1.028\pm 0.032& (PlanckTT,TE,EE+LowE+lensing\\ & +SNe+BAO).\end{array}$$

This value have been achieved at 68% confidence level through implementation of various observational techniques. We also observe that the cosmic diagnostic state-finder parameters for our derived models are compatible with the most recent limits and constraint over the kinematics of the universe [48,49]. Furthermore, the second non-conserved model is stable as well as well-behaved model as the squared speed of sound parameter is quite zero for past, present and some phase of future regime. It only shows some unphysical situation for very very late-time cosmic expansion. It is worth mentioning here that our results are consistent with those of reconstructed THDE model in general relativity [28] as well as THDE BD model [39].