A Fuzzy Programming Method for Modeling Demand Uncertainty in the Capacitated Road–Rail Multimodal Routing Problem with Time Windows

Abstract

Demand uncertainty is an important issue that influences the strategic, tactical, and operational-level decision making in the transportation/logistics/supply chain planning. In this study, we explore the effect of demand uncertainty on the operational-level freight routing problem in the capacitated multimodal transportation network that consists of schedule-based rail transportation and time-flexible road transportation. Considering the imprecise characteristic of the demand, we adopt fuzzy set theory to model its uncertainty and use trapezoidal fuzzy numbers to represent the fuzzy demands. We set multiple transportation orders as the optimization object and employ soft time windows to reflect the customer requirement on on-time transportation. Under the above situation, we establish a fuzzy mixed integer nonlinear programming (FMINLP) model to formulate the capacitated road–rail multimodal routing problem with demand uncertainty and time windows. We first use the fuzzy expected value model and credibility measure based fuzzy chance-constrained programming to realize the defuzziness of the model and then adopt linearization technique to reformulate the crisp model to finally generate an equivalent mixed integer linear programming (MILP) model that can be solved by standard mathematical programming software. Finally, a numerical case is presented to demonstrate the feasibility of the proposed method. Sensitivity analysis and fuzzy simulation are combined to quantify the effect of demand uncertainty on the routing problem and also reveal some helpful insights and managerial implications.

1. Introduction

As an effective alternative to the road transportation that is the most typical representative of traditional monomodal transportation, road–rail multimodal transportation combines the good mobility of road transportation in short- or medium-distance pickup and delivery and the mass capacity and outstanding reliability of rail transportation in long-distance transportation, which can provide the customers with seamless door-to-door services [1,2]. Furthermore, by using the standard containers to carry the goods, the mechanization of transportation can be significantly improved, which leads to a remarkable enhancement of the transportation efficiency [3]. Nierat [4,5] points out that transportation distance is an important factor that influences the economic competition between road–rail multimodal transportation and the monomodal road transportation. As for the long-haul transportation setting, empirical studies conducted by Janic [6], Bookbinder and Fox [7], Du et al. [8] and Göçmen and Erol [9] show that multimodal transportation is more competitive than the monomodal transportation in improving not only the transportation economy but also efficiency and sustainability, especially in an extensive global commodity circulation network. The freight industry in Europe is mainly enabled by road transportation [6]. In Northern America (including the United States, Canada, and Mexico) and Asia, the focus is mainly shifting transportation to more cost-efficient and environmental-friendly modes. There, multimodal transportation is more economically and environmentally viable and shows better competition than road transportation, and thereby gets wide utilization in these areas [6,7,8]. Especially in China, since the 1980s, road–rail multimodal transportation was widely applied in the container transportation and now plays an important role in China’s inland transportation system for both international and domestic business. The transportation industry attached great importance to promote the road–rail multimodal transportation in practice, which motivates its optimization research. Among relative optimization problems (e.g., network design problem [10,11,12] and location problem [13,14]), the road–rail multimodal routing problem, an operational-level planning problem, drew attention from both researchers and practitioners and has become one of the forefronts in the transportation optimization field [15,16].

The road–rail multimodal routing problem is related to the optimal utilization of the existing transportation facilities and equipment in the multimodal transportation network. It aims at planning the best origin-to-destination routes to move the containers through the road–rail multimodal transportation network based on the transportation orders proposed by customers [3,17,18]. As a service-oriented planning, the road–rail multimodal routing always take satisfying the customer demand by providing the best transportation scheme as its goal.

First of all, the customers would like to pay least expenditure to accomplish their transportation orders, so that they cut down on the logistics cost to reduce the entire product cost in order to make more profit [19]. Consequently, minimizing the customers’ expenditure used to accomplish their transportation orders is always set as an essential optimization objective of the multimodal routing modelling, regardless of single-objective modelling (e.g., Sun and Lang [17], Sun et al. [3], Ayar and Yaman [20], and Hrušovský et al. [21]) or multi-objective modelling (e.g., Chang [19], Xiong and Wang [22], Xiong and Dong [23], and Sun and Chen [24]). A state-of-the-art representation that can be used to formulate the expenditure paid to accomplish the transportation orders is “generalized costs” [25]. Generalized costs covers all the expenditure created in the whole transportation process, including the transportation costs created in the pre-haul, long-haul and end-haul processes, handling costs (mainly refer to the loading/unloading operation costs) and inventory costs created in the transshipment process [20,26]. Moreover, generalized costs also contains penalty costs when there are soft due dates and on-time delivery is considered [21] and emission costs (e.g., carbon emission costs) when sustainability issues are considered [17]. Therefore in this study, minimizing the generalized costs for accomplishing multiple transportation orders will be the optimization objective of our road–rail multimodal routing model.

Secondly, besides transportation economy, customers also show considerable concern if their transportation orders can be accomplished punctually, especially when the ‘just-in-time’ production strategy gets more and more popular and is employed by various industries [27,28]. As a result, improving the transportation efficiency is another important goal demanded by customers’ due dates of accomplishing the transportation order shows the customer requirement on transportation efficiency. Majority of the existing literature formulates the due dates as time points and constructs a hard constraint that the accomplishment of a transportation order should not be later than its due date [3,17,26,29,30,31,32]. Zhang et al. [33] formulate the due dates as time windows and also propose a hard constraint that the accomplishment of a transportation order must falls into its time window. There are also studies that consider the due dates represented by time points are soft and could be violated to a certain degree [21,34]. To make the setting of the due date better match the customer requirement on transportation efficiency, we consider a soft time window more suitable than the above forms, because (1) compared with time point, it can better describe the customer requirement on on-time transportation that the transportation orders should be accomplished neither too early nor too late, and (2) compared with hard due date, it can reflect the fact that customer can tolerate the early or delayed accomplishment of a transportation order with some extent. In this study, we use a positive parameter named penalty costs per TEU per hour to try to avoid the early or delayed accomplishment of all the transportation orders. The entire penalty costs of all the transportation orders are integrated into the generalized costs. The minimization of the generalized costs helps to lower the penalty costs, which further helps to optimize the timeliness of accomplishing the transportation orders. The setting of penalty costs has already been employed by Hrušovský [21] and Zhao et al. [34] in improving the transportation efficiency of the multimodal routing that uses time points to represent the due dates. However, these two studies only use penalty costs to avoid delayed accomplishment.

Last but not least, growing attention is paid to the reliability of transportation plans that is influenced by uncertainty [35]. The uncertainty can disrupt the transportation process, which will influence whether the transportation orders can be accomplished successfully [3]. Thus, improving the reliability of road–rail multimodal routing by considering uncertainty is vitally necessary. The uncertain source from the side of customers is their demands [36]. The road–rail multimodal routing decision making is an advance work that should be done earlier than the actual transportation starts [18,37]. During the decision-making process, the rapidly changed market makes customers difficult to determine their demands ahead of time, and the lack of effective information communication between customers and planners will also lead to the imprecision of demand data [38]. The customers can define their demands only when the actual transportation starts [35]. Therefore, demand uncertainty exists in the road–rail multimodal routing decision-making process.

Majority of the current studies on the multimodal routing neglects the demand uncertainty and use deterministic numbers to represent the demands [2,3,17,19,20,21,22,23,24,26,29,30,31,32,34]. When using deterministic data to estimate the uncertain parameters, underestimation and overestimation might exist [18]. The multimodal transportation network is capacitated [18]. Underestimation on the demand might result in the infeasibility of the planned road–rail multimodal route since the actual demand might exceed the capacities of some transportation services on the route. Overestimation might mean that the actual best road–rail multimodal route is identified to be infeasible since the estimated demand exceeds the capacities of some transportation services on the actual best route, while the actual demand satisfies the capacity constraint. When the decision makers need to serve multiple transportation orders, underestimation and overestimation of the demands might exist simultaneously, which makes the situation more complicated. Consequently, using deterministic demands in the road–rail multimodal routing problem is clearly infeasible. The demand uncertainty hence should be integrated into the problem in order to improve the transportation reliability.

Demand uncertainty can be formulated by fuzzy programming and stochastic programming. Currently, there are limited studies on the road–rail multimodal routing problem that consider the demand uncertainty. Existing literature addresses the demand uncertainty by fuzzy programming. Fazayeli et al. [36], Sun et al. [37], and Yu et al. [39] utilize triangular fuzzy numbers to represent the uncertain demands when optimizing the multimodal (location-) routing problem and employ fuzzy possibility measure to model the objective and constraints with fuzzy demands. To the best of our knowledge, there is no literature that adopts stochastic programming to deal with the demand uncertainty in the multimodal routing problem. However, stochastic programming gains wide application in the vehicle routing problem with demand uncertainty, an optimization problem that also belongs to the operational level of transportation planning [40]. Various studies on the vehicle routing problem with stochastic demands can be found, e.g., Gaur et al. [41], Gutierrez et al. [42], Mendoza et al. [43], and Bianchi et al. [44].

In most cases, are not enough data for decision makers to fit the probability distributions of demands [10,45,46], which reduces the feasibility of stochastic programming in dealing with the uncertainty. However, it is easier for decision makers to give their own estimations on the uncertain parameter. The estimation might be pessimistic, optimistic, and moderately optimistic [47]. Therefore, it is worthwhile to use fuzzy logic to address the uncertainty according to the expert experiences and opinions. There are three forms of fuzzy numbers that are most commonly used in the fuzzy programming model, i.e., interval numbers, triangular fuzzy numbers and trapezoidal fuzzy numbers [48]. Compared with triangular fuzzy numbers that have already been used in modeling the road–rail multimodal routing problem with demand uncertainty [36,37,39], trapezoidal fuzzy numbers is more flexible since it allows that different decision makers hold different opinions on the most likely values of the demand and hence better match the practical decision-making situation [18]. Consequently, in this study, we select trapezoidal fuzzy numbers to model the uncertain demand.

Additionally, the existing studies [36,37,39] use fuzzy possibility measure to build the fuzzy chance constraint(s). As stressed by Zarandi et al. [45] and Zheng and Liu [46], fuzzy possibility measure is not self-dual, i.e., a fuzzy event might fail even its possibility is 1. However, fuzzy credibility measure is self-dual, i.e., a fuzzy event must hold when its credibility is 1 and must fail when its credibility is 0. Therefore, fuzzy credibility measure is more suitable to build fuzzy chance constraint(s) and will be applied in this study.

Above all, as for the road–rail multimodal routing problem, there is still research potential to improve its efficiency and reliability by considering soft due date time windows and demand uncertainty, respectively. Furthermore, as demonstrated in various vehicle routing studies [45,46,49], the reliability of routing related to demand uncertainty or travel time uncertainty influences its economy and efficiency. Therefore, it is meaningful to explore the effect of demand uncertainty on the capacitated road–rail multimodal routing problem with time windows, which will be the main contribution of this study.

The remaining sections of this study are organized as follows. In Section 2, we formulate demand uncertainty by trapezoidal fuzzy numbers. In Section 3, we describe a multimodal routing scenario with a specific network topology and a schedule-constrained transportation process. In Section 4, a FMINLP model is established for the capacitated road–rail multimodal routing problem with fuzzy demands and soft due date time windows under the given scenario, in which the objective is to minimize the generalized costs for accomplishing multiple transportation orders. In Section 5, we present a fuzzy programming method to address the fuzzy problem by using fuzzy expected value model and fuzzy chance constraint based on fuzzy credibility measure to separately deal with the fuzzy objective and fuzzy constraint. Linearization technique is then used in the same section to generate an equivalent MILP model so that the problem can be solved by standard mathematical programming software. In Section 6, a numerical case is given to demonstrate the feasibility of the proposed method. We quantify the effect of demand uncertainty on the economy and efficiency of the road–rail multimodal routing by sensitivity analysis, and proposing a framework based on fuzzy simulation to help decision makers to make effective tradeoff among transportation economy, efficiency, and reliability. Finally, the conclusions of this study are drawn in Section 7.

2. Modeling Demand Fuzziness

Considering the infeasibility of formulating stochastic demand that has been stated in Section 1, in this study, we employ fuzzy set theory to model demand uncertainty by using trapezoidal fuzzy numbers. Trapezoidal fuzzy numbers use four prominent points to describe the imprecise parameters, which can be seen in Figure 1 [45]. For a trapezoidal fuzzy number $\tilde{e}=\left(e_1, e_2, e_3, e_4\right)$ that measures a fuzzy demand [50], the definition of its prominent points are as follows.

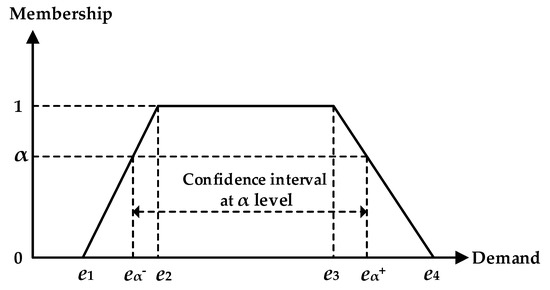
Figure 1. Fuzzy demand represented by trapezoidal fuzzy number.

(1) The value $e_1$ is the most pessimistic estimation, which is unlikely in practice but still slightly possible in the real world if the case turns out badly.

(2) The interval $\left[e_2, e_3\right]$ is the most likely estimation and corresponds to the most realistic case. It matches the fact that different decision makers might hold different opinions on the most likely values of a demand.

(3) The value $e_4$ is the most optimistic estimation, which is as unlikely as $e_1$ in the real world but might be possible if the case turns out well.

The membership function of trapezoidal fuzzy number $\tilde{e}$ is as Equation (1) [18].

$${\mu }_{\tilde{e}}\left(e\right)=\{\begin{array}{c}\hspace{1em}\frac{e-e_1}{e_2-e_1},\mathrm{if}{e}_1\le e<e_2\\ 1,\mathrm{if}{e}_2\le e<e_3\hfill \\ \hspace{1em}\frac{e-e_4}{e_3-e_4},\mathrm{if}{e}_3\le e<e_4\\ 0,\mathrm{otherwise}\hfill \end{array}$$

(1)

The α-cut level of trapezoidal fuzzy number $\tilde{e}$ is ${\tilde{e}}_{\alpha }=\left\{e|{\mu }_{\tilde{e}}\left(e\right)\ge \alpha \right\}$ where $\alpha \in \left[0, 1\right]$. As illustrated by Figure 1, $\left[e_{\alpha }^{-}, e_{\alpha }^{+}\right]$ is the confidence interval of $\tilde{e}$ at α level where $e_{\alpha }^{-}$ and $e_{\alpha }^{+}$ are the lower bound and upper bound of the interval, respectively.

3. Road–Rail Multimodal Routing Scenario

The road–rail multimodal routing should be modelled under a specific scenario, in which the consolidation network to model the transportation system should be determined [51] and schedules should be included in the routing modelling when scheduled transportation modes (e.g., rail and maritime) are considered [19].

3.1. Multimodal Transportation Network

Road–rail multimodal transportation combines the scheduled rail transportation and unscheduled (time-flexible) road transportation to move containers from origins to destinations. The most typical transportation chain utilized in practice has three stages: pick-up (or pre-haul), long haul, and delivery (end-haul) [2,52]. By considering the advantages of road transportation for short- or medium-distance collection and distribution and of rail transportation for long-distance transportation, the pick-up and delivery are carried out by road and the long haul is by rail [4,10]. Consequently, the transportation network possesses a hub-and-spoke structure. A hub-and-spoke network is most suitable for a road–rail multimodal transportation system by integrating the respective advantages of rail and road transportation [53]. The hub-and-spoke network is thereby the backbone of the road–rail multimodal transportation system explored in this study. In such a network, the rail terminals play the role of the multimodal hubs where transshipments between rail and road transportation are conducted. The origins and destinations are the spokes.

It should be also noted that there might exist some transportation orders with tight due dates [54]. Such transportation orders should be accomplished in a short period. However, rail transportation should be operated according to fixed schedules [55], which reduces its flexibility in space and time. Therefore, it might be infeasible to involve rail transportation in accomplishing such transportation orders. The transportation of containers of such transportation orders might be limited to the all-road transportation [3]. Above all, the multimodal transportation network is a combination of hub-and-spoke network and point-to-point network, which is shown as Figure 2 [3].

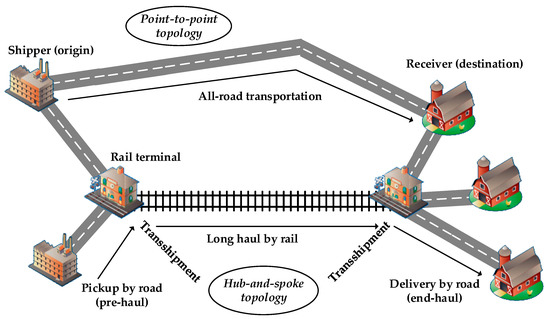
Figure 2. Topological structure of the multimodal transportation network.

3.2. Schedule-Constrained Multimodal Transportation Process

Unlike many studies that only consider fixed departure time [21,56,57,58] or fixed service/operation time window [19,20] of scheduled transportation, we formulate the rail schedule that regulates by more than just scheduled departure time or operation time window to make the routing optimization better match the real-world transportation situation. The schedule of rail transportation restricts the route feasibility in space by fixed train routes and in time by scheduled departure/arrival times and scheduled operation time windows at rail terminals. Such rail schedule-based constraints have been stressed in our previous studies [3,17,26] and are of the key factors to ensure that the planned best road–rail multimodal routes are feasible in both space and time.

The multimodal routing problem in this study is in the context of a transportation network that combines hub-and-spoke and point-to-point structures. The hub-and-spoke network is a three-stage full-truck-load (FTL) system [35]. The vehicle usage strategy applied by container trucks when serving pickup and delivery is thereby FTL. The point-to-point transportation by road is to move containers of a transportation order from an origin to the associated destination directly, which is also a FTL strategy [59]. Above all, all the road transportation implements FTL strategy in the road–rail multimodal transportation network. A road transportation arc contains a group of container truck fleets, and a fleet of container trucks only serves one transportation order. Consequently, as for this study, there is a direct transportation problem instead of a vehicle routing problem associated with a less-than-truck-load (LTL) strategy that is involved in the road transportation.

Using the most representative “pickup-long haul-delivery” route in the road–rail multimodal transportation system for demonstration, the transportation process that coordinates the scheduled rail transportation and time-flexible road transportation is shown as Figure 3. Such schedule-constrained multimodal transportation process will be modelled in the road–rail multimodal routing problem.

Figure 3. Schedule-constrained multimodal transportation process.

4. Mathematical Model

4.1. Presenting the Hypotheses

The routing problem is oriented on the following hypotheses to make the optimization modeling rigorous.

Hypothesis 1.

All containers are ISO standardized and are measured in 20 ft equivalent units (TEU) [34].

Hypothesis 2.

The batch of containers in one transportation order is unsplittable to ensure the integrity of each transportation order, i.e., the transportation of the containers of each transportation order is required to follow one origin-to-destination route [17,60].

Hypothesis 3.

All containers punctually depart from their origins at their prescribed release times claimed in the corresponding transportation orders [17,34].

Hypothesis 4.

The route for each transportation order can be either a combination of rail and road or an all-road transportation chain.

Hypothesis 5.

The violation of the due date time windows, i.e., early and delayed accomplishment of transportation orders, leads to penalty costs.

4.2. Defining the Parameters and Variables

In this study, we adopt the parameters and variables defined in Table 1 to construct the optimization model of the specific road–rail multimodal routing problem.

Table 1. Symbols and their representations.

Parameters regarding the Transportation Orders
$F$	Set of all the targeted transportation orders in the road–rail multimodal routing problem.
$f$	Index of transportation orders, and $f\in F$.
${\tilde{e}}_f$	Fuzzy demand of the containers of transportation order $f$, and ${\tilde{e}}_f=\left(e_f^1,e_f^2, e_f^3, e_f^4\right)$.
${\omega }_f^{-}$	Index of the origin of transportation order $f$.
${\omega }_f^{+}$	Index of the destination of transportation order $f$.
$releas{e}_f$	Release time of the containers of transportation order $f$ at its origin.
$\left[du{e}_f^{-},du{e}_f^{+}\right]$	Due date time window of transportation order $f$ claimed by customer, where ${\mathrm{due}}_f^{-}$ and ${\mathrm{due}}_f^{+}$ are separately the lower bound and upper bund of the time window.
Parameters regarding the Road–Rail Multimodal Transportation Network
$N$	Node set of the network.
$A$	Directed arc set of the network.
$V$	Transportation service set in the network.
$h,i,j$	Indices of the nodes, and $h,i,j\in N$.
$\left(i,j\right)$	Directed arc from node $i$ to node $j$, and $\left(i,j\right)\in A$.
$k,l$	Indices of the transportation services, and $k,l\in V$.
$V_{ij}$	Transportation service set on directed arc $\left(i,j\right)$, and $V_{ij}\subseteq V$.
$U_{ij}$	Set of rail services operated on directed arc $\left(i,j\right)$, and $U_{ij}\subseteq V_{ij}$.
$W_{ij}$	Set of road services operated on directed arc $\left(i,j\right)$, and $W_{ij}\subseteq V_{ij}$.
$N_i^{-}$	Set of the predecessor nodes to node $i$, and $N_i^{-}\subseteq N$
$N_i^{+}$	Set of the successor nodes to node $i$, and $N_i^{+}\subseteq N$
Parameters regarding the Transportation Services
$\left[o{p}_{ki}^{-},o{p}_{ki}^{+}\right]$	Operation time window of rail service $k$ at node $i$, where $o{p}_{ki}^{-}$ is the operation start instant and $o{p}_{ki}^{+}$ is the operation cutoff instant.
$q_{ijk}$	Capacity of transportation service $k$ on directed arc $\left(i,j\right)$. For rail service $k$, $q_{ijk}$ is the available carrying capacity of a freight train. For road service $k$, $q_{ijk}$ is the entire capacity of a group of truck fleets that it can provide.
$t_{ijk}$	Travel time in hour of road service $k$ on directed arc $\left(i,j\right)$.
$d_{ijk}$	Travel distance in km of transportation service $k$ on directed arc $\left(i,j\right)$.
$c_{ijk}$	Transportation costs per TEU of transportation service $k$ on directed arc $\left(i,j\right)$.
$c_k$	Loading/unloading operation costs per TEU of transportation service $k$.
$c_{store}$	Inventory costs per TEU per hour.
$c_{pen}$	Penalty costs per TEU per hour.
Other Parameter
$L$	Large enough positive number.
Decision Variables
$x_{ijk}^f$	0–1 variable: if the containers of transportation order $f$ is transported by transportation service $k$ on directed arc $\left(i,j\right)$, $x_{ijk}^f$ = 1; otherwise, $x_{ijk}^f$ = 0.
$y_i^f$	Non-negative variable: the arrival time of the containers of transportation order $f$ at node $i$.
$z_{ijk}^f$	Non-negative variable: the inventory time in hour of the containers of transportation order $k$ at node $i$ before being transported by rail service $k$ on directed arc $\left(i,j\right)$.

4.3. Establishing the Optimization Objective

The objective of the model is to minimize the total generalized costs for accomplishing multiple transportation orders. In this study, the generalized costs include transportation costs en route (Equation (2)), loading/unloading operation costs at terminals (Equation (3)), inventory costs at terminals (Equation (4)) and penalty costs caused by early or delayed accomplishment of transportation orders (Equation (5)).

$$minimize{\displaystyle \sum }_{f\in F}{\displaystyle \sum }_{\left(i,j\right)\in A}{\displaystyle \sum }_{k\in V_{ij}}{c}_{ijk}·{\tilde{e}}_f·x_{ijk}^f$$

(2)

$$+{\displaystyle \sum }_{f\in F}{\displaystyle \sum }_{i\in N}{\displaystyle \sum }_{h\in N_i^{-}}{\displaystyle \sum }_{l\in V_{hi}}{c}_l·{\tilde{e}}_f·x_{hil}^f+{\displaystyle \sum }_{f\in F}{\displaystyle \sum }_{i\in N}{\displaystyle \sum }_{j\in N_i^{+}}{\displaystyle \sum }_{k\in V_{ij}}{c}_k·{\tilde{e}}_f·x_{ijk}^f$$

(3)

$$+{\displaystyle \sum }_{f\in F}{\displaystyle \sum }_{\left(i,j\right)\in A}{\displaystyle \sum }_{k\in U_{ij}}{c}_{store}·{\tilde{e}}_f·z_{ijk}^f$$

(4)

$$+{\displaystyle \sum }_{f\in F}{c}_{pen}·{\tilde{e}}_f·\left[max\left\{du{e}_f^{-}-y_{{\omega }_f^{+}}^f,0\right\}+max\left\{y_{{\omega }_f^{+}}^f-du{e}_f^{+},0\right\}\right]$$

(5)

4.4. Formulating the the Constraints

4.4.1. Container Flow Conservation Constraint

Equation (6) ensures the smooth connection between the nodes and arcs on the route of each transportation order.

$$\begin{array}{c}{\displaystyle \sum _{j\in N_i^{+}}}{\displaystyle \sum _{k\in V_{ij}}}{x}_{ijk}^f-{\displaystyle \sum _{h\in N_i^{-}}}{\displaystyle \sum _{l\in V_{hi}}}{x}_{hil}^f=\{\begin{array}{cc}1\hfill & \forall i={\omega }_f^{-}\\ 0\hfill & \forall i\in N\backslash \left\{{\omega }_f^{-},{\omega }_f^{+}\right\}\hspace{1em}\forall f\in F\\ -1\hfill & \forall i={\omega }_f^{+}\end{array}\end{array}$$

(6)

4.4.2. Constraint Representing Hypothesis 2

Equation (7) ensures that no more than one transportation service operated on a certain arc can be used to move the containers of each transportation order.

$$\begin{array}{ccc}{\displaystyle \sum _{k\in V_{ij}}}{x}_{ijk}^f\le 1& \forall f\in F& \forall \left(i,j\right)\in A\end{array}$$

(7)

4.4.3. Bundle Capacity Constraint

Bundling is the core process of transportation sector [61]. In this study, the capacitated road–rail multimodal transportation network consists of point-to-point structure and hub-and-spoke structure and accordingly is a combination of direct bundling network and complex bundling network [61,62]. We formulate the bundle capacity constraint as Equation (8) to ensure that the containers of different transportation orders bundled in a common train (when $k\in U_{ij}$) or a common group of truck fleets (when $k\in W_{ij}$) do not exceed the corresponding capacity.

$$\begin{array}{ccc}{\displaystyle \sum _{f\in F}}{\tilde{e}}_f·x_{ijk}^f\le q_{ijk}& \forall \left(i,j\right)\in A& \forall k\in V_{ij}\end{array}$$

(8)

4.4.4. Constraint Representing Hypothesis 3

Equation (9) ensures that the containers of each transportation order will punctually depart from the origin at the corresponding release time.

$$\begin{array}{cc}{y}_{{\omega }_f^{-}}^f=releas{e}_f& \forall f\in F\end{array}$$

(9)

4.4.5. Operation Time Window Constraint

Equation (10) ensures that if a rail service is selected to move the containers of a transportation order, the arrival time of the containers at the transshipping node should not be later than the upper bound of the rail service’s operation time window at the same node.

$$\begin{array}{cc}\begin{array}{cc}{y}_i^f\le o{p}_{ki}^{+}·x_{ijk}^f+L·\left(1-x_{ijk}^f\right)& \forall f\in F\end{array}& \begin{array}{cc}\forall \left(i,j\right)\in A& \forall k\in U_{ij}\end{array}\end{array}$$

(10)

4.4.6. Compatibility Requirement Constraints among Variables

Equations (11) and (12) compute the arrival time of the containers of each transportation order at the nodes covered on the planned route separately by road services and rail services. Note that when using rail service to move containers from node $i$ to node $j$, the arrival time of the containers of transportation order $f$ at node $j$ should be $o{p}_{kj}^{-}$ instead of the scheduled arrival instant of rail service $k$ at node $j$, because the containers should wait until $o{p}_{kj}^{-}$ and then start to get transshipped from container train to trucks. Equation (13) computes the inventory times of the containers of each transportation order at the road-to-rail transshipping nodes covered on the planned route. Note that the inventory is needed only when the arrival time of the containers at road-to-rail the transshipping nodes are earlier than the lower bound of the operation time window of the selected successor rail service. When such the arrival time falls into the operation time window, the transshipment of the containers will be operated immediately without inventory.

$$\begin{array}{cc}\begin{array}{cc}\left(y_i^f+t_{ijk}-y_j^k\right)·x_{ijk}^f=0& \forall f\in F\end{array}& \begin{array}{cc}\forall \left(i,j\right)\in A& \forall k\in W_{ij}\end{array}\end{array}$$

(11)

$$\begin{array}{cc}\begin{array}{cc}\left(o{p}_{kj}^{-}-y_j^k\right)·x_{ijk}^f=0& \forall f\in F\end{array}& \begin{array}{cc}\forall \left(i,j\right)\in A& \forall k\in U_{ij}\end{array}\end{array}$$

(12)

$$\begin{array}{cc}\left(\max \left\{0,o{p}_{kj}^{-}-y_i^f\right\}-z_{ijk}^f\right)·x_{ijk}^f=0& \begin{array}{ccc}\forall f\in F& \forall \left(i,j\right)\in A& \forall k\in U_{ij}\end{array}\end{array}$$

(13)

4.4.7. Variable Domain Constraints

Equations (14)–(16) constrain the domains of the three variables according to their definitions.

$$\begin{array}{cc}\begin{array}{cc}{x}_{ijk}^f\in \left\{0,1\right\}& \forall f\in F\end{array}& \begin{array}{cc}\forall \left(i,j\right)\in A& \forall k\in V_{ij}\end{array}\end{array}$$

(14)

$$\begin{array}{ccc}{y}_i^f\ge 0& \forall f\in F& \forall i\in N\end{array}$$

(15)

$$\begin{array}{cc}\begin{array}{cc}{z}_{ijk}^f\ge 0& \forall f\in F\end{array}& \begin{array}{cc}\forall \left(i,j\right)\in A& \forall k\in U_{ij}\end{array}\end{array}$$

(16)

5. Solution Method

The proposed mathematical model in Section 4 is a FMINLP model. To solve the fuzzy road–rail multimodal routing problem, first of all, defuzziness of the fuzzy model should be conducted to generate a crisp model [63]. Then, in order to enable the problem to be solved by any standard mathematical programming software, the nonlinear model should be converted into a linear model [3,17,26]. Finally, we obtain a MILP model that we can solve it by Branch-and-Bound Algorithm run by mathematical programming software Lingo to get the global optimal solution. In summary, the two-stage solution procedure for the problem is illustrated by Figure 4.

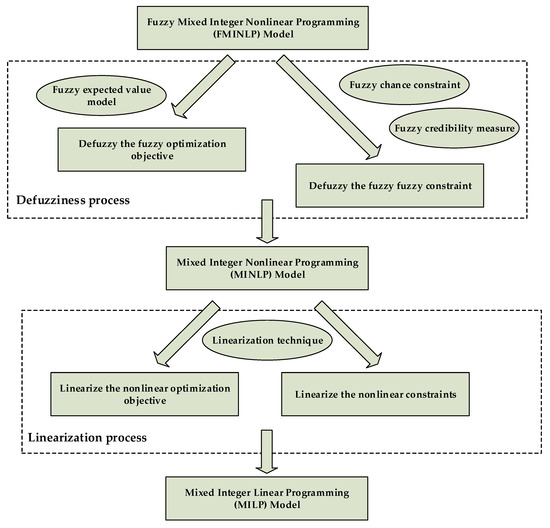
Figure 4. Solution procedure for the road–rail multimodal routing problem.

5.1. Defuzzying the Fuzzy Optimization Objective by Fuzzy Expected Value Model

Fuzzy expected value model is widely used to deal with the objective functions with fuzzy parameters [10,63,64]. It aims at minimizing the expected value of the objective functions (Equation (17)).

$$\begin{gathered} minimize{\displaystyle \sum }_{f\in F}{\displaystyle \sum }_{\left(i,j\right)\in A}{\displaystyle \sum }_{k\in V_{ij}}{c}_{ijk}·E\left[{\tilde{e}}_f\right]·x_{ijk}^f \\ +{\displaystyle \sum }_{f\in F}{\displaystyle \sum }_{i\in N}{\displaystyle \sum }_{h\in N_i^{-}}{\displaystyle \sum }_{l\in V_{hi}}{c}_l·E\left[{\tilde{e}}_f\right]·x_{hil}^f+{\displaystyle \sum }_{f\in F}{\displaystyle \sum }_{i\in N}{\displaystyle \sum }_{j\in N_i^{+}}{\displaystyle \sum }_{k\in V_{ij}}{c}_k·E\left[{\tilde{e}}_f\right]·x_{ijk}^f \\ +{\displaystyle \sum }_{f\in F}{\displaystyle \sum }_{\left(i,j\right)\in A}{\displaystyle \sum }_{k\in U_{ij}}{c}_{store}·E\left[{\tilde{e}}_f\right]·z_{ijk}^f \\ +{\displaystyle \sum }_{f\in F}{c}_{pen}·E\left[{\tilde{e}}_f\right]·\left[max\left\{du{e}_f^{-}-y_{{\omega }_f^{+}}^f,0\right\}+max\left\{y_{{\omega }_f^{+}}^f-du{e}_f^{+},0\right\}\right] \end{gathered}$$

(17)

For a fuzzy demand ${\tilde{e}}_f=\left(e_f^1,e_f^2, e_f^3, e_f^4\right)$, its expected value is $E\left[{\tilde{e}}_f\right]=\frac{e_f^1+e_f^2+e_f^3+e_f^4}{4}$ and can express the corresponding auxiliary crisp value of ${\tilde{e}}_f$. Based on the fuzzy expected value model, the fuzzy objective functions (Equations (2)–(5)) of the FMINLP model can be reformulated by the following crisp functions.

$$\begin{gathered} minimize{\displaystyle \sum }_{f\in F}{\displaystyle \sum }_{\left(i,j\right)\in A}{\displaystyle \sum }_{k\in V_{ij}}{c}_{ijk}·\frac{e_f^1+e_f^2+e_f^3+e_f^4}{4}·x_{ijk}^f \\ +{\displaystyle \sum }_{f\in F}{\displaystyle \sum }_{i\in N}{\displaystyle \sum }_{h\in N_i^{-}}{\displaystyle \sum }_{l\in V_{hi}}{c}_l·\frac{e_f^1+e_f^2+e_f^3+e_f^4}{4}·x_{hil}^f+{\displaystyle \sum }_{f\in F}{\displaystyle \sum }_{i\in N}{\displaystyle \sum }_{j\in N_i^{+}}{\displaystyle \sum }_{k\in V_{ij}}{c}_k·\frac{e_f^1+e_f^2+e_f^3+e_f^4}{4}·x_{ijk}^f \\ +{\displaystyle \sum }_{f\in F}{\displaystyle \sum }_{\left(i,j\right)\in A}{\displaystyle \sum }_{k\in U_{ij}}{c}_{store}·\frac{e_f^1+e_f^2+e_f^3+e_f^4}{4}·z_{ijk}^f \\ +{\displaystyle \sum }_{f\in F}{c}_{pen}·\frac{e_f^1+e_f^2+e_f^3+e_f^4}{4}·\left[max\left\{du{e}_f^{-}-y_{{\omega }_f^{+}}^f,0\right\}+max\left\{y_{{\omega }_f^{+}}^f-du{e}_f^{+},0\right\}\right] \end{gathered}$$

(17)

5.2. Defuzzying the Fuzzy Constraint by Fuzzy Chance Constraint and Fuzzy Credibility Measure

Fuzzy chance constraint can be applied to find the corresponding auxiliary crisp form of the fuzzy constraint based on fuzzy possibility, necessity, and credibility measures [45,46,65]. Considering the self-dual property of fuzzy credibility measure over the rest two measures, in this study, we employ a fuzzy chance constraint based on fuzzy credibility measure to deal with the bundling capacity constraint that involve fuzzy demands in it. The corresponding fuzzy chance constraint of Equation (8) is as Equation (18) where $\alpha$ is the confidence level that is determined by decision makers subjectively and falls into range $\left[0, 1\right]$.

$$\begin{array}{ccc}Cr\left\{{\displaystyle \sum _{f\in F}}{\tilde{e}}_f·x_{ijk}^f\le q_{ijk}\right\}\ge \alpha & \forall \left(i,j\right)\in A& \forall k\in V_{ij}\end{array}$$

(18)

$Cr\left\{{\displaystyle {\sum }_{f\in F}}{\tilde{e}}_f·x_{ijk}^f\le q_{ijk}\right\}$ in Equation (18) can be transformed into Equation (19) according to the operational rule of fuzzy numbers.

$$Cr\left\{\left(q_{ijk}-{\displaystyle \sum }_{f\in F}{e}_f^4·x_{ijk}^f,q_{ijk}-{\displaystyle \sum }_{f\in F}{e}_f^3·x_{ijk}^f,q_{ijk}-{\displaystyle \sum }_{f\in F}{e}_f^2·x_{ijk}^f,q_{ijk}-{\displaystyle \sum }_{f\in F}{e}_f^1·x_{ijk}^f\right)\ge 0\right\}$$

(19)

Given a deterministic number $a$ and a trapezoidal fuzzy number $\tilde{b}=\left(b_1, b_2, b_3, b_4\right)$, they have following relationship when fuzzy credibility measure is adopted [18,45].

$$Cr\left\{a\le \tilde{b}\right\}=\{\begin{array}{l}1,\mathrm{if}a\le b_1\\ \frac{2b_2-b_1-a}{2\left(b_2-b_1\right)},\mathrm{if}{b}_1\le a\le b_2\\ \frac{1}{2},\mathrm{if}{b}_2\le a\le b_3\\ \frac{b_4-a}{2\left(b_4-b_3\right)},\mathrm{if} b_3\le a\le b_4\\ 0,\mathrm{otherwise}\end{array}$$

(20)

According to Equation (20), $Cr\left\{a\le \tilde{b}\right\}\ge \alpha$ equlas $b_4-a\ge 2\alpha \left(b_4-b_3\right)$ when $\alpha \in \left[0, 0.5\right]$ and $2b_2-b_1-a\ge 2\alpha \left(b_2-b_1\right)$ when $\alpha \in (0.5, 1]$. Consequently, Equation (18) can be reformulated as Equation (21) when $\alpha \in \left[0, 0.5\right]$ and Equation (22) when $\alpha \in (0.5, 1]$. Both the following two equations are crisp linear constraints.

$$\begin{array}{ccc}{q}_{ijk}-{\displaystyle \sum _{f\in F}}{e}_f^1·x_{ijk}^f\ge 2·\alpha ·{\displaystyle \sum _{f\in F}}\left(e_f^2-e_f^1\right)·x_{ijk}^f& \forall \left(i,j\right)\in A& \forall k\in V_{ij}\end{array}$$

(21)

$$\begin{array}{ccc}{q}_{ijk}+{\displaystyle \sum _{f\in F}}\left(e_f^4-2·e_f^3\right)·x_{ijk}^f\ge 2·\alpha ·{\displaystyle \sum _{f\in F}}\left(e_f^4-e_f^3\right)·x_{ijk}^f& \forall \left(i,j\right)\in A& \forall k\in V_{ij}\end{array}$$

(22)

5.3. Reformulating the Nonlinear Model by Linearization Technique

According to the proof given by Sun et al. [3], by using two non-negative auxiliary variables ${\rho }_f$ and ${\phi }_f$ to replace the nonlinear sections $max\left\{du{e}_f^{-}-y_{{\omega }_f^{+}}^f , 0\right\}$ and $max\left\{y_{{\omega }_f^{+}}^f-du{e}_f^{+} , 0\right\}$ and adding the auxiliary constraints shown as Equations (24)–(27), the nonlinear objective function can be linearized as Equation (23).

$$\begin{gathered} minimize {\displaystyle \sum }_{f\in F}{\displaystyle \sum }_{\left(i, j\right)\in A}{\displaystyle \sum }_{k\in V_{ij}}{c}_{ijk}·\frac{e_f^1+e_f^2+e_f^3+e_f^4}{4}·x_{ijk}^f \\ +{\displaystyle \sum }_{f\in F}{\displaystyle \sum }_{i\in N}{\displaystyle \sum }_{h\in N_i^{-}}{\displaystyle \sum }_{l\in V_{hi}}{c}_l·\frac{e_f^1+e_f^2+e_f^3+e_f^4}{4}·x_{hil}^f+{\displaystyle \sum }_{f\in F}{\displaystyle \sum }_{i\in N}{\displaystyle \sum }_{j\in N_i^{+}}{\displaystyle \sum }_{k\in V_{ij}}{c}_k·\frac{e_f^1+e_f^2+e_f^3+e_f^4}{4}·x_{ijk}^f \\ +{\displaystyle \sum }_{f\in F}{\displaystyle \sum }_{\left(i, j\right)\in A}{\displaystyle \sum }_{k\in U_{ij}}{c}_{store}·\frac{e_f^1+e_f^2+e_f^3+e_f^4}{4}·z_{ijk}^f \\ +{\displaystyle \sum }_{f\in F}{c}_{pen}·\frac{e_f^1+e_f^2+e_f^3+e_f^4}{4}·\left({\rho }_f+{\phi }_f\right) \end{gathered}$$

(23)

$$\begin{array}{cc}{\rho }_f\ge du{e}_f^{-}-y_{{\omega }_f^{+}}^f& \forall f\in F\end{array}$$

(24)

$$\begin{array}{cc}{\phi }_f\ge y_{{\omega }_f^{+}}^f-du{e}_f^{+}& \forall f\in F\end{array}$$

(25)

$$\begin{array}{cc}{\rho }_f\ge 0& \forall f\in F\end{array}$$

(26)

$$\begin{array}{cc}{\phi }_f\ge 0& \forall f\in F\end{array}$$

(27)

According to Sun and Lang [17], nonlinear constraints Equations (11), (12), and (13) separately equal linear Equations (28) and (29), Equations (30) and (31), and Equations (32) and (33).

$$\begin{array}{cc}\begin{array}{cc}{y}_i^f+t_{ijk}-y_j^k\ge L·\left(x_{ijk}^f-1\right)& \forall f\in F\end{array}& \begin{array}{cc}\forall \left(i, j\right)\in A& \forall k\in W_{ij}\end{array}\end{array}$$

(28)

$$\begin{array}{cc}\begin{array}{cc}{y}_i^f+t_{ijk}-y_j^k\le L·\left(1-x_{ijk}^f\right)& \forall f\in F\end{array}& \begin{array}{cc}\forall \left(i, j\right)\in A& \forall k\in W_{ij}\end{array}\end{array}$$

(29)

$$\begin{array}{cc}\begin{array}{cc}o{p}_{kj}^{-}-y_j^k\ge L·\left(x_{ijk}^f-1\right)& \forall f\in F\end{array}& \begin{array}{cc}\forall \left(i, j\right)\in A& \forall k\in U_{ij}\end{array}\end{array}$$

(30)

$$\begin{array}{cc}\begin{array}{cc}o{p}_{kj}^{-}-y_j^k\le L·\left(1-x_{ijk}^f\right)& \forall f\in F\end{array}& \begin{array}{cc}\forall \left(i, j\right)\in A& \forall k\in U_{ij}\end{array}\end{array}$$

(31)

$$\begin{array}{cc}{z}_{ijk}^f\ge L·\left(x_{ijk}^f-1\right)+o{p}_{kj}^{-}-y_i^f& \begin{array}{ccc}\forall f\in F& \forall \left(i, j\right)\in A& \forall k\in U_{ij}\end{array}\end{array}$$

(32)

$$\begin{array}{cc}{z}_{ijk}^f\le L·x_{ijk}^f& \begin{array}{ccc}\forall f\in F& \forall \left(i, j\right)\in A& \forall k\in U_{ij}\end{array}\end{array}$$

(33)

After defuzziness in Section 5.1 and Section 5.2 and linearization in Section 5.3, we can get a MILP model for the capacitated road–rail multimodal routing problem with fuzzy demands and soft due date time windows. The optimization objective of the model is Equation (23) and its constraints include Equations (6), (7), (10), (14)–(16), (21), (22), and (24)–(33).

6. Computational Experiment

6.1. Numerical Case

In this section, we present a numerical case to demonstrate the feasibility of the proposed method and further discuss the effect of demand uncertainty on the capacitated road–rail multimodal routing problem with time windows. The multimodal transportation network in the case is shown as Figure 5.

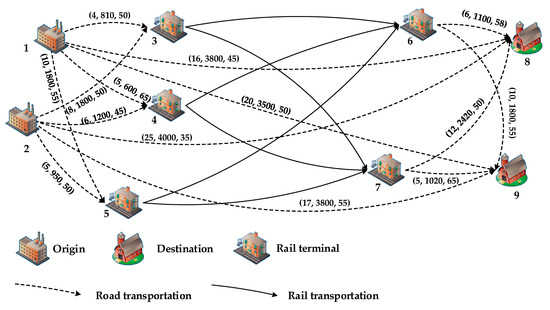
Figure 5. Multimodal transportation network in the numerical case.

The schedules of all the rail services in the multimodal transportation network are given in Table 2. The numbers listed along the road transportation arcs are their travel times in hour, transportation costs in CNY per TEU and transportation capacities in TEU, successively.

Table 2. Schedules of the rail services in the multimodal transportation network.

Rail Service	(3, 6)	(3, 7)	(4, 6)	(4, 7)	(5, 6)	(5, 7)
Operation time window at the predecessor terminal	[5, 7]	[7, 9]	[14, 15]	[11, 12]	[15, 17]	[10, 12]
Lower bound of the operation time window at the successor terminal	11	13	19	15	21	15
Operation period in the number of trains operated per day *	1	1	1	1	1	1
Transportation costs in CNY per TEU	950	1300	1000	1100	1150	800
Transportation capacity in TEU	90	90	80	100	100	85

* The same rail service in different periods is modelled as different services.

The loading/unloading operation costs per TEU of rail service and road service are separately 195 CNY and 20 CNY. The inventory costs per TEU per hour are 3 CNY. The penalty costs per TEU per hour are 50 CNY. It should be noted that the unit penalty costs is set by the decision makers and reflect relative importance of transportation efficiency in the multimodal routing. In practical decision making, multiple attribute decision-making methods, e.g., classical analytic hierarchy process (AHP) method, can be used to help decision makers to set the value in a more precise way [10]. The transportation orders that need to be accomplished in the numerical case is presented in Table 3. Note that all the numbers regarding release time and due date time window are all discretized.

Table 3. Transportation orders in the numerical case.

Order No.	Origin	Destination	Release Time	Due date Time Window	Fuzzy Demand in TEU
1	1	8	8	[18, 27]	(10, 14, 19, 24)
2	1	8	11	[30, 45]	(14, 17, 24, 28)
3	1	9	4	[17, 23]	(7, 11, 16, 21)
4	1	9	13	[40, 50]	(10, 15, 21, 23)
5	2	8	2	[23, 30]	(10, 13, 16, 18)
6	2	8	10	[32, 38]	(6, 11, 13, 15)
7	2	9	3	[18, 27]	(15, 19, 22, 25)
8	2	9	6	[25, 31]	(9, 13, 18, 21)

6.2. Illustration of the Best Road–Rail Multimodal Routes

We use the standard Branch-and-Bound Algorithm to solve the problem formulated by the MILP model. The algorithm is run by Lingo 12 developed by LINDO Systems Inc., Chicago, IL, USA [66]. All the computation is carried out on a ThinkPad Laptop with Intel Core i5-5200U 2.20 GHz CPU 8 GB RAM. When the confidence level $\alpha$ is set to 0.9 by the decision makers, the best road–rail multimodal routes are planned as shown in Table 4.

Table 4. Best road–rail multimodal routes when confidence level is 0.9.

Order No.	Routes	Accomplishment Time	Status
1	$1-$$\mathrm{Road}\to$$4-$$\mathrm{Rail}\to$$6-$$\mathrm{Road}\to$ 8	25	on time
2	$1-$$\mathrm{Road}\to$$3-$$\mathrm{Rail}\to$$6-$$\mathrm{Road}\to$ 8	41	on time
3	$1-$$\mathrm{Road}\to$$4-$$\mathrm{Rail}\to$$7-$$\mathrm{Road}\to$ 9	20	on time
4	$1-$$\mathrm{Road}\to$ 9	33	early
5	$2-$$\mathrm{Road}\to$ 8	27	on time
6	$2-$$\mathrm{Road}\to$ 8	35	on time
7	$2-$$\mathrm{Road}\to$$5-$$\mathrm{Rail}\to$$7-$$\mathrm{Road}\to$ 9	20	on time
8	$2-$$\mathrm{Road}\to$$5-$$\mathrm{Rail}\to$$7-$$\mathrm{Road}\to$ 9	20	early

6.3. Sensivity Analysis of the Capacitated Road–Rail Multimodal Routing with Respect to the Confidence Level

In the fuzzy chance constraint, the confidence level is set by decision makers manually, which might influence the optimization results [3,18,67]. Therefore, it is necessary to explore whether and how demand uncertainty influences the capacitated road–rail multimodal routing via confidence level $\alpha$. In this study, we use sensitivity analysis to test if the routing results change with the variation of confidence level $\alpha$. We increase confidence level $\alpha$ from 0.1 to 1.0 with a step size of 0.1 and gain the best road–rail multimodal routes and corresponding minimal generalized costs, which can be seen in Figure 6.

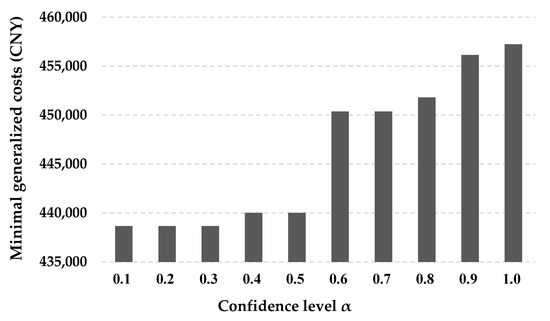
Figure 6. Sensitivity of the minimal generalized costs of the capacitated road–rail multimodal routing problem with respect to the confidence level.

As we can see from Figure 6, following conclusions can be drawn for the case presented in Section 6.1:

(1) The capacitated road–rail multimodal routing is sensitive to the confidence level in the fuzzy chance constraint regarding fuzzy demand. The sensitivity is significant when the confidence level exceeds 0.5.

(2) Increasing confidence level will result in the increase of the minimal generalized costs corresponding to the best road–rail multimodal routes, and the increase is stepwise.

(3) It is impossible for decision makers to plan the best road–rail multimodal routes that can achieve the best transportation economy and best transportation reliability simultaneously.

We also calculate the total hours that lead to penalty costs under different confidence level, which can be seen in Figure 7. As we can see from Figure 7, as for the case presented in Section 6.1, the confidence level also influence the transportation efficiency of the capacitated road–rail multimodal routing.

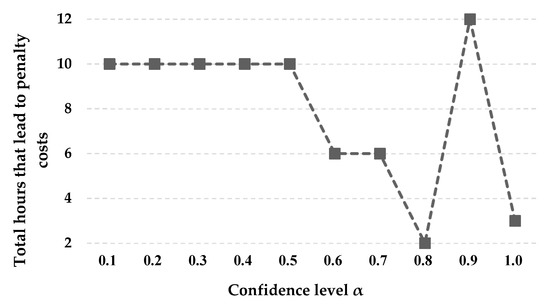
Figure 7. Sensitivity of the total hours that lead to penalty costs with respect to the confidence level.

6.4. Fuzzy Simulation to Determine the Best Confidence Level

As shown in Section 6.3, the confidence level has significant effect on the capacitated multimodal routing with soft due date time windows. Therefore, the decision makers have to decide which confidence level is optimal if they would like to gain a crisp solution to the problem [63].

In the practical decision-making process, the decision makers prefer reliable plans on the road–rail multimodal routes, so that all the transportation orders can be successfully accomplished. Since the transportation efficiency is modeled by penalty costs that are caused by violation of the due date time windows, the generalized costs can reflect a combination of transportation economy and transportation efficiency. Then under acceptable reliability, the decision makers prefer plans with lower generalized costs.

The actual transportation situation should be known to test if the planned road–rail multimodal routes are reliable and if the planned road–rail multimodal routes can lower the generalized costs for accomplishing the transportation orders. However, as claimed in Section 1, the actual demands of all the transportation orders cannot be known exactly during the decision-making process. Still we can simulate the actual transportation situation by using fuzzy simulation [3,18,37].

Fuzzy simulation can randomly generate the actual demand of each transportation order by using the fuzzy membership function of the trapezoidal fuzzy numbers expressed by Equation (1). To better simulate the actual transportation situation, fuzzy simulation should be implemented several times (in this study, the times is set to 50) and we can do some statistical analysis on the planned road–rail multimodal routes under different confidence levels. The procedure of the fuzzy simulation is as Figure 8. The fuzzy simulation results are given in Appendix A.

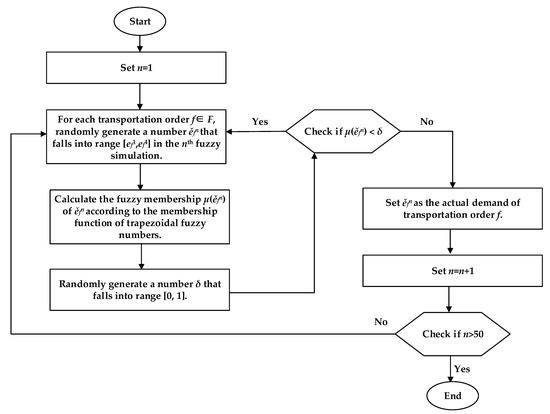
Figure 8. Fuzzy simulation.

In the $n^{th}$ fuzzy simulation ($n$ = 1, 2, …, 50), the simulated actual demand of transportation order $f\in F$ is ${\check{e}}_f^n$. The fuzzy constraint Equation (8) can be transformed into a deterministic constraint as Equation (34).

$$\begin{array}{ccc}{\displaystyle \sum _{f\in F}}{\check{e}}_f^n·x_{ijk}^f\le q_{ijk}& \forall \left(i,j\right)\in A& \forall k\in V_{ij}\end{array}$$

(34)

Using these simulated actual demands, we can first analyze the reliability of the planned best road–rail multimodal routes by testing if Equation (34) is satisfied. If satisfied, the plan is successful for the $n^{th}$ fuzzy simulation, otherwise, failed. The successful ratios of the plans under different confidence levels in the entire 50 fuzzy simulations can quantify the transportation reliability and are indicated by Figure 9. As we can see from Figure 9, for the sake of ensuring that the planned road–rail multimodal routes for the presented case in Section 6.1 are exactly feasible in practice, the confidence level can be 0.6, 0.7, 0.8, 0.9, and 1.0.

Figure 9. Ratio of the successful plans in the 50 fuzzy simulations.

Then we should determine under which confidence level, the planned best road–rail multimodal routes are closer to the actual best road–rail multimodal routes. The actual multimodal routes in the $n^{th}$ fuzzy simulation ($n$ = 1, 2, …, 50) can be simulated by a MILP model whose optimization objective is as Equation (35) and constraints include Equations (6), (7), (10), (14)–(16), (24)–(34).

$$\begin{gathered} minimize {\displaystyle \sum }_{f\in F}{\displaystyle \sum }_{\left(i, j\right)\in A}{\displaystyle \sum }_{k\in V_{ij}}{c}_{ijk}·{\check{e}}_f^n·x_{ijk}^f \\ +{\displaystyle \sum }_{f\in F}{\displaystyle \sum }_{i\in N}{\displaystyle \sum }_{h\in N_i^{-}}{\displaystyle \sum }_{l\in V_{hi}}{c}_l·{\check{e}}_f^n·x_{hil}^f+{\displaystyle \sum }_{f\in F}{\displaystyle \sum }_{i\in N}{\displaystyle \sum }_{j\in N_i^{+}}{\displaystyle \sum }_{k\in V_{ij}}{c}_k·{\check{e}}_f^n·x_{ijk}^f \\ +{\displaystyle \sum }_{f\in F}{\displaystyle \sum }_{\left(i, j\right)\in A}{\displaystyle \sum }_{k\in U_{ij}}{c}_{store}·{\check{e}}_f^n·z_{ijk}^f \\ +{\displaystyle \sum }_{f\in F}{c}_{pen}·{\check{e}}_f^n·\left[max\left\{du{e}_f^{-}-y_{{\omega }_f^{+}}^f , 0\right\}+max\left\{y_{{\omega }_f^{+}}^f-du{e}_f^{+} , 0\right\}\right] \end{gathered}$$

(35)

By comparing the generalized costs of transporting containers with their simulated actual demands along the planned best road–rail multimodal routes under different confidence levels with the generalized costs of the simulated actual best road–rail multimodal routes in the 50 fuzzy simulations, we can identify a crisp plan on the road–rail multimodal routs that better match the actual transportation situation. The comparison is illustrated by Figure 10 (we only give the first 15 simulations due to the limited space).

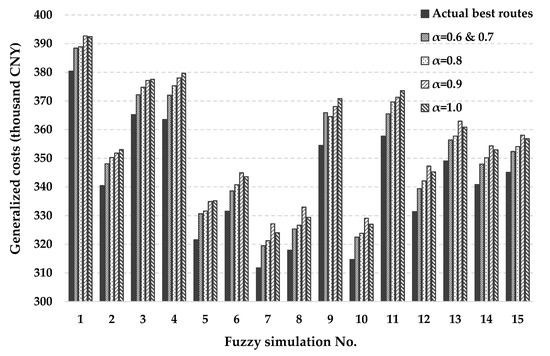
Figure 10. Comparison between the planned best routes and the actual best routes.

Through Figure 10, we can identify that the planned best road–rail multimodal routes under confidence levels of 0.6 and 0.7 are closest to the actual best situation and can lower the generalized costs compared with confidence levels of 0.8, 0.9, and 1.0. As a result, as for the case presented in Section 6.1, the best confidence levels are 0.6 and 0.7. The road–rail multimodal routes planned under such confidence levels can be used in practice.

6.5. Comparing the Fuzzy Demands with Deterministic Demands in the Road–Rail Multimodal Routing

In the previous studies, deterministic demands are considered in the road–rail multimodal routing problem. In this study, we use the fuzzy simulation results in Appendix A to simulate the decision makers’ behavior when estimating the demands in the multimodal routing problem with deterministic demands. As a result, we construct following four deterministic scenarios.

(1) Deterministic scenario 1 is that decision makers prefer to use the average value $\frac{{{\displaystyle \sum }}_{n=1}^{50}{\check{e}}_f^n}{50}$ in the 50 fuzzy simulations to represent the deterministic demand of transportation order $f$.

(2) Deterministic scenario 2 is that decision makers prefer to use the value that emerges more than others in the 50 fuzzy simulations to represent the deterministic demand of transportation order $f$.

(3) Deterministic scenario 3 is that decision makers prefer to use the minimum value $\underset{n=1,\dots ,50}{min}\left\{{\check{e}}_f^n\right\}$ in the 50 fuzzy simulations to represent the deterministic demand of transportation order $f$.

(4) Deterministic scenario 3 is that decision makers prefer to use the maximum value $\underset{n=1,\dots ,50}{max}\left\{{\check{e}}_f^n\right\}$ in the 50 fuzzy simulations to represent the deterministic demand of transportation order $f$.

As for deterministic scenario $g$ ($g$ = 1, 2, 3, 4), the corresponding MILP model is with optimization objective Equation (36) and constraints Equations (6), (7), (10), (14)–(16), (24)–(33), and (37), where $e_f^{DSg}$ is the deterministic demand of transportation order $f$ in deterministic scenario $g$. For example, $e_f^{DSg}=e_f^{DS1}=\frac{{{\displaystyle \sum }}_{n=1}^{50}{\check{e}}_f^n}{50}$ in deterministic scenario 1.

$$\begin{gathered} minimize {\displaystyle \sum }_{f\in F}{\displaystyle \sum }_{\left(i, j\right)\in A}{\displaystyle \sum }_{k\in V_{ij}}{c}_{ijk}·e_f^{DSg}·x_{ijk}^f \\ +{\displaystyle \sum }_{f\in F}{\displaystyle \sum }_{i\in N}{\displaystyle \sum }_{h\in N_i^{-}}{\displaystyle \sum }_{l\in V_{hi}}{c}_l·e_f^{DSg}·x_{hil}^f+{\displaystyle \sum }_{f\in F}{\displaystyle \sum }_{i\in N}{\displaystyle \sum }_{j\in N_i^{+}}{\displaystyle \sum }_{k\in V_{ij}}{c}_k·e_f^{DSg}·x_{ijk}^f \\ +{\displaystyle \sum }_{f\in F}{\displaystyle \sum }_{\left(i, j\right)\in A}{\displaystyle \sum }_{k\in U_{ij}}{c}_{store}·e_f^{DSg}·z_{ijk}^f \\ +{\displaystyle \sum }_{f\in F}{c}_{pen}·e_f^{DSg}·\left[max\left\{du{e}_f^{-}-y_{{\omega }_f^{+}}^f , 0\right\}+max\left\{y_{{\omega }_f^{+}}^f-du{e}_f^{+} , 0\right\}\right] \end{gathered}$$

(36)

$$\begin{array}{ccc}{\displaystyle \sum _{f\in F}}{e}_f^{DSg}·x_{ijk}^f\le q_{ijk}& \forall \left(i,j\right)\in A& \forall k\in V_{ij}\end{array}$$

(37)

Then we can obtain the planned best road–rail multimodal routes and corresponding generalized costs in the above four deterministic scenarios. Furthermore, we can test their reliability in the fuzzy simulation designed in Section 6.4. The results are given in Table 5.

Table 5. Computational results of the four deterministic road–rail multimodal routing scenarios.

Deterministic Scenario	Generalized Costs (CNY) of the Best Road–Rail Multimodal Routes	Successful Ratio of the Road–Rail Multimodal Routes in the Fuzzy Simulation
$e_f^{DS1}$	379,224	68%
$e_f^{DS2}$	288,399	68%
$e_f^{DS3}$	274,280	68%
$e_f^{DS4}$	521,203	100%

Same to the discussion around Figure 10, we can also compare the planned best road–rail multimodal routes with fuzzy demands when confidence level is set to 0.6 or 0.7 with the planned best routes with deterministic demands, which can be seen in Figure 11 (we only give the first 15 simulations due to the limited space). From Figure 11, based on a statistical viewpoint, we find that:

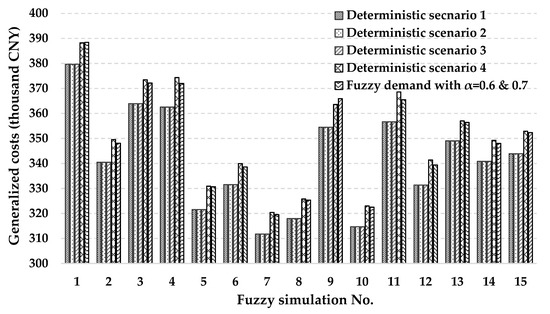
Figure 11. Comparison between the planned best routes considering fuzzy demands and the ones considering deterministic demands.

(1) Compared with deterministic scenarios 1, 2, and 3, the road–rail multimodal routing with fuzzy demands can significantly improve the transportation reliability from 68% to 100% by approximately 47% by slightly increasing the generalized costs by averagely 2.4%.

(2) Compared with deterministic scenario 4, the road–rail multimodal routing with fuzzy demands can reduce the generalized costs by averagely 0.26% and meanwhile maintain same reliability that is 100% feasible.

Therefore, the road–rail multimodal routing with fuzzy demands performs better than the one with deterministic demands. Consequently, we can draw the conclusion that considering the demand uncertainty (fuzziness) can improve the performance of the capacitated road–rail multimodal routing problem with soft due date time windows by making effective tradeoff among transportation economy, efficiency and reliability.

6.6. Managerial Implications

Although the computational experiment is based on a numerical case, its results show important managerial implications for dealing with demand uncertainty when planning the road–rail multimodal routes.

(1) The demand uncertainty exists in practice and has significant effect on the planning. Comparing with deterministic demands, it is more meaningful to consider demand uncertainty when planning the routes, since the demand uncertainty can help decision makers make better tradeoff among different transportation goals.

(2) Increasing the confidence level in the fuzzy chance constraint will increase the generalized costs for accomplishing the targeted transportation orders; however, it will also reduce the risk that the planned road–rail multimodal routes violate the bundle capacity constraint, which is helpful to improve the transportation reliability.

(3) To obtain a crisp plan on the road–rail multimodal routes under demand certainty, it is necessary for decision makers to determine the best confidence value. By using the fuzzy simulation-based comparison, such confidence level can be effectively identified. It should be noted that the best confidence level is sensitive to the setting of the case. It might change if the case changes.

7. Conclusions

In this study, we mainly explore the effect of demand uncertainty on a capacitated road–rail multimodal routing problem with soft due date time windows. A fuzzy programming method is developed to formulate the uncertain demands and model the specific routing problem with demand fuzziness. The case study combining sensitivity analysis and fuzzy simulation indicates that the demand uncertainty influence the planning on the best road–rail multimodal routes and considering fuzzy demands can help decision makers make better tradeoff among transportation economy, efficiency and reliability when optimizing the road–rail multimodal routes. Above all, the main contributions made by this study are three fold.

(1) We improve the modelling of demand uncertainty in the road–rail multimodal routing problem by using trapezoidal fuzzy numbers to represent fuzzy demands and using fuzzy expected value model, fuzzy chance constraint and fuzzy credibility measure to deal with fuzzy routing problem.

(2) We propose soft time windows to formulate the due dates claimed by customers and integrate such formulation into the road–rail multimodal routing problem to improve the transportation efficiency.

(3) We develop a framework that combines sensitivity analysis and fuzzy simulation to quantify the effect of demand uncertainty on a capacitated road–rail multimodal routing problem with soft due date time windows, and reveal some helpful insights to help decision makers better organize the road–rail multimodal transportation.

In this study, we only consider the source of uncertainty from the customers’ side. Actually, the multimodal transportation network itself also possesses uncertainty, such as time uncertainty and demand uncertainty. Formulating multiple sources of uncertainty can further improve the performance of the road–rail multimodal routing compared with the consideration of only one source of uncertainty. In our future work, we will discuss the road–rail multimodal routing problem that contains multiple sources of uncertainty including demand, time and capacity uncertainty.