Abstract
In the age of the knowledge-based economy and the rapid development of information technology, enterprise management is facing great challenges and has entered an era of prudent management. Traditional enterprise performance evaluation focuses on the interests of shareholders. Investors take financial data as their base and pay attention to the study of material attraction and the results; if they do not, they cannot adjust to a new economy period. Therefore, enterprise performance reflects the interests of shareholders and business strategists for the needs of stakeholders, which is important for the future of lively competition. With that in mind, aggregation of information is an important research tool that has recently drawn the attention of researchers for information analysis. In this paper, we have developed multiple-attribute decision-making methods for enterprise performance evaluation with picture fuzzy information. We have applied Hamacher aggregation operators such as the picture fuzzy Hamacher weighted averaging (PFHWA) operator and picture fuzzy Hamacher weighted geometric (PFHWG) operator in picture fuzzy environment for the assessment of the best enterprise selection. Finally, we justified the proposed approach with the existing methods for feasibility and effectiveness.
1. Introduction
Financial management is an important part of strategic management research, which investigates how enterprises exploit proper strategies to create and maintain competitive advantages. Presently, research into competition has grown exponentially. Mintzberg et al. [1] criticized overly analytical orientation, upper management slant, lack of attention to action and learning, and neglect of the elements that lead to the creation of strategies. Shrivastava [2] focused his research on organizational learning processes; this has the potential to offer insights into these identified drawbacks. Brockman and Morgan [3] showed that organizational knowledge is the basis for gaining and defending competitive advantage and a key variable in the amplification of firm performance. Furthermore, some studies showed evidence of a useful relationship between organizational learning and inflexible performance. For example, Baker and Sinkula [4] proved that learning intention has a direct effect on firm performance. Ussahawanitchakit [5] practiced an advance measure of knowledge and obtained similar issues. Enterprise performance estimation is not only development of market economy within a certain time, but also a scientific method and constructive tool to supervise enterprises for a nation with current market economy. Work for the evaluation of enterprise performance of our country, how to change our economy, social environment, and the trend of internationalization and how to show a system of performance appraisal that fits our economic development plays an especially important operational significance for enhancing the health of our enterprises, improving the management level, sharpening the enterprise competitiveness, and further improving the economic growth quality. Many MCDM or multiple attribute decision making (MADM) problems (such as business and strategic financial management, medical diagnosis etc.) have been developed with the use of aggregation [6,7,8] operators under probabilistic environment. Merigo et al. [9] introduced order weighted averaging operator, induce aggregation operators, weighted averaging operator and then used these operators to develop strategic decision making theory. Li [10] have studied decision and game theory in management in the environment of intuitionistic fuzzy information. The study of aggregation functions under different fuzzy environment is an important research instrument in decision science. In next paragraph, we briefly overview of some fuzzy aggregation functions and their corresponding decision making problems.
It is very difficult to take real attribute values, because of complexity presented in serious level in the field of decision environment. In 1965, Zadeh [11] introduced theory of fuzzy sets (FS), a new mathematical notion to handle easily multi-criteria decision making MCDM [12,13] problems and multi-criteria group decision making MCGDM [14,15] problems. It is known to all that intuitionistic fuzzy sets (IFSs) and interval-valued intuitionistic fuzzy sets (IVIFSs) [16] are the generalization of IFS. All these traditional theories are very interesting research topics which have engaged attention of the researchers, because these theories have successful applications in different directions such as decision-making, medical diagnosis, pattern recognition, cluster analysis etc. Then many scholars expressed intuitionistic fuzzy information in their excellent study as follows, Chen and Chou [17] used particle swarm optimization method to develop a MADM problem under the information IVIF numbers. Du and Liu [18] proposed to study a MADM problem based on VIKOR method using intuitionistic trapezoidal fuzzy information. Garg [19] studied an MCDM problem with unknown attribute values by defining a new score and accuracy function under IVIF environment. Kumar and Garg [20] contributed an MADM problem for INVIF environment based on SPA. Li [21] proposed a MADM to develop a closeness coefficient of nonlinear programming method based on IVIF values in which preference values of the attribute are unknown. Lourenzutti and Krohling [22] used IFVs to develop MCDM method using fuzzy-TODIM technique. Wan and Li [23,24] used to develop heterogeneous MAGDM problems with A-IF (A-IVIF) information and then applicability of the proposed method is justified with an example of real supplier selection. Ye [25] motivated to analyze MCDM based on novel accuracy function under IVIF environment. Recently, researchers have drawn attention to model covering-based IF rough sets with their applications to MADM problems [26,27]. Additionally, intuitionistic fuzzy rough graphs are helpful to understand these models and can solved decision-making problems, which is explained in [28].
All the execution of the criteria for alternatives, weighted and order weighted aggregation operators [29,30], have a major role in the course of the document aggregation. In that view, Xu [31,32] introduced some weighted aggregation operators to solve MAGDM problems. Recently, aggregation of information for operators is an interesting research subject, receiving great attention of the researchers in the light of Hamacher operations. The operation introduced by Hamacher [33], known as “Hamacher operation (HO)”, is a combination of algebraic TN and TCN, and Einstein TN and TCN [34]. Huang [35] introduced intuitionistic fuzzy Hamacher aggregation operators and gave application of these operators in MADM. Liu [36] presented some interval-valued intuitionistic fuzzy Hamacher aggregation operators and applied it to MAGDM problems. Xiao [37] proposed order weighted Hamacher geometric operator under IVIF environment. Li [38] gave the attention to the study of Hamacher correlated averaging (HCA) operator with the help of Hamacher sum and the Hamacher product operations based on IVIF information. The readers can get more information about Hamacher and other aggregation functions and developed decision-making methods from the following references [39,40,41,42,43,44,45,46,47,48,49,50,51].
Although IFS and IVIFS have been successfully applied to solve real world problems, in reality there are some conditions which cannot be handled by IFSs. Suppose, that in case of voting, human outlook involved more responses such as yes, abstain, no, refusal, which cannot be perfectly presented by traditional FS and IFS. To overcome this situation, the notion of picture fuzzy (PFS) set was originated by Cuong [52,53,54] as a new mathematical tool for computational intelligence problems. A PFS is identified by functions called (positive, neutral, refusal)-membership function during the information analysis. With this point of view, a PFS can be considered as a generalization of IF and the fuzzy sets. Recently, many researchers have studied PFSs and its applications: Sing [55] suggested correlation coefficient of PFS, and gave an application in clustering analysis. Jana et al. [56] used weighted Dombi aggregation operators in picture fuzzy environment, and using these operators developed software selection method. Based on some new fuzzy algorithms on the basis of PFSs environment, Son and others [57,58] provided weather forecasting and time series forecasting. Thong [59] studied a novel fuzzy hybrid model for PF-clustering, and IF-systems for Medical diagnosis and health care support systems. Son [60] investigated generalized PF-distance measure, and applied it to solve clustering analysis problems under PFSs environment. Wei and others [61,62] used PF-information aggregation to find ranking of EPR systems, picture 2-tuple linguistic Bonferroni mean-based model, picture 2-tuple linguistic model for the solution of multi attribute decision making problems. To see more information about PFS applied to risk management, picture preference relation and picture 2-tuple linguistic [63,64,65] information used to find their corresponding decision making. Recently, Wei [66] introduced Hamacher aggregation operator on picture fuzzy set. He studied different kinds of Hamacher aggregation operators under picture fuzzy environment such as (PFHA) operators, (PFHG) operators, (PFHCA) operators, (IPFHA) operators, (IPFHCA) operators, (PFHPA) operators, (PFHPA) operators, and then provided a MADM problem for the utility and flexibility of proposed method. Therefore, based on Hamacher operation, how to aggregate these PFS is a very useful topic. In this paper, we shall define some PF Hamacher aggregation operators on the basis of traditional arithmetic [29,30,32], geometric operations [31], and Hamacher operations [33,66].
The PFS has a powerful ability to model the ambiguous and imprecise information of the real world. In literature, there are many different works related to applications of fuzzy aggregation method in decision making problem based on Hamacher operations. With this motivation, we used picture fuzzy Hamacher weighted averaging (PFHWA) operator, picture fuzzy Hamacher weighted geometric (PFHWGA) operator to access the best enterprise on the basis of performance evaluation of enterprises.
2. Preliminaries
In this section, some basic definitions and operations related intuitionistic fuzzy sets and picture fuzzy sets are recalled briefly.
2.1. Intuitionistic Fuzzy Sets
Let X be universe of discourse. Then, an intuitionistic fuzzy set (IFS) [16] is defined as follows:
where and are called membership function and non-membership function of IFS A, respectively. Here for all and is called degree of indeterminacy of in IFS A. The pair is called intuitionistic fuzzy value (IFV) or intuitionistic fuzzy number (IFN) by Xu [31].
2.2. Picture Fuzzy Sets
Let X be a universe of discourse objects. A picture fuzzy set over X, denoted by , is defined in [52,53] as follows:
where , and are called positive (neutral, negative)-degree of membership of picture fuzzy set , respectively. Here for all . Besides, denotes degree of refusal of , and is defined as . The pair is called picture fuzzy value (PFV) or picture fuzzy element (PFE).
Definition 1
([67]). Let be a PFN. Then, the score function of PFN , denoted by , is defined as follows:
Definition 2
([67]). Let be a PFN. Then, the accuracy function of PFN , denoted by is defined as follows:
Here, the larger value of implies a greater degree of accuracy of the PFE .
3. Hamacher Operations (HOs) on the Picture Fuzzy Set
3.1. Hamacher Operations
The TN and TCN are useful notions in fuzzy set theory, that are used to define general union and intersection of fuzzy sets [68]. The definitions and conditions of TN and TCN are proposed by Roychowdhury and Wang [69]. The generalized union and generalized intersection of intuitionistic fuzzy sets based on TN and TCN were provided by Deschrijver and Kerre [70]. In 1978, Hamacher [33] introduced HOs known as Hamacher product (⨂) and Hamacher sum (⨁), which are examples of TN and TCN, respectively. Hamacher TN and Hamacher TCN are provided in the following definition
Usually, when , then Hamacher TN and TCN will reduce to the form
which represent algebraic TN and TCN. When , then Hamacher TN and Hamacher TCN will conclude to the form
which are called Einstein TN and TCN respectively.
3.2. Hamacher Operations(HOs) of Picture Fuzzy Set
Here, given some Hamacher operations on PFNs which are provided by Wei [66]. Let A and B be two PFSs and . Then, Hamacher product and Hamacher sum of the two PFSs A and B are denoted by and , respectively, and defined by
- .
Now, we have drawn the attention on picture fuzzy Hamacher weighted averaing operator (PFHWA) and picture fuzzy Hamacher weighted geometric (PFHWG) operator introduced by Wei [66] that are as follows.
Definition 3
([66]). Let be several picture fuzzy number (PFNs).
A picture fuzzy Hamacher weighted average (PFHWA) operator is defined as a mapping from to as follows:
where is the weight vector of with and .
Now, we considered two special cases subsequently for the PFHWA operator when the parameter takes the values 1 or 2.
Case 1. If , then PFHWA operator will reduce to PFWA operator (Wei, 2017):
Case 2. If , then PFHWA operator will reduce to picture fuzzy Einstein weighted averaging (PFEWA) operator:
Definition 4
([66]). Let ( be several PFNs. A picture fuzzy Hamacher weighted geometric (PFHWG) operator is defined as a mapping by
where is the weight vector of such that and .
Case 1. If , PFHWG operator reduces to picture fuzzy weighted geometric (PFWG) operator:
Case 2. If , then PFHWG operator reduces to a picture fuzzy Einstein weighted geometric (PFEWG) operator:
4. Model for MADM Using Picture Fuzzy Information
To this part, multiple attribute decision making (MADM) method is proposed based on PFHA operators of which weights of attributes are real numbers and values of attributes are PFNs. To illustrate effectiveness of the proposed MADM method, an application in evaluation of enterprises performance under picture fuzzy information is given. Let be the discrete set of alternatives and be the set of attributes.
Let be the weight vector of the attribute such that and , and be a picture fuzzy decision matrix. Here, is the degree of the positive membership for which alternative satisfies the attribute given by the decision makers, denote the degree of neutral membership such that alternative does not satisfy the attribute , and provides the degree that the alternative does not satisfy the attribute given by the decision maker, where , and such that , and .
In the following algorithm, a MADM method using PFHWA and PFHWG operators is proposed to solve problems involving picture fuzzy information.
Step 1. Construction of decision matrix R by decision makers under PF-information:
Step 2. Finding of values of based on decision matrix R: These values are found by using PFHWA (or PFHWG) given as follow:
to obtain the overall preference values of the alternative .
Step 3. Calculate the score by using Equation (3) based on overall PF-information in order to rank all the alternative to choose the best choice . If score values of and are equal, accuracy degrees of and based on overall picture fuzzy information of and are calculated, and rank the alternative depending with the accuracy of and .
Step 4. To rank the alternatives , choose the best one(s) in accordance with .
Step 5. Select the best alternative.
Step 6. Stop.
5. Numerical Example and Comparative Analysis
5.1. Numerical Example
The long-term stable development of enterprise hampered due to these issues: Development of production, environmental pollution, poor quality production, waste of resources, and lack of protection of the interests of the employees, as a result shareholders lose interest to invest their wealth, and they urge to special-purpose investment to the company and bear the investment risk. Thus, an enterprise’s growth and survival depends on its ability to effectively deal with the relationship among various shareholders. The strategic management experts gradually realized that it is a small-minded behavior for enterprises if they want to achieve the goal of shareholder value in the production of process, regardless of the interest of other stakeholders requirements. From the standpoint of stakeholders, as a supervision and management system, the enterprise’s financial performance is not only an enterprise’s important self-monitoring, self-restraint, self-evaluation, but also have a vital instrumentation to effectively communicate with stakeholders, coordinating each stakeholder’s interest, and finally achieving the strategic management goal of enterprise. In this part, we shall present a project for the selection of best enterprise alternative(s) on the basis of the present trend of enterprise financial performances in order to investigate our proposed method. Here, we have evaluated the enterprise overall performance of five possible enterprises . A company invests its money to an enterprize with the enterprise performances, and seeks to maximize the expected profit. In that view, it is required to calculate the enterprise performance of five possible enterprises as to select the desirable one. The whole decision-making process is presented by a flow-chart in Figure 1. The investment company take a decision depending on the following four attributes:
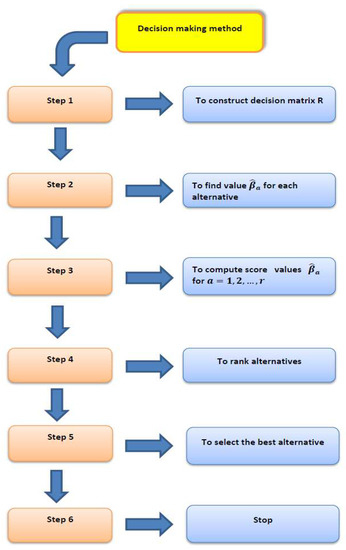
Figure 1.
A flow chart of PFNs based on multiple attribute decision making (MADM) problem.
- Financial performance
- Customer performance
- Internal processes of performance
- Staff performance
To keep away from dominating each other, decision makers are required to exempted the five possible enterprises under the considered attributes whose weight vector determined by decision makers. According to opinions of decision makers, decision matrix is constructed under picture fuzzy information as in Table 1.

Table 1.
Decision matrix R under picture fuzzy (PF)-information.
- Step 1. Decision matrix R is constructed by decision maker or expert under PF information as follows:
- Step 2. Let . By using the PFHWA operator of the overall performance values of enterprises, are obtained as follows:by a similar way, , , and are obtained as follows: , , , .
- Step 3. By using Equation (3) the score values of the overall PFNs are obtained as follows:By a similar way, , , , .
- Step 4. The ranking order in the performance of enterprises in accordance with the value of the score functions of the overall PFNs is as follows: .
- Step 5. is selected as the most desirable enterprises.
- Step 6. Stop.
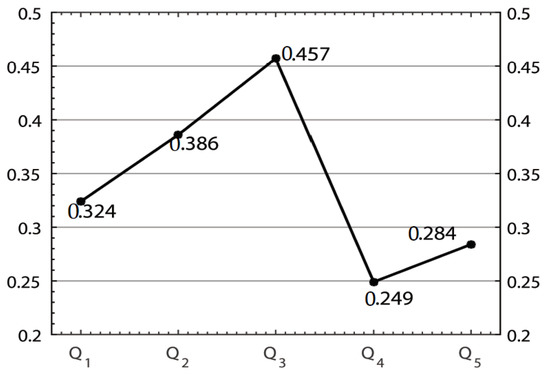
Figure 2.
Graph of score values of obtained by picture fuzzy Hamacher weighted averaging (PFHWA) operator.
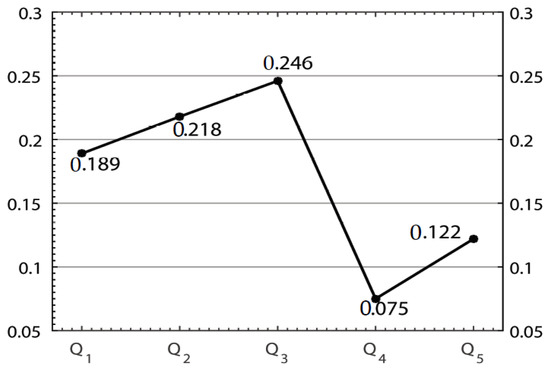
Figure 3.
Graph of score values of obtained by picture fuzzy Hamacher weighted geometric (PFHWG) operator.
If PFHWG operator is implemented instead, then the problem can be solved similarly as above.
- Step 1. Let us consider Table 1.
- Step 2. Let , using the PFHWG operator to evaluate the overall performance values of enterprisesby a similar way, , , and are obtained as , , , .
- Step 3. Calculate the values of the score functions of the overall picture fuzzy numbers as follows:, by a similar way, the other score values are obtained as follows , , , .
- Step 4. Rank all of the enterprises according to score values of the overall PFNs as .
- Step 5. Return is selected as the most desirable enterprise.
- Step 6. Stop.
5.2. Comparison Analysis
In ordered to compare our proposed method more effective to the existing method [56,71], we use PFDWA (PFDWGA) and PFWA (PFWGA) operators to aggregate picture fuzzy input arguments (Table 1) for the given decision matrix in Table 2 and their corresponding score values are given in Table 3 as follows:

Table 2.
Aggregated values of the alternatives using PFWA (PFWGA) and PFDWA (PFDWGA) operators.

Table 3.
Score values of alternatives using PFWA (PFWGA) and PFDWA (PFDWG) operators.
It follows from Table 4 that although overall rating values of the alternatives are different for these two operators, the most desirable alternative is . In comparison with the other existing method [56,71], the ranking order of alternatives is slightly different but the optimum alternative is almost same. Thus, our proposed method is stable and can be applicable to handle different uncertain environments. It is also notified in order to compare the effectiveness of the proposed technique for MADM problems using PF-Hamacher aggregation, operators with other existing methods for MADM problems based on IF Hamacher aggregation operators [35] and bipolar fuzzy Hamacher aggregation operators [50] have some restraints and are not provided overall information about the situation. Picture fuzzy set is a more generalization of IFS. Therefore, picture fuzzy Hamacher set has provided more information (positive, neutral, negative, and refusal)-membership degrees to analyze systems of information, whereas IF-Hamacher set provides (membership, non-membership)-degree and BF-Hamacher set gives (positive, negative)-membership degree only. Therefore, the developed models PF-Hamacher set can be regarded as a further generalization of IF-Hamacher set [35]. Thus, our developed models are careful about the degrees of (positive, neutral, negative)-membership, and the soundness of the information of refusal degree of membership. Thus, existing models for IF-Hamacher set are particular cases of the proposed models of PF-Hamacher set. Hence, the developed models and algorithms in this paper not only solve MADM technique under PF-Hamacher environment, but also the MADM method with IF-Hamacher information, although the method given in [35] is only suitable for MADM problems for IF-Hamacher information.

Table 4.
Ranking order of the alternatives.
6. Conclusions
Enterprises are an important factor of stockholders, employees, creditor, customer, government, and other stakeholders. In the performance of enterprises, two characteristics should be considered: Economic and society, hence we should consider all stakeholders’ benefit in performance of enterprise evaluating time. We set up a performance evaluating system on the basis of stakeholder benefits. In this article, we have studied a multi-attribute decision-making problem for emerging technology enterprise performance evaluation with picture fuzzy information. We used a picture fuzzy Hamacher weighted averaging (PFHWA) operator and a picture fuzzy Hamacher weighted geometric (PFHWGA) operator to assess the best enterprise on the basis of performance evaluation of enterprises. In the future, the application of our proposed model can be applied in decision-making theory, risk evaluation, and other domains under ambiguous environments.
Author Contributions
Conceptualization, C.J.; formal analysis, M.P.; writing—original draft preparation, C.J.; writing—review and editing, C.J. and M.P.; supervision, M.P.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mintzberg, H.; Ahlstrand, B.W.; Lampel, J. Strategy safari: A guided tour through the wilds of strategic management. Manag. Serv. 2009, 48, 152. [Google Scholar]
- Shrivastava, P. Advances in Strategic Management: Organizational Learning and Strategic Management; Emerald Group: Greenwicht, UK, 1997. [Google Scholar]
- Brockman, B.K.; Morgan, R.M. The Role of Existing Knowledge in New Product Innovativeness and Performance. Dec. Sci. 2003, 34, 385–419. [Google Scholar] [CrossRef]
- Baker, W.E.; Sinkula, J.M. The synergistic effect of market orientation and learning orientation on organizational performance. J. Acad. Mark. Sci. 1999, 27, 411–427. [Google Scholar] [CrossRef]
- Ussahawanitchakit, P. Impacts of organizational learning on innovation orientation and firm efficiency: An empirical assessment of accounting firms in Thailand. Int. J. Bus. Res. 2008, 8, 1–12. [Google Scholar]
- Merigó, J.M. Probabilities in the OWA operator. Expert Syst. Appl. 2012, 39, 11456–11467. [Google Scholar] [CrossRef]
- Merigó, J.M.; Casanovas, M.; Yang, J.B. Group decision making with expertons and uncertain generalized probabilistic weighted aggregation operators. Eur. J. Oper. Res. 2014, 235, 215–224. [Google Scholar] [CrossRef]
- Merigó, J.M. Decision-making under risk and uncertainty and its application in strategic management. J. Bus. Econ. Manag. 2015, 16, 1–24. [Google Scholar] [CrossRef]
- Merigó, J.M.; Gil-Lafuente, A.M.; Aluja, J.G. A new aggregation method for strategic decision making and its application in assignment theory. Afr. J. Bus. Manag. 2011, 5, 4033–4043. [Google Scholar]
- Li, D.F. Decision and Game Theory in Management with Intuitionistic Fuzzy Sets; Springer: Berlin, Germany, 2014; Volume 308, pp. 1–441. ISBN 978-3-642-40711-6. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inform. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Adrian, C.; Abdullah, R.; Atan, R.; Jusoh, Y.Y. Conceptual Model Development of Big Data Analytics Implementation Assessment Effect on Decision-Making. Int. J. Interact. Multimed. Artif. Intell. 2017, 4, 28–33. [Google Scholar] [CrossRef]
- Idrus, A.; Mahmoud, M.A.; Ahmad, M.S.; Yahya, A.; Husen, H. A Solution Generator Algorithm for Decision Making-based Automated Negotiation in the Construction Domain. Int. J. Artif. Intell. Interact. Multimed. 2018, in press. [Google Scholar] [CrossRef]
- Morente-Molinera, J.A.; Kou, G.; González-Crespo, R.; Corchado, J.M.; Herrera-Viedma, E. Solving multi-criteria group decision making problems under environments with a high number of alternatives using fuzzy ontologies and multi-granular linguistic modelling methods. Knowl.-Based Syst. 2017, 137, 54–64. [Google Scholar] [CrossRef]
- Morente-Molinera, J.A.; Kou, G.; González-Crespo, R.; Corchado, J.M.; Herrera-Viedma, E. Managing multi-criteria group decision making environments with high number of alternatives using fuzzy ontologies. SOMET 2018, 303, 493–506. [Google Scholar]
- Atanassov, K.T. Intuitionistic Fuzzy Sets: Theory and Applications, Studies in Fuzziness and Soft Computing; Physica-Verlag: Heidelberg, Germany; New York, NY, USA, 1999; Volume 35. [Google Scholar]
- Chen, S.M.; Chiou, C.H. Multiattribute decision making based on interval-valued intuitionistic fuzzy sets, PSO techniques, and evidential reasoning methodology. IEEE Trans. Fuzzy Syst. 2015, 23, 1905–1916. [Google Scholar] [CrossRef]
- Du, Y.; Liu, P. Extended fuzzy VIKOR method with intuitionistic trapezoidal fuzzy numbers. Inf. Int. Interdiscip. J. 2011, 14, 2575–2583. [Google Scholar]
- Garg, H. A new generalized improved score function of interval-valued intuitionistic fuzzy sets and applications in expert systems. Appl. Soft Comput. 2016, 38, 988–999. [Google Scholar] [CrossRef]
- Kumar, K.; Garg, H. TOPSIS method based on the connection number of set pair analysis under interval-valued intuitionistic fuzzy set environment. Comput. Appl. Math. 2016. [Google Scholar] [CrossRef]
- Li, D.F. Closeness coefficient-based nonlinear programming method for interval-valued intuitionistic fuzzy multiattribute decision making with incomplete preference information. Appl. Soft Comput. 2011, 11, 3402–3418. [Google Scholar] [CrossRef]
- Lourenzutti, R.; Krohling, R.A. A study of TODIM in a intuitionistic fuzzy and random environment. Expert Syst. Appl. 2013, 40, 6459–6468. [Google Scholar] [CrossRef]
- Wan, S.P.; Li, D.F. Atanassovs intuitionistic fuzzy programming method for heterogeneous multiattribute group decision making with atanassovs intuitionistic fuzzy truth degrees. IEEE Trans. Fuzzy Syst. 2014, 22, 300–312. [Google Scholar] [CrossRef]
- Wan, S.P.; Li, D.F. Fuzzy mathematical programming approach to heterogeneous multiattribute decision-making with interval-valued intuitionistic fuzzy truth degrees. Inform. Sci. 2015, 325, 484–503. [Google Scholar] [CrossRef]
- Ye, J. Multicriteria fuzzy decision-making method based on a novel accuracy function under interval-valued intuitionistic fuzzy environment. Expert Syst. Appl. 2009, 36, 899–6902. [Google Scholar] [CrossRef]
- Zhang, L.; Zhan, J.; Xu, Z.S. Covering-based generalized IF rough sets with applications to multi-attribute decision-making. Inform. Sci. 2019, 478, 275–302. [Google Scholar] [CrossRef]
- Zhan, J.; Sun, B. Covering-based intuitionistic fuzzy rough sets and applications in multi-attribute decision-making. Artif. Intell. Rev. 2018. [Google Scholar] [CrossRef]
- Zhan, J.; Malik, H.M.; Akram, M. Novel decision-making algorithms based on intuitionistic fuzzy rough environment. Int. J. Mach. Learn. Cybern. 2018. [Google Scholar] [CrossRef]
- Yager, R.R. On ordered weighted avergaing aggregation operators in multi-criteria decision making. IEEE Trans. Syst. Man Cybern. 1988, 18, 183–190. [Google Scholar] [CrossRef]
- Yager, R.R.; Kacprzyk, J. The Ordered Weighted Averaging Operators: Theory and Applications; Kluwer: Boston, MA, USA, 1997. [Google Scholar]
- Xu, Z.S.; Yager, R.R. Some geometric aggregation operators-based on intuitionistic fuzzy sets. Int. J. Gen. Syst. 2006, 35, 417–433. [Google Scholar] [CrossRef]
- Xu, Z.S. Intuitionistic fuzzy aggregation operators. IEEE Trans. Fuzzy Syst. 2007, 15, 1179–1187. [Google Scholar]
- Hamacher, H. Uber logische verknunpfungenn unssharfer Aussagen undderen Zugenhorige Bewertungsfunktione. In Progress in Cybernatics and Systems Research; Trappl, K.R., Ed.; Hemisphere: Washington, DC, USA, 1978; Volume 3, pp. 276–288. [Google Scholar]
- Beliakov, G.; Pradera, A.; Calvo, T. Aggregation Functions: A Guide For Practitioner; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Huang, J.Y. Intuitionistic fuzzy Hamacher aggregation operators and their application to multiple attribute decision making. J. Intell. Fuzzy Syst. 2014, 27, 505–513. [Google Scholar]
- Liu, P.D. Some Hamacher aggregation operators based on the interval-valued intuitionistic fuzzy numbers and their application to group decision making. IEEE Trans. Fuzzy Syst. 2014, 22, 83–97. [Google Scholar] [CrossRef]
- Xiao, S. Induced interval-valued intuitionistic fuzzy Hamacher ordered weighted geometric operator and their application to multiple attribute decision making. J. Intell. Fuzzy Syst. 2014, 27, 527–534. [Google Scholar]
- Li, W. Approaches to decision making with interval-valued intuitionistic fuzzy information and their application to enterprise financial performance assessment. J. Intell. Fuzzy Syst. 2014, 27, 1–8. [Google Scholar]
- He, Y.D.; Chen, H.Y.; He, Z.; Zhou, L.G. Multi-attribute decision making based on neutral averaging operators for intuitionistic fuzzy information. Appl. Soft Comput. 2015, 27, 64–76. [Google Scholar] [CrossRef]
- Jana, C.; Pal, M.; Wang, J.-Q. Bipolar fuzzy Dombi aggregation operators and its application in multiple attribute decision making process. J. Ambient Intell. Humaniz. Comput. 2018. [Google Scholar] [CrossRef]
- Jana, C.; Pal, M.; Karaaslan, F.; Wang, J.-Q. Trapezoidal neutrosophic aggregation operators and its application in multiple attribute decision -making process. Sci. Iran. E 2019, in press. [Google Scholar]
- Karaaslan, F. Correlation coefficients of single-valued neutrosophic refined soft sets and their applications in clustering analysis. Neural Comput. Appl. 2017, 28, 2781–2793. [Google Scholar] [CrossRef]
- Karaaslan, F. Possibility neutrosophic soft sets and PNS-decision making method. Appl. Soft Comput. 2017, 54, 403–414. [Google Scholar] [CrossRef]
- Khameneh, A.Z.; Kilicman, A. m-polar fuzzy soft weighted aggregation operators and their applications in group decision-making. Symmetry 2018, 10, 636. [Google Scholar] [CrossRef]
- Lu, M.; Wei, G.W.; Alsaadi, F.E.; Hayat, T.; Alsaedi, A. Hesitant pythagorean fuzzy hamacher aggregation operators and their application to multiple attribute decision making. J. Intell. Fuzzy Syst. 2017, 33, 1105–1117. [Google Scholar] [CrossRef]
- Tan, C.Q.; Yi, W.T.; Chen, X.H. Hesitant fuzzy Hamacher aggregation operators for multicriteria decision making. Appl. Soft Comput. 2015, 26, 325–349. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.; Liu, X.D. Prioritized aggregation operators and correlated aggregation operators for hesitant 2-tuple linguistic variables. Symmetry 2018, 10, 39. [Google Scholar] [CrossRef]
- Wei, G.W. Some geometric aggregation functions and their application to dynamic multiple attribute decision making in intuitionistic fuzzy setting. Int. J. Uncertain. Fuzz. Knowl.-Based Syst. 2009, 17, 179–196. [Google Scholar] [CrossRef]
- Wei, G.W.; Lu, M. Dual hesitant pythagorean fuzzy Hamacher aggregation operators in multiple attribute decision making. Arch. Control Sci. 2017, 27, 365–395. [Google Scholar] [CrossRef]
- Wei, G.W.; Alsaadi, F.E.; Hayat, T.; Alsaedi, A. Bipolar fuzzy Hamacher aggregation operators in multiple attribute decision Making. Int. J. Fuzzy Syst. 2018, 20, 1–12. [Google Scholar] [CrossRef]
- Zhou, L.Y.; Zhao, X.F.; Wei, G.W. Hesitant fuzzy Hamacher aggregation operators and their application to multiple attribute decision making. J. Intell. Fuzzy Syst. 2014, 26, 2689–2699. [Google Scholar]
- Cuong, B.C. Picture Fuzzy Sets-First Results, Part 1, Seminar Neuro-Fuzzy Systemswith Applications; Tech. Rep.; Instiute of Mathematics: Hanoi, Vietnam, 2013. [Google Scholar]
- Cuong, B.C. Picture Fuzzy Sets-First Results, Part 2, Seminar Neuro-Fuzzy Systemswith Applications; Tech. Rep.; Instiute of Mathematics: Hanoi, Vietnam, 2013. [Google Scholar]
- Cuong, B.C. Picture fuzzy sets. J. Comput. Sci. Cybern. 2014, 30, 409–420. [Google Scholar]
- Singh, P. Correlation coefficients for picture fuzzy sets. J. Intell. Fuzzy Syst. 2014, 27, 2857–2868. [Google Scholar]
- Jana, C.; Senapati, T.; Pal, M.; Yager, R.R. Picture fuzzy Dombi aggregation operators: Application to MADM process. Appl. Soft Comput. 2019, 74, 99–109. [Google Scholar] [CrossRef]
- Son, L. DPFCM: A novel distributed picture fuzzy clustering method on picture fuzzy sets. Expert Syst. Appl. 2015, 2, 51–66. [Google Scholar] [CrossRef]
- Thong, P.H.; Son, L.H. A new approach to multi-variables fuzzy forecasting using picture fuzzy clustering and picture fuzzy rules interpolation method. In Proceedings of the 6th International Conference on Knowledge and Systems Engineering, Hanoi, Vietnam, 9–11 October 2014; pp. 679–690. [Google Scholar]
- Thong, N.T. HIFCF An effective hybrid model between picture fuzzy clustering and intuitionistic fuzzy recommender systems for medical diagnosis. Expert Syst. Appl. 2015, 42, 3682–3701. [Google Scholar] [CrossRef]
- Son, L.H. Generalized picture distance measure and applications to picture fuzzy clustering. Appl. Soft Comput. 2016, 46, 284–295. [Google Scholar] [CrossRef]
- Wei, G.W. Picture fuzzy cross-entropy for multiple attribute decision making problems. J. Bus. Econ. Manag. 2016, 17, 491–502. [Google Scholar] [CrossRef]
- Wei, G.W. Picture 2-tuple linguistic Bonferroni mean operators and their application to multiple attribute decision making. Int. J. Fuzzy Syst. 2017, 19, 997–1010. [Google Scholar] [CrossRef]
- Nie, R.X.; Wang, J.Q.; Li, L. A shareholder voting method for proxy advisory firm selection based on 2-tuple linguistic picture preference relation. Appl. Soft Comput. 2017, 60, 520–539. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, H.Y.; Wang, J.Q.; Li, L. Picture fuzzy normalized projection-based VIKOR method for the risk evaluation of construction project. J. Intell. Fuzzy Syst. 2018, 64, 216–226. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Wang, J.Q.; Hu, J.H. On novel operational laws and aggregation operators of picture 2-tuple linguistic information for MCDM problems. Int. J. Fuzzy Syst. 2017. [Google Scholar] [CrossRef]
- Wei, G.W. Picture fuzzy Hamacher aggregation operators and their application to multiple attribute decision making. Fundam. Inform. 2018, 157, 271–320. [Google Scholar] [CrossRef]
- Chen, S.M.; Tan, J.M. Handling multicriteria fuzzy decision-making problems based on vague set theory. Fuzzy Sets Syst. 1994, 67, 163–172. [Google Scholar] [CrossRef]
- Deschrijver, G.; Cornelis, C.; Kerre, E.E. On the representation of intuitionistic fuzzy t-norms and t-conorms. IEEE Trans. Fuzzy Syst. 2004, 12, 45–61. [Google Scholar] [CrossRef]
- Roychowdhury, S.; Wang, B.H. On generalized Hamacher families of triangular operators. Int. J. Approx. Reason. 1998, 19, 419–439. [Google Scholar] [CrossRef]
- Deschrijver, G.; Kerre, E.E. Ageneralization of operators on intuitionistic fuzzy sets using triangular norms and conorms. Notes Intuitionistic Fuzzy Sets 2002, 8, 19–27. [Google Scholar]
- Wei, G.W. Picture fuzzy aggregation operators and their application to multiple attribute decision making. J. Intell. Fuzzy Syst. 2017, 33, 713–724. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).