Stochastic Bifurcation of a Strongly Non-Linear Vibro-Impact System with Coulomb Friction under Real Noise
Abstract
:1. Introduction
1.1. Background
1.2. Literature Survey
1.3. Formulation of the Problem
1.4. Contribution of this Study
1.5. Organization
2. System Description and Non-Smooth Transformation
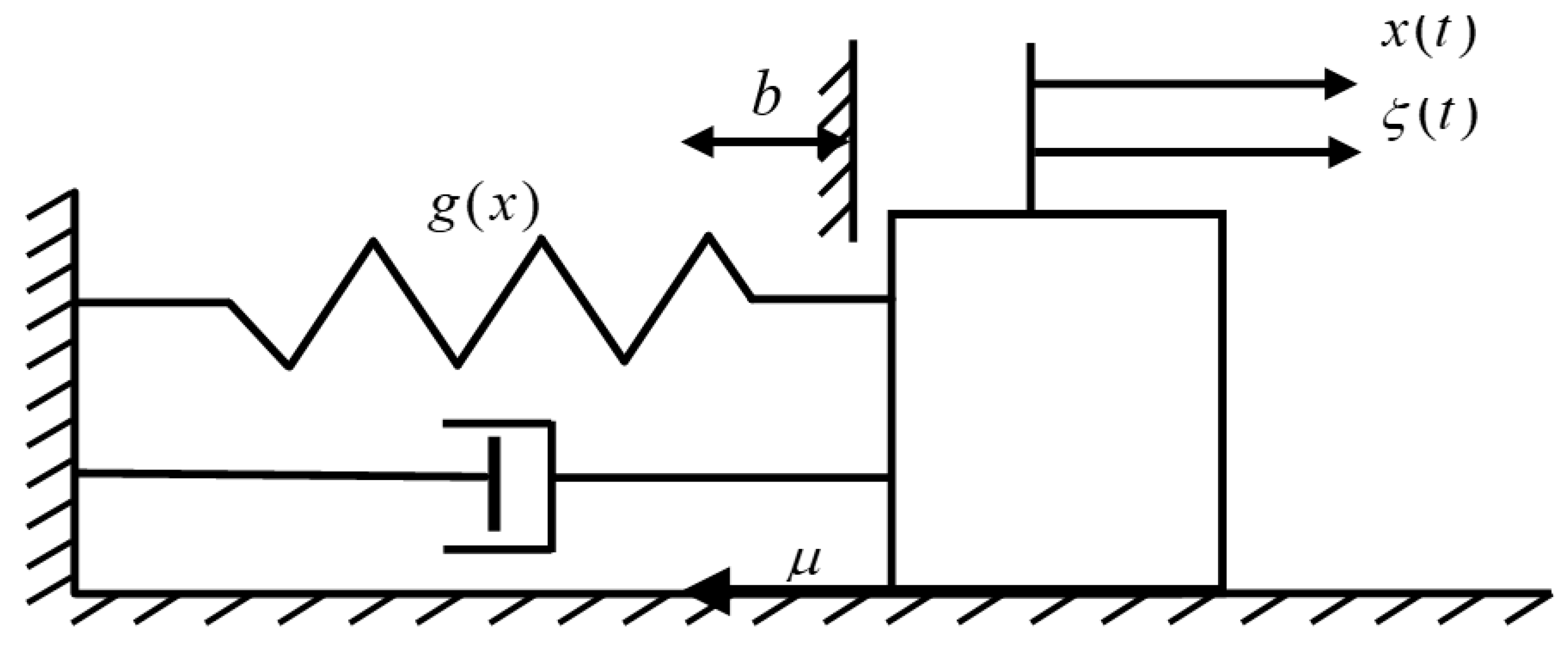
2.1. System Description
2.2. Non-Smooth Transformation
3. Stochastic Averaging Procedure
4. Response Probability Density Functions
5. Example
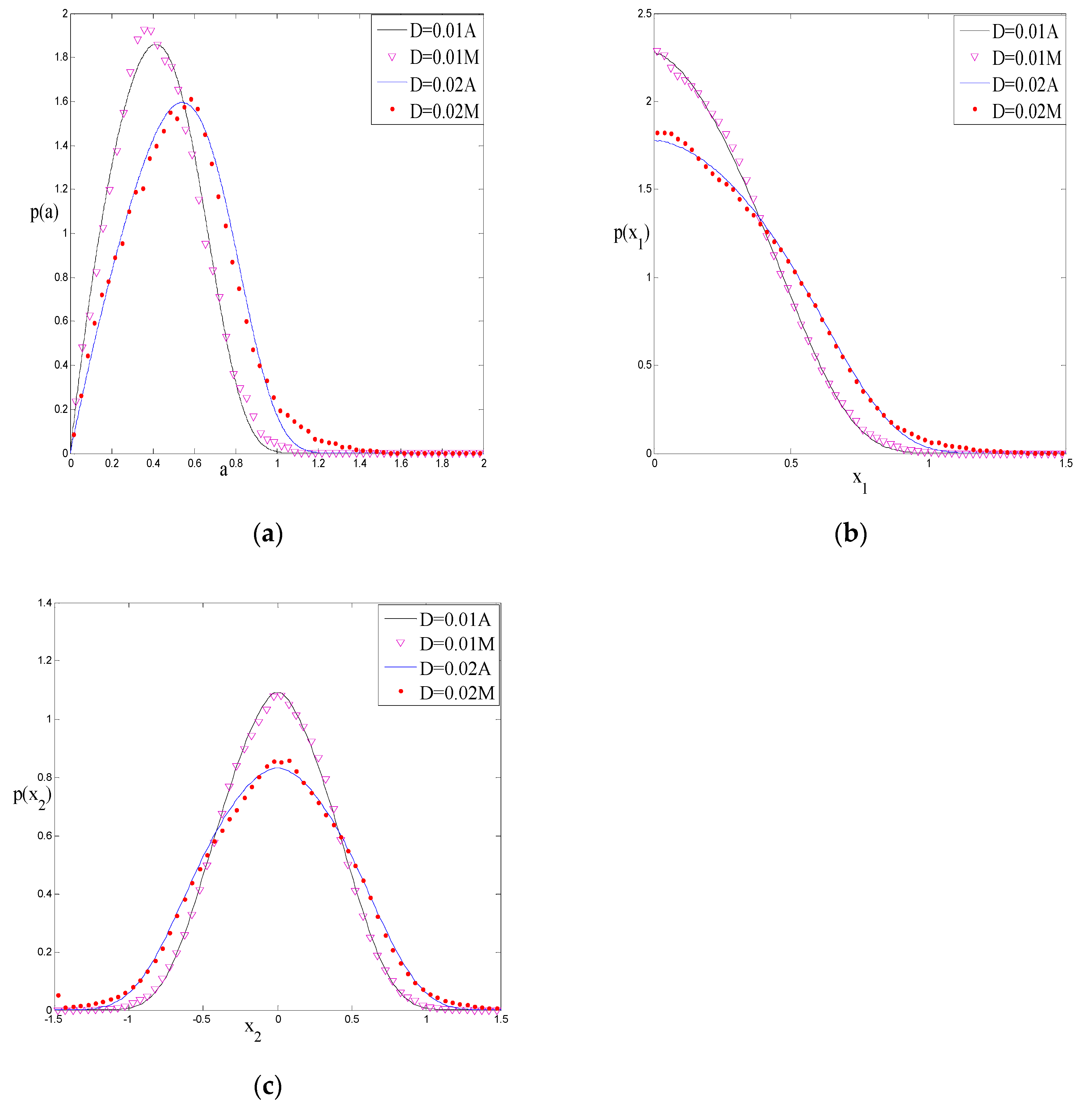
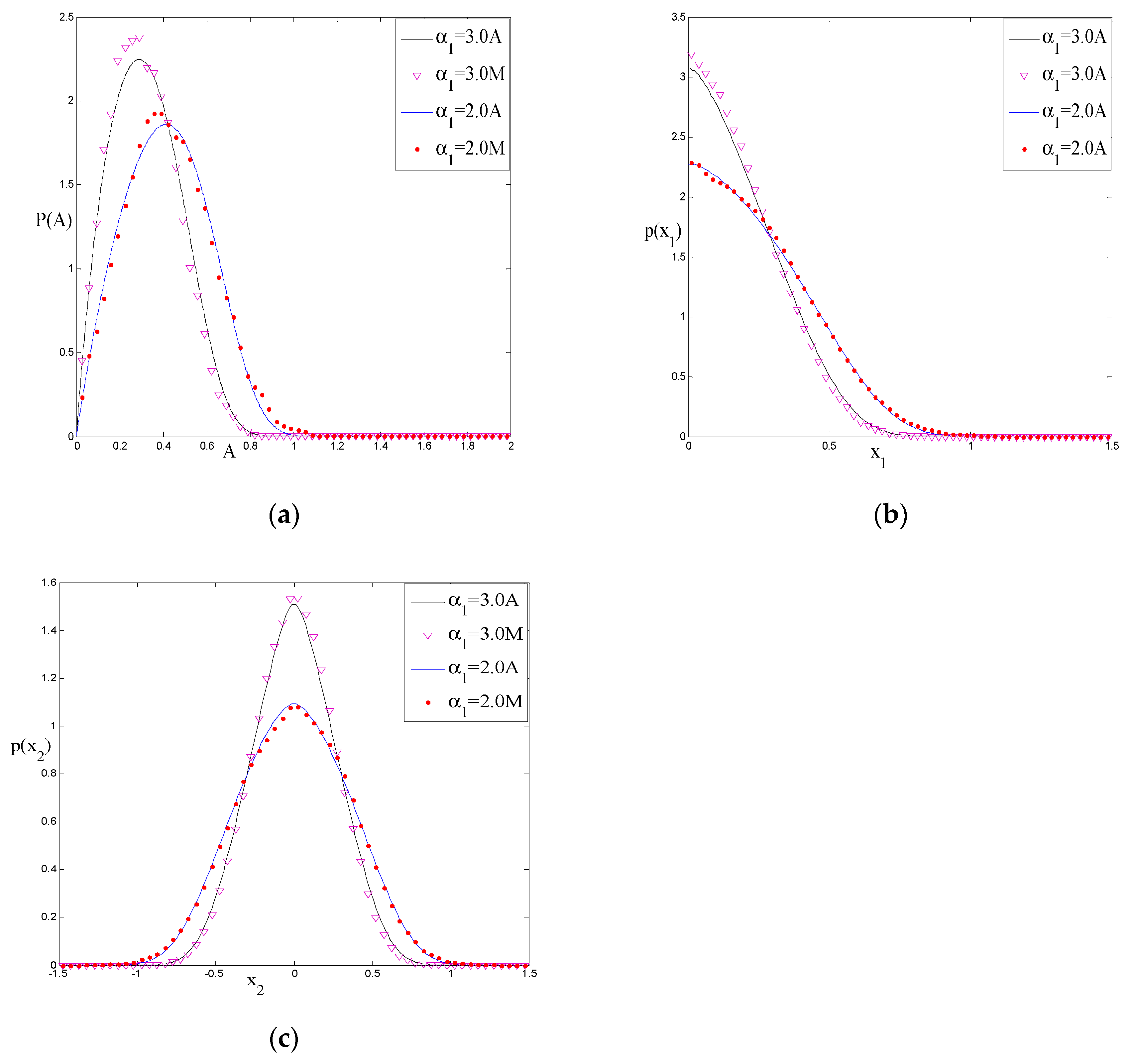
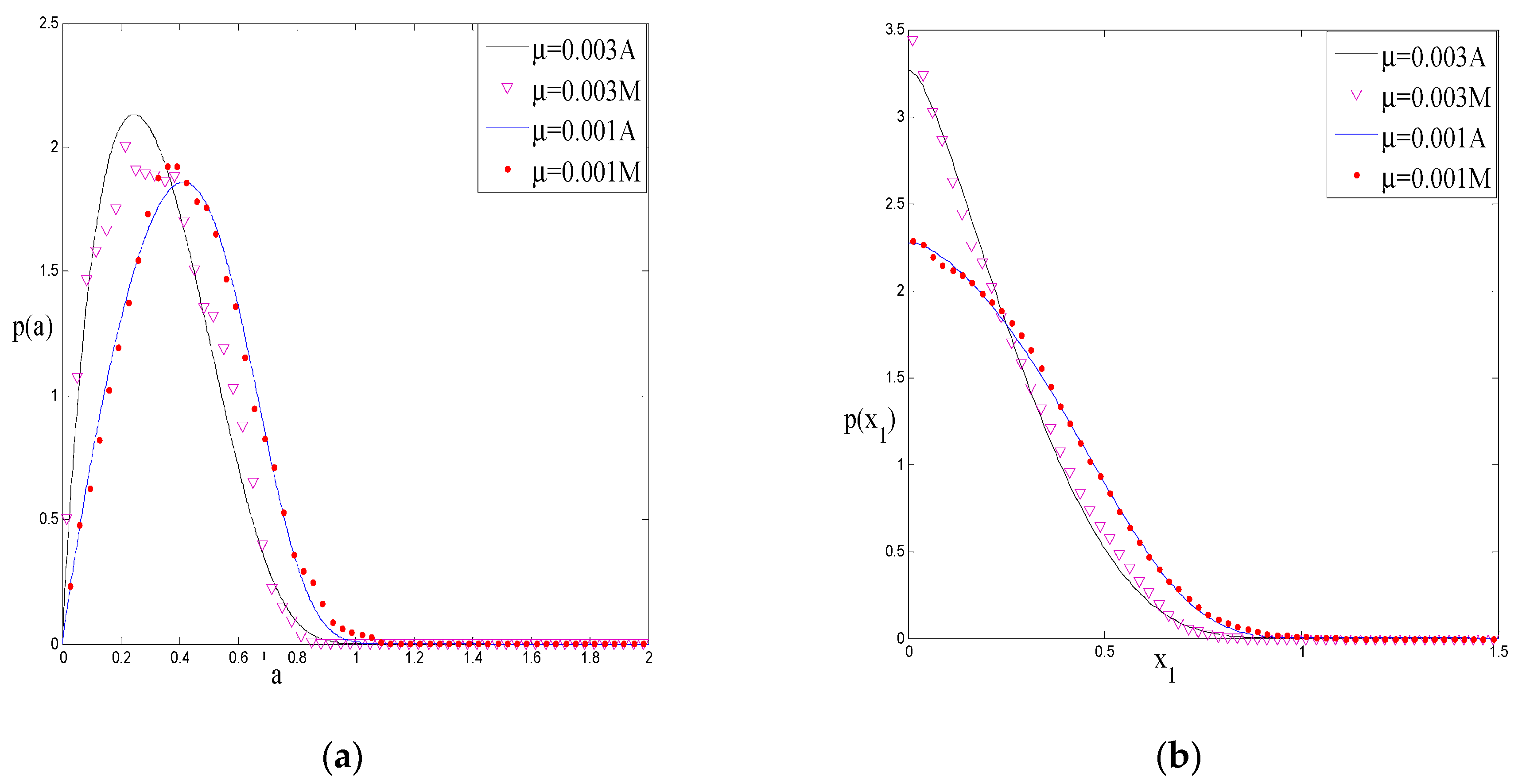
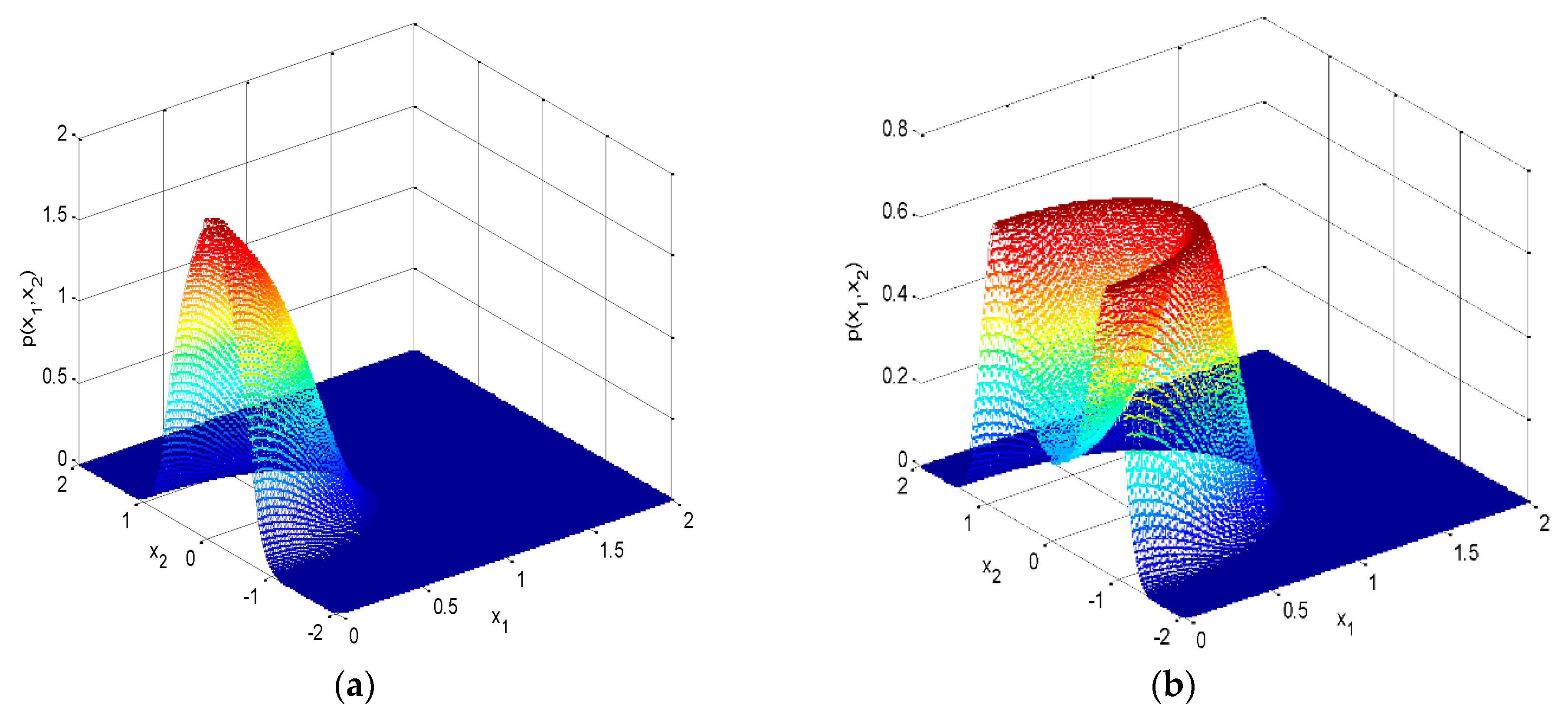
5.1. The Effect of System Parameters on Response
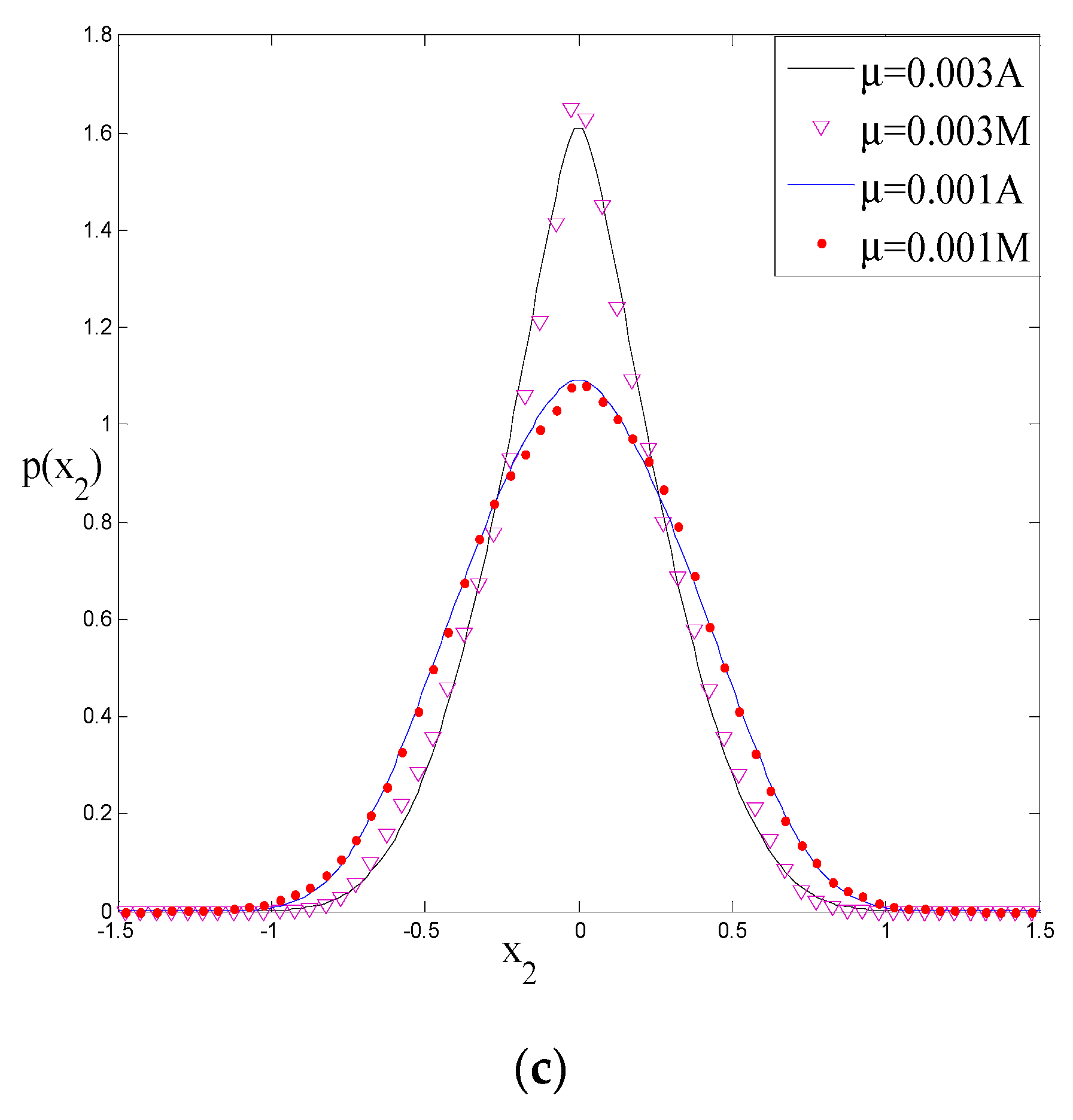
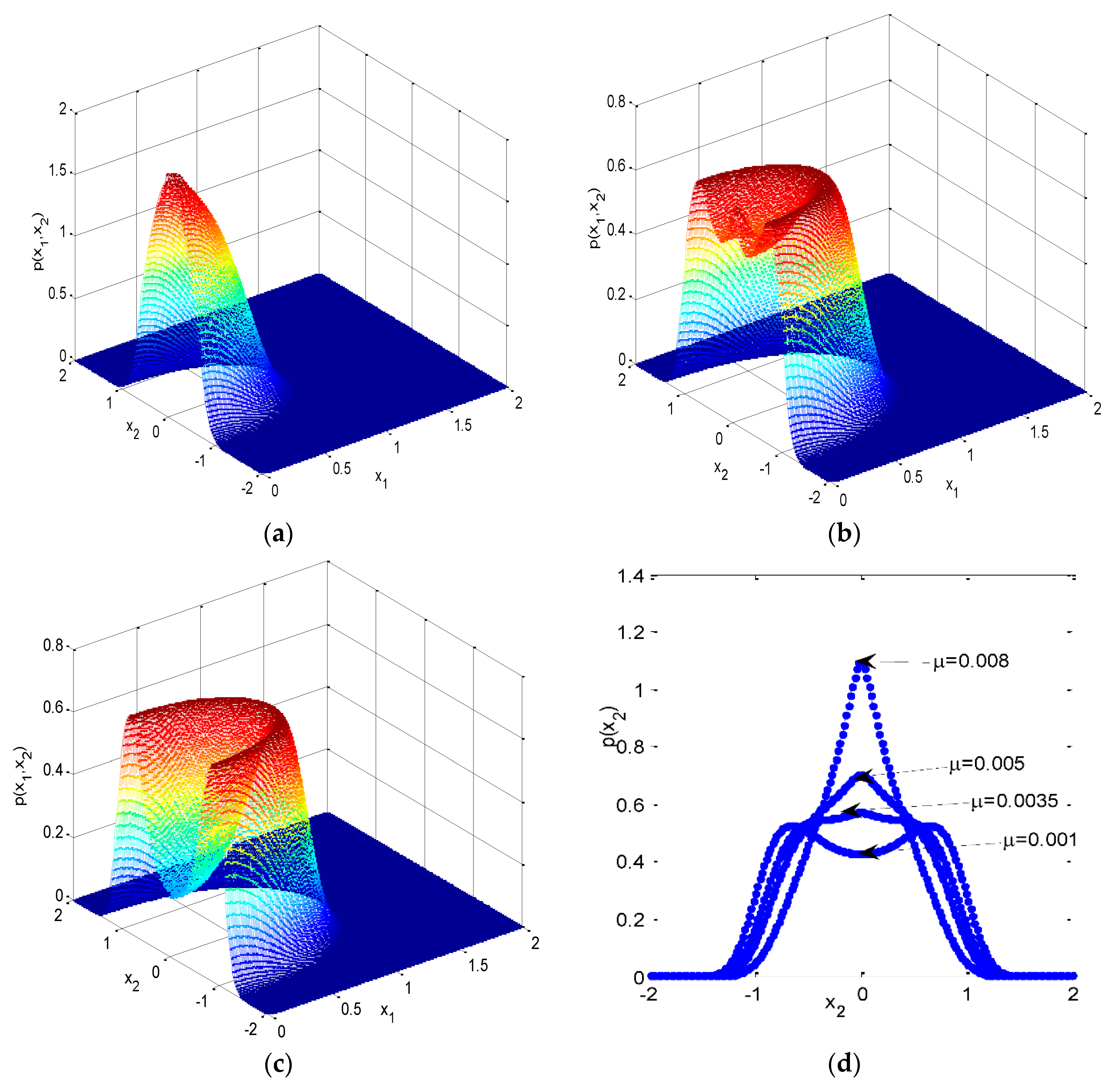
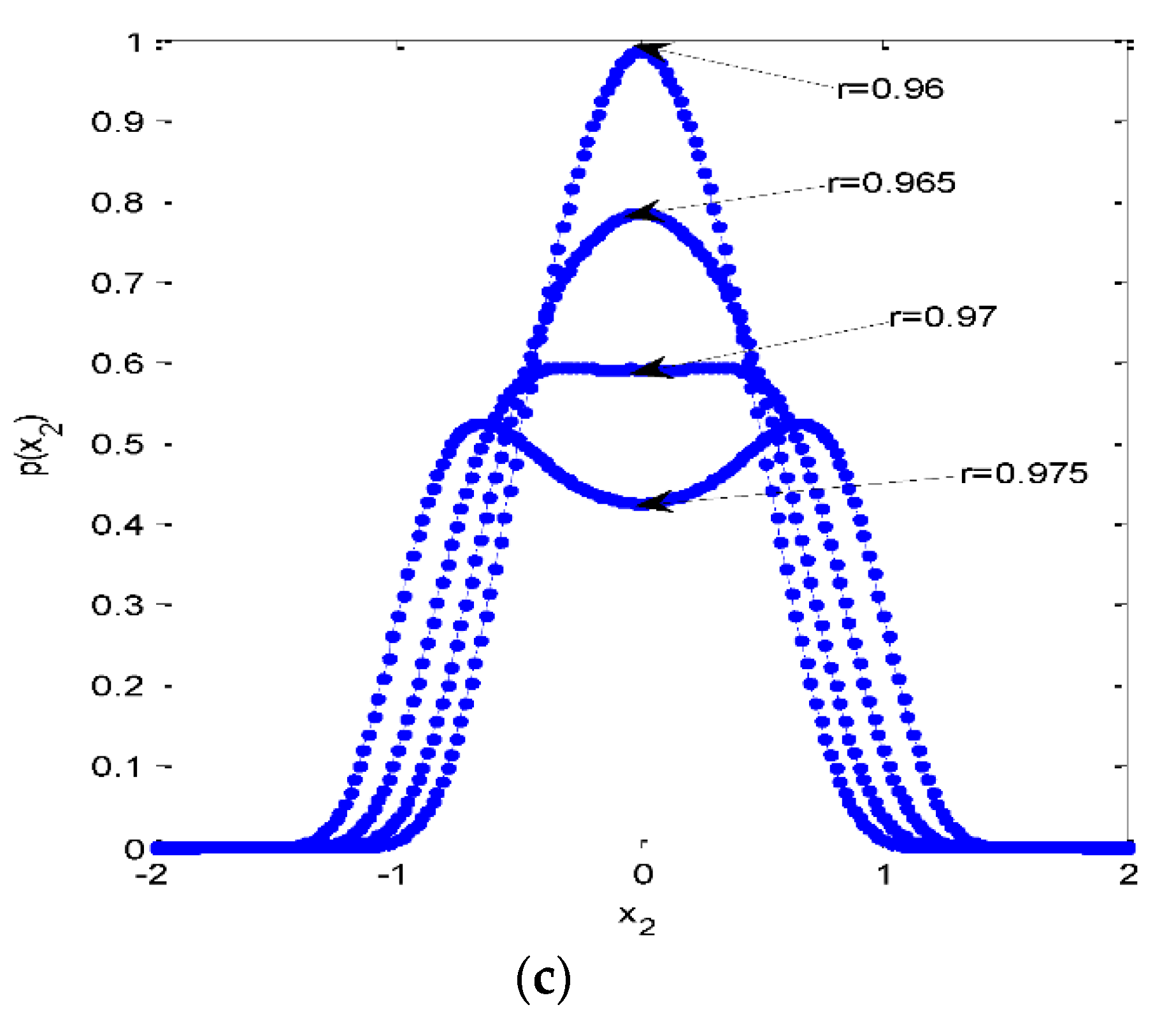
5.2. Stochastic Bifurcations
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ibrahim, R.A. Modeling Mapping and Application. In Vibro-impact Dynamics; Springer: Berlin, Germany, 2009. [Google Scholar]
- Di Bernardo, M.; Nordmark, A.; Olivar, G. Discontinity-induced bifurcations of quilibria in piecewise smooth and impacting dynamical systems. Phys. D Nonlinear Phenom. 2008, 237, 119–136. [Google Scholar] [CrossRef]
- Luo, G.W.; Chu, Y.D.; Zhang, Y.L.; Zhang, J.G. Double Neimark-Sacker bifurcation and torus bifurcation of a class of vibratory systems with symmetrical rigid stops. J. Sound Vib. 2006, 298, 154–179. [Google Scholar] [CrossRef]
- Wagg, D.J.; Bishop, S.R. Chatter sticking and chaotic impacting motion in a two degree of freedom impact oscillator. Int. J. Bifurc. Chaos 2001, 11, 57–71. [Google Scholar] [CrossRef]
- Namachchivaya, N.S.; Park, J.H. Stochastic dynamics of impact oscillators. J. Appl. Mech. 2005, 72, 862–870. [Google Scholar] [CrossRef]
- Park, J.H.; Namachchivaya, N.S. Noisy impact oscillators. In Proceedings of the ASME 2004 International Mechanical Engineering Congress and Exposition, Anaheim, CA, USA, 13–19 November 2004. [Google Scholar]
- Huang, Z.; Liu, Z.; Zhu, W. Stationary response of multi-degree-of-freedom vibro-impact systems under white noise excitation. J. Sound Vib. 2004, 275, 223–240. [Google Scholar] [CrossRef]
- Xu, M.; Wang, Y.; Jin, X.; Huang, Z.; Yu, T. Random response of vibro-impact systems with inelastic contact. Int. J. Non-Linear Mech. 2013, 52, 26–31. [Google Scholar] [CrossRef]
- Rong, H.; Wang, X.; Xu, W.; Fang, T. Subharmonic response of a single-degree-of freedom nonlinear 8vibro-impact system to a randomly disordered periodic excitation. J. Sound Vib. 2009, 327, 173–182. [Google Scholar] [CrossRef]
- Yang, G.; Xu, W.; Jia, W.; He, M. Random vibrations of Rayleigh vibroimpact oscillator under parametric poisson white noise. Commun. Nonlinear Sci. Numer. Simul. 2016, 33, 19–29. [Google Scholar] [CrossRef]
- Zhu, H. Stochastic response of vibro-impact Duffing oscillators under external and parametric Gaussian white noises. J. Sound Vib. 2013, 333, 945–961. [Google Scholar] [CrossRef]
- Zhu, H. Probabilistic solution of vibro-impact stochastic Duffing systems with a unilateral non-zero offset barrier. Phys. A Stat. Mech. Appl. 2014, 40, 335–344. [Google Scholar] [CrossRef]
- Green, P.L.; Worden, K.; Sims, N.D. On the identification and modeling of friction in a randomly excited energy harvester. J. Sound Vib. 2013, 332, 4696–4708. [Google Scholar] [CrossRef]
- Sun, J.Q. Random vibration analysis of a non-linear system with dry friction damping by the short-time Gaussian cell mapping method. J Sound Vib. 1995, 180, 785–795. [Google Scholar] [CrossRef]
- Kumar, P.; Narayanan, S.; Gupta, S. Stochastic bifurcation analysis of a Duffing oscillator with Coulomb friction excited by Poisson White noise. Procedia Eng. 2016, 144, 998–1006. [Google Scholar] [CrossRef]
- Sun, J.J.; Xu, W.; Lin, Z.F. Research on the reliability of friction system under combined additive and multiplicative random excitations. Commun. Nonlinear Sci. Numer. Simul. 2018, 54, 1–12. [Google Scholar] [CrossRef]
- Rigatos, G.G.; Siano, P. Sensorless control of electric motors with Kalman Filters: Applications to robotic and industrial system. Int. J. Adv. Robot. Syst. 2011, 8, 71. [Google Scholar] [CrossRef]
- Rigatos, G.; Siano, P. Sensorless nonlinear control of induction motors using Unscented Kalman Filtering. In Proceedings of the IECON 2012-38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 4654–4659. [Google Scholar]
- Bryson, A.E.; Ho, Y.-C. Applied Optimal Control: Optimization, Estimation and Control. Routledge: London, UK, 1935. [Google Scholar]
- Pappalardo, C.M.; Guida, D. Use of the Adjoint Method for Controlling the Mechanical Vibrations of Nonlinear Systems. Machines 2018, 6, 19. [Google Scholar] [CrossRef]
- Pappalardo, C.M.; Guida, D. System algorithm for computing the Modal Parameters of linear mechanical Systems. Machines 2018, 6. [Google Scholar] [CrossRef]
- Ibrahim, R.A. Vibro-Impact Dynamics Modeling, Mapping and Applications; Springer: Berlin, Germany, 2009. [Google Scholar]
- Dimentberg, M.F.; Iourtchenko, D.V. Random vibrations with impacts: A review. Nonlinear Dyn. 2004, 36, 229–254. [Google Scholar] [CrossRef]
- Zhu, W.Q.; Huang, Z.L.; Suzuki, Y. Response and stability of strongly non-linear oscillators under wide-band random excitation. Int. J. Non-Linear Mech. 2011, 36, 1235–1250. [Google Scholar] [CrossRef]
- Zhu, W.; Cai, G. Random vibration of viscoelastic system under broad-band excitations. Int. J. Non-Linear Mech. 2011, 46, 720–726. [Google Scholar] [CrossRef]
- Ling, Q.; Jin, X.; Huang, Z. Response and stability of SDOF viscoelastic system under wideband noise excitations. J. Franklin Inst. 2008, 345, 499–507. [Google Scholar] [CrossRef]
- Zhuravlev, V.F. A method for analyzing vibration-impact systems by means of special function. Mech. Solids 1976, 11, 23–27. [Google Scholar]
- Stratonovich, R.L. Topics in the Theory of Random Noise; Gordon Breach: New York, NY, USA, 1963. [Google Scholar]
- Khasminskii, R.Z. A limit theorem for the solution of differential equations with random right-band sides. Theory Probab. Appl. 1966, 11, 390–405. [Google Scholar] [CrossRef]
- Xu, W.; He, Q.; Rong, H.; Fang, T. Global analysis of stochastic bifurcation in Ueda system. In Proceedings of the Fifth International Conference on stochastic Structural Dynamics-SSD03, Hangzhou, China, 26–28 May 2003; pp. 509–515. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Xu, W.; Yue, X.; Huang, D. Stochastic Bifurcation of a Strongly Non-Linear Vibro-Impact System with Coulomb Friction under Real Noise. Symmetry 2019, 11, 4. https://doi.org/10.3390/sym11010004
Liu L, Xu W, Yue X, Huang D. Stochastic Bifurcation of a Strongly Non-Linear Vibro-Impact System with Coulomb Friction under Real Noise. Symmetry. 2019; 11(1):4. https://doi.org/10.3390/sym11010004
Chicago/Turabian StyleLiu, Li, Wei Xu, Xiaole Yue, and Dongmei Huang. 2019. "Stochastic Bifurcation of a Strongly Non-Linear Vibro-Impact System with Coulomb Friction under Real Noise" Symmetry 11, no. 1: 4. https://doi.org/10.3390/sym11010004
APA StyleLiu, L., Xu, W., Yue, X., & Huang, D. (2019). Stochastic Bifurcation of a Strongly Non-Linear Vibro-Impact System with Coulomb Friction under Real Noise. Symmetry, 11(1), 4. https://doi.org/10.3390/sym11010004




