Applying Graph Centrality Metrics in Visual Analytics of Scientific Standard Datasets
Abstract
1. Introduction
1.1. Graph Visualisation
1.2. Modelling Scientific Standards into Graphs
1.3. Graph Centrality Metrics
- Betweenness centrality. A node has high betweenness centrality if it serves as an intermediate between many other nodes, that is, it lies between them with respect to their shortest path. In other words, if we calculate the total set of shortest paths, then a node with high betweenness centrality is present with a large proportion of this set. Again, the higher this metric is, the more important the node is, since it controls the flow of information between many other nodes [41]. The highest betweenness node is on the closest link between other nodes [42].
1.4. Motivations and Contributions
2. Method
2.1. Data Processing
- Standard Name: The standard’s name. E.g. 12207:2008: It is a common framework for describing the life cycle of systems created by humans, which defines a set of processes and associated terminology.
- Standard Publisher: Standard’s publisher. E.g. 12207:2008’s publisher is ISO/IEC.
- Standard Type: Standards can refer to other standards normatively or informatively. Normative standards contain clauses that can become contractually required; Informative standards are there to give advice.
- Related Reference Standard: Connected standards as references. For example, standard 9126:1991 is a reference to 12207:2008.
- Reference Type: Same as the standard type mentioned.
- Reference Publisher: Same as the standard publisher mentioned.
- Reference Detail: To show more information about the reference.
2.2. Data Visualisation
2.2.1. FR (Fruchterman and Reingold)
2.2.2. FA2 (ForceAtlas2)
2.3. Centrality Measure Model
2.4. Graph Layout Generation
- Node’s colour depth: Dark green indicates larger centrality values of Weighted Degree, PageRank and Eigenvector etc., while light green represents smaller values on the opposite;
- Node’s size: Larger size expresses larger centrality values, while smaller size indicates smaller centrality values;
- Edge thickness: To show the edge weights: thick edges represent stronger connections while thin edges indicate weaker relations.
2.5. Hypotheses
2.6. Procedure
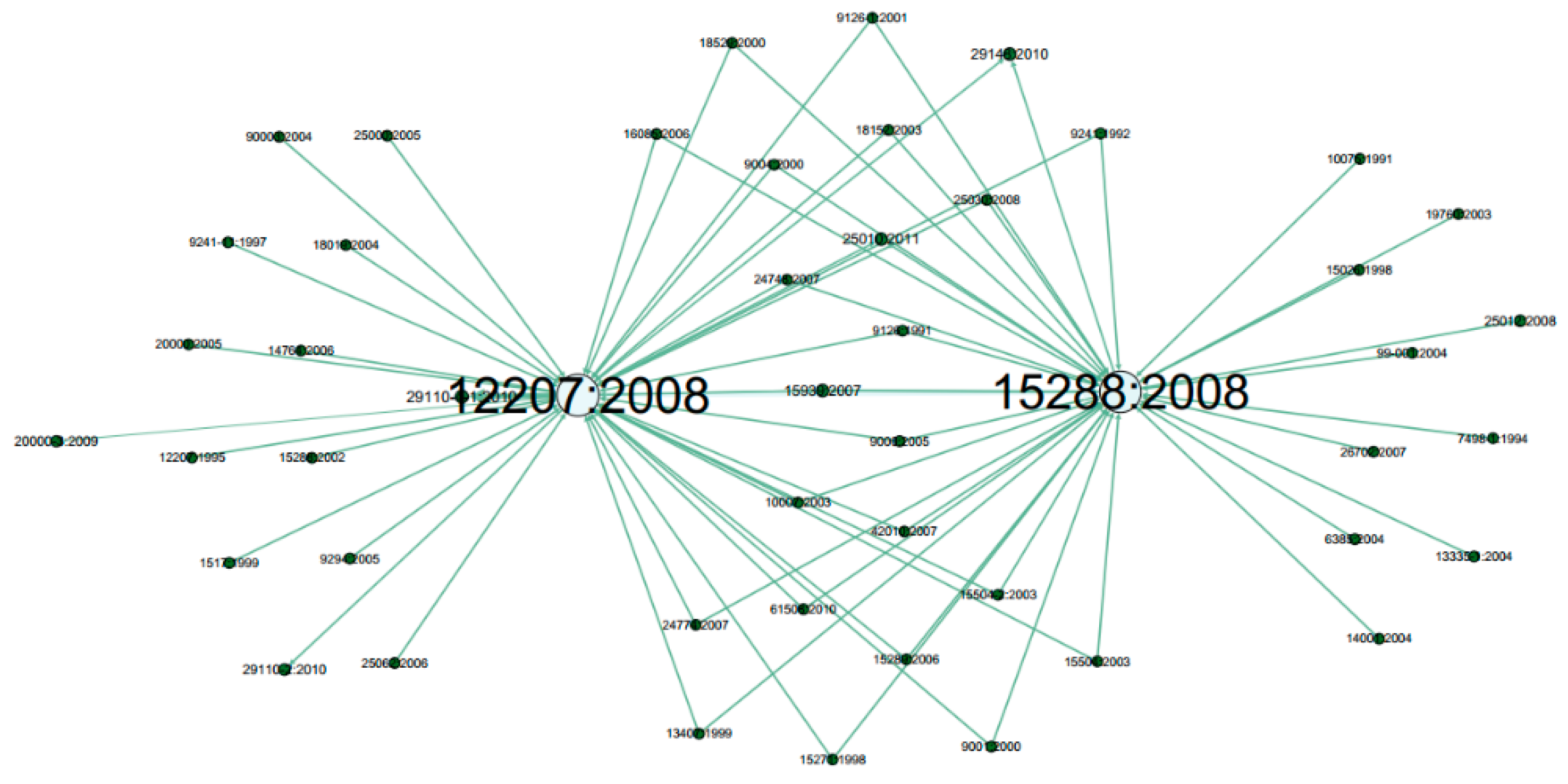
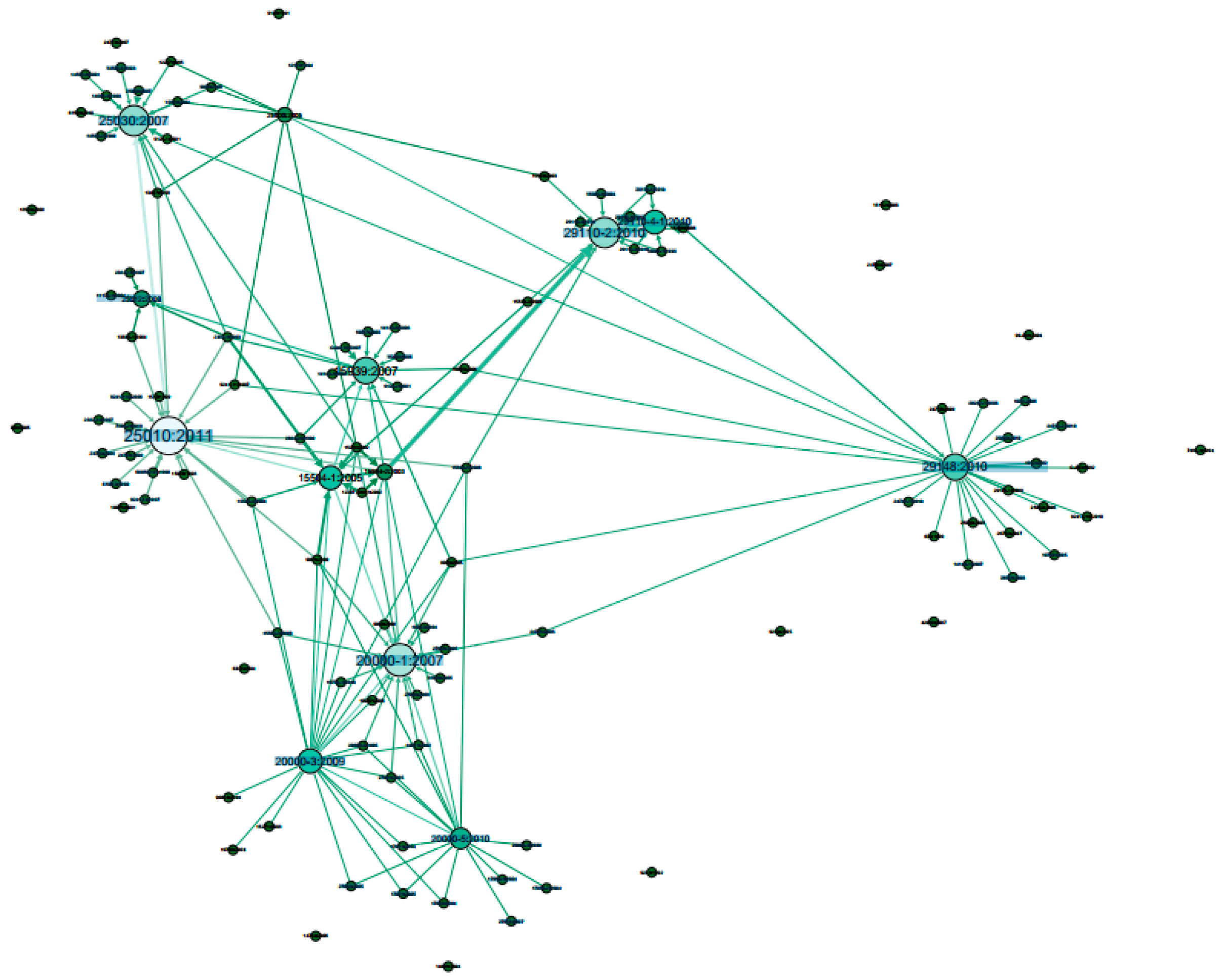
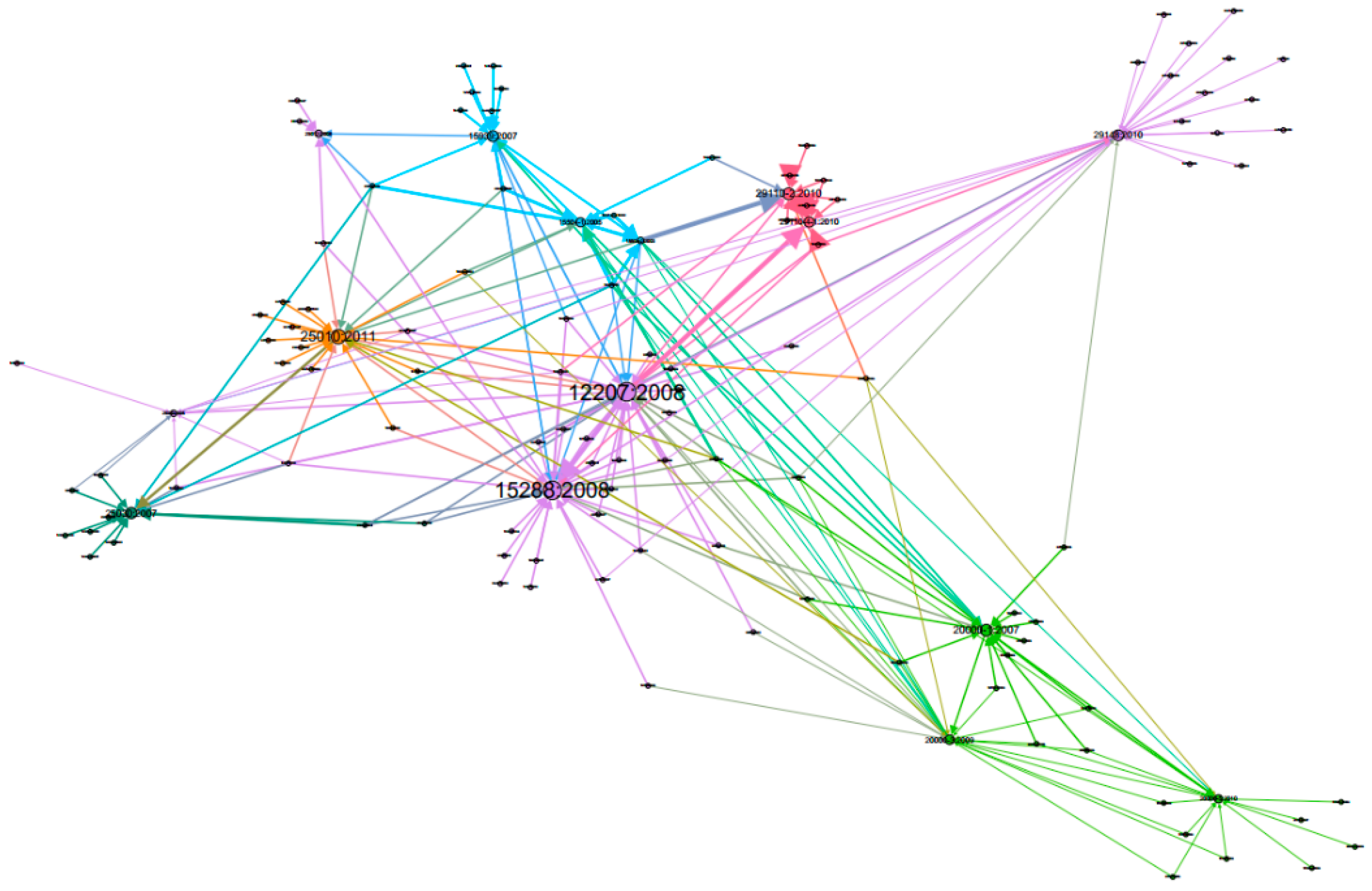
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Yarmey, L.; Baker, K.S. Towards Standardization: A Participatory Framework for Scientific Standard-Making. Int. J. Digit. Curation 2013, 8, 157–172. [Google Scholar] [CrossRef]
- International Organization for Standardization (ISO): ISO/IEC 12207:2008 Information Technology—Software Life Cycle Processes; ISO: Geneva, Switzerland, 2008.
- Ribaud, V.; Saliou, P.; Connor, R.V.O.; Laporte, C.Y. Software Engineering Support Activities for Very Small Entities. In Proceedings of the European Conference on Software Process Improvement (EuroSPI 2010), Grenoble, France, 1–3 September 2010; pp. 165–176. [Google Scholar]
- Yergeau, F. UTF-8, A Transformation Format of ISO 10646 (No. RFC 3629); ISO: Geneva, Switzerland, 2003. [Google Scholar]
- Milgram, S. Obedience to Authority. Available online: https://www.panarchy.org/milgram/obedience.html. (accessed on 19 December 2018).
- Woods, S.P.; Scott, J.C.; Sires, D.A.; Grant, I.; Heaton, R.K.; Tröster, A.I.; HIV Neurobehavioral Research Center (HNRC) Group. Action (verb) fluency: Test-retest reliability, normative standards, and construct validity. J. Int. Neuropsychol. Soc. 2005, 11, 408–415. [Google Scholar] [PubMed]
- Finkbeiner, M.; Inaba, A.; Tan, R.; Christiansen, K.; Klüppel, H.J. The new international standards for life cycle assessment: ISO 14040 and ISO 14044. Int. J. Life Cycle Assess. 2006, 11, 80–85. [Google Scholar] [CrossRef]
- Kenny, D. ISO and CEN documents on quality in medical laboratories. Clin. Chim. Acta 2001, 309, 121–125. [Google Scholar] [CrossRef]
- Lohmann, G.; Margulies, D.S.; Horstmann, A.; Pleger, B.; Lepsien, J.; Goldhahn, D.; Schloegl, H.; Stumvoll, M.; Villringer, A.; Turner, R. Eigenvector centrality mapping for analyzing connectivity patterns in fMRI data of the human brain. PLoS ONE 2010, 5, e10232. [Google Scholar] [CrossRef] [PubMed]
- Batagelj, V.; Andrej, M. Pajek—Analysis and visualization of large networks. In International Symposium on Graph Drawing; Springer: Berlin/Heidelberg, Germany, 2001; pp. 477–478. [Google Scholar]
- Battista, G.D.; Eades, P.; Tamassia, R.; Tollis, I.G. Graph Drawing Algorithms for the Visualization of Graphs; PrenticeHall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Eades, P. A heuristic for graph drawing. Congr. Numer. 1984, 42, 149–160. [Google Scholar]
- Huang, W.; Huang, M.L.; Lin, C.-C. Evaluating Overall Quality of Graph Visualizations Based on Aesthetics Aggregation. Inf. Sci. 2016, 330, 444–454. [Google Scholar] [CrossRef]
- Huang, M.L.; Huang, W. Innovative Approaches of Data Visualization and Visual Analytics; IGI Group: Hershey, PA, USA, 2014; 464p. [Google Scholar]
- Huang, T.-H.; Huang, M.L.; Nguyen, Q.V.; Zhao, L.; Huang, W.; Chen, J. A Space-Filling Multidimensional Visualization (SFMDVis) for Exploratory Data Analysis. Inf. Sci. 2017, 390, 32–53. [Google Scholar] [CrossRef]
- Hua, J.; Huang, M.L.; Huang, W.; Wang, J.; Nguyen, Q.V. Force-directed graph visualization with pre-positioning-Improving convergence time and quality of layout. In Proceedings of the 16th International Conference on Information Visualisation, Montpellier, France, 11–13 July 2012; pp. 124–129. [Google Scholar]
- Brandes, U.; Wagner, D. Analysis and visualisation of social networks. In Graph Drawing Software; Springer: Berlin/Heidelberg, Germany, 2004; pp. 1–20. [Google Scholar]
- Handcock, M.S.; Hunter, D.R.; Butts, C.T.; Goodreau, S.M.; Morris, M. Statnet: Software Tools for the Representation, Visualisation, Analysis and Simulation of Network Data. J. Stat. Softw. 2005, 14, 1–11. [Google Scholar] [CrossRef]
- Ripley, R.; Boitmanis, K.; Snijders, T.A.B. RSiena: Siena—Simulation Investigation for Empirical Network Analysis. R Package Version 1.1-232. 2013. Available online: http://CRAN.R-project.org/package=RSiena (accessed on 19 December 2018).
- Csárdi, G.; Nepusz, T. The igraph software package for complex network research. Int. J. Comp. Syst. 2006, 1695, 1–9. [Google Scholar]
- Borgatti, S.P.; Everett, M.G.; Freeman, L.C. UCINET 6.0 Version 1.00; Analytic Technologies: Natick, MA, USA, 1999. [Google Scholar]
- Hansen, D.L.; Shneiderman, B.; Smith, M.A. Analyzing Social Media Networks with NodeXL: Insights from a Connected World; Morgan Kaufmann: Burlington, MA, USA, 2010. [Google Scholar]
- Kolaczyk, E.D.; Csardi, G. Statistical Analysis of Network Data with R. J. Stat. Softw. 2005, 14, 1–6. [Google Scholar]
- Grunspan, D.Z.; Wiggins, B.L.; Goodreau, S.M. Understanding classrooms through social network analysis: A primer for social network analysis in education research. CBE Life Sci. Educ. 2014, 13, 167–178. [Google Scholar] [CrossRef] [PubMed]
- Rossi, R.A.; Ahmed, N.K. The Network Repository: An Interactive Data Repository with Multi-scale Visual Analytics. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; pp. 4292–4293. [Google Scholar]
- Bollen, J.; van de Sompel, H.; Hagberg, A.; Chute, R. A Principal Component Analysis of 39 Scientific Impact Measures. PLoS ONE 2009, 4, e6022. [Google Scholar] [CrossRef] [PubMed]
- Newman, J.R. Leonhard Euler and the Konigsberg Bridges. Sci. Am. 1953, 189, 66–70. [Google Scholar]
- Huang, W.; Hong, S.H.; Eades, P. Effects of sociogram drawing conventions and edge crossings in social network visualization. J. Graph Algorith. Appl. 2007, 11, 397–429. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 6684, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Baraba, A.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–513. [Google Scholar]
- Freeman, L. The Development of Social Network Analysis: A Study in the Sociology of Science; Empirical Press: Vancouver, BC, USA, 2004. [Google Scholar]
- Friedkin, N.E. Theoretical foundations for centrality measures. Am. J. Sociol. 1991, 96, 1478–1504. [Google Scholar] [CrossRef]
- Eigenvector Centrality. Available online: https://www.sci.unich.it/~francesc/teaching/network/eigenvector.html (accessed on 19 December 2018).
- Du, D. Social Network Analysis: Centrality Measures. Available online: http://www2.unb.ca/~ddu/6634/Lecture_notes/Lecture_4_centrality_measure.pdf. (accessed on 19 December 2018).
- Bonacich, P. Some unique properties of eigenvector centrality. Soc. Netw. 2007, 29, 555–564. [Google Scholar] [CrossRef]
- Page, L.; Brin, S.; Motwani, R.; Winograd, T. The Pagerank Citation Ranking: Bringing Order to the Web; Stanford InfoLab: Stanford, CA, USA, 1998. [Google Scholar]
- Langville, A.N.; Meyer, C.D. Google’s PageRank and Beyond: The Science of Search Engine Rankings; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Barrat, A.; Barthelemy, M.; Pastor-Satorras, R.; Vespignani, A. The architecture of complex weighted networks. Natl. Acad. Sci. USA 2004, 101, 3747–3752. [Google Scholar] [CrossRef]
- Opsahl, T.; Agneessens, F.; Skvoretz, J. Node Centrality in Weighted Networks: Generalizing degree and shortest paths. Soc. Netw. 2010, 32, 245–251. [Google Scholar] [CrossRef]
- Tang, X.; Wang, J.; Zhong, J.; Pan, Y. Predicting essential proteins based on weighted degree centrality. IEEE/ACM Trans. Comput. Biol. Bioinform. 2014, 11, 407–418. [Google Scholar] [CrossRef] [PubMed]
- Newman, M. The Mathematics of Networks; University of Michigan: Ann Arbor, MI, USA, 2002. [Google Scholar]
- Krebs, V. Power in Networks. 2004. Available online: http://www.orgnet.com (accessed on 12 December 2018).
- Yoon, J.; Blumer, A.; Lee, K. An algorithm for modularity analysis of directed and weighted biological networks based on edge-betweenness centrality. Bioinformatics 2006, 22, 3106–3108. [Google Scholar] [CrossRef] [PubMed]
- da Silva, M.R.; Ma, H.; Zeng, A.P. Centrality, network capacity, and modularity as parameters to analyze the core-periphery structure in metabolic networks. Proc. IEEE 2008, 96, 1411–1420. [Google Scholar] [CrossRef]
- de Domenico, M.; Solé-Ribalta, A.; Cozzo, E.; Kivelä, M.; Moreno, Y.; Porter, M.A.; Gómez, S.; Arenas, A. Mathematical formulation of multilayer networks. Phys. Rev. X 2013, 3, 041022. [Google Scholar] [CrossRef]
- Newman, M.E. Modularity and community structure in networks. Proc. Natl. Acad. Sci. USA 2006, 103, 8577–8582. [Google Scholar] [CrossRef] [PubMed]
- Parsons, P.; Sedig, K.; Didandeh, A.; Khosravi, A. Interactivity in Visual Analytics: Use of Conceptual Frameworks to Support Human-Centered Design of a Decision-Support Tool. In Proceedings of the 48th Hawaii International Conference on System Sciences (HICSS), Kauai, HI, USA, 5–8 January 2015; pp. 1138–1147. [Google Scholar]
- Sedig, K.; Parsons, P. Design of Visualizations for Human-Information Interaction: A Pattern-Based Framework; Morgan & Claypool Publishers: San Rafael, CA, USA, 2016. [Google Scholar]
- Eichelberg, M.; Aden, T.; Riesmeier, J. A Survey and Analysis of Electronic Healthcare Record Standards. ACM Comput. Surv. 2005, 37, 277–315. [Google Scholar] [CrossRef]
- Huang, W.; Huang, M.; Lin, C. Aesthetic of Angular Resolution for Node-Link Diagrams: Validation and Algorithm. In Proceedings of the IEEE Symposium on Visual Languages and Human-Centric Computing (VL/HCC’11), Pittsburgh, PA, USA, 18–22 September 2011; pp. 18–22. [Google Scholar]
- Huang, W.; Eades, P.; Hong, S.H.; Lin, C.C. Improving Force-Directed Graph Drawings by Making Compromises Between Aesthetics. In Proceedings of the IEEE Symposium on Visual Languages and Human-Centric Computing (VL/HCC 2010), Leganes, Spain, 21–25 September 2010; pp. 176–183. [Google Scholar]
- Huang, W.; Huang, M. Exploring the Relative Importance of Number of Edge Crossings and Size of Crossing Angles: A Quantitative Perspective. Int. J. Adv. Intell. 2011, 3, 25–42. [Google Scholar]
- Omote, H.; Sugiyama, K. Force-Directed Drawing Method for Intersecting Clustered Graphs. In Proceedings of the 6th International Asia-Pacific Symposium on Visualization, Sydney, Australia, 5–7 February 2007; pp. 85–92. [Google Scholar]
- Lin, C.C.; Yen, H.C. A New Force-Directed Graph Drawing Method Based on Edge-Edge Repulsion. In Proceedings of the Ninth International Conference on Information Visualisation, London, UK, 6–8 July 2005; pp. 329–334. [Google Scholar]
- Kobourov, S.G. Force-directed drawing algorithms. In Handbook of Graph Drawing and Visualization (Discrete Mathematics and Its Applications); CRC Press: Boca Raton, FL, USA, 2013; pp. 383–408. [Google Scholar] [CrossRef]
- Gansner, E.R.; North, S.C. Improved force-directed layouts. In Proceedings of the International Symposium on Graph Drawing and Network Visualization, Montreal, QC, Canada, 13–15 August 1998; pp. 364–373. [Google Scholar]
- Jacomy, M.; Heymann, S.; Venturini, T.; Bastian, M. Force Atlas 2, A Graph Layout Algorithm for Handy Network Visualisation. Available online: https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0098679. (accessed on 19 December 2018).
- Bastian, M.; Heymann, S.; Jacomy, M. Gephi: An Open Source Software for Exploring and Manipulating Networks. In Proceedings of the Third International ICWSM Conference, San Jose, CA, USA, 17–20 May 2009. [Google Scholar]
- Schiffer, E.; Hauck, J. Net-Map: Collecting Social Network Data and Facilitating Network Learning through Participatory Influence Network Mapping. Field Methods 2010, 22, 231–249. [Google Scholar] [CrossRef]
- Gao, Y.C.; Zeng, Y.; Cai, S.M. Influence network in the Chinese stock market. J. Stat. Mech. Theory Exp. 2015, 2015, P03017. [Google Scholar] [CrossRef]
- Li, J.; Peng, W.; Li, T.; Sun, T.; Li, Q.; Xu, J. Social network user influence sense-making and dynamics prediction. Expert Syst. Appl. 2014, 41, 5115–5124. [Google Scholar] [CrossRef]
- Newman, M. Networks: An Introduction; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Huang, W. An Eye Tracking Study into the Effects of Graph Layout. Available online: https://arxiv.org/pdf/0810.4431.pdf. (accessed on 19 December 2018).
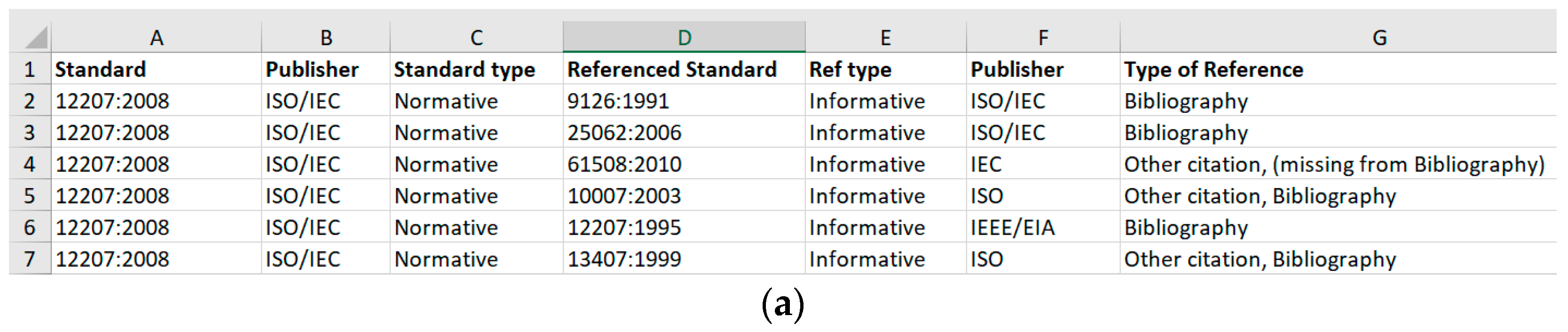

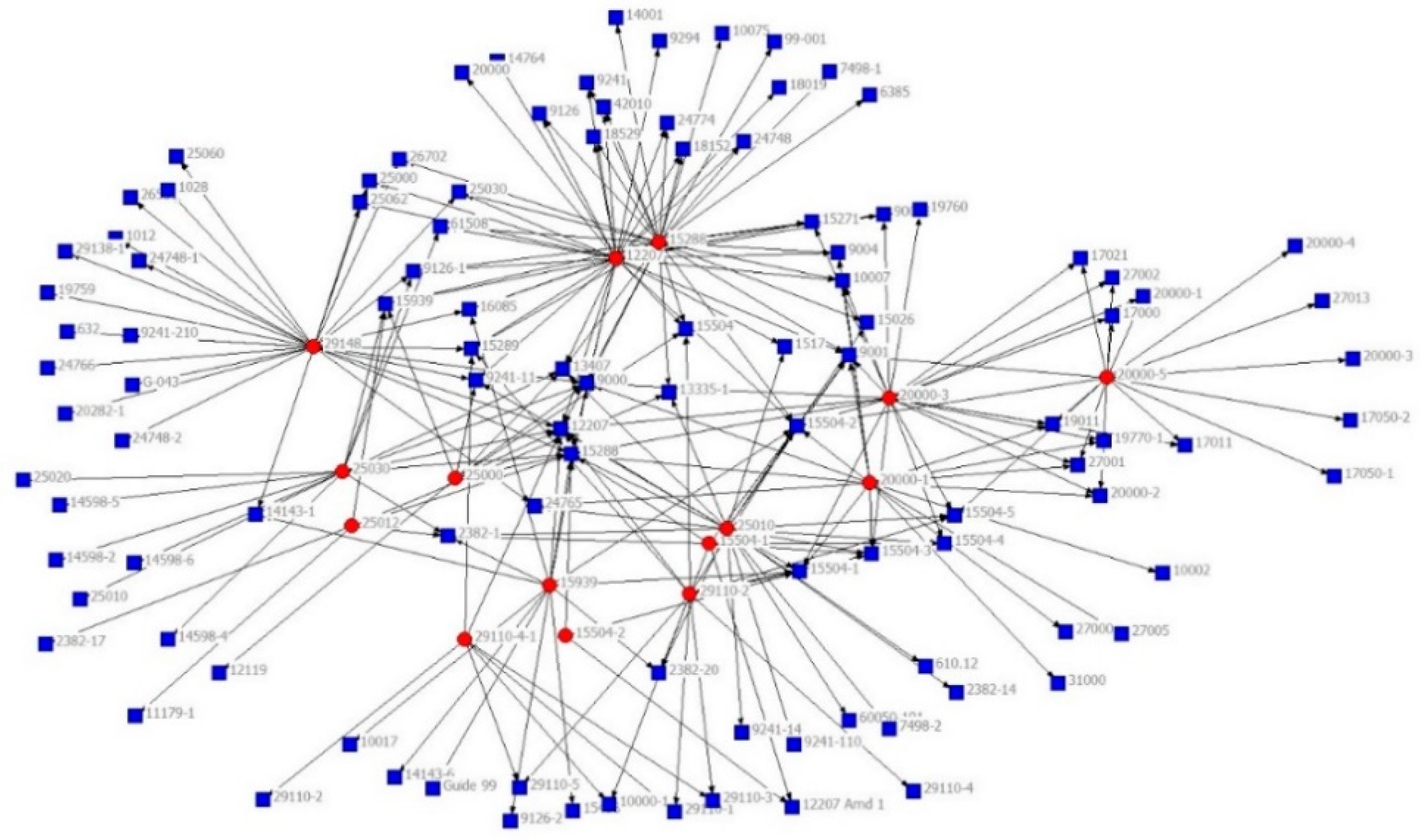
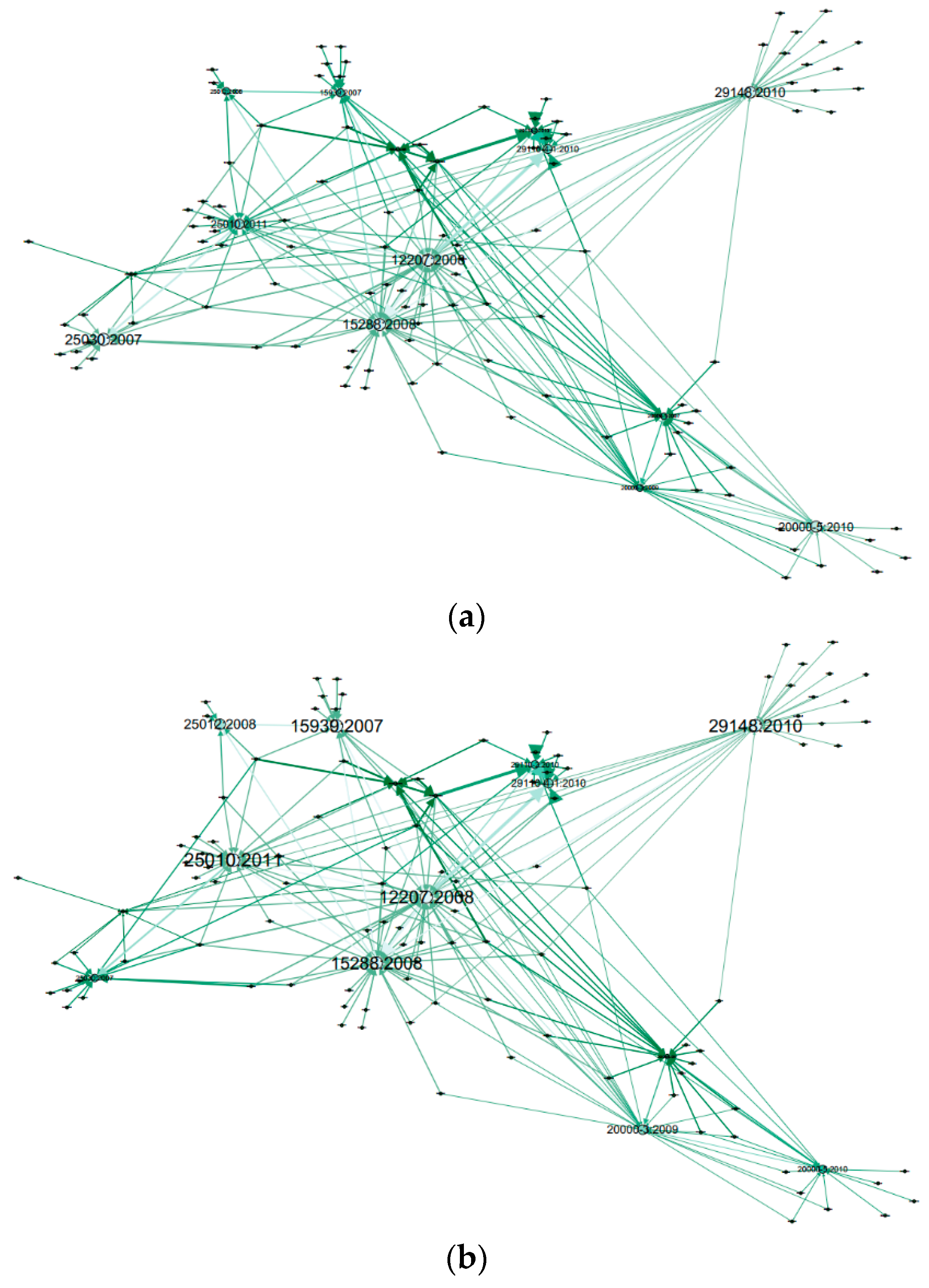

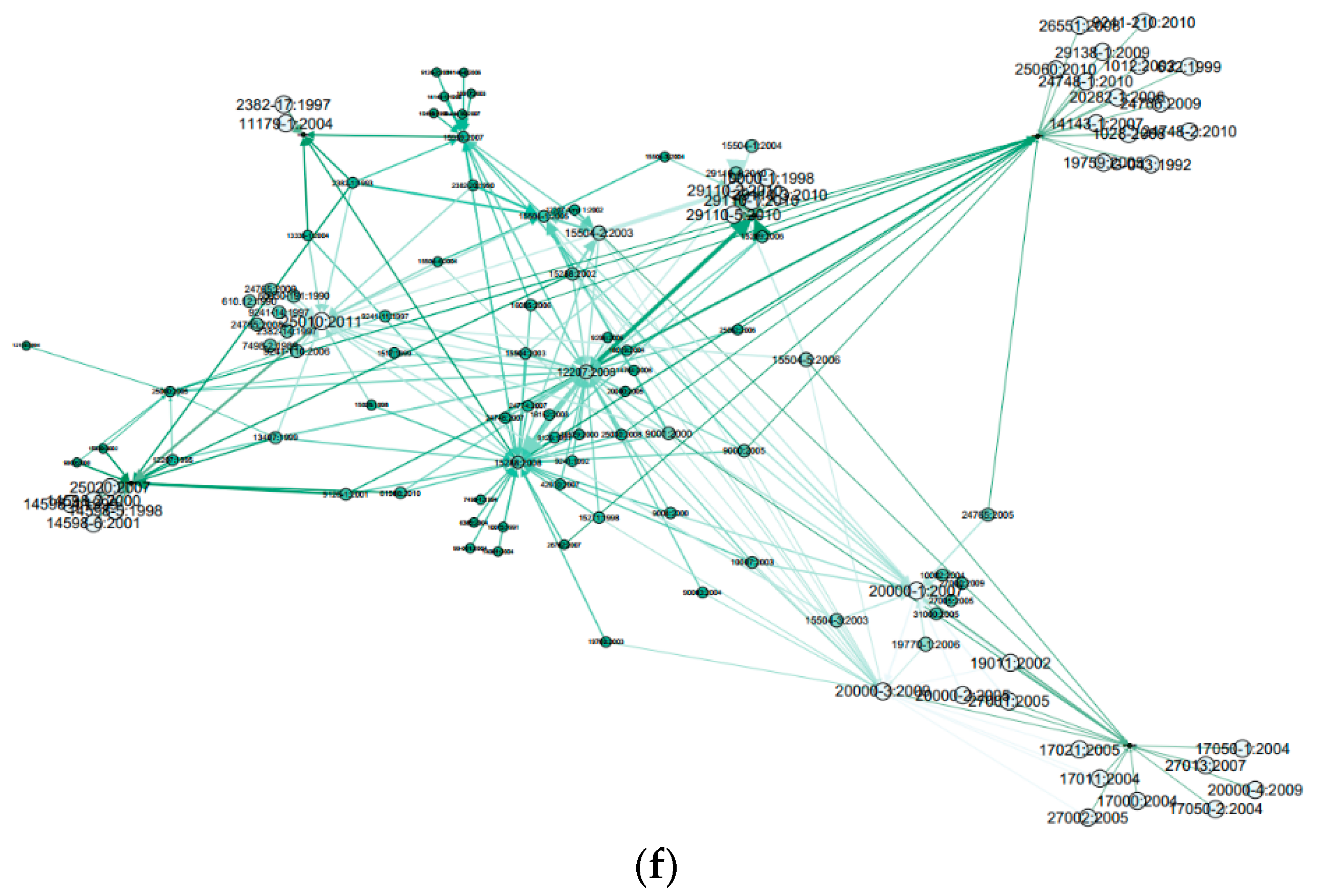
| Standard | Related Reference | |||||
|---|---|---|---|---|---|---|
| Name | Publisher | Type | Name | Type | Publisher | Detail |
| 12207:2008 | ISO/IEC | Normative | 9126:1991 | Informative | ISO/IEC | Bibliography |
| 12207:2008 | ISO/IEC | Normative | 61508:2010 | Informative | IEC | Other citation |
| Standard Relations | Edge Weight |
|---|---|
| Normative Standard—Normative Standard | 3 |
| Normative Standard—Informative Standard | 2 |
| Informative Standard—Informative Standard | 1 |
| PageRank | Eigenvector Centrality | |||||
| Standard | Value | Catalogue | Standard | Value | Catalogue | |
| 1 | 25030:2007 | 0.074 | Software engineering—Software product Quality Requirements and Evaluation (SQuaRE)—Quality requirements | 25010:2011 | 1 | Systems and software engineering—SQuaRE—System and software quality models |
| 2 | 12207:2008 | 0.072 | Systems and software engineering—Software life cycle processes | 12207:2008 | 0.981 | Systems and software engineering—Software life cycle processes |
| 3 | 15288:2008 | 0.071 | Systems and software engineering—System life cycle processes | 29148:2010 | 0.967 | Systems and software engineering—Life cycle processes—Requirements engineering |
| 4 | 29148:2010 | 0.069 | Systems and software engineering—Life cycle processes—Requirements engineering | 15939:2007 | 0.962 | Systems and software engineering—Measurement process |
| 5 | 20000-5:2010 | 0.064 | Information technology—Service management—Part 5: Exemplar implementation plan for ISO/IEC 20000-1 | 15288:2008 | 0.956 | Systems and software engineering—System life cycle processes |
| 6 | 25010:2011 | 0.057 | Systems and software engineering—SQuaRE—System and software quality models | 25012:2008 | 0.798 | Software engineering—SQuaRE—Data quality model |
| 7 | 29110-4-1:2010 | 0.048 | Software engineering—Lifecycle profiles for Very Small Entities (VSEs)—Part 4-1: Profile specifications: Generic profile group | 20000-3:2009 | 0.700 | Information technology—Service management—Part 3: Guidance on scope definition and applicability of ISO/IEC 20000-1 |
| 8 | 15939:2007 | 0.044 | Systems and software engineering—Measurement process | 29110-4-1:2010 | 0.656 | Software engineering—Lifecycle profiles for VSEs—Part 4-1: Profile specifications: Generic profile group |
| 9 | 25012:2008 | 0.035 | Software engineering—SQuaRE—Data quality model | 20000-5:2010 | 0.524 | Information technology—Service management—Part 5: Exemplar implementation plan for ISO/IEC 20000-1 |
| 10 | 20000-3:2009 | 0.034 | Information technology—Service management—Part 3: Guidance on scope definition and applicability of ISO/IEC 20000-1 | 29110-2:2010 | 0.504 | Software engineering—Lifecycle profiles for VSEs—Part 2: Framework and taxonomy |
| Weighted In-Degree | Weighted Out-Degree | |||||
| Standard | Value | Catalogue | Standard | Value | Catalogue | |
| 1 | 12207:2008 | 66.0 | Systems and software engineering—Software life cycle processes | 12207:2008 | 1 | Systems and software engineering—SQuaRE—System and software quality models |
| 2 | 15288:2008 | 65.0 | Systems and software engineering—System life cycle processes | 15504-2:2003 | 0.981 | Information technology—Process assessment—Part 2: Performing an assessment |
| 3 | 25010:2011 | 46.0 | Systems and software engineering—SQuaRE—System and software quality models | 15288:2002 | 0.967 | Systems engineering—System life cycle processes |
| 4 | 20000-1:2007 | 34.0 | Information technology—Service management | 15289:2006 | 0.962 | Systems and software engineering—Content of systems and software life cycle process information products (Documentation) |
| 5 | 29110-2:2010 | 33.0 | Software engineering—Lifecycle profiles for VSEs—Part 2: Framework and taxonomy | 9001:2000 | 0.956 | Quality management systems—Requirements |
| 6 | 25030:2007 | 31.0 | Software engineering—SQuaRE—Quality requirements | 2382-1:1993 | 0.798 | Information technology—Vocabulary—Part 1: Fundamental terms |
| 7 | 15939:2007 | 29.0 | Systems and software engineering—Measurement process | 15288:2008 | 0.700 | Systems and software engineering—System life cycle processes |
| 8 | 29148:2010 | 29.0 | Systems and software engineering—Life cycle processes—Requirements engineering | 15504-1:2005 | 0.656 | Information technology—Process assessment—Part 1: Concepts and vocabulary |
| 9 | 29110-4-1:2010 | 26.0 | Software engineering—Lifecycle profiles for VSEs—Part 4-1: Profile specifications: Generic profile group | 9000:2005 | 0.524 | Quality management systems—Fundamentals and vocabulary |
| 10 | 20000-3:2009 | 23.0 | Information technology—Service management—Part 3: Guidance on scope definition and applicability of ISO/IEC 20000-1 | 29110-1:2010 | 0.504 | Software engineering—Lifecycle profiles for VSEs—Part 1: Overview |
| Betweenness Centrality | Closeness Centrality | |||||
| Standard | Value | Catalogue | Standard | Value | Catalogue | |
| 1 | 12207:2008 | 297.4 | Systems and software engineering—Software life cycle processes | 25010:2011 | 1.0 | Systems and software engineering—SQuaRE—System and software quality models |
| 2 | 15288:2008 | 153.2 | Systems and software engineering—System life cycle processes | 20000-3:2009 | 1.0 | Information technology—Service management—Part 3: Guidance on scope definition and applicability of ISO/IEC 20000-1 |
| 3 | 15939:2007 | 87.93 | Systems and software engineering—Measurement process | 20000-1:2007 | 1.0 | Information technology—Service management |
| 4 | 25010:2011 | 60.0 | Systems and software engineering—SQuaRE—System and software quality models | 29110-2:2010 | 1.0 | Software engineering—Lifecycle profiles for VSEs—Part 2: Framework and taxonomy |
| 5 | 20000-3:2009 | 50.67 | Information technology—Service management—Part 3: Guidance on scope definition and applicability of ISO/IEC 20000-1 | 19011:2002 | 1.0 | Guidelines for auditing management systems |
| 6 | 15504-1:2005 | 34.03 | Information technology—Process assessment—Part 1: Concepts and vocabulary | 27001:2005 | 1.0 | Information technology—Security techniques—Information security management systems—Requirements |
| 7 | 25000:2005 | 32.66 | Software Engineering—Software product Quality Requirements and Evaluation (SQuaRE)—Guide to SQuaRE | 20000-2:2005 | 1.0 | Information technology—Service management—Part 2: Code of practice |
| 8 | 15504-2:2003 | 21.73 | Information technology—Process assessment—Part 2: Performing an assessment | 17011:2004 | 1.0 | Conformity assessment—General requirements for accreditation bodies accrediting conformity assessment bodies |
| 9 | 20000-1:2007 | 15.17 | Information technology—Service management | 17021:2005 | 1.0 | Conformity assessment—Requirements for bodies providing audit and certification of management systems |
| 10 | 29110-2:2010 | 6.17 | Software engineering—Lifecycle profiles for VSEs—Part 2: Framework and taxonomy | 27002:2005 | 1.0 | Information technology—Security techniques—Code of practice for information security management |
| Group 0 | 12207:2008, 9126:1991, 25062:2006, 12207:1995, 13407:1999, 14764:2006, 15271:1998, 15288:2008, 15504:2003, 16085:2006, 18019:2004, 18152:2003, 18529:2000, 20000:2005, 24748:2007, 24774:2007, 25000:2005, 25030:2008, 42010:2007, 90003:2004, 9004:2000, 9241:1992, 9241-11:1997, 9294:2005, 10075:1991, 13335-1:2004, 14001:2004, 19760:2003, 26702:2007, 6385:2004, 7498-1:1994, 99-001:2004, 12119:1994, 25012:2008, 11179-1:2004, 2382-17:1997, 29148:2010, 1012:2002, 25060:2010, 26551:2008, 1028-2008, 14143-1:2007, 19759:2005, 20282-1:2006, 24748-1:2010, 24748-2:2010, 24766:2009, 29138-1:2009, 632:1999, 9241-210:2010, G-043:1992 |
| Group 1 | 15288:2002, 15504-2:2003, 15939:2007, 15504-1:2005, 12207-1:2002, 15504-3:2004, 2382-1:1993, 2382-20:1990, 10017:2003, 14143-1:1998, 14143-6:2006, 15498:1996, 9126-2:2001, 2315-99:2007 |
| Group 2 | 10007:2003, 9000:2005, 9001:2000, 20000-1:2007, 10002:2004, 19011:2002, 24765:2005, 27001:2005, 27005:2005, 31000:2005, 15504-3:2003, 19770-1:2006, 20000-2:2005, 27000:2009, 20000-3:2009, 17011:2004, 17021:2005, 27002:2005, 17000:2004, 20000-5:2010, 27013:2007, 17050-1:2004, 17050-2:2004, 20000-4:2009 |
| Group 3 | 1517:1999, 15026:1998, 15504-4:2004, 15504-5:2006, 25010:2011, 24765:2008, 2382-14:1997, 24765:2009, 60050-191:1990, 610.12:1990, 7498-2:1989, 9241-110:2006, 9241-14:1997 |
| Group 4 | 61508:2010, 9126-1:2001, 15939:2002, 9000:2000, 25030:2007, 14598-2:2000, 14598-4:1999, 14598-5:1998, 14598-6:2001, 25020:2007 |
| Group 5 | 15289:2006, 29110-2:2010, 10000-1:1998, 15504-1:2004, 29110-1:2010, 29110-3:2010, 29110-4:2010, 29110-5:2010, 29110-4-1:2010 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hua, J.; Huang, M.L.; Huang, W.; Zhao, C. Applying Graph Centrality Metrics in Visual Analytics of Scientific Standard Datasets. Symmetry 2019, 11, 30. https://doi.org/10.3390/sym11010030
Hua J, Huang ML, Huang W, Zhao C. Applying Graph Centrality Metrics in Visual Analytics of Scientific Standard Datasets. Symmetry. 2019; 11(1):30. https://doi.org/10.3390/sym11010030
Chicago/Turabian StyleHua, Jie, Mao Lin Huang, Weidong Huang, and Chenglin Zhao. 2019. "Applying Graph Centrality Metrics in Visual Analytics of Scientific Standard Datasets" Symmetry 11, no. 1: 30. https://doi.org/10.3390/sym11010030
APA StyleHua, J., Huang, M. L., Huang, W., & Zhao, C. (2019). Applying Graph Centrality Metrics in Visual Analytics of Scientific Standard Datasets. Symmetry, 11(1), 30. https://doi.org/10.3390/sym11010030




