Parallel Computing Based Dynamic Programming Algorithm of Track-before-Detect
Abstract
1. Introduction
2. Models and Method Statement
2.1. Target Dynamic Model and Measurement Model
2.2. Basic Dynamic Programming Track-before-Detect (TBD) Algorithm
3. Multi-Target Dynamic Programming for Track-before-Detect
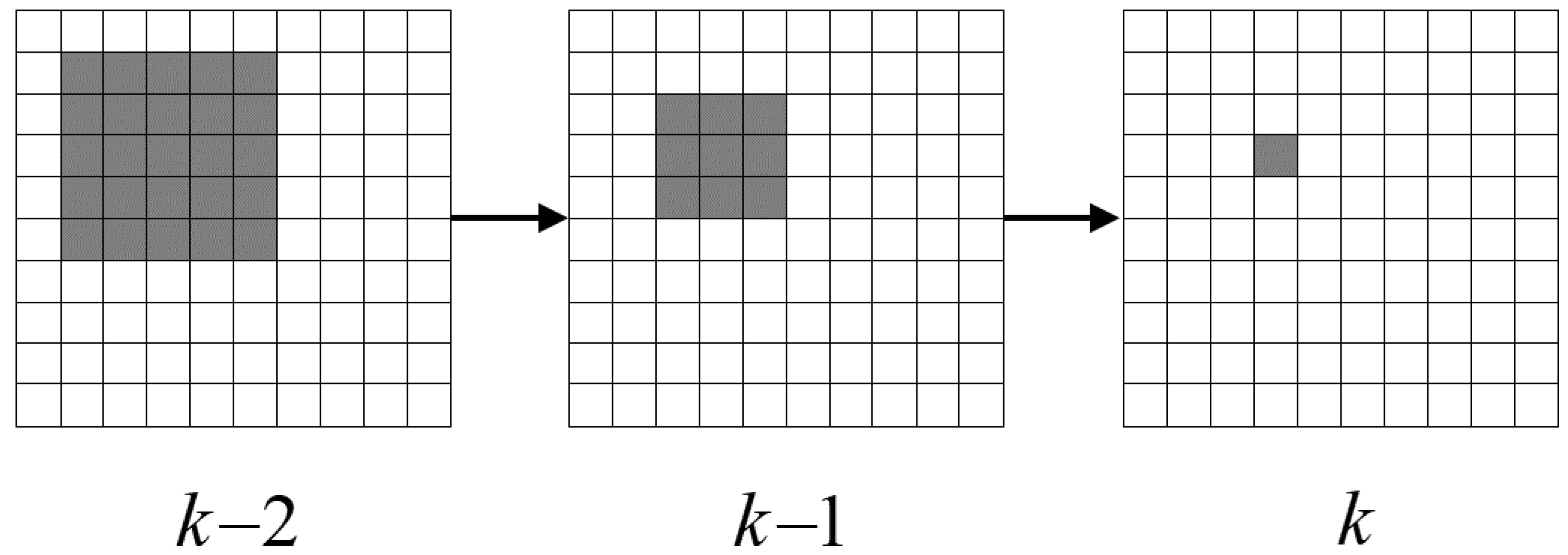
3.1. Target Cancellation
3.2. Parallel Computing-Based DP-TBD
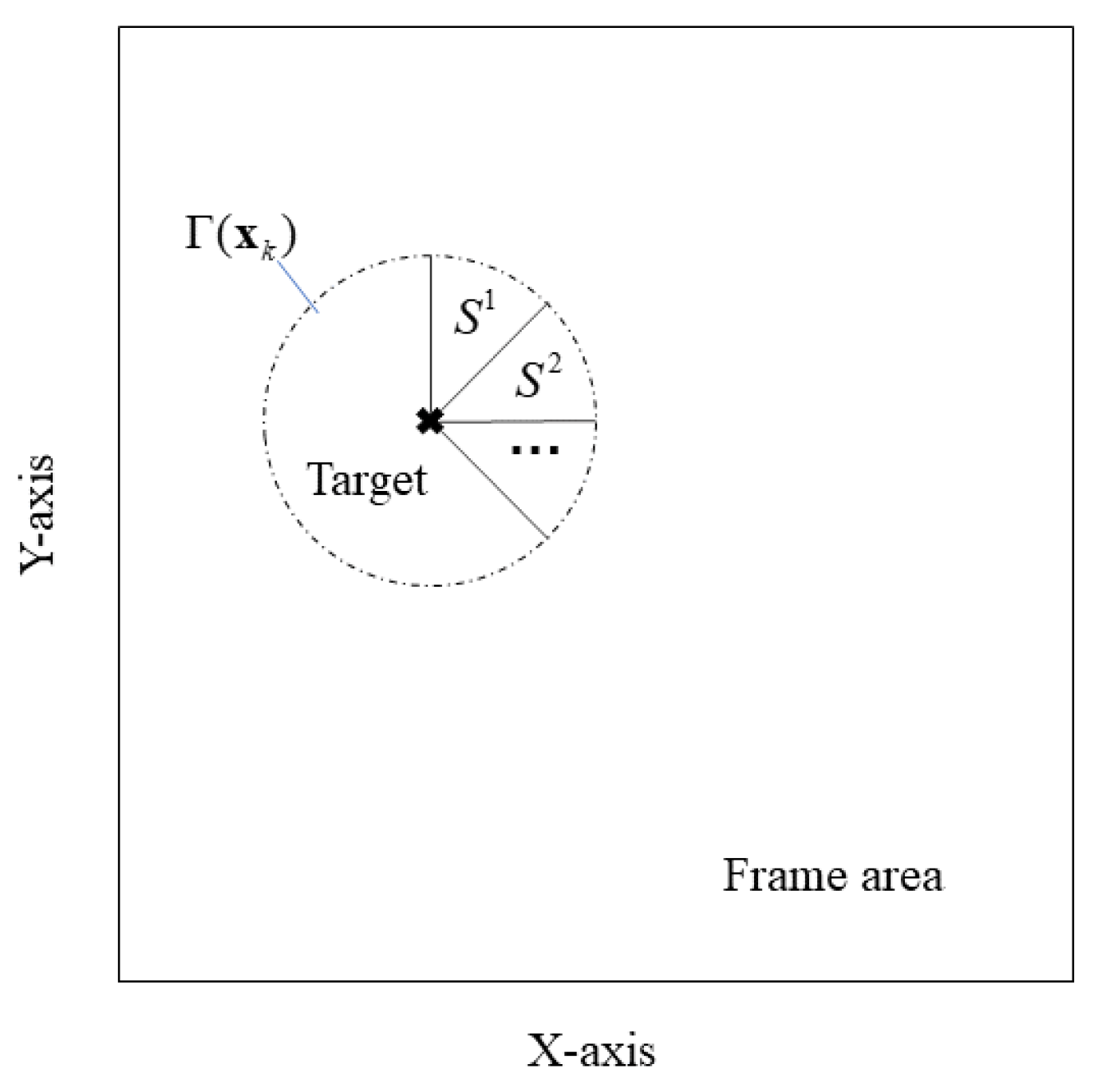
3.2.1. Partition of the Target State Transition Set
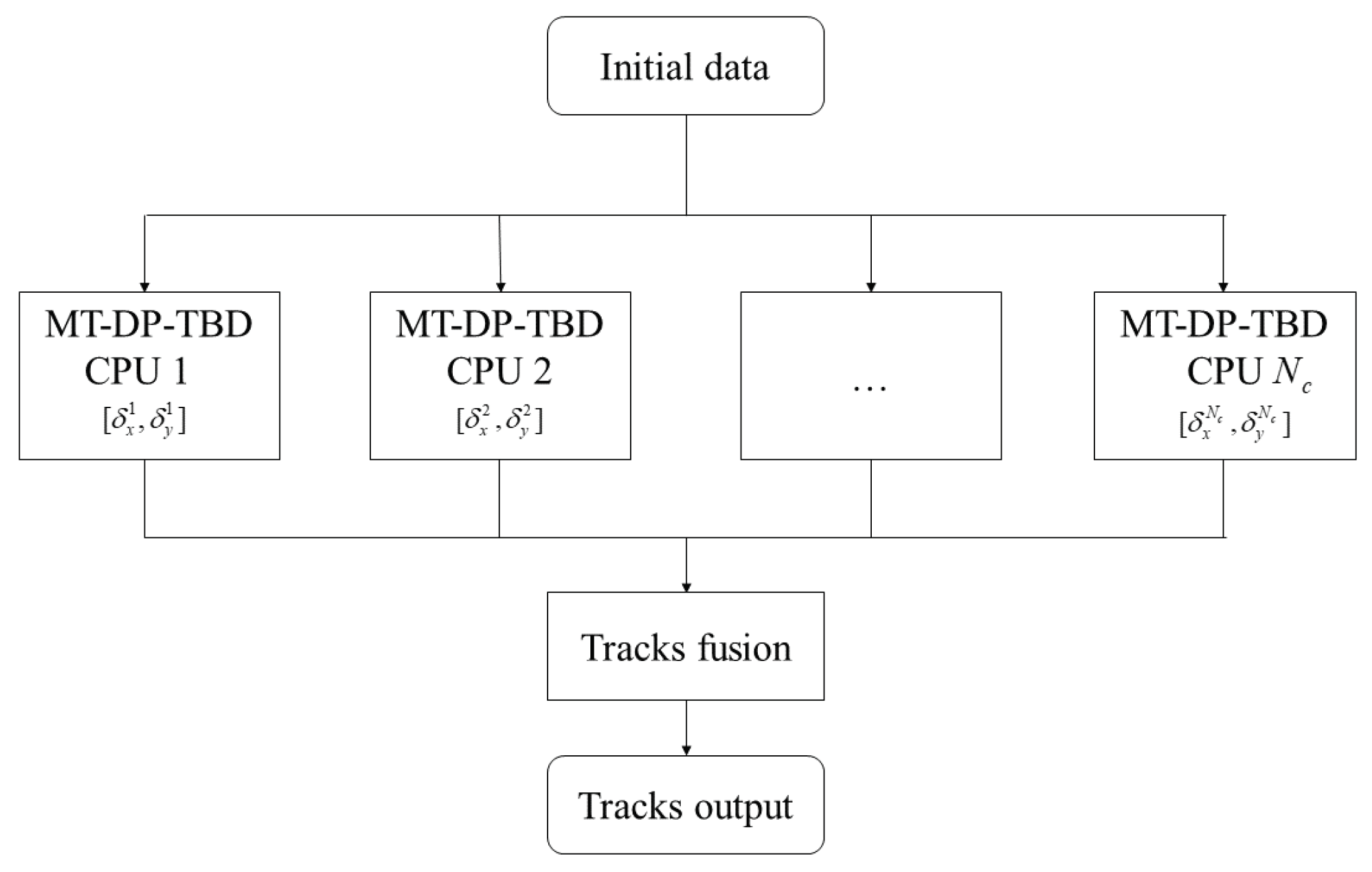
3.2.2. Implementation Steps Based on Parallel Computing
- Step 1:
- According to (11), partition the state transition set by:where and are the numbers of cells contained in towards the X-axis and Y-axis, respectively, which are determined by .
- Step 2:
- Implement MT-DP-TBD in computing cores with transition subset , respectively. For :
- Step 2.1:
- DP integration: For and all :This procedure is a recursive process of DP-TBD demonstrated in Section 2.2
- Step 2.2:
- Obtain a candidate target state at the scan:
- Step 2.3:
- Target cancellation: Backtrack the trajectory by defined in (10), and detach the measurement information related to from the original measurement data , then go to Step 2.1. Step 2 is a recursive process and ends when . Then, each computing core gets a track collection .
- Step 3:
- Merge the track collections. If the coincidence of every two tracks exceeds 50%, they will be merged and considered to belong to one target. Then, the final estimation of all tracks is given as . This method avoids the trajectories’ repetition caused by the operation of different transition sets and eliminates the false trajectories generated due to the spread of target energy.
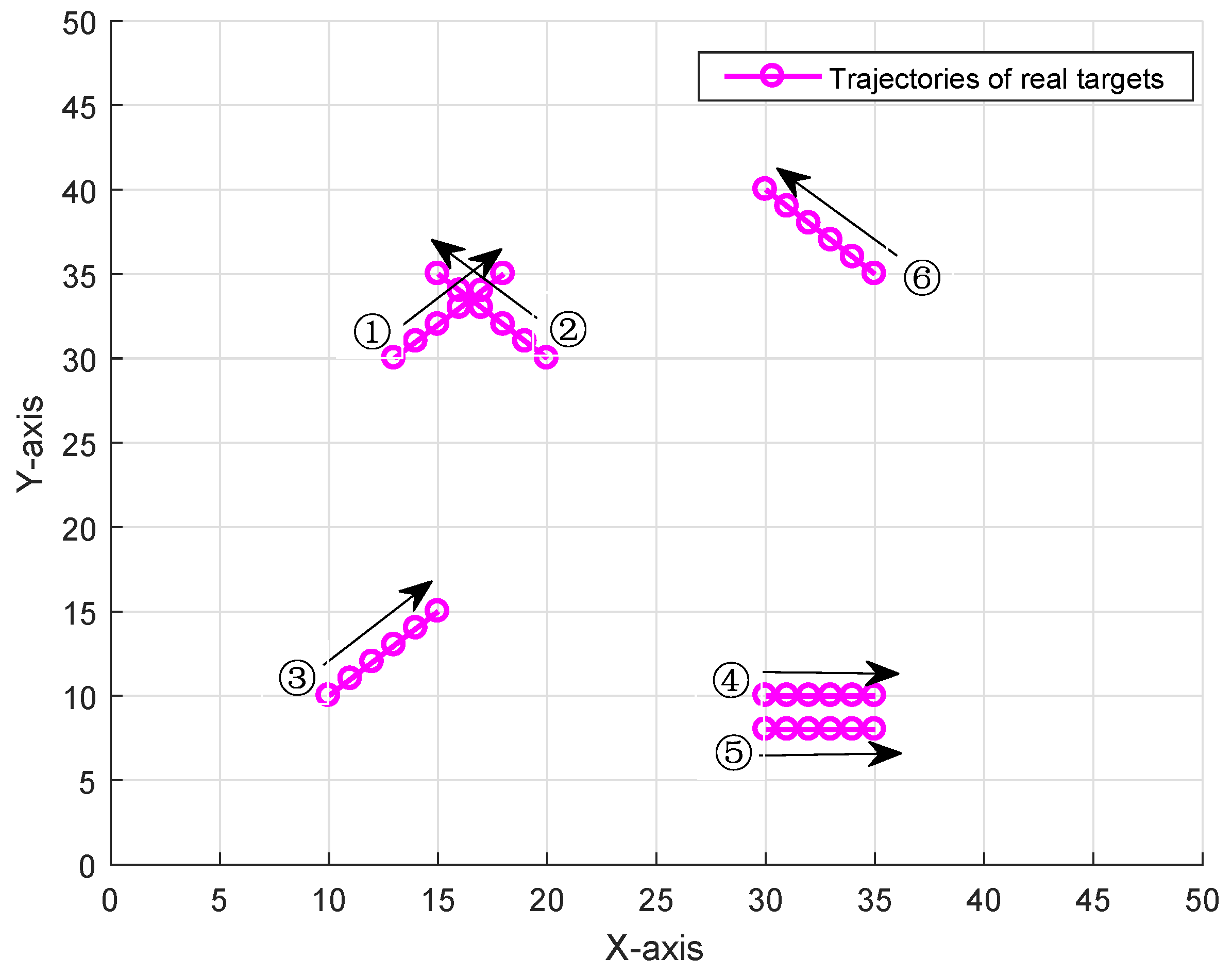
4. Simulations and Analysis
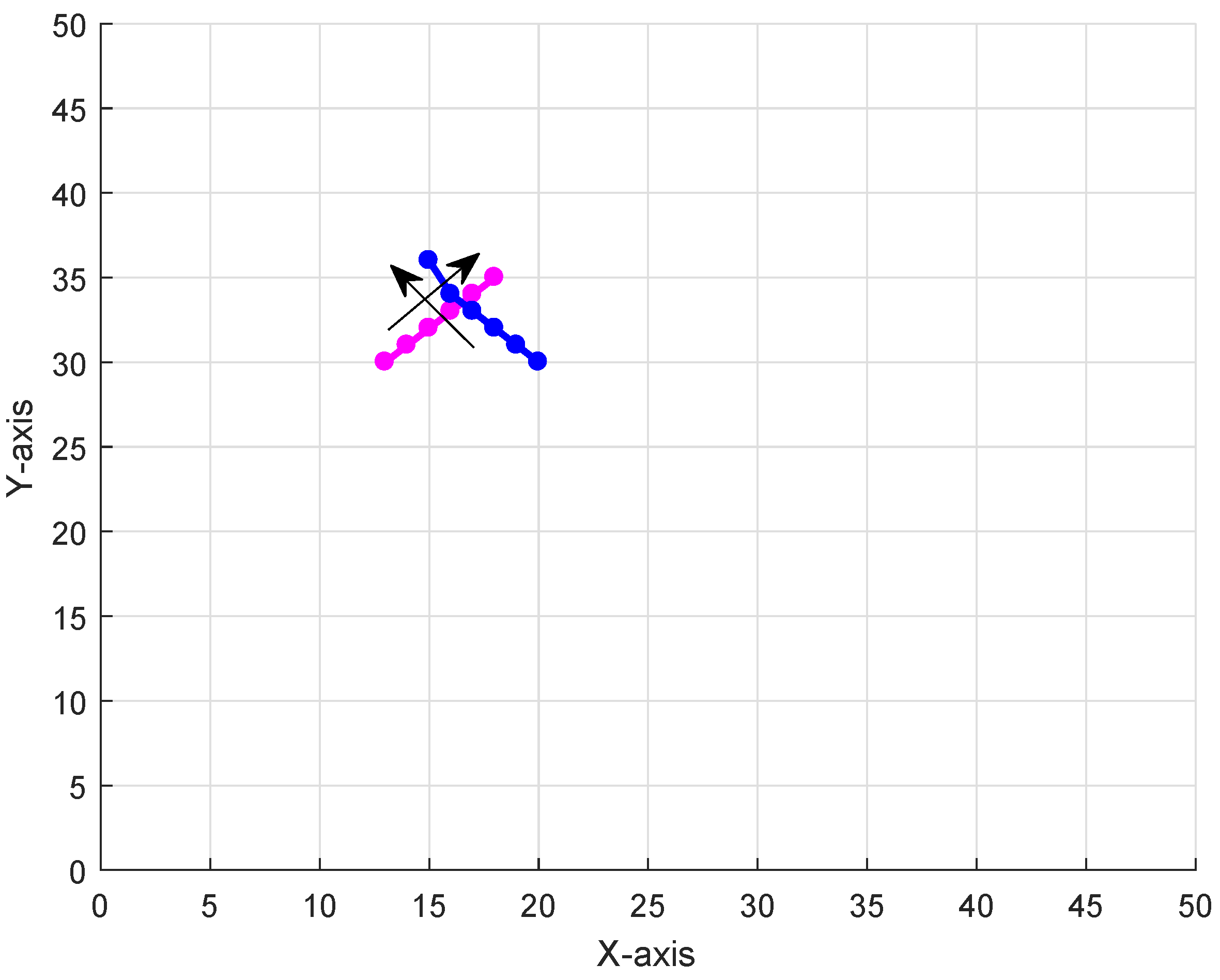
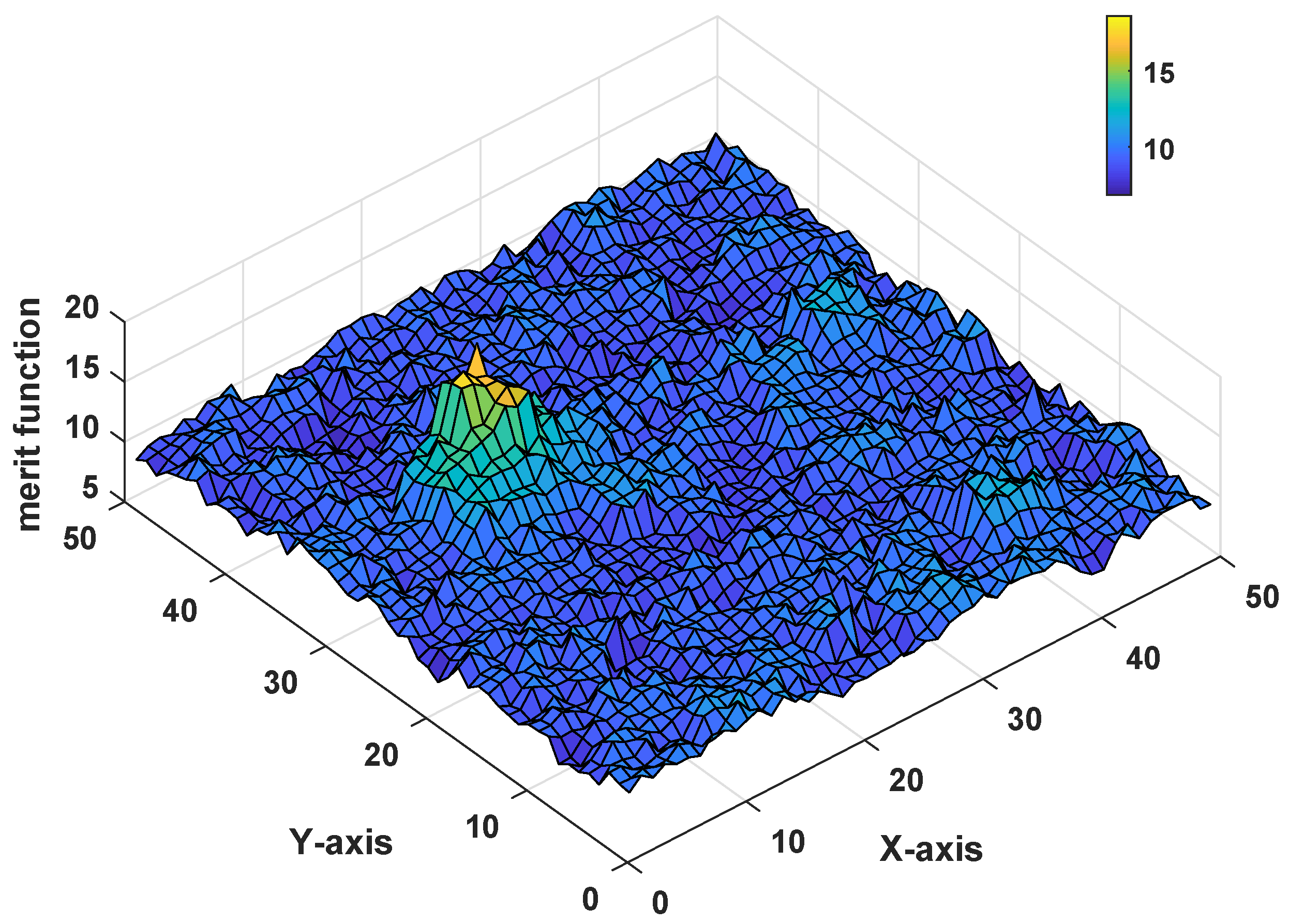
4.1. Interference of Cross Targets
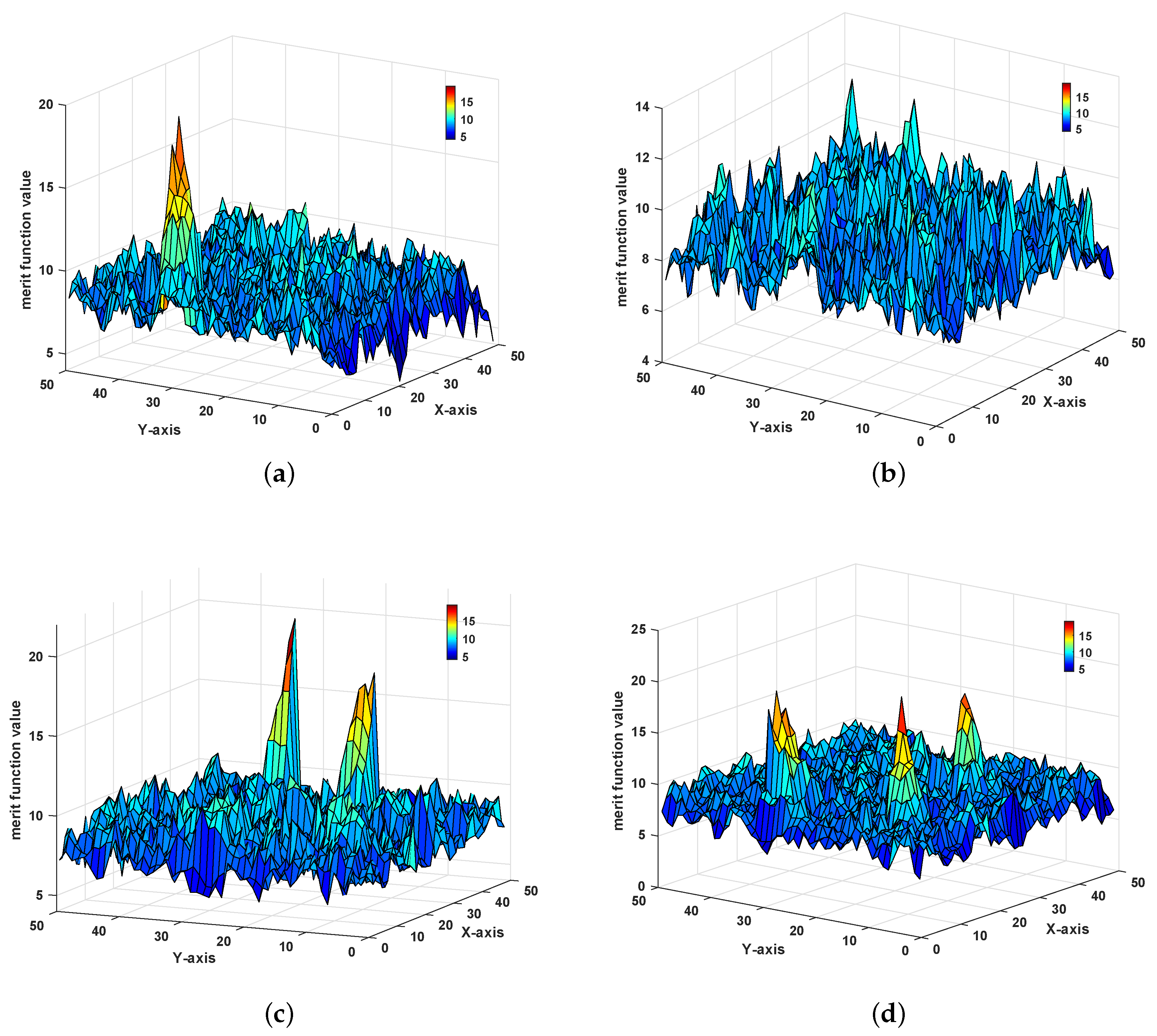
4.2. Simulation of PC-DP-TBD
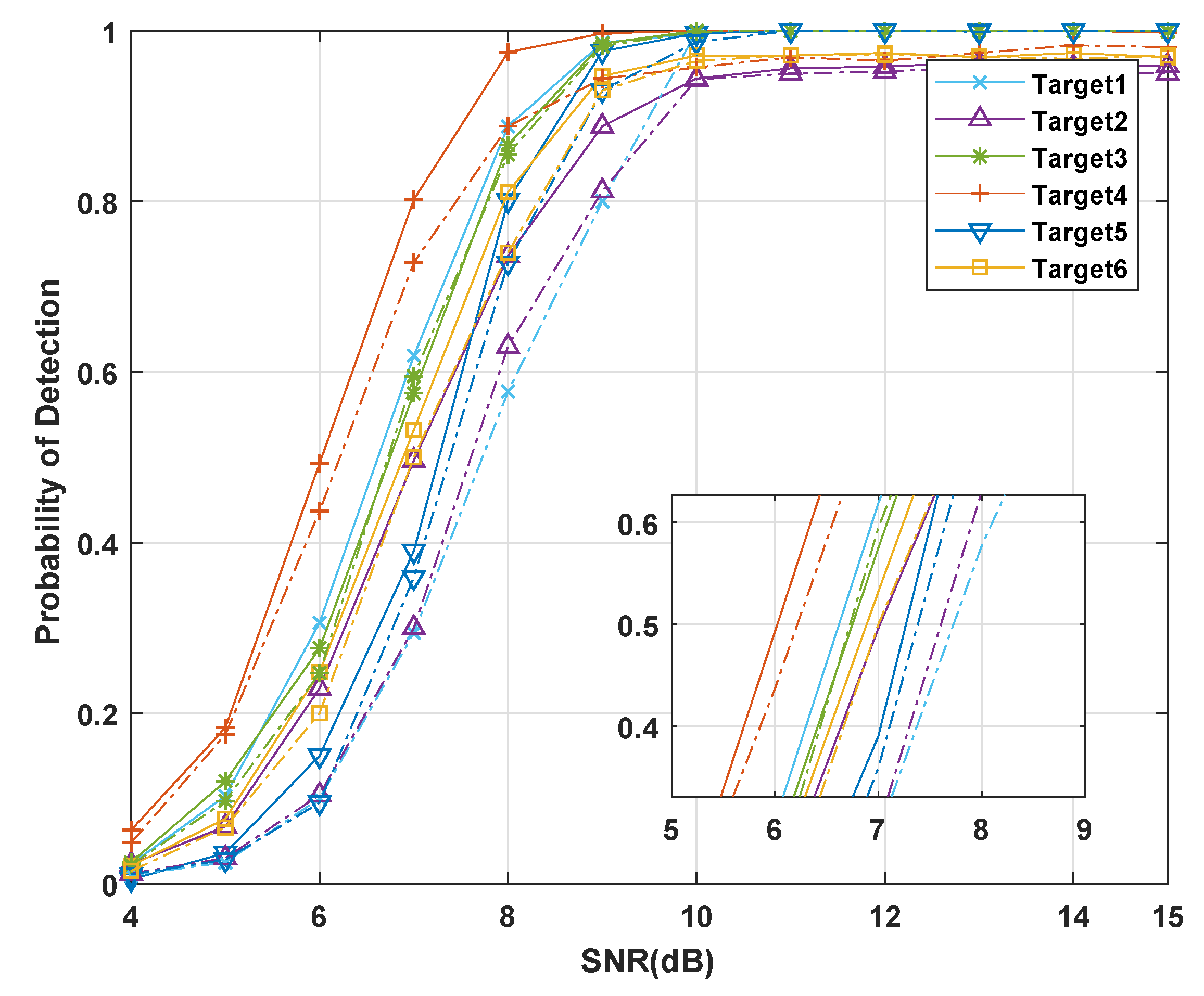
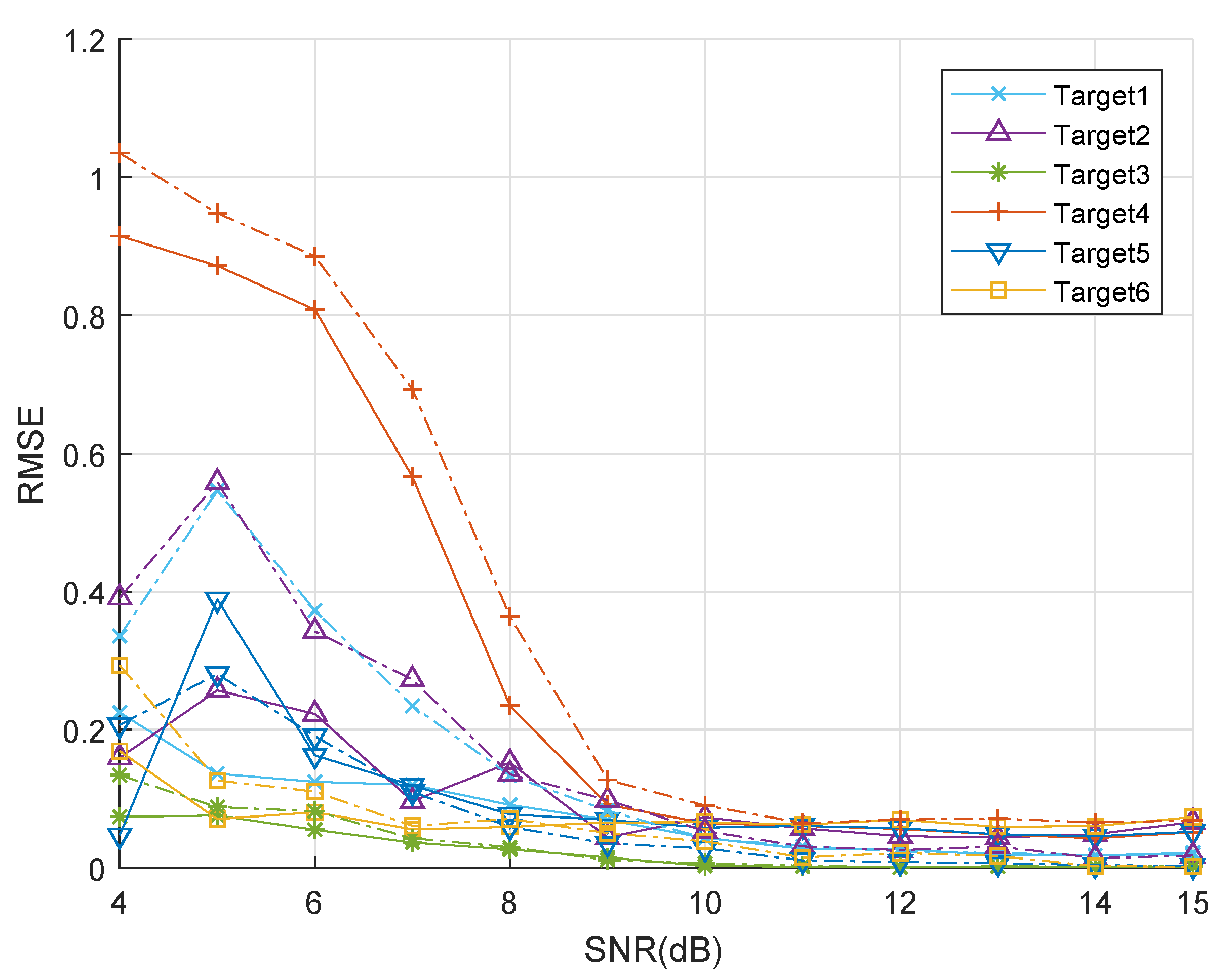
4.3. Performance Analysis
4.4. Computational Expense
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Davey, S.J.; Rutten, M.G.; Cheung, B. A comparison of detection performance for several track-before-detect algorithms. Eurasip J. Adv. Signal Process. 2007, 22–27. [Google Scholar] [CrossRef]
- Larson, R.; Peschon, J. A dynamic programming approach to trajectory estimation. IEEE Trans. Autom. Control 1966, 11, 537–540. [Google Scholar] [CrossRef]
- Huang, X.; Zhao, Y.; Hao, Y. Dynamic Programming Algorithm for Track-Before-Detect Technology. Command Inf. Syst. Technol. 2015, 53–71. [Google Scholar] [CrossRef]
- Tonissen, S.; Evans, R. Peformance of dynamic programming techniques for Track-Before-Detect. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 1440–1451. [Google Scholar] [CrossRef]
- Cai, F.; Fan, H.; Fu, Q. Dual-Channel Particle Filter Based Track-Before-Detect for Monopulse Radar. Math. Probl. Eng. 2014, 2014, 750279. [Google Scholar] [CrossRef]
- Rutten, M.G.; Ristic, B.; Gordon, N.J. A comparison of particle filters for recursive track-before-detect. In Proceedings of the 2005 7th International Conference on Information Fusion, Philadelphia, PA, USA, 25–28 July 2005; Volume 1, p. 7. [Google Scholar] [CrossRef]
- Jing, C.; Lin, Z.; Li, J. Detection and tracking of an underwater target using the combination of a particle filter and track-before-detect. In Proceedings of the OCEANS 2016-Shanghai, Shanghai, China, 10–13 April 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Bi, X.; Du, J.; Zhang, Q.; Wang, W. Improved multi-target radar TBD algorithm. J. Syst. Eng. Electron. 2015, 26, 1229–1235. [Google Scholar] [CrossRef]
- Carlson, B.D.; Evans, E.D.; Wilson, S.L. Search radar detection and track with the Hough transform. I. system concept. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 102–108. [Google Scholar] [CrossRef]
- Buzzi, S.; Lops, M.; Venturino, L.; Ferri, M. Detection of an Unknown Number of Targets via Track-Before-Detect Procedures. In Proceedings of the 2007 IEEE Radar Conference, Boston, MA, USA, 17–20 April 2007; pp. 180–185. [Google Scholar]
- Yi, W.; Morelande, M.R.; Kong, L.; Yang, J. An Efficient Multi-Frame Track-Before-Detect Algorithm for Multi-Target Tracking. IEEE J. Sel. Top. Signal Process. 2013, 7, 421–434. [Google Scholar] [CrossRef]
- Grossi, E.; Lops, M.; Venturino, L. A Track-Before-Detect Algorithm With Thresholded Observations and Closely-Spaced Targets. IEEE Signal Process. Lett. 2013, 20, 1171–1174. [Google Scholar] [CrossRef]
- Bruno, M.G.S.; Moura, J.M.F. Multiframe detector/tracker: optimal performance. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 925–945. [Google Scholar] [CrossRef]
- Yan, B. Track-before-detect algorithm based on dynamic programming for multi-extended-targets detection. IET Signal Process. 2017, 11, 674–686. [Google Scholar] [CrossRef]
- McDonald, M.; Balaji, B. Impact of Measurement Model Mismatch on Nonlinear Track-Before-Detect Performance for Maritime RADAR Surveillance. IEEE J. Ocean. Eng. 2011, 36, 602–614. [Google Scholar] [CrossRef]
- Jiang, H.; Yi, W.; Cui, G.; Kong, L.; Yang, X. Knowledge-Based Track-Before-Detect Strategies for Fluctuating Targets in K-Distributed Clutter. IEEE Sens. J. 2016, 16, 7124–7132. [Google Scholar] [CrossRef]
- Moyer, L.R.; Spak, J.; Lamanna, P. A Multi-Dimensional Hough Transform-Based Track-Before-Detect Technique for Detecting Weak Targets in Strong Clutter Backgrounds. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 3062–3068. [Google Scholar] [CrossRef]
- Johnston, L.A.; Krishnamurthy, V. Performance analysis of a track before detect dynamic programming algorithm. In Proceedings of the 2000 IEEE International Conference on Acoustics, Speech, and Signal Processing, Istanbul, Turkey, 5–9 June 2000; Proceedings (Cat. No.00CH37100). Volume 1, pp. 49–52. [Google Scholar] [CrossRef]
- Johnston, L.A.; Krishnamurthy, V. Performance analysis of a dynamic programming track before detect algorithm. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 228–242. [Google Scholar] [CrossRef]
- Orton, M.; Fitzgerald, W. A Bayesian approach to tracking multiple targets using sensor arrays and particle filters. IEEE Trans. Signal Process. 2002, 50, 216–223. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Q.; Li, Z.; Song, W.; Fu, W. Parallel Computing Based Dynamic Programming Algorithm of Track-before-Detect. Symmetry 2019, 11, 29. https://doi.org/10.3390/sym11010029
Guo Q, Li Z, Song W, Fu W. Parallel Computing Based Dynamic Programming Algorithm of Track-before-Detect. Symmetry. 2019; 11(1):29. https://doi.org/10.3390/sym11010029
Chicago/Turabian StyleGuo, Qiang, Zhenwu Li, Wenming Song, and Wenyu Fu. 2019. "Parallel Computing Based Dynamic Programming Algorithm of Track-before-Detect" Symmetry 11, no. 1: 29. https://doi.org/10.3390/sym11010029
APA StyleGuo, Q., Li, Z., Song, W., & Fu, W. (2019). Parallel Computing Based Dynamic Programming Algorithm of Track-before-Detect. Symmetry, 11(1), 29. https://doi.org/10.3390/sym11010029



