Mathematical Modeling of Tissue Folding and Asymmetric Tissue Flow during Epithelial Morphogenesis
Abstract
1. Introduction
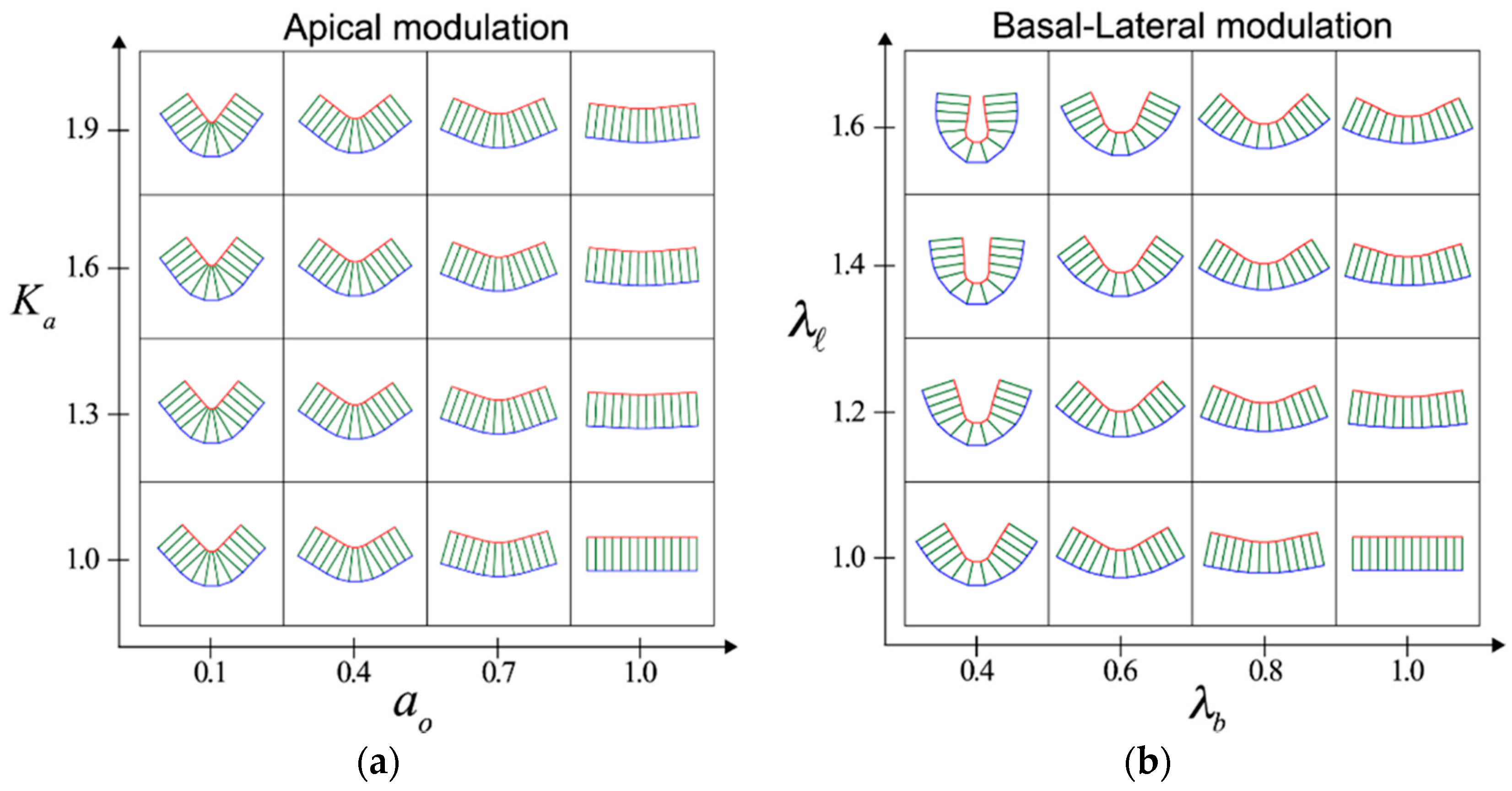
2. Cell-Autonomous Mechanisms that Induce Tissue Folding: Apical Constriction and Basal–Lateral Modulation
3. Unidirectional Tissue Flow Induced by a Combination of Chirality and Junctional Remodeling
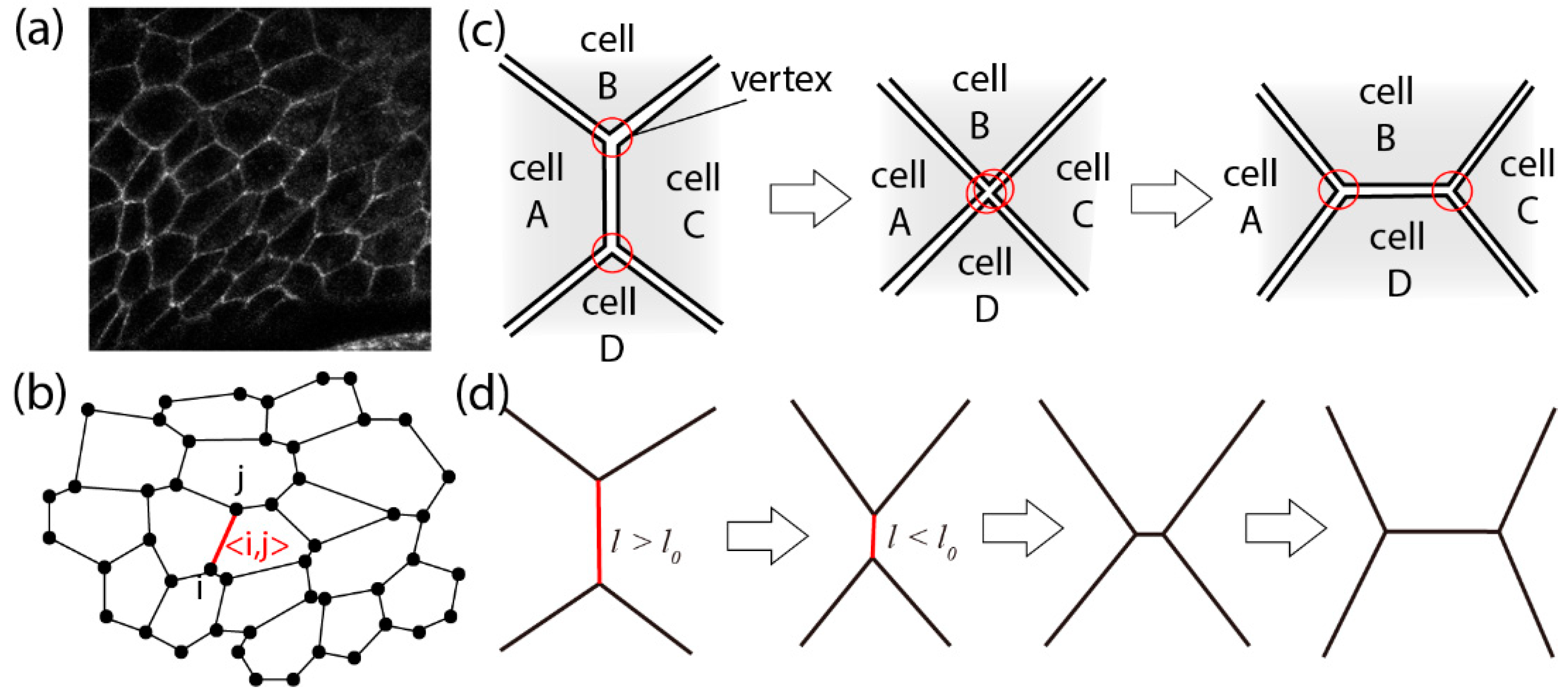
3.1. Vertex Model in an Apical Plane
3.2. Junctional Remodeling and Tissue Morphogenesis
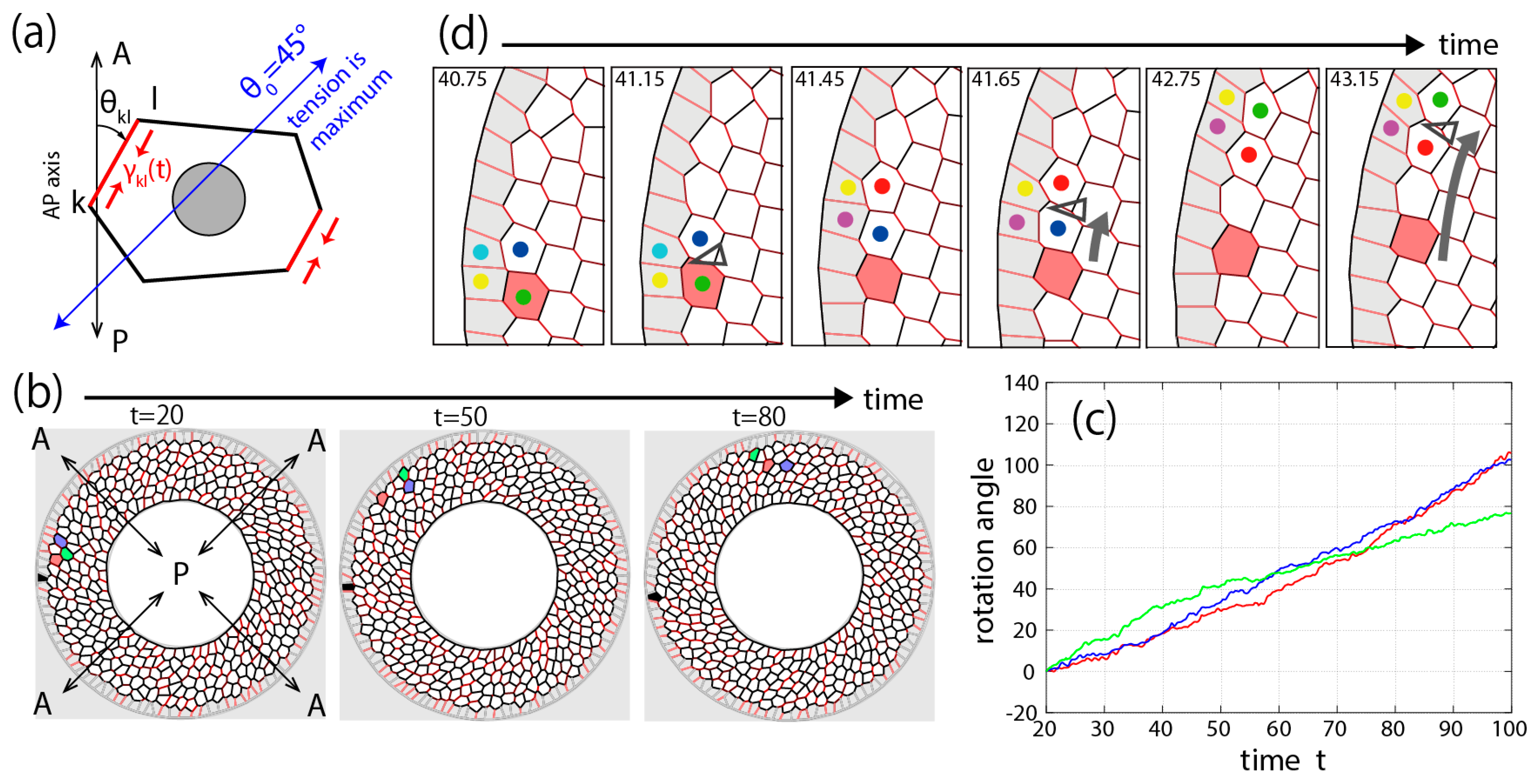
3.3. Theory and Numerical Simulation of Genitalia Rotation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Umetsu, D.; Kuranaga, E. Planar polarized contractile actomyosin networks in dynamic tissue morphogenesis. Curr. Opin. Genet. Dev. 2017, 45, 90–96. [Google Scholar] [CrossRef] [PubMed]
- Khan, Z.; Wang, Y.-C.; Wieschaus, E.F.; Kaschube, M. Quantitative 4D analyses of epithelial folding during Drosophila gastrulation. Development 2014, 141, 2895–2900. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Amourda, C.; Shagirov, M.; Hara, Y.; Saunders, T.E.; Toyama, Y. Basolateral protrusion and apical contraction cooperatively drive Drosophila germ-band extension. Nat. Cell Biol. 2017, 19, 375–383. [Google Scholar] [CrossRef] [PubMed]
- Hutson, M.S. Forces for Morphogenesis Investigated with Laser Microsurgery and Quantitative Modeling. Science 2003, 300, 145–149. [Google Scholar] [CrossRef] [PubMed]
- Toyama, Y.; Peralta, X.G.; Wells, A.R.; Kiehart, D.P.; Edwards, G.S. Apoptotic Force and Tissue Dynamics During Drosophila Embryogenesis. Science 2008, 321, 1683–1686. [Google Scholar] [CrossRef] [PubMed]
- Hara, Y.; Shagirov, M.; Toyama, Y. Cell Boundary Elongation by Non-autonomous Contractility in Cell Oscillation. Curr. Biol. 2016, 26, 2388–2396. [Google Scholar] [CrossRef] [PubMed]
- Polyakov, O.; He, B.; Swan, M.; Shaevitz, J.W.; Kaschube, M.; Wieschaus, E. Passive Mechanical Forces Control Cell-Shape Change during Drosophila Ventral Furrow Formation. Biophys. J. 2014, 107, 998–1010. [Google Scholar] [CrossRef]
- Bertet, C.; Sulak, L.; Lecuit, T. Myosin-dependent junction remodelling controls planar cell intercalation and axis elongation. Nature 2004, 429, 667–671. [Google Scholar] [CrossRef]
- Nishimura, T.; Honda, H.; Takeichi, M. Planar Cell Polarity Links Axes of Spatial Dynamics in Neural-Tube Closure. Cell 2012, 149, 1084–1097. [Google Scholar] [CrossRef]
- Sato, K.; Hiraiwa, T.; Maekawa, E.; Isomura, A.; Shibata, T.; Kuranaga, E. Left–right asymmetric cell intercalation drives directional collective cell movement in epithelial morphogenesis. Nat. Commun. 2015, 6, 10074. [Google Scholar] [CrossRef]
- Taniguchi, K.; Maeda, R.; Ando, T.; Okumura, T.; Nakazawa, N.; Hatori, R.; Nakamura, M.; Hozumi, S.; Fujiwara, H.; Matsuno, K. Chirality in Planar Cell Shape Contributes to Left-Right Asymmetric Epithelial Morphogenesis. Science 2011, 333, 339–341. [Google Scholar] [CrossRef] [PubMed]
- Perez-Mockus, G.; Mazouni, K.; Roca, V.; Corradi, G.; Conte, V.; Schweisguth, F. Spatial regulation of contractility by Neuralized and Bearded during furrow invagination in Drosophila. Nat. Commun. 2017, 8, 1594. [Google Scholar] [CrossRef] [PubMed]
- Martin, A.C.; Goldstein, B. Apical constriction: Themes and variations on a cellular mechanism driving morphogenesis. Development 2014, 141, 1987–1998. [Google Scholar] [CrossRef] [PubMed]
- Heisenberg, C.-P.; Bellaïche, Y. Forces in Tissue Morphogenesis and Patterning. Cell 2013, 153, 948–962. [Google Scholar] [CrossRef] [PubMed]
- Heller, E.; Fuchs, E. Tissue patterning and cellular mechanics. J. Cell Biol. 2015, 211, 219–231. [Google Scholar] [CrossRef]
- Sánchez-Corrales, Y.E.; Röper, K. Alignment of cytoskeletal structures across cell boundaries generates tissue cohesion during organ formation. Curr. Opin. Cell Biol. 2018, 55, 104–110. [Google Scholar] [CrossRef]
- Hara, Y. Contraction and elongation: Mechanics underlying cell boundary deformations in epithelial tissue. Dev. Growth Differ. 2017, 59, 340–350. [Google Scholar] [CrossRef]
- Lee, J.-Y. Uncorking gastrulation: The morphogenetic movement of bottle cells. Wiley Interdiscip. Rev. Dev. Biol. 2012, 1, 286–293. [Google Scholar] [CrossRef]
- Popov, I.K.; Ray, H.J.; Skoglund, P.; Keller, R.; Chang, C. The RhoGEF protein Plekhg5 regulates apical constriction of bottle cells during gastrulation. Development 2018, 145, dev.168922. [Google Scholar] [CrossRef]
- Fletcher, A.G.; Cooper, F.; Baker, R.E. Mechanocellular models of epithelial morphogenesis. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 2017, 372, 20150519. [Google Scholar] [CrossRef]
- Ninomiya, H.; Elinson, R.P.; Winklbauer, R. Antero-posterior tissue polarity links mesoderm convergent extension to axial patterning. Nature 2004, 430, 364–367. [Google Scholar] [CrossRef] [PubMed]
- Williams, M.L.; Solnica-Krezel, L. Regulation of gastrulation movements by emergent cell and tissue interactions. Curr. Opin. Cell Biol. 2017, 48, 33–39. [Google Scholar] [CrossRef] [PubMed]
- Kuranaga, E.; Matsunuma, T.; Kanuka, H.; Takemoto, K.; Koto, A.; Kimura, K.-I.; Miura, M. Apoptosis controls the speed of looping morphogenesis in Drosophila male terminalia. Development 2011, 138, 1493–1499. [Google Scholar] [CrossRef] [PubMed]
- Hatori, R.; Ando, T.; Sasamura, T.; Nakazawa, N.; Nakamura, M.; Taniguchi, K.; Hozumi, S.; Kikuta, J.; Ishii, M.; Matsuno, K. Left–right asymmetry is formed in individual cells by intrinsic cell chirality. Mech. Dev. 2014, 133, 146–162. [Google Scholar] [CrossRef] [PubMed]
- Inaki, M.; Hatori, R.; Nakazawa, N.; Okumura, T.; Ishibashi, T.; Kikuta, J.; Ishii, M.; Matsuno, K.; Honda, H. Chiral cell sliding drives left-right asymmetric organ twisting. Elife 2018, 7, e32506. [Google Scholar] [CrossRef] [PubMed]
- Spéder, P.; Ádám, G.; Noselli, S. Type ID unconventional myosin controls left–right asymmetry in Drosophila. Nature 2006, 440, 803–807. [Google Scholar] [CrossRef]
- Hiraiwa, T.; Kuranaga, E.; Shibata, T. Wave Propagation of Junctional Remodeling in Collective Cell Movement of Epithelial Tissue: Numerical Simulation Study. Front. Cell Dev. Biol. 2017, 5, 66. [Google Scholar] [CrossRef]
- Sato, K. Direction-dependent contraction forces on cell boundaries induce collective migration of epithelial cells within their sheet. Dev. Growth Differ. 2017, 59, 317–328. [Google Scholar] [CrossRef]
- Wen, F.-L.; Wang, Y.-C.; Shibata, T. Epithelial Folding Driven by Apical or Basal-Lateral Modulation: Geometric Features, Mechanical Inference, and Boundary Effects. Biophys. J. 2017, 112, 2683–2695. [Google Scholar] [CrossRef]
- Osterfield, M.; Du, X.; Schüpbach, T.; Wieschaus, E.; Shvartsman, S.Y. Three-Dimensional Epithelial Morphogenesis in the Developing Drosophila Egg. Dev. Cell 2013, 24, 400–410. [Google Scholar] [CrossRef]
- Murisic, N.; Hakim, V.; Kevrekidis, I.G.; Shvartsman, S.Y.; Audoly, B. From discrete to continuum models of three-dimensional deformations in epithelial sheets. Biophys. J. 2015, 109, 154–163. [Google Scholar] [CrossRef] [PubMed]
- Ogura, Y.; Wen, F.-L.; Sami, M.M.; Shibata, T.; Hayashi, S. A Switch-like Activation Relay of EGFR-ERK Signaling Regulates a Wave of Cellular Contractility for Epithelial Invagination. Dev. Cell 2018, 46, 162–172.e5. [Google Scholar] [CrossRef] [PubMed]
- Hočevar Brezavšček, A.; Rauzi, M.; Leptin, M.; Ziherl, P. A Model of Epithelial Invagination Driven by Collective Mechanics of Identical Cells. Biophys. J. 2012, 103, 1069–1077. [Google Scholar] [CrossRef] [PubMed]
- Štorgel, N.; Krajnc, M.; Mrak, P.; Štrus, J.; Ziherl, P. Quantitative Morphology of Epithelial Folds. Biophys. J. 2016, 110, 269–277. [Google Scholar] [CrossRef] [PubMed]
- Misra, M.; Audoly, B.; Kevrekidis, I.G.; Shvartsman, S.Y. Shape Transformations of Epithelial Shells. Biophys. J. 2016, 110, 1670–1678. [Google Scholar] [CrossRef] [PubMed]
- Hannezo, E.; Prost, J.; Joanny, J.-F. Theory of epithelial sheet morphology in three dimensions. Proc. Natl. Acad. Sci. USA 2014, 111, 27–32. [Google Scholar] [CrossRef]
- Krueger, D.; Tardivo, P.; Nguyen, C.; De Renzis, S. Downregulation of basal myosin-II is required for cell shape changes and tissue invagination. EMBO J. 2018, 37, e100170. [Google Scholar] [CrossRef] [PubMed]
- Okuda, S.; Takata, N.; Hasegawa, Y.; Kawada, M.; Inoue, Y.; Adachi, T.; Sasai, Y.; Eiraku, M. Strain-triggered mechanical feedback in self-organizing optic-cup morphogenesis. Sci. Adv. 2018, 4, eaau1354. [Google Scholar] [CrossRef] [PubMed]
- Nagai, T.; Honda, H. A dynamic cell model for the formation of epithelial tissues. Philos. Mag. B 2001, 81, 699–719. [Google Scholar] [CrossRef]
- Li, B.; Sun, S.X. Coherent Motions in Confluent Cell Monolayer Sheets. Biophys. J. 2014, 107, 1532–1541. [Google Scholar] [CrossRef]
- Bi, D.; Yang, X.; Marchetti, M.C.; Manning, M.L. Motility-driven glass and jamming transitions in biological tissues. Phys. Rev. X 2016, 6, 021011. [Google Scholar] [CrossRef] [PubMed]
- Coburn, L.; Lopez, H.; Caldwell, B.J.; Moussa, E.; Yap, C.; Priya, R.; Noppe, A.; Roberts, A.P.; Lobaskin, V.; Yap, A.S.; et al. Contact inhibition of locomotion and mechanical cross-talk between cell–cell and cell–substrate adhesion determine the pattern of junctional tension in epithelial cell aggregates. Mol. Biol. Cell 2016, 27, 3436–3448. [Google Scholar] [CrossRef] [PubMed]
- Lecuit, T.; Lenne, P.-F.; Munro, E. Force Generation, Transmission, and Integration during Cell and Tissue Morphogenesis. Annu. Rev. Cell Dev. Biol. 2011, 27, 157–184. [Google Scholar] [CrossRef]
- Jha, A.; van Zanten, T.S.; Philippe, J.-M.; Mayor, S.; Lecuit, T. Quantitative Control of GPCR Organization and Signaling by Endocytosis in Epithelial Morphogenesis. Curr. Biol. 2018, 28, 1570–1584.e6. [Google Scholar] [CrossRef]
- Fletcher, A.G.; Osterfield, M.; Baker, R.E.; Shvartsman, S.Y. Vertex Models of Epithelial Morphogenesis. Biophys. J. 2014, 106, 2291–2304. [Google Scholar] [CrossRef] [PubMed]
- Collinet, C.; Rauzi, M.; Lenne, P.-F.; Lecuit, T. Local and tissue-scale forces drive oriented junction growth during tissue extension. Nat. Cell Biol. 2015, 17, 1247–1258. [Google Scholar] [CrossRef]
- Sato, K.; Hiraiwa, T.; Shibata, T. Cell Chirality Induces Collective Cell Migration in Epithelial Sheets. Phys. Rev. Lett. 2015, 115, 188102. [Google Scholar] [CrossRef] [PubMed]
- Tee, Y.H.; Shemesh, T.; Thiagarajan, V.; Hariadi, R.F.; Anderson, K.L.; Page, C.; Volkmann, N.; Hanein, D.; Sivaramakrishnan, S.; Kozlov, M.M.; et al. Cellular chirality arising from the self-organization of the actin cytoskeleton. Nat. Cell Biol. 2015, 17, 445–457. [Google Scholar] [CrossRef]
- Lebreton, G.; Géminard, C.; Lapraz, F.; Pyrpassopoulos, S.; Cerezo, D.; Spéder, P.; Ostap, E.M.; Noselli, S. Molecular to organismal chirality is induced by the conserved myosin 1D. Science 2018, 362, 949–952. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hiraiwa, T.; Wen, F.-L.; Shibata, T.; Kuranaga, E. Mathematical Modeling of Tissue Folding and Asymmetric Tissue Flow during Epithelial Morphogenesis. Symmetry 2019, 11, 113. https://doi.org/10.3390/sym11010113
Hiraiwa T, Wen F-L, Shibata T, Kuranaga E. Mathematical Modeling of Tissue Folding and Asymmetric Tissue Flow during Epithelial Morphogenesis. Symmetry. 2019; 11(1):113. https://doi.org/10.3390/sym11010113
Chicago/Turabian StyleHiraiwa, Tetsuya, Fu-Lai Wen, Tatsuo Shibata, and Erina Kuranaga. 2019. "Mathematical Modeling of Tissue Folding and Asymmetric Tissue Flow during Epithelial Morphogenesis" Symmetry 11, no. 1: 113. https://doi.org/10.3390/sym11010113
APA StyleHiraiwa, T., Wen, F.-L., Shibata, T., & Kuranaga, E. (2019). Mathematical Modeling of Tissue Folding and Asymmetric Tissue Flow during Epithelial Morphogenesis. Symmetry, 11(1), 113. https://doi.org/10.3390/sym11010113




