1. Introduction
Unmanned Aerial Vehicles (UAVs) cluster intelligence and cooperation depend on timely and effective information exchange between different nodes, therefore the communication network is one of the most important design issues of multi-UAV system [
1]. UAVs exchange data or instructions through one or more hops in FANET, which is a center-free ad hoc network between UAVs [
2]. In three-dimensional single-connected FANET networks, the movement or failure of some UAVs will lead to the disconnection of communication links or network partition, resulting in data transmission failure [
3,
4,
5]. Therefore, it is an urgent problem to establish fault-tolerant networks to ensure the reliable end-to-end connection between UAVs.
A network is defined as bi-connected if there are two disjoint communication paths between any pair of UAV nodes in the network, which is the basic goal of the FANET network fault-tolerant design [
6]. Topology control is an effective method to realize fault-tolerant networks [
7], which can be divided into three categories. The first method is to maintain network connectivity by adjusting the transmit power of nodes in the network [
8,
9]. Fidel Aznar [
10] proposed a theoretical model of the swarm energy consumption to describe the UAVs energy consumed. R. Ramanathan [
11] proposed two distributed heuristic algorithms, which adaptively adjust the transmit power of nodes according to the topology changes and attempts to maintain the topology connectivity using the minimum power. In [
12], an adaptive topology control algorithm is proposed to improve the network performance by controlling the transmit power to change the transmission range. M. Mozaffari [
13] and F. Lagum [
14] analyzed the deployment of a UAV as a flying base station and minimized the total required transmit power of UAV while covering the entire area. However, sometimes the distance between UAVs is so long that the maximum transmit power may be unable to achieve connectivity. The second method is to add relay nodes to the network to improve the fault tolerance capability of UAV network [
15,
16]. Kashyap A [
17] reconstructed the topology of ad hoc network by adding relay nodes to meet the fault tolerance requirements of the network. Jie LI [
18] proposed maintaining the fault tolerance UAV ad hoc network through the speed control of relay nodes. However, the additional relay nodes increase the UAV quantity cost. The third method is to use UAV movement in cluster to achieve bi-connected fault-tolerant network [
19]. Prithwish first proposed the centralized block movement algorithm [
20], but the global topology information of UAV cluster is difficult to obtain and the distance of deviation from original track is too long. Shantanu proposed the distributed node movement algorithm to implement a bi-connected fault-tolerant network [
21], but the algorithm causes the disconnection of the original communication link, and the recovery success rate in the sparse network is not high. UAV moves in three-dimensional space, but the existing research on mobile topology control is based on two-dimensional space [
19,
20,
21,
22]. Therefore, the research of distributed movement control based on three-dimensional space is of great significance to improve the fault tolerance of UAV dynamic network.
To realize fault-tolerant network, we adopt local movement management to control the network topology. As every UAV has its own task, we can only change its movement in a limited range and direction, which is challenging work. In this paper, we propose the localized fault-tolerant algorithm based on node movement freedom degree (LFTMF) for single-connected FANET networks to realize fault-tolerant network with minimum movement cost. The main contributions are as follows. Firstly, the movement freedom degree model of UAV nodes is established based on k-hop local topology of UAV nodes in three-dimensional FANET. Then, we analyze the consistency of k-hop cut points and global cut points. Finally, we adopt local cascade movement management to achieve bi-connected fault tolerant networks.
The rest of this paper is organized as follows. In
Section 2, the system model and problem analysis are introduced.
Section 3 presents the local cut point detection algorithm and LFTMF algorithm. Simulation results are discussed in
Section 4 and
Section 5 gives conclusion.
2. Model and Problem Analysis
The signal transmission in space will cause the change of the receiving power, which will decrease with the increase of the distance between the transmission node and the receiving node. This phenomenon is called large-scale fading model, which is the most basic channel model for FANET network research. When a UAV node
sends a wireless signal to
in FANET, the receiving power
of UAV node j is shown in Equation (
1).
Equation (
1) is Fries transfer formula, where
is the transmission power of node
, and
is the carrier wavelength of the wireless signal.
is the distance between the transmission node
and the receiving node
.
is the path loss coefficient and the worse the environment, the greater the value.
is the antenna gain of the transmission node and
is the antenna gain of the receiving node.
is the loss factor.
In free space, the value of power
of noise and interference is assumed to be constant.
is the threshold of SNR. Then, the receiving power
satisfies Equation (
2).
When
,
, and
, the maximum transmission distance
is shown as Equation (
3).
The paper assumes that the transmitters are the same and the receivers are the same in FANET network. The values of
,
and
are constant. Then, the definition of constant
C is shown as Equation (
4).
Equation (
3) is further abbreviated as Equation (
5).
From Equation (
5), it can be seen that the maximum transmission distance
is proportional to the powers of transmission power
. Given the value of transmission power, the value of the maximum transmission distance of the signal is unique. Therefore, we use the distance to represent transmission power in the latter sections.
UAV cluster carries out reconnaissance tasks in three-dimensional barrier-free space, flying in a straight line and every UAV is equipped with GPS and a wireless transceiver with communication distance
. If the distance between two UAVs is not greater than
, the two UAV nodes are neighbors and have bi-way communication links. This paper assumes that FANET is an isomorphic network. Nodes
corresponds to UAVs and the bi-way communication links between nodes is represented as edges
. UAV nodes and communication links constitute three-dimensional FANET networks topology graph
, and the network topology schematic diagram is shown in
Figure 1. As the network topology only represents the relative position relationship between UAVs, the topology is planform of three-dimensional network topology in this paper.
At the initial time, the FANET network is single connected, but it is prone to be partitioned, which leads to the failure of communication links. Therefore, it is necessary to construct fault-tolerant network and minimize the distance of deviation from original track.
2.1. Node Movement Freedom Degree Model
To better describe the node movement freedom degree model, some symbols and their definitions are shown in
Table 1.
Some important definitions are as follows.
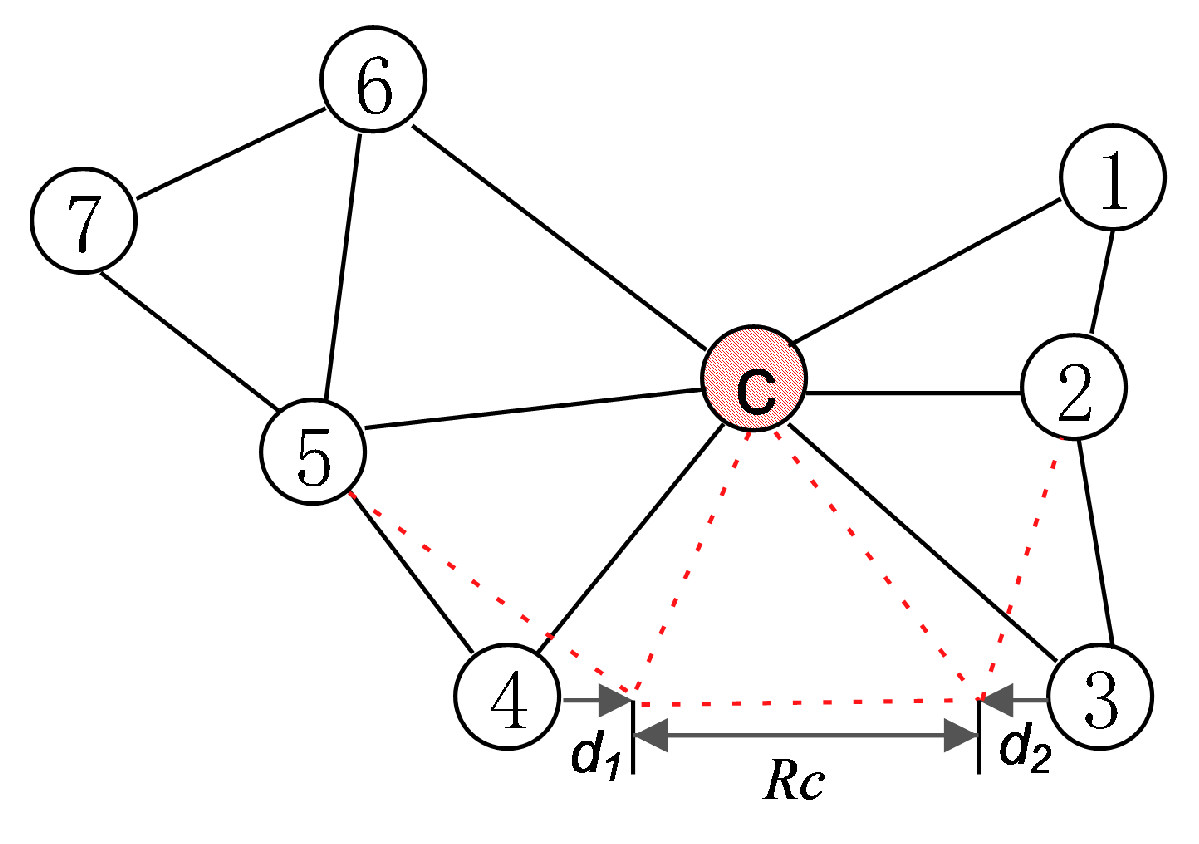
Definition 1. k-hop local topology, also known as k-hop derived subgraph. Suppose is a node in the network topology graph G and is the derived subgraph of G. If all the nodes in are composed of and its k-hop neighbors, then G is the k-hop local topology of of G.
Definition 2. k-hop cut point. In the network topology graph G, if c is the cut point of its k-hop local topology, then c is the k-hop cut point.
Definition 3. Network node density, also called average node degree. The ratio value of the node degree of all nodes in the network topology graph G to the total number of nodes in G is the network node density.
Definition 4. Generalized leaf nodes. Nodes with a node degree of 1 in the network topology graph G are called leaf nodes. For a cut point c, there exists a set , and the neighbor nodes of any node in set A satisfy condition , then the nodes in set A are called generalized leaf nodes.
In the
k-hop topology of cut point
c, the the movement freedom degree
of node
on direction
is defined as the maximum distance that node
could move while maintaining connectivity with all its neighbors
in direction
. That is to say, the minimum value of the maximum distance of deviation from original track on direction
on the premise that node
is connected to each neighbor node
, and the details are shown in Equation (
6).
where
is the maximum distance matrix of deviation from original track of node
on direction
, constrained by its neighbor node
. Element
in
denotes the maximum movement distance of node
on direction
only under the constraint of its neighbor
. According to cosine theorem,
satisfies Equation (
7).
where
represents the angle between vector
and vector
and
represents the set of
kth-hop neighbor nodes of cut point
c. The conditions under which Equation (
7) has a feasible solution are shown as the inequality in Equation (
8).
The inequality in Equation (
8) is always established. Thus, the solution of Equation (
7) is shown in Equation (
9), and the derivation process is as follows.
2.2. Problem Analysis
To describe the problem more conveniently, some of the theorems are as follows.
Theorem 1. If the network is bi-connected, there are no global cut-points in the network topology. If there are no global cut-points in the network topology, the network is bi-connected at least, which means that the network has bi-connectivity or higher connectivity.
Proof of Theorem 1. Firstly, if the network topology graph G satisfies bi-connectivity, there will be at least two disjoint communication paths between any pair of nodes and in the graph G. Assuming that there is a global cut-point c in the topology graph of a bi-connected network G and a pair nodes . After removing node c, there is no communication path between and , which is in contradiction with that G satisfies bi-connectivity. Therefore, if the network topology graph G satisfies bi-connectivity, there is no global cut-point in the G. Then, if the network topology graph G does not have global cut-points, removing any node will not lead to network partition. Therefore, G is not single-connected and it is bi-connected at least. □
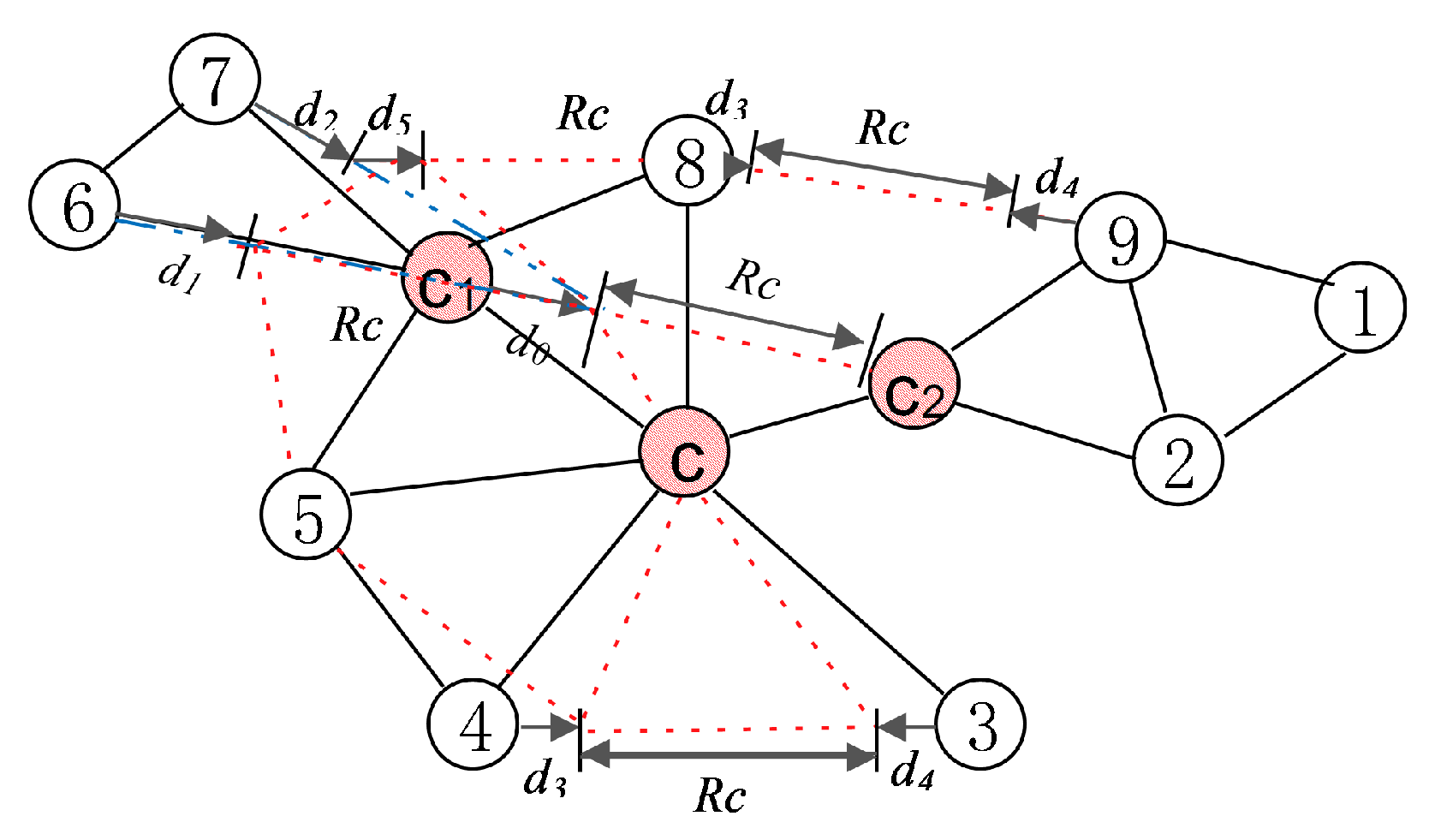
A network topology graph G is defined as k-connected if there are k disjoint communication paths between any pair of UAV nodes in the network. When , the network topology G is single connected and when , the network topology G has fault-tolerant ability and good invulnerability. Therefore, is set to construct a bi-connected fault-tolerant network in this paper. According to Theorem 1, the construction of bi-connected fault-tolerant network can be transformed into the problem of changing cut-points into non-cut points in the network. As the global topology information is unknown, it is necessary to study the cut-point detection algorithm based on k-hop local topology, and approximately minimize the node offset distance based on k-hop local topology of cut-points. The offset distance is the distance of deviation from original track of UAV in this paper.
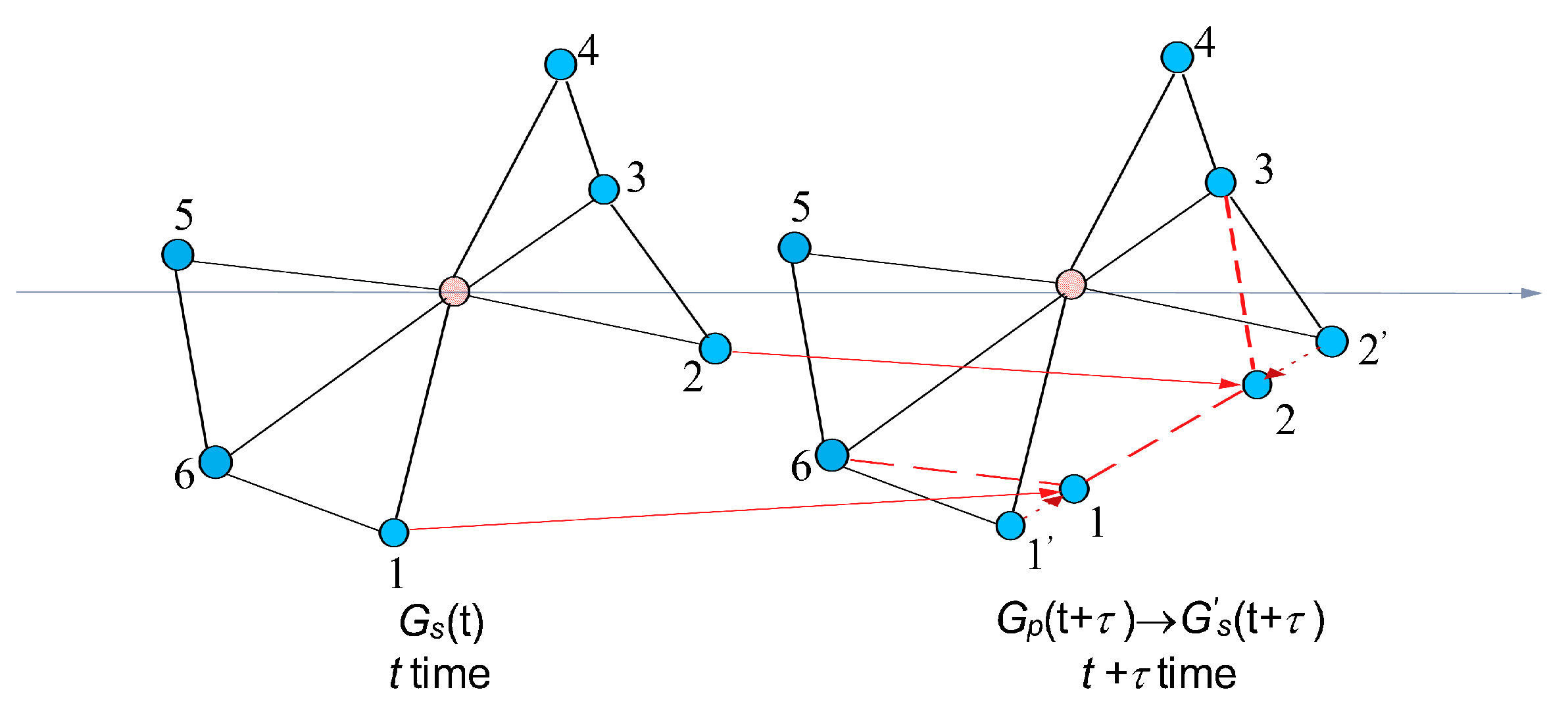
FANET network fault-tolerant control problem is abstracted as the closed-loop control model shown in
Figure 2, and the red node in the predicted topology is cut-point.
The initial network topology is single connected and every UAV executes the control flow.
Step 1: The location of every UAV in the cluster is at time t, and the location predictor of predicts its location of time . The k-hop local topology information, which contains the ID of each node and the location information of every UAV at time t and time , is obtained by k times information exchange with its neighbors. According to the location relationship of nodes, we could get the k-hop local topology of time t and the k-hop local topology of time .
Step 2: The cut-point detector on executes the cut-point detection algorithm based on to determine whether itself is a cut-point. If is a cut-point, update the cut-point information of the k-hop local topology and then obtain by once information exchange with its neighbors.
Step 3: The topology controller of node recalculates the location of UAV nodes in the k-hop local topology of time according to the network fault-tolerance requirements and the predicted local network topology . Then, the movement instructions are sent to the destination UAV node through k times information exchange. Finally, the destination UAV node updates its speed according to the decision rules.
4. Simulation Result
To verify the feasibility of the LFTMF algorithm and test its performance, we conducted simulation experiments to compare the performance of LFTMF algorithm, global block movement algorithm [
17] and localized movement control algorithm [
18]. The test simulated the application layer to transfer data and assumed an ideal MAC layer underneath, with no communication loss and instantaneous delivery of messages.
4.1. Simulation Environment and Parameter Setting
UAV carried out reconnaissance tasks in three-dimensional obstacle-free environment. UAV nodes were randomly distributed within a certain range, and the height distribution of the UAV cluster was kept within 100 m. UAV’s speed was 30 m/s, if it did not participate in the bi-connected fault-tolerant network adjustment. The UAV that participates in the adjustment can reach the destination on time during the adjustment period. The maximum communication range of UAV was m, and the duration of each topology update period was s. FANET was isomorphic and the initial network was single-connected.
4.2. Evaluating Indicator
Five hundred randomly single-connected network topologies were selected in the experiment and the number of maximum adjustment period was five equivalent to time t to time . The success rate of the achievement of fault-tolerant network, the average distance of deviation from original track, the ratio of nodes participating in cascade movement and the average adjustment period were taken as evaluation indexes. Definitions are as follows.
The consistency of k-hop cut-points and global cut-points is defined as the ratio of the number of global cut-points to the number of k-hop cut-points.
The success rate of achieving FANET fault-tolerant network (
) is defined as:
where
is the total number of single-connected network topologies and
B is the number of bi-connected fault-tolerant network topologies in five adjustment periods.
The average distance of deviation from original location (
) is also called average offset distance, which is the total distance that all UAV nodes deviate from their original track in the process of realizing a bi-connected fault-tolerant network in a single-connected network.
where
is the location of every node in the adjusted UAV cluster, and
is the original location of every node in the UAV cluster assuming no adjustment.
The ratio of UAV nodes participating in cascade movement (
) is defined as:
where
is the number of nodes involved in cascade movement and
is the total number of nodes in the network topology.
reflects the degree of change in the original network topology, and has a great impact on computing and communication cost. The larger is the
, the greater are the computing cost and communication cost.
The average adjustment period is the number of periods required for a single-connected network to become a bi-connected fault-tolerant network. The smaller is the , the smaller is the communication cost.
4.3. Discussion of Simulation Results
4.3.1. Experiment 1: Consistency of k-Hop Cut-Points and Global Cut-Points
The value of k was and the number of nodes . Simulated experiment of cut-points detection was carried in 500 random three-dimensional single-connected networks.
Figure 8 shows the relationship between the consistency of
k-hop cut-points and global cut-points and network node density when
k takes different values. With the increase of network node density, the consistency between
k-hop cut-points and global cut-points increased. If the node degree were certain, the greater was the value of
k, the greater was the consistency. The larger was the value of
k, the higher was the communication cost. However, too small a value of
k led to too many
k-hop cut-points, which means non-global cut-points being recognized as global cut-points, resulting in unnecessary movement cost. Therefore, the value of
k was 3 in subsequent experiments. It is worth noting that the global cut-points must be
k-hop cut-points, so eliminating all
k-hop cut-points means eliminating all global cut-points.
4.3.2. Experiment 2: With a Certain Number of UAV Nodes, Analyses of the Relationships among the Performances of LFTMF Algorithm, Global Block Movement Algorithm, Localized Movement Control Algorithm and the Network Node Density by Simulation
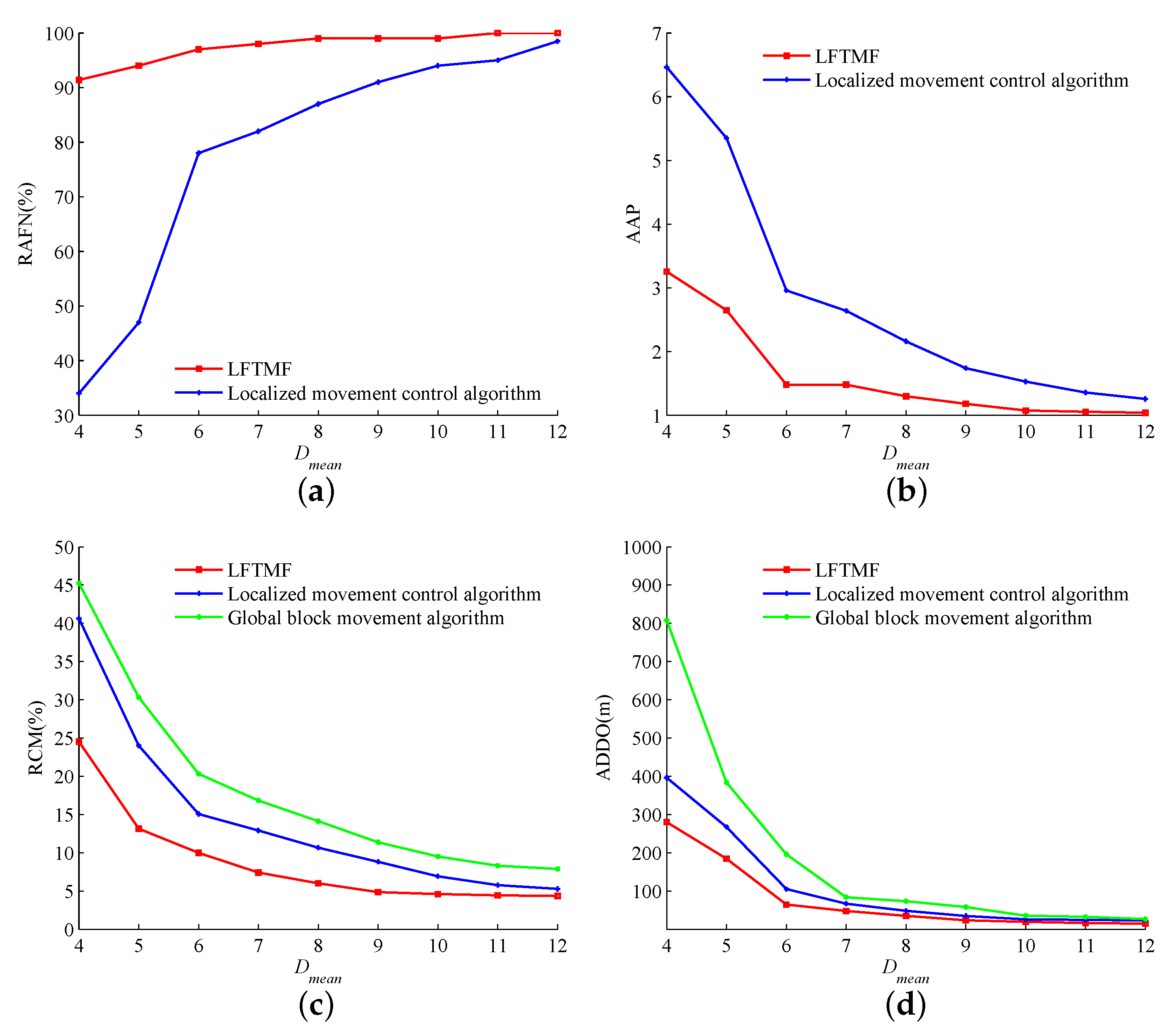
First,
and the number of UAV nodes
were set. Based on 500 random three-dimensional single-connected networks, the relationship between the performance of different algorithms and the network node density was tested, as shown in
Figure 9.
A parse networks means
. In
Figure 9a, it can be seen that, when the network was sparse, the success rate of the achievement of bi-connected fault-tolerant network was more than 90%, while the success rate of the localized movement control algorithm was only 35–45%. When
, the success rate of the localized movement control algorithm increased with the increase of
, and finally reached more than 90%. in
Figure 9b, it can be seen that, in sparse networks, the adjustment period of LFTMF algorithm was much shorter than that of localized movement control algorithm. With the increase of
, the value of
was close to 1, but the value of
of LFTMF algorithm was always smaller than that of localized movement control algorithm.
The reasons for the above results are as follows. In sparse networks, there are many consecutive cut-points without the constraint of movement freedom degree in the localized movement control algorithm. The movement of some nodes leads to the disconnection of the original communication link and the generation of new cut-points. In LFTMF algorithm, the movement freedom degree of the third-hop node of cut-point is 0, and it does not participate in movement, forming a “barrier” to ensure the connectivity with the external topology. With the constraint of node freedom, no new cut-points will be generated. When the network node density is large, the number of cut-points is small, and both algorithms have higher success rate and smaller adjustment period.
In
Figure 9c,d, it can be seen that the ratio of UAV nodes participating in cascade movement and average offset distance of the global block movement algorithm were larger than those of the two distributed algorithms. This is because the nodes move in blocks in block movement algorithm, resulting in more UAV nodes participating in the movement and a larger offset distance. Compared with LFTMF algorithm, localized movement control algorithm has a larger ratio of nodes participating in cascade movement and movement cost because it may lead to the generation of new cut-points, and the adjustment period is longer.
In summary, the performance of all the algorithms improved with the increase of network node density when the number of UAV nodes was certain. Compared with localized movement control algorithm, LFTMF algorithm has obvious advantages in sparse network.
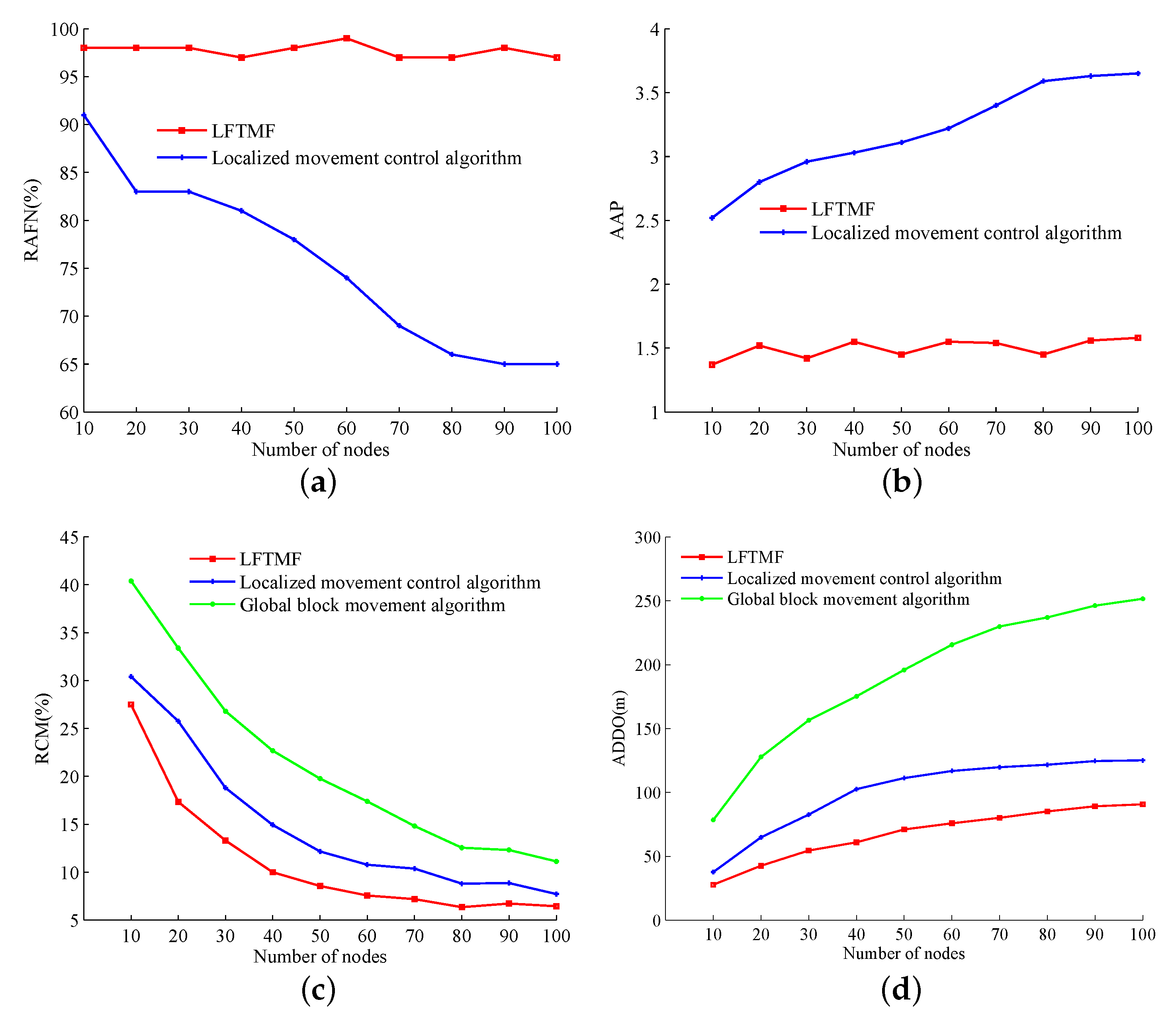
4.3.3. Experiment 3: With a Certain Network Node Density, Analyses of the Relationships among the Performances of LFTMF Algorithm, Global Block Movement Algorithm, Localized Movement Control Algorithm and the Number of UAV Nodes by Simulation
First,
and the network node density
were set. Based on 500 random three-dimensional single-connected networks, the relationship between the performance of different algorithms and the number of UAV nodes was tested, as shown in
Figure 10.
It can be seen in
Figure 10a,b that, with the increase of the number of nodes, the success rate of LFTMF algorithm remained above 95%, and the adjustment period was about 1.5, independent of the number of nodes. The success rate of the localized movement control algorithm decreased continuously, and finally stabilized at about 65%. The adjustment period increased continuously, and finally stabilized at about 3.5. The reasons is that, when the network scale increases, the 3-hop local topology cannot represent the global topology. Localized movement control algorithm will cause the disconnection between the local topology and the rest of the nodes in the global topology, resulting in new cut-points. When the number of nodes reached more than 80, the influence tended to be stable. In the LFTMF algorithm, the third-hop nodes of 3-hop local topology do not participate in the migration, and the movement freedom degree can effectively maintain the connectivity of the original link.
In
Figure 10c,d, it can be seen that the performance of the local algorithm was better than that of the global block movement algorithm when the network scale was large, because the block movement algorithm participated in the movement as a block. The ratio of UAV nodes participating in cascade movement of the three algorithms decreased with the increase of network scale, and the average offset distance increased with the increase of network scale. The reason is that most of the nodes will participate in the movement when the network scale is small. Only the nodes around the cut-points participate in the movement when the network scale is large and at this point. The ratio of nodes participating in cascade movement is small, but the number of nodes involved in the movement increases leading to the increase of offset distance. Compared with localized movement control algorithm, the LFTMF algorithm had smaller ratio of participating in cascade movement and average offset distance.
In summary, when the network node density was certain, with the increase of network scale, the success rate of LFTMF algorithm in realizing bi-connected fault-tolerant network was always above 95%, and the overall performance was better than global block movement algorithm and localized movement control algorithm.