Abstract
We construct families of ground state representations of the -current net and of the Virasoro nets with central charge . We show that these representations are not covariant with respect to the original dilations, and those on the -current net are not solitonic. Furthermore, by going to the dual net with respect to the ground state representations of , one obtains possibly new family of Möbius covariant nets on .
1. Introduction
A model of quantum field theory may be in various states: in quantum theory, a system is defined by the algebra of observables and a physical state is realized as a normalized positive linear functional on it [1]. Among them, the most important state on a quantum field theory is the vacuum state, and indeed, notable axiomatizations of quantum field theory are formulated in terms of the vacuum state or the vacuum correlation functions. Yet, some other states are of particular interest. For example, DHR (Doplicher-Haag-Roberts [2]) representations correspond to charged states. KMS (Kubo-Martin-Schwinger [3] (Section 5.3)) states represent thermally equilibrium states. Limiting cases of KMS states, where the temperature is zero, are called ground states and they enjoy particular properties. In this paper, we construct ground states on chiral components of certain two-dimensional conformal field theories.
Ground states can be characterized in various ways, see e.g., [3]. In one of them, ground states are invariant under the dynamics and the generator of the dynamics has positive generator. In the operator-algebraic setting, this is particularly interesting, because if one has a ground state on a one-dimensional Haag-Kastler net, one can take the dual net in the GNS (Gelfand-Naimark-Segal [4] (Section 2.3.3)) representation, The dual net should be considered not as an extension but as a possibly new, different model from the original net, because it has a different Möbius symmetry. Let us recall that there is a certain relation between the failure of Haag duality and symmetry breaking (see [5] (Section 1) for this and some implications on Goldstone bosons), but this does not necessarily hold in -dimensions, because a Haag-Kastler net is not always the fixed point net of a larger net with respect to a Lie group.
In this work, we focus on the simplest class of quantum field theory: chiral components of two-dimensional conformal field theory. Previously we studied KMS states on them [6,7] (let us stress that we study here KMS states and ground states with respect to the spacetime translations. We studied the KMS states with respect to rotations in a previous work [8] and discussed possible applications to 3d black holes.).Differently from KMS states, it appears to be difficult to classify ground states for a given net: the techniques to classify KMS states do not directly apply to ground states, because we do not have a direct connection between ground states and modular automorphisms, which was crucial in [6] (Section 4.2.1, Appendix B) (the arguments for the case of maximal nets [6] (Theorem 4.7) might still work for ground states), nor extension results of KMS states to larger net (cf. [7] (Appendix A), [9]) are available for ground states. On the other hand, we classified ground states on loop algebras [10], yet it is still unclear whether the results passes to ground states on the corresponding Haag-Kastler nets. Therefore, rather than classifying them, we try to construct various examples.
Contrary to the case of loop algebras where ground state is unique [10], we find that the -current net and the Virasoro nets with admit continuously many ground states. It turns out that the -current net admits a one-parameter family of automorphisms commuting with translations, and by composing them with the vacuum state, we obtain a family of ground states. As the Virasoro nets with restricted to can be embedded in the -current net [11], they also admit a family of ground states. In this way, we construct a family of pure ground states on the -current net parametrized by , and those on the Virasoro nets with parametrized by . In the GNS representations of these ground states, one can take the dual net. While the dual nets in the case of the ground states on the -current net are unitarily equivalent to the -current net itself, for the case of the Virasoro nets with the dual nets must be different from the original net, since the latter are not strongly additive.
We also obtain explicit expressions of the current and the stress-energy tensor in the GNS representation. These expressions in turn serve to show that the GNS representations of the -current net are not normal on half-lines. This shows that the implication “positivity of energy ⟹ solitonic representation”, conjectured in [12] (Conjecture 34) for loop groups, does not hold for the -current net.
This paper is organized as follows. In Section 2 we recall Möbius covariant nets, operator-algebraic setting of chiral components of conformal field theory and collect general facts on ground states. In Section 3 we introduce examples of Möbius covariant nets, the -current net and the Virasoro nets. In Section 4 we construct ground states on these nets and study their property. We conclude with some open problems in Section 5.
2. Preliminaries
2.1. Möbius Covariant Net on Circle
The following is a mathematical setting for chiral components of two-dimensional conformal field theory. These chiral components are essentially quantum field theories on the real line , and by conformal covariance they extend to . In the operator-algebraic setting, they are realized as nets (precosheaves) of von Neumann algebras on . More precisely, let be the set of open, non-dense, non empty intervals in . A Möbius covariant net is a triple of the map , where is a von Neumann algebra on a Hilbert space and is the set of all bounded operators on , U a strongly continuous representation of the group on and a unit vector satisfying the following conditions:
- (MN1)
- Isotony: If , then .
- (MN2)
- Locality: If , then and commute.
- (MN3)
- Möbius covariance: for , .
- (MN4)
- Positive energy: the generator of rotations is positive.
- (MN5)
- Vacuum: is the unique (up to a phase) invariant vector for and (the Reeh-Schlieder property).
From (MN1)–(MN5), one can prove the following [13,14]:
- (MN6)
- Haag duality: , where is the interior of the complement of I.
- (MN7)
- Additivity: If , then .
We consider also the following additional properties:
- Strong additivity: If and are the intervals obtained from I by removing one point, then .
- Conformal covariance: U extends to a projective unitary representation of the group of orientation preserving diffeomorphisms and , and if .
Strong additivity does not follow from (MN1)–(MN5), and indeed the Virasoro nets with fail to have strong additivity [11] (Section 4). If conformal covariance holds, is called a conformal net.
Concrete examples relevant to this work will be presented in Section 3.
2.2. Ground State Representations
Let us identify with a dense interval in by the stereographic projection. By convention, the point of infinity ∞ corresponds to . We denote by the net of algebras restricted to finite open intervals in the real line . Translations and dilations acts on , and they are elements of .
acts on as an automorphism. A state on is by definition a state on the -algebra . Let be a state on and let be the GNS representation with respect to . If extends to in the -weak topology, then we say that is solitonic. If there is a representation of the translation group such that , then we say that is translation-covariant. Furthermore, if the generator of can be taken positive, then we say is a positive-energy representation.
If a state on is invariant under , then is automatically translation-covariant, because one can define , where is the GNS vector for . If furthermore has positive energy, then we say that it is a ground state representation, and the state is called the ground state. By the Reeh-Schlieder argument (see e.g., [15] (Theorem 1.3.2), [16] (Theorem 3.2.1)), the GNS vector is cyclic for for any .
If is a ground state representation with the ground state vector , then one can consider the translation-covariant net on intervals in on the GNS representation space . Its dual net is defined by and . By ([17] (Corollary 1.9)), extends uniquely to a strongly additive Möbius covariant net on :
Theorem 1
(Guido-Longo-Wiesbrock). There is a one-to-one correspondence between
- Isomorphism classes of strongly additive Möbius covariant nets
- Isomorphism classes of Borchers triples , ( is a von Neumann algebra, U is a representation of with positive generator, Ω is cyclic and separating for and such that for ) with the property that Ω is cyclic for
Even if the given net is conformally covariant, it is not known whether the net is conformally covariant. Although is -covariant in the natural sense, where is the group of diffeomorphisms of with compact support, we do not have the uniqueness results of -action (cf. [18] (Theorem 5.5)) for a uniqueness theorem for -action). See [19] (Chapter 4) for some attempts to construct -covariance), and [20] (Section 4.2) for some examples in -dimensions where Möbius covariance gets lost by passing to the dual net.
The purpose of this paper is to construct ground state representations of certain nets. One of the ideas to construct ground state representations is the following: an automorphism of the net is a family of automorphisms of such that for . extends naturally to .
Lemma 1.
If α commutes with , then is a ground state, where is the vacuum state.
Proof.
The GNS representation of is given by , where is the vacuum representation, the identity map. As commutes with , the same representation with positive energy implements translations. □
Furthermore, combining [6] (Lemmas 4.4 and 4.5), we obtain the following dichotomy: if admits one nontrivial ground state, then there must be continuously many ground states.
Proposition 1.
If there is an automorphism α of commuting with translations and if , then are mutually different and their GNS representations are mutually unitarily inequivalent.
Note that as in Proposition 1 cannot be implemented by a unitary operator, because is unique up to a phase. Hence, the second statement implies that the dilation automorphisms are not unitarily implemented in the GNS representations (namely, there are no such that ): if they were implemented, then it would imply that and are unitarily equivalent, which is a contradiction.
3. Main Examples
Here we introduce examples of conformal nets. Although our emphasis is on their restriction to , they are most conveniently defined on . Our treatment of these models follows that of [7] (Section 4.1).
3.1. The -Current Net
Buchholz, Mack and Todorov obtained some fundamental results in the operator-algebraic treatment of the -current algebra [21]. The current can be defined by the Fourier modes , where satisfy the following commutation relations and hence the current J as a quantum field on satisfies the following relation: , for . It admits a vacuum state such that for , and the representation is uniquely determined by this property, unitarity and the commutation relation. The smeared current , where and is the Fourier-coefficient, is essentially self-adjoint on the subspace spanned by vectors , .
The vacuum state is invariant under -transformations , hence this can be implemented by a unitary operator , and in this way we obtain a unitary representation U of with positive energy.
The exponential is called the Weyl operator. They satisfy , where . If we define von Neumann algebras by , then is a Möbius covariant net. This is called the -current net. It is known that it satisfies strong additivity [11] (Equation (4.21) and below), and conformal covariance [22] (Section 5.3).
We can also define J in the real line picture. To do this, note that the above commutation relation is invariant under diffeomorphisms. Therefore, if we introduce for by where is the Cayley transform mapping (with a slight abuse of notation: the definition of depends on whether or ), we obtain the same commutation relation
We call it J in the real line picture. Again by the diffeomorphism covariance, translations and dilations acts on J in the natural way: if is such a transformation, then .
Lemma 2.
For a function f on such that , and can be defined by continuity.
Proof.
Note first that if , then in the strong operator topology. Indeed, recall that [16] (Section 6.5) and . Therefore, it is straightforward to see that, if , then and . It then follows that for a fixed g
and since is total and are unitary, this implies the claimed strong convergence.
For a smooth function f on , , and hence J can be extended by continuity to any -function f on such that . □
If f is piecewise smooth and continuous, then . Indeed, as an operator on , is self-adjoint on the following domain [23] (X.1 Example 1)
and , therefore, . These facts can be seen as an easier version of [18] (Proposition 4.5), [24] (Lemma 2.2).
3.2. The Virasoro Nets
On the Hilbert space of the -current net, one can construct another quantum field. Let where the normal ordering means with negative k comes to the left [25] (2.9). Then they satisfy the Virasoro algebra with the central charge . The stress-energy tensor is essentially self-adjoint on and satisfies the commutation relations . In particular, if f and g have disjoint support, they commute. By the linear energy bound [18] (Proposition 4.5), [26] (Lemma 3.2) and the Driessler-Fröhlich theorem [27] [Theorem 3.1) (or its adaptation to the case of operators [26] (Theorem 3.4)), they actually strongly commute. For , it holds that with a certain , where is the pullback of f as a vector field by [28] (Proposition 3.1). Moreover, integrates to the representation U in the sense that up to a phase [29] (Section 4), see also [28] (Proposition 5.1).
Let us denote and call it the Virasoro subnet. By Haag duality, it holds that . Furthermore, by the Reeh-Schlieder argument, does not depend on I. The restriction of and U to together with is called the Virasoro net with and we denote it by .
We can also consider the real line picture for T. For a vector field f on , or more precisely , we define . Conversely, a vector field f on corresponds to .
In [7] (Proof of Theorem 4.7), we also computed the exponentiation of the relation between and :
where this equality holds on .
To obtain the Virasoro nets with , we need to perturb T as in [11] (4.6), We have computed its real-line picture [7] (Section 5.3):
then satisfies the commutation relation
hence the central charge is . Define . We have seen that , but is covariant only with respect to U restricted to translations and dilations. Yet, does not depend on I again by the Reeh-Schlieder argument. It was shown in [11] (Section 4, (4.8)) that by exploiting the Möbius invariance of n-points functions of , the restriction of to can be extended to a conformal net, the Virasoro net with central charge . does not satisfy strong additivity [11] (Section 4, (4.13)). It is an open problem whether the dual net of is conformal (-covariant).
4. Ground States
4.1. On the -Current Net
Following Lemma 1, we construct automorphisms of commuting with translations. This has been done in [7] (Proposition 4.1). Let us recall it in our present notations.
Lemma 3.
For , there is an automorphism of commuting with translations such that .
Proof.
Let . There is a smooth function with compact support such that . By commutation relation (1), for f with we have
We define . This does not depend on the choice of within the restriction above, because is generated by with . commutes with translations because is invariant under translations. □
From here, it is immediate to construct ground states by Lemma 1. We collect some properties of the resulting GNS representations.
Theorem 2.
We have the following.
- The states are mutually different ground states of , and they are connected with each other by dilations. Dilations are not implemented unitarily.
- The GNS vector of is in the domain of , where and . In particular, it holds that
- The GNS representations do not extend to in the weak operator topology, hence are not solitonic.
- The dual nets are equal to the original net .
Proof.
As are automorphisms commuting with translations, the states are ground states by Lemma 1, and their GNS representations are . They are different states because they give the scalar to . It follows from Proposition 1 that they are connected by dilations and dilations are not implemented unitarily.
Let us recall the action . From this it is immediate that
We also showed [7] (Lemma 4.6) that is invariant under Weyl operators , hence we have, the following equation of operators on :
is a core of , and hence of by the commutator theorem [23] (Theorem X.37) and the estimate , see the computations in [30] (Proposition 1) (this estimate is known since [11] (below (2.23)). Since is invariant under , to apply the commutator theorem with slightly different assumptions [23] (Theorem X.36), it is enough to have a linear bound ).
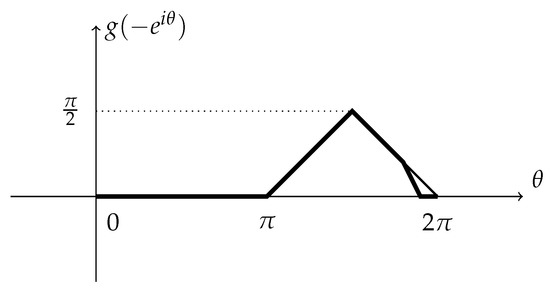
To show the non-normality on the half line ( is analogous), we take a sequence of smooth functions on (see Figure 1):

Figure 1.
The functions (the thick line) and (the thin line above), restricted to .
It is clear that each is piecewise smooth (linear) and continuous, and both converges in the -norm to
Therefore, and hence in the strong operator topology, and in the weak operator topology, too. On the other hand, , where
Note that, , and behaves as as , hence . Accordingly, is not convergent.
The last claim follows immediately because are automorphisms, hence and by strong additivity of . □
In this case it is trivial that the dual net coincides with the original net. In contrast, we have a markedly different result for .
The fact that suggests that q is an analogue of the lowest weight g of [21] (Section 1C), cf. [10] (Lemmas 5.3, 5.6) and the state has uniform charge density q.
The -Current as a Multiplier Representation of the Loop Group
Let be the group of smooth maps from into with winding number 0 with pointwise multiplication [22] (Section 5.1). These elements can be identified with smooth functions on in by logarithm, and the group operation becomes addition. Recall the Weyl relation : this can be seen as a multiplier representation of with the cocycle . From this perspective, one can also consider the subgroup of functions f on such that for all [12] (Section 2.1.2).
Let us observe that is a multiplier representation of functions f whose support does not contain , because for such f, is defined and respects product. We claim that this extends to . Indeed, for such f, is a rapidly decreasing smooth function, hence we can find compactly supported test functions in the topology of Schwartz-class functions, and then . On the other hand, we have seen in Theorem 2 that the representation is not normal (continuous in the -weak topology, which coincides with the weak operator topology on norm-bounded sets) on any half-line.
Henriques conjectured that any positive-energy representation of should be normal on half-lines [12] (Conjecture 34), where G is a simple and simply connected compact group. The above observation shows that an analogous conjecture for does not hold. On the other hand, we have also shown that for such G, the only ground state of the algebra of Schwartz-class maps in is the vacuum state [10] (Corollary 5.8). This supports to some extent the conjecture for . Yet, there are many other positive-energy representations of without ground state, and the situation is not conclusive.
4.2. On Virasoro Nets
We can simply restrict the states to the Virasoro nets . Let us denote , where and this does not depend on I by the Reeh-Schlieder argument. Let us denote the GNS representation by , where is the projection onto .
Theorem 3.
We have the following.
- The states are mutually different ground states of for different , and they are connected with each other by dilations. Dilations are not implemented unitarily in .
- The GNS vector of is in the domain of , where and on .
- If , the dual nets are not unitarily equivalent to any of , .
Proof.
Let us first prove the second statement. We have seen in [7] (Lemma 4.6) that preserves and for it holds on that
Furthermore, we have , and . Applying term by term, we obtain on
since , and this operator has in its domain.
To show that they are different states for different , it is enough to observe that
giving different values.
Let us also check that these states depend only on and not on . To see this, note that is a vacuum-preserving automorphism of commuting with translations. This automorphism clearly intertwines and . Under , is mapped to itself because it is quadratic in J, therefore, is mapped to . Since and give the same state on , they depend only on .
They are connected by dilation on the larger algebra and from the action (formally, J has scaling dimension 1: . By integrating this equation again f, we obtain , where . Similarly, the stress-energy tensor T has scaling dimension 2: and ) of dilations it follows that
Hence ,
Since is the unique translation-invariant vector, it follows that are irreducible (see the arguments of [15] (Corollary 1.2.3)). If dilations were implemented by unitary operators, they would bring a vector state to another vector state which are again translation-invariant, which contradicts the uniqueness of invariant vector.
As are not strongly additive while dual nets are strong additive, they cannot be unitarily equivalent. □
We expect that the GNS representations are not normal on . A candidate for a convergent sequence which is not convergent in is , where are smooth functions on , supported in and converging to a function f which decays as . We expect that is self-adjoint, while is divergent. To do this, the commutator theorem would not suffice (because formally would not be defined for this f) but one would need an analysis similar to [18] (Theorem 4.4).
Here the value can be viewed as the energy density of the state , hence the representation as a whole has infinite energy with respect the original vacuum, cf. [31] where it was shown that, under certain conditions, translation-invariant states cannot be created by finite energy. This also supports that are not normal even on half-lines.
Even for the case , the dual nets cannot be easily identified with any known conformal net. We remark that strong additivity of the original net does not appear to imply that is already dual, cf. [6] (Lemma 3.2).
5. Outlook
Classification. As we have seen, the ground states we constructed in this paper are characterized by a number q (for the -current net) or (for the Virasoro nets). This is a structure very similar to the invariant of [10] (Lemma 5.3). If one studies corresponding Lie algebras, it should be possible to classify ground state representations as in [10] (Theorem 5.6).
More precisely, to the net there corresponds the central extension of the Lie algebra of compactly supported smooth functions on with the relation . To the Virasoro nets one considers the central extension of smooth vector fields on with . By positivity of energy, one should be able to determine the representation in terms of q and , respectively.
Actually, for the -current net, the direct classification of ground states might be possible. Some techniques from [7] (Section 4.2) used to classify KMS states should be useful, although the boundary condition ( for -KMS states) is missing for ground states. As for the Virasoro nets, it is still not clear whether such classification results pass to the Virasoro nets. For that implication, one needs that the ground state vector is infinitely differentiable. We are currently not able to do this, because the corresponding Lie group of compactly supported diffeomorphisms of do not possess any compact subgroup (in contrast to which contains finite covers of , which is the key to differentiate representations [32] (Appendix), cf. [33]).
Dual Nets. The most fundamental properties of the dual nets remain open. Among them is conformal covariance. Conformal covariance implies the split property [34], and even the split property is unknown to hold in these dual nets. The split property may fail in the dual net in two-dimensional Haag-Kastler net [20] (Section 4.2), therefore, it may be worthwhile to try to (dis)prove the split property in these nets.
More Positive-Energy Representations. Ground states consist only a particular class of positive-energy representations. It was shown in [35,36] that there is a huge class of locally normal positive-energy representations of the free massless fermion field in -dimensions. A similar construction should be possible in one dimension. Furthermore, important conformal nets, including some loop group nets, can be realized as subnets of (the tensor product of ) the free fermion field nets (see [37] (Examples 4.13–16)). Among them, there might be counterexamples to [12] (Conjecture 34).
Funding
Supported by Programma per giovani ricercatori, anno 2014 “Rita Levi Montalcini” of the Italian Ministry of Education, University and Research.
Acknowledgments
We acknowledge the MIUR Excellence Department Project awarded to the Department of Mathematics, University of Rome Tor Vergata, CUP E83C18000100006.
Conflicts of Interest
The author declares no conflict of interest.
References
- Haag, R. Local Quantum Physics, 2nd ed.; Texts and Monographs in Physics; Springer: Berlin, Germany, 1996. [Google Scholar]
- Doplicher, S.; Haag, R.; Roberts, J. Fields, observables and gauge transformations. I. Commun. Math. Phys. 1969, 13, 1–23. [Google Scholar] [CrossRef]
- Bratteli, O.; Robinson, D. Operator Algebras and Quantum Statistical Mechanics. 2. Equilibrium States. Models in Quantum Statistical Mechanics, 2nd ed.; Texts and Monographs in Physics; Springer: Berlin, Germany, 1997. [Google Scholar]
- Bratteli, O.; Robinson, D. Operator Algebras and Quantum Statistical Mechanics. 1. C*- and W*-Algebras, Symmetry Groups, Decomposition of States, 2nd ed.; Texts and Monographs in Physics; Springer: New York, NY, USA, 1987. [Google Scholar]
- Buchholz, D.; Doplicher, S.; Longo, R.; Roberts, J.E. A new look at Goldstone’s theorem. Rev. Math. Phys. 1992, 1, 49–83. [Google Scholar] [CrossRef]
- Camassa, P.; Longo, R.; Tanimoto, Y.; Weiner, M. Thermal states in conformal QFT. I. Commun. Math. Phys. 2012, 309, 703–735. [Google Scholar] [CrossRef]
- Camassa, P.; Longo, R.; Tanimoto, Y.; Weiner, M. Thermal States in Conformal QFT. II. Commun. Math. Phys. 2012, 315, 771–802. [Google Scholar] [CrossRef]
- Longo, R.; Tanimoto, Y. Rotational KMS states and type I conformal nets. Commun. Math. Phys. 2018, 357, 249–266. [Google Scholar] [CrossRef]
- Araki, H.; Kastler, D.; Takesaki, M.; Haag, R. Extension of KMS states and chemical potential. Commun. Math. Phys. 1977, 53, 97–134. [Google Scholar] [CrossRef]
- Tanimoto, Y. Ground state representations of loop algebras. Ann. Henri Poincaré 2011, 12, 805–827. [Google Scholar] [CrossRef]
- Buchholz, D.; Schulz-Mirbach, H. Haag duality in conformal quantum field theory. Rev. Math. Phys. 1990, 2, 105–125. [Google Scholar] [CrossRef]
- Henriques, A. Loop groups and diffeomorphism groups of the circle as colimits. arXiv, 2017; arXiv:1706.08471. [Google Scholar]
- Fredenhagen, K.; Jörß, M. Conformal Haag-Kastler nets, pointlike localized fields and the existence of operator product expansions. Commun. Math. Phys. 1996, 176, 541–554. [Google Scholar] [CrossRef]
- Gabbiani, F.; Fröhlich, J. Operator algebras and conformal field theory. Commun. Math. Phys. 1993, 155, 569–640. [Google Scholar] [CrossRef]
- Baumgärtel, H. Operator Algebraic Methods in Quantum Field Theory; Akademie Verlag: Berlin, Germany, 1995. [Google Scholar]
- Longo, R. Real Hilbert subspaces, modular theory, SL(2,R) and CFT. In Proceedings of the Von Neumann Algebras in Sibiu: Conference, Theta, Bucharest, 25 November 2008; pp. 33–91. [Google Scholar]
- Guido, D.; Longo, R.; Wiesbrock, H.-W. Extensions of conformal nets and superselection structures. Commun. Math. Phys. 1998, 192, 217–244. [Google Scholar] [CrossRef]
- Carpi, S.; Weiner, M. On the uniqueness of diffeomorphism symmetry in conformal field theory. Commun. Math. Phys. 2005, 258, 203–221. [Google Scholar] [CrossRef]
- Weiner, M. Conformal Covariance and Related Properties of Chiral Qft. Ph.D. Thesis, Universitá di Roma “Tor Vergata”, Rome, Italy, 2005. [Google Scholar]
- Morinelli, V.; Tanimoto, Y. Scale and Möbius covariance in two-dimensional haag-kastler net. arXiv, 2018; arXiv:1807.04707. [Google Scholar]
- Buchholz, D.; Mack, G.; Todorov, I. The current algebra on the circle as a germ of local field theories. Nucl. Phys. B Proc. Suppl. 1988, 5B, 20–56. [Google Scholar] [CrossRef]
- Ottesen, J.T. Infinite-Dimensional Groups and Algebras in Quantum Physics; Lecture Notes in Physics. New Series M: Monographs; Springer: Berlin, Germany, 1995; Volume 27. [Google Scholar]
- Reed, M.; Simon, B. Methods of Modern Mathematical Physics. II. Fourier Analysis, Self-Adjointness; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Weiner, M. Conformal covariance and positivity of energy in charged sectors. Commun. Math. Phys. 2006, 265, 493–506. [Google Scholar] [CrossRef]
- Kac, V.G.; Raina, A.K. Bombay Lectures on Highest Weight Representations Of Infinite-Dimensional Lie Algebras; Advanced Series in Mathematical Physics; World Scientific Publishing Co. Inc.: Teaneck, NJ, USA, 1987; Volume 2. [Google Scholar]
- Bischoff, M.; Tanimoto, Y. Construction of Wedge-Local Nets of Observables through Longo-Witten Endomorphisms. II. Commun. Math. Phys. 2013, 317, 667–695. [Google Scholar] [CrossRef]
- Driessler, W.; Fröhlich, J. The reconstruction of local observable algebras from the euclidean green’s functions of relativistic quantum field theory. Ann. L’Institut Henri Poincare Sect. Phys. Theor. 1977, 27, 221–236. [Google Scholar]
- Fewster, C.; Hollands, S. Quantum energy inequalities in two-dimensional conformal field theory. Rev. Math. Phys. 2005, 17, 577–612. [Google Scholar] [CrossRef]
- Goodman, R.; Wallach, N. Projective unitary positive-energy representations of Diff(S1). J. Funct. Anal. 1985, 63, 299–321. [Google Scholar] [CrossRef]
- Lechner, G. Polarization-free quantum fields and interaction. Lett. Math. Phys. 2003, 64, 137–154. [Google Scholar] [CrossRef]
- Dybalski, W. A sharpened nuclearity condition and the uniqueness of the vacuum in QFT. Commun. Math. Phys. 2008, 283, 523–542. [Google Scholar] [CrossRef]
- Carpi, S. On the representation theory of Virasoro nets. Commun. Math. Phys. 2004, 244, 261–284. [Google Scholar] [CrossRef]
- Zellner, C. On the existence of regular vectors. In Representation Theory—Current Trends and Perspectives; EMS Series of Congress Reports; EMS Publishing House: Zürich, Switzerland, 2017; pp. 747–763. [Google Scholar]
- Morinelli, V.; Tanimoto, Y.; Weiner, M. Conformal covariance and the split property. Commun. Math. Phys. 2018, 357, 379–406. [Google Scholar] [CrossRef]
- Doplicher, S.; Spera, M. Representations obeying the spectrum condition. Commun. Math. Phys. 1982, 84, 505–513. [Google Scholar] [CrossRef]
- Doplicher, S.; Spera, M. Local normality properties of some infrared representations. Commun. Math. Phys. 1983, 89, 19–25. [Google Scholar] [CrossRef]
- Tener, J. Geometric realization of algebraic conformal field theories. arXiv, 2016; arXiv:1611.01176. [Google Scholar]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).