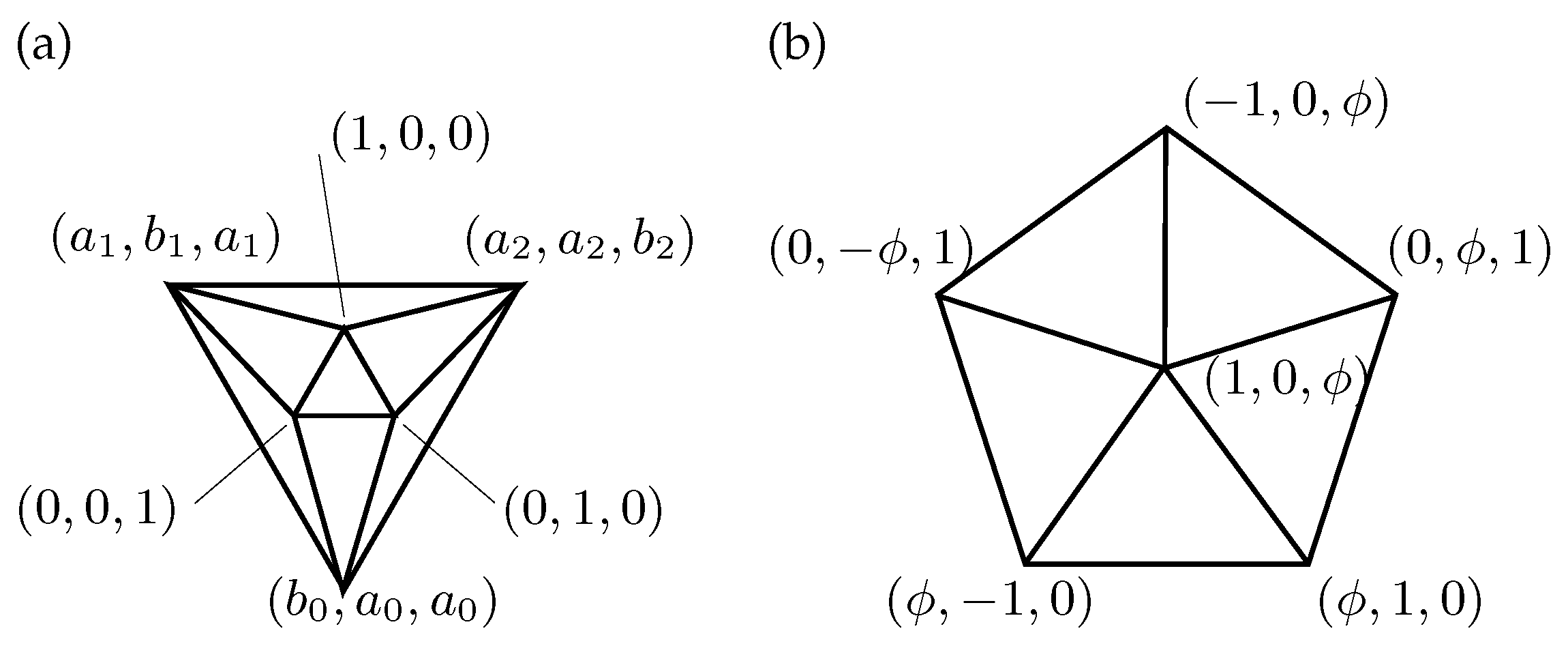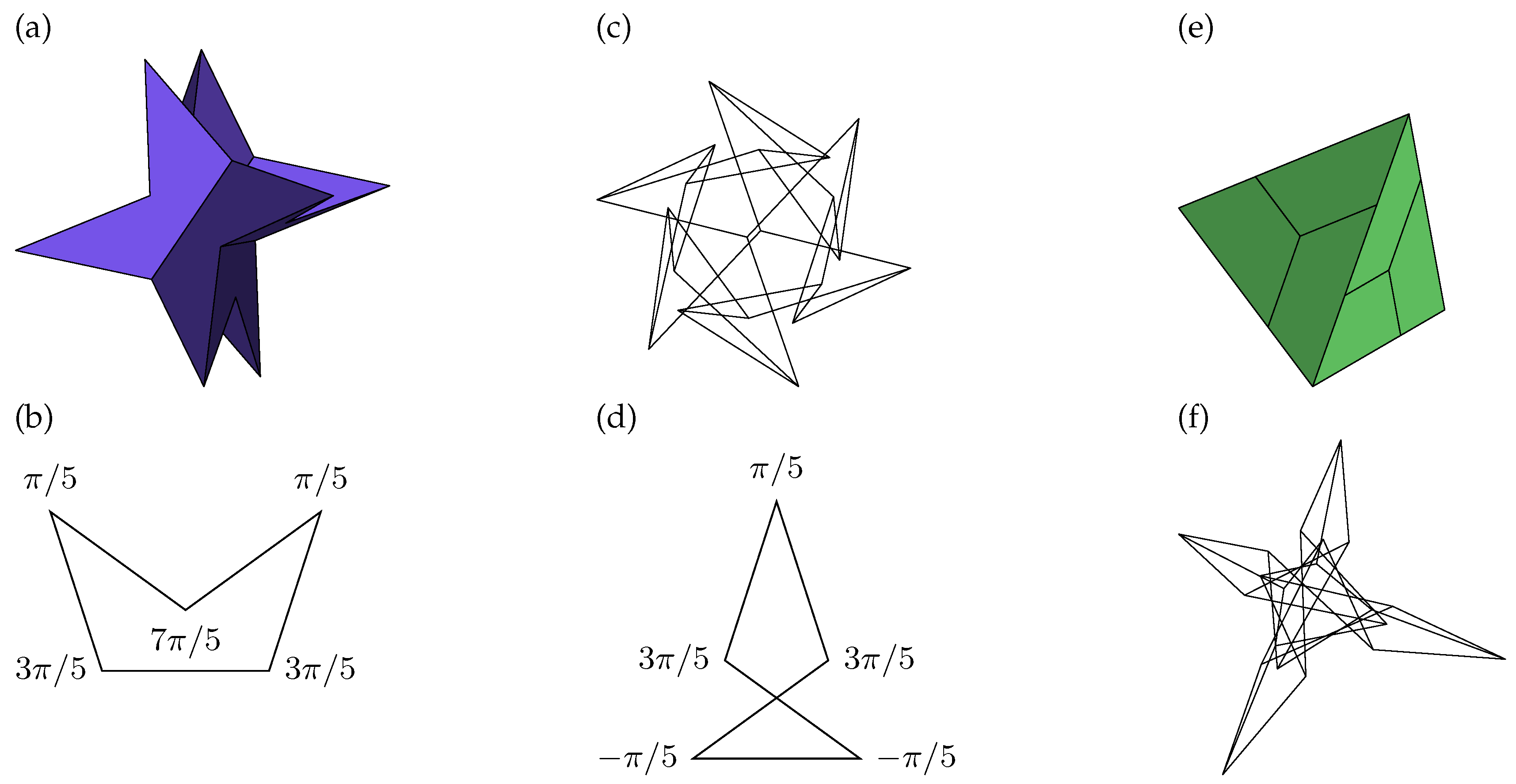2. Definitions and Preliminaries
To properly define what is meant by an “equilateral solid”, we need to consider the planar graph (or cage) formed by the vertices, edges and faces of a solid and the coordinates of its vertices in space:
Definition 1.
Let Γ denote a three-connected planar graph. Let μ denote an embedding of Γ into three-dimensional Euclidian space, i.e., a function that maps vertices of Γ onto coordinate triplets in . We call μ equiplanarized, or an EP-embedding in short, if and only if it satisfies the following properties:
The Euclidian distance is the same for every edge of Γ, i.e., all edges in the embedding have the same length.
If vertices belong to the same face of V, then lie in the same plane, i.e., all faces in the embedding are planar.
Note that the set of vertices, edges and faces in three-dimensional space that results from an EP-embedding does not always form a polyhedron in the strict sense. For example, Definition 1 does not require the set of points to be convex. It does not exclude coplanar faces, collinear edges and intersecting edges and faces. In full generality, the definition even allows different vertices of to map to the same point in three-dimensional space.
We are interested in determining all EP-embeddings for a given planar graph . To tackle this problem, we set up a system of equations (which we call the EP-equations for ) that correspond to Definition 1. For this purpose, we assign coordinates to each vertex of and express the defining properties of an EP-embedding as equations with the variables , and , , and , … as unknowns. There are exactly coordinates, where V denotes the number of vertices of .
Before we proceed, it is important to define at what point we consider two embeddings to be the same. For example, we may embed the complete graph on four vertices as a tetrahedron with vertex coordinates , , and , but we can also use the following coordinates instead: , , and , obtained from the first by adding to each point. Essentially, the second embedding is obtained by translating the result of the first to a different position. These two embeddings are therefore considered equivalent.
Similarly, the embedding with coordinates
,
,
and
are again considered “the same” as the original, because it corresponds to a reflection of the original about one of the coordinate planes. More formally:
Definition 2.
Two EP-embeddings are equivalent (or isometric) if one can be obtained from the other by applying an isometry, i.e., a translation and/or rotation and/or reflection.
Note that rescaling an embedding (by a factor other than ) is not considered an equivalence by Definition 2. For our purposes, this is not really relevant, as we always fix a side length of an EP-embedding beforehand. An embedding can be translated with three degrees of freedom and rotated with a further three degrees of freedom. This is important when we count distinct (i.e., nonequivalent) solutions of the EP-equations below.
We consider two types of EP-equation: edge equations and face equations.
For each edge
of
, the following edge equation needs to be satisfied:
The constant
L denotes the edge length of the embedding. We can always choose
, but in some cases it turns out that other values of
L lead to solutions that are more elegant. There are
E equations of this type, where
E is the number of edges of
.
If the vertices
form a face of
, then the planarity condition holds for that face if and only if the following matrix
has rank at most 3. In terms of equations, this condition can be expressed as the following face equation
for every quadruple
of vertices in a face.
The face equations for a given face are not algebraically independent. They form a variety of dimension
, where
n is the number of vertices in the face. Intuitively,
corresponds to the fact that three of the vertices of a planar
n-gon can be chosen freely in three-dimensional space, but for every subsequent vertex we need to impose the condition that it lies in the plane spanned by the first three. However, this argument only works if it is certain that the first three vertices chosen are not collinear. As we are working with unknown coordinates, this condition cannot easily be guaranteed. (In practice, we always use either
n versions of Equation (
3) or else formulate the fact that the matrix in Equation (
2) has rank at most 3 in a different way.)
In short, the number of restrictions imposed by the face equations is equal to for each n-gonal face, which summed over all faces of amounts to , where F is the number of faces of .
Summing up, we obtain a system of equations with restrictions on unknowns, yielding a total of degrees of freedom. Using Euler’s formula for planar graphs, we see that this number is exactly 6. Because six degrees of freedom provide three translations and three rotations, the solutions of the EP-equations up to equivalence generally leave no further degrees of freedom.
An alternative approach to the issue of equivalence is to restrict the solutions as follows:
Fix the coordinates of to be . Indeed, if there is a solution, then we can always move it so that has exactly these coordinates.
Similarly, we may fix to be of the form , for we can always rotate a solution in such a way that becomes the X-axis.
Finally, we can choose to be of the form by rotating the plane around the X-as so that it coincides with the -plane.
This method drops the variables , , , , and from the EP-equations, yielding variables in all, the same as the number of EP-equations.
Consequently, if the equations for a given polyhedron have no further dependencies, then we expect there to be a finite number of inequivalent solutions. An upper bound for this number of solutions can be derived from Bézout’s theorem: the edge equations are of degree 2, and the face equations are of degree 3, so the total number of solutions (counting multiplicities) is equal to , usually a huge number.
Of course, this bound is only a very rough approximation. Many of the solutions have values for the unknowns that are complex numbers and often the same solution is obtained more than once because of roots with higher multiplicity. In addition, solutions usually come in isometric pairs, where one solution is an inversion of the other with respect to the origin (unless the solution itself has mirror symmetry). Indeed, the equations are invariant under a simultaneous sign change of all unknowns.
Although this is mostly a philosophical issue, we are convinced that the fact that the numbers of equations and variables are equal is an indication that the notion of equiplanarity is a proper mathematical notion to pursue.
We must however point out that, although the system of EP-equations is well-constrained, there is no guarantee that the solution space is zero-dimensional. In other words, it is certainly possible that for a given planar graph the equations have further algebraic dependencies, making the story more complicated. The primary example of a case with dependent equations is the cube. Indeed, every parallelepiped with edges of the same length is a valid EP-embedding of a cube, and there is a three-fold infinity of those solutions. The same phenomenon occurs with other zonohedra. Except in very simple cases, it is very hard to determine the dimension of the solution manifold a priori, except by producing the actual solutions.
In [
5], a different method is used to determine the EP-embeddings of cubic (=trivalent) planar graphs, letting the internal angles of the polygonal faces serve as unknowns instead of the vertex coordinates, but the conclusion was the same: equal numbers of equations and degrees of freedom.
3. Analytic Solutions
Whereas, in [
5], mostly numerical methods are employed, in the present paper, we concentrate on finding the analytic (exact) solutions of the EP-equations. (One disadvantage of solving the equations numerically is that it is very hard to guarantee that all solutions have been found.) Unfortunately, finding all analytic solutions to the EP-equations is only possible in small cases. To illustrate some of the difficulties that may be encountered in the attempt, we determine all EP-embeddings of the octahedron. The corresponding planar graph
is depicted as a Schlegel diagram in
Figure 1a.
Without loss of generality, we may fix the coordinates of one of the equilateral triangles to be , and . This makes the edge length L equal to . This choice already removes the six degrees of freedom that stem from translations or rotations. Note however that for each solution there is still a second (isometric) solution that arises from a reflection about the plane that contains the chosen triangle.
Three vertices remain to be assigned coordinates, for a total of nine unknowns. We use the unknowns
,
,
, …,
,
, and
as indicated in the diagram. Our special choice of coordinates for the first triangle already ensures us that 3 of the 12 edges have the correct length. We introduce nine edge equations for the remaining edges:
Because the faces are triangles, faces are automatically planar, hence there are no face equations in this case.
There are thus nine quadratic equations in nine variables. Assuming the equations are independent, we expect solutions. Fortunately, it turns out that many of these solutions are identical.
Although it is possible to solve the system of Equation (
4) by hand, we have instead chosen to use a computer algebra system to compute the solutions. In particular, we have used the program Singular [
6] through the general purpose system Sage [
7]. Using an automated method ensures that we do not forget any special cases.
According to the computer algebra system, there are eight cases to consider, depending on whether each of the values for
,
and
is equal to or different from 0. The cases where either none or all of these unknowns are zero yield one solution each:
These correspond to the classical embedding of the octahedron and its reflection with respect to the plane .
Each of the other six cases have an infinity of solutions. When exactly one of is zero, say , then one pair of opposite points of the octahedral graph coincide in the embedding, i.e., . Consequently, the eight faces collapse into four coincident pairs, yielding a configuration with four equilateral triangles through a common vertex. The relative position of these triangles can be chosen with one degree of freedom.
When two of are zero, there are two coincident point pairs and the entire configuration collapses to two equilateral triangles through a common edge, again with a single degree of freedom. This configuration is essentially a special case of the above.
Finally, when we do not only find the classical solution given before, but also the solution where three opposite point pairs coincide and all eight faces are mapped to the same triangle. Again, this embedding is a special case of the above.
This example illustrates that solving the EP-equations for even a simple planar graph is already non-trivial and may lead to many solutions that are of little interest. The situation becomes even worse when there are non-triangular faces, because then also face equations are needed, and these are cubic equations (as opposed to quadratic equations for the edges).
Fortunately, in the case of quadrangles, the face equation can be reduced to linear equations. Indeed, in an equilateral quadrangle opposite sides must be parallel. There are two cases. Either the vectors representing opposite sides have the same direction, and then we find
where subsequent vertices of the quadrangle are given coordinates
, or vectors representing opposite sides have opposite direction, in which case one pair of opposite points coincides. Therefore, if we are only interested in EP-embeddings that have no coincident points, the face equation for a quadrangle can be replaced by the system in Equation (
5). Unfortunately, no such simplifications are possible for faces with more than four sides.
5. Symmetric Solutions
In
Section 3, we manage to obtain all EP-embeddings for the graph of the octahedron. In
Section 2, we mention that there is a threefold infinity of EP-embeddings of the graph of the cube. It is also fairly easy to see that the regular tetrahedron is the only EP-embedding of the complete graph on four vertices.
From these examples, the reader might get the impression that finding the EP-embedings of most well-known polyhedral graphs is a simple matter of setting up the correct EP-equations and handing them to a computer algebra system. Unfortunately, it turns out that already for small graphs the EP-equations are too complex and too high in number for even the current state of the art in computer algebra systems. At this moment we have not yet succeeded in solving the EP-equations for the icosahedron (a system of 30 equations) in full generality, let alone those of the dodecahedron (54 equations).
Although it is generally not feasible to obtain all analytic solutions for a given set of EP-equations, it remains possible to find some of them by adding some additional constraints. In this paper, we impose a certain symmetry on the results. In other words, we only seek those solutions that have a given symmetry group acting on them. This group is necessarily a subgroup of the full symmetry group of the original graph.
The graphs that we consider in this paper are the graphs of the Platonic and Archimedean solids. These solids have full symmetry groups of type , I, , O or . However, the symmetry group that we impose on the embedding is not the full symmetry group of these graphs, but rather the chiral tetrahedral group T, which is a subgroup of all these groups.
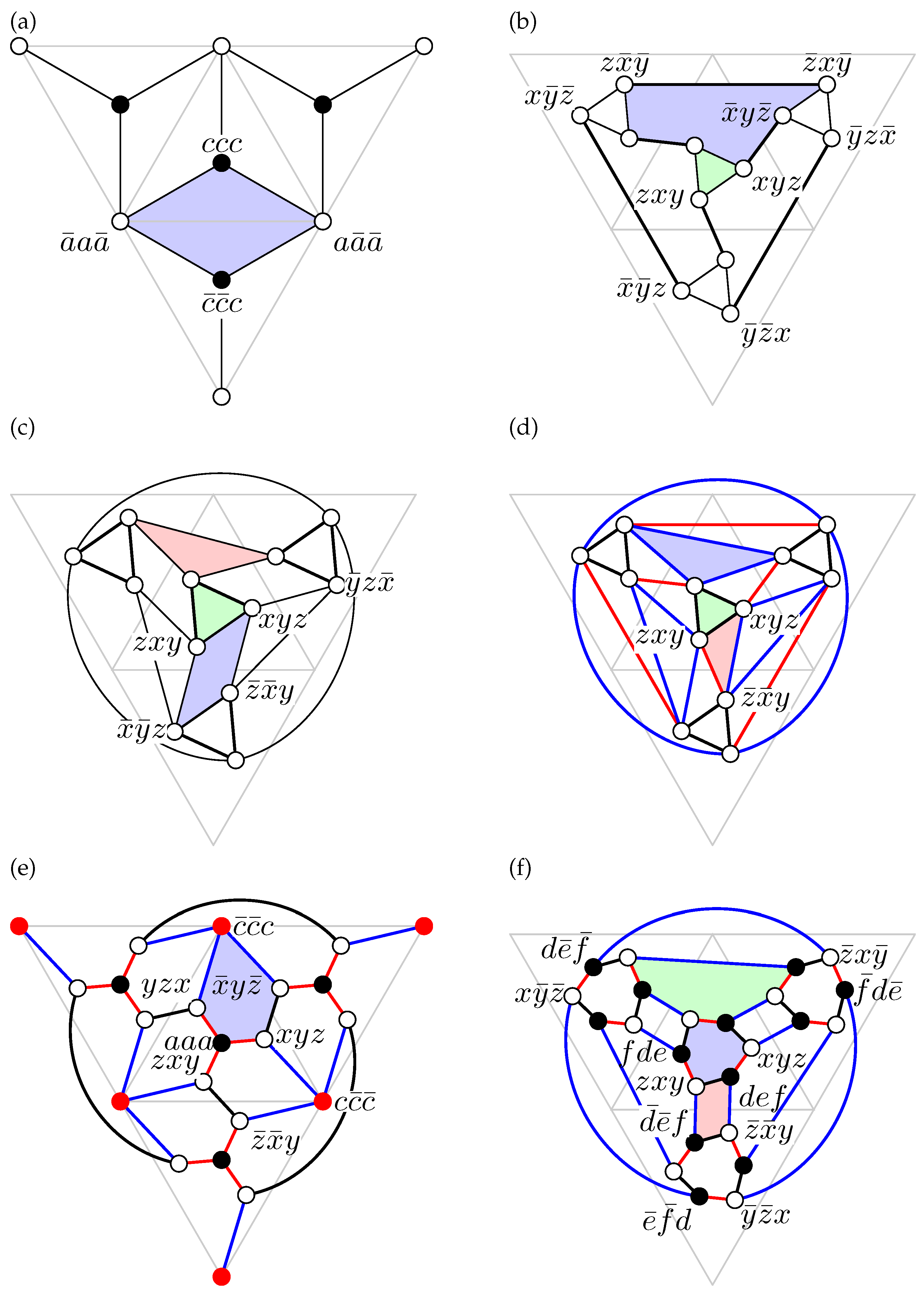
In the following pages, we use a schematic representation of the group
T and its action on three-dimensional space as presented in
Figure 3a. The four triangles in this picture represent the faces of a regular tetrahedron (the reference tetrahedron) that is “folded open”. The three points marked
and joined by dashed arcs, actually indicate the same point in three-dimensional space. Similarly, each pair of outer edges in the picture (e.g., the two top horizontal edges) corresponds to the same edge in three-dimensional space.
The group
T consists of the identity, three rotations of order 2 (with a rotation angle of
) and eight rotations of order 3 (with a rotation angle of
). The three rotations of order 2 are shown as green arrows in the picture and have the X-, Y- and Z-axes as rotation axes. These axes intersect the midpoints of the edges of the reference tetrahedron. These rotations have a simple representation in terms of coordinates:
The eight rotations of order 3 are shown as blue double arrows in the picture. Their axes go through the centers of the four faces of the reference tetrahedron and, although not immediately apparent in the picture, also through the opposite vertex. The rotation with axis through
, i.e., the central blue arrow in the picture, acts by “shifting” the coordinates:
There are several ways to extend T to a larger point group (of which T is a subgroup):
Extending T with the inversion yields the pyritohedral group . This group contains (among other elements) the three mirror symmetries with respect to the coordinate planes, mapping to , and , respectively.
Extending T with the coordinate transpositions , and yields the full tetrahedral group . The coordinate transpositions are mirror symmetries with respect to the planes , and .
Doing both extensions above at the same time yields the full octahedral group
. This group contains (among other elements) six rotations of order 4 (i.e., with a rotation angle of
), with the X-, Y- and Z-axes as rotation axes:
Extending T with the rotations above, but not with any of the mirror symmetries, yields the chiral octahedral group O.
In addition, the icosahedral groups (full) and I (chiral) have T as a subgroup. They can be obtained by extending or T by a rotation of order 5 (with a rotation angle of ). This rotation does not have an elegant representation in the coordinate system that we have chosen here.
The group T has three different types of orbit on the points of the three-dimensional space (excluding the trivial orbit that only contains the center of symmetry).
A first type consists of four points that lie on the four axes of three-fold rotation. These points have coordinates of the form
, where the subscript “even” indicates that of the eight choices of signs, we only consider those with an even number of minus signs.
Figure 3b,c shows two different representations of these points. The fact that we use a two-dimensional representation of a three-dimensional set of points, together with the “folding open” of the reference tetrahedron, might be a bit confusing at first. The reader should think of each point on the picture as representing all points in three-dimensional space on a line through the origin. This explains why the point
is placed in the same position as the vertex
of the reference tetrahedron, although in general this is not the same point. Moreover, the line connecting
with the origin intersects the tetrahedron twice, once in a vertex, but also once in the center of the opposite face. In
Figure 3c, we have chosen the center of a face to represent the line.
Note that a can also be negative. It might help to think of both representations as corresponding to a different sign of a (and each point representing only half a line). If we extend T to , O or , then two orbits of this type collapse to a single orbit of six points, with coordinates of the form , without sign restrictions.
A second type of orbit has size 6 and corresponds to points on the axes of twofold rotation. Their coordinates are of the form
as shown in
Figure 3d. Note that the points with “negative” coordinates are shown twice, as indicated by the dashed arcs (but recall that
b is allowed to be a negative number). Orbits of this type remain the same when we extend the group to either of the tetrahedral or octahedral groups.
The third type of orbit is that of a general point. This orbit has size 12 and contains points with coordinates
,
or
. This orbit is represented in
Figure 3e. In general, two orbits of this type collapse to a single orbit of size 24 when
T is extended to
,
or
O, and four orbits collapse to an orbit of size 48 when
T is extends to
. There are however some specific cases, in which the orbits remain smaller:
The orbit size for the point remains 12 in all cases.
The orbit size for the point , with remains 12 for and becomes 24 for , O and .
The orbit size for the point , with remains 12 for and becomes 24 for , O and .
6. Archimedean and Platonic Solids
We now use the information of the previous section to set up the EP-equations with forced tetrahedral symmetry for all Platonic and Archimedean solids. In
Table 1, we list these uniform solids with their names and vertex configurations, i.e., the sizes of the faces that occur at each vertex, e.g., in a rhombicuboctahedron (3.4.5.4), each vertex is contained in a triangle, a square, a pentagon and a square, in that order. We treat the various cases in increasing order of complexity of the EP-equations. (This roughly corresponds to the increasing number of vertices and number of edges, but the occurrence of quadrangular faces reduces the complexity somewhat.)
Imposing symmetry on the solutions reduces the number of variables and equations substantially. Instead of setting up edge and face equations for all edges and faces, we need to do so only for one edge or face per orbit of the group T. Similarly, the variables in the equations now correspond to the coordinates of only one vertex per orbit instead of all vertices.
Table 2,
Table 3 and
Table 4 list the number of orbits of group
T of each type for all Platonic and Archimedean solids. The bottom section of each table contains a “measure of difficulty” for the EP-equations that need to be solved in each case. The row marked “Variables” contains the number of variables in the equations after simplification. The row marked “Bézout” contains the products of the degrees of the equations.
In the pictures that accompany the various cases on the following pages (
Figure 4), we have used colors to indicate the different orbits of vertices and edges. (For each face orbit, we highlight only a single representative face.) In these pictures we use a condensed notation for coordinates: we drop parentheses and commas (instead of
we write
) and the minus sign is replaced by a bar (for
we write
).
These orbits are not too hard to compute explicitly, but each case needs to be treated separately. A reader familiar with the topic can easily reproduce our results, for instance by reasoning on a three-dimensional model.
Note. We provide a website with three-dimensional models of all the embedded polyhedra that are reported in this and the following section (
http://caagt.ugent.be/ep-embeddings/). The models can be rotated to give a clear impression of their three-dimensional structure.
Tetrahedron (3.3.3) The four vertices of the (graph of the) tetrahedron form a single orbit of
T. If the EP-embedding is to be invariant for
T, then the coordinates of these vertices must be of the form
, as explained in
Section 5. Every vertex is connected to every other vertex by an edge. The edges form a single orbit of
T, and hence there is only a single edge equation. Because the faces are triangles, there are no face equations.
For an edge length , the edge equation becomes with two solutions . (The edge lengths are chosen differently for each case to reduce the number of square roots in the solutions.) These solutions correspond to two EP-embeddings: one with vertex coordinates , and the other with vertex coordinates . Both embeddings are equivalent: one is mapped to the other by the inversion .
Octahedron (3.3.3.3). The six vertices of the (graph of the) octahedron form a single orbit and therefore map to coordinates
,
and
, as explained in
Section 5. The edges form a single orbit, where
is a typical edge. This representation leads to a single edge equation
(this time we choose edge length
). There are no face equations. Both solutions
lead to the same result, i.e., the regular octahedron with vertices
,
and
.
Cube (4.4.4). The eight vertices of the (graph of the) cube form two orbits of size 4, as denoted by filled and unfilled vertices in
Figure 4a, with coordinates
and
. (They form a single orbit under the full automorphism group of the graph, but here we only consider the subgroup
T.) The 12 edges form a single orbit, where
is a typical edge. This leads to the edge equation
with edge length
. There is also a single orbit of quadrangular faces.
Following
Section 3, if we are not interested in embeddings with coincident points, we may use Equation (
5) to simplify the corresponding face equation to
. This simplification yields the solutions
, both corresponding to the “classical embedding” of the cube with vertices
.
Three-fold rotational symmetry. Before proceeding with the more complex polyhedra, we would like to illustrate how the three-fold rotational symmetry that we impose helps to simplify the face equations for certain hexagonal faces. Consider a hexagon through points with coordinates of the following form:
This hexagon is invariant under the three-fold rotation with axis
. It is planar if and only if it lies in a plane perpendicular to the axis, and hence, if and only if
Instead of the three cubic equations that we would obtain in the general case for a hexagonal face, the symmetry that we enforce reduces these equations to a single linear equation.
Truncated tetrahedron (3.6.6). The 12 vertices of the truncated tetrahedron form a single orbit with representative
(
Figure 4b). There are two orbits of edges, as denoted in the picture by two thicknesses of edges. One orbit, generated by
has size 12. The other orbit, generated by
, has size 6. There is one orbit of four triangles, and one orbit of four hexagons. (One hexagon
H lies “behind” the others in the picture.) Each hexagon is rotation invariant for one of the rotation axes of
T through a vertex of the reference tetrahedron, as is evident for
H in the picture.
The edge equations for this configuration are
with
. Because it is rotation invariant, we may apply Equation (
6) to
H, with the following vertices
We find
, i.e.,
. Combining these equations, we obtain
with the following solutions
The solutions come in isometric pairs. The first pair corresponds to the classical embedding of the regular truncated tetrahedron. The second is degenerate insofar as it has coincident points, e.g., . It is therefore not considered a “proper” solution. (The vertices become those of a regular tetrahedron.)
Cuboctahedron (3.4.3.4). The 12 vertices of a cuboctahedron form a single orbit. The edges form two orbits of 12 edges generated by
and
. There are two orbits of triangles and one of quadrangles (
Figure 4c).
The edge equations for this configuration are
with
. The face equations of the quadrangle become
, by Equation (
5). Combining these results, yields
with solutions
The first pair corresponds to the classical embedding of the regular cuboctahedron. The second is degenerate and has coincident points, e.g., . (The vertices become those of a regular octahedron.)
Icosahedron (3.3.3.3.3). The 12 vertices of an icosahedron still form a single orbit under the subgroup
T of its full symmetry group
(
Figure 4d). The edges, on the other hand, now form three orbits (as denoted in the picture by three different colors) generated by
The last edge lies in an orbit of size 6, the other orbits have size 12. Three edges that lie “behind” the picture have been drawn here as curved lines. The triangles come in two orbits of 4 (invariant for three-fold rotations) and one orbit of size 12. There are now three edge equations:
Subtracting the first two equations gives
. Adding them yields
, and from the last equation we then obtain
. Simplified:
First assume
. Then, we find
or
, where
is the golden ratio, and
its algebraic conjugate (cf.
Section 4). These pairs correspond to the classical embedding of the regular icosahedron (
Figure 2c) and its conjugate (
Figure 2d).
Second, assume
and hence
by Equation (
7). We then find the solutions
. These are four degenerate solutions that reduce the icosahedron to a tetrahedron.
Dodecahedron (5.5.5). The 20 vertices of the dodecahedron come in two orbits of size 4, generated by
and
, and one orbit of size 12, generated by
(
Figure 4e).
The edges form threee orbits, with representatives
The last edge lies in an orbit of size 6, the other orbits have size 12. There is one orbit of 12 pentagonal faces, with representative vertices
It is not difficult to verify that the EP-equations are invariant under the (simultaneous) transformations
and under inversion. It follows that in principle for every solution we find three others. (They turn out always to be equal or equivalent to the original solution.)
In this case, it is no longer feasible to solve the EP-equations “by hand” so instead we have used a computer algebra system. Groebner basis calculations with variable order
yield a polynomial of degree 24 in
y (of degree 12 in
) that factors as follows:
We investigate each factor separately.
Case 1. . This yields a degenerate solution with and coincident points.
Case 2.
, i.e.,
or
. The first value of
y yields the coordinates of the classical embedding of the regular dodecahedron (
Figure 2e):
The second yields its algebraic conjugate (
Figure 2f). The factor
of Equation (
9) leads to the same solution, but inverted with respect to the origin.
Case 3.
, i.e.,
or
. For
we find
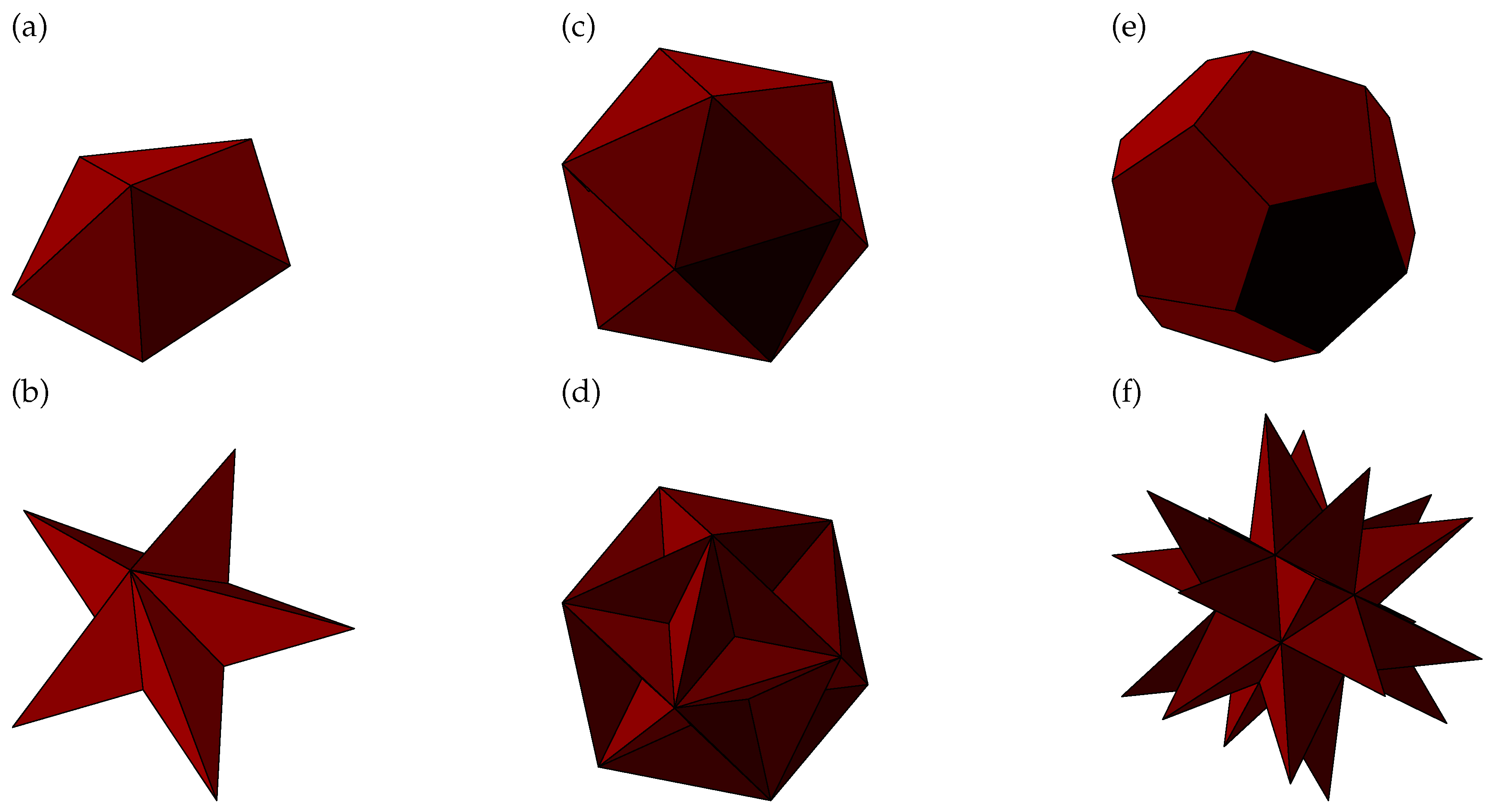
We have dubbed this embedding the equilateral dodecastemma (
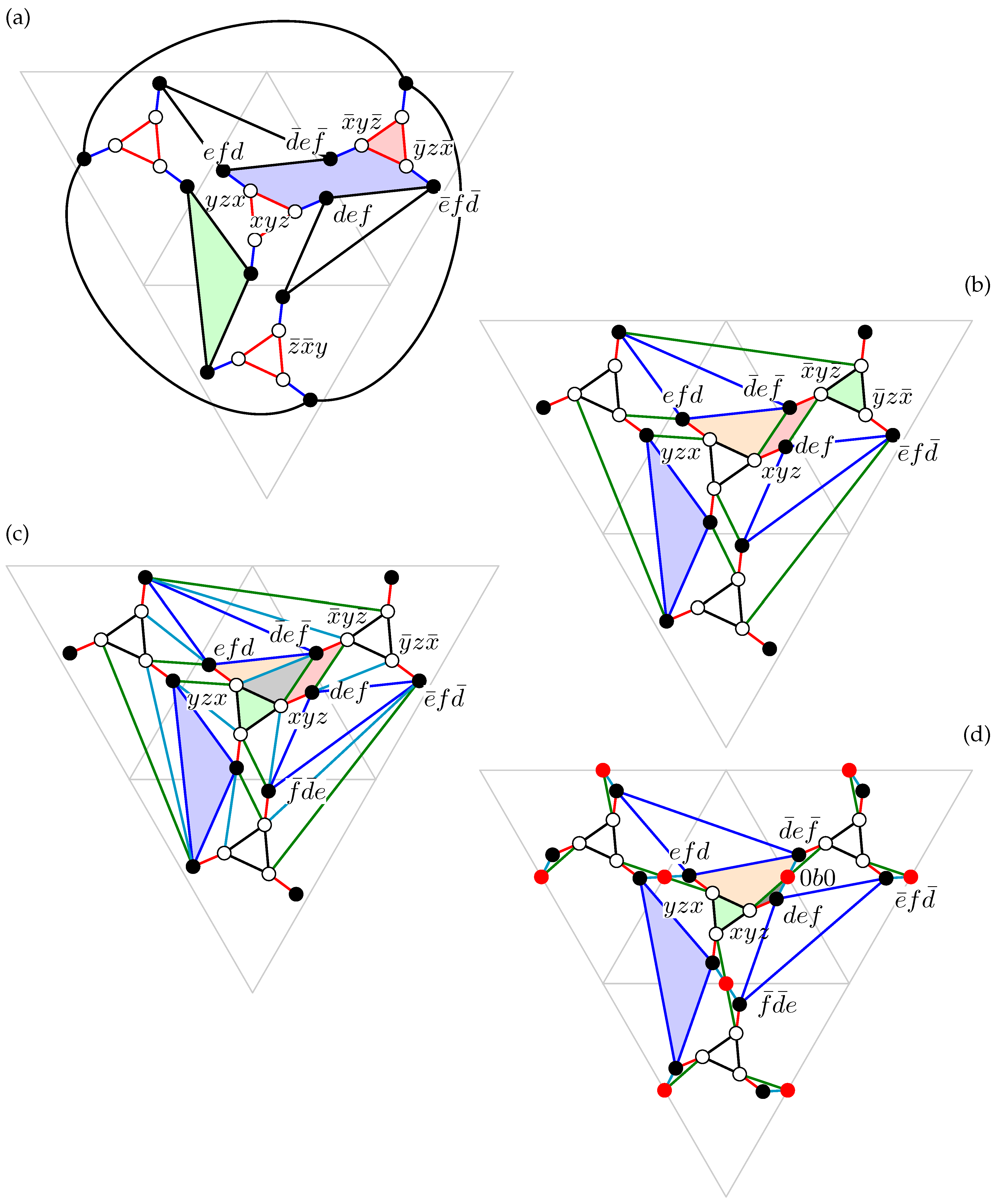
Figure 5a), meaning “twelve crowns” as the faces (
Figure 5b) somewhat resemble crowns. It is a face-transitive polyhedron (an isohedron) and as such it was already discovered as a member of an infinite family with
symmetry by B. Grünbaum and G. C. Shephard [
8]. (The other members of that family have faces with a similar shape but with one edge that differs in length from the others. The paper does not explicitly mention that there is an equilateral polyhedron among these examples.)
In addition, the algebraic conjugate of Equation (
10) provides a solution (
Figure 5c). The latter embedding has faces and edges that intersect each other (
Figure 5d). Note that inversion leaves this solution invariant. The symmetry group of the equilateral dodecastemma (and of its conjugate) is therefore equal to
, and not just
T, merging the two vertex orbits of size 4 and the two edge orbits of size 12. The factor
of Equation (
9) yields the same embedding.
Case 4.
, i.e.,
. (We only discuss the plus sign, as the minus sign yields an equivalent embedding, inverted with respect to the origin.) This case corresponds to the following solution
This embedding is convex but has coplanar faces and collinear edges. (
Figure 5e.) It can be constructed by decorating the faces of a tetrahedron with three trapezoids that serve as equilateral pentagons. The same equations lead to another (equivalent) solution that can be obtained from this one by applying Equation (
8). Because interchanging two coordinate positions leaves the set of vertices invariant, the symmetry group of this solution is
.
Case 5.
is a root of the equation
This equation has only one real positive solution, leading to 4 EP-embeddings that are equivalent. One of these is the following:
The others are obtained by inversion and/or applying Equation (
9). This solution has chiral tetrahedral symmetry
T. It has intersecting faces and edges (
Figure 5f).
Note that it is not necessary to resort to numerical methods to determine the number of real roots of a univariate polynomial, or the number of real roots that are positive. This can be done by computing the Sturm sequence of the polynomial symbolically and applying Sturm’s Theorem [
9].
Truncated cube (3.8.8). The 24 vertices of the truncated cube come in two orbits of size 12, generated by
and
(
Figure 6a). There are three edge orbits of size 12, with the following representatives:
There are two orbits of four triangles, and one orbit of six octagons, with representative vertices
Note that this octagon is invariant under a rotation of order 2 around the Y-axis. If this octagon is planar, its plane must be invariant under the same rotation. There are two possibilities, either this plane is the -plane or the plane contains the Y-axis.
In the first case, the Y-coordinate of each vertex of the octagon should be the same, i.e.,
In the second case, the vertices are coplanar if and only if their projections onto the
-plane are collinear, i.e., if
The edge equations for the truncated cube are the following
Note that the EP-equations are invariant for the transformation , for the transformation , and, as always, for inversion with respect to the origin.
For the case in Equation (
11), the equations can still be solved “by hand”. They reduce to
with the following solutions:
The classical embedding of the truncated cube, with coordinates
The algebraic conjugate of the above, with coordinates
An embedding with coordinates
which is equivalent to its algebraic conjugate. This solution is invariant to coordinate transpositions and has symmetry group
. It has intersecting faces.
The case that corresponds to Equation (
12) is slightly more difficult to solve. It results in eight equivalent solutions that (somewhat unexpectedly) involve the golden ratio
:
This solution is also equivalent to its algebraic conjugate. Its symmetry group is T and it has intersecting faces.
Truncated octahedron (4.6.6). The EP-embeddings of the truncated octahedron with 24 vertices turn out to be much easier to compute than those of the truncated cube. There are two orbits of 12 vertices, generated by
and
(
Figure 4f), and three orbits of 12 edges, with the following representatives:
There are one orbit of six quadrangles and two orbits of four hexagons. The edge equations are
The face equation for the quadrangle reduces to
, by Equation (
5). The hexagons are invariant for a three-fold rotation and their face equations reduce to
Combining all this information leads to
yielding the solution
,
, the classical embedding of the truncated octahedron, and two degenerate embeddings, reducing the polyhedron to a cuboctahedron or an octahedron.
Rhombicuboctahedron (3.4.4.4). The 24 vertices of the rhombicuboctahedron come in two orbits of 12 vertices, generated by
and
(
Figure 6b). There are four orbits of 12 edges, with the following representatives:
(Six “outer” edges have been omitted from the picture for reasons of clarity.) There are two orbits of 4 triangles, one orbit of 6 quadrangles and one orbit of 12 quadrangles. The edge equations read
The face equations of the quadrangles reduce to
by Equation (
5). Combining these equations yields
from which we obtain de solution
,
, the classical embedding, and also its algebraic conjugate
,
.
Snub cube (3.3.3.3.4). The last Archimedean solid with 24 vertices again has two orbits of 12 vertices, generated by
and
(
Figure 6c), and this time five orbits of 12 edges:
(Again, some edges have been omitted from the picture.) There are two orbits of 4 triangles, two orbits of 12 triangles and one orbit of 6 quadrangles. The edge equations read
and the face equations of the quadrangle reduce to
. The transformation
leaves these equations invariant. Groebner basis calculations with variable order
yield a polynomial of degree 18 in
e (of degree 9 in
) that factors as follows:
The first factor leads to a solution that degenerates to the vertices of the octahedron.
For the second factor, note that
only has a single real root
, leading to
. The full solution for the positive value of
e is
This is the classical embedding of a snub cube. The equalities between variables illustrate that the symmetry group of the snub cube is
O and not just
T. Now consider the third factor of Equation (
13). The polynomial
has two real roots of which only one is positive (
), and then
. For each value of
e there are two solutions yielding a total of four embeddings that turn out to be equivalent:
Icosidodecahedron (3.5.3.5). The 24 vertices come in two orbits of size 12, generated by
and
, and one orbit of size 6, generated by
(
Figure 6d). There are five orbits of 12 edges, with the following representatives:
There are two orbits of 4 triangles, and one orbit of 12 triangles. There is also one orbit of 12 pentagons. The face equations become
and the edge equations read
Note that the transformation leaves the EP-equations invariant. Consequently, applying this transformation to any solution yields another solution, that is however not necessarily new. If after transformation the solution remains the same, then the corresponding embedding has symmetry.
The face equations make this a complicated set of equations to solve. Using Groebner basis calculations with variable order yield a polynomial of degree 71 in b leading to the following cases:
Case 1. . Degenerates to a cuboctahedron with all vertices connected to the origin.
Case 2. . Degenerates to an octahedron.
Case 3.
. We find
. This embed- ding has coplanar faces and can be obtained by “decorating” a truncated tetrahedron appropriately (
Figure 7a). This solution is left invariant for coordinate transpositions and therefore has symmetry group
.
Case 4. . We find , . This is the classical embedding of the icosidodecahedron. This embedding has an algebraic conjugate that is not equivalent to it.
Case 5.
is a root of the polynomial
and then
,
and
. (These equalities imply that the result has the larger symmetry group
instead of just
T.) There are two real roots of this polynomial, i.e.,
and
, yielding the following solutions:
The second solution is particularly interesting because it yields a result that has no intersecting faces, although it is not convex (
Figure 7b).
Case 6. Finally, there is a polynomial of degree 48 in
b (degree 24 in
). This polynomial has seven positive real roots, six of which yield a solution in real numbers. Four of these solutions have intersecting faces, the other two have no intersecting faces but are not convex (
Figure 7c,d). All these solutions have
T as their symmetry group.
Truncated cuboctahedron (4.6.8). (For this case and the cases that follow, we have omitted the corresponding pictures as they become too crowded.) The 48 vertices of the truncated cuboctahedron come in 4 orbits of size 12 with generators
,
,
,
. The edges have the following representatives (6 orbits of size 12):
There is one orbit of 12 quadrangles, with corresponding face equations
There are two orbits of hexagons with rotational symmetry, yielding
Adding the last two equations and simplifying already yields
and therefore
Finally, there is one orbit of octagons, containing the points
which is invariant for a rotation of order 2 around the Y-axis. To set up the face equations for this octagon we use the same techniques as with the truncated cube (cf. Equations (
11) and (
12)). We obtain that either
or
Apart from inversion with respect to the origin, the following transformations also preserve the equations.
Equation (
15) yields sixteen solutions. Twelve of these have coincident points. The others are equivalent to either the classical embedding of the truncated cuboctahedron—where vertices have coordinates of the form
or permutations of these—or its algebraic conjugate.
Equation (
16) yields sixteen solutions that reduce to two inequivalent ones. Both have intersecting faces. The first solution is
The second is the algebraic conjugate that results from replacing by . (Replacing by results in an equivalent embedding.) Both embeddings have T as their symmetry group.
Rhombicosidodecahedron (3.4.5.4). The 60 vertices of the rhombicosidodecahedron come in five orbits of 12 vertices with representatives
,
,
,
and
. There are 10 orbits of 12 edges each, with the following representatives
There are two orbits of 12 quadrangles, and one orbit of 6 quadrangles:
There are also two orbits of 4 triangles, one orbit of 12 triangles and one orbit of 12 pentagons.
The face equations of the quadrangles yield the following linear equations, by Equation (
5):
and the face equation of the pentagon reads
Note that the EP-equations are invariant under the transformation
Already quite some simplification of the formulas can be done by hand. First by adding the equations of Equation (
18) three by three, we obtain
and hence, subtracting and using
, we find
, and then
Equation (
18) reduces the 10 edge equations to the following 6:
We introduce three new variables
,
,
. Then
From the second line of Equation (
21), we obtain
which simplifies to
Subtracting these equalities leads to
The second equation on the third line of Equation (
21) can be rewritten as
If
and hence
this equation transforms to
or
. In combination with Equation (
22), we obtain
. There are three cases to consider.
Case 1.
and then
from Equation (
24) and
from Equation (
22). There turn out to be several subcases:
1a. . We only need to consider the plus sign, as the minus sign yields an equivalent solution. There are 16 solutions, in eight conjugate pairs. Each solution is invariant for . Three pairs have and one pair has and therefore contain coincident vertices.
The remaining solutions are as follows:
The first of these solutions is the classical embedding. The second solution yields an embedding that does not have intersecting faces (but is also not convex). It is depicted in
Figure 8a. The pentagonal faces are the same as those of the equilateral dodecastemma of
Figure 5a.
1b.
. Again, we only need to consider the plus sign. There are eight solutions coming in two sets of four conjugates. Applying Equation (
19) to one solution yields another, so in all there is only a single set of four solutions up to equivalence. The solution below is depicted in
Figure 8b. (Note that the pentagonal faces are embedded as trapezoids.)
The others (i.e., the conjugate solutions) are obtained by changing the sign of everywhere, by substituting for , or by doing both transformations at the same time.
1c. . All solutions turn out to have and have coincident points.
1d. . This equation has only two real roots: . Again, we need only consider the positive sign. There turn out to be four inequivalent solutions. All of them have intersecting faces.
Case 2.
and then
from Equation (
24) and
, from Equation (
23).
2a. . In this case, there are coincident vertices.
2b. . It turns out that in this case and again there are coincident vertices.
2c.
. There are four solutions, i.e., the following solution
and its conjugates. All of these have intersecting faces.
2d. . In this case, we have and then there are coincident points.
2e. Finally, there is a factor of degree 24 in F (12 in ) that yields four more solutions. All of these have intersecting faces.
Case 3.
and then
from Equation (
23) and
from Equation (
24). This case results from the previous case by applying the transformation in Equation (
19) and yields isometric solutions (after inversion).
7. The Remaining Cases
There remain four Archimedean solids to consider: the truncated icosahedron, the truncated dodecahedron, the snub icosahedron (each with 60 vertices) and, finally, the truncated icosidodecahedron (with 120 vertices). Unfortunately, in each of these cases, the EP-equations are too hard to solve for the current computer algebra systems and most likely result in polynomials of high degree.
However, if we strengthen the symmetry requirements and restrict ourselves to solutions that have (at least) symmetry (or I symmetry in the case of the snub icosahedron), then the problem becomes manageable again. The corresponding results and computations are provided below.
Truncated icosahedron (5.6.6) The 60 vertices of this polyhedron are split into one orbit of 12 vertices, with coordinates of the form
and two orbits of 24 vertices with representative
and
. The edges have the following representatives:
Note that the edge equation for the first edge is
, and hence, with
this reduces to
. Without loss of generality, we may choose
. The solutions with
can then be obtained by applying inversion to the solutions with
. Similarly, the last edge equation reduces to
. The edge equations for the remaining three edges become
There is one orbit of 12 pentagons, with representative
The face equations for this pentagon are
(Here, we have used the fact that .)
There is one orbit of eight hexagons, with representative
and corresponding face equations
There is also one orbit of 12 hexagons, with representative
and face equations
We first consider the case where
. Note that Equation (30) can be rewritten as
. From Equation (28), we then obtain
Because
, this can be rewritten as
Now, assume that the first factor of this expression is 0, i.e., . Then, by Equation (28), it follows that , and hence for any solution in real numbers. This is a solution with coincident points.
On the other hand, the second factor is 0 if and only if either or . The first case again leads to coincident vertices. We can therefore assume that . From Equation (30) we then derive that either (with coincident points) or .
Applying Groebner basis calculations with variable order to these results yields a polynomial of degree 8 in z with factors of degree 2, 2 and 4, leading to the following cases.
Case 1.
, i.e.,
or
. We find four solutions. Two solutions have
and therefore have coincident points. The other solutions correspond to the classical embedding of the truncated icosahedron
and its algebraic conjugate.
Case 2.
, i.e.,
. Note that in this case either
or
and then by Equation (
26) or (28) there are no solutions in real numbers.
Case 3. , or . In addition, in this case, either or , and there are no solutions in real numbers.
The case where is not easily simplified by hand, and finding the solution is not easy. Applying Groebner basis calculations with variable order yields a polynomial of degree 49 in e. The first factor is e (and leads to embeddings with coincident points) and there are two additional factors of degree 24. One of these has no real roots, the other has six, corresponding to six EP-embeddings. All of these have intersecting faces.
Truncated dodecahedron (3.10.10) The 60 vertices of this polyhedron come in three orbits, and we may choose the same representatives
,
and
as in the case of the truncated icosahedron. There are five orbits of edges:
As with the truncated icosahedron, we may derive from this that
and
. There are one orbit of 8 triangles, one orbit of 12 triangles and one orbit of 12 decagons. The following matrix displays the coordinates of the vertices of one representative of the latter:
The rank of this matrix must be 3, which is equivalent to
To solve these EP-equations, we applied Groebner basis calculations with variable order . For , this yields a polynomial in z with two linear factors, two quadratic factors and one factor of degree 16, leading to the following cases.
Case 1. . We find that which has no solutions in real numbers.
Case 2. . We find that which again has no solutions in real numbers.
Case 3.
, i.e.,
or
. We find the classical embedding of the truncated dodecahedron:
and its algebraic conjugate.
Case 4.
, i.e.,
or
, with solution
and its algebraic conjugate. (Both have intersecting faces.)
Case 5. z satisfies some polynomial of degree 16. This case yields eight different solutions, all with intersecting faces.
The remaining case is again more difficult to solve. We find that either or z must satisfy a polynomial of degree 22. We find six solutions in all that have no coincident vertices. Because f and p have a different sign, in each of these embeddings, the dodecagonal faces have intersecting edges.
Truncated icosidodecahedron (4.6.10) There are 120 vertices in five orbits of 24. We choose
,
,
,
and
as representatives for these orbits. There is one orbit of 12 decagons. The following matrix displays the coordinates of the vertices of one representative:
This matrix must have rank 3, and because of the special form of the coordinates, this reduces to the following face equations:
There is one orbit of 8 hexagons and there is one orbit of 12 hexagons:
The first hexagon is invariant under the three-fold rotation and hence its face equations reduce to
The special form of the coordinates of its vertices allow the face equations of the second hexagon to be reduced to
Finally, there is one orbit of 6 quadrangles and one of 24 quadrangles
For the first quadrangle the face equations are trivially satisfied. The second quadrangle yields
Note that the following are edges of the polyhedron:
It follows that , or equivalently , , . Without loss of generality we may fix the sign of one of these solutions, say . The remaining choices then essentially split the solutions of the EP-equations into four different cases.
It turns out that only the case
could be solved by a computer algebra system (with reasonable time and memory restrictions). One reason that this case is simpler to solve is that, in this case, the EP-equations are invariant for the transformation
(involving all 15 variables). This transformation yields an embedding that is not equivalent to the original embedding.
Groebner basis calculations show that E satisfies a polynomial with ten factors. As before, we treat each factor separately.
Case 1. . This case leads to coincident points.
Case 2. . Yields a polynomial in F of degree 24 that has no real roots.
Case 3.
. This yields the classical embedding of the truncated icosidodecahedron:
and its conjugate.
Case 4. . This case can be obtained by applying the transformation in Equation (31) to Case 2. There are therefore also no real solutions in this case.
Case 5. , i.e., or . Now, we find and hence the embedding has coincident vertices.
Case 6. , i.e., . There now are eight solutions coming in two sets of four that are conjugate. One of these has and therefore results in coincident vertices. The other set of solution has and hence again has coincident vertices.
Case 7. , i.e., or . This case results from applying the transformation in Equation (31) to Case 5. This solution has coincident vertices.
Case 8. , i.e., . We now have and again the embedding has coincident vertices.
Cases 9 and 10. or . Neither polynomial has real roots.
Snub dodecahedron (3.3.3.3.5) Because the graph of the snub dodecahedron has an automorphism group (i.e.,
I) that does not contain
as a subgroup, we cannot find solutions with this symmetry. Enforcing the even larger symmetry group
I on our solution yields only the classical embedding and its three (real) conjugates. Indeed, because of the enforced symmetry, the pentagonal faces embed as regular pentagons and hence the embedding is a uniform polyhedron, all of which have been classified before [
4].