Time-Dependent Behavior of a Circular Symmetrical Tunnel Supported with Rockbolts
Abstract
:1. Introduction
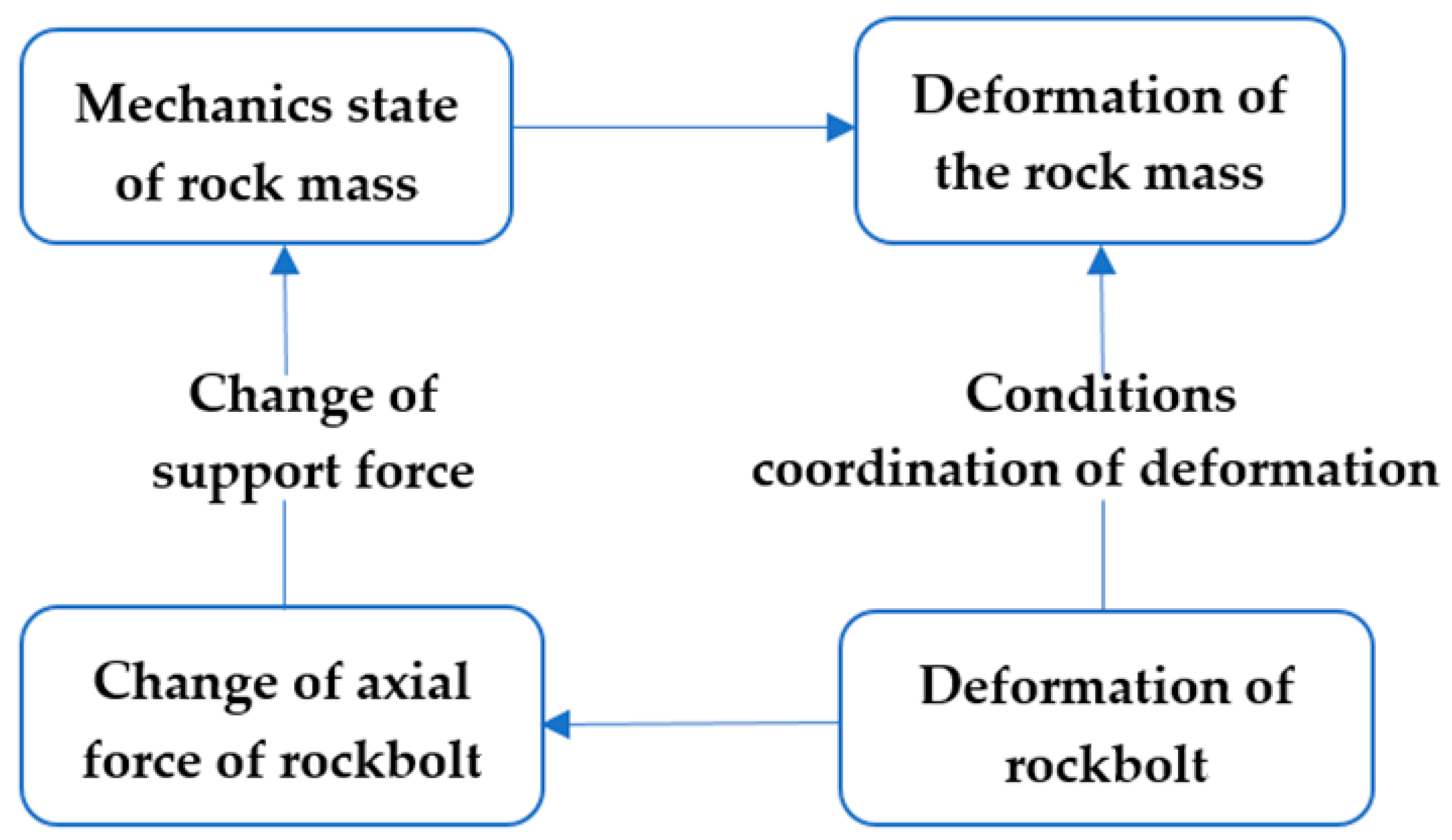
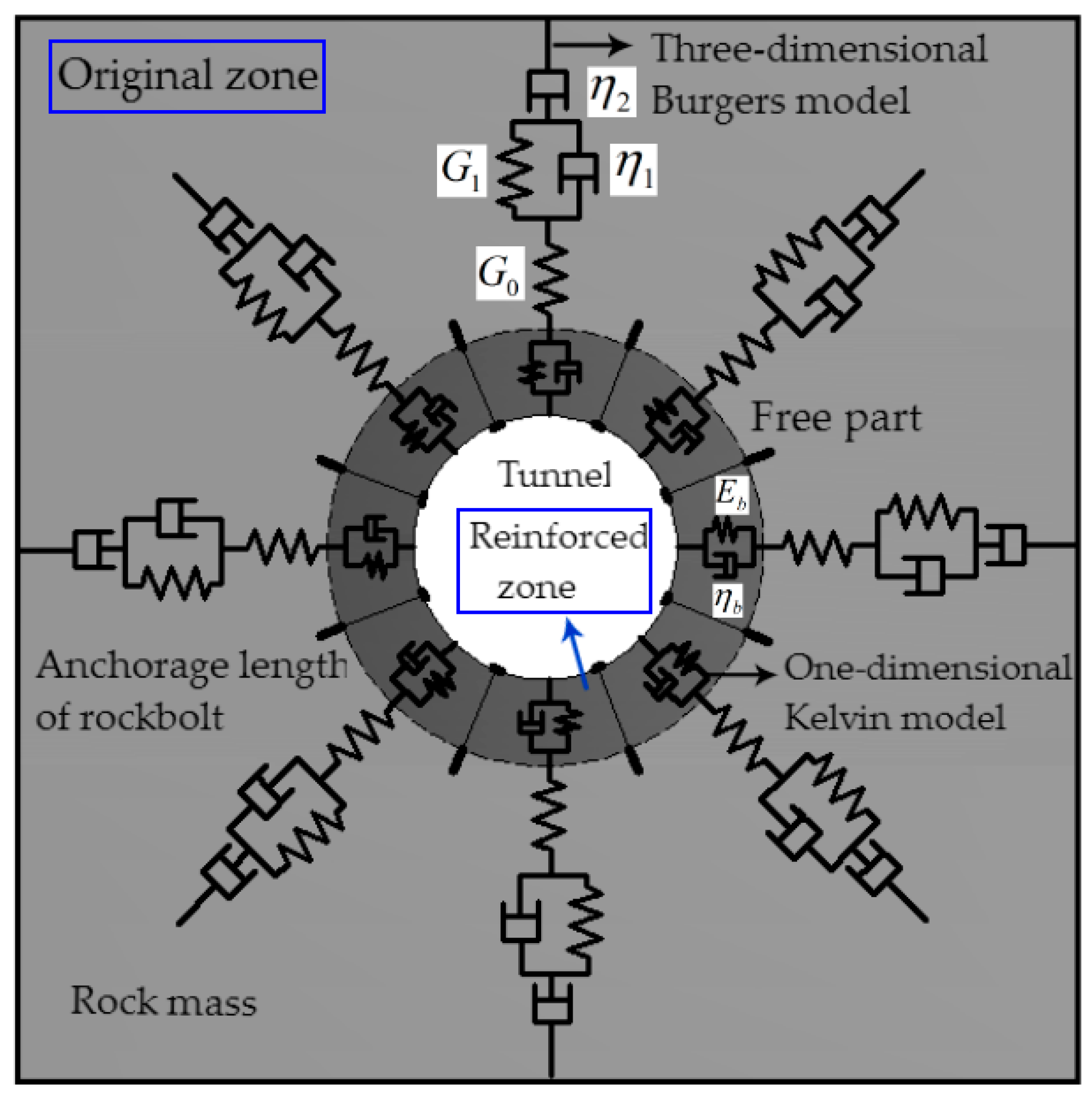
2. Coupling Mechanical Model of the Rockbolt and Rock Mass System
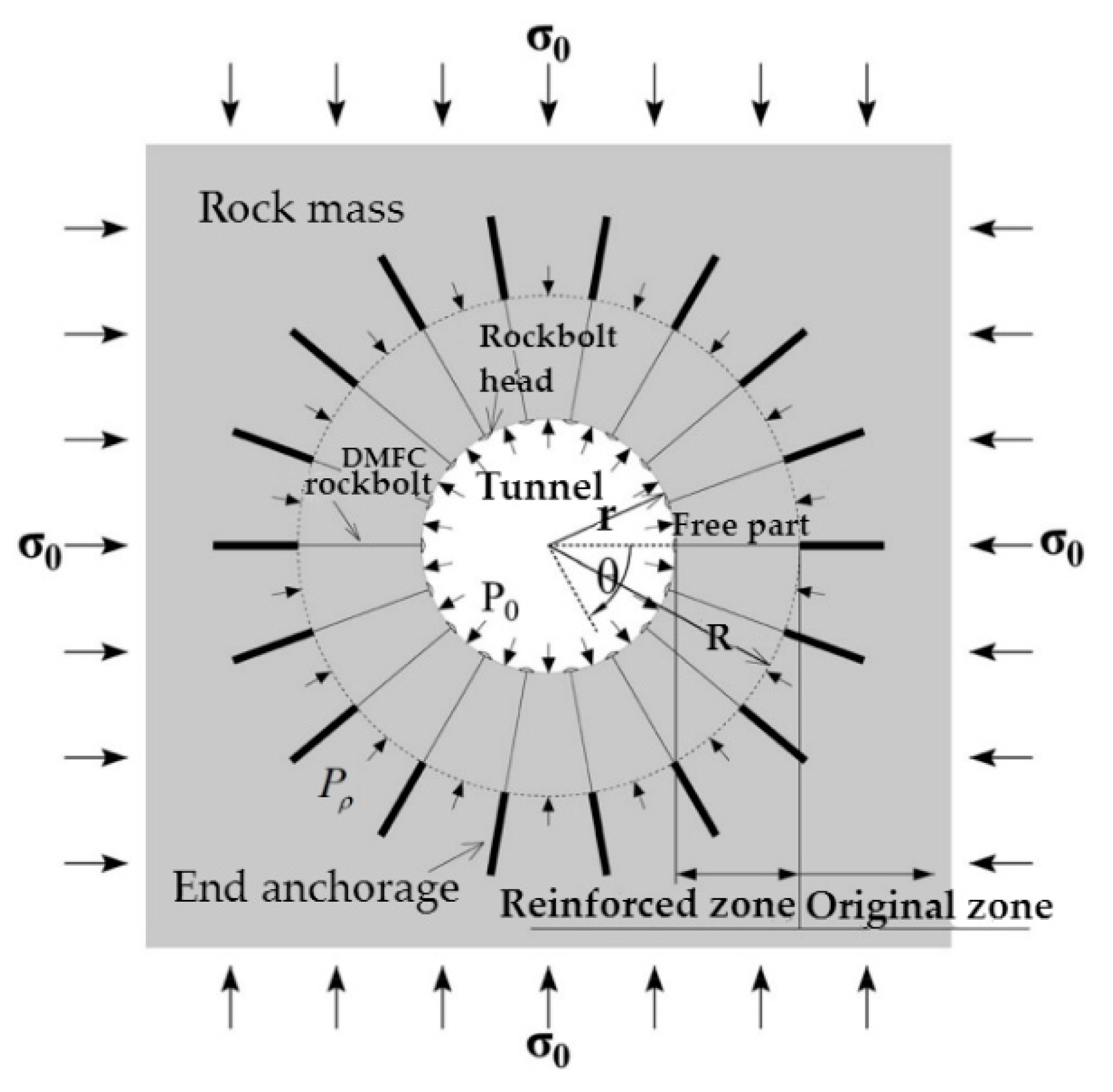
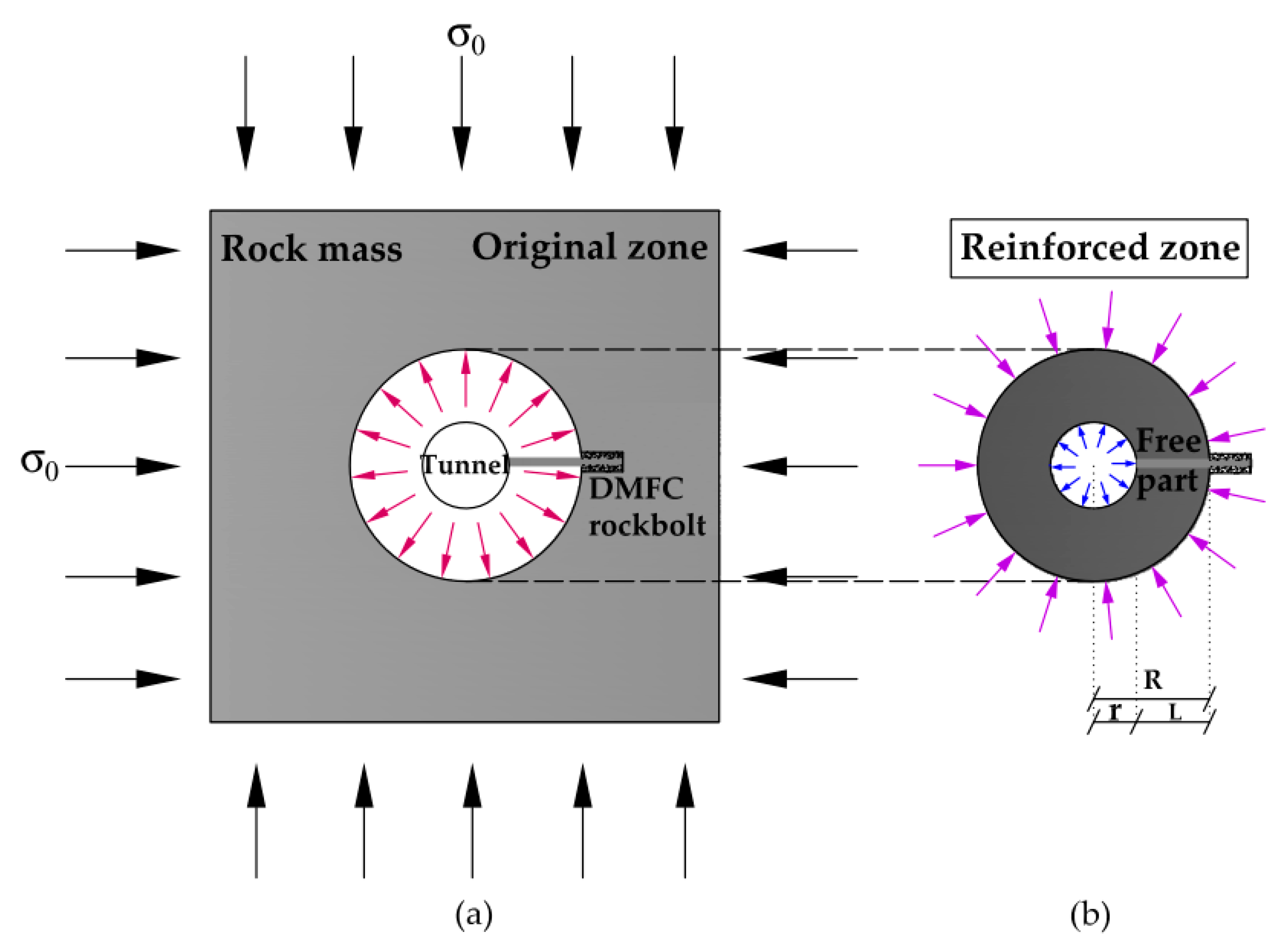
2.1. Principle of the Coupling Model
2.2. Elastic Solutions
2.3. Viscoelastic Solutions
2.3.1. Rheological Model of Rockbolt and Definition of Operator Function
2.3.2. Rheological Model of Rock Mass and Definition of Operator Function
2.4. Analytical Solutions in the Laplace Space
3. Analysis of the Analytical Solution Using Engineering Parameters
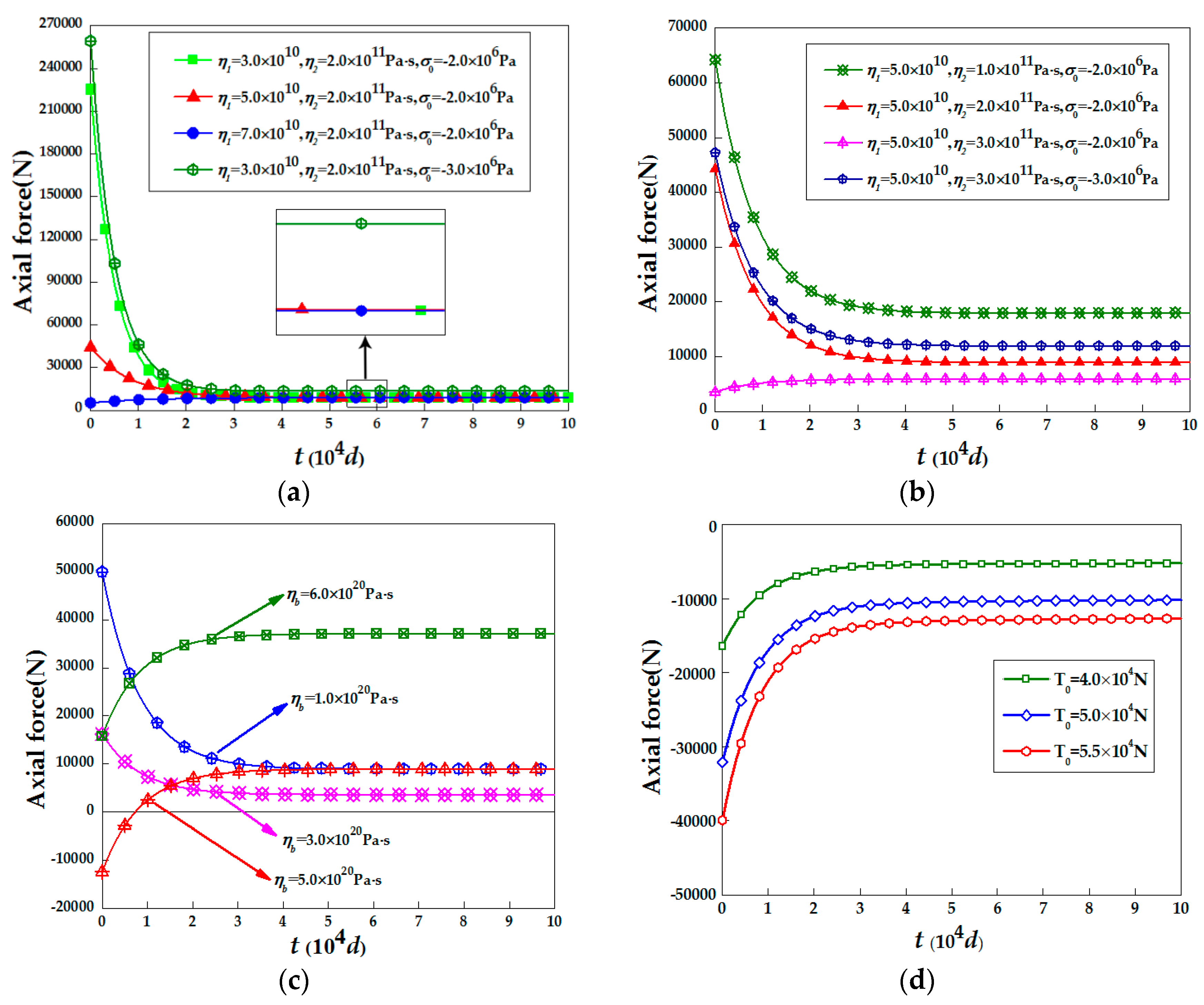
3.1. Axial Force Changes over Time
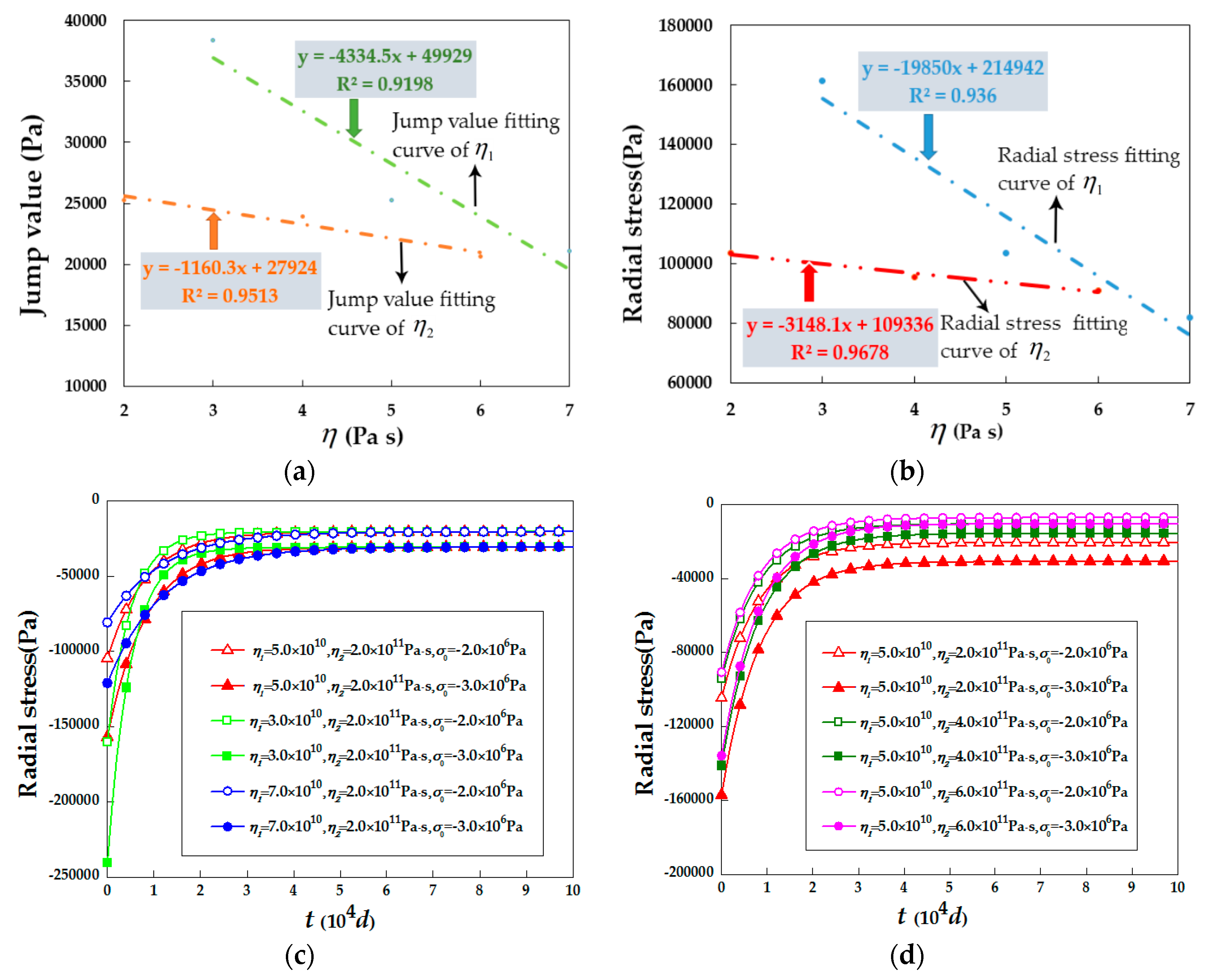
3.2. Radial Stress Changes over Time
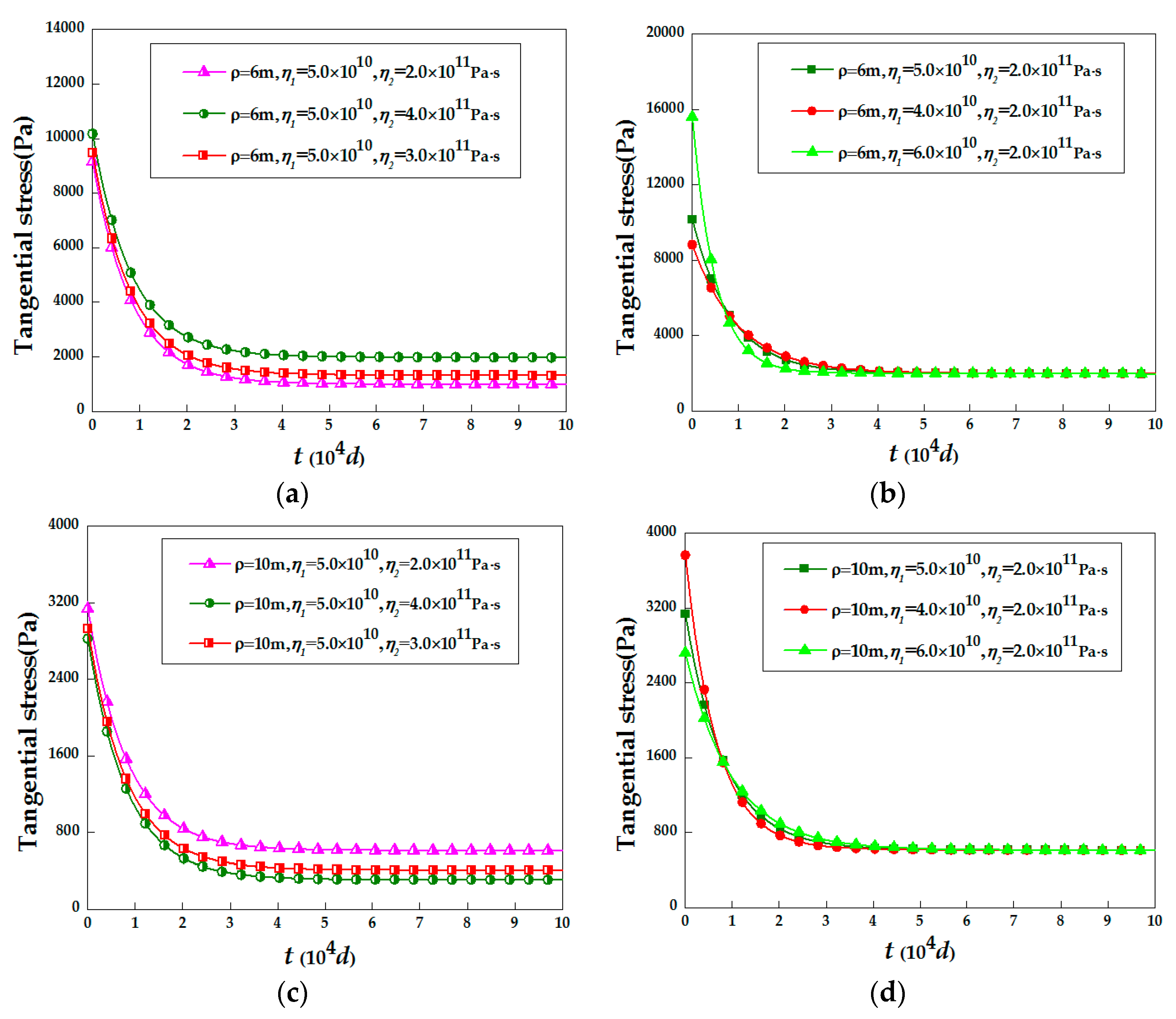
3.3. Tangential Stress Changes over Time
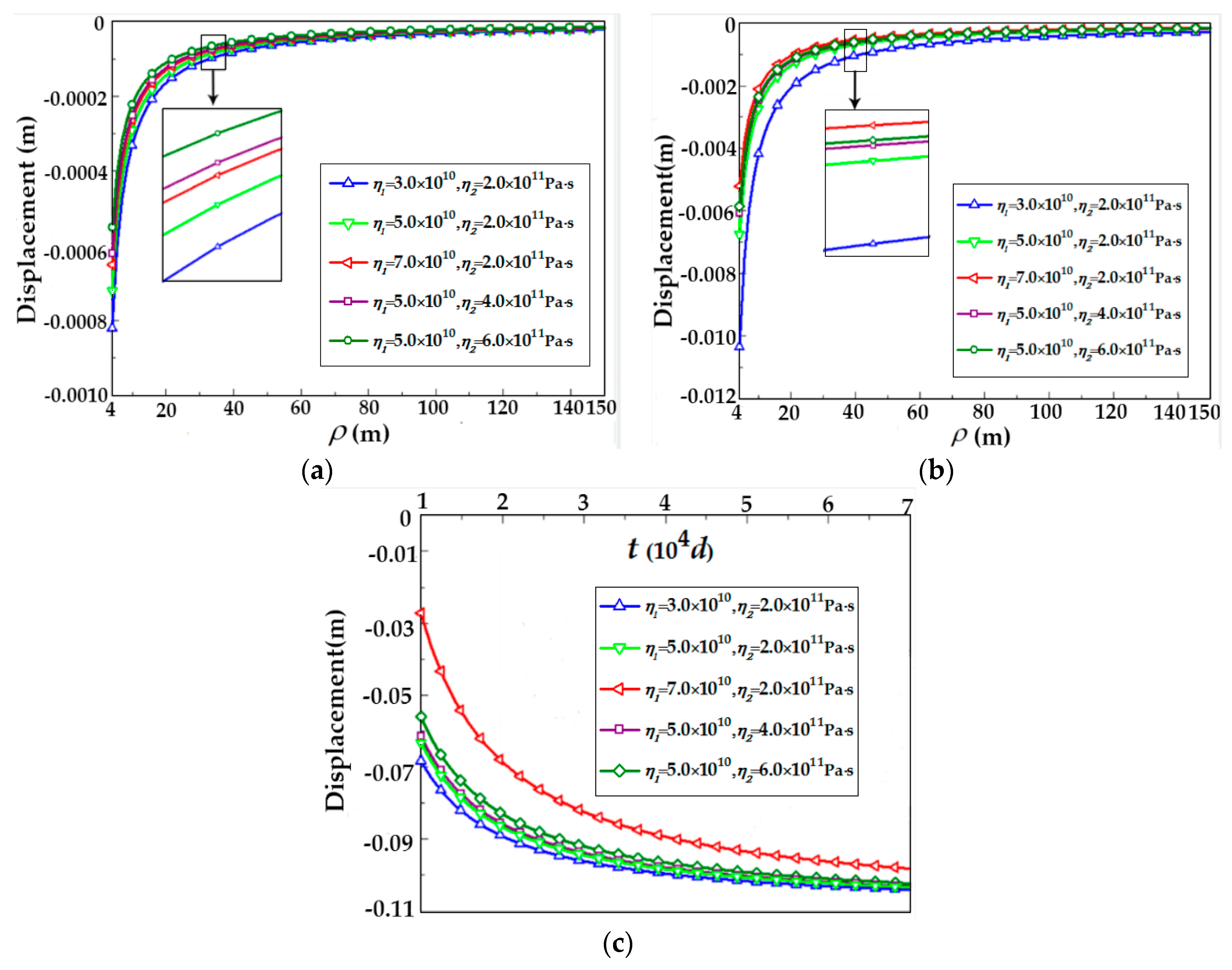
3.4. Displacement Evolution over Time
4. Conclusions
- (1)
- The axial force of DMFC rockbolts are positively correlated with the support force at the excavation face in a tunnel, and the greater the convergence value of the axial force is, the better the support effect. In addition, the greater the pre-tension of rockbolt, the better the reinforcement effect, however, when the pre-tension is too large, the rock bolt support effect will not increase significantly.
- (2)
- The η1 of the three-dimensional Burgers model influences the early support effect, η2 of three-dimensional Burgers model affects both the early and the ultimate reinforcement effect. In addition, there is a significant negative correlation between rock mass displacement and η1 or η2. Therefore, important support measures should be taken when η1 or η2 is small.
- (3)
- In this paper, the interaction model elastic solutions were solved based on the distributed force model. However, the axial force of the rockbolt is similar to the concentrated force to rock mass (Bobet 2006), Hence, a more suitable theoretical model should be explored to solve the coupling model in future.
- (4)
- Continuously Mechanically Coupled (CMC) rockbolts applications are more extensive than DMFC rockbolts, the reasonable and simplified method for the theoretical model of CMC rockbolts can be further studied based on this model, which lays a foundation of the preliminary research for solving the theoretical model of CMC rockbolts.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Ab | Area of the rockbolt cross-section |
| L | Length of rockbolt free part |
| ρ | Radial coordinate |
| r | Radius of tunnel |
| T | Axial force of the rockbolt bolt |
| P0 | Support force in tunnel opening |
| k | Stiff of the support system |
| σρ1 | Radial stress in the reinforced zone |
| σθ1 | Tangential stress in the reinforced zone |
| uρ1 | Displacement in the reinforced zone |
| σρ1s | Radial stress of the reinforced zone in Laplace |
| σθ1s | Tangential stress of the reinforced zone in Laplace |
| uρ1s | Displacement of the reinforced zone in Laplace |
| Sθ | Rockbolt spacing in the tangential direction |
| ηb | Viscosity coefficient of the rock bolt |
| η2 | Viscosity coefficient of the second creep stage |
| Δx | Pre-tension length of the rockbolt |
| G1 | Viscoelastic shear modulus of rock mass |
| t | Time |
| Sij | Partial stress tensor |
| Operator functions of the Kelvin model | |
| Operator function of rock mass viscoelastic constitutive model | |
| Er | Deformation modulus of the rock mass |
| Eb | Deformation modulus of the rockbolt |
| θ | Circumferential angle |
| σ0 | Initial stress |
| μ | Poisson’s ratio of rock mass |
| Pρ | Reinforcement force |
| R | Radius of the reinforced rock zone |
| σρ2 | Radial stress in the original zone |
| σθ2 | Tangential stress in the original zone |
| uρ2 | Displacement in the original zone |
| σρ2s | Radial stress of the original zone in Laplace |
| σθ2s | Tangential stress of the original zone in Laplace |
| uρ2s | Displacement of the original zone in Laplace |
| Sz | Rockbolt spacing in the longitudinal direction |
| η1 | Viscosity coefficient of the first creep stage |
| ΔL | Deformation of rockbolt in the axial direction |
| G0 | Elastic shear modulus of the rock mass |
| K | Elastic bulk modulus of the rock mass |
| σij | Stress tensor |
| eij | Partial strain tensor |
| Operator functions of the Kelvin model in Laplace space | |
| Operator function of rock mass viscoelastic constitutive model after Laplace transformation |
Appendix A
References
- Kovári, K. History of the sprayed concrete lining method—Part I. Milestones up to the 1960s. Tunn. Undergr. Space Technol. 1992, 18, 57–69. [Google Scholar] [CrossRef]
- Cai, Y.; Tetsuro, E.; Jiang, Y.J. A rock bolt and rock mass interaction model. Int. J. Rock Mech. Min. Sci. 2004, 41, 1055–1067. [Google Scholar] [CrossRef]
- Sun, J. Rock rheological mechanics and its advance in engineering applications. Chin. J. Rock Mech. Eng. 2007, 26, 1081–1106. [Google Scholar]
- Phienwej, N.; Thakur, P.K.; Cording, E.J. Time-dependent response of tunnels considering creep effect. Int. J. Geomech. 2007, 7, 296–306. [Google Scholar] [CrossRef]
- Goodman, R. Introduction to Rock Mechanics; Wiley: New York, NY, USA, 1989. [Google Scholar]
- Nomikos, P.; Rahmannejad, R.; Sofianos, A. Supported axisymmetric tunnels within linear viscoelastic Burgers rocks. Rock Mech. Rock Eng. 2011, 44, 553–564. [Google Scholar] [CrossRef]
- Ladanyi, B.; Gill, D.E. Tunnel lining design in creeping rocks. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1985, 22, A17. [Google Scholar] [CrossRef]
- Sulem, J.; Panet, M.; Guenot, A. An analytical solution for time-dependent displacements in circular tunnel. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1987, 24, 155–164. [Google Scholar] [CrossRef]
- Ladanyi, B. Time-dependent response of rock around tunnels. In Comprehensive Rock Engineering; Hudson, J., Ed.; Pergamon: London, UK, 1993; Volume 2, pp. 77–112. [Google Scholar]
- Panet, M. Understanding deformations in tunnels. In Comprehensive Rock Engineering; Hudson, J., Ed.; Pergamon: London, UK, 1993; Volume 1, pp. 663–690. [Google Scholar]
- Ghaboussi, J.; Gioda, G. On the time-dependent effects in advancing tunnels. Int. J. Numer. Methods Geomech. 1977, 1, 249–269. [Google Scholar] [CrossRef]
- Gioda, G. A finite element solution of non-linear creep problems in rock. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1981, 18, 35–46. [Google Scholar] [CrossRef]
- Peila, D.; Oreste, P.; Rabajuli, G.; Trabucco, E. The pre-tunnel method, a new Italian technology for full-face tunnel excavation: A numerical approach to design. Tunn. Undergr. Space Technol. 1995, 10, 367–374. [Google Scholar] [CrossRef]
- Li, J.J.; Zheng, B.L.; Xu, C.Y. Numerical analyses of creep behavior for prestressed anchor rods. Chin. Q. Mech. 2007, 28, 124–128. [Google Scholar]
- Wang, G.; Liu, C.Z.; Jiang, Y.J.; Wu, X.Z.; Wang, S.G. Rheological Model of DMFC Rockbolt and Rockmass in a Circular Tunnel. Rock Mech. Rock Eng. 2015, 48, 2319–2357. [Google Scholar] [CrossRef]
- Sharifzadeh, M.; Tarifard, A.; Moridi, M.A. Time-dependent behavior of tunnel lining in weak rock mass based on displacement back analysis method. Tunn. Undergr. Space Technol. 2013, 38, 348–356. [Google Scholar] [CrossRef]
- Labiouse, V. Ground response curves for rock excavations supported by ungrouted tensioned rockbolts. Rock Mech. Rock Eng. 1996, 29, 19–38. [Google Scholar] [CrossRef]
- Bobet, A. A simple method for analysis of point anchored rockbolts in circular tunnels in elastic ground. Rock Mech. Rock Eng. 2006, 39, 315–338. [Google Scholar] [CrossRef]
- Carranza-Torres, C.; Fairhurst, C. Application of the convergence–confinement method of tunnel design to rock masses that satisfy the Hoek-Brown failure criterion. Tunn. Undergr. Space Technol. 2000, 15, 187–213. [Google Scholar] [CrossRef]
- Bobet, A.; Einstein, H.H. Tunnel reinforcement with rockbolts. Tunn. Undergr. Space Technol. 2011, 26, 100–123. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Li, Y.P. Rock Rheology Theory and Numerical Simulation; Science Press: Beijing, China, 2008. [Google Scholar]
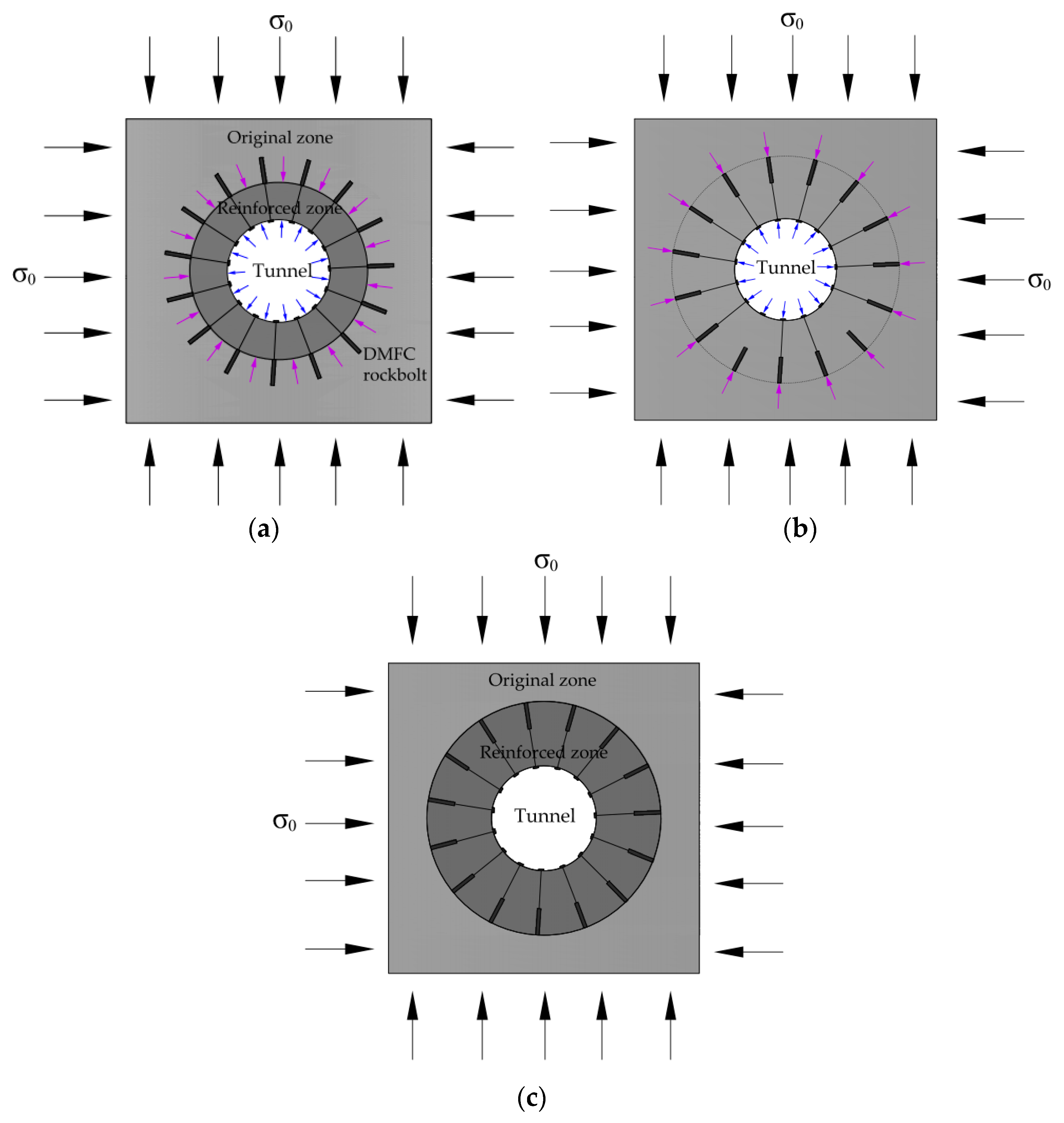
| Parameters | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | Case 6 | Case 7 | Case 8 |
|---|---|---|---|---|---|---|---|---|
| R/m | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 |
| r/m | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| Ab/10−4 m2 | 3.0 | 3.0 | 3.0 | 3.0 | 3.0 | 3.0 | 3.0 | 3.0 |
| Eb/1011 Pa | 2.0 | 2.0 | 2.0 | 2.0 | 2.0 | 2.0 | 2.0 | 2.0 |
| L/m | 4.0 | 4.0 | 4.0 | 4.0 | 4.0 | 4.0 | 4.0 | 4.0 |
| K/109 Pa | 2.2 | 2.2 | 2.2 | 2.2 | 2.2 | 2.2 | 2.2 | 2.2 |
| G0/109 Pa | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 |
| G1/1010 Pa | 6.0 | 6.0 | 6.0 | 6.0 | 6.0 | 6.0 | 6.0 | 6.0 |
| ηb/1020 Pa·s | 3.0 | 3.0 | 3.0 | 3.0 | 3.0 | 3.0 | 3.0 | 3.0 |
| η1/1010 Pa·s | 5.0 | 3.0 | 7.0 | 5.0 | 5.0 | 5.0 | 5.0 | 5.0 |
| η2/1011 Pa·s | 2.0 | 2.0 | 2.0 | 4.0 | 6.0 | 2.0 | 2.0 | 2.0 |
| T0/104 N | 4.0 | 4.0 | 4.0 | 4.0 | 4.0 | 5.0 | 5.5 | 4.0 |
| σ0/106 Pa | −2.0 | −2.0 | −2.0 | −2.0 | −2.0 | −2.0 | −2.0 | −3.0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, W.; Wang, G.; Liu, C.; Luan, H.; Wang, K. Time-Dependent Behavior of a Circular Symmetrical Tunnel Supported with Rockbolts. Symmetry 2018, 10, 381. https://doi.org/10.3390/sym10090381
Han W, Wang G, Liu C, Luan H, Wang K. Time-Dependent Behavior of a Circular Symmetrical Tunnel Supported with Rockbolts. Symmetry. 2018; 10(9):381. https://doi.org/10.3390/sym10090381
Chicago/Turabian StyleHan, Wei, Gang Wang, Chuanzheng Liu, Hengjie Luan, and Ke Wang. 2018. "Time-Dependent Behavior of a Circular Symmetrical Tunnel Supported with Rockbolts" Symmetry 10, no. 9: 381. https://doi.org/10.3390/sym10090381
APA StyleHan, W., Wang, G., Liu, C., Luan, H., & Wang, K. (2018). Time-Dependent Behavior of a Circular Symmetrical Tunnel Supported with Rockbolts. Symmetry, 10(9), 381. https://doi.org/10.3390/sym10090381






