Abstract
BM123-64 block cipher, which was proposed by Minh, N.H. and Bac, D.T. in 2014, was designed for high speed communication applications factors. It was constructed in hybrid controlled substitution–permutation network (CSPN) models with two types of basic controlled elements (CE) in distinctive designs. This cipher is based on switchable data-dependent operations (SDDO) and covers dependent-operations suitable for efficient primitive approaches for cipher constructions that can generate key schedule in a simple way. The BM123-64 cipher has advantages including high applicability, flexibility, and portability with different algorithm selection for various application targets with internet of things (IoT) as well as secure protection against common types of attacks, for instance, differential attacks and linear attacks. However, in this paper, we propose methods to possibly exploit the BM123-64 structure using related-key attacks. We have constructed a high probability related-key differential characteristics (DCs) on a full eight rounds of BM123-64 cipher. The related-key amplified boomerang attack is then proposed on all three different cases of operation-specific designs with effective results in complexity of data and time consumptions. This study can be considered as the first cryptographic results on BM123-64 cipher.
1. Introduction
The BM123-64 [1] has a 64-bit block size covering 256-bit secret key size and a total of eight function rounds. This cipher is based on switchable data-dependent operations (SDDO) [2], which is designed to combine data-dependent operations in functions and new feature of hybrid-controlled substitution–permutation network (CSPN) models. By this way, BM123-64 is considered as a solution for a more flexible and suitable approach for appropriate application targets with each specific design. The cipher has advantages including better suitability, applicability with different algorithm designs for specific targets, and high reliability of securing against well-known attacks, for instance, linear attacks and differential attacks.
Although lots of researchers have focused on how to enhance the security of construction designs using different operations and functions, for instance, DDP (Data-Dependent Permutation) -based ciphers (such as DDP-64 [3], Cobra-family [3] and SCO (Switchable Controlled Operation) -family [2]), DDO (Data-Dependent Operation) -based ciphers (such as MD-64 [4], KT-64 [5], CTPO (Controlled Two-Place Operation) [6] and DDO-64 [7]), and SDDO-based ciphers (such as XO-64 [8] or BMD-128 [9]), their weaknesses have been recently explored with common related attacks. A simple key schedule generator for high speed transformation and lightweight targets can lead to an attack possibility for cryptanalysis using common related-key attack methods.
Related-key amplified boomerang attack [10] is an extension of the related-key boomerang attack proposed by Biham et al., 2005 [11] and Wagner, 1999 [12]. The idea of this attack is that it explores two distinctive related-key differentials to construct the related-key boomerang with high probability. Compared to other attacks, the attack was designed as an adaptive chosen plaintext attack that has become a popular and effective method to exploit many types of block ciphers. Previous studies that have applied this attack on various SDDO-based ciphers - such as COCONUT98, IDEA [11], MARS, Serpent [12], DDO-64 [13], MD-64 [14], BMD-128 [15], XO-64 [16], etc.—showed efficiency and high probabilities in cryptanalytic results.
In this paper, we propose attack methods on BM123-64 constructions with related-key approach. By constructing high probability differentials with two related-key boomerangs in distinctive designs, this attack expects to exploit a full eight rounds of BM123-64 with effective cryptanalytic results. The proposed attack requires about 267 data complexity, 270 memory bytes, and time complexity of 267 encryptions with Case 1 design. For Case 2 and Case 3 designs of BM-123-64 constructions, 251 data complexity, 254 memory bytes, and time complexity of 265 are required. This study shows that like lots of other ciphers designed on data-dependent operations, BM123-64 still has weaknesses and is insecure against related-key cryptanalysis. The cipher construction should therefore be based on more secure primitive security approach.
The rest of this paper is organized as follows: The BM123-64 construction is briefly reviewed in Section 2. In Section 3, the proposed attacks on BM123-64 cipher is discussed, including differential characteristics (DCs), analysis methods, and security assessments. Finally, in Section 4, conclusions of the paper are presented.
2. BM123-64 Block Cipher Description
2.1. Preliminaries
This section explains notations used in this paper. With x1 as the most significant bit and xn as the least significant bit, a cipher X can be assigned as X = (x1, x2, …, xn).
The DCs applied to the attack methods include descriptions of differential relation of block ciphers, such as input, output, and function round key.
- -
- r denotes each function round of block cipher.
- -
- ∆Xr denotes input difference value that occurs in each r.
- -
- ∆Yr denotes output difference value that occurs in each r.
- -
- ∆Ur, ∆Qr denote round key difference values that occur in each r.
- -
- ei denotes the data bit changing within each round function, with i value considered as an active bit; at the ith position, the bit value is “1”, and the remaining bits are “0” in each block data. for instance, e1,3 = (1, 0, 1, 0, …, 0)).
2.2. BM123-64 Construction
BM123-64 [1] is described as a 64-bit SDDO-based block cipher with 256-bit secret key and eight function rounds in total. Each Crypt(e) round function in the cipher structure does the same operation from the first round to the final round to generate output ciphertext.
The Crypt(e) of BM123-64 covers three types of fixed permutation functions (I, I1, and I2), an extension box E, hybrid-controlled substitution–permutation networks CSPNs, and SDDO-based functions (F16/64, F −116/64, F16/32, F −116/32) based on basic controlling element F2/2.
The process of BM123-64 encryption is described in the algorithm below.
- 64-bit input plaintext splits into two 32-bit block A and block B.
- From rounds r = 1 to 7, they have the same operations for each round:(A, B) = Crypt(0) (A, B, Ur, Qr)(A, B) = (B, A)
- In the last round, there is final transformation to output ciphertext:(A, B) = Crypt(0) (A, B, U8, Q8)(A, B) = (L ⊕ UFT, R ⊕ QFT)(A, B) = (A, B).
Figure 1 and Figure 2 illustrate the Crypt(0) round function in detail. Reference [1] contains more description of the BM123-64 construction.
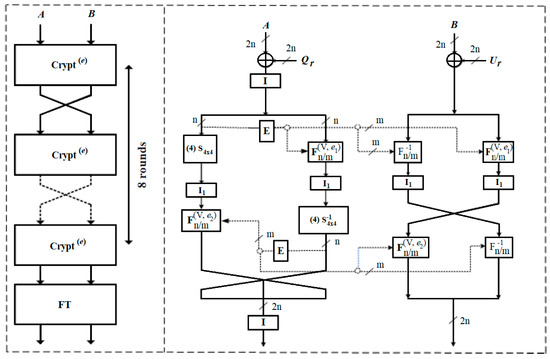
Figure 1.
(a) The general structure (left); and (b) round function Crypt(0) (right) of BM123-64.
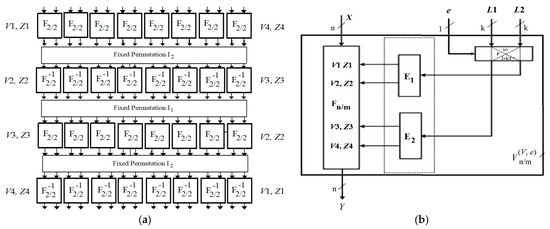
Figure 2.
(a) Switchable data-dependent operations (SDDO)-based functions F16/64, F−116/64; and (b) F16/32, F−116/32.
The SDDO-based functions F16/64, F −116/64 are constructed based on elementary function F2/2, since F2/2 is described as ((x1, x2), [v, z]/(y1, y2)). For better performance on implementation with the target of a specific application and expansion of encryption space, the function is designed in three different operations with three different description of the basic element F2/2.
- Case 1:
- y1 = vzx1 ⊕ vz ⊕ vx1 ⊕ vx2 ⊕ v ⊕ z ⊕ x1 ⊕ 1y2 = vzx2 ⊕ vz ⊕ vx1 ⊕ vx2 ⊕ zx1 ⊕ x2 ⊕ v ⊕ z ⊕ 1y3 = vzx1 ⊕ vzx2 ⊕ zx1 ⊕ x1 ⊕ x2.
- Case 2:
- y1 = vzx1 ⊕ vzx2 ⊕ vx1 ⊕ vx2 ⊕ zx1 ⊕ zx2 ⊕ z ⊕ v ⊕ x2y2 = vzx1 ⊕ vzx2 ⊕ vz ⊕ vx1 ⊕ vx2 ⊕ zx1 ⊕ zx2 ⊕ x1y3 = vz ⊕ v ⊕ z ⊕ x1 ⊕ x2.
- Case 3:
- y1 = vx2 ⊕ x2 ⊕ x1 ⊕ v ⊕ 1y2 = vx1 ⊕ x2.
The three fixed permutations I, I1, and I2 are denoted as follows:
I1 = (1) (2,5) (3,9) (4,13) (5,2) (6) (7,10) (8,14) (9,3) (10,7) (11) (12,15) (13,4) (14,8) (15,12) (16).
I2 = (1) (2,3) (3,2) (4) (5) (6,7) (7,6) (8) (9) (10,11) (11,10) (12) (13) (14,15) (15,14) (16).
I = (1) (2,18) (3) (4,20) (5) (6,22) (7) (8,24) (9) (10,26) (11) (12,28) (13) (14,30) (15) (16,32) (17)
(18,2) (19) (20,4) (21) (22,6) (23) (24,8) (25) (26,10) (27) (28,12) (29) (30,14) (31) (32,16).
The expansion function E takes a 16-bit input X, since E(X) = (X, X<<<4, X<<<8, X<<<12); it then outputs 64-bit controlled vector (V, Z) = (V1, V2, V3, V4, Z1, Z2, Z3, Z4).
The hybrid CSPN construction is designed based on the description of permutation function structure covering eight 4 × 4 S-boxes (S0, S1, S2, S3 and S−10, S−11, S−12, S−13) with SDDO-based function . Figure 3 presents the CSPN with its S-boxes in structure.
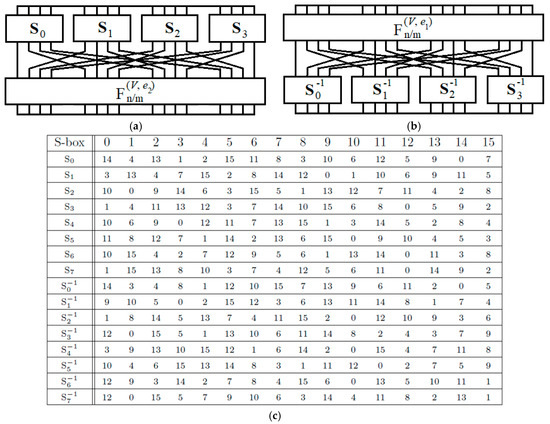
Figure 3.
Controlled substitution–permutation network (CSPN) model in (a) left and (b) right of data sub-block; (c) different 4 × 4 S-boxes.
Like other data-dependent ciphers, BM123-64 is constructed with a very simple key schedule for high-speed transformation target. To generate function keys used in each round, 256-bit secret key K is divided into eight 32-bit subkeys K = (K1, K2, …, K7, K8). The key scheduling is provided with different parameters as shown in Table 1.

Table 1.
Key schedule of BM123-64.
3. Proposed Attack Methods on BM123-64 Construction
Differential properties of operations in each round function are fundamental features to build differential characteristics and explore the related-key attack methods. Based on these properties, we can construct high probability DCs on a full eight rounds of BM123-64 with Crypt(e) function. Furthermore, the related-key amplified boomerang attacks will be addressed with effective complexity results.
3.1. BM123-64 Crypt(e) Function Properties
The Crypt(e) function in BM123-64 cipher consists of several functions having appropriate differential properties to construct the high probability DCs.
3.1.1. Differential Properties of F2/2 Function
x1 and x2 are assumed as input parameters, with a pair (v, z) controlled vector of F2/2 function. Therefore, the controlled element F2/2 can be described as F2/2 (x1, x2, [v, z]). Based on different distribution applied to different descriptions of F2/2 in BM123-64, we have differential properties for each case as the following:
- Case 1:
- y1 = vzx1 ⊕ vz ⊕ vx1 ⊕ vx2 ⊕ v ⊕ z ⊕ x1 ⊕ 1y2 = vzx2 ⊕ vz ⊕ vx1 ⊕ vx2 ⊕ zx1 ⊕ x2 ⊕ v ⊕ z ⊕ 1Pr [F2/2 (x1, x2, [v, z]) ⊕ F2/2 (x1 ⊕ 1, x2, [v, z]) = (1, 0)] = 2−2.
- Case 2:
- y1 = vzx1 ⊕ vzx2 ⊕ vx1 ⊕ vx2 ⊕ zx1 ⊕ zx2 ⊕ z ⊕ v ⊕ x2y2 = vzx1 ⊕ vzx2 ⊕ vz ⊕ vx1 ⊕ vx2 ⊕ zx1 ⊕ zx2 ⊕ x1Pr [F2/2 (x1, x2, [v, z]) ⊕ F2/2 (x1 ⊕ 1, x2, [v, z]) = (1, 0)] = 2−1.
- Case 3:
- y1 = vx2 ⊕ x2 ⊕ x1 ⊕ v ⊕ 1;y2 = vx1 ⊕ x2Pr [F2/2 (x1, x2, [v, z]) ⊕ F2/2 (x1 ⊕ 1, x2, [v, z]) = (1, 0)] = 2−1.
For each case of F2/2 description, in order to get the (1, 0) output difference with the (x1 ⊕ 1, 0) input difference and the (0, 0) controlled vector difference, the probability will be 2−2, 2−1, and 2−1 for Case 1, Case 2, and Case 3, respectively.
3.1.2. Differential Properties of F16/64 and F −116/64 Functions
In the same way, we can get the properties of SDDO-based functions F16/64 and F −116/64 using the properties above. Here, X is the input parameters for F16/64 and F −116/64 and (V, Z) is the controlled vector. Based on the properties of F2/2, we can get the following:
- Case 1:
- Pr [F16/64 (X, V, Z) ⊕ F16/64 (X ⊕ e16, V, Z) = e16] = 2−8Pr [F−116/64 (X, V, Z) ⊕ F−116/64 (X ⊕ e16, V, Z) = e16] = 2−8
- Case 2:
- Pr [F16/64 (X, V, Z) ⊕ F16/64 (X ⊕ e16, V, Z) = e16] = 2−4Pr [F−116/64 (X, V, Z) ⊕ F−116/64 (X ⊕ e16, V, Z) = e16] = 2−4
- Case 3:
- Pr [F16/64 (X, V, Z) ⊕ F16/64 (X ⊕ e16, V, Z) = e16] = 2−4Pr [F−116/64 (X, V, Z) ⊕ F−116/64 (X ⊕ e16, V, Z) = e16] = 2−4
With the F16/64 and F −116/64 function designs, we can see that there is a total of four active layers F2/2 within each construction, as shown in Figure 2.
3.2. Related-Key Boomerang of BM123-64
Here, we describe the way to generate related-key differential boomerangs on a full eight rounds of BM123-64 using the obtained properties in Section 3.1 with the key schedule generator.
We construct two related-key differentials as follows:
The first four rounds of related-key differential E0 = ( → ) holds with chosen input difference = (0, 0) and key difference (0, e32) from the first round to the fourth round with output difference = (0, 0). The key difference, based on the key schedule generator given in Table 1, is to control differential propagation and get high probability. The first related-key differential achieves this with probability p = 2−16, 2−8, and 2−8 for each case of F2/2 description.
The second related-key differential E1 = ( → ) = (0, e32) “ (0, e16) covering the last four rounds with input difference = (0, e32) and key difference (0, e32) from the fifth round gives output difference = (0, e16) after the final transformation. The second related-key differential obtains probability q = 2−16, 2−8, and 2−8, respectively. In total, the related-key differential characteristics constructed on a full eight rounds of BM123-64 designs give us the probability of 2−32 for Case 1, 2−16 for Case 2, and 2−16 for Case 3. Figure 2 illustrates the DCs propagation of some specific BM123-64 rounds in Case 2 and Case 3.
The differential amplified boomerang can be explored based on the two related-key differentials above.
We can take any chosen plaintexts, namely (P, P*, P’, P’*) with input difference = (0, 0) described as ∆P = P ⊕ P* = P’ ⊕ P’*, to give respective ciphertexts with output difference = (0, 0) using related-keys (K, K*, K’, K’*) defined as ∆K = K ⊕ K* = K’ ⊕ K’* = (0, e16, e32, 0, 0, 0, 0, 0). We can hold the first four rounds related-key boomerang with probability of 2−16 for Case 1, 2−8 for Case 2, and 2−8 for Case 3. Furthermore, by pretending an additional round with intermediate differential values (I, I*, I’, I’*) described as I ⊕ I* = I’ ⊕ I’* = (0, e32) using another related-key differences ∆K’ = K ⊕ K’ = K* ⊕ K’* = (0, e32, 0, 0, 0, 0, 0, 0), we can build the second related-key boomerang on the last four rounds of 2−16 probability for Case 1, and 2−8 for both Case 2 and Case 3.
In Table 2, the detailed DCs of a full eight rounds of BM123-64 with corresponding probabilities is shown. And, Figure 4 illustrates the DCs in Crypt(e) function of BM123-64 with Case 2 and Case 3 at several rounds.

Table 2.
Related-key DCs of a full eight rounds of BM123-64 in distinctive designs.
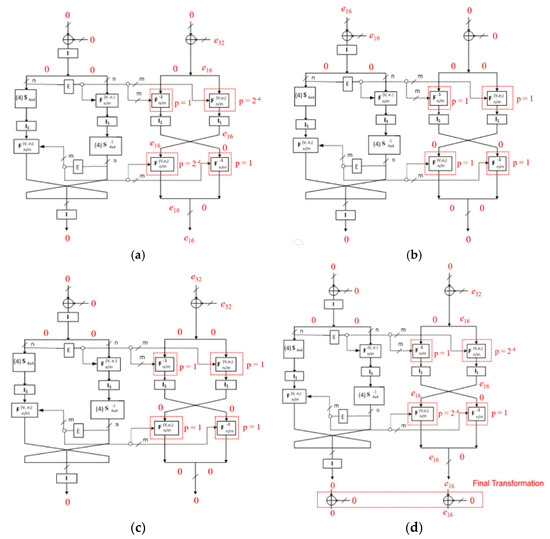
Figure 4.
Differential characteristics (DCs) in Crypt(e) function at (a) the first round; (b) the second round; (c) the fifth round; and (d) the eighth round and final transformation of BM123-64 with Case 2 and Case 3.
See (Appendix A) for more descriptions of DCs with Case 1.
3.3. Related-Key Amplified Boomerang Attack on the BM123-64 Designs
With the two obtained differentials, we expect that having m2∙2−128 of encrypted quartets for Case 1 is right. For Case 2 and Case 3, the expected number is m2∙2−96 right quartets. Furthermore, in the case of an ideal cipher, the related-key boomerang differentials applied on a full eight rounds of BM123-64 with probabilities of 2−128, 2−96, and 2−96 (2−64∙p2∙q2) for each case, respectively. For the least expected right quartets number of 8, we take a set of 266 pairs of plaintexts (m2∙2−128 = 23) for the attack process in Case 1 and 250 pairs of plaintexts (m2∙2−96 = 23) for the attacks in Case 2 and Case 3.
The attacker follows the below steps for a full related-key attack method on BM123-64:
- (1)
- We pick a set of 266 pairs of plaintexts (Pj, Pj *), (j = 1, …, 266), then we expand into another set of 2131 quartets of plaintexts, denoted as (Pi, Pi *, Pi ’, Pi ’*), (i = 1, …, 2131) in Case 1, or 250 pairs of plaintexts (Pj, Pj *), (j = 1, …, 250) and generate 299 quartets of plaintexts (Pi, Pi *, Pi ’, Pi ’*), (i = 1, …, 299) in Case 2 and Case 3, with input difference = (0, 0). We ask for encryption of all the quartets (Pi, Pi *, Pi ’, Pi ’*) using the related-keys (K, K*, K’, K’*) difference, described as two terms of relation: ∆K = K ⊕ K* = K’ ⊕ K’* = (0, e16, e32, 0, 0, 0, 0, 0) and ∆K’ = K ⊕ K’ = K* ⊕ K’* = (0, e32, 0, 0, 0, 0, 0, 0) to output respective quartets of ciphertexts (Ci, Ci *, Ci ’, Ci ’*).
- (2)
- We do XOR with all possible values of Ci and Ci’, Ci *, and Ci’* for each i value, then check whether the output result is (0, e16) and store all these difference values to apply in the previous eight rounds.
- (3)
- By this way, at the final transformation, we expect to hold a 64-bit subkey including K1 and K3, then get the remaining subkeys (K1*, K3*), (K1’, K3’), and (K1’*, K3’*) of the quartets of subkeys.
- (a)
- Similarly, at the eighth round, we ask for decryption of all quartets of ciphertexts values obtained from Step 2 with subkey quartets of K1 and K3 to hold 64-bit input values (Xj, Xj*, Xj’, Xj’*) at the left side process of round function.
- (b)
- We do XOR with all possible values of Xj and Xj’, Xj *, and Xj’* for each j value, then check whether the output result is 0.
- (4)
- After passing Step 3, all values of quartets of two subkeys K1 and K3 are explored. We can do brute force attacks to obtain the remaining 192-bit subkeys (K2, K4, K5, K6, K7, K8) with all K1 and K3.
4. Results and Discussion
With Case 1, the proposed attack requires 266 pairs of plaintexts and 267 related-key chosen plaintexts in data complexity, since the related-key DC is 2−32. Furthermore, it needs about 270 (=267 × 8) bytes of memory.
With Case 2 and Case 3, the attack requires 250 pairs of plaintexts and 251 related-key chosen plaintexts in data complexity, while the related-key DCs are 2−16. The attack takes about 254 (=251 × 8) bytes of memory.
At Step 1 of the attack, the complexity of time is a unit of 267 encryptions (Case 1), or 251 encryptions (Case 2 and Case 3) of the full eight rounds of BM123-64. Each quartet of ciphertext is planned to achieve Step 2 of the attack with 2−64 probability. In addition, we will get 267 (=2131 × 2−64) right quartets of ciphertext (Case 1) or 235 right quartets of ciphertext (=299 × 2−64) (Case 2 and Case 3) that will achieve Step 2. At Step 3 and Step 4, the complexity of time is a unit of 262 (=264 × 4 × 1/8 × 1/2) and 265 (=264 × 1 × 2) for a full eight rounds of BM123-64 encryptions, respectively. Finally, the results show that all the attacks require total time complexity of 267 (≈267 + 262 + 265) (Case 1) or 265 (≈251 + 262 + 265) (Case 2 and Case 3) for a full eight rounds of BM123-64 encryptions on average. In Table 3, a comparison of cryptanalysis results between the scheme proposed and other data-dependent ciphers in terms of complexity of data and time is given.

Table 3.
Cryptanalysis results on constructions based on DDP (Data-Dependent Permutation), DDO (Data-Dependent Operation), and SDDO (switchable data-dependent operation).
At Step 4 of the attack, outputting a wrong quartet of subkey takes 2−64 of probability. With our cryptanalysis methods, the results shown with the output possibility in case of a wrong key is lower than the ideal case. These proposed related-key amplified boomerang attacks can potentially exploit the BM123-64 constructions at all three specific cases.
5. Conclusions
This paper proposes effective attacks on one of the recent SDDO-based constructions, BM123-64. The methods addressed in the study present main issues in security mechanisms of ciphers based on data-dependent operations that is used in many cipher designs for high speed transformation and lightweight targets. The simple key schedule generator with basic parameters when changed and substituted leads to a possibility of exploiting the structure weaknesses by related-key cryptanalysis. The work presented related-key amplified boomerang attacks on a full eight rounds of BM123-64 in distinctive designs with effective complexity results. This shows that with Case 1, it requires 266 related-key chosen plaintexts and 267 encryptions consumptions, and 250 related-key chosen plaintexts and 265 encryptions consumptions are required with Case 2 and Case 3. The results of this study can be applied on many construction designs of these types of ciphers. Along with some new cryptanalysis techniques like Fr Trust or RARE, our research will further enhance performance and is expected to develop novel approaches for a wide range of applications and devices in the IoT environment.
Author Contributions
Conceptualization, T.S.D.P., C.L.; Methodology, T.S.D.P.; Writing-Original Draft Preparation, T.S.D.P.; Writing-Review & Editing, T.S.D.P.; Supervision, C.L.; Funding Acquisition, C.L.
Funding
This work was supported by the Korea Institute of Energy Technology Evaluation and Planning (KETEP) and the Ministry of Trade, Industry & Energy (MOTIE) of the Republic of Korea (Development of Cyber Security Technology for Non-safety Grade Control System (DCS) in Nuclear Power Plants, No. 20161510101810).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Figure A1 illustrates the differential propagation at several rounds of BM123-64 cipher with Crypt(e) function in Case 1.
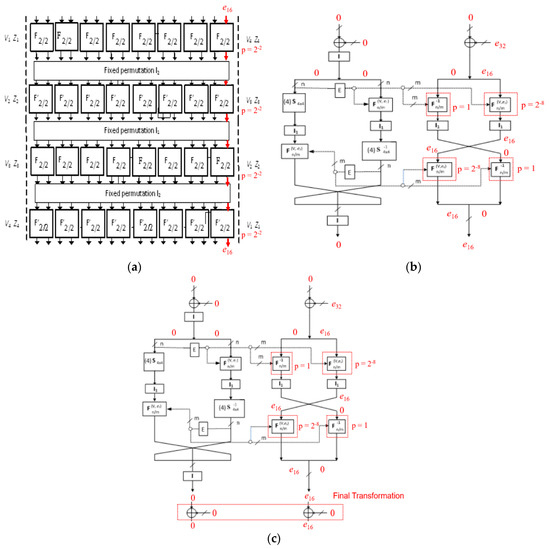
Figure A1.
(a) The differential propagation of F16/64, F −116/64 function and the DCs in Crypt(e) function at (b) the 1st round and (c) the eighth round and final transformation of BM123-64 with Case 1.
We pick a set of 266 pairs of plaintexts (Pj, Pj *) and expand to 2131 quartets of plaintexts (Pi, Pi*, Pi’, Pi’*). The SDDO-based function in BM123-64 structure includes F16/64 and F −116/64, which has four layers with eight F2/2 element function in each. Based on the differential properties mentioned in Section 3.1, we can construct two related-key boomerangs on a full eight rounds of BM123-64 in Case 1 with total probability of 2−32. The first four rounds of related-key boomerang holds with the probability p = 2−16; the last four rounds of related-key boomerang also obtains with the probability q = 2−16. It requires about 267 chosen plaintexts in complexity of data as input, and the memory required is about 270 (=267 × 8) bytes.
References
- Bac, D.; Minh, N. High-Speed Block Cipher Algorithm Based on Hybrid Method. In Ubiquitous Information Technologies Applications; Lecture Notes in Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2014; Volume 280, pp. 285–291. [Google Scholar]
- Moldovyan, N. On Cipher Design Based on Switchable Controlled Operations. In MMM-ACNS, LNCS; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2776, pp. 316–327. [Google Scholar]
- Bac, D.; Minh, N.; Duy, H. An Effective and Secure Cipher Based on SDDO. Int. J. Comput. Netw. Inf. Secur. 2012, 4, 1. [Google Scholar]
- Bac, D.; Minh, N.; Duy, H. New SDDO-Based Block Cipher for Wireless Sensor Network Security. Int. J. Comput. Netw. Inf. Secur. 2010, 10, 54–60. [Google Scholar]
- Minh, N.; Luan, N.; Dung, L. KT-64: A New Block Cipher Suitable to Efficient FPGA Implementation. IJCSNS Int. J. Comput. Netw. Inf. Secur. 2010, 19, 10–18. [Google Scholar]
- Minh, N.; Duy, H.; Dung, L. Design and Estimate of a New Fast Block Cipher for Wireless Communication Devices. In Proceedings of the International Conference on Advanced Technologies for Communications, Hanoi, Vietnam, 6–9 October 2008; pp. 409–412. [Google Scholar]
- Moldovyan, N.; Moldovyan, A.; Sklavos. Controlled Elements for Designing Ciphers Suitable to Efficient VLSI Implementation. Telecommun. Syst. J. 2006, 32, 149–163. [Google Scholar] [CrossRef]
- Kang, J.; Jeong, K.; Lee, C.; Hong, S. Distinguishing attack on SDDO-based block cipher BMD-128. In Ubiquitous Information Technologies and Applications; Springer: Berlin/Heidelberg, Germany, 2014; Volume 280, pp. 595–602. [Google Scholar]
- Phuc, T.S.D.; Lee, C.; Xiong, N. Cryptanalysis of the XO-64 Suitable for Wireless Systems. Wirel. Pers. Commun. 2017, 93, 589–600. [Google Scholar] [CrossRef]
- Izotov, B.V.; Moldovyan, N.; Moldovyan, A. Controlled Operations as a Cryptographic Primitive. In Information Assurance in Computer Networks; Springer: Berlin/Heidelberg, Germany, 2001; Volume 2052, pp. 230–241. [Google Scholar]
- Kang, J.; Jeong, K.; Yeo, S.; Lee, C. Related-key Attack on the MD-64 Block Cipher Suitable for Pervasive Computing Environment. In Proceedings of the International Conference on Advance Information Networking and Application Workshops, Fukuoka, Japan, 26–29 March 2012; pp. 726–731. [Google Scholar] [CrossRef]
- Lee, C.; Kim, J.; Sung, J.; Hong, S.; Lee, S. Security analysis of the full-round DDO-64 block cipher. J. Syst. Softw. 2008, 84, 2328–2335. [Google Scholar] [CrossRef]
- Moldovyan, N.; Moldovyan, A. Data-driven Ciphers for Fast Telecommunication Systems. In Auerbach Publication; Talor & Francis Group: New York, NY, USA; London, UK, 2008; pp. 77–185. ISBN 1420054112 9781420054118. [Google Scholar]
- Biham, E.; Dunkelman, O.; Keller, N. Related-key boomerang and rectangle attacks. In Advances in Cryptology—EUROCRYPT’05, LNCS; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3494, pp. 507–525. [Google Scholar]
- Kelsey, J.; Kohno, T.; Schneier, B. Amplified Boomerang Attacks against Reduced-Round MARS and Serpent. In Proceedings of Fast Software Encryption 7; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2000; Volume 1978, pp. 75–93. [Google Scholar] [CrossRef]
- Wagner, D. The Boomerang Attack. In Proceedings of Fast Software Encryption 6; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1999; Volume 1636, pp. 156–170. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).