Optimizing the High-Level Maintenance Planning Problem of the Electric Multiple Unit Train Using a Modified Particle Swarm Optimization Algorithm
Abstract
:1. Introduction
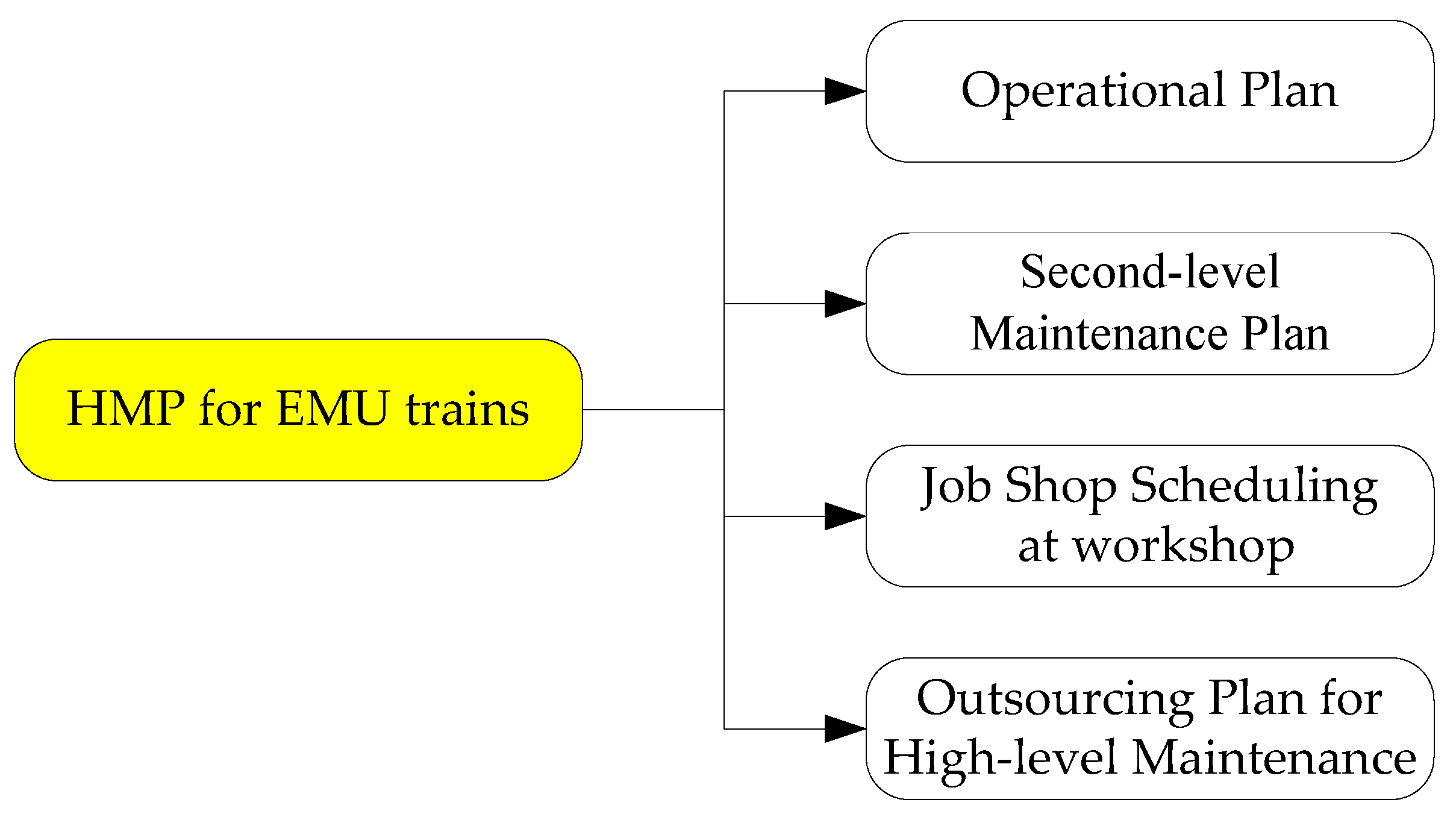
2. HMP Problem at CR
3. Mathematical Model of the HMP Problem
3.1. Notations
3.2. Optimization Objective
3.3. Constraints Analysis
3.4. Model Construction
4. Modified Particle Swarm Optimization Algorithm
4.1. Processing of Model Constraints
4.2. General Particle Swarm Optimization Algorithm
4.3. MPSO and Solution Strategy
4.3.1. Inertia Weight
4.3.2. Learning Factor
4.3.3. Update Equations
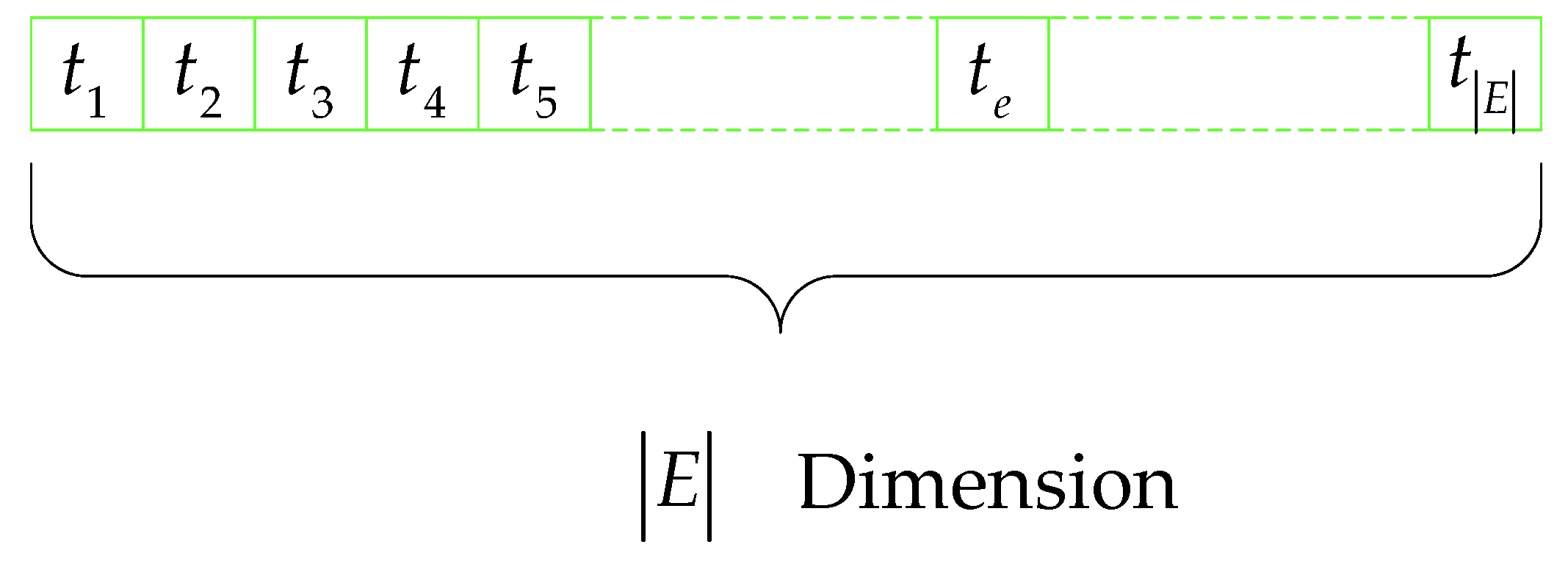
4.3.4. Encoding Rules and Initial Solution
4.4. Algorithm Steps
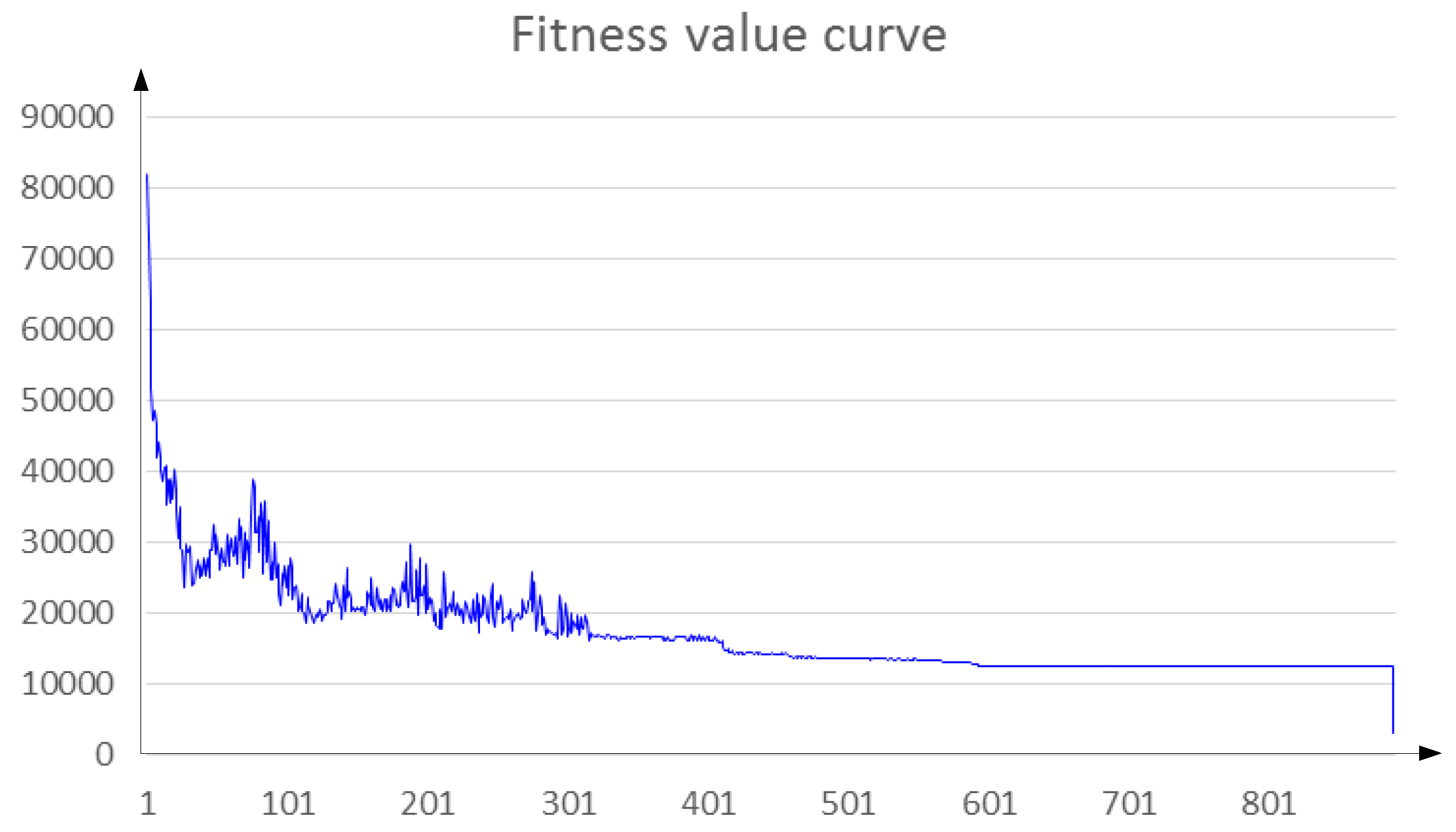
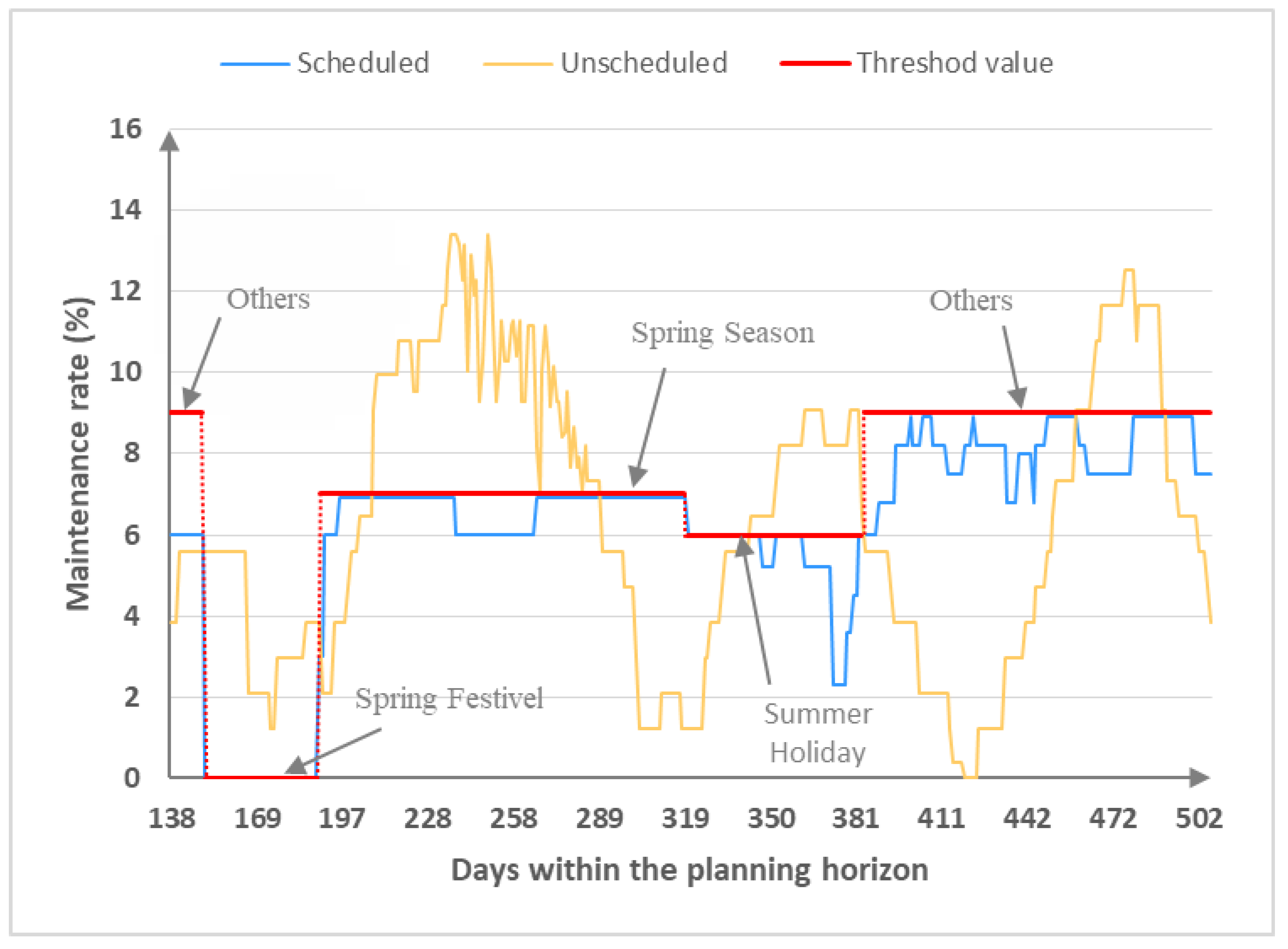
5. Case Study
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- China Railway. User Manual for EMU Operation and Maintenance Procedures, 1st ed.; Railway Publishing House: Beijing, China, 2013. [Google Scholar]
- Stuchly, V.; Grencik, J.; Poprocky, R. Railway vehicle maintenance and information systems. WIT Trans. Built Environ. 2000, 50, 885–894. [Google Scholar]
- Rezvanizanianil, S.M.; Valibeiglool, M.; Asgharil, M.; Barabady, J.; Kumar, U. Reliability centered maintenance for rolling stock: A case study in coaches’ wheel sets of passenger trains of Iranian railway. In Proceedings of the IEEE International Conference on Industrial Engineering and Engineering Management, Singapore, 8–11 December 2008; pp. 516–520. [Google Scholar]
- Shimada, N. Rolling stock maintenance for safe and stable transport. Jpn. Railw. Eng. 2006, 46, 4–7. [Google Scholar]
- Cheng, Y.H.; Tsao, H.L. Rolling stock maintenance strategy selection, spares parts’ estimation, and replacements’ interval calculation. Int. J. Prod. Econ. 2010, 128, 404–412. [Google Scholar] [CrossRef]
- Maróti, G.; Kroon, L. Maintenance routing for train units: The transition model. Transp. Sci. 2005, 39, 518–525. [Google Scholar] [CrossRef]
- Maróti, G.; Kroon, L. Maintenance routing for train units: The interchange model. Comput. Oper. Res. 2007, 34, 1121–1140. [Google Scholar] [CrossRef]
- Tsuji, Y.; Kuroda, M.; Imoto, Y. Rolling stock planning for passenger trains based on ant colony optimization. Trans. Jpn. Soc. Mech. Eng. Part C 2010, 76, 397–406. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, J.; Miao, J.R. Column generation algorithms based optimization method for maintenance scheduling of multiple units. China Railw. Sci. 2010, 31, 115–120. [Google Scholar]
- Giacco, G.L.; D’Ariano, A.; Pacciarelli, D. Rolling stock rostering optimization under maintenance constraints. J. Intell. Transp. Syst. 2014, 18, 95–105. [Google Scholar] [CrossRef]
- Ziaratia, K.; Soumisa, F.; Desrosiers, J.; Gélinas, S.; Saintonge, A. Locomotive assignment with heterogeneous consists at CN North America. Eur. J. Oper. Res. 1997, 97, 281–292. [Google Scholar] [CrossRef]
- Lingaya, N.; Cordeau, J.F.; Desaulniers, G.; Desrosiers, J.; Soumis, F. Operational car assignment at VIA Rail Canada. Transp. Res. B Meth. 2002, 36, 755–778. [Google Scholar] [CrossRef]
- Wang, L.; Ma, J.J.; Lin, B.L.; Chen, L.; Wen, X.H. Method for optimization of freight locomotive scheduling and routing problem. J. China Railw. Soc. 2014, 36, 7–15. [Google Scholar] [CrossRef]
- Moudania, W.E.; Félix, M.C. A dynamic approach for aircraft assignment and maintenance scheduling by airlines. J. Air Transp. Manag. 2000, 6, 233–237. [Google Scholar] [CrossRef] [Green Version]
- Mehmet, B.; Bilge, Ü. Operational aircraft maintenance routing problem with remaining time consideration. Eur. J. Oper. Res. 2014, 235, 315–328. [Google Scholar] [CrossRef]
- Budai, G.; Huisman, D.; Dekker, R. Scheduling preventive railway maintenance activities. J. Oper. Res. Soc. 2006, 57, 1035–1044. [Google Scholar] [CrossRef] [Green Version]
- Grigoriev, A.; Klundert, J.V.D.; Spieksma, F.C.R. Modeling and solving the periodic maintenance problem. Eur. J. Oper. Res. 2006, 172, 783–797. [Google Scholar] [CrossRef] [Green Version]
- Lin, B.L.; Lin, R.X. An Approach to the high-level maintenance planning for EMU trains based on simulated annealing. arXiv. 2017. Available online: https://arxiv.org/abs/1704.02752 (accessed on 10 April 2017).
- Wu, J.P.; Lin, B.L.; Wang, J.X.; Liu, S.Q. A network-based method for the EMU train high-level maintenance planning problem. Appl. Sci. 2018, 8, 2. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, W.J.; Jia, Z.K. Forecast method of annual senior over haul amount for EMU. J. Transp. Eng. 2013, 13, 102–107. [Google Scholar]
- Wang, D.W.; Wang, J.W.; Wang, H.F.; Zhang, R.Y; Guo, Z. Intelligent Optimization Method; High Education Press: Beijing, China, 2007; pp. 217–259. [Google Scholar]
- Li, J.; Lin, B.L.; Wang, Z.K.; Chen, L.; Wang, J.X. A pragmatic optimization method for motor train set assignment and maintenance scheduling problem. Discrete Dyn. Nat. Soc. 2016, 3, 1–13. [Google Scholar] [CrossRef]
- Wang, J.X.; Lin, B.L.; Jin, J.C. Optimizing the shunting schedule of electric multiple units depot using an enhanced particle swarm optimization algorithm. Comput. Intell. Neurosci. 2016, 1, 1–11. [Google Scholar] [CrossRef] [PubMed]
| Notations | Definition |
|---|---|
| The index of EMU trains; | |
| The set of all EMU trains; | |
| An empty set; | |
| The eta of the HM for the EMU train ; | |
| The type of the EMU train ; | |
| The maintenance level of the EMU train ; | |
| The maximum value of the difference between the actual operating mileage before the HM and the for the train of which the type is and maintenance level is ; | |
| The maximum value of the difference between the and the actual operating mileage before the HM for the train of which the type is and the maintenance level is ; | |
| The average daily operating mileage for the EMU train before HM. |
| Notations | Definition |
|---|---|
| Indices | |
| The index of EMU trains; | |
| The index of types for the EMU trains; | |
| The index of dates during the planning horizon; | |
| The index of the maintenance level; | |
| Set | |
| The set of all EMU trains; | |
| The set of all types; | |
| The set of all dates during the planning horizon; | |
| The set of all maintenance levels; | |
| Input parameters | |
| The maintenance level of the EMU train ; | |
| The type of the EMU train ; | |
| The unit penalty fee for the unused mileage before the HM; | |
| The eta for the EMU train ; | |
| The average daily operating mileage for the EMU train before the HM; | |
| The first date of the time window for the EMU train , (See Section 2); | |
| The last date of the time window for the EMU train , (See Section 2); | |
| The conversion coefficient for train of which the type is , indicates whether the train includes sixteen cars or not, if yes, then = 2; otherwise, = 1; | |
| The maximum HM rate on the t-th day; | |
| The fleet size (the standard set); | |
| The maximum number of an EMU train in the HM state for the type on the t-th day; | |
| The maximum number of an EMU train in the -th level maintenance state; | |
| The maximum number of an acceptable EMU train in the -th level maintenance state at the same time; | |
| A sufficiently large positive number; | |
| The maintenance service time for an EMU train with the -th type and the -th level; | |
| The minimum interval time for delivering another train after an EMU train with the -th type and the -th level enters the workshop; | |
| The length of the planning horizon; | |
| The number of the EMU trains which need to be maintained during the planning horizon; | |
| Decision Variables | |
| Binary variable, indicates whether the EMU train selects the -th day to start the HM procedures during the planning horizon, = 1 if yes, = 0 otherwise; | |
| Binary variable, indicates whether the EMU train in the -th level maintenance state on the -th day during the planning horizon, = 1 if yes, = 0 otherwise; | |
| Binary variable, indicate whether the EMU train in the -th level delivery interval on the -th day during the planning horizon, = 1 if yes, = 0 otherwise; | |
| ID | Type | Time Window | Level | (Day) | |
|---|---|---|---|---|---|
| 1 | m1 | 1600 | [64,164] | 3 | 50 |
| 2 | m1 | 1600 | [64,164] | 3 | 50 |
| 3 | m1 | 1600 | [90,190] | 3 | 50 |
| 4 | m1 | 1600 | [124,224] | 3 | 50 |
| 5 | m1 | 1600 | [144,244] | 3 | 50 |
| 6 | m1 | 1600 | [188,288] | 3 | 50 |
| 7 | m1 | 1600 | [200,300] | 3 | 50 |
| 8 | m1 | 1600 | [274,374] | 4 | 55 |
| 9 | m1 | 1600 | [370,470] | 4 | 55 |
| 10 | m1 | 1600 | [379,479] | 4 | 55 |
| 11 | m1 | 1600 | [429,479] | 4 | 55 |
| 12 | m2 | 1600 | [72,172] | 3 | 50 |
| 13 | m2 | 1600 | [158,258] | 3 | 50 |
| 14 | m2 | 1600 | [216,316] | 3 | 50 |
| 15 | m2 | 1600 | [264,354] | 3 | 50 |
| 16 | m2 | 1600 | [387,484] | 3 | 50 |
| 17 | m2 | 1600 | [396,484] | 3 | 50 |
| 18 | m2 | 1600 | [409,484] | 3 | 50 |
| 19 | m2 | 1600 | [443,484] | 4 | 55 |
| 21 | m3 | 2000 | [134,234] | 5 | 60 |
| 21 | m3 | 2000 | [149,249] | 3 | 40 |
| 22 | m3 | 2000 | [150,250] | 3 | 40 |
| 23 | m3 | 2000 | [153,253] | 3 | 40 |
| 24 | m3 | 2000 | [158,258] | 5 | 60 |
| 25 | m3 | 2000 | [158,258] | 3 | 40 |
| 26 | m3 | 2000 | [159,259] | 3 | 40 |
| 27 | m3 | 2000 | [167,267] | 3 | 40 |
| 28 | m3 | 2000 | [172,272] | 4 | 55 |
| 29 | m3 | 2000 | [172,272] | 3 | 40 |
| 30 | m3 | 2000 | [182,282] | 3 | 40 |
| 31 | m3 | 2000 | [184,284] | 3 | 40 |
| 32 | m3 | 2000 | [185,285] | 3 | 40 |
| 33 | m3 | 2000 | [190,290] | 3 | 40 |
| 34 | m3 | 2000 | [190,290] | 3 | 40 |
| 35 | m3 | 2000 | [191,291] | 3 | 40 |
| 36 | m3 | 2000 | [192,292] | 3 | 40 |
| 37 | m3 | 2000 | [193,293] | 3 | 40 |
| 38 | m3 | 2000 | [206,306] | 3 | 40 |
| 39 | m3 | 2000 | [209,309] | 3 | 40 |
| 40 | m3 | 2000 | [211,311] | 3 | 40 |
| 41 | m3 | 2000 | [211,311] | 3 | 40 |
| 42 | m3 | 2000 | [249,349] | 3 | 40 |
| 43 | m3 | 2000 | [276,376] | 3 | 40 |
| 44 | m3 | 2000 | [280,380] | 3 | 40 |
| 45 | m3 | 2000 | [281,381] | 3 | 40 |
| 46 | m3 | 2000 | [289,389] | 3 | 40 |
| 47 | m3 | 2000 | [290,390] | 3 | 40 |
| 48 | m3 | 2000 | [299,399] | 3 | 40 |
| 49 | m3 | 2000 | [300,400] | 3 | 40 |
| 50 | m3 | 2000 | [309,409] | 3 | 40 |
| 51 | m3 | 2000 | [309,409] | 3 | 40 |
| 52 | m3 | 2000 | [320,420] | 3 | 40 |
| 53 | m3 | 2000 | [321,421] | 3 | 40 |
| 54 | m3 | 2000 | [325,425] | 3 | 40 |
| 55 | m3 | 2000 | [395,494] | 3 | 40 |
| 56 | m3 | 2000 | [398,494] | 3 | 40 |
| 57 | m3 | 2000 | [425,494] | 3 | 40 |
| 58 | m3 | 2000 | [429,494] | 3 | 40 |
| 59 | m3 | 2000 | [448,494] | 3 | 40 |
| 60 | m3 | 2000 | [459,494] | 3 | 40 |
| e | e | e | e | e | e | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 108 | 11 | 481 | 21 | 182 | 31 | 280 | 41 | 310 | 51 | 409 |
| 2 | 103 | 12 | 142 | 22 | 220 | 32 | 252 | 42 | 349 | 52 | 419 |
| 3 | 153 | 13 | 212 | 23 | 250 | 33 | 278 | 43 | 376 | 53 | 421 |
| 4 | 193 | 14 | 333 | 24 | 240 | 34 | 273 | 44 | 379 | 54 | 425 |
| 5 | 198 | 15 | 360 | 25 | 248 | 35 | 282 | 45 | 381 | 55 | 472 |
| 6 | 300 | 16 | 460 | 26 | 188 | 36 | 276 | 46 | 388 | 56 | 498 |
| 7 | 312 | 17 | 492 | 27 | 218 | 37 | 238 | 47 | 390 | 57 | 500 |
| 8 | 387 | 18 | 458 | 28 | 268 | 38 | 303 | 48 | 398 | 58 | 502 |
| 9 | 482 | 19 | 490 | 29 | 270 | 39 | 243 | 49 | 400 | 59 | 496 |
| 10 | 480 | 20 | 190 | 30 | 246 | 40 | 308 | 50 | 407 | 60 | 494 |
| Method | z (km) | Time Consumption (s) |
|---|---|---|
| Gurobi | 3,213,121 | 3186 s |
| MPSO | 3,213,121 | 500 s |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Lin, B.; Wang, H.; Zhang, X.; Wang, Z.; Wang, J. Optimizing the High-Level Maintenance Planning Problem of the Electric Multiple Unit Train Using a Modified Particle Swarm Optimization Algorithm. Symmetry 2018, 10, 349. https://doi.org/10.3390/sym10080349
Wu J, Lin B, Wang H, Zhang X, Wang Z, Wang J. Optimizing the High-Level Maintenance Planning Problem of the Electric Multiple Unit Train Using a Modified Particle Swarm Optimization Algorithm. Symmetry. 2018; 10(8):349. https://doi.org/10.3390/sym10080349
Chicago/Turabian StyleWu, Jianping, Boliang Lin, Hui Wang, Xuhui Zhang, Zhongkai Wang, and Jiaxi Wang. 2018. "Optimizing the High-Level Maintenance Planning Problem of the Electric Multiple Unit Train Using a Modified Particle Swarm Optimization Algorithm" Symmetry 10, no. 8: 349. https://doi.org/10.3390/sym10080349
APA StyleWu, J., Lin, B., Wang, H., Zhang, X., Wang, Z., & Wang, J. (2018). Optimizing the High-Level Maintenance Planning Problem of the Electric Multiple Unit Train Using a Modified Particle Swarm Optimization Algorithm. Symmetry, 10(8), 349. https://doi.org/10.3390/sym10080349






