A Neutrosophic Set Based Fault Diagnosis Method Based on Multi-Stage Fault Template Data
Abstract
1. Introduction
2. Preliminaries
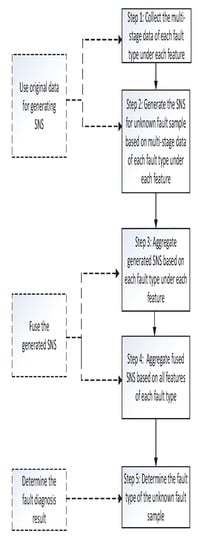
3. The Proposed Method
- Step 1
- Collect the multi-stage data of fault types under each feature. Suppose that there are m fault types () with n features (). Firstly, collect the multi-stage data of each fault type under each feature. Each stage’s data for each fault type under each feature are obtained by continuously collecting within the time interval (T). Suppose that data from k stages of every fault type under every feature are obtained. The multi-stage data of each fault type under each feature are shown as follows:where and .
- Step 2
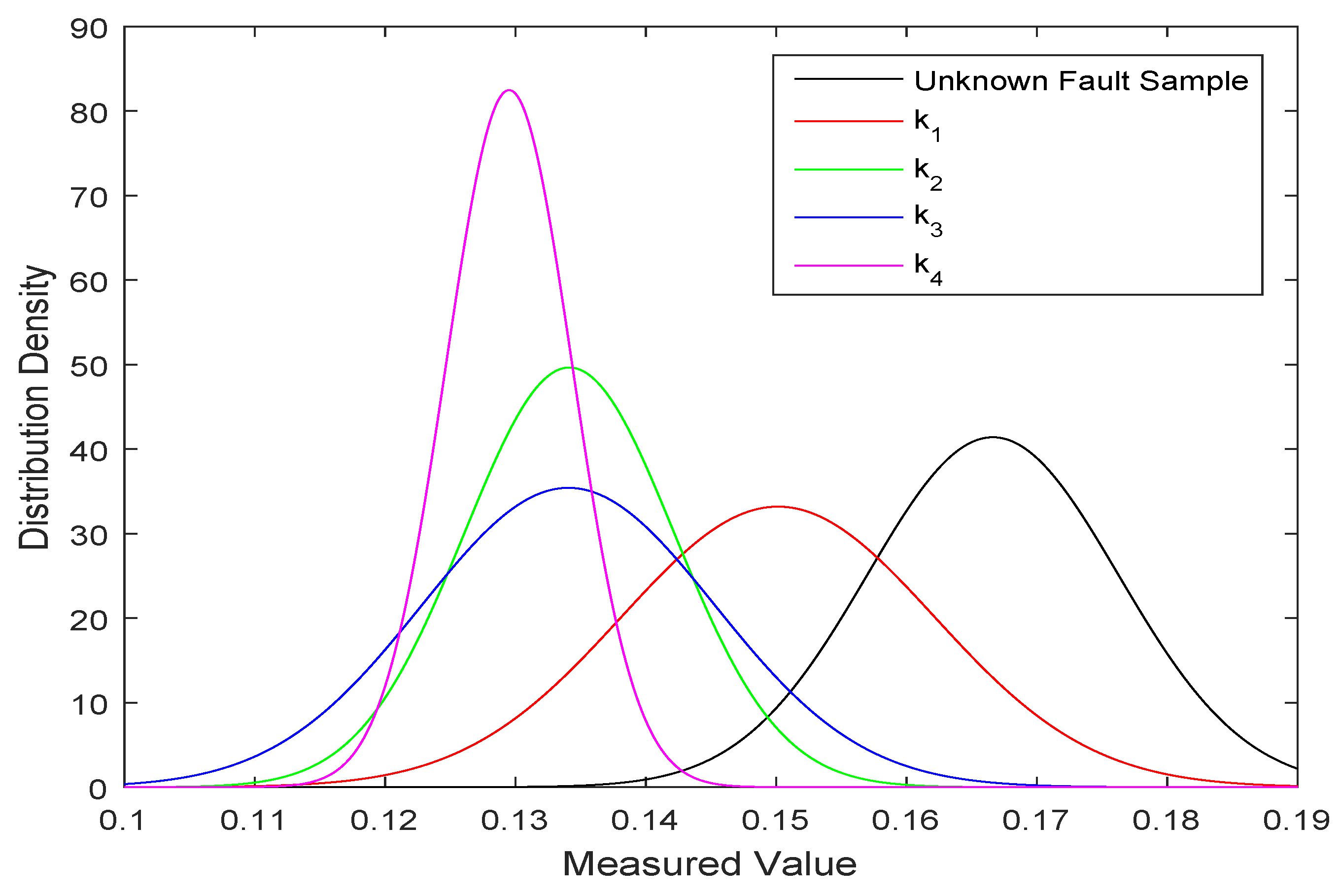
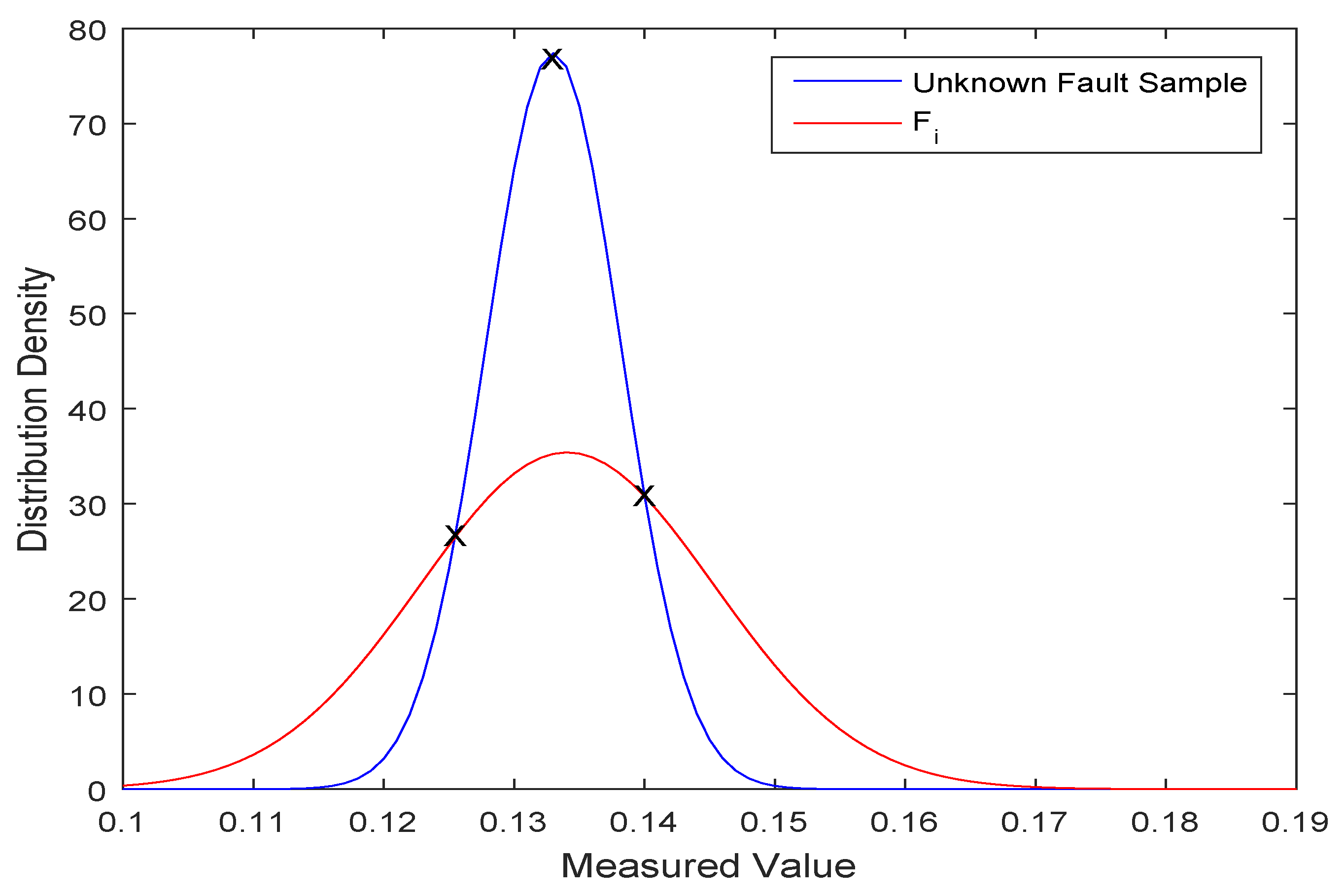
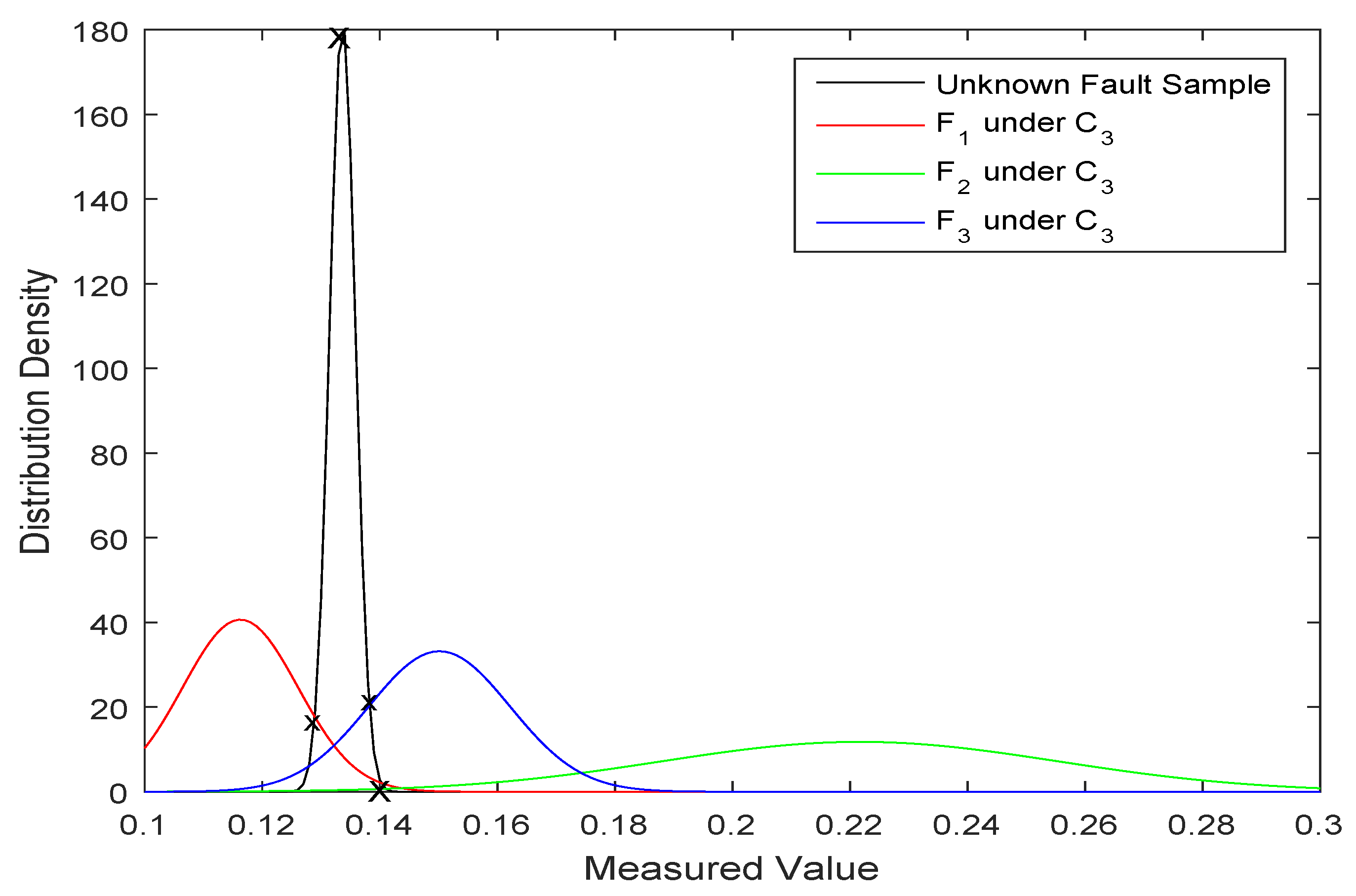
- Generate the SNS for an unknown fault sample (S) based on the multi-stage data of each fault type under each feature. For each stage’s data for each fault type under every feature, and for the data of every feature of the unknown fault sample (S), a normal distribution model is established which is obtained by using the arithmetic average (m) and variance () of a stage’s data as the arithmetic average and standard deviation of the normal distribution model, denoted as . Then, k normal distribution models and k normal distribution figures are generated according to k stages of data of each fault type under each feature. In addition, a normal distribution model is generated based on the data of the unknown fault sample under each feature. The normal distribution figures generated from the data of of unknown fault sample S and k stages of data for of are shown in Figure 2. As the figure shows, each stage’s data collected drift to a certain extent in a certain range. In particular, there are distinct differences between the fault type’s data collected in the fourth stage and the data of the unknown fault sample.The normal distribution function indicates the distribution probability density of the data. The membership degree of SNS is defined as the ratio of the maximum value of the vertical coordinate of the intersection point between the unknown fault sample and the fault type and the peak value of the unknown fault sample. The two normal distribution curves (Figure 3) and the definition of the membership degree () are as follows:where represents the maximum value of the vertical coordinate of the intersection point of distribution between the unknown fault sample (S) and the fault type (), and represents the peak value of the unknown fault sample’s distribution.As the figure shown, the intersection points of distribution between the unknown fault sample and are marked with X, and the peak point of S’ distribution is marked with X in the same way. Then, from the Equation (6), the membership degree is generated.In this paper, it is assumed that the non-membership degree and the membership degree are interdependent. The indeterminacy-membership degree indicates the uncertainty degree of neutrosophic information. Entropy represents the uncertainty of the information and has been widely used in many fields. Shannon introduced the quantitative and qualitative model of communication as a statistical process that underlies information theory [55], which is a formalism that was originally applied to digital communication. The indeterminacy-membership degree and non-membership degree are defined as follows:The indeterminacy-membership degree () represents the Shannon entropy of the membership degree () and the non-membership degree (), and equals 0 if or equal 0. Hence, the SNS can be obtained. The generated SNS is shown in Table 1:
- Step 3
- Aggregate the generated SNS based on each fault type under each feature. In this paper, it is assumed that the weights of data from k stages collected under the same working conditions are equal. The k SNNs of each fault type under each feature are fused via the SNWA operator, as shown in Equation (5). For instance,Then, the fused SNS matrix (A) is as follows:where and .
- Step 4
- Aggregate the fused SNS based on all features of each fault type. If the weights of n features are equal, n SNNs of each fault type are fused via the SNWA operator, as shown in Equation (5). For instance,Then, the fused SNS matrix (F) is as follows:
- Step 5
- Determine the fault type of the unknown fault sample. Considering the fuzziness of the unknown fault sample and the fault types, direct application of the defuzzification method can intuitively reflect the results of the fault diagnosis and reduce the amount of calculation in the process of fault diagnosis. The crisp number of each SNN is defuzzied and calculated as follows [56]:is the degree to which the information extracted from the data of untested fault supports each fault type. As a result, the ranking order of all the fault types can be determined according to the descending order of their crisp numbers ().
4. Illustrative Example and Discussion
- : The vibration amplitude when the acceleration frequency of the rotor is the basic frequency, .
- : The vibration amplitude when the acceleration frequency of the rotor is the frequency .
- : The vibration amplitude when the acceleration frequency of the rotor is the frequency .
- : The average amplitude of vibration displacement in the time-domain.
- Step 1
- Collect the multi-stage data of each fault type under each feature. There are three fault types set up on the test-bed:
- : Rotor imbalance.
- : Rotor misalignment.
- : Support base loosening.
For each feature of each fault type, data from five stages were collected, and for each stage’s data, forty consecutive observation values were collected continuously within a time interval of 16 s. The data in this paper originated from Reference [57]. For instance, the first stage’s data of under was as follows: - Step 2
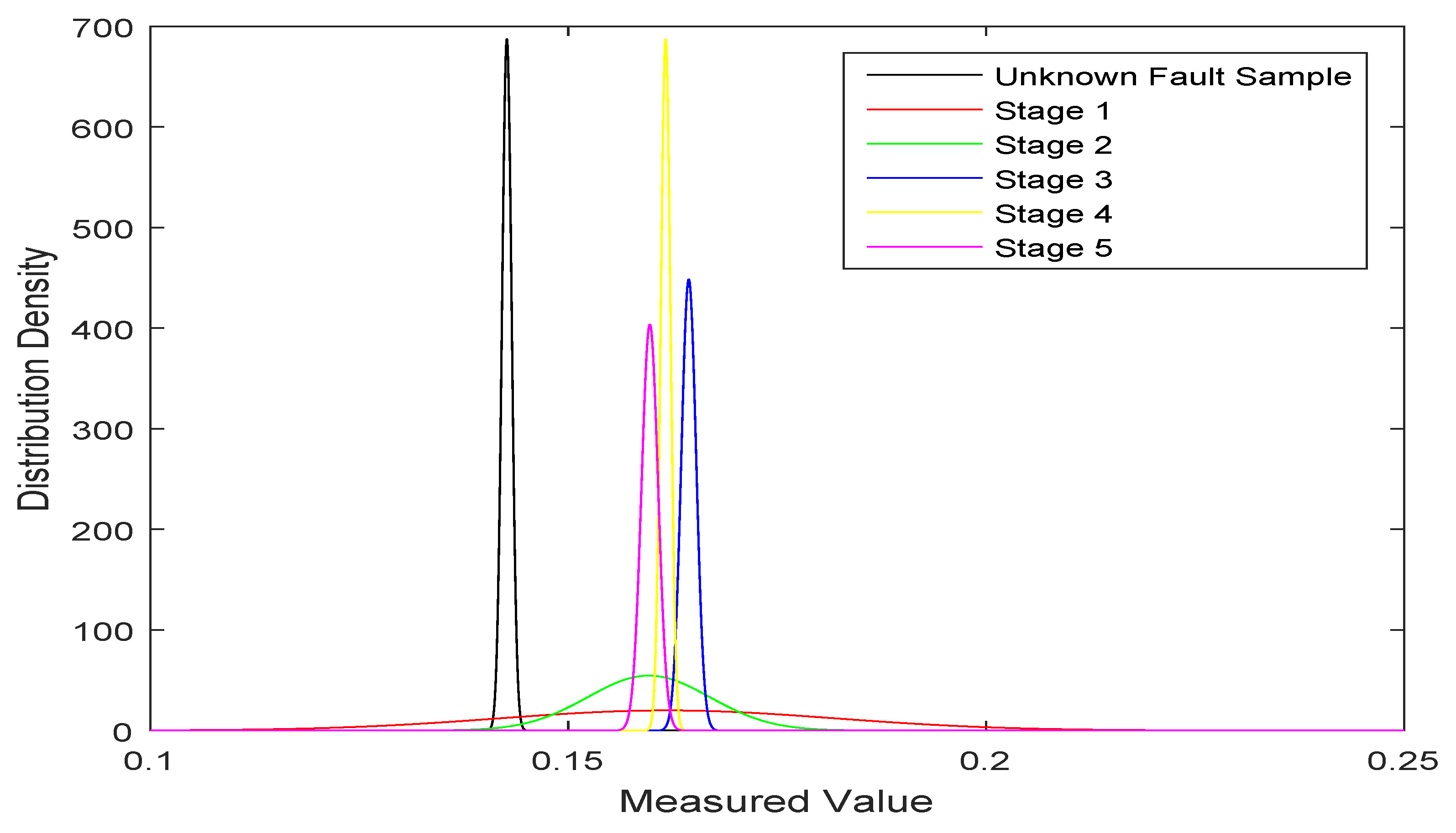
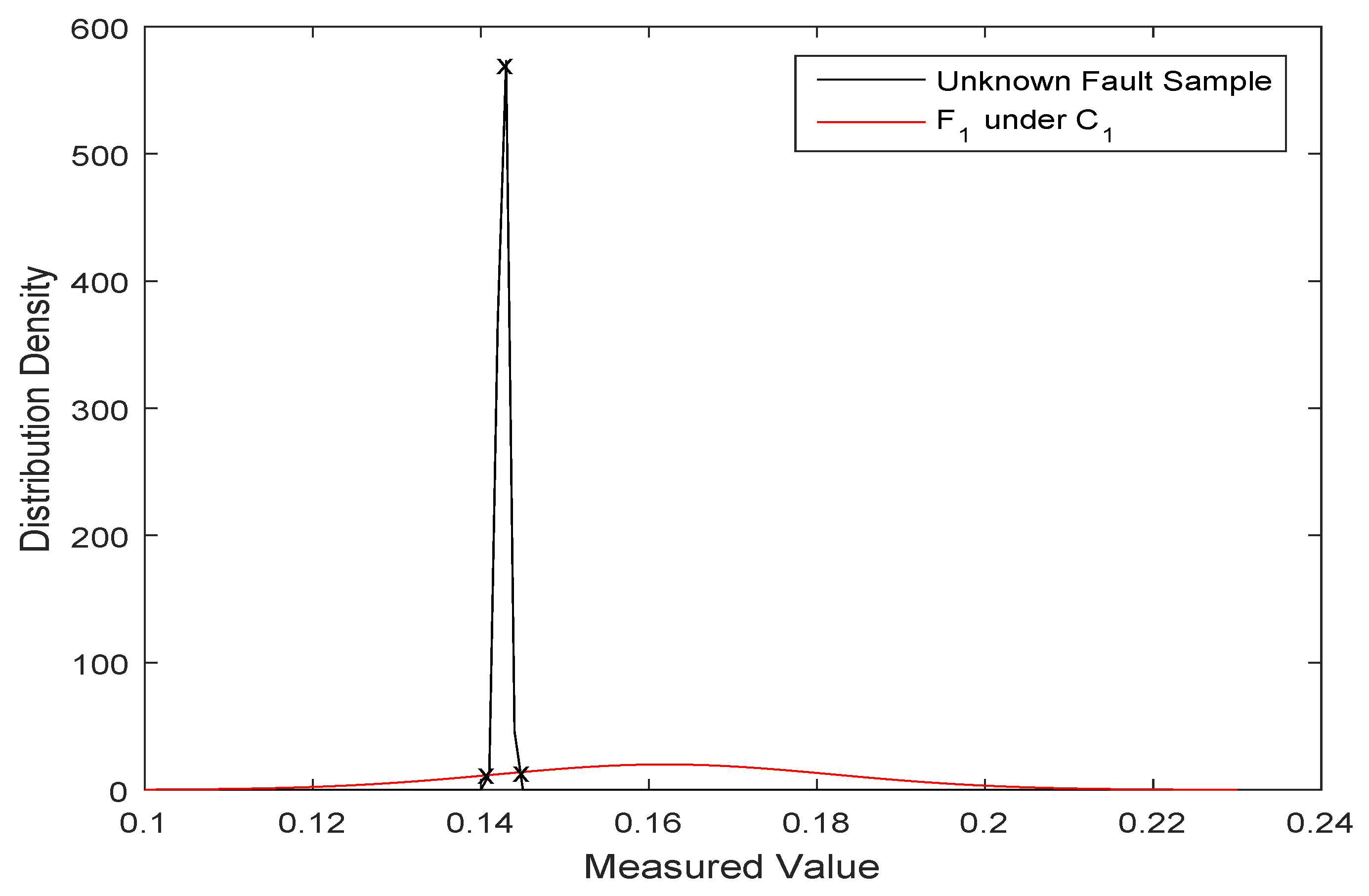
- Generate the SNS for the unknown fault sample based on the multi-stage data from each fault type under each feature. Each stage’s data collected is used to establish the normal distribution model. The generated normal distributions of fault types and the unknown fault sample are listed in Table 2. For instance, the normal distribution of data and with five stages of data is shown in Figure 4. As the figure shows, each stage’s data collected drift to a certain extent in a certain range. In particular, there were distinct differences between the fault types collected in each stage and the data of unknown fault samples. Therefore, it is significant to collect data in multiple stages and to use its integration with the neutrosophic set to deal with the uncertainty of fault information.Then, are calculated with Equations (6) and (7). For instance, the distribution of was , the normal distribution of ’s first stage of data was , and the membership degree of SNN generated from the two distributions is shown in Figure 5. As the figure shows, the intersection points of distribution between the unknown fault sample () and ’s first stage data are marked with X, and the peak point of ’s distribution is marked with X in the same way. Then, from the Equations (6) and (7), the SNN was generated and denoted as . The generated SNSs are listed in Table 3.
- Step 3
- Aggregate the generated SNSs based on each fault type under each feature. Fuse the five stages of SNNs for each fault type under each feature with the SNWA operator, Equation (5). It is assumed that the weights (w) of the five SNNs are . For example, the SNNs based on the fault type under feature could be fused as follows:The others are shown in Table 4.
- Step 4
- Aggregate the fused SNSs based on all features of each fault type. Fusing the SNNs is based on the four features of each fault type by the SNWA operator, Equation (5). In addition, it is supposed the weights (w) of the four SNNs are . For example, the SNNs based on fault type could be fused as follows:The others are shown in Table 5.
- Step 5
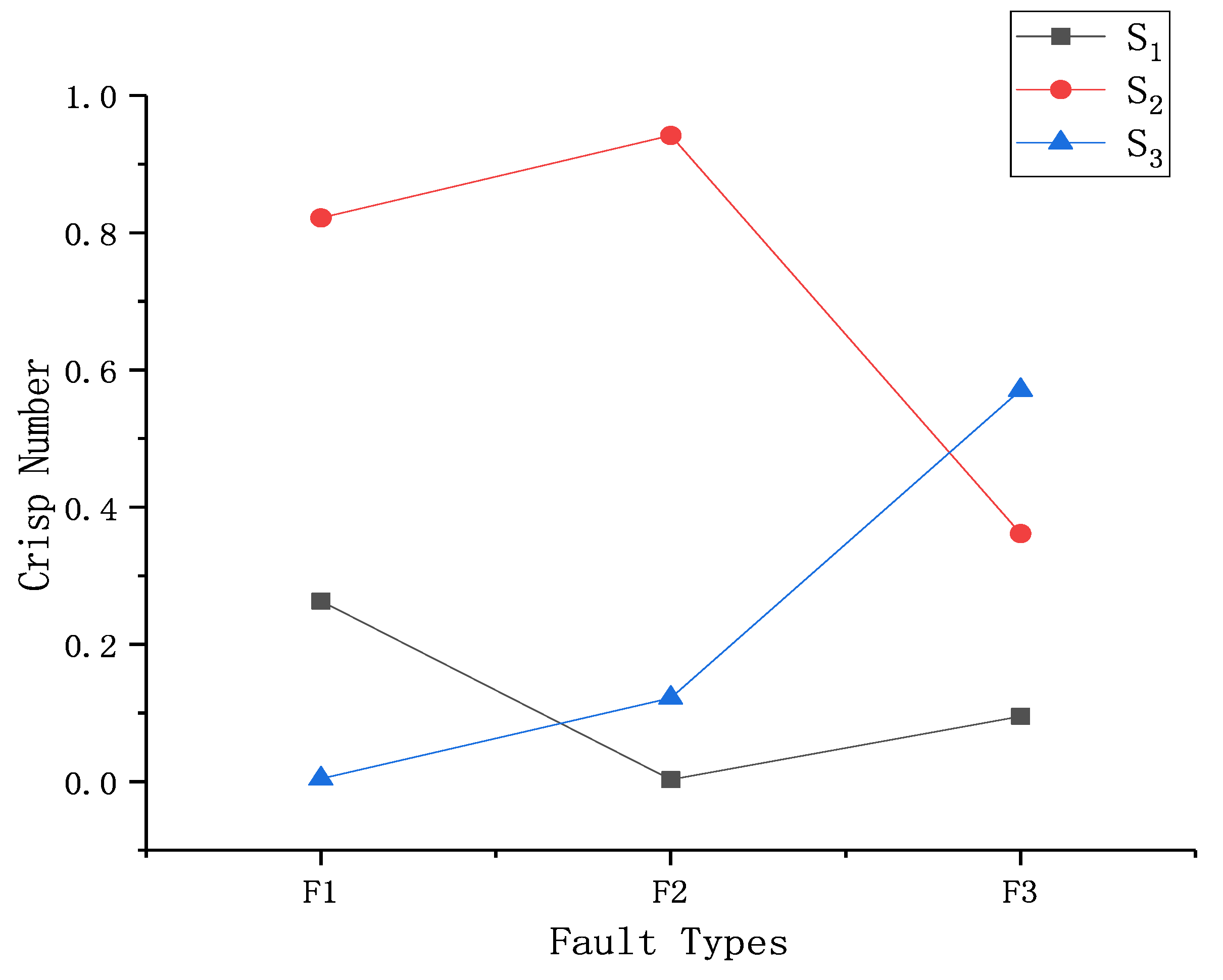
- Determine the fault type of the unknown fault sample. Finally, Table 5 can be regarded as an SNN fault diagnosis matrix which can be used to rank the three fault types via the defuzzification method (Equation (10)). The descendant ranks of the crisp numbers of the three fault types are shown in Table 6.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Caliskan, F.; Zhang, Y.; Wu, N.E.; Shin, J.Y. Actuator fault diagnosis in a Boeing 747 model via adaptive modified two-stage Kalman filter. Int. J. Aerosp. Eng. 2014, 2014, 1–10. [Google Scholar] [CrossRef]
- Zieja, M.; Golda, P.; Zokowski, M.; Majewski, P. Vibroacoustic technique for the fault diagnosis in a gear transmission of a military helicopter. J. Vibroeng. 2017, 19, 1039–1049. [Google Scholar] [CrossRef]
- Strydom, J.J.; Miskin, J.J.; McCoy, J.T.; Auret, L.; Dorfling, C. Fault diagnosis and economic performance evaluation for a simulated base metal leaching operation. Miner. Eng. 2018, 123, 128–143. [Google Scholar] [CrossRef]
- Gong, X.; Qiao, W. Bearing fault diagnosis for direct-drive wind turbines via current-demodulated signals. IEEE Trans. Ind. Electron. 2013, 60, 3419–3428. [Google Scholar] [CrossRef]
- Zhang, C.; Li, D.; Broumi, S.; Sangaiah, A.K. Medical diagnosis based on single-valued neutrosophic probabilistic rough multisets over two universes. Symmetry 2018, 10, 213. [Google Scholar] [CrossRef]
- Oliveira, C.C.; Da Silva, J.M. Fault diagnosis in highly dependable medical wearable systems. J. Electron. Test. 2016, 32, 467–479. [Google Scholar] [CrossRef]
- Glowacz, A.; Glowacz, Z. Diagnosis of stator faults of the single-phase induction motor using acoustic signals. Appl. Acoust. 2016, 117, 20–27. [Google Scholar] [CrossRef]
- Gai, J.; Hu, Y. Research on Fault Diagnosis Based on Singular Value Decomposition and Fuzzy Neural Network. Shock Vib. 2018, 2018, 1–7. [Google Scholar] [CrossRef]
- Deng, X.; Xiao, F.; Deng, Y. An improved distance-based total uncertainty measure in belief function theory. Appl. Intell. 2017, 46, 898–915. [Google Scholar] [CrossRef]
- Deng, X.; Jiang, W. Dependence assessment in human reliability analysis using an evidential network approach extended by belief rules and uncertainty measures. Ann. Nucl. Energy 2018, 117, 183–193. [Google Scholar] [CrossRef]
- Deng, X. Analyzing the monotonicity of belief interval based uncertainty measures in belief function theory. Int. J. Intell. Syst. 2018, 33, 1869–1879. [Google Scholar] [CrossRef]
- Xu, S.; Jiang, W.; Deng, X.; Shou, Y. A modified Physarum-inspired model for the user equilibrium traffic assignment problem. Appl. Math. Model. 2018, 55, 340–353. [Google Scholar] [CrossRef]
- Xiao, F. Multi-sensor data fusion based on the belief divergence measure of evidences and the belief entropy. Inf. Fusion 2019, 46, 23–32. [Google Scholar] [CrossRef]
- Tay, F.E.; Shen, L. Fault diagnosis based on rough set theory. Eng. Appl. Artif. Intell. 2003, 16, 39–43. [Google Scholar] [CrossRef]
- Yao, X.; Li, S.; Hu, J. Improving rolling bearing fault diagnosis by DS evidence theory based fusion model. J. Sens. 2017, 2017, 1–14. [Google Scholar] [CrossRef]
- Bian, T.; Zheng, H.; Yin, L.; Deng, Y. Failure mode and effects analysis based on Dnumbers and TOPSIS. Qual. Reliab. Eng. Int. 2018, 34, 501–515. [Google Scholar] [CrossRef]
- Dromigny, A.; Zhu, Y.M. Improving the dynamic range of real-time X-ray imaging systems via Bayesian fusion. J. Nondestruct. Eval. 1997, 16, 147–160. [Google Scholar] [CrossRef]
- Rodrigues, M.A.; Liu, Y.; Bottaci, L.; Rigas, D.I. Learning and diagnosis in manufacturing processes through an executable Bayesian network. In Proceedings of the International Conference on Industrial, Engineering and Other Applications of Applied Intelligent Systems, New Orleans, LA, USA, 19–22 June 2000; pp. 390–396. [Google Scholar]
- Lucas, P.J. Bayesian model-based diagnosis. Int. J. Approx. Reason. 2001, 27, 99–119. [Google Scholar] [CrossRef]
- Basir, O.; Yuan, X. Engine fault diagnosis based on multi-sensor information fusion using Dempster–Shafer evidence theory. Inf. Fusion 2007, 8, 379–386. [Google Scholar] [CrossRef]
- Dempster, A.P. Upper and lower probabilities induced by a multivalued mapping. Ann. Math. Stat. 1967, 38, 325–339. [Google Scholar] [CrossRef]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976. [Google Scholar]
- Jiang, W.; Chang, Y.; Wang, S. A method to identify the incomplete framework of discernment in evidence theory. Math. Probl. Eng. 2017, 2017. [Google Scholar] [CrossRef]
- Jiang, W.; Hu, W. An improved soft likelihood function for Dempster-Shafer belief structures. Int. J. Intell. Syst. 2018, 33, 1264–1282. [Google Scholar] [CrossRef]
- Kaftandjian, V.; Dupuis, O.; Babot, D.; Zhu, Y. Uncertainty modelling using Dempster–Shafer theory for improving detection of weld defects. Pattern Recognit. Lett. 2003, 24, 547–564. [Google Scholar] [CrossRef]
- Glowacz, A. Acoustic based fault diagnosis of three-phase induction motor. Appl. Acoust. 2018, 137, 82–89. [Google Scholar] [CrossRef]
- Glowacz, A.; Glowacz, W.; Glowacz, Z.; Kozik, J. Early fault diagnosis of bearing and stator faults of the single-phase induction motor using acoustic signals. Measurement 2018, 113, 1–9. [Google Scholar] [CrossRef]
- Jozwik, J.; Wac-Wlodarczyk, A.; Michalowska, J.; Kloczko, M. Monitoring of the noise emitted by machine tools in industrial conditions. J. Ecol. Eng. 2018, 19, 83–93. [Google Scholar] [CrossRef]
- Lee, L.; Cheng, Y.; Xie, L.; Jiang, L.; Ma, N.; Lu, M. An integrated method of set pair analysis and association rule for fault diagnosis of power transformers. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 2368–2378. [Google Scholar]
- He, S.; Xiao, L.; Wang, Y.; Liu, X.; Yang, C.; Lu, J.; Gui, W.; Sun, Y. A novel fault diagnosis method based on optimal relevance vector machine. Neurocomputing 2017, 267, 651–663. [Google Scholar] [CrossRef]
- Xi, W.; Li, Z.; Tian, Z.; Duan, Z. A feature extraction and visualization method for fault detection of marine diesel engines. Meas. J. Int. Meas. Confed. 2017, 116, 429–437. [Google Scholar] [CrossRef]
- Krolczyk, G.M.; Krolczyk, J.B.; Legutko, S.; Hunjet, A. Effect of the disc processing technology on the vibration level of the chipper during operations. Teh. Vjesn. 2014, 21, 447–450. [Google Scholar]
- Merizalde, Y.; Hernandez-Callejo, L.; Duque-Perez, O. State of the art and trends in the monitoring, detection and diagnosis of failures in electric induction motors. Energies 2017, 10, 1056. [Google Scholar] [CrossRef]
- Smarandache, F. A unifying field in logics: Neutrosophic logic. Mult. Valued Logic 1999, 8, 489–503. [Google Scholar]
- Ali, M.; Smarandache, F. Complex neutrosophic set. Neural Comput. Appl. 2017, 28, 1817–1834. [Google Scholar] [CrossRef]
- Zhang, X.; Bo, C.; Smarandache, F.; Park, C. New operations of totally dependent-neutrosophic sets and totally dependent-neutrosophic soft sets. Symmetry 2018, 10, 187. [Google Scholar] [CrossRef]
- Ali, M.; Smarandache, F.; Khan, M. Study on the development of neutrosophic triplet ting and neutrosophic triplet field. Mathematics 2017, 6, 46. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X.; Park, C. Generalized interval neutrosophic choquet aggregation operators and their applications. Symmetry 2018, 10, 85. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Jiang, W.; Wei, B.; Liu, X.; Li, X.; Zheng, H. Intuitionistic fuzzy power aggregation operator based on entropy and its application in decision making. Int. J. Intell. Syst. 2018, 33, 49–67. [Google Scholar] [CrossRef]
- Turksen, I.B. Interval valued fuzzy sets based on normal forms. Fuzzy Sets Syst. 1986, 20, 191–210. [Google Scholar] [CrossRef]
- Wang, H.; Smarandache, F.; Zhang, Y.; Sunderraman, R. Single valued neutrosophic sets. In Proceedings of the 8th Joint Conference on Information Sciences, Salt Lake, UT, USA, 21–26 July 2005; pp. 94–97. [Google Scholar]
- Ye, J. A multicriteria decision-making method using aggregation operators for simplified neutrosophic sets. J. Intell. Fuzzy Syst. 2014, 26, 2459–2466. [Google Scholar]
- Liu, P.; Wang, Y. Multiple attribute decision-making method based on single-valued neutrosophic normalized weighted Bonferroni mean. Neural Comput. Appl. 2014, 25, 2001–2010. [Google Scholar] [CrossRef]
- Peng, J.; Wang, J.; Wang, J.; Zhang, H.; Chen, X. Simplified neutrosophic sets and their applications in multi-criteria group decision-making problems. Int. J. Syst. Sci. 2016, 47, 2342–2358. [Google Scholar] [CrossRef]
- Ye, J. Single-valued neutrosophic similarity measures based on cotangent function and their application in the fault diagnosis of steam turbine. Soft Comput. 2017, 21, 817–825. [Google Scholar] [CrossRef]
- Ye, J. Fault diagnoses of hydraulic turbine using the dimension root similarity measure of single-valued neutrosophic sets. Intell. Autom. Soft Comput. 2016, 1–8. [Google Scholar] [CrossRef]
- Kong, L.; Wu, Y.; Ye, J. Misfire fault diagnosis method of gasoline engines using the cosine similarity measure of neutrosophic numbers. Neutrosophic Sets Syst. 2015, 8, 42–45. [Google Scholar]
- Zhang, C.; Zhai, Y.; Li, D.; Mu, Y. Steam turbine fault diagnosis based on single-valued neutrosophic multigranulation rough sets over two universes. J. Intell. Fuzzy Syst. 2016, 31, 2829–2837. [Google Scholar] [CrossRef]
- Jiang, W.; Xie, C.; Zhuang, M.; Tang, Y. Failure Mode and Effects Analysis based on a novel fuzzy evidential method. Appl. Soft Comput. 2017, 57, 672–683. [Google Scholar] [CrossRef]
- He, Z.; Jiang, W. An evidential dynamical model to predict the interference effect of categorization on decision making. Knowl. Based Syst. 2018, 150, 139–149. [Google Scholar] [CrossRef]
- Zheng, X.; Deng, Y. Dependence Assessment in Human Reliability Analysis Based on Evidence Credibility Decay Model and IOWA Operator. Ann. Nucl. Energy 2018, 112, 673–684. [Google Scholar] [CrossRef]
- Xu, X.; Zhou, Z.; Wen, C. Data fusion algorithm of fault diagnosis considering sensor measurement uncertainty. Int. J. Smart Sens. Intell. Syst 2013, 6, 171–190. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. ACM SIGMOBILE Mob. Comput. Commun. Rev. 2001, 5, 3–55. [Google Scholar] [CrossRef]
- Boran, F.E.; Genç, S.; Kurt, M.; Akay, D. A multi-criteria intuitionistic fuzzy group decision making for supplier selection with TOPSIS method. Expert Syst. Appl. 2009, 36, 11363–11368. [Google Scholar] [CrossRef]
- Xu, X.; Wen, C. Theory and Application of Multi-Source and Uncertain Information Fusion; Science Press: Beijing, China, 2012; pp. 98–108. [Google Scholar]
| Fault Type | Stage | Feature | |||
|---|---|---|---|---|---|
| ⋯ | |||||
| 1 | ⋯ | ||||
| 2 | ⋯ | ||||
| ⋮ | ⋮ | ⋮ | ⋱ | ⋮ | |
| k | ⋯ | ||||
| 1 | ⋯ | ||||
| 2 | ⋯ | ||||
| ⋮ | ⋮ | ⋮ | ⋱ | ⋮ | |
| k | ⋯ | ||||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋱ | ⋮ |
| 1 | ⋯ | ||||
| 2 | ⋯ | ||||
| ⋮ | ⋮ | ⋮ | ⋱ | ⋮ | |
| k | ⋯ | ||||
| Fault Type | Stage | Feature | |||
|---|---|---|---|---|---|
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| 1 | |||||
| Fault Type | Stage | Feature | |||
|---|---|---|---|---|---|
| 1 | (0.0197, 0.0969, 0.9803) | (0.7400, 0.5731, 0.2600) | (0.0973, 0.3191, 0.9027) | (0.0841, 0.2888, 0.9159) | |
| 2 | (0.0092, 0.0521, 0.9908) | (0.6576, 0.6426, 0.3424) | (0.0000, 0.0000, 1.0000) | (0.0000, 0.0000, 1.0000) | |
| 3 | (0.0000, 0.0000, 1.0000) | (0.6382, 0.6545, 0.3618) | (0.0000, 0.0000, 1.0000) | (0.0388, 0.1641, 0.9612) | |
| 4 | (0.0000, 0.0000, 1.0000) | (0.8108, 0.4851, 0.1892) | (0.0000, 0.0000, 1.0000) | (0.0001, 0.0006, 0.9999) | |
| 5 | (0.0000, 0.0000, 1.0000) | (0.7177, 0.5951, 0.2823) | (0.0004, 0.0032, 0.9996) | (0.0003, 0.0026, 0.9997) | |
| 1 | (0.0021, 0.0152, 0.9979) | (0.0000, 0.0000, 1.0000) | (0.0000, 0.0000, 1.0000) | (0.0000, 0.0000, 1.0000) | |
| 2 | (0.0000, 0.0000, 1.0000) | (0.0000, 0.0000, 1.0000) | (0.0000, 0.0000, 1.0000) | (0.0010, 0.0082, 0.9990) | |
| 3 | (0.0001, 0.0010, 0.9999) | (0.0000, 0.0000, 1.0000) | (0.0038, 0.0249, 0.9962) | (0.0486, 0.1944, 0.9514) | |
| 4 | (0.0000, 0.0000, 1.0000) | (0.0000, 0.0000, 1.0000) | (0.0000, 0.0000, 1.0000) | (0.0164, 0.0836, 0.9836) | |
| 5 | (0.0000, 0.0000, 1.0000) | (0.0000, 0.0000, 1.0000) | (0.0000, 0.0000, 1.0000) | (0.0000, 0.0000, 1.0000) | |
| 1 | (0.0000, 0.0000, 1.0000) | (0.0001, 0.0008, 0.9999) | (0.1118, 0.3502, 0.8882) | (0.0000, 0.0000, 1.0000) | |
| 2 | (0.0000, 0.0000, 1.0000) | (0.0000, 0.0000, 1.0000) | (0.2525, 0.5650, 0.7475) | (0.0000, 0.0000, 1.0000) | |
| 3 | (0.0000, 0.0000, 1.0000) | (0.0000, 0.0000, 1.0000) | (0.1847, 0.4785, 0.8153) | (0.0000, 0.0000, 1.0000) | |
| 4 | (0.0000, 0.0000, 1.0000) | (0.0000, 0.0000, 1.0000) | (0.3815, 0.6648, 0.6185) | (0.0000, 0.0000, 1.0000) | |
| 5 | (0.0000, 0.0000, 1.0000) | (0.0000, 0.0000, 1.0000) | (0.4364, 0.6850, 0.5636) | (0.0000, 0.0000, 1.0000) | |
| Fault Type | ||||
|---|---|---|---|---|
| (0.0058, 0.0000, 0.9942) | (0.7200, 0.5868, 0.2800) | (0.0203, 0.0000, 0.9797) | (0.0252, 0.0008, 0.9748) | |
| (0.0004, 0.0000, 0.9996) | (0.0000, 0.0000, 1.0000) | (0.0008, 0.0000, 0.9992) | (0.0134, 0.0038, 0.9866) | |
| (0.0000, 0.0000, 1.0000) | (0.0000, 0.0000, 1.0000) | (0.2836, 0.5332, 0.7164) | (0.0000, 0.0000, 1.0000) |
| Fault Type | SNS |
|---|---|
| (0.2633, 0.0000, 0.7367) | |
| (0.0030, 0.0000, 0.9970) | |
| (0.0952, 0.0000, 0.9048) |
| Fault Type | Crisp Number | Rank |
|---|---|---|
| 0.263335 | 1 | |
| 0.003040 | 3 | |
| 0.095221 | 2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, W.; Zhong, Y.; Deng, X. A Neutrosophic Set Based Fault Diagnosis Method Based on Multi-Stage Fault Template Data. Symmetry 2018, 10, 346. https://doi.org/10.3390/sym10080346
Jiang W, Zhong Y, Deng X. A Neutrosophic Set Based Fault Diagnosis Method Based on Multi-Stage Fault Template Data. Symmetry. 2018; 10(8):346. https://doi.org/10.3390/sym10080346
Chicago/Turabian StyleJiang, Wen, Yu Zhong, and Xinyang Deng. 2018. "A Neutrosophic Set Based Fault Diagnosis Method Based on Multi-Stage Fault Template Data" Symmetry 10, no. 8: 346. https://doi.org/10.3390/sym10080346
APA StyleJiang, W., Zhong, Y., & Deng, X. (2018). A Neutrosophic Set Based Fault Diagnosis Method Based on Multi-Stage Fault Template Data. Symmetry, 10(8), 346. https://doi.org/10.3390/sym10080346