Abstract
In this paper, we discuss some relations between the semigroup, , of all groupoids and graphs. We discuss mimimum (mutual) covering sets in several groupoids and discuss distances of graphs with groupoids. Finally, we obtain some results on frame graphs with groupoids.
1. Introduction
J. Neggers [1] defined the notion of a pogroupoid, obtained a functorial connection between pogroupoids and posets and associated structure mappings. J. Neggers and H. S. Kim [2] proved that a pogroupoid is modular if and only if its associated poset is -free . Given a pogroupoid , the relation, , is transitive for any fuzzy subset, , of X if and only if the associated poset, , of is -free [3]. In a sequence of papers, Nebeský [4,5,6] discussed various properties of a graph with its associated groupoid . Although it is not identical in terms of outlook, there are some similarities between Nebeský’s work and results which are discussed in this paper.
As we note below, our point of view permits us to consider arbitrary (simple) graphs as particular groupoids. By using this model, it is possible to assign to groupoids of a particular (locally zero) type to certain simple graphs as well. Using the viewpoint developed, we can then assign the theoretical parameters of graphs to groupoids in a meaningful way. How this is done is the topic of what follows. We concentrate on two such parameters: “covering” and “shortest distance”. It is clear that a great deal more work remains to be done and can be done in a straightforward manner.
2. Preliminaries
A non-empty set, X, with a constant 0 and a binary operation , satisfying the following axioms, (i) , (ii) , and (iii) , where implies for all is said to be a d-algebra [7]. For general references on d-algebras, we refer to [8,9,10,11].
A d-algebra is said to be a -algebra [12] if it satisfies the following additional axioms:
- (iv)
- ,
- (v)
- for all .
Example 1.
Let be a set with the following table [11]: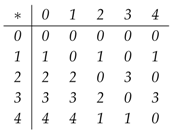 Then, is a d-algebra which is not a -algebra.
Then, is a d-algebra which is not a -algebra.
 Then, is a d-algebra which is not a -algebra.
Then, is a d-algebra which is not a -algebra.For general references on -algebras, we refer to references [12,13,14]. Given a non-empty set, X, we denote the collection of all groupoids , where is a map, by . Given elements and of , define a product “□" on these groupoids as follows:
where
for any . Using that notion, H. S. Kim and J. Neggers proved the following theorem.
Theorem 1.
[15] is a semigroup, i.e., the operation “□", as defined in general, is associative. Furthermore, the left- zero-semigroup for which for all is the identity for this operation.
Another element with interesting properties in is the right-zero-semigroup, i.e., the groupoid for which for all . Fayoumi [16] is not referred in main text, please check. showed that a groupoid commutes relative to the operation, □, of if and only if any two element subset of is a subgroupoid which is either a left-zero-semigroup or a right-zero-semigroup. Thus, is an element of the center, , of if and only if for any pair of elements or . Therefore, among these groupoids, the left-zero-semigroup on X and the right-zero-semigroup on X are extreme cases. Furthermore, it is easily seen that is itself a semigroup with identity—a subsemigroup of the semigroup .
3. Graphs and Binary Systems
Let be an element of . Suppose, in addition, that we construct a graph, , as follows: and —the edge set of provided that . Thus, if , then as well, and we identify as an undirected edge of . Similarly, since is an element of , if , then and determines the absence of an edge, directed or otherwise. Since in any case, we do not consider this to be of particular graphical interest. The mapping accomplishes the following:
Theorem 2.
If is a simple graph with vertex set and edge set , then G determines a unique groupoid, , in the center of the semigroup by defining the binary operation “*" as if and if .
Theorem 3.
If is a simple graph and is defined as in Theorem 2, then and , so that .
Proof.
The proofs of both theorems are straightforward. ☐
Proposition 1.
If is the left-zero-semigroup, then is the complete graph on X. If , then .
Proof.
From the definition, it is clear that if , then , so that , and the conclusion follows. ☐
Proposition 2.
If is the right-zero-semigroup, then is the null(empty) graph on X, i.e., , while .
Proof.
From the definition, it is clear that if , then , so that , i.e., and the conclusion follows. ☐
To illustrate the close relationship between simple graphs and groupoids, we note the following.
Theorem 4.
If is a simple graph and is the groupoid associated with G, then for the right-zero-semigroup defined on X, defines as the complementary graph of G.
Proof.
Suppose that . Then, . Hence, and . Thus, . Similarly, if , then , so that is the opposite groupoid of , with , while is the complementary graph of G, with if and only if . ☐
Example 2.
The operation “□" on induces an operation “□" on the graphs with vertex set X as well as edges illustrated in the proof of Theorem 4. Let and consider two simple graphs on vertex set X. Then, we have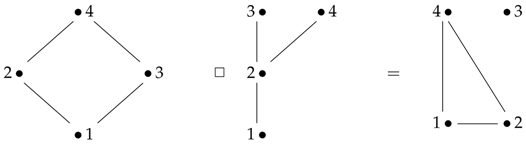 Based on the fact that is a semigroup, it follows that this product is associative as well. For groupoids, we have tables and a resultant (product) table:
Based on the fact that is a semigroup, it follows that this product is associative as well. For groupoids, we have tables and a resultant (product) table: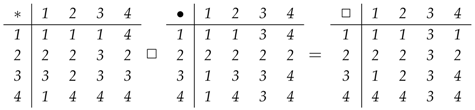 Hence, by reconstructing the graph, , we obtain
Hence, by reconstructing the graph, , we obtain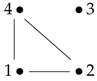 as pictured.
as pictured.
 Based on the fact that is a semigroup, it follows that this product is associative as well. For groupoids, we have tables and a resultant (product) table:
Based on the fact that is a semigroup, it follows that this product is associative as well. For groupoids, we have tables and a resultant (product) table: Hence, by reconstructing the graph, , we obtain
Hence, by reconstructing the graph, , we obtain as pictured.
as pictured.4. Graphs with Groupoids
If is a simple graph, then the covering number, is the cardinal number of a minimal covering set which is the smallest among these cardinal numbers. A covering set is a set of vertices such that any vertex not in the set is connected to an element in the set via an edge. A covering set is minimal if no vertex can be deleted from the set and still maintain the property of being a covering set. Thus, e.g., , since for any n-graph containing a , i.e., a star or a complete bipartite graph partitioned into two classes containing 1 and elements respectively. The number is an example of a graph parameter which can be directly taken over by groupoids. Indeed, we shall consider an element, x, of a groupoid to cover an element, y, of a groupoid if and mutually y covers x if as well. In the setting of graphs with the constructions made above, it follows that if is a simple graph, then if , it follows that as well whenever . Thus, for simple graphs, the two notions are equivalent. However, in the context of groupoids, they are not the same.
Example 3.
Suppose that is a poset with a minimal element of 0. The standard -algebra for this poset is defined by setting if and otherwise. Now and for all , and thus, 0 mutually covers every element x of X. On the other hand, if and , then if and x covers y. If , then , and x and y mutually cover each other. Thus, we may consider the Hasse diagram of the poset in terms of this relationship, for example, the poset 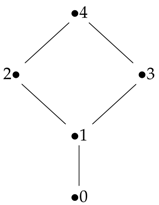 has a standard -algebra table, as follows:
has a standard -algebra table, as follows: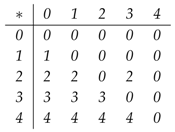 In terms of the covering relation, we obtain
while the mutual covering relation yields
In terms of the covering relation, we obtain
while the mutual covering relation yields
 has a standard -algebra table, as follows:
has a standard -algebra table, as follows: In terms of the covering relation, we obtain
In terms of the covering relation, we obtainFollowing the analogy pathway, it is clear that in this case, if is the cardinal of a minimum covering set (i.e., a minimal covering set of the smallest cardinal number), then . If is the cardinal number of a minimum mutual covering set, then as well.
Proposition 3.
If is a groupoid for which a mutual covering set exists, then
Proof.
Suppose that is a mutual covering set for . Then, S is also a covering set for . Hence, if S is a minimum mutual covering set for , then it is a covering set for , and hence, it has a cardinal at least as large as . ☐
Example 4.
If is a left-zero-semigroup, then and implies that elements x and y mutually cover each other. Thus, any singleton is a minimal mutual covering set, and , so that as well.
Proposition 4.
If is a -algebra, then .
Proof.
This follows from the fact that for all . Hence, is a mutual covering set. ☐
Proposition 5.
If is a d-algebra, then .
Proof.
This follows on from the fact that for all .
Example 5.
Let K be a field and let for all . Then, is a d-algebra. Since for all , is a minimal covering set, and thus, . Let in K. Then, , and thus, is not a mutual covering set. If is a covering set, then for all . It follows that for all —a contradiction. Hence, is the only minimal covering set of .
Proposition 6.
If is a simple graph and is the associated groupoid. Then, , the covering number of G.
Example 6.
Given a simple graph, as shown below, we see that covers .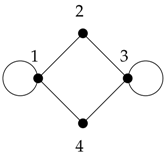 Since 1 does not cover 3, it follows that . Since both 2 and 4 cover 1 and 3, is a mutual covering set which is minimal, i.e., .
Since 1 does not cover 3, it follows that . Since both 2 and 4 cover 1 and 3, is a mutual covering set which is minimal, i.e., .
 Since 1 does not cover 3, it follows that . Since both 2 and 4 cover 1 and 3, is a mutual covering set which is minimal, i.e., .
Since 1 does not cover 3, it follows that . Since both 2 and 4 cover 1 and 3, is a mutual covering set which is minimal, i.e., .Proposition 7.
If is a group, then , the cardinal of X.
Proof.
If , then . Hence, it follows that the smallest covering set of is . Now, if and , then . Hence is not a mutual covering set, i.e., the smallest mutual covering set is X itself, i.e., , as claimed.
Proposition 8.
Let be a groupoid with . The defined set is a minimum mutual covering set, }. Then, is a subsemigroup of the groupoid and a left-zero-semigroup.
Proof.
Suppose . Then, , since . It follows that is a left-zero-semigroup, as claimed, and as such, it is a subsemigroup of . ☐
Corollary 1.
If is a -algebra, then .
Proof.
This follows immediately from Propositions 4 and 8. ☐
5. Distances of Graphs with Groupoids
Given a groupoid we consider the shortest distance, , to be , if, for , we have , where , and there is no set with fewer elements having this property. The mutual shortest distance, , is for elements , if, for , we have , and there is no set with fewer elements having this property. We set for any .
Proposition 9.
If is a -algebra, then for all .
Proof.
If , then , and thus, . ☐
Example 7.
If is a poset with a standard -algebra , then implies , and thus, , since . If , then and , so that in that situation as well.
Proposition 10.
If is any groupoid for which the (mutual) shortest distance exists for all , then
- (i)
- ,
- (ii)
- ,
- (iii)
- ,
- (iv)
- .
Proof.
This follows immediately from the definition. ☐
Given a groupoid and , the cycle number is the sum if , and exists. Since, , the mutual cycle number, . is simply .
Proposition 11.
If is any groupoid with the property that and if exists and is finite, then .
Proof.
Suppose , with intermediate elements . Then, so that could serve as a set of intermediate elements for and z. The proposition follows.
Given a poset , it is said to be strongly connected if for all . It is said to be strongly mutually connected if for all . In Proposition 10(i), , so strongly mutually connected groupoids are also strongly connected.
Proposition 12.
If is a commutative (abelian) groupoid, i.e., for all , then implies . Hence, if , then .
Proof.
If and is a set of intermediate elements for , then implies , and by continuation, —a contradiction. It follows that . ☐
Example 8.
Let be the digraph with diagram . Then, the associated groupoid has the following Cayley table: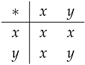 . It follows that is commutative, and . If , then has the Cayley table
. It follows that is commutative, and . If , then has the Cayley table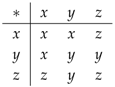 so that is a commutative groupoid. We have , so that is strongly connected, but not strongly mutually connected.
so that is a commutative groupoid. We have , so that is strongly connected, but not strongly mutually connected.
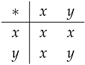 . It follows that is commutative, and . If , then has the Cayley table
. It follows that is commutative, and . If , then has the Cayley table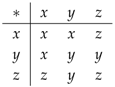 so that is a commutative groupoid. We have , so that is strongly connected, but not strongly mutually connected.
so that is a commutative groupoid. We have , so that is strongly connected, but not strongly mutually connected.Proposition 13.
Let be a groupoid such that implies and exists. Then, .
Proof.
Suppose that and is a set of intermediate elements. Then, implies which implies which implies . Hence, is also a set of intermediate elements for , i.e., . From Proposition 10(i), , and thus, . ☐
We consider the groupoids of Proposition 13 to be undirected groupoids.
Proposition 14.
If is an (undirected) simple graph, then the associated groupoid is an undirected groupoid.
Proof.
This follows from the definition. ☐
Example 9.
Consider the groupoid with and Cayley table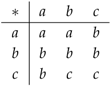 . Then, , and is an undirected groupoid, since implies . However, it does not correspond to a simple graph. If we compute , we obtain an undirected graph as follows:
. Then, , and is an undirected groupoid, since implies . However, it does not correspond to a simple graph. If we compute , we obtain an undirected graph as follows:  . Thus, the undirected groupoid is also strongly mutually connected.
. Thus, the undirected groupoid is also strongly mutually connected.
 . Then, , and is an undirected groupoid, since implies . However, it does not correspond to a simple graph. If we compute , we obtain an undirected graph as follows:
. Then, , and is an undirected groupoid, since implies . However, it does not correspond to a simple graph. If we compute , we obtain an undirected graph as follows:  . Thus, the undirected groupoid is also strongly mutually connected.
. Thus, the undirected groupoid is also strongly mutually connected.6. Frame Graphs with Groupoids
Given a groupoid , we consider the frame of to be the collection of all pairs such that . From the frame of we may construct a simple graph, , where is a pair in the frame for some y in X}, and is a pair in the frame }. is the frame graph of , and every groupoid has a frame graph.
From the diframe of , we may construct a simple digraph, , with or belongs to the diframe of for some , and an ordered pair in the diframe }. is the diframe graph of and every groupoid has such a diframe graph. The frame graph, , is seen to be a subdigraph of the diframe graph, , in a natural way, i.e., the undirected edge, , of generates a pair of directed edges, and , in .
Given a groupoid with a frame, , a groupoid is generated, where implies if and otherwise, i.e., the groupoid is an element of , the frame groupoid of .
Example 10.
The groupoid in Example 9 has a frame  , has the Cayley table
, has the Cayley table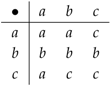 . If, for the groupoid , we consider the diframe graph, , then the associated algebraic structure is the groupoid , where if , i.e., if . Since implies as well, it follows that in such a case that and represent the edge . Hence, in this sense, the frame graph, , is a subdigraph of the diframe graph, .
. If, for the groupoid , we consider the diframe graph, , then the associated algebraic structure is the groupoid , where if , i.e., if . Since implies as well, it follows that in such a case that and represent the edge . Hence, in this sense, the frame graph, , is a subdigraph of the diframe graph, .
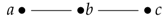 , has the Cayley table
, has the Cayley table . If, for the groupoid , we consider the diframe graph, , then the associated algebraic structure is the groupoid , where if , i.e., if . Since implies as well, it follows that in such a case that and represent the edge . Hence, in this sense, the frame graph, , is a subdigraph of the diframe graph, .
. If, for the groupoid , we consider the diframe graph, , then the associated algebraic structure is the groupoid , where if , i.e., if . Since implies as well, it follows that in such a case that and represent the edge . Hence, in this sense, the frame graph, , is a subdigraph of the diframe graph, .Example 11.
In Example 9, the condition yields as not being elements of , and thus, in , i.e., and have exactly the same Cayley table.
Example 12.
Suppose that is the groupoid with , and is the digraph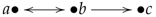 . Then, is the frame graph, . The table for can be filled in as
. Then, is the frame graph, . The table for can be filled in as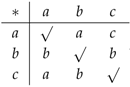 , where √ can be filled with any element of X. For the table is
, where √ can be filled with any element of X. For the table is . Also, for , the Cayley table is
. Also, for , the Cayley table is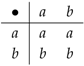 .
.
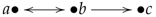 . Then, is the frame graph, . The table for can be filled in as
. Then, is the frame graph, . The table for can be filled in as , where √ can be filled with any element of X. For the table is
, where √ can be filled with any element of X. For the table is . Also, for , the Cayley table is
. Also, for , the Cayley table is .
.Example 13.
Let be a groupoid with the following general table: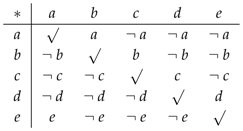 where means “not x”, i.e., anything but x in X, and √ can be filled with any element of X. Then, is the following graph:
where means “not x”, i.e., anything but x in X, and √ can be filled with any element of X. Then, is the following graph: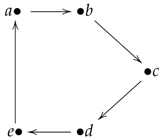 i.e., for any , . Also, has , since there is no pair with elements of .
i.e., for any , . Also, has , since there is no pair with elements of .
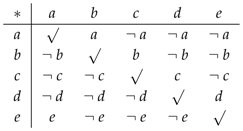 where means “not x”, i.e., anything but x in X, and √ can be filled with any element of X. Then, is the following graph:
where means “not x”, i.e., anything but x in X, and √ can be filled with any element of X. Then, is the following graph: i.e., for any , . Also, has , since there is no pair with elements of .
i.e., for any , . Also, has , since there is no pair with elements of .The groupoid has the associated table:

Example 14.
Let be a groupoid with the following general table: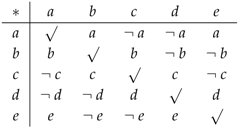 where means “not x", i.e., anything but x in X, and √ can be filled with any element of X. Then, is the simple graph:
where means “not x", i.e., anything but x in X, and √ can be filled with any element of X. Then, is the simple graph: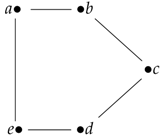 The corresponding groupoid (or ) has the following multiplication table:
The corresponding groupoid (or ) has the following multiplication table:
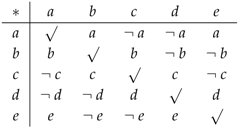 where means “not x", i.e., anything but x in X, and √ can be filled with any element of X. Then, is the simple graph:
where means “not x", i.e., anything but x in X, and √ can be filled with any element of X. Then, is the simple graph: The corresponding groupoid (or ) has the following multiplication table:
The corresponding groupoid (or ) has the following multiplication table:
The question is then how to represent the undirected cyclical nature of the groupoid in the most elegant way, such as we were able to do in Example 14.
Theorem 5.
Let be an onto homomorphism for groupoids. Define a binary operation “⇝" on X by with for any . If we define , then the graph, , is a subdigraph of .
Proof.
If is an onto homomorphism for groupoids, then implies . Thus, either or maps to from to . Furthermore, if is an arrow (directed edge) in , then if . Hence, , i.e., . Thus, if we consider the digraph to have the vertex set and edge set , then f induces a mapping by setting . The mapping is a surjection of graphs (or a graph epimorphism). Hence the graph is naturally a subdigraph of . ☐
Example 15.
Let be a mapping defined by for all . Then, , and f is a group(oid) epimorphism. Now, means , and thus, . Thus, means and for all x, while means . Hence, . The mapping given by , as a mapping of graphs maps an edge, , to an edge, , and it is an epimorphism of graphs, in fact, it is an isomorphism. Note that implies that (i.e., ), and implies and implies as well.
7. Final Considerations
From the constructions made above, we see clearly that we may now infuse the theory of with a multitude of graph theoretical notions. As a further illustration, we may consider the eccentricity, , of a vertex, x, of a groupoid as the maximum, , and if the maximum is finite, assign that number to the vertex, x. From the eccentricity function, we may now derive the concepts of radius and diameter. Incidentally we may do the same with respect to the mutual distance to obtain the mutual eccentricity function After having done so, types of groupoids can be discussed in terms of these parameters. We have a selection of possibilities:
- (1)
- Groupoids in , such that (i.e., diameter) or equivalently e is a constant;
- (2)
- Groupoids in , such that for , where A is an interesting subset of X, e.g., ;
- (3)
- Groupoids in with a small but being as large as possible;
- (4)
- Groupoids in with .
Obviously, there are many other interesting parameters of a graph’s theoretical nature which may be introduced. Hence, it may be of interest in certain applications to pursue the subject further. In the interest of producing an article which is clear but manageable in size, we have decided not to go into more detail in this paper.
Author Contributions
The authors had the same contributions to complete the paper.
Acknowledgments
The authors are deeply grateful to the referee for the valuable suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Neggers, J. Partially ordered sets and groupoids. Kyungpook Math. J. 1976, 16, 7–20. [Google Scholar]
- Neggers, J.; Kim, H.S. Modular posets and semigroups. Semigroup Forum 1996, 53, 57–62. [Google Scholar] [CrossRef]
- Kim, H.S.; Neggers, J. Fuzzy pogroupoids. Inf. Sci. 2005, 175, 108–119. [Google Scholar] [CrossRef]
- Nebeský, L. An algebraic characterization of geodetic graphs. Czechoslov. Math. J. 1998, 48, 701–710. [Google Scholar] [CrossRef]
- Nebeský, L. A tree as a finite nonempty set with a binary operation. Math. Bohem. 2000, 125, 455–458. [Google Scholar]
- Nebeský, L. Travel groupoids. Czechoslov. Math. J. 2006, 56, 659–675. [Google Scholar] [CrossRef]
- Neggers, J.; Kim, H.S. On d-algebras. Math. Slovaca 1999, 49, 19–26. [Google Scholar]
- Neggers, J.; Dvurečenskij, A.; Kim, H.S. On d-fuzzy functions in d-algebras. Found. Phys. 2000, 30, 1805–1815. [Google Scholar] [CrossRef]
- Allen, P.J.; Kim, H.S.; Neggers, J. Companion d-algebras. Math. Slovaca 2007, 57, 93–106. [Google Scholar] [CrossRef]
- Allen, P.J.; Kim, H.S.; Neggers, J. Deformations of d/BCK-algebras. Bull. Korean Math. Soc. 2011, 48, 315–324. [Google Scholar] [CrossRef]
- Neggers, J.; Jun, Y.B.; Kim, H.S. On d-ideals in d-algebras. Math. Slovaca 1999, 49, 243–251. [Google Scholar]
- Meng, J.; Jun, Y.B. BCK-Algebras; Seoul Kyung Moon Sa Co.: Seoul, Korea, 1994. [Google Scholar]
- Huang, Y. BCI-Algebra; Science Press: Bejing, China, 2006. [Google Scholar]
- Iorgulescu, A. Algebras of Logic as BCK-Algebras; Editura ASE: Bucharest, Romania, 2008. [Google Scholar]
- Kim, H.S.; Neggers, J. The semigroups of binary systems and some perspectives. Bull. Korean Math. Soc. 2008, 45, 651–661. [Google Scholar] [CrossRef]
- Fayoumi, H. Locally-zero groupoids and the center of Bin(X). Comm. Korean Math. Soc. 2011, 26, 163–168. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).