1. Introduction
Multiple criteria decision-making (MCDM) problems occur in numerous practical fields [
1,
2,
3]. For a specific purpose, several possible plans may be presented as the alternatives; then, decision makers assess the alternatives concerning the related criteria to determine the best one. Traditionally, crisp numbers are utilized to express the evaluation information. However, in real life, the data are inevitably incomplete and complex, and decision makers may be uncertain when evaluating the alternatives. To deal with the fuzziness of evaluation information, the fuzzy set (FS) [
4] was proposed to improve the information form. During the past decades, many scholars devoted themselves to the study of the fuzzy MCDM problems [
1]. Furthermore, in recent years, along with the complexity of the MCDM problems, how to improve the FS theory to deal with different specific situations has been a hot topic.
Although FS is a valid form to express the uncertain evaluation information, it cannot solve several complex situations in real life. For more effective expression of the evaluation information, many generalized forms of FS were proposed [
5,
6,
7,
8,
9,
10]. The purpose of this paper is to propose a new information form; the picture hesitant fuzzy set (PHFS) theory is put forward combined with the concepts of picture fuzzy set (PFS) [
7] and hesitant fuzzy set (HFS) [
8]. As a generalized form of FS, intuitionistic fuzzy set (IFS) [
5], PFS, and HFS, PHFS can express the uncertainty and complexity of human opinions in practice; furthermore, the positive, neutral, negative, and refusal membership degrees are represented by several possible values that are given by decision makers.
In practice, the uncertain and complex evaluation information will be inevitably given by decision makers. For example, ten business managers discuss an investment project; five suggest agreement, two present disagreement, and the other business managers choose to abstain. Obviously, FS can only indicate the membership degree of evaluation information; thus, the opinions of the 10 business managers cannot be represented by FS. For overcoming the limitation of FS, Atanassov [
5] put forward the non-membership function and developed the IFS. Then, the evaluation information in the aforementioned example can be expressed by IFS accurately. Later, the interval numbers were used to substitute the crisp numbers in IFS; then, the interval-valued intuitionistic fuzzy set (IVIFS) was developed [
6]. To convey the indeterminate information of decision makers more effectively, Ye [
9] and Liu and Yuan [
11] extended the FS to triangular and trapezoidal intuitionistic fuzzy set, respectively. However, in some particular situations, it is not convincing to represent the evaluation information combined with IFS or IVIFS. For instance, there is a vote for a specific matter, the voting opinions of voters can be divided into four types, namely, vote for, abstain, vote against, and a refusal of the voting [
12]. Therefore, Cuong [
7,
13] put forward the PFS, which is composed by the positive, neutral, negative, and refusal membership functions; thus, PFS can express the opinions of decision makers accurately in the example above. Subsequently, the correlation coefficient, distance measure, and cross-entropy measure of PFS were investigated in detail [
14,
15,
16].
On the other hand, sometimes the accurate membership degree of evaluation information is difficult to be determined, which is also another shortcoming of FS. Therefore, the HFS was developed [
17], in which the membership degrees are represented by several possible crisp numbers. Next, the interval numbers were introduced to extend the membership function of HFS and the interval-valued hesitant fuzzy set (IVHFS) theory was proposed [
18]. According to the IFS and HFS, several potential membership and non-membership functions were expressed to put forward the dual hesitant fuzzy set (DHFS) [
10]. Later, Farhadinia [
19] constructed the dual interval-valued hesitant fuzzy set (DIVHFS) combined with DHFS. Nevertheless, HFS in the existing research cannot express all types of human opinions in the aforementioned example.
According to the evaluation information of the individual decision makers, the collective evaluation information of each alternative is obtained through the information fusion. Due to the important role of aggregation tools in MCDM problems, many scholars have investigated the aggregation operators of different fuzzy information. For example, Xu and Yager [
20] developed the operations of intuitionistic fuzzy numbers (IFNs) and proposed the intuitionistic fuzzy geometric aggregation operators. Later, Xu [
21] put forward the intuitionistic fuzzy weighted averaging aggregation operators to aggregate the IFNs. Next, several interval-valued intuitionistic fuzzy aggregation operators were constructed to deal with the MCDM [
22,
23,
24]. With respect to the picture fuzzy (PF) evaluation information, Wei [
25] defined the operations of picture fuzzy numbers (PFNs) according to the study of [
21] and proposed the picture fuzzy weighted aggregation operators. In addition, several PF aggregation operators according to different operations were put forward [
12,
26]. Besides, a great time of hesitant fuzzy aggregation operators and their generalized forms were constructed [
27], and several aggregation operators under dual hesitant fuzzy and dual interval-valued hesitant fuzzy environment were developed [
28,
29,
30].
In some practical MCDM problems, the related criteria may be at different priority levels. For instance, a young couple wants to choose a toy for their child, the criteria of the toy they will consider are safety and price; obviously, the criteria safety has a higher priority than price. However, the aforementioned aggregation operators cannot fuse the aggregated arguments that are in different priority levels. In response to these situations, Yager [
31] proposed the prioritized averaging (PA) operator. Inspired by Yager [
31], Yu et al. [
32,
33] constructed the intuitionistic fuzzy prioritized fuzzy and interval-valued intuitionistic fuzzy prioritized fuzzy aggregation operators. Besides, the hesitant fuzzy prioritized aggregation operators were proposed to aggregate the evaluation information that is at different priorities [
34]. Nevertheless, to our best knowledge, few researches have extended the PA operator to solve the MCDM problems under PF environment.
In summary, this paper defines the PHFS based on the PFS and HFS and develops the operations laws of picture hesitant fuzzy elements (PHFEs) according to the operations of IFNs [
21]. Then, the generalized picture hesitant fuzzy aggregation operators and generalized picture hesitant fuzzy prioritized aggregation operators are put forward, and the properties and reduced operators of them are investigated. Furthermore, the proposed operators are utilized to solve diverse situations during MCDM processes under picture hesitant fuzzy (PHF) environment.
The rest of this paper is structured as follows. Definitions of the PFS, HFS, and PA operator are presented in
Section 2. The concept of PHFS is defined, and the comparison method and operations of PHFEs are proposed in
Section 3.
Section 4 constructs the generalized picture hesitant fuzzy weighted averaging (GPHFWA), generalized picture hesitant fuzzy weighted geometric (GPHFWG), generalized picture hesitant fuzzy prioritized weighted averaging (GPHFPWA), and generalized picture hesitant fuzzy prioritized weighted geometric (GPHFPWG) operators. In
Section 5, two MCDM methods are constructed according to the proposed operators.
Section 6 applies the proposed methods into two numerical examples and an application of web service selection to show the effectiveness and advantages of the proposed methods. Finally, some conclusions are summarized in
Section 7.
3. PHFS
According to the PFS and UTHFS, we can define the PHFS that is composed by four membership functions, namely, positive, neutral, negative, and refusal membership functions. The four membership degrees are denoted by several values belonging to , respectively, which can convey the hesitancy of decision makers.
Definition 10. Letbe a non-empty and finite set, a PHFSon is defined bywhere,, andare three sets of several values in, representing the potential positive, neutral, and negative membership degrees. The degrees above satisfy the condition of, where,, and. For convenience, we callis a PHFE, denoted by.
During the process of applying the PHFEs to the practical MCDM problems, it is necessary to rank the PHFEs; thus, we develop the score and accuracy functions of PHFEs.
Definition 11. Letbe a PHFE, the numbers of values inare, respectively. Thus, the score function is defined as the accuracy function is expressed as Based on the score and accuracy values of PHFEs, we can determine the order relations between two PHFEs as in the following.
Definition 12. Letandbe two PHFEs, then
- (1)
If, then;
- (2)
If, then
- a.
If, then;
- b.
If, then;
- c.
If, then
For example, let and be two PHFEs, according to the Definition 11, we have , , and , then .
Inspired by the operational laws of PFNs and UTHFEs, i.e., the Definition 3 and 8, we propose the operational laws of PHFEs as follows.
Definition 13. Let,, andbe three PHFEs,, andis the complementary set of, and the operations of PHFEs are represented as For example, letandbe two PHFEs,, then
- (1)
, ;
- (2)
- (3)
- (4)
- (5)
,
Obviously, the following theorem can be obtained based on the Definition 13.
Theorem 1. Let,, andbe three PHFEs,, then
- (1)
- (2)
- (3)
- (4)
- (5)
- (6)
- (7)
4. Generalized Picture Hesitant Fuzzy Aggregation Operators
Combined with the concept and operations of PHFS, the GPHFWA, GPHFWG, GPHFPWA, and GPHFPWG operators are developed. Then, several properties of them are discussed, and some other aggregation operators under PHF environment that reduced by the proposed operators are presented.
4.1. The GPHFWA Operator
Definition 14. Letbe a collection of PHFEs, the GPHFWA operator is a mappingaswhereis the weight vector of PHFEs, and satisfies the conditions ofand.
Based on the Definition 13, we can obtain the theorems as follows.
Theorem 2. Let be a collection of PHFEs, then their aggregated value by using the GPHFWA operator is also a PHFE, and Theorem 3. (Idempotency) Letbe a collection of PHFEs, if all the PHFEs are equal, i.e.,,, then Theorem 4. (Boundedness) Letbe a collection of PHFEs, ifand, where,,,,, and, thus Theorem 5. (Monotonicity) Letandbe two collections of PHFEs, if, then Proof. Theorem 5 can be obtained by the Theorem 4. □
Under some specific situations, we can obtain the reduced operators of the GPHFWA operator.
Case 1. If
, then the GPHFWA operator is reduced to the picture hesitant fuzzy weighted averaging (PHFWA) operator
Case 2. If
and
, then the GPHFWA operator is reduced to the picture hesitant fuzzy arithmetic averaging (PHFAA) operator
4.2. The GPHFWG Operator
Similarly, the GPHFWG operator can be defined as in the following.
Definition 15. Letbe a collection of PHFEs, the GPHFWG operator is a mappingaswhereis the weight vector of PHFEs, and satisfies the conditions ofand.
According to the operational laws of PHFEs, the theorem can be obtained as follows.
Theorem 6. Let be a collection of PHFEs, then their aggregated value by using the GPHFWG operator is also a PHFE, and It can be proven by the same process as Theorem 3–5 that the GPHFWG operator also has several properties.
Theorem 7. (Idempotency) Letbe a collection of PHFEs, if all the PHFEs are equal, i.e.,,, then Theorem 8. (Boundedness) Letbe a collection of PHFEs, ifand, where,,,,, and, thus Theorem 9. (Monotonicity) Letandbe two collections of PHFEs, if, then Several reduced operators of the GPHFWG operator are presented as:
Case 3. If
, then the GPHFWG operator is reduced to the picture hesitant fuzzy weighted geometric (PHFWG) operator
Case 4. If
and
, then the GPHFWG operator is reduced to the picture hesitant fuzzy geometric averaging (PHFGA) operator
4.3. The GPHFPWA Operator
In real life, the criteria sometimes have different priority levels. For example, safety has a higher priority than price when a couple chooses a toy for their child. Obviously, the GPHFWA and GPHFWG operators cannot deal with this situation; then, the GPHFPWA and GPHFPWG operators are developed according to the PA operator proposed by Yager [
31].
Definition 16. Letbe a collection of PHFEs, the GPHFPWA operator is a mappingaswhere, , and is the score value of PHFE.
Similarly, the following theorem can be put forward.
Theorem 10. Let be a collection of PHFEs, then their aggregated value by using the GPHFPWA operator is also a PHFE, and The GPHFPWA operator also has the properties as follows.
Theorem 12. (Idempotency) Letbe a collection of PHFEs, if all the PHFEs are equal, i.e.,,, then Theorem 13. (Boundedness) Letbe a collection of PHFEs,and, where,,,,, and, thus Theorem 14. (Monotonicity) Letandbe two collections of PHFEs, if, then Then, the reduced operators of the GPHFPWA operator can be obtained.
Case 5. If
, then the GPHFPWA operator is reduced to the picture hesitant fuzzy prioritized weighted averaging (PHFPWA) operator
Case 6. If
and the criteria are at the same priority, then the GPHFPWA operator is reduced to the PHFWA operator
Case 7. If
,
, and the criteria are at the same priority, then the GPHFPWA operator is reduced to the PHFAA operator
4.4. The GPHFPWG Operator
Similarly, the GPHFPWG operator is constructed as below.
Definition 17. Letbe a collection of PHFEs, the GPHFPWG operator is a mappingaswhere,, and is the score value of PHFE.
Combined with the operations of PHFEs, the following theorems are obtained.
Theorem 15. Let be a collection of PHFEs, then their aggregated value by using the GPHFPWG operator is also a PHFE, and Theorem 16. (Idempotency) Letbe a collection of PHFEs, if all the PHFEs are equal, i.e.,,, then Theorem 17. (Boundedness) Letbe a collection of PHFEs, ifand, where,,,,, and, thus Theorem 18. (Monotonicity) Letandbe two collections of PHFEs, if, then Several reduced operators of the GPHFPWG operator are presented as below:
Case 8. If
, then the GPHFPWG operator is reduced to the picture hesitant fuzzy prioritized weighted geometric (PHFPWG) operator
Case 9. If
and the criteria are at the same priority, then the GPHFPWG operator is reduced to the PHFWG operator
Case 10. If
,
and the criteria are at the same priority, then the GPHFPWG operator is reduced to the PHFGA operator
5. MCDM Methods under PHF Environment
We utilize the proposed operators to deal the different MCDM problems under PHF environment in this section. Let
be a collection of alternatives and
be a set of criteria; decision maker evaluates the
alternatives concerning the
criteria by using the PHFEs. Thus, suppose that
is the PHF evaluation matrix, and
is the evaluation information when the alternative
is evaluated concerning the criteria
. In general, the criteria can be divided into two types in practice, namely, the cost criteria and benefit criteria; therefore, the evaluation information concerning the cost criteria should be transformed into the evaluation information concerning the benefit criteria to obtain the standardized PHF evaluation matrix
as
According to the aforementioned assumptions, when the criteria of a specific MCDM problem are in same priority level, and let
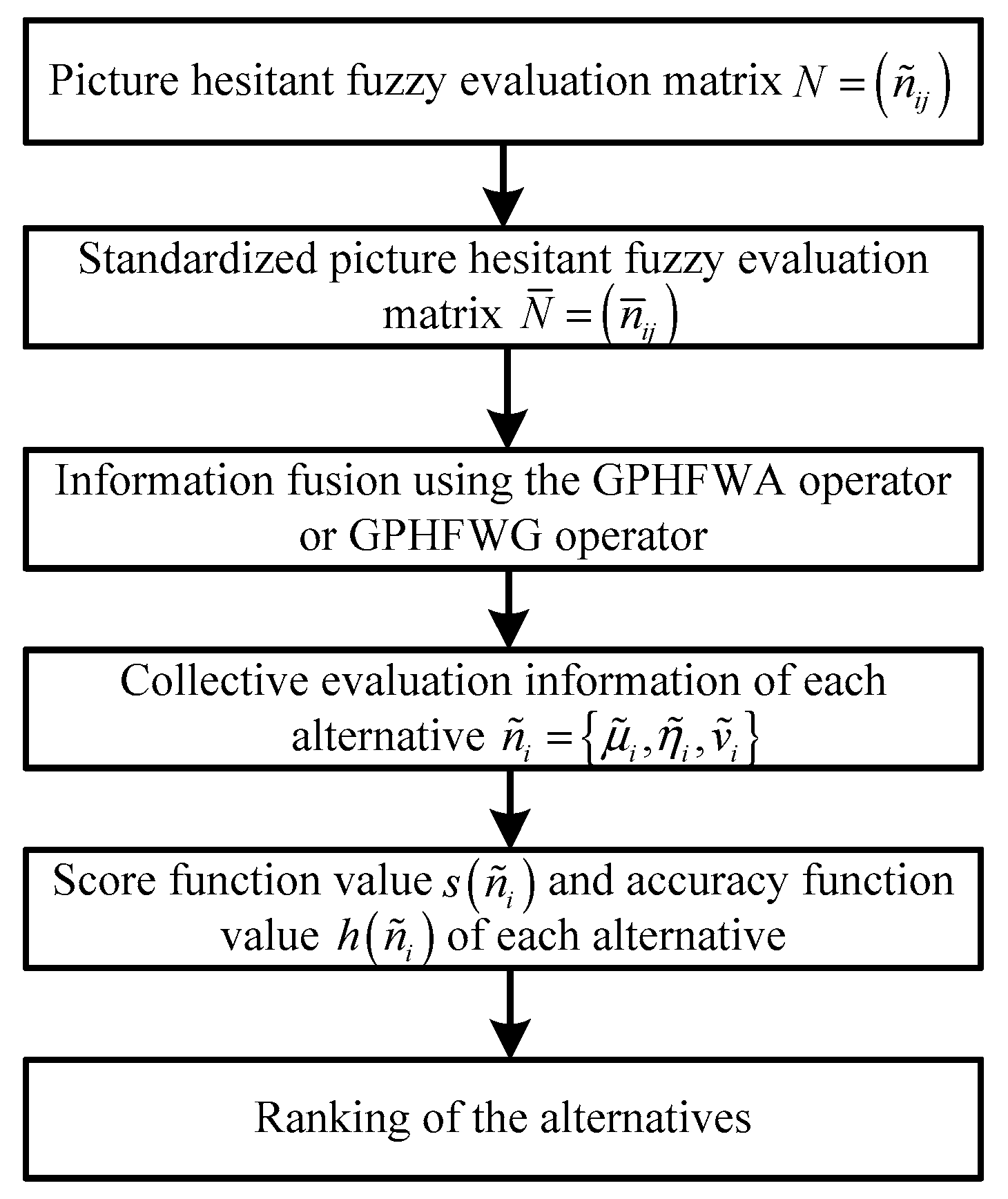
be the weight vector of the criteria. We can construct a novel approach, i.e., Algorithm 1 to solve it based on the GPHFWA or the GPHFWG operator. The flow diagram of the Algorithm 1 is presented in
Figure 1, and the ranking result can be obtained by the following steps.
| Algorithm 1. MCDM method based on the GPHFWA or the GPHFWG operator. |
| 1: Normalize the PHF evaluation matrix to obtain the standardized PHF evaluation matrix combined with Equation (51). |
| 2: Utilize the GPHFWA operatoror the GPHFWG operator
to aggregate the standardized PHF evaluation matrix to obtain the collective evaluation information of each alternative, i.e., . |
| 3: Compute the score and accuracy values of each alternative using Equation (14) and (15). |
| 4: Based on the comparison method of PHFEs, rank the alternatives. |
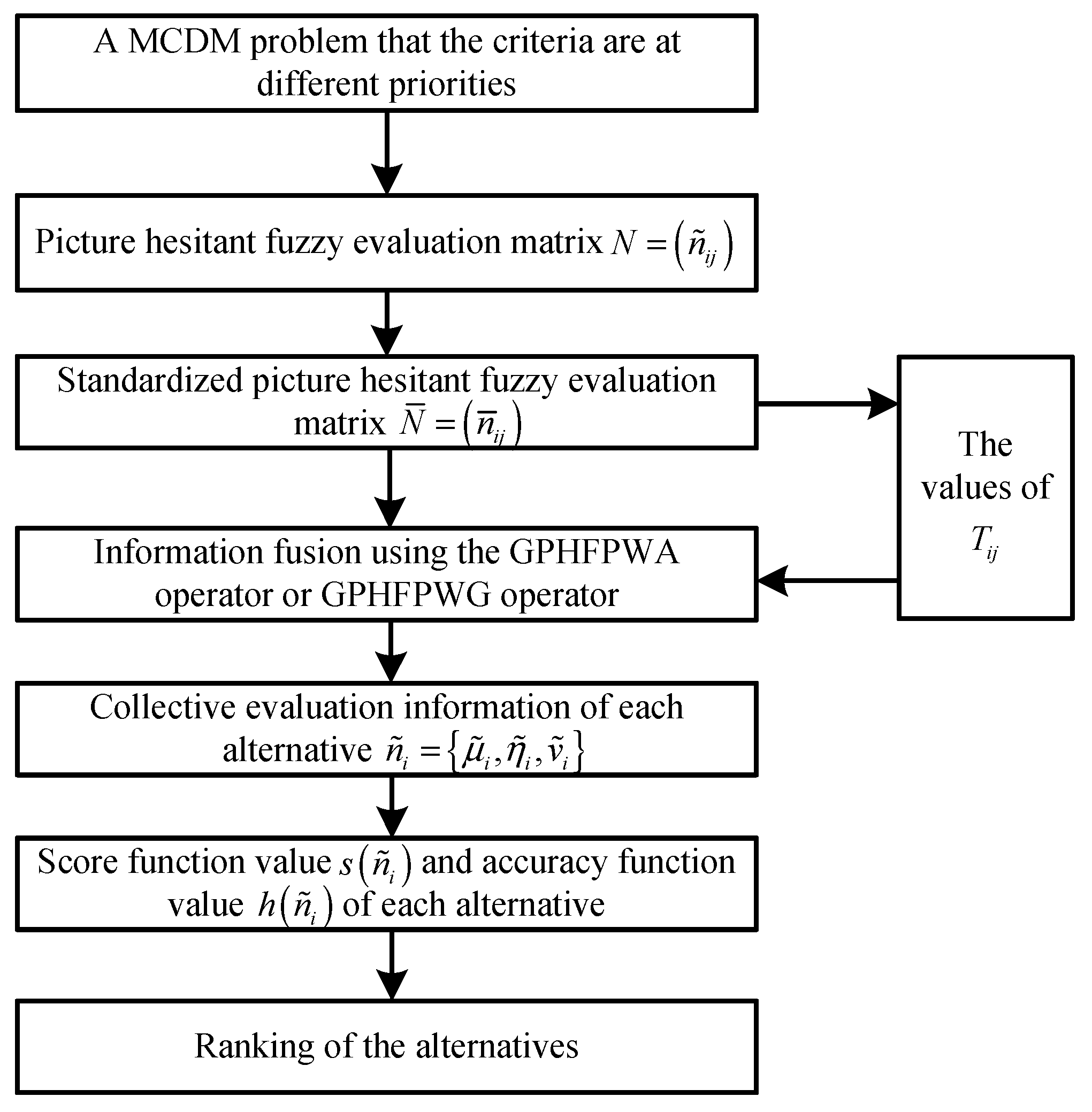
When the criteria are in different priorities, we can solve the MCDM problem combined with the Algorithm 2 based on the GPHFPWA or the GPHFPWG operator. The flow diagram of Algorithm 2 is presented in
Figure 2, and the ranking result can be obtained by the following steps.
| Algorithm 2. MCDM method based on the GPHFPWA or the GPHFPWG operator. |
| 1: Normalize the PHF evaluation matrix to obtain the standardized PHF evaluation matrix combined with Equation (51). |
| 2: Compute the values of using the equations as |
| 3: Utilize the GPHFPWA operatoror the GPHFPWG operatorto aggregate the standardized PHF evaluation matrix to obtain the collective evaluation information of each alternative, i.e., . |
| 4: Compute the score and accuracy values of each alternative using Equation (14) and (15). |
| 5: Based on the comparison method of PHFEs, rank the alternatives. |
6. Numerical Examples
We adopt two numerical examples of MCDM problems from the study of [
25] and [
34] and an application of web service selection [
37] to show the feasibility and advantages of the proposed methods.
6.1. Implementation
Example 1. Suppose that an organization wants to construct the enterprise resource planning (ERP) system [25]. After investigating the existing vendors of ERP systems on the market, five potential ERP systems are primary determined to be chosen from, i.e., Ai (
i = 1, 2, 3, 4, 5)
. Decision makers utilize the PHFEs to evaluate the five alternatives with respect to four criteria, namely, function and technology (C1), strategic fitness (C2), ability of vendor (C3), and reputation of vendor (C4), and the weight vector of the criteria is w = (0.2, 0.1, 0.3, 0.4)
. Subsequently, the PHF evaluation matrix is obtained as shown in Table 1. Then, we can determine the ranking of the five potential ERP systems using the Algorithm 1, which are presented as below.
Step 1: Because of all the criteria are the benefit type, the standardized PHF evaluation matrix is as same as the PHF evaluation matrix .
Step 2: Use the GPHFWA (
) operator to aggregate the standardized PHF evaluation matrix
, and the collective evaluation information of each alternative is obtained as
Step 3: Compute the score values of each alternative combined with Equation (14):
Step 4: According to the score values, the ranking result of the five ERP systems is determined as .
If the GPHFWG operator is utilized in the steps above to complete the information fusion, the ranking procedures are presented as follows.
Example 2. Suppose a university wants to introduce excellent foreign professors to improve the level of teaching and scientific research [34]. There are five foreign professors who are selected by the University’s human resources department. Based on the priority level, the criteria of investigation is successively morality (C1), research ability (C2), teaching capacity (C3), and educational experience (C4); a priority relationship exists between the criteria. Then, the PHF evaluation matrix is presented in Table 2. Subsequently, we can determine the ranking of the five foreign professors using the Algorithm 2, which are presented as follows.
Step 1: Because of all the criteria are the benefit type, the standardized PHF evaluation matrix is as same as the PHF evaluation matrix .
Step 2: Compute the values of
using the Equation (54)
Step 3: Use the GPHFPWA (
) operator to aggregate the standardized PHF evaluation matrix
, and the collective evaluation information of each alternative is obtained as
Step 4: Compute the score values of each alternative combined with Equation (14)
Step 5: According to the score values, the ranking result of the five foreign professors is determined as .
If the GPHFPWG operator is utilized in the steps above to complete the information fusion, the ranking procedures are presented as follows.
6.2. Sensitivity Analysis
To explore the impact of the parameter
on the ranking results, different possible values of
are used in the algorithms of two aforementioned numerical examples, such as 0.001, 0.5, 1, 2, 3, 5, 10, 20, and 50. Then, combined with the proposed methods, the different rankings of alternatives are presented in
Table 3,
Table 4,
Table 5 and
Table 6. From
Table 3 and
Table 4, we can find that the best potential ERP system in Example 1 is always
using both the GPHFWA operator and GPHFWG operator; however, some differences exist between the ranking results concerning different values of
.
Table 5 and
Table 6 show that when we utilize the GPHFPWA operator to complete the information fusion, the best foreign professor is
for
, but the best alternative is
for
. In addition, when the GPHFPWG operator is used in Algorithm 2, the best foreign professor is
for
, but the best alternative is
for
. On the other hand, the score values of all the alternatives vary with different values of
; the reason is that the aggregation processes of the proposed operators have changed. For instance, when
, the GPHFWA operator can be reduced to the picture hesitant fuzzy weighted quadratic averaging (PHFWQA) operator as
when
, the GPHFWA operator can be reduced to the picture hesitant fuzzy weighted cubic averaging (PHFWCA) operator as
- (1)
In Example 1, the score values of each alternative obtained by the GPHFWA operator are bigger than those obtained by the GPHFWG operator, and the difference between them increases along with the increasing of . It means that the GPHFWA operator is more suitable to aggregate the PHFEs of optimistic decision makers, while the GPHFWG operator can reflect the opinion of pessimistic decision makers. Furthermore, the level of optimism and pessimism are greater with the bigger value of .
- (2)
In Example 2, the score values of each alternative obtained by the GPHFPWA and GPHFPWG operators are relatively stable when the different values of are used; the parameter cannot reflect the attitude of decision makers. In addition, the best alternative varies when the value of is relatively high, while the best alternative is always the same in Example 1. It means that the rankings obtained by the GPHFPWA and GPHFPWG operators are more affected by the parameter than those obtained by the GPHFWA and GPHFWG operators.
The aforementioned sensitivity analysis results show that the value of plays a very important role in MCDM problems, especially when the value of is relatively high. The value of can be determined based on the personal preference of decision makers to obtain different ranking results; thus, the proposed methods are highly flexible to deal with different situations in practice.
6.3. Comparative Analysis
To prove the feasibility of the proposed MCDM methods, the rankings of Example 1 in this paper are compared with the rankings obtained by the existing MCDM methods as presented in
Table 7; including the PFWA and PFWG operators [
25], and the picture fuzzy cross-entropy method [
16]. Similarly, a comparison of Example 2 between the GPHFPWA and GPHFPWG operators and the HFPWA and HFPWG operators [
34] is presented in
Table 8.
Table 7 shows that the best alternative of Example 2 obtained by the MCDM methods based on the GPHFWA and GPHFWG operators is always
, which is consistent with the existing methods; the results can demonstrate the feasibility of the proposed method. Compared with the PFS that is used in the study of [
25] and [
16], PHFS proposed in this paper can convey the human opinions more effectively, including yes, abstain, no, and refusal. For instance, the evaluation information of the alternative
concerning the criteria
that are given by decision maker is expressed as a PFN (0.53,0.33,0.09) [
16,
25]. In practice, decision maker may feel doubtful to determine an exact value of each membership level. Obviously, PFS cannot deal with this situation; however, we can use PHFS to represent the evaluation information as a PHFE {{0.43,0.53}, {0.33}, {0.06,0.09}} as shown in
Table 1. Consequently, the proposed method can solve the MCDM problems when decision makers feel difficulty to determine the accurate value of each membership level. On the other hand, when the numbers of the criteria are relatively large, the aggregation process of the proposed operators will be more complicated than the existing methods and the data size will be relatively large; it is the limitation of the proposed method.
Table 8 shows that the best alternative of Example 2 obtained by the HFPWA operator is
, but the result of other MCDM methods is
. The main reason of the difference is that the MCDM methods combined with the HFPWA and HFPWG operators ignore some complex evaluation information of decision makers in practice. UTHFS allows the decision makers to give several values of positive membership level, for instance, the evaluation information of the alternative
concerning the criteria
that are given by decision maker is expressed as a UTHFE (0.4,0.5,0.7) [
34]. Nevertheless, in some particular situations, it is not convincing to express the evaluation information that only considers the positive membership level of decision makers; many scholars have focused on this problem and made some improvements to UTHFS [
10,
19]. Thus, we can overcome the limitation of UTHFS combined with the proposed method. It is worth noting that the GPHFPWA and GPHFPWG operators also have the same disadvantage as the GPHFWA and GPHFWG operators.
According to the aforementioned comparison results, we can summarize the advantages and disadvantages of the different MCDM methods (see
Table 9), as well as their respective fields of application (see
Table 10). In addition, the benefits of the aggregation process by using the proposed operators are presented as in the following.
(1) The Expansion of the Evaluation Information
The GPHFWA, GPHFWG, GPHFPWA, and GPHFPWG operators can solve the MCDM problems under PHF environment. PHFS proposed in this paper can express the different human opinions in real life and allow the decision makers to give several possible values of the different membership levels; thus, it can simultaneously depict the uncertainty and hesitancy of decision makers’ evaluation information, which cannot be achieved by PFS and UTHFS. Therefore, when decision makers are not fully aware of the evaluation target and feel doubtful about each membership level, it is reasonable to deal with these MCDM problems combined with the proposed methods. Furthermore, as a generalized form of FS, IFS, PFS, and UTHFS, we can transform the proposed methods into the existing MCDM methods if necessary.
(2) The Flexibility of Information Aggregation with Different Values of
Recall the sensitivity analysis in
Section 6.2, the proposed operators can be reduced to other specific PHF aggregation operators by varying the value of
; thus, the proposed methods are highly flexible to deal with different situations. Furthermore, the parameter
can also be regarded as a measure of the optimism and pessimism level of decision makers in the information fusion of the GPHFWA and GPHFWG operators; and the value of
can be determined by decision makers according to their preferences in practice.
(3) The Simplicity of Dealing with Different Types of Criteria
During the MCDM process, the weight values of criteria play an important role and will affect the final ranking results. The criteria can be divided into two categories: one is in the same priority, the other is in different priorities. On the one hand, when the criteria have the same priority level, we can utilize the proposed method based on the GPHFWA and GPHFWG operators combined with the weight vector of criteria to solve the MCDM problem. On the other hand, when the criteria have different priority levels, the GPHFPWA and GPHFPWG operators can be introduced to determine the ranking of alternatives. In practice, we can use different aggregation operators in this paper to deal with different situations.
6.4. Application of Web Service Selection
To investigate the applications of the proposed methods in a more realistic scenario, we use the proposed methods to solve the Quality of Service (QoS) based web service selection problem [
37]. According to the study of [
37], the evaluation information of QoS is measured by a crisp number scale of 1–9, and the related criteria are availability (
), throughput (
), successability (
), reliability (
), compliance (
), best practices (
), documentation (
), latency (
), and response time (
). Due to the criteria latency and response time are the cost type criteria, the closer the evaluation values concerning these two criteria are to 1, the better the alternative.
Suppose there are 20 web services to be evaluated concerning the aforementioned nine criteria, i.e.,
; the evaluation information of each web service is presented in
Table 11. As each evaluation value in [
37] is expressed by an exact crisp number, the PHFS can be reduced to the PFS to represent the evaluation information of each web service. Based on the relationship between the linguistic variables and IFNs [
38], we develop the transformation relationship between the linguistic variables and PFNs as presented in
Table 12. Then, the evaluation information in
Table 11 can be transformed into a PF evaluation matrix
, and the ranking of the 20 web services can be obtained by the Algorithm 1 in this paper. Subsequently, the ranking result will be compared with the rankings determined by AHP, TOPSIS, COPRAS, VIKOR, and SAW methods in [
37]. It is worth noting that, in order to compare different MCDM methods, more effectively we suppose each criteria is considered equally important, i.e.,
. Then, the ranking of the 20 web services can be determined by the following steps.
Step 1: According to the Definition 3, normalize the PF evaluation matrix
to the standardized PF evaluation matrix
as
Step 2: Utilize the GPFWA (
) operator
to aggregated the PF evaluation matrix
, and the collective PFNs of each web service are obtained.
Step 3: Compute the score values of each web service using the equation
Then, the ranking of the 20 web services can be determined; the lager the score value, the better the web service. The related data of the ranking are presented in
Table 13.
To verify the accuracy of the ranking obtained by the proposed method, we use AHP, TOPSIS, COPRAS, VIKOR, and SAW methods to solve the web service selection problem combined with the evaluation information in
Table 11. Subsequently, the ranking results of different MCDM methods are presented in
Table 14. The Spearman’s rank correlation coefficient is a powerful tool for measuring the similarity between two MCDM methods [
39]. Then, we can calculate the Spearman’s rank correlation coefficients between the proposed method and the other five MCDM methods as shown in
Table 15.
Table 15 shows that the Spearman’s rank correlation coefficients between the proposed method and AHP and TOPSIS are 0.9722 and 0.9549, respectively, which demonstrate that the proposed method is highly correlated with these two methods. AHP and TOPSIS methods have been approved to be the most suitable two methods to solve web service selection problems [
39]; thus, the comparison results above illustrate the feasibility of the proposed method.
From the information aggregation of the proposed method, we can find that the calculating procedure of the proposed method is more complicated than AHP and TOPSIS methods. In addition, TOPSIS method does not require the transformation of the evaluation information concerning cost and benefit type criteria. However, when decision makers are not sure if it is 3 or 4 about the evaluation information of the web service concerning the criteria , AHP and TOPSIS methods cannot deal with this situation in practice; we can use PHFS to express the evaluation information above, i.e., {{0.25,0.35},{0.05},{0.55,0.65}}. On the other hand, when the criteria are in different priorities, the GPHFPWA and GPHFPWG operators can be used to aggregation the evaluation information. Thus, the AHP, TOPSIS, and proposed methods have their own advantages and disadvantages; in real life, decision makers can determine to utilize which MCDM methods to solve problems according to the actual situations.
7. Conclusions
Combined with the picture fuzzy set and uniformly typical hesitant fuzzy set, this paper develops the picture hesitant fuzzy set, in which the positive, neutral, negative, and refusal membership degrees are expressed by several possible values. Then, the operations and comparison method of picture hesitant fuzzy elements are developed. To solve the multiple criteria decision-making problems under picture hesitant fuzzy environment, the generalized picture hesitant fuzzy weighted averaging and generalized picture hesitant fuzzy weighted geometric operators are put forward to aggregate the picture hesitant elements given by decision maker. Furthermore, considering the different priorities between the related criteria in practice, the generalized picture hesitant fuzzy prioritized weighted averaging and generalized picture hesitant fuzzy prioritized weighted geometric operators are proposed. Meanwhile, some desirable properties and the reduced operators of them are investigated in detail. Finally, two kinds of multiple criteria decision-making methods combined with the proposed operators are constructed to solve the multiple criteria decision-making problems in different situations. Subsequently, two numerical examples and an application of web service selection are provided to indicate the applications and advantages of the proposed methods.
In future research, we will investigate other operations of picture hesitant fuzzy elements and develop different aggregation operators to aggregate picture hesitant fuzzy elements. In addition, we will propose the consensus model to improve the proposed methods; then, the non-consensus evaluation information of decision makers will be revised to obtain a more accurate ranking result.