Abstract
In this paper, we propose a methodology for the step-by-step solution of problems, which can be incorporated into a computer algebra system. Our main aim is to show all the intermediate evaluation steps of mathematical expressions from the start to the end of the solution. The first stage of the methodology covers the development of a formal grammar that describes the syntax and semantics of mathematical expressions. Using a compiler generation tool, the second stage produces a parser from the grammar description. The parser is used to convert a particular mathematical expression into an Abstract Syntax Tree (AST), which is evaluated in the third stage by traversing al its nodes. After every evaluation of some nodes, which corresponds to an intermediate solution step of the related expression, the resulting AST is transformed into the corresponding mathematical expression and then displayed. Many other algebra-related issues such as simplification, factorization, distribution and substitution can be covered by the solution methodology. We currently focuses on the solutions of various problems associated with the subject of derivative, equations, single variable polynomials, and operations on functions. However, it can easily be extended to cover the other subjects of general mathematics.
1. Introduction
Mathematics has an important root in human evolutionary history. Computers are very good at solving problems if right commands are used. The first generation of programming languages, namely assembly, did not have special statements to work with mathematical expressions except for four basic operations of add, subtract, multiply and divide. Although the basic operations can be used to work with the hardware, given high-level programming languages, more sophisticated expressions are supported and break down to those operations. The breaking-down process is generally controlled by compilers which translate all statements and expressions in a high-level programming language into low-level or machine code. Due to very effective outcomes of the process, many advanced languages and systems have been introduced [1,2]. Mathematics systems are categorized into two main groups such as numerical computation and symbolic computation. Although numeric computation is widely used [3], the output is always an approximated value. Unfortunately the difference between the exact value and the approximate value can cause errors and failures. Error propagation happens in various forms such as floating-point calculation, estimated values, uncertainty, etc. For very accurate systems, using numeric computation is not preferred. Symbolic computation or algebraic computation refers to the development and evaluation of mathematical expressions. Symbolic computation offers exact solutions with expressions that can contain variables or symbols. If symbols are not set to any value, then the output will also be another expression of variables. Computer applications that can conduct symbolic calculations are called Computer Algebra Systems (CAS) or symbol manipulation systems [4]. The increasing use of CAS systems has enlarged the role of computer systems in the teaching of mathematics [5,6,7]. For example, computer algebra has an important role in designing and experimenting formulas that are required in numerical programs. CAS can be used for two separate areas of general purposes and specific purposes [8,9,10]. General-purpose applications such as Matlab, Maple and Mathematica provide rich computing facilities for complex and difficult mathematical problems. Programs such as MyAlgebra, MathWay, webMath, which produce mathematical questions and DELIA working on deferential equations, provide special uses of algebraic and general mathematics. But most applications of CAS are commercial, and there exist very few open source and academic projects. Academic researches are conducted to increase the stock of knowledge in the scope of symbolic computation. In this paper, we propose a methodology to solve mathematical problems using symbolic computation. Symbolic solving of algebraic problems uses a divide and conquer strategy, where large expressions are divided into small pieces and each piece is separately handled to obtain the complete solution of the original problem. In recent years, much research has been done on working with mathematical expressions. The production of math phrases is one of the things that are referred in [11]. In this study, using grammars, the template-based production of mathematical expressions has been carried out. The common point of the study is the use of a formal grammar to work with mathematical expressions. As the referred article discusses the production of mathematical expressions, we address the solution of mathematical problems in our research.
The solution of the problem pieces helps the production of intermediate or step-by-step solutions using the divide and conquer strategy. With object oriented programming constructs which facilitate the implementation process of this strategy as a result of supporting the inheritance between classes, it is quite possible to manage the evaluation, simplification and printing stages, required for mathematical operations involved in, for example, the derivation of expressions.
Mathematical expressions can have many distinct aspects that must be evaluated by different solution strategies. The evaluation steps need to perform a special collection of operations based on the kinds of expression components. It is possible to embed a particular expression directly into program code, using programming language constructs, and then employ some evaluation methods, without considering the syntactic and semantic structure of the expression. But, this approach does not support the convenient manipulation of the in-code expression, especially for some intermediate or symbolic evaluations such as simplification and derivation, which involves in expression analysis. To manipulate expressions appropriately, there is need to represent them at a more abstract level. Our methodology uses a grammar-based approach to convert mathematical expressions into abstract syntax trees (AST) on which new methods can be developed for different evaluation or interpretation requirements. In this way, users can dynamically enter expressions and all the intermediate operations on them can successfully be achieved through AST nodes.
Context Free Grammars (CFG) is used to parse and produce mathematical expressions. Input string passes through a parser which verifies the syntax of that input and also creates an Abstract Syntax Tree (AST). This tree structure serves as the main core part of the proposed methodology to apply various improvement algorithms on input string. It is possible to create a symbolic computation environment via the methodology, where a mathematical problem can be generated and its step-by-step solution can be obtained. In the other words, it can play an important role in constructing a general framework for dealing with mathematical expressions. Given the internal representations of expressions, the framework can easily be equipped with new solution methods of mathematical problems. It can also be a good platform for the development of educational products in the field of mathematics, which can display all problem-solving steps.
2. Materials and Methods
2.1. Review of the Literature
From the beginning of computer science on, many algorithms, methods, and techniques have being developed. With the development of computer systems and their increasing use, it has been easier to see the effects of the technology on several different fields including education and health. In recent years, there have inevitably been many technological changes on educational practices and materials. Among educational disciplines, mathematical education, especially general mathematics, has attracted more attention [5].
Most of the current e-learning systems such as Coursera and Edventure have provided support for automatic assessment, but only with multiple-choice questions as it is a great challenge to support other question formats. Recently, there has been a growing interest in intelligent tutoring systems for supporting mathematical learning such as geometry construction [12], algebra problem generation [13] and automatic solution assessment [14,15].
Currently, there are three main approaches for automatic mathematical solution assessment, namely computer algebraic approach, rule-based approach and structural approach. The computer algebraic approach is based on symbolic algebraic computation [16,17] for automatic mathematical solution assessment. This technique is implemented in commercial Computer Algebra Systems (CAS) such as Mathematica and Maple. The rule-based approach [18,19] is based on mathematical rules for equivalence assessment. Starting with a mathematical expression, this approach transforms it into another equivalent expression and compares it with the intended target expression for equivalence verification. The structural approach [20,21] is based on the tree representation of a mathematical expression. In this approach, two mathematical expressions are first represented as two mathematical expression trees. Then, tree matching algorithm [22] is used to compare the two trees using dynamic programming [23] for equivalence verification.
The development of CAS has led to the idea of use of these systems in teaching mathematics. However, there are different discussions about the use of these systems in mathematical curricula [24]. The application of CAS systems to teaching programs has been approached from two perspectives: The first approach focuses on the use of CAS systems as part of mathematical teaching programs like instructing materials including solving equations, derivate, etc. [6,25,26]. The other approach examines the development of teaching programs based on technology, which changes the course of teaching methods and structures [27,28,29,30].
In recent years, different researches on the impacts of use of CAS systems on improvement in mathematical teachings have been conducted, showing their favorable impact [31,32,33]. Also, studies on the use of technological educational systems for teaching the derivative subject have been performed [6,25,34,35]. The efforts made on the use of CAS systems in mathematical teachings have usually been in the form of non-numerical solutions and, in some cases, graphical representations, where the results suggest improvement in educational quality while utilizing these systems.
In 1986, the paper entitled “Computer Algebra System, Tools for Reforming Calculus Instruction”, [36] addressed the use of CAS in development of conceptual comprehension, teaching method, wrong conception analysis, exercises, test questions, and finally the overcoming of restrictions leading to deficiency in algebraic operations.
Automatic mathematical solution assessment is different from other similarity-based solution assessment problems such as automatic essay grading [37] and short text marking [38].
It can be argued that the problem-based learning is more effective than traditional learning, and increases students’ ability to solve the problems [39]. On the other hand, textbooks cannot be suitable as a source of questions, because they are limited, and not interactive. In addition, textbooks do not usually solve the problem step-by-step and do not have appropriate visual features for motivation. In these resources, often there are not adequate facilities for on line helps to students. Therefore, the use of information and computer-based technologies in education, especially physics (e.g., CAPA) [40], mathematics (e.g., Mathway) [41,42] and electronics (e.g., CHARLIE) [43] is widespread. The literature also has systems that emerged for generating and solving the questions [44,45].
Many methods have been developed for solving algebraic equations and some of them have been used with automatic computers [46,47]. The methods which are most suitable for use with automatic computers are ones that are applied to a wide class of equations and that are relatively rapid when the degree of the equation is large.
In addition to general-purpose computer algebra systems, there is some special-purpose software for mathematics and physics, developed to solve problems in a particular area. Typical examples are Cayley and GAP software, developed for group theory [48,49], PARI, SIMATH, and KANT for number theory, CoCoA for commutative algebra [50], Macaulay for algebraic geometry and LiE for Lie theory [51].
Math software tools used in mathematics curriculum can serve in the five categories as: practical, public, private, environment, and communications [52]. Besides, Handal and Herrington [53] have identified exercises, lessons, games, simulations, hypermedia, and tools as other computer-based mathematics education categories.
2.2. Methodology Illustration
In this paper we propose a grammar based methodology to solve mathematical expressions step-by-step, which is designed as a multi-party system. The system uses an extended grammar to parse input data, and then converts it into a tree data structure, which provides an appropriate model for easily processing a particular mathematical expression. Each node of the tree includes a symbol or term of the input expression, and its relations with other symbols or terms, where symbols can be operators, numbers, etc.
The tree representation also helps to apply recursive operations over a node and its children. For example, the evaluation of a node requires firstly evaluating the children of that node. Besides a certain combination of nodes can define a pattern to which some other specific operations needs applying. A typical example would be a basic distributive transformation where a complex representation of summation expression is simplified to a simple one.
The methodology consists of the following phases and steps:
- Phase 1:
- Parser definitionSteps: Grammar design, grammar conversion, compiler-compiler input construction, code generation
- Phase 2:
- Input data analysisSteps: Token generation, syntax analysis, AST generation
- Phase 3:
- Evaluation and interpretationSteps: Solving expressions, simplification, printing intermediate evaluation results.
Some of these phases and steps are also shown in Figure 1.
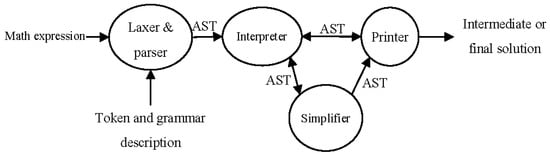
Figure 1.
Some important phases and steps of the proposed methodology.
Using the steps shown in Figure 1, one can implement a framework to process mathematical expressions. In this paper, we will work on algebraic expressions to illustrate some applications of the methodology. The methodology can be integrated with systems developed to solve many practical or real-world problems in education, business or industry. It has the potential to serve as a major component in all the systems for which a mathematical model can be developed. For example, a possible area of usage can be the solution of a linear or nonlinear system of equations derived from the analysis of electrical circuits. The other one can be the evaluation, refinement and application of many numerical analysis methods, including root-finding, function interpolation, polynomial approximation, curve fitting. It can also be used to identify and solve differential equations of various types.
2.3. Evaluation of Mathematical Expressions
2.3.1. BNF Grammar Definition
The BNF notation is used to define context-free grammars for formal languages, especially programming languages. It has simple notations and recursive structures. Many compiler generation tools, such as YACC [54], LEX [55], and JavaCC [56,57] use a BNF-like description of a source language.
Mathematical expressions can contain operations such as addition or subtraction, functions such as sin or cos, special symbols such as integral, etc. Given a grammar developed for a particular mathematical expression, all operators, functions, symbols, variables and numbers will be members of the terminal set. The nonterminal set will be determined based on the production rules of the grammar. The designed grammar must generate arithmetic expressions with an operator and its operands, or a mathematical function with arguments. An operand or argument itself might be a number, a variable, or another mathematical expression.
The production rules of grammar might be recursive, since there are operands of a type “expression”, shortly called expr. In addition, the decimal (or integer) numbers can be generated up to desired number of digits. Every different kind of mathematical expressions requires the use of different grammars. In this section, a derivative system is implemented by developing an extended BNF Grammar with some modifications to the one presented in [58], which is shown in Listing 1.
| Listing 1. An Extended-BNF grammar for mathematical expression. |
| G = {Σ, T, V, P, S} V = {expr, op, func, var, number, digit}⊆ Σ T = {x, Sin, Cos, Tan, Log, Exp, Sqrt, +, -, *, /}⊆Σ Σ = T ∪ V, S = { expr } <expr>::= <expr> <op> <expr> |(<expr>) |<func>(<expr>) |<var> |<Number> <op>::=‘+’ | ‘-’ | ‘*’ | ‘/’ | ‘^’ <func>::= ‘Sin’ | ‘Cos’ | ‘Tan’ | ‘Log’ |’Exp’ | ‘Sqrt’ <var>::=‘x’ <number>::= ‘-’ ? <digit> + (‘. ‘ <digit> +)? <digit>::=[‘ 0’-’9’] |
The grammar given in Listing 1 has five operators and six functions that can reside in simple mathematical expression. However, it can be modified with the insertion of some other operators, functions, and symbols.
When the above grammar is used to describe, for example, the expression “”, it will confront a semantics problem. Since the grammar definition does not consider the priority of the operators, the expression will be given a different meaning from what is done in mathematics and thus will not be evaluated in the right order of operations. In the next section, the grammar will be modified to resolve such semantics problems.
2.3.2. Grammar Conversion
Parsing an expression means processing expression structure via a grammar. One of the most important connections between grammar and expression is the type of parse tree derivation. This connection can be determined by a parsing method, which works under some certain conditions. In this paper, we focus on LL parsers.
The grammar designed in Listing 1 has to be converted to use one of the conventional parsing methods. There are various tools developed for parser generation called compiler-compiler or CC. Each CC is suitable for a specific kind of parsing methods. These tools in fact are compiler generators where they take the syntax rules of a formal language as input, and return a compiler for that language as output.
In this paper, we use JavaCC as a parser generator, which is a compiler-compiler tool developed for the top-down parsing. Top-down parsers can easily work with public grammars.
It is easy to see that, given the grammar in Listing 1, all operators have the same level of precedence. As we know, this will make it an ambiguous grammar. In order to use a compiler-compiler tool like JavaCC, the grammar has to be LL(1). Listing 2 shows the equivalent LL(1) grammar, which is modified by considering the operator precedence and associativity.
| Listing 2. A LL(1) grammar for mathematical expressions. |
| G = {Σ, T, V, P, S} V = {expr, element, term, unary, power, func, number, digit}⊆Σ T = {x, Sin, Cos, Tan, Log, Exp, Sqrt, (,), +, -, *, /, ^}⊆Σ Σ = T ∪ V, S = { expr } <expr>→<unary> <term> [(“+” | ”-”) <term>]* <unary>→(“+” | ”-”)? <term>→<power> [(“*” | ”/”)<power>]* <power>→<element> (“^”<power>)? <element>→<func> (<expr>) | <number> | “x” <func>→”Sin “ | “Cos” | “Tan” | “Log” | “Exp” | “Sqrt” <number>→”-”? <digit> + (“.”<digit>+)? <digit>→[“ 0”-”9”] |
The grammar in Listing 2 is an optimized version of normal LL(1) grammar where all extra non-terminals are combined back to the original non-terminal.
Given the tree structure created by the grammar, the operators with higher priority will first be evaluated and the ones with lower priority later. If there is a need for other mathematical operators, they must be added in the grammar with the level of its priority. In this way, the expression “” will be evaluated consistently with mathematics.
2.3.3. Definition of Syntax Classes
Syntax is the writing rules of a language. Mathematical expressions, as well as other languages, have certain syntax where there is a finite combination of components. Numbers, variables, operations, functions, symbols of grouping, and other syntactic symbols are used in math expressions. Each component has a specific structure which needs to be defined.
We use syntax classes that are implemented using the object oriented concepts of Java. Table 1 shows some syntax classes and their attributes adapted to our work.

Table 1.
The syntax classes for some mathematical components.
As in Table 1 the additional syntax classes can be defined for other operators, functions, or symbols. In object-oriented programming, each rule is generally defined by a class, which is then used to evaluate the expressions. Listing 3 shows the definitions of some classes given in Table 1.
The syntax classes can be used to create some structure. The AST tree structure is the most suitable one for mathematical expressions. Unlike parse trees, an AST can hold essential sections of input in the form of a tree. An AST can be defined simultaneously with a parser that produces it.
| Listing 3. The definition of some syntax classes shown in Table 1. |
| public abstract class Exp { public Exp exp1, exp2; public Exp (Exp e1, Exp e2){ this.exp1 = e1; this.exp2 = e2; } } public class Plus extends Exp { … } … public class Sin extends Exp { public Sin(Exp e) {super(e, null); } } … public class Num extends Exp { public double num; public Num(double n){ this.num = n; } } public class Var extends Exp { private String var; public Var() { super(null, null) } public Var(String var) { super(null, null); this.var = var; } } |
The syntax classes defined at this stage should be coded in accordance with the properties of their respective operators in mathematics. As seen in Listing 4, the Exp class is defined as abstract, and depending on the various operations that may be performed on expressions, methods can be added to this class. For example, to calculate the result of an expression, a method such as public abstract double Eval (int x); can be added in Exp class. The Listing 4 displays the definitions of this method for some operators.
| Listing 4. The definition of some syntax classes for eval() method. |
| abstract class Exp { … public abstract double Eval(int x); } class Plus extends Exp { Exp exp1, exp2, tmp; public Plus(Exp e1, Exp e2) { exp1 = e1; exp2 = e2; } public double Eval(int x) { return (exp1.Eval(x)+exp2.Eval(x)); } … } class Minus extends Exp { Exp exp1, exp2; Data val2; Exp tmp; public Minus(Exp e1, Exp e2) { exp1 = e1; exp2 = e2; } public double Eval(int x) { return (exp1.Eval(x)- exp2.Eval(x)); } … } class Times extends Exp { Exp exp1, exp2, tmp; Data val2; public Times(Exp e1, Exp e2) { exp1 = e1; exp2 = e2; } public double Eval(int x) { return (exp1.Eval(x)*exp2.Eval(x)); } … } class Var extends Exp { public Var(String var) { this.var = var; } public double Eval(int x) { return (x); } … } |
Using the method defined in Listing 4, it is easy to calculate the numerical value of a mathematical expression such as “” with a given value for the variable x.
2.3.4. Parser Construction
The parser generator tools often create AST. The structure of AST depends on the language in which the tool generates code. There are many different parser tools generating parser code for various languages. Some of these tools are developed for code generation in imperative languages, such as yacc [54], and bison [59], and the others such as ml-yacc [60], and happy [61] generates code for functional languages, as well as those generating code for object-oriented languages, including t-gen [62] and JavaCup [63]. Each of these tools requires defining a special type of grammar. Some tools are suitable for LL(k), and some others are suitable for LR(k) etc. Therefore, after selecting a tool for the parser, the grammar must be developed according to the specifications of that parser generator.
Token Specification
A token manufacturer (scanner) with input analysis from the perspective of the word produces a series of tokens. Any word within the input data, which cannot divided into smaller parts, is called token. Tokens are all elements in terminal set (T ⊆ Σ) which is defined by the grammar given in Listing 2. For the grammar in Listing 2, the tokens are shown in Listing 5, following the specification rules of JavaCC.
| Listing 5. JavaCC token declarations of the terminals in the grammar Listing 2. |
| TOKEN : { < NUMBER : ([“0”-”9”])+(“.” ([“0”-”9”])+)? > } TOKEN : { < EOL : “\n” > } TOKEN : /* OPERATORS */ { < PLUS: “+” > | < MINUS: “-” > | < TIMES: “*” > | < DIV : “/” > | < POW : “^” > …… } TOKEN : /* FUNCTIONS */ { < SQRT: “sqrt” > | < SIN: “sin” > | < COS: “cos” > …… } TOKEN : /* SYMBOLS */ { < X: “x” > | < LPR: “(“ > | < RPR: “)” > } SKIP : { “ “ | “\t” | “\r” } |
In Listing 5 each token is defined by the keyword TOKEN. For simplicity, we separate all tokens and categorize them into the groups of numbers, operators, etc. The keyword SKIP specifies the characters which should be discarded. In a similar way, the other tokens in the grammar can be added into Listing 5.
In fact, at this stage, the tokens are defined by regular expressions, which are understood by a lexical analyzer produced via JavaCC. For example, the expression “” will have a stream of the following tokens:
NUMBER TIMES VAR PLUS VAR POW NUMBER DIV NUMBER
Parser Definition
A parser analyzes input data in terms of productivity based on a series of produced tokens. It checks whether the sequence of tokens is generated or not, examining them from the perspective of grammar rules. Therefore, we need a mechanism for verification of tokens and their appearance order based on the language rules. Of course, in the process of analysis, the system must also do a semantic analysis for acceptable input data before evaluation. However, the syntax analyzer (parser) can guarantee the evaluation ability of those data due to the structures of mathematical expressions. The parser can be designed by hand-written functions or using parser generator tools. The use of a parser generation tool involves developing the desired grammar based on the description conditions of that parser. For example, a grammar for Yacc++ must be developed in LR and for CppCC in LL form. In this paper we use JavaCC for the parser generation and validity test of entries.
The name of functions or methods in JavaCC declaration is determined according to the non-terminal set in the grammar in Listing 2. In general, a method must be defined for each non-terminal in a grammar. In some cases it may be useful to combine several non-terminal symbols, defining only a method for them. For example, consider the non-terminal <expr> in Listing 1. For this non-terminal, there is a rule as <expr>→<term> <expr’>. Therefore, a method can be defined for it in the parse generator. But it can arise some difficulties in parse tree generation for the related non-terminal <expr’>. For such cases, these non-terminals can be merged, resulting in one non-terminal, and can be represented by only one method in the parse generator tool. Table 2 shows the typical examples of the merging operation.

Table 2.
The usual and combined rules for some non-terminals.
All the parser methods are defined in accordance with the structure of the grammar rules. In Table 3, some JavaCC defined methods of the LL(1) grammar are shown.

Table 3.
Sample JavaCC method definitions for LL(1) grammar rules.
The other methods for the grammar rules can be defined in the same way as seen in Table 3. The whole definitions of the tokens and rules must be specified with the extension “.jj”, which is taken by JavaCC as input. The output of JavaCC is java code that serves as a parser for the related grammar. This parser can be used for determining the authenticity of input data. In Table 3, the tokens <EOL> and <EOF> represent the end of line and the end of data entries, respectively.
This stage can be used to check the correctness of the expression structure or lead to the production of the syntax tree. The mathematical expression defined in the previous stage is evaluated structurally based on a specific grammar. It is easy to see that the expression “” is well-formed, which has no syntax error.
2.3.5. Generating Abstract Syntax Tree (AST)
In the previous section, we have discussed about creating a parser to determine the accuracy of data entry. However, for being able to do some operation on mathematical expressions, it is necessary not only to detect the accuracy but also generate the desired data structure. One of the useful structures for mathematical expressions is the syntax tree.
A syntax tree (or mainly object tree) is composed of many nodes linked together in a hierarchical structure. Each node is derived from a syntax class, and is constructed by an object that represents a statement or expression of source data. The syntax tree is usually created with the help of a super class type. Subclasses that inherit from the same super class can be used to create the nodes of an object tree, but these nodes on the tree can be represented by the reference of super class.
By adding a various java statements in JavaCC, it is possible to generate AST. Listing 6 shows the commands to be added to the code in Table 3 to generate the nodes of AST.
| Listing 6. The Java statements added to produce AST. |
| Exp parse() : { Exp a; }{ a = expr() (<EOF> | <EOL>) { return a; } } Exp expr() : { Exp a, b; }{ a = term() ( <PLUS> b = term() { a = new Plus(a, b); } | <MINUS> b = term() { a = new Minus(a, b); } )* { return a; } } … Exp power() : { Exp a, b; }{ a = element() ( <POWER> b = power() { a = new Power(a, b); } )? { return a; } }… Exp element() : { Token t; Exp a; } { t=<NUMBER> { return (new Num(Double.parseDouble(t.image))); } | <X> { return (new Var()); } | <LPR> a = expr() <PPR> { return a;} | <SIN> <LPR> a=expr() <PPR> { return new Sin(a);} … }... |
Codes added to Table 3 produce output data, verifying the input string. Figure 2 demonstrates the steps required to produce the AST for our mathematical grammar.
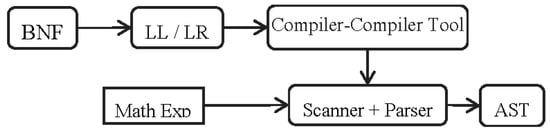
Figure 2.
The steps required to produce the AST for the mathematical grammar.
For example, the expression “” will be converted to an AST, as graphically illustrated in Figure 3.
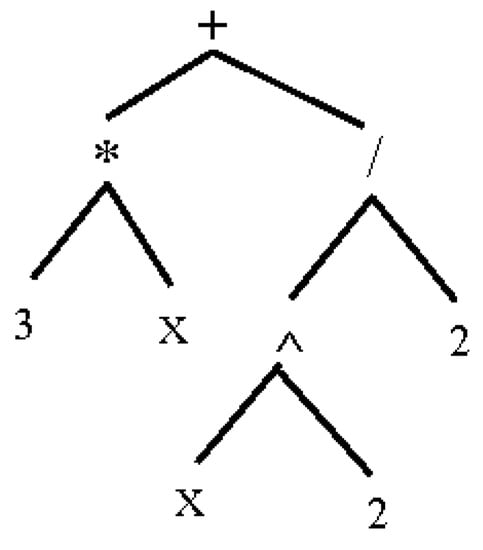
Figure 3.
The AST produced for the expression “3x + x^2/2”.
In fact, this AST is programmatically constructed in the parser as follows:
Exp ast = new Plus(new Time(new Num(3), new Var()), new Divide(new Pow(new Var(), new Num(2)), new Num(2)))
To improve the readability of all AST examples in this paper, we adapt a more elegant representation of the above AST like
Exp ast = Plus(Time(Num(3), Var()), Divide(Pow(Var(), Num(2)), Num(2)))
2.3.6. Evaluation of Mathematical Expressions
The phase of verifying the input data results in the construction of the related AST. The next phase handles the evaluation of this AST. In general, a mathematical expression can be evaluated in two approaches, either directly or using AST of that expression. The first approach refers to the evaluation of the token components of the expression during the verification phase of the parser. The other approach involves evaluating the AST representation of the expression visiting its token residing nodes. These two approaches are described in the following sections.
Direct Evaluation of Mathematical Expressions
The evaluation of simple mathematical expressions can be conducted at the time of parsing. In this case, there is no need to create any data structure from an input expression and the desired evaluation can directly be embedded in the parser. As seen in the previous section, it is possible to issue programming language statements in the process of utilizing parser generator tools. So, the desired operation can be performed by adding the evaluation code into the parser methods. As an example, let us consider calculating a mathematical expression based on a certain value of a variable. For this purpose, the value of the variable is passed as an argument to the methods. Within each method, the corresponding operation is performed on the related piece of the expression, and the result is returned, which can be a double. Listing 7 shows some of these methods of in JavaCC.
A significant difference between the functions given in Listing 5 and Listing 6 is associated with the type of their return values. The functions in Listing 6 must always return a number. Given a simple example of the expression “3x3 + 7x + 1” evaluated for x = 2, the combined process of parameter passing and evaluation will return 39.
| Listing 7. Some JavaCC functions for string-based evaluation. |
| double parse(double x) : { double a; } { a = expr(x) (<EOF> | <EOL>) { return a; } } double expr(double x) : { double a, b; }{ a = term(x) ( <PLUS> b = term(x) { a = a+b; } | <MINUS> b = term(x) { a = a-b; } )* { return a; } } double power(double x) : { double a, b; }{ a = element(x) ( <POWER> b = power(x) { a = Math.pow (a, b); } )? { return a; } } double element(double x) : { Token t; double a;} { t = <NUMBER> { return Double.parseDouble(t.image); } | <X> { return x; } | <LPR> a = expr(x) <RPR> { return a; } | <SIN> <LPR> a = expr(x) <RPR> { return Math.sin(a); } … } |
Evaluation of Mathematical Expressions Using AST
This approach works on the intermediate representation of expressions, which is demonstrated through some particular applications of the methodology in this paper. As we know, the parsing process produces a hierarchical structure of objects with the components of a source expression, namely AST. For an example, input string “3x + x^2/2” will be converted by the parser into an AST as follows:
where the class constructor Var represents the variable x. For the expressions with more than one variable, we can pass the name of the variable as an argument to the constructor. In this paper, we basically use the approach of adding methods into syntax classes. However, in some cases, a combination of two approaches is required to implement the evaluation. In this way, the instanceof operator is mainly used in the methods that are added into the syntax classes. This is due to the need to identify the type of the child of each node, when these nodes are visited. To show the intermediate solution steps, when a node is visited, we need to know if that node has the child for further evaluation. For example, if the type of the child node is Num, it is clear that such nodes would need no more evaluation.
Plus(Time(Num(3), Var()), Divide(Pow(Var(), Num(2)), Num(2))).eval()
2.4. Representation of Mathematical Expressions
On each evaluation step of a mathematical expression through the relevant AST, the resulting expression needs converting into one of human-readable formats such as LaTex, or MathML. This is especially necessary to display the current expression in the AST modified by an evaluation process. Traversing AST with the technique of binary search will allow us to get the proper terms to construct the desired output. Figure 4 shows the AST of the expression “(3cos (x + 1))/2”.
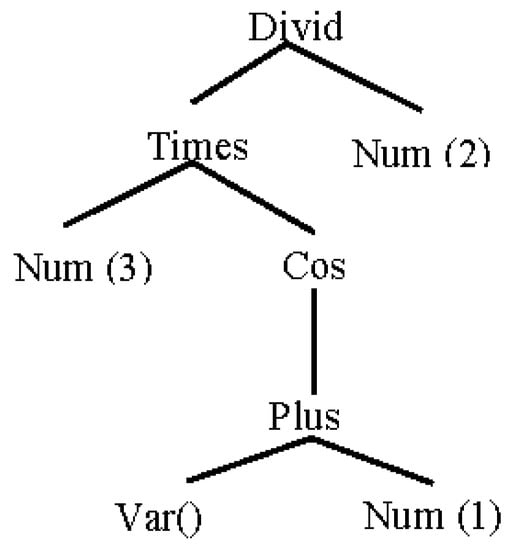
Figure 4.
The AST for the expression “(3cos (x + 1))/2”.
The result of binary traverse or simply syntax tree of Figure 4 is
Divide (Times(Num(3), Cos(Plus(Var(), Num(1)))), Num(2))
To display mathematical expressions on AST, they can be converted to different formats which are addressed in the following sections.
2.4.1. Human-Readable Format
By applying the format-converting methods to each class, the required output format can be generated. Displaying mathematical expressions in human-readable format needs the conversion of the expressions in syntax tree to a string that can be obtained from binary traverse of AST. Table 4 shows the Print methods for some classes.

Table 4.
Print method added to classes to generate human-readable output.
The output of these methods can directly be displayed to the user. Additional codes and methods can be added to produce more pretty results. The output of the methods will be an expression such as, for example, “(3cos(x + 1))/2”.
2.4.2. LaTex Format
LaTex is widely used by scientific community. Similar to other formats of displaying AST in output, a LaTex document can be created by adding outputting codes to parser codes. Table 5 shows the LaTex method provided by some syntax classes, which outputs the Latex-formatted data.

Table 5.
LaTex method to generate LaTex statements.
MathML also accept LaTex input. Therefore, one can export the result to LaTex format and then use MathML renderer to display it. As mentioned before, LaTex is a very popular format and is supported by many other tools.
It is easy to understand the LaTex output; for example, the output of “(3cos(x + 1))/2” in LaTex format is generated as “\frac{(3\sin(x + 1))}{2}”.
2.4.3. MathML Format
MathMl has become very popular due to its use in web-pages. To product a string in MathML format, it is possible to use built-in functions within MathML SDK. However, by adding some simple Print methods, this can also be achieved with AST.
As in the previous section, each syntax class has its own print method, but the output will be wrapped between MathML tags. For example, Num and Var classes must be surrounded with <mi> and <mo> tags, respectively. Table 6 shows the MathML method for some classes.

Table 6.
MathML method to generate MathML statement.
The output of this method requires MathML parser/render, where it needs to be linked within the web-page. As an example, the raw view of “(3cos(x + 1))/2” as well as its rendered form are displayed in Table 7.

Table 7.
MathML example of “(3cos(x + 1))/2”.
2.5. Automatic Simplification
One of important and underlying operations in symbolic computation is simplification. However, it has many difficulties in implementation, because some concepts of simplification are naturally challenging. For example, responding the question “which part is simplified?” will justify this claim.
Automatic simplification is defined as a collection of algebraic and trigonometric simplified transformations that are applied to an expression as a part of the evaluation process.
Table 8 shows some simplifications in classes using the basic transformations.

Table 8.
Simplifications performed in classes.
Transformations, similar to generating output from AST, can be achieved by inserting methods into the simplifier component. More than one transformation might be applied for a simple operator or class. Table 9 shows some methods to implement the simplification.

Table 9.
An implementation of some simplification methods.
The result of the simplification process is also an AST. It can be used instead of the initial AST as it might speed-up the evaluation time if any simplification is performed.
The simplification of expressions is not limited to basic operations that are listed in Table 8. There are other transformations that can be applied by combining basic properties of some operators. The following are some of these samples. As a rule, all simplification methods will be applied until no change is made.
2.5.1. Similar Operands
The summation of two expressions that have similar types, numbers or variables, can easily be performed. Operators are merged and replaced with their evaluation result or more general term, Figure 5.
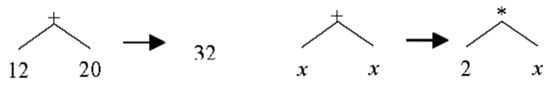
Figure 5.
Simplification of similar operands.
For all Plus nodes, this simplification can easily be applied. Listing 8 shows codes that perform this transformation:
| Listing 8. Simplifying similar operands for Num and Var in Plus. |
| if (exp1 instanceOf Num && exp2 instanceOf Num) return new Num(exp1.getNum()+ exp2.getNum()); if (exp1 instanceOf Var && exp2 instanceOf Var ) return new Times (new Num(2), exp1); |
Figure 6 shows an example of multiple simplifications applied to an AST.
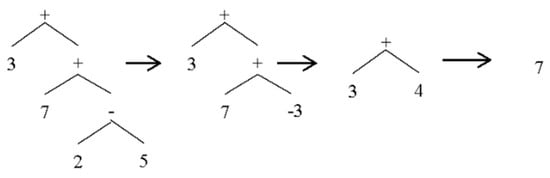
Figure 6.
Simplifying expression “3 + 7 + 2 − 5”.
2.5.2. Similar Operands on Different Levels
Similar operands might be at different levels of AST, therefore normal evaluation of these cases due to different types of operands cannot be performed. Assume that we want to simplify the expression “2 + x + 6 + x”. The equivalent AST for this expression is “Plus(Num(2),Plus(Var(), Plus(Num(6),Var())))”.
The expression in Figure 7 can be simplified to “8 + 2*x”; however, operand types differ at each level of tree. The solution to perform more accurate transformation for Plus is to change the tree from binary to a list and then check if any evaluation can be performed or not. Figure 8 shows the changed structure from Figure 7.
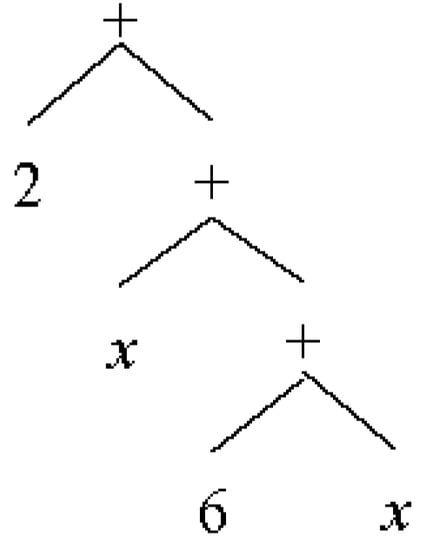
Figure 7.
AST of expression “2+ x + 6 + x”.

Figure 8.
Binary tree to list of operands.
The summation can be applied for all operands in the list, as the operator is a Plus node. To implement this transformation in code, an array list is used to keep all operands of operator nodes. The same code can also be used for Minus, Multiply, and Division nodes.
In each operator node, or class, instead of similar operators, a list of all operands is collected and merged together. Listing 9 shows the related code for collecting the operands of all similar operator nodes.
| Listing 9. Collecting operands for similar operators. |
| public ArrayList<Exp> sameOpList (){ ArrayList<Exp> a=new ArrayList<Exp>(); ArrayList<Exp> b=new ArrayList<Exp>(); if(exp1 instanceOf Plus || exp1 instanceOf Minus) a = exp1.sameOpList(); else a.add(exp1); if(exp2 instanceOf Plus || exp2 instanceOf Minus) b = exp2.sameOpList(); else b.add(exp2); return mergeList(a, b); } |
In Listing 9, mergeList() is a simple method that concatenates two lists. Using basic distributive transformation, the list will be simplified. To add the new result back to the main AST, a new parse will be performed over the result and it will be added as a sub-AST. It is quite possible that some other operators within the Plus or Minus nodes may exist. Therefore, it is also needed to do the same simplifications over those nodes. An example of expression “x + 3 + 2*x” is displayed in Figure 9.
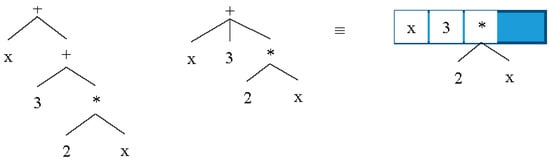
Figure 9.
Structural form of “x + 3 + 2*x” expression.
If no simplification can be done, the process will be aborted. Similar concept is true for other operators.
2.5.3. Fraction Simplification
Numbers and variables can be evaluated and simplified for a fraction operator. This case is similar to basic division transformation. If we consider the structure of the Multiply and Division operators alike, then we can perform the simplification for expressions that have both numbers and variables. Figure 10 shows both the tree and list views of expression “6x/12”.

Figure 10.
Tree and list views of “6x/12”.
In such hybrid cases of numbers and variables, each type will individually be evaluated with the same type and then the results will be merged back as a sub-AST to main AST. In the cases that a number cannot completely be divided by another number, a way for simplifying a fraction is to eliminate common parts or greatest common divisor (GCD). A typical example of the expression “35/30” is shown in Figure 11.
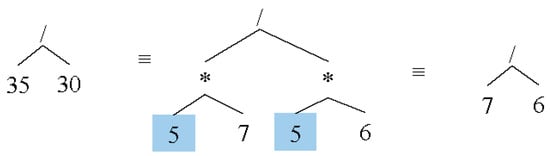
Figure 11.
Simplification stages of expression “35/30”.
If one operand is a fraction, and the one on the other side an integer, then integer operand must be converted to a fraction and then be evaluated for simplifications.
Listing 10 shows changes in Divide class to perform this simplification.
| Listing 10. The simplify() method for Divide class. |
| public class Divide extends Exp { public Exp simplify() { if (exp1 instanceof Divide || exp2 instanceof Divide){ if (!exp1 instanceof Divide) exp1 = new Divide(exp1, new Num(1)); if (!exp2 instanceof Divide) exp2 = new Divide(exp2, new Num(1)); } … //codes for GCD … return new Divide(exp1.simplify(), exp2.simplify()); } } |
If two operands of a fraction are fractions, then they need to be transformed into multiplications and a fraction. We use one of fraction properties for this case, which is shown in Figure 12.
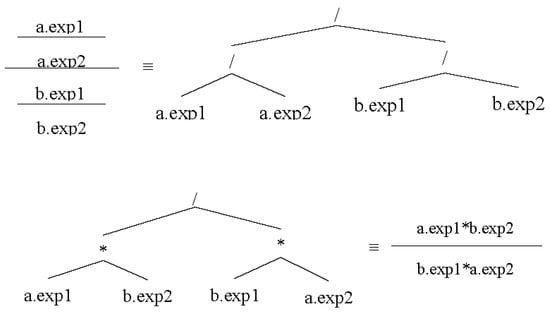
Figure 12.
AST of fraction children of a fraction node.
Listing 11 shows additional codes added to Listing 10 in Divide class.
| Listing 11. Changes in the simplify() method for Divide class. |
| exp1 = new Times(exp1.exp1.simplify(), exp2.exp2.simplify()).simplify(); exp2 = new Times(exp2.exp1.simplify(), exp1.exp2.simplify()).simplify(); … //codes for GCD … |
Figure 13 shows an example of fraction simplification for
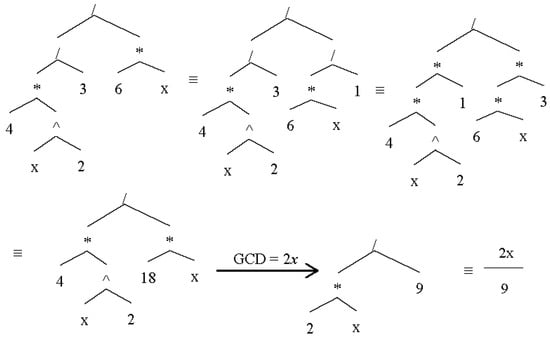
Figure 13.
An example of recursive fraction.
Other complex simplifications can be performed if operator types of Plus or Minus are multiplications or divisions. Here is an example that shows a fraction expression as operands.
This case indicates that if one side of the operator is a fraction, the other side should be a fraction, too. So it has to be converted into a fraction and then will be simplified as a whole new expression. Some modifications applied to the Simplify() method of Plus is displayed in Listing 12.
| Listing 12. Modifications in class Plus. |
| … if (exp1 instanceOf Divide || exp2 instanceOf Divide){ if (!exp1 instanceOf Divide) exp1 = new Divide (exp1, new Num(1)); if (!exp2 instanceOf Divide) exp2 = new Divide (exp2, new Num(1)); Exp a = exp1.exp1; Exp b = exp1.exp2; Exp c = exp2.exp1; Exp d = exp2.exp2; Exp G = polynomialLCM (b, d); a = new Times (a, polynomialDivide(G, b).result); c = new Times (c, polynomialDivide(G, d).result); return new Divide(new Plus(a, c), G); } … |
The same portions of code must be implemented for other classes. However, code factoring can be applied to reduce the number of changes in base codes for each class.
2.5.4. Exponential Simplifications
The use of the power operator is very convenient due to the removal of repeated multiplications for numbers and variables. The exponent part is placed on the top of base by a number or an expression, and refers to the number of times it is multiplied by itself.
The power operator and exponential expressions can be simplified in various ways. An example would be the expression that is equivalent to or xa*b*c in terms of left-associativity.
All exponentials will be considered to be multiplies and will be replaced by only one exponential. Figure 14 shows an example.
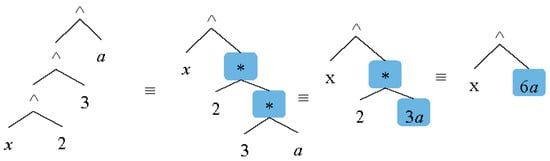
Figure 14.
Simplifying exponential expressions.
In these cases the power operator can be changed to multiple operators. Duplicate powers always appear in exp1 (i.e., left child). It is possible to identify this situation, examining the value of exp1. The Simplify method for Power class must contain the codes in Listing 13.
| Listing 13. Simplify method for Power class. |
| public class Power extends Exp { … public ArrayList<Exp> sameOpList(){ ArrayList<Exp> a = new ArrayList<Exp>(); if(exp2 instanceOf Power ) return mergeList(a, exp2.sameOpList()); else return exp2.simplify(); } … public Exp simplify() { Exp b = exp1.exp1; Exp e = new Num(1); ArrayList<Exp> pow = sameOpList(); for(Exp tmp: pow) e = new Times(e, tmp); return new Power(b, e); } … } |
There is another interpretation of the power operator where the right side of the expression has higher precedence that is to say; the operator is right-associative. For example, the expression will be evaluated as , instead of . Also there are some other cases for power expressions such as un.vn and un.vm.
2.5.5. Removal of Radical Expression in Denomination
If a radical expression appears as a dominator, it can be removed by multiplying that expression to nominator and itself. An example is where the simplified form will be . Another example for this case where the expression is simplified to is shown in Figure 15. Later this can be simplified by the Multiply() method to obtain the result .
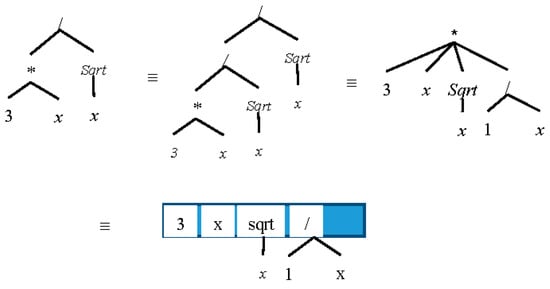
Figure 15.
Simplification of a radical expression as dominator.
Listing 14 shows codes added to Divide class to cover this case.
| Listing 14. Simplify method for Divide class. |
| … if (exp2 instanceof Sqrt){ Exp sq = exp2.exp1; return new Divide(new Times(exp1, sq), sq); } … |
2.5.6. Equality of Expressions
The isEquals() method checks if two expressions are equivalent. The elements of expressions can have different permutations; therefore, isEquals() should detect these differences. An example would be and . Figure 16 shows the related AST for each of these expressions.
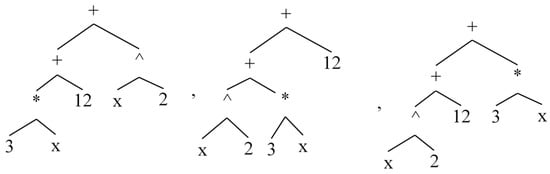
Figure 16.
Equivalent expressions of different ASTs.
However, checking the similarity of expressions seems computationally exhaustive. One solution is to check all permutation of operators and operands and find a matching one. Another solution is to divide two equations; if two equations are equal, then the result will be 1 and a value “true” will be returned. Before division, if nominator and denominator are both zero, then isEquals() directly will return true, which is defined as seen in Listing 15.
| Listing 15. Equality of mathematical expressions. |
| public class Exp{ public boolean isEqual(Exp e) { Exp a = this.simplify(); Exp b = e.simplify(); if(a.eval().equal(“0”) && b.eval().equal(“0”)) return true; Exp res = new Divide(a, b); return res.eval().equal(“0”); } } |
2.5.7. Other Simplifications
In addition to those presented above, there are many other formulas and equations that can be simplified. Here are some transformations for which we develop some code in this work.
However, it is not easy to correctly decide the selection of the related components of an expression for some simplifications. Each component can be a part of different simplifications. The result of the simplification may differ from what one expects, which can be handled by some controlling methods that decide whether it should allow a formula to be factored, expanded or ignored.
2.6. Controlling the Step-by-Step Solution
One goal of the paper is to help students or users to see the solution steps for a given mathematical expression. The solution comes into existence once a user evaluates the expression in an AST. However, a step-by-step solution will increase the user’s understanding of handling an expression. Besides, for hundreds of random expressions, the solution can be produced via the tool prepared with this work, which will be helpful to increase the math solving skill for students.
Automatic evaluation and simplification on an expression are discussed in the previous sections. The solution process uses a method of the recursive implementation of simplification transformations.
The eval() method invoked by the root element of an AST recursively calls the eval() methods of the children. This process will continue, until it reaches to the leaves which are only numbers or variables. The return value of each eval() method is a number, variable or another expression node. It is worth mentioning that, on assigning values to variables, the result will be always a number. Finally the result of the evaluated nodes will be displayed to the user.
Simplifying an expression slightly differs from evaluating it, where all variables should be kept as strings, and also performing each transformation might change the view of the final output. Considering these two properties, at some point, depending on if a user wants to see the steps of the solution, the transformations at each level must be reported.
There are two main techniques that can be used to show each transformation:
- Print the transformation into an output buffer, and continue.
- Return to the root node after performing each transformation
In the first technique, there should always be an object which we can use as a pointer to the address of the output buffer. However, it is also possible to use a static object, or a global method which is accessible by all AST nodes. Each node should call a method to report the changes and therefore, the method must be imported into the classes such as Plus, Multiply and Sin. Other approaches like addressing one node or retrieving parent nodes with the transformations to them also require extra methods and data to access the parent nodes.
However, in the second technique, a flag is used to check if a simplification should be performed or not. In this method, once a change is applied to the related AST, it triggers the flag and stops the simplification process for other nodes. The effect of this action will be only one change at a time, and therefore, it must be done with a loop. In each time, we reset the flag and then continue the process until there is no more simplifications to perform in which case the flag status stays the same. Listing 16 shows the main loop for simplifications.
| Listing 16. The main loop for simplifications. |
| public Exp performSimplification(Exp root){ do{ Controls.resetFlags(); root = root.simplify(); if(Controls.hasError() != null){ System.out.println(Controls.getError()); return null; } root.Print(); } while ( Controls.isSkipSimplifying() ); root.Print(); return root; } |
The second technique guarantees that we obtain the exact AST at each iteration of the loop, so we can call the Print() method of the AST in one position. Listing 17 shows the relevant code added to the simplify() method of each class.
| Listing 17. Modifications for the simplify() method. |
| public Exp simplify(){ if(Controls.isSkipSimplifying()) return this; … // rest of the codes simplifying the element … // in case of performing any // simplification call Controller.skipSimplification(); … } |
Expression Simplification Control
Each step of simplification can be controlled by a class called Controls which denotes which transformation to perform or not. As an example, we use a skip simplification method, isSkipSimplifying(), when we want to return to the main loop and report the current state of the AST. Another example is hasError() where we can perform illegal evaluations like division by zero, negative value for root square, etc.
Varieties of other flags are used to control each transformation. Some of these flags are listed in Table 10.

Table 10.
Some of variables and their applications.
These flags are customizable for each object. Listing 18 shows an example of how to control the removal of a fraction in dominator.
The same controls can be added to other objects as well. However, to control errors, some code will be added to eval() method of each class. Division by zero and other mathematical errors are semantic ones that should have to be prevented. Syntactical errors have been resolved once we create AST, so no such errors will occur.
| Listing 18. The control of the simplification of radical removal using control flags. |
| public Exp simplify(){ if(Controls.isSkipSimplifying()) return this; … if (exp2 instanceof Sqrt && Controls.isSqrtRemoveal()){ Exp sq = exp2.exp1; // Notify the transformation to controller Controller.skipSimplification(); return new Divide(new Times(exp1, sq), sq); } … } |
3. Conclusions and Results
In this paper, we propose a grammar-based methodology for step-by-step solving of mathematical problems. The methodology is basically designed to handle algebraic expressions that can be evaluated or simplified into a more concise form. From this perspective, on the contrary of numerical computation methods, we aim to produce the exact values of mathematical expressions, using symbolic computation approaches. There are many algebra-related topics such as simplification, factorization, distribution and substitution that can easily be covered by the solution methodology. The study currently supports univariate operations on these algebra topics, but can also be adapted to operate on multivariate expressions. It can make a crucial contribution to the practical application of mathematics via software. The underlying structure can be used to develop mathematical problem-solving systems. The other outcome can be the easier production of educational systems, where the intermediate solution steps of a problem can be integrated with such systems to fulfill regular learning or teaching requirements.
The form of expressions is represented via LL(1) grammars that exhibit an unambiguous aspect. Using the JavaCC tool, we develop LL(1) parsers which always follow a unique derivation for every kind of mathematical expressions. The implementation of such parsers is relatively easy as it involves the mapping of the grammar rules into corresponding methods. We illustrate the use of the tool through the implementation of the different parts of the solution methodology.
We model an input expression by using Abstract Syntax Tree (AST) which has a hierarchical structure. The tree represents the precedence and associativity of operators, and thus establishes the semantic-based relations among its nodes. It is quite possible to make the different interpretations of an AST, however, we use it to evaluate simplify and optimize the expressions. The well-known applications such as LISP and Maxima use a similar tree structure for manipulation of expressions.
Using AST, the step-by-step solutions for mathematical expressions are proposed. The simplification ways of equations and similar expressions are discussed. Simplifying a node in an AST simply depends on the type of that node. Different occurrences of an operator or function node and its children confront different simplifications or transformations. Each transformation resolves a part of the complexity that exists in a node.
AST supports the execution of the evaluating operations in a recursive manner. In this way, the simplification process goes down in the tree until it encounters the leaves that contain numbers or variables and terminates when transformation cannot further be applied to the tree. However, there are some special cases where we need to define control flags, for example, to decide how to use algebraic identities (i.e., product and factoring formulas). This is to prevent those formulas from triggering several times, ensuring that no infinite loops occur.
A different type of mathematical expressions requires a different style of simplification. We introduce some basic and sophisticated transformations on AST nodes, but they can be extended to construct new ones operating on other states of nodes. The examples of basic transformations are commutative and power, and the examples of sophisticated transformations are linearization of nested operators; fraction, power and radical simplifications, and radical removal from fractions.
In terms of the step-by-step solution, these transformations of the simplification process are considered as the steps of solving the problem. The result of each transformation is a new AST; therefore this operation advances the solution one step towards the final one.
Various documents or reports can be produced to print the applied transformations and the resulting expression. We prefer to use a document formatting system in which the content of AST is printed. The differences between two consecutive prints of the output show the progress of solving the given input through a symbolic computation system.
The evaluation of AST is quite simple. The tree contains variables and numbers, therefore by initializing variables such as x, a, and b into some values, the numerical result can be calculated.
Several experiments are conducted to compare the benefits and drawbacks of the proposed methodology. We use Matlab Symbolic Computation Toolbox and a real person as our test competitors. The results are listed in Table 11.

Table 11.
Symbolic calculation of some math questions.
For further analysis of the solution methodology, we conduct some experiments for time complexity. The results are listed in Table 12.

Table 12.
Time and space complexity.
In the methodology, a new recursive model based on AST is used. With object-oriented features in programming languages, it is easy to implement various transformations suggested for simplifications. The step-by-step solutions can be reported using each applied transformation.
Given the issues that can be determined comprehensively and recursively, the experimental results are very favorable. Particularly, one result demonstrates the high percentage of the similarities between the steps of the automatic solution of the problem and the steps of solving it manually. In addition, it leads to a useful structure for those who want to work with mathematical expressions, supporting the development of iterative or recursive methods in applying the basic rules of mathematical operations. An important one of the observed disadvantages is that the methodology fails if a solution strategy needs to solve a problem by transforming it into another one. Compared to manual solving, this involves additional solution steps with the aim of determining the type of the problem and applying another solution strategy.
The methodology currently deals with arithmetic, polynomial, and algebraic expressions. Due to the different characteristics that other types of mathematical expressions can have, the underlying structure may need to be modified. Besides, the methodology attempts to solve problems under normal circumstances, and must be extended for other ones. For example, to find the limit of an expression involving multiple functions, first it must be checked if it is a limit of indeterminate forms. If this is the case, a different method must be considered in accordance with the indeterminate form.
Author Contributions
S.H., M.M.R.A.M. and H.P. contributed to the design and implementation of the methodology, to the achievement of the results and to the writing of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Finkel, R.A.; Finkel, R.A. Advanced Programming Language Design; Addison-Wesley Reading: Boston, MA, USA, 1996. [Google Scholar]
- Watt, D.A.; Findlay, W.; Hughes, J. Programming Language Concepts and Paradigms; Prentice Hall Englewood Cliffs: Upper Saddle River, NJ, USA, 1990; Volume 234. [Google Scholar]
- Thisted, R.A. Elements of Statistical Computing: Numerical Computation; Routledge: Abingdon, UK, 2017. [Google Scholar]
- Van Hulzen, J.; Calmet, J. Computer algebra systems. In Computer Algebra; Springer: Berlin/Heidelberg, Germany, 1983; pp. 221–243. [Google Scholar]
- Dunham, P.H.; Dick, T.P. Research on graphing calculators. Math. Teach. 1994, 87, 440. [Google Scholar]
- Palmiter, J.R. Effects of computer algebra systems on concept and skill acquisition in calculus. J. Res. Math. Educ. 1991, 22, 151–156. [Google Scholar] [CrossRef]
- Artigue, M. Learning mathematics in a cas environment: The genesis of a reflection about instrumentation and the dialectics between technical and conceptual work. Int. J. Comput. Math. Learn. 2002, 7, 245. [Google Scholar] [CrossRef]
- Pfister, G.-M.G.G.; Schonemann, H. Singular—A Computer Algebra System for Polynomial Computations. In Symbolic Computation and Automated Reasoning: The CALCULEMUS-2000 Symposium; AK Peters/CRC Press: Bocaton, FL, USA, 2001; p. 227. [Google Scholar]
- Peeters, K. Introducing cadabra: A symbolic computer algebra system for field theory problems. arXiv, 2007; arXiv:hep-th/0701238. [Google Scholar]
- Kajler, N. Cas/pi: A Portable and Extensible Interface for Computer Algebra Systems. In Proceedings of the Papers from the International Symposium on Symbolic and Algebraic Computation, Berkeley, CA, USA, 27–29 July 1992; ACM: New York, NY, USA, 1992; pp. 376–386. [Google Scholar]
- Hosseinpour, S.; Milani, M.M.R.A.; Pehlivan, H. A grammar-based methodology for producing mathematical expressions. Int. J. Innov. Stud. Sci. Eng. Technol. 2017, 3, 27–36. [Google Scholar]
- Gulwani, S.; Korthikanti, V.A.; Tiwari, A. Synthesizing Geometry Constructions; ACM SIGPLAN Notices; ACM: New York, NY, USA, 2011; pp. 50–61. [Google Scholar]
- Singh, R.; Gulwani, S.; Rajamani, S.K. Automatically Generating Algebra Problems; AAAI: Palo Alto, CA, USA, 2012. [Google Scholar]
- Rasila, A.; Harjula, M.; Zenger, K. Automatic Assessment of Mathematics Exercises: Experiences and Future Prospects. In Proceedings of the ReflekTori 2007 Symposium of Engineering Education, Espoo, Finland, 3–4 December 2007; pp. 70–80. [Google Scholar]
- Rasila, A.; Havola, L.; Majander, H.; Malinen, J. Automatic assessment in engineering mathematics: Evaluation of the impact. In Proceedings of the ReflekTori 2010 Symposium of Engineering Education, Espoo, Finland, 9–10 December 2010; pp. 37–45. [Google Scholar]
- Cohen, J.S. Computer Algebra and Symbolic Computation: Mathematical Methods; Universities Press: Telangana, India, 2003. [Google Scholar]
- Von zur Gathen, J.; Gerhard, J. Modern Computer Algebra; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Buchberger, B.; Loos, R. Algebraic simplification. In Computer Algebra; Springer: Berlin/Heidelberg, Germany, 1982; pp. 11–43. [Google Scholar]
- Moses, J. Algebraic Simplification A Guide for the Perplexed. In Proceedings of the Second ACM Symposium on Symbolic and Algebraic Manipulation, Los Angeles, CA, USA, 23–25 March 1971; ACM: New York, NY, USA, 1971; pp. 282–304. [Google Scholar]
- Shatnawi, M.; Youssef, A. Equivalence Detection Using Parse-Tree Normalization for Math Search. In Proceedings of the 2nd International Conference on Digital Information Management, Lyon, France, 28–31 October 2007; pp. 643–648. [Google Scholar]
- Youssef, A.; Shatnawi, M. Math search with equivalence detection using parse-tree normalization. In Proceedings of the 4th International Conference on Computer Science and Information Technology, Yangon, Myanmar, 23–24 February 2006. [Google Scholar]
- Apostolico, G. Pattern Matching Algorithms; Oxford University Press on Demand: Don Mills, ON, Canada, 1997. [Google Scholar]
- Zhang, K.; Shasha, D. Simple fast algorithms for the editing distance between trees and related problems. SIAM J. Comput. 1989, 18, 1245–1262. [Google Scholar] [CrossRef]
- Demana, F.; Waits, B.K. Calculators in mathematics teaching and learning. Past, present, and future. In Learning Mathematics for a New Century; National Concil of Teachers of Mathematics: Reston, VA, USA, 2000; pp. 51–66. [Google Scholar]
- Judson, P.T. Effects of Modified Sequencing of Skills and Applications in Introductory Calculus; University of Texas at Austin: Austin, TX, USA, 1988. [Google Scholar]
- Runde, D.C. The Effect of Using the ti-92 on Basic College Algebra Students’ Ability to Solve Word Problems; ERIC Document Reproduction Service No. ED409046; Manatee Community College: Bradenton, FL, USA, 1997. [Google Scholar]
- Brown, R. Computer Algebra Systems in the Junior High School. In Proceedings of the 3rd International Derive/TI-92 Conference, Gettysburg, PA, USA, 14–17 July 1998. [Google Scholar]
- Drijvers, P. Assessment and new technologies: Different policies in different countries. Int. J. Comput. Algebra Math. Educ. 1998, 5, 81–94. [Google Scholar]
- Heid, M.K. Resequencing skills and concepts in applied calculus using the computer as a tool. J. For Res. Math. Educ. 1988, 1, 3–25. [Google Scholar] [CrossRef]
- Herget, W.; Heugl, H.; Kutzler, B.; Lehmann, E. Indispensable Manual Calculation Skills in a Cas Environment. Micromath 2000, 16, 8–17. [Google Scholar]
- Bennett, G. Calculus for general education in a computer classroom. Int. Derive J. 1995, 2, 3–11. [Google Scholar]
- Day, R.P. Algebra and technology. J. Comput. Math. Sci. Teach. 1993, 12, 29–36. [Google Scholar]
- Tall, D. Functions and calculus. In International Handbook of Mathematics Education; Springer: Berlin/Heidelberg, Germany, 1996; pp. 289–325. [Google Scholar]
- Heid, M.K. The technological revolution and the reform of school mathematics. Am. J. Educ. 1997, 106, 5–61. [Google Scholar] [CrossRef]
- Repo, S. Understanding and reflective abstraction: Learning the concept of derivative in a computer environment. Int. Derive J. 1994, 1, 97–113. [Google Scholar]
- Small, D.B.; Hosack, J.M. Computer algebra system, tools for reforming calculus instruction. In Toward a Lean and Lively Calculus; Tulane University: New Orleans, LA, USA, 1986; pp. 143–155. [Google Scholar]
- Hearst, M.A. The debate on automated essay grading. IEEE Intell. Syst. Their Appl. 2000, 15, 22–37. [Google Scholar] [CrossRef]
- Mohler, M.; Bunescu, R.; Mihalcea, R. Learning to grade short answer questions using semantic similarity measures and dependency graph alignments. In Proceedings of the 49th Annual Meeting of the Association for Computational Linguistics: Human Language Technologies—Volume 1, Portland, OR, USA, 19–24 June 2011; pp. 752–762. [Google Scholar]
- Farnsworth, C.C. Using computer simulations in problem-based learning. In Proceedings of the Thirty-Fifth ADCIS Conference, Nashville, TN, USA, 15–19 February 1994; pp. 137–140. [Google Scholar]
- Kashy, E.; Sherrill, B.; Tsai, Y.; Thaler, D.; Weinshank, D.; Engelmann, M.; Morrissey, D. Capa—An integrated computer-assisted personalized assignment system. Am. J. Phys. 1993, 61, 1124–1130. [Google Scholar] [CrossRef]
- Dragon, T.; Mavrikis, M.; McLaren, B.M.; Harrer, A.; Kynigos, C.; Wegerif, R.; Yang, Y. Metafora: A web-based platform for learning to learn together in science and mathematics. IEEE Trans. Learn. Technol. 2013, 6, 197–207. [Google Scholar] [CrossRef]
- Gutierrez-Santos, S.; Geraniou, E.; Pearce-Lazard, D.; Poulovassilis, A. Design of teacher assistance tools in an exploratory learning environment for algebraic generalization. IEEE Trans. Learn. Technol. 2012, 5, 366–376. [Google Scholar] [CrossRef]
- Barker, D.S. Charlie: A Computer-managed homework, assignment and response, learning and instruction environment. In Proceedings of the Frontiers in Education 1997 27th Annual Conference, Teaching and Learning in an Era of Change, Pittsburgh, PA, USA, 5–8 November 1997; pp. 1503–1509. [Google Scholar]
- Baldwin, D. Three Years’ Experience with Gateway Labs; ACM SIGCSE Bulletin: New York, NY, USA, 1996; pp. 6–7. [Google Scholar]
- Bridgeman, S.; Goodrich, M.T.; Kobourov, S.G.; Tamassia, R. Pilot: An Interactive Tool for Learning and Grading; ACM SIGCSE Bulletin: New York, NY, USA, 2000; pp. 139–143. [Google Scholar]
- Brooker, R. The Solution of Algebraic Equations on the Edsac; Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1952; pp. 255–270. [Google Scholar]
- Maehly, H.J. Zur iterativen auflösung algebraischer gleichungen. Zeitschrift für Angewandte Mathematik und Physik ZAMP 1954, 5, 260–263. [Google Scholar] [CrossRef]
- Butler, G.; Cannon, J. The Design of Cayley—A Language for Modern Algebra. In Proceedings of the International Symposium on Design and Implementation of Symbolic Computation Systems, Gmunden, Austria, 15–17 September 1993; Springer: Berlin/Heidelberg, Germany, 1990; pp. 10–19. [Google Scholar]
- Schönert, M.; Besche, H.U.; Breuer, T.; Celler, F.; Eick, B.; Felsch, V.; Hulpke, A.; Mnich, J.; Nickel, W.; Pfeiffer, G. Groups Algorithms and Programming; Lehrshuhl D fur Mathematik, RWTH Aachen: Aachen, Germany, 1994. [Google Scholar]
- Capani, A.; Niesi, G. Cocoa User’s Manual (v. 3.0 b); Department of Mathematics, University of Genova: Genova, Italy, 1996. [Google Scholar]
- Van Leeuwen, M. Lıe, a software package for lie group computations. Euromath. Bull. 1994, 1, 83–94. [Google Scholar]
- Kurz, T.L.; Middleton, J.A.; Yanik, H.B. A taxonomy of technological tools for mathematics instruction. Contemp. Issues Technol. Teach. Educ. 2005, 5, 123–137. [Google Scholar]
- Handal, B.; Herrington, A. Mathematics teachers’ beliefs and curriculum reform. Math. Educ. Res. J. 2003, 15, 59–69. [Google Scholar] [CrossRef]
- Johnson, S.C. Yacc: Yet Another Compiler-Compiler; Bell Laboratories: Murray Hill, NJ, USA, 1975; Volume 32. [Google Scholar]
- Levine, J.R.; Levine, J.R.; Mason, T.; Brown, D. Lex & Yacc; O’Reilly Media, Inc.: Sebastopol, CA, USA, 1992. [Google Scholar]
- Kodaganallur, V. Incorporating language processing into java applications: A javacc tutorial. IEEE Softw. 2004, 21, 70–77. [Google Scholar] [CrossRef]
- Viswanadha, S. Java Compiler Compiler (javacc)—The Java Parser Generator. Available online: https://javacc.org/ (accessed on 15 April 2018).
- Ryan, C.; O’Neill, M.; Collins, J. Grammatical Evolution: Solving Trigonometric Identities. In Proceedings of the Mendel, Brno, Czech Republic, 24–26 June 1998. [Google Scholar]
- Donnelly, C.; Stallmen, R. The Bison Manual: Using the Yacc-Compatible Parser Generator, for Bison Version 1.875; GNU Press: Boston, MA, USA, 2004. [Google Scholar]
- Earley, J. An efficient context-free parsing algorithm. Commun. ACM 1970, 13, 94–102. [Google Scholar] [CrossRef]
- Gill, A.; Marlow, S. Happy: The Parser Generator for Haskell; University of Glasgow: Glasgow, Scotland, UK, 1995. [Google Scholar]
- Graver, J.O. The evolution of an object-oriented compiler framework. Softw. Pract. Exp. 1992, 22, 519–535. [Google Scholar] [CrossRef]
- Hudson, S. Javacup: Lalr Parser Generator for Java; GVU Center, Georgia Institute of Technology: Atlanta, GA, USA, 1996. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).