1. Introduction
An interesting topic in graph theory is the study of the different types of products of graphs [
1]. In particular, given two graphs
, the
direct product is defined as the graph with vertices the (Cartesian) product of
and
, and two vertices
are connected by an edge if and only if
and
. The direct product is associative and commutative. Direct product was introduced in Principia Mathematica by Russell and Whitehead.
Weichsel observed that
is connected if and only if the graphs
and
are connected and
or
is not a bipartite graph [
2], i.e., there exists an odd cycle. The direct product is known with different names: tensor product, conjunction, categorical product, Kronecker product and cardinal product. There are many works studying several properties of direct products. These works include structural results [
3,
4,
5,
6,
7,
8], hamiltonian properties [
9,
10], and above all the well-known Hedetniemi’s conjecture (see [
11,
12]). Imrich has an algorithm in [
13] which can recognize in polynomial time if a graph is a direct product; furthermore, the algorithm provides a factorization if the graph is a direct product. This fact facilitates the computational use of the direct product of graphs.
Hyperbolic spaces are an important tool in geometry and group theory [
14,
15,
16]. Gromov hyperbolicity is a meeting point for different spaces: some of them continuous (hyperbolic plane and many Riemannian manifolds with negative curvature) and some of them discrete (trees and many graphs) [
14,
15,
16].
Gromov hyperbolicity was introduced in the context of finitely generated groups [
16], and it was applied, in the science of computation, to the study of automatic groups [
17,
18]. Gromov hyperbolicity is useful in networking, algorithms and discrete mathematics [
19,
20,
21,
22,
23,
24]; also, many real networks are hyperbolic [
25,
26,
27,
28,
29]. Besides, there are several important applications of hyperbolic spaces to the Internet [
30,
31,
32,
33,
34] and to random graphs [
35,
36,
37]. It has recently been pointed out that also some aspects of biological systems require hyperbolicity for proper functioning [
38]. In [
39], it was proven that, for a large class of Riemannian surfaces endowed with a metric of negative curvature, there is a very simple graph related with the surface such that the surface is hyperbolic if and only if the graph is hyperbolic; therefore, it is interesting to study hyperbolic graphs to understand hyperbolic surfaces.
All these facts show the increasing interest of hyperbolic graphs (see, e.g., [
19,
24,
25,
26,
27,
32,
33,
35,
36,
37,
39,
40,
41,
42,
43,
44,
45,
46,
47] and the references therein).
In this paper, let us denote by a connected graph with . We consider that the length of each edge is 1. In addition, we assume that the graph does not have either multiple edges or loops.
Trees are the graphs with hyperbolicity constant zero. Thus, we can view the hyperbolicity constant as a measure of how “tree-like” the space is. This is an important subject (see, e.g., [
48,
49]).
From a computational viewpoint, we can obtain
in time
for graphs with
n vertices [
50]. In addition, there is an algorithm which decides if a Cayley graph is hyperbolic [
51]. In [
52], this algorithm is improved, allowing to obtain
in time
, but only if the graph is given in terms of its distance-matrix. However, it is usually very difficult to decide if an infinite graph is hyperbolic. Therefore, it is useful to study hyperbolicity for particular classes of graphs. There are many works dealing with the hyperbolicity of different types of graphs: median graphs [
53], line graphs [
54,
55,
56], cubic graphs [
57], complement graphs [
58], regular graphs [
59], chordal graphs [
25,
42,
45,
60], planar graphs [
61,
62], bipartite and intersection graphs [
63], vertex-symmetric graphs [
64], periodic graphs [
65,
66], expanders [
34], bridged graphs [
67], short graphs [
68], graph minors [
69], graphs with small hyperbolicity constant [
70], Mycielskian graphs [
71], geometric graphs [
56,
72], and some types of products of graphs: Cartesian product and sum [
46,
73], strong product [
74], lexicographic product [
75], and corona and join product [
76].
Some of these works give results about the hyperbolicity of some unary operations in graphs:
A line graph is hyperbolic if and only if the original graph does [
54,
55,
56].
For a large class of minor graphs, the minor graph is hyperbolic if and only if the original graph does [
69].
Mycielskian graphs are always hyperbolic [
71].
Now, we summarize the known results about the hyperbolicity of the main class of binary operations in graphs: products of graphs.
The Cartesian product is hyperbolic if and only if one factor graph is bounded and the other one is hyperbolic [
46].
The same holds for the strong product [
74].
The corona product
is hyperbolic if and only if the first factor
is hyperbolic, and the join
is always hyperbolic [
76].
The Cartesian sum
is always hyperbolic, if the factors have at least two vertices [
73].
The lexicographic product graph
is hyperbolic if and only if
does, if the first factor has at least two vertices [
75].
The goal of this paper is the characterization in many cases of the direct product of graphs which are hyperbolic. Here, the situation is more complicated than with other products of graphs. This is partly because the direct product of two bipartite graphs (i.e., graphs without odd cycles) is already disconnected and the formula for the distance in is more complicated that in the case of other products of graphs. The symmetry of this product allows us to show that, if is hyperbolic, then one factor is hyperbolic and the other one is bounded (see Theorem 10). Besides, we prove that this necessary condition is also sufficient in many cases. If is a hyperbolic graph and is a bounded graph, then we prove that is hyperbolic when has some odd cycle (Theorem 3) or and do not have odd cycles (Theorem 4). One could think that otherwise (if has some odd cycle and does not have odd cycles) this necessary condition is also sufficient; however, Theorem 15 allows constructing in an easy way examples (with hyperbolic and bounded) such that is not hyperbolic. This shows that the characterization of hyperbolic direct products is a more difficult task when has some odd cycle and does not have odd cycles. Theorems 11 and 12 provide sufficient conditions for non-hyperbolicity and hyperbolicity, respectively. Besides, Theorems 15 and Corollary 5 characterize the hyperbolicity of under some additional conditions. Furthermore, we obtain good bounds, and even formulas in many cases, for the hyperbolicity constant of the direct product of some important graphs; in particular, Theorem 18 provides the hyperbolicity constant of many direct products of bipartite graphs, and Theorems 17 and 19 give the hyperbolicity constant of many direct products of path and cycle graphs.
We want to remark that, in a general context, the hypothesis on the existence (or non-existence) of odd cycles is artificial in the context of Gromov hyperbolicity. However, it is an essential hypothesis in the works on direct products (see Theorem 1). Throughout the development of this work, we have verified that the existence of odd cycles is also essential in the study of hyperbolic product graphs.
2. Definitions and Background
Let be a metric space, and denote by L the length associated to the distance d. A geodesic is a curve satisfying for every (here, is the restriction of g to ). We say that the metric space X is a geodesic metric space if for each there is a geodesic connecting them; we denote by any geodesic form p to q. Hence, a geodesic metric space is a connected space. When X is a graph and , denotes the edge connecting p and q if they are adjacent.
Along this paper, we consider the graphs as geodesic metric spaces. To do that, we identify any edge with the real interval ; therefore, the points in a graph are the vertices and also the points in the interior of the edges. Hence, we can define a natural distance on the points of a connected graph G by taking shortest paths in G, and so, we consider G as a metric graph. If p and q are points in different connected components of the graph, we define .
Some authors do not consider the internal points of edges in the study. Although this approach has some advantages, we prefer to consider the internal points since these graphs are geodesic metric spaces. We use this approach since to work with geodesic metric spaces provides an interesting geometric viewpoint (for instance, Theorem 2 holds for geodesic metric spaces).
Given a geodesic metric space X and three points , the geodesic triangle is the union of three geodesics , and . The points are the vertices of the triangle T. The geodesic triangle T is -thin if any side of T is contained in the -neighborhood of the union of the two other sides. We define the thin constant of the triangle T by and the hyperbolicity constant of the space X as The space X is hyperbolic if , and it is -hyperbolic if X is hyperbolic and the constant satisfies . We say that a triangle with two identical vertices is a “bigon”. Of course, each bigon in a space (which is -hyperbolic) is -thin. If are the connected components of X, then we can define , and X is hyperbolic if and only if .
We want to remark that in the classical references on hyperbolicity [
14,
15,
77] appear many different definitions of Gromov hyperbolicity. However, the definitions are equivalent: if
X is
-hyperbolic for a definition, then it is
-hyperbolic for every definition, where the constant
can be obtained from
.
We refer to the classical book [
1] for definitions and background about direct product graphs.
We need bounds for the distance between points in the direct product. We use the definition given in [
1].
Definition 1. Let and be two graphs. Thedirect product of and has as vertex set, so that two distinct vertices and of are adjacent if and .
If and are isomorphic, we write . It is clear that, if , then .
It is clear that the direct product of two graphs is commutative, i.e., . Therefore, the conclusion of every result in this paper with some “non-symmetric” hypothesis also holds if we change the roles of and (see, e.g., Theorems 3, 4, 11, 12 and 15 and Corollary 5).
Denote by the projection map for . In fact, this projection is well defined as a map for .
We need some previous results of [
1]. If
, then by a
-
walk in
G we mean a path joining
u and
where repeating vertices is allowed.
Proposition 1. ([1], Proposition 5.7) Suppose and are vertices of the direct product , and n is an integer for which has a -walk of length n and has a -walk of length n. Then, has a walk of length n from to . The smallest such n (if it exists) equals . If no such n exists, then . Proposition 2. ([1], Proposition 5.8) Suppose x and y are vertices of . Then,where it is understood that if no such n exists. Definition 2. If G is a connected graph, the diameter of its vertices isand the diameter of G is Corollary 1. We have for every and, consequently, Furthermore, if and have the same parity, thenand, consequently, By trivial graph, we mean a graph which has only a vertex.
The following result characterizes when a direct product is connected. By cycle, we mean a simple closed curve, i.e., a path with different vertices, unless the last one, which is equal to the first vertex.
Theorem 1. ([1], Theorem 5.9) Suppose and are connected non-trivial graphs. If at least one of or has an odd cycle, then is connected. If both and are bipartite, then has exactly two connected components. Corollary 2. ([1], Corollary 5.10) A direct product of connected non-trivial graphs is connected if and only if at most one of the factors is bipartite. In fact, the product has connected components, where k is the number of bipartite factors. Consider the metric spaces
and
. Given constants
, a map
is an
-
quasi-isometric embedding if
for
. We say that
f is
-
full if for each
there is
with
.
We say that f is a quasi-isometry if there exist constants such that f is an -full -quasi-isometric embedding.
Two metric spaces X and Y are quasi-isometric if there exists a quasi-isometry . One can check that to be quasi-isometric is an equivalence relation. An -quasi-geodesic in X is an -quasi-isometric embedding between an interval of and X.
We need the following result ([
15], p. 88).
Theorem 2 (Invariance of hyperbolicity). Let be an -quasi-isometric embedding between the geodesic metric spaces X and Y. If Y is -hyperbolic, then X is -hyperbolic, where is a constant which just depends on .
Besides, if f is ε-full for some (a quasi-isometry) and X is -hyperbolic, then Y is -hyperbolic, where is a constant which just depends on .
There are several explicit expressions for
, some of them very complicated. In [
78] appears the best possible formula for
:
for some explicit constants
.
3. Hyperbolic Direct Products
Let us start with a necessary condition for hyperbolicity.
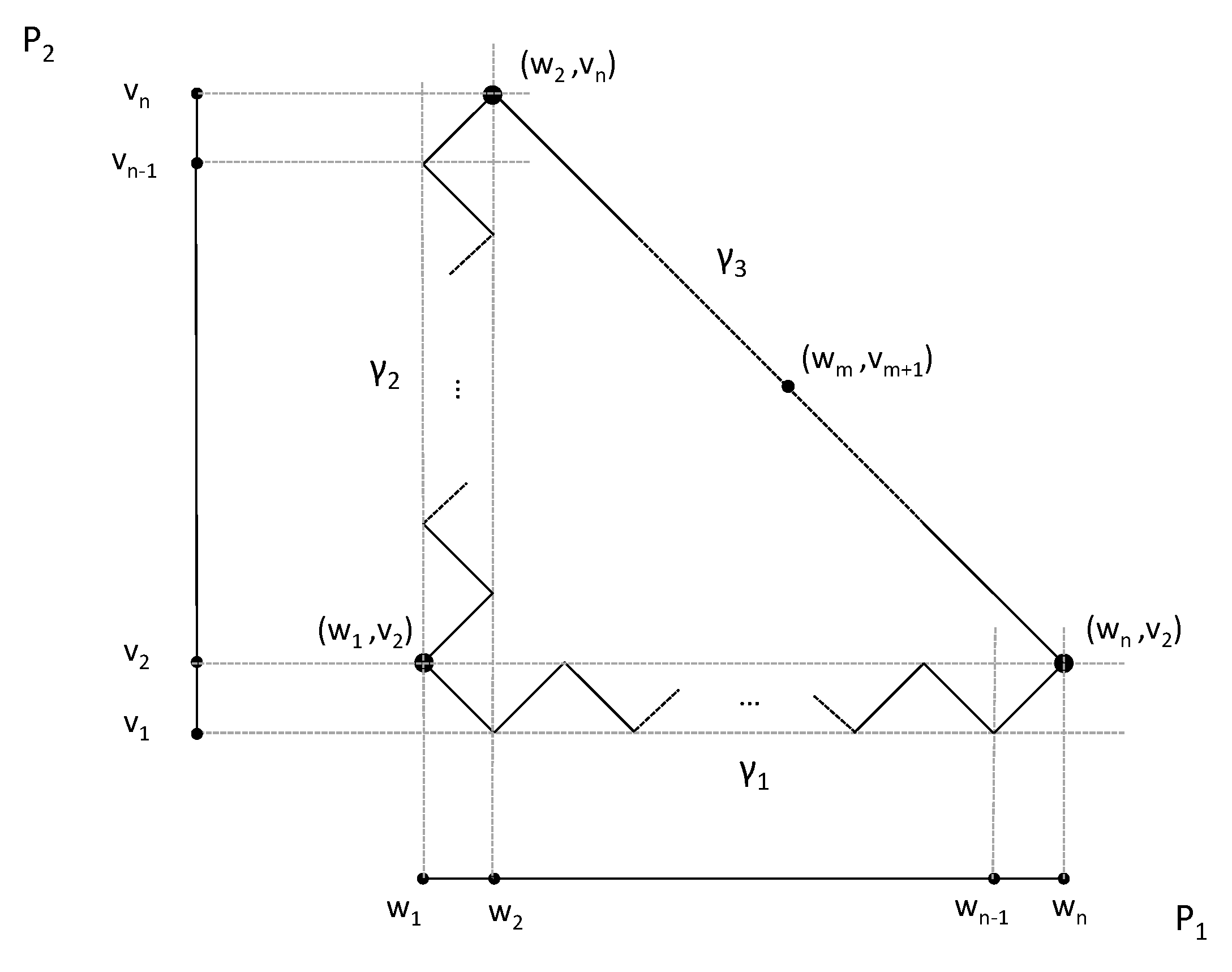
Proposition 3. Let and be two unbounded connected graphs. Then, is not hyperbolic.
Proof. Since
and
are unbounded graphs, for each positive integer
n there exist two geodesic paths
in
and
in
. If
n is odd, then we can consider the geodesic triangle
T in
(see
Figure 1) defined by the following geodesics:
Corollary 1 gives that are geodesics.
Let and consider the vertex in . For every vertex in , we have by Corollary 1. We have for every vertex in , , by Corollary 1, . Hence, and . Since n is arbitrarily large, is not hyperbolic. □
Lemma 1. Consider two connected graphs and . If is an -quasi-isometric embedding, then there exists an -quasi-isometric embedding with on . In addition, if f is ε-full, then g is -full.
Proof. For each
, let us choose a closest point
from
x, and define
. Note that
if
and so
on
. Given
we have
and
g is an
-quasi-isometric embedding, since
.
In addition, if f is -full, then g is -full since . □
Given a graph G, let denote the odd girth of G, that is, the length of the shortest odd cycle in G.
Theorem 3. Let be a connected graph and be a non-trivial bounded connected graph with some odd cycle. Then, is hyperbolic if and only if is hyperbolic.
Proof. Fix with contained in an odd cycle C with . Consider the map such that for every .
By Corollary 1, for every , . In addition, Proposition 2 gives the following.
If a geodesic joining
and
has even length, then
If a geodesic joining
and
has odd length, then
C defines a
-walk with odd length and
Thus, i is a quasi-isometric embedding.
Consider any
. Then, if the geodesic joining
v and
has even length,
If a geodesic joining
v and
has odd length,
defines a
-walk with even length. Therefore,
Thus, i is -full.
Hence, by Lemma 1, there is a -full -quasi-isometry, , and is hyperbolic if and only if is hyperbolic by Theorem 2. □
Theorem 4. Let be a connected graph without odd cycles and be a non-trivial bounded connected graph without odd cycles. Then, is hyperbolic if and only if is hyperbolic.
Proof. Fix some vertex and some edge .
By Theorem 1, there are exactly two components in . Since there are no odd cycles, there is no -walk in . Thus, let us denote by the component containing the vertex and by the component containing the vertex .
Consider defined as for every such that every -walk has even length and for every such that every -walk has odd length.
By Proposition 2, for every and i is a -quasi-isometric embedding.
Let . Let with such that every -walk has even length. Then, by Proposition 2, . Therefore, i is -full.
Hence, by Lemma 1, there is a -full -quasi-isometry, , and is hyperbolic if and only if is hyperbolic by Theorem 2.
The same argument proves that is hyperbolic. □
Denote by the path graph with two vertices and an edge.
Lemma 2. Let be a connected graph with some odd cycle and a non-trivial bounded graph without odd cycles. Then, and are quasi-isometric and .
Proof. By Theorem 1, we know that and are connected graphs.
Denote by and the vertices of and fix . The map defined as for every and is an isomorphism of graphs; hence, it suffices to prove that and are quasi-isometric.
Consider the inclusion map . Since is a subgraph of , we have for every .
Since
is a graph without odd cycles, every
-walk has odd length and every
-walk has even length for
. Thus, Proposition 2 gives, for every
,
Furthermore, for every
and
Hence, for every , and the inclusion map i is an -quasi-isometric embedding. Therefore, .
Since
is a graph without odd cycles, given any
, we have either that every
-walk has even length and every
-walk has odd length or that every
-walk has even length and every
-walk has odd length. In addition, since
is connected, for each
there is some
such that
. Therefore, by Proposition 2, for every
, if
is even, then
and if
is odd, then
In both cases,
and
i is
-full. By Lemma 1, there exists a
-full
-quasi-isometry
. □
A subgraph Γ of G is said isometric if for any . One can check that Γ is isometric if and only if for any .
Lemma 3. ([47], Lemma 5) If Γ is an isometric subgraph of G, then . A -walk g in G is a shortcut of a cycle C if and where denotes the length metric on C.
A cycle is a reduction of the cycle C if both have odd length and is the union of a subarc of C and a shortcut of C joining the endpoints of . Note that . We say that a cycle is minimal if it has odd length and it does not have a reduction.
Lemma 4. If C is a minimal cycle of G, then .
Proof. We prove first that C is an isometric subgraph of G. Assume that C is not an isometric subgraph. Thus, there exists a shortcut g of C with endpoints . There are two subarcs of C joining u and v; since C has odd length, we can assume that has even length and has odd length. If g has even length, then is a reduction of C. If g has odd length, then is a reduction of C. Hence, C is not minimal, a contradiction, and so C is an isometric subgraph of G.
It is easy to show that any isometric cycle C has length . This fact and Lemma 3 give . □
Given any
-walk
in
and
, if
is either odd or even, then we define the
-walk for
,
respectively.
Remark 1. By Proposition 2, if g is a geodesic path in , then is a geodesic path in .
Let us define the map as and for every , and the path as .
Let us define the map which is an isometry on the edges and such that if j is even and if j is odd. In addition, let be the map defined by .
Given a graph G, denote by the set of minimal cycles of G.
Lemma 5. Let be a connected graph with some odd cycle and . Consider a geodesic in . Let us define and , i.e., or if k is odd or even, respectively. Then, for every .
Proof. Choose such that . Since is odd, we have for some positive integer t. Thus, .
If is a cycle, then let us define . Thus, and for every . Otherwise, we may assume that for some . If , then let us define (where ). Hence, is a cycle, and .
If
is not minimal, then consider a reduction
of
. Let us repeat the process until we obtain a minimal cycle
. Note that
and for every point
,
. Now, repeating the argument, for every
,
and for every point
,
. Therefore,
Corollary 3. Let be a hyperbolic connected graph with some odd cycle and . Consider a geodesic in . Let us define and . Then, we have for every , Proof. Corollary 1 and Lemma 5 give and , and these inequalities provide the lower bound of .
Consider a geodesic
joining
and
with
and the
-walk
One can check that
is a
-walk in
, and so Lemma 4 gives
□
If is an edge of G, then the point with is the midpoint of the edge . Denote by the set of vertices and midpoints of edges in G. Consider the set of geodesic triangles T in G which are cycles and such that the vertices of T are in . We denote by the infimum of the constants such that any triangle in is -thin.
The following three results are used throughout the paper.
Theorem 5. ([40], Theorem 2.5) For every connected graph G, we have . Theorem 6. ([40], Theorem 2.6) Let G be any connected graph. Then, is always a multiple of . Theorem 7. ([40], Theorem 2.7) For any hyperbolic connected graph G, there exists a geodesic triangle such that . Consider the set of geodesic triangles T in G that are cycles and such that the three vertices of the triangle T are also vertices of G. denotes the infimum of the constants such that every triangle in is -thin.
Theorem 8. For every connected graph G, we have . Hence, G is hyperbolic if and only if . Furthermore, if G is hyperbolic, then there are a geodesic triangle and such that . In addition, is an integer multiple of .
Proof. The inequality is direct.
Consider the set
of geodesic triangles
T in
G such that the three vertices of the triangle
T belong to
, and denote by
the infimum of the constants
such that every triangle in
is
-thin. The argument in the proof of (ref. [
79], Lemma 2.1) gives that
.
Let us prove now
. Let us assume that
G is hyperbolic. If
, then the inequality is trivial. Thus, it suffices to consider the case
. By Theorem 7, there is a triangle
that is a cycle with
and
such that
. Assume that
(otherwise, the argument is simpler). Let
such that
and
. Since
is a geodesic hexagon with vertices in
, it is
-thin and every point
verifies
, we have
Assume that G is not hyperbolic. Therefore, for each there is a triangle which is a cycle with and with . The previous argument gives and, since M is arbitrary, we conclude .
Finally, consider any geodesic triangle in . Since , attains its maximum value when . Hence, is a multiple of for any triangle . Since the set of non-negative numbers that are multiple of is a discrete set, is an integer multiple of if G is hyperbolic, and there is a triangle and with . This finishes the proof. □
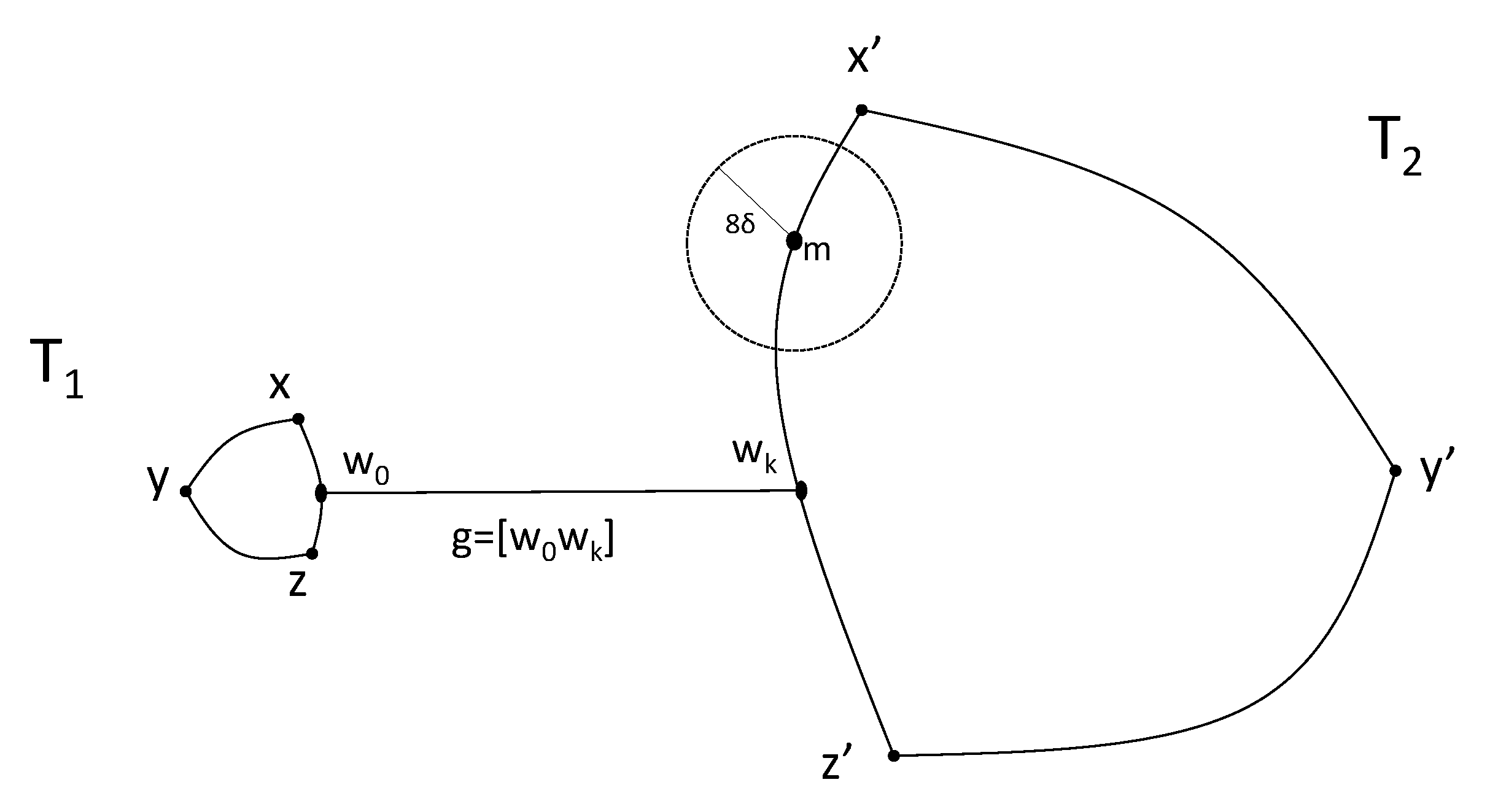
Theorem 9. If is a non-hyperbolic connected graph, then is not hyperbolic.
Proof. Since is not hyperbolic, by Theorem 8, given any there exists a triangle wich is a cycle, with and such that T is not R-thin. Therefore, there exists some point , let us assume that , such that .
Seeking for a contradiction let us assume that is -hyperbolic.
Suppose that for some , there is a geodesic triangle that is an even cycle in , with and such that T is not R-thin. Consider the (closed) path . Then, since T has even length, the path defines a cycle in . Let , , be the paths in corresponding to , respectively. By Corollary 1, the curves , and are geodesics, and , leading to contradiction.
Suppose that, for every , there is a geodesic triangle which is an odd cycle, with and such that T is not R-thin.
Let be a geodesic triangle as above and let us assume that .
Let be another triangle as above such that is not -thin, this is, there is a point m in one of the sides, let us call it , of such that .
Let
with
and
be a shortest geodesic in
joining
and
(if
and
intersect, just assume that
g is a single vertex,
, in the intersection). See
Figure 2.
Let us assume that
and
. Then, let us consider the closed path
C in
given by the union of the geodesics in
,
g, the geodesics in
and the inverse of
g from
to
, this is,
Since are odd cycles, C is an even closed cycle. Therefore, defines a cycle in . Moreover, by Remark 1, is a geodesic decagon in with sides , , , , , , , , and .
Since we are assuming that is -hyperbolic, then for every and every point , .
Let .
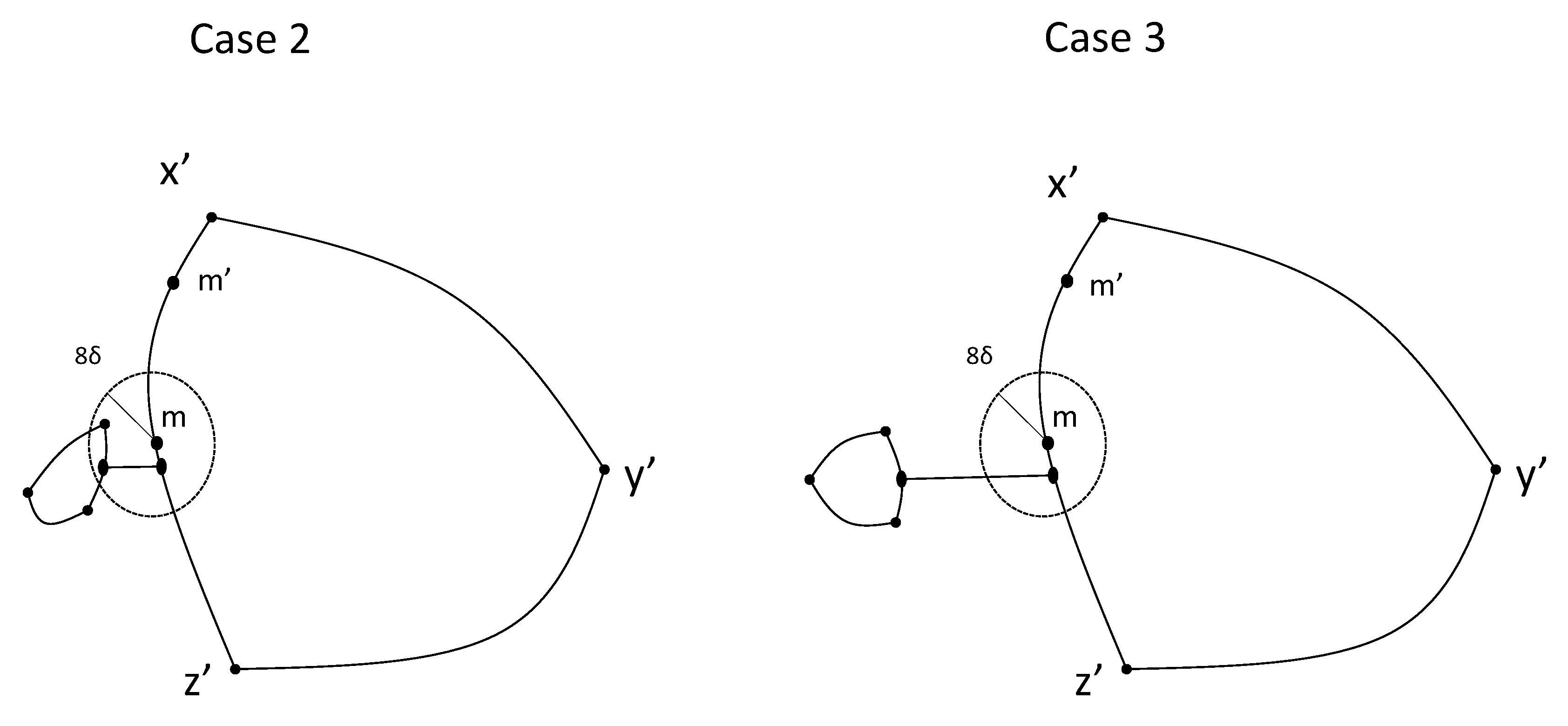
Case 1. Suppose that
. See
Figure 2.
By assumption, . If (resp. ), then (resp. ) and, by Corollary 1, (resp. ) leading to contradiction. If , since , let us assume . Then, since , it follows that . Thus, and, by Corollary 1, leading to contradiction.
Case 2. Suppose that
and
. See the left side of
Figure 3. Then, for every point
q in
,
. In particular,
. Therefore,
and let us assume that
. Since
, there is a point
such that
. Then,
. In addition, it is trivial to check that
and since
is a geodesic,
. Thus, if
, then
and, by Corollary 1,
leading to contradiction.
Case 3. Suppose that
and
. See the right side of
Figure 3. Since
g is a shortest geodesic in
joining
and
, this implies that
and
. Moreover,
. Otherwise, there is a point
such that
and
which means that
and
leading to contradiction.
Since , . Let us assume that . Since , there is a point such that . Let us see that . Suppose there is some such that . Since and g is a shortest geodesic joining and , . However, which is a contradiction. Hence, . In addition, it is trivial to check that and since is a geodesic, . Thus, if , then and, by Corollary 1, leading to contradiction. □
Proposition 3, Lemma 2 and Theorems 3, 4 and 9 have the following consequence.
Corollary 4. If is a non-hyperbolic connected graph and is some non-trivial connected graph, then is not hyperbolic.
Proposition 3 and Corollary 4 provide a necessary condition for the hyperbolicity of .
Theorem 10. Let be non-trivial connected graphs. If is hyperbolic, then one factor graph is hyperbolic and the other one is bounded.
Theorems 3 and 4 show that this necessary condition is also sufficient if either has some odd cycle or and do not have odd cycles (when is a hyperbolic graph and is a bounded graph). We deal now with the other case, when has some odd cycle and does not have odd cycles.
Theorem 11. Let be a connected graph with some odd cycle and a non-trivial bounded connected graph without odd cycles. Assume that satisfies the following property: for each there exist a geodesic g joining two minimal cycles of and a vertex with . Then, is not hyperbolic.
Proof. If is not hyperbolic, then Corollary 4 gives that is not hyperbolic. Assume now that is hyperbolic. By Theorem 2 and Lemma 2, we can assume that and .
Fix and choose a geodesic joining two minimal cycles in and with .
Define the paths
and
in
as
and
. Since
, we have
Hence,
and
are geodesics in
. Choose geodesics
and
in
. Since
is odd, Proposition 2 gives
Since belongs to a minimal cycle, by Lemma 4. In a similar way, we obtain .
Consider the geodesic quadrilateral in . Thus, . Since , we deduce .
Let
with
. Let us define
and
. Thus, Lemma 5 gives
and since
M is arbitrarily large, we deduce that
is not hyperbolic. □
Lemma 6. Let be a hyperbolic connected graph and suppose there is some constant such that for every vertex , . Then, is hyperbolic.
Proof. Denote by and the vertices of . Let defined as for every .
For every
, by Corollary 1,
. By Corollary 3,
Therefore, is a -quasi-isometric embedding.
Notice that for every , . In addition, for any , since is connected, there is some edge and we have . Therefore, is 1-full.
Thus, by Lemma 1, and are quasi-isometric and, by Theorem 2, is hyperbolic. □
Theorem 3 and Lemmas 2 and 6 give the following result.
Theorem 12. Let be a hyperbolic connected graph and some non-trivial bounded connected graph. If there is some constant such that for every vertex , , then is hyperbolic.
We finish this section with a characterization of the hyperbolicity of , under an additional hypothesis. We present first some lemmas.
Let J be a finite or infinite index set. Now, given a graph , we define some graphs related to which will be useful in the following results. Let with and , for any , such that if , and every odd cycle C in satisfies for some . Denote by the subgraph of induced by . Let . Denote by the graph with , where are additional vertices, and . We have .
Lemma 7. Let be a connected graph as above. Then, there is a quasi-isometry such that for every .
Proof. Let defined as for every , and for every . It is clear that is 0-full.
Now, we focus on proving that is a -quasi-isometric embedding. For every , it is clear that .
Let us prove the other inequality. Fix and consider an oriented geodesic in from to .
Assume that . If , then . If , then meets some . Since is a compact set, it intersects only a finite number of ’s, which we denote by . Since is an oriented curve from to , we can assume that meets in this order.
Let us define the following vertices in
for every
. Note that
for every
(it is possible to have
).
Since
and
, we have
for every
. Thus,
Assume that
. Therefore, there exists
j with
and
Assume now that
u and/or
v does not belong to
and
. Let
be the closest vertices in
to
, respectively (it is possible to have
or
). Since
,
, we have
and
. Hence,
If , then . If , then , and .
Finally, we conclude that is a -quasi-isometric embedding. Thus, Lemma 1 provides a quasi-isometry with the required property. □
Definition 3. Given a connected graph and some index set J, let be a family of balls where with , for any , and if . Suppose that every odd cycle C in satisfies that for some . If there is some constant such that for every , there is an odd cycle such that with , then we say that is M-regular.
Remark 2. If J is finite, then there exists such that is M-regular.
Denote by the graph with , where is a graph as above and are additional vertices, and .
Lemma 8. Let be a connected graph as above and with . If is hyperbolic and as above is M-regular, then there exists a quasi-isometry with for every and .
Proof. Let defined as for every , and for every . It is clear that is 0-full. Recall that we denote by the projection map. Define as on and for every x with for some .
Now, we focus on proving that
is a quasi-isometric embedding. For every
, one can check
To prove the other inequality, let us fix
(the inequalities in other cases can be obtained from the one in this case, as in the proof of Lemma 7). Consider a geodesic
in
. If
, then
If , then meets some . Since is a compact set, intersects just a finite number of ’s, which we denote by . We consider as an oriented curve from to ; thus we can assume that meets in this order.
Let us define the following set of vertices in
for every
, such that
. Note that
for every
and
since
.
If for some , then . Since for , we have that in this case.
If for some , then is odd.
Since is M-regular, consider an odd cycle C with and , and let and geodesics in . Thus, and have different parity which means that one of them has different parity from . Then, . Since for , we have that in this case.
Thus, we have that
for every
and
for every
. Therefore,
We conclude that is a quasi-isometric embedding. Thus, Lemma 1 provides a quasi-isometry with the required property. □
Definition 4. Given a geodesic metric space X and closed connected pairwise disjoint subsets of X, we consider another copy of X. The double of X is the union of X and obtained by identifying the corresponding points in each and .
Definition 5. Let us consider , a metric space X, and subsets . The set is called the H-neighborhood of Y in X. The Hausdorff distance of Y to Z is defined by .
The following results in [
15,
80] will be useful.
Theorem 13. ([80], Theorem 3.2) Let us consider a geodesic metric space X and closed connected pairwise disjoint subsets of X, such that the double is a geodesic metric space. Then, the following conditions are equivalent: - (1)
is hyperbolic.
- (2)
X is hyperbolic and there exists a constant such that for every and we have for every .
- (3)
X is hyperbolic and there exist constants such that for every and we have for every x in some -quasi-geodesic joining a with b in X.
Theorem 14. ([15], p. 87) For each , and , there exists a constant with the following property: Let us consider a δ-hyperbolic geodesic metric space X and an -quasigeodesic g starting in x and finishing in y. If γ is a geodesic joining x and y, then .
This property is called geodesic stability. It is well-known that hyperbolicity is, in fact, equivalent to geodesic stability [
81].
Theorem 15. Let be a connected graph and with and , for any , such that , if , and every odd cycle C in satisfies for some . Suppose is M-regular for some . Let be a non-trivial bounded connected graph without odd cycles. Then, the following statements are equivalent:
- (1)
is hyperbolic.
- (2)
is hyperbolic and there exists a constant , such that for every and , there exists a geodesic in with for every .
- (3)
is hyperbolic and there exist constants , such that for every we have for every x in some ()-quasi-geodesic joining with in .
Proof. Items and are equivalent by geodesic stability in (see Theorem 14).
Assume that holds. By Lemma 7, there exists an -quasi-isometry with for every . Given is an -quasi-geodesic with endpoints and in . Given , we have with and . Taking and for every , Theorem 13 gives that is hyperbolic. Now, Lemma 8 gives that is hyperbolic and we conclude that is hyperbolic by Lemma 2.
Now, suppose holds. By Lemma 2, is hyperbolic and, by Theorem 9, is hyperbolic. Then, Lemma 8 gives that is hyperbolic and taking and for every , by Theorem 13, holds. □
Theorem 15 and Remark 2 have the following consequence.
Corollary 5. Let be a connected graph and suppose that there are a positive integer K and a vertex , such that every odd cycle in intersects the open ball . Let be a non-trivial bounded connected graph without odd cycles. Then, is hyperbolic if and only if is hyperbolic.
4. Bounds for the Hyperbolicity Constant of Some Direct Products
The following well-known result will be useful (see a proof, e.g., in ([
47], Theorem 8)).
Theorem 16. In any connected graph G the inequality holds.
Remark 3. Note that, if is a bipartite connected graph, then . Furthermore, if is a bipartite connected graph, then the product has exactly two connected components, which are denoted by and , where each one is a bipartite graph and, consequently, for .
Remark 4. Let be two path graphs with . The product has exactly two connected components, which will be denoted by and . If for , then and .
Furthermore, if and , then .
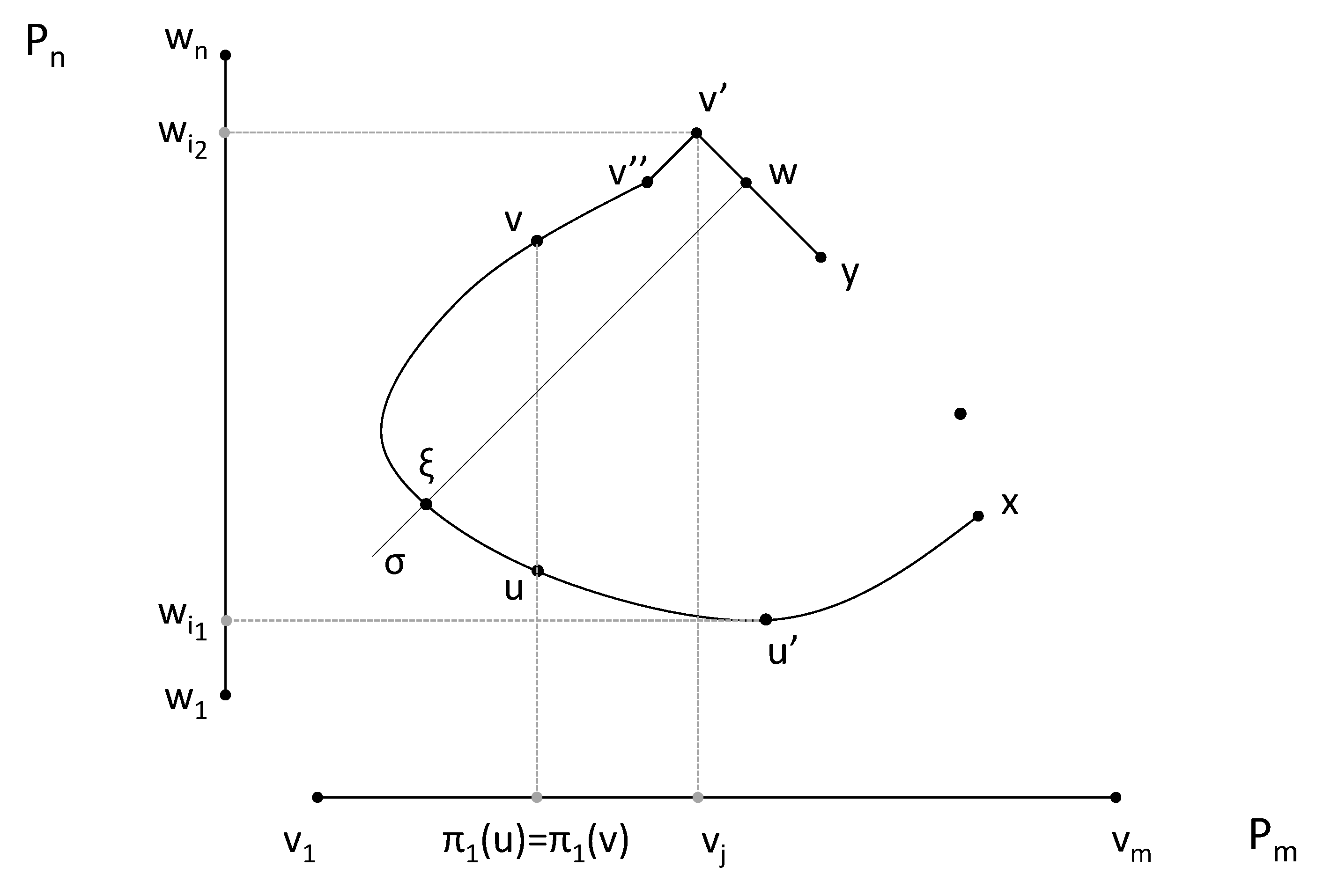
Lemma 9. Let be two path graphs with , and let γ be a geodesic in such that there are two different vertices in γ, with . Then, .
Remark 5. Note that the conclusion of Lemma 9 does not hold for , since we always have .
Proof. Let
, and let
be the sets of vertices in
, respectively, such that
and
for
. Seeking for a contradiction, assume that
. Notice that if
denotes the geodesic contained in
joining
u and
v, then
restricted to
is injective. Consider two vertices
such that
,
is injective in
and
,
with
maximal under these conditions. See
Figure 4.
Since , either there is an edge in such that or there is an edge in such that . In addition, since , notice that is not injective in . Moreover, since is maximal, if , then , and since , and . Thus, either or .
Hence, let us assume that there is an edge in such that with (otherwise, if there is an edge in such that with , the proof is similar).
Suppose . Let be the vertex in such that . Then, by construction of , since , it follows that . Therefore, in particular, .
Assume that (if , then the argument is similar). Therefore, .
Since , there is a vertex of in . Let with . Let be the geodesic contained in joining and w. Let be the geodesic contained in joining and s. Hence, leading to contradiction. □
Theorem 17. Let be two path graphs with . If , then . If , then Furthermore, if and m is odd, then .
Proof. If , then has two connected components isomorphic to , and .
Assume that . By symmetry, it suffices to prove the inequalities for . Hence, Theorem 16 and Remark 4 give . By Theorem 7, there exists a geodesic triangle with , and . Let such that .
To prove , we consider two cases.
Assume first that there is at least a vertex
such that
. If
, then
and
If
, then
by Lemma 9, and
Assume now that there is not a vertex
such that
. Then, there exist two different vertices
in
such that
, and
. If
or
belongs to
, then
. Otherwise,
. Lemma 9 gives
, and we have that
To prove the lower bound, denote the vertices of and by and , with for and for .
Let be the connected component of containing .
Assume first that
. Consider the following curves in
:
Corollary 1 gives that
are geodesics. If
B is the geodesic bigon
, then Remark 4 gives that
If
m is odd with
, then
and we can consider the curves in
:
Corollary 1 gives that
are geodesics. If
, then Remark 4 gives that
By Remark 4, if
m is even with
, then we have that
Furthermore, if and m is odd, then we have proven . □
Theorem 18. If and are bipartite connected graphs with and such that , then Furthermore, if and is even, then .
Proof. Corollary 1, Theorem 16 and Remark 3 give us the upper bound.
To prove the lower bound, we can see that there exist two path graphs
which are isometric subgraphs of
and
, respectively. It is easy to check that
is an isometric subgraph of
. By Lemma 3 and Theorem 17, we have
Using a similar argument as above, we have and . Thus, since and for , we obtain the first statement.
Furthermore, if and is odd, then Theorem 17 gives , and we conclude . □
The following result deals just with odd cycles since otherwise we can apply Theorem 18.
Theorem 19. For every odd number and every , Proof. Let
and
be the sets of vertices in
and
, respectively, such that
and
for
,
. Note that for
and
we have
, if
, or
, if
. Besides, we have
, i.e.,
if
, and
if
. Thus, by Theorem 16, we have
Assume first that . Note that and is an isometric subgraph of , if . By Lemma 3, we have , and we obtain the result in this case.
Assume now that
. Consider the geodesic triangle
T in
defined by the following geodesics
where
(respectively,
) is an endpoint of either
or
, depending of the parity of
n. Since
T is a geodesic triangle in
, we have
. If
and
M is the midpoint of the geodesic
, then
. Therefore, the result for
follows.
Finally, assume that . Let us consider such that . Thus, . To finish the proof, it suffices to prove that . Seeking for a contradiction, assume that . By Theorems 6 and 7, there is a geodesic triangle and with . Then, . Let (respectively, ) be the closest vertex to x (respectively, y) in , and consider a vertex in such that . Note that implies that . Since , we have and, consequently, is a geodesic in . Since is a path in joining and , there exists a vertex such that and . Therefore, and, consequently, , leading to contradiction. □