On the Diameter and Incidence Energy of Iterated Total Graphs

Abstract

The total graph of G, $\mathcal{T}\left(G\right)$ is the graph whose vertex set is the union of the sets of vertices and edges of G, where two vertices are adjacent if and only if they stand for either incident or adjacent elements in G. For $k\ge 2$, the k-th iterated total graph of G, ${\mathcal{T}}^k\left(G\right)$, is defined recursively as ${\mathcal{T}}^k\left(G\right)=\mathcal{T}\left({\mathcal{T}}^{k-1}\left(G\right)\right),$ where ${\mathcal{T}}^1\left(G\right)=\mathcal{T}\left(G\right)$ and ${\mathcal{T}}^0\left(G\right)=G.$ If G is a connected graph, its diameter is the maximum distance between any pair of vertices in G. The incidence energy $IE\left(G\right)$ of G is the sum of the singular values of the incidence matrix of G. In this paper, for a given integer k we establish a necessary and sufficient condition under which $diam\left({\mathcal{T}}^{r+1}\left(G\right)\right)>k-r,$ $r\ge 0$. In addition, bounds for the incidence energy of the iterated graph ${\mathcal{T}}^{r+1}\left(G\right)$ are obtained, provided G is a regular graph. Finally, new families of non-isomorphic cospectral graphs are exhibited.

1. Introduction

Let G be a simple connected graph of order n, and $v_1,v_2,\dots ,v_n$ its vertices. An edge e with end vertices u and v will be denoted by $\left(uv\right)$. Sometimes, after a labeling of the vertices of G, a vertex $v_i$ is simply referred to by its label i, and an edge $v_i{v}_j$ is simply referred to as $\left(ij\right)$. The incident vertices to the edge $\left(ij\right)$ are i and j. The distance between two vertices $v_i$ and $v_j$ in G is equal to the length of the shortest path in G joining $v_i$ and $v_j$, denoted by $d_G(v_i,v_j)$. The diameter of G, denoted by $diam\left(G\right)$, is the maximum distance between any pair of vertices in G. The above distance provides the simplest and most natural metric in graph theory, and its study has recently received increasing interest in discrete mathematics research. As usual, $K_n$, $P_n$, $C_n$, and $S_n$ denote, respectively, the complete graph, the path, the cycle, and the star of n vertices.

The line graph of G, denoted by $\mathcal{L}\left(G\right)$, is the graph whose vertices are the edges of G, where two vertices are adjacent if the corresponding edges in G have a common vertex. The k-th iterated line graph of G is defined recursively as ${\mathcal{L}}^k\left(G\right)=\mathcal{L}\left({\mathcal{L}}^{k-1}\left(G\right)\right)$, $k\ge 2$, where ${\mathcal{L}}^1\left(G\right)=\mathcal{L}\left(G\right)$ and ${\mathcal{L}}^0\left(G\right)=G$. Metric properties of the line graph have recently been extensively studied in the mathematical literature [1,2,3,4,5], and it found remarkable applications in chemistry [6,7,8,9].

The total graph of G, denoted by $\mathcal{T}\left(G\right)$, is the graph whose vertex set corresponds union of set of vertices and edges of G, where, two vertices are adjacent if their corresponding elements are either adjacent or incident in G. The k-th iterated total graph of G is defined recursively as ${\mathcal{T}}^k\left(G\right)=\mathcal{T}\left({\mathcal{T}}^{k-1}\left(G\right)\right)$, $k\ge 2$, where $\mathcal{T}\left(G\right)={\mathcal{T}}^1\left(G\right)$ and $G={\mathcal{T}}^0\left(G\right)$.

The incidence matrix, $I\left(G\right),$ is the $n\times m$ matrix whose $(i,j)$-entry is 1 if $v_i$ is incident to $e_j$, and 0 otherwise. It is known that

$$I\left(G\right)I^T\left(G\right)=Q\left(G\right)$$

(1)

and

$$I^T\left(G\right)I\left(G\right)=2I_m+A\left(\mathcal{L}\left(G\right)\right),$$

(2)

where $Q\left(G\right)$ is the signless Laplacian matrix of G and $A\left(\mathcal{L}\right(G\left)\right)$ is the adjacency matrix of the line graph of G. Our results can be applied to several disciplines—in engineering for example, solid materials with discrete lattices are modeled to this type of graph. Some recent papers have focused on this application (see, for instance, [10,11,12] and references therein). In [13,14], the authors introduced the concept of the incidence energy $IE\left(G\right)$ of G as the sum of the singular values of the incidence matrix of G. It is well-known that the singular values of a matrix M are the nonzero square roots of $M{M}^T$ or $M^{T}M$, as these matrices have the same nonzero eigenvalues. From these facts and (1), it follows that

$$IE\left(G\right)=\sum _{i=1}^n\sqrt{q_i},$$

where $q_1,q_2,\dots ,q_n$ are the signless Laplacian eigenvalues of G.

In [13], Gutman, Kiani, Mirzakhah, and Zhou proved that

Theorem 1

([13]). Let G be a regular graph on n vertices of degree r. Then,

$$IE\left({\mathcal{L}}^{k+1}\left(G\right)\right)\le {\displaystyle \frac{n_k(r_k-2)}{2}}\sqrt{2r_k-4}+\sqrt{4r_k-4}+\sqrt{(n_k-1)[(3r_k-4)(n_k-1)-r_k]},$$

where $n_k$ and $r_k$ are the order and degree of ${\mathcal{L}}^{k+1}\left(G\right)$, respectively. Equality holds if and only if ${\mathcal{L}}^k\left(G\right)\cong K_n$.

This paper is organized as follows. In Section 2, we establish conditions on a graph G, so that the diameter of $\mathcal{T}\left(G\right)$ does not exceed k, $k\ge 2$. Additionally, conditions so that the diameter of $\mathcal{T}\left(G\right)$ is greater than or equal to k, $k\ge 3$, are established. Moreover, we establish a necessary condition so that the diameter of ${\mathcal{T}}^{r+1}\left(G\right)$ is not greater than or equal to $k-r$, $k\ge 2$, $r\ge 0$. In Section 3, we derive upper and lower bounds on the incidence energy for the iterated total graphs of regular graphs. Additionally, we construct some new families of non-isomorphic cospectral graphs.

2. Diameter of Total Graphs

In this section, for $k\ge 2$ we establish necessary and sufficient conditions for a graph G, so that the diameter of $\mathcal{T}\left(G\right)$ does not exceed $k$. Moreover, for $k\ge 2$ we establish necessary and sufficient conditions for a graph G, so that the diameter of $\mathcal{T}\left(G\right)$ is strictly greater than $k$.

2.1. Main Results

Before proceeding, we need the following definitions.

Definition 1.

A path P with end vertices u and v in a connected graph G is called a diameter path of G if P has $diam\left(G\right)+1$ vertices and $d_G(u,v)=diam\left(G\right)$.

Definition 2.

A subgraph H of a connected graph G is called diameter subgraph of G if H has a diameter path of G as a subgraph.

Definition 3.

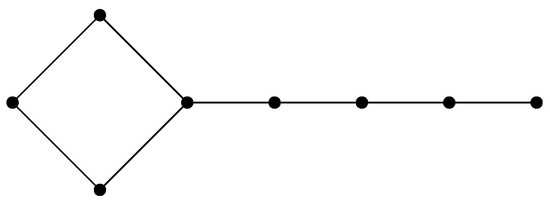
The Lollipop $Lo{l}_{n,g}$ is the graph obtained from a cycle with g vertices by identifying one of its vertices with a vertex of path length $n-g$. Note that this graph has n vertices and diameter $n-g+1+⌊\frac{g}{2}⌋$. In Figure 1 we display an example of Lollipop $Lo{l}_{8,4}$.

Figure 1. A Lollipop $Lo{l}_{8,4}$.

In [15] it was conjectured that $Lo{l}_{3,n-3}$ is the non-bipartite graph of order n with minimum smallest signless Laplacian eigenvalue $q_n.$

Lemma 1.

Let G be a connected graph on n vertices. Then, either $diam\left(\mathcal{T}\right(G\left)\right)=diam\left(G\right)$ or $diam\left(\mathcal{T}\right(G\left)\right)=diam\left(\mathcal{L}\right(G\left)\right)$ or $Lo{l}_{l+diam\left(G\right)+1,2l+1}$ is a diameter subgraph of G for some $1\le l\le diam\left(G\right)$, where $diam\left(\mathcal{T}\right(G\left)\right)=diam\left(G\right)+1$.

Proof. 

The result can be easily verified for graphs of order $n\le 3$. Consequently, we assume $n>3$. If $diam\left(G\right)<diam\left(\mathcal{T}\right(G\left)\right)$, then $diam\left(\mathcal{L}\right(G\left)\right)<diam\left(\mathcal{T}\right(G\left)\right)$, and $Lo{l}_{l+diam\left(G\right)+1,2l+1}$ is not a diameter subgraph of G for all $1\le l\le diam\left(G\right)$, where $diam\left(\mathcal{T}\right(G\left)\right)=diam\left(G\right)+1$. We claim that $d_{\mathcal{T}\left(G\right)}(u,v)<diam\left(\mathcal{T}\left(G\right)\right)$ for any pair of vertices $u,v$ in $\mathcal{T}\left(G\right)$. Let $v_a$, $v_b$ be two vertices in $\mathcal{T}\left(G\right)$ such that $d_{\mathcal{T}\left(G\right)}(v_a,v_b)\ge diam\left(\mathcal{T}\left(G\right)\right)$. Then, there must exist $diam\left(\mathcal{T}\right(G\left)\right)-1$ vertices in $\mathcal{T}\left(G\right)$, say $v_1,v_2,\dots ,v_{diam\left(\mathcal{T}\right(G\left)\right)-1}$, such that $v_i$ is adjacent to $v_{i+1}$, $i=1,2,\dots ,diam\left(\mathcal{T}\right(G\left)\right)-2$, where $v_a$ is adjacent to $v_1$.

• If $v_a,v_b$ are vertices of G, then we can assume that $v_i$ is a vertex of G, $i=1,2,\dots ,diam\left(\mathcal{T}\right(G\left)\right)-1$. Then, $diam\left(G\right)\ge diam\left(\mathcal{T}\right(G\left)\right)$, which is impossible.
• If $v_a,v_b$ are vertices of the line graph of G, that is to say if $v_a,v_b$ are edges of G, then we can assume that $v_i$ is an edge of G, $i=1,2,\dots ,diam\left(\mathcal{T}\right(G\left)\right)-1$. Thus, $diam\left(\mathcal{L}\right(G\left)\right)\ge diam\left(\mathcal{T}\right(G\left)\right)$, which is impossible.
• If $v_a$ is a vertex of G and $v_b$ is an edge of G, say $v_b=\left(b_1{b}_2\right)$, we can assume without loss of generality that $v_i$ is a vertex of $G,$$i=1,2,\dots ,diam\left(\mathcal{T}\right(G\left)\right)-1,$ or $v_i$ is an edge of $G,$$i=1,2,\dots ,diam\left(\mathcal{T}\right(G\left)\right)-1$. Suppose that $v_i$ is a vertex of $G,$$i=1,2,\dots ,diam\left(\mathcal{T}\right(G\left)\right)-1$. Then, $d_G(v_a,b_1)\ge diam\left(\mathcal{T}\left(G\right)\right)-1$. Since $diam\left(G\right)<diam\left(\mathcal{T}\right(G\left)\right)$, then $d_G(v_a,b_1)=diam\left(\mathcal{T}\left(G\right)\right)-1=diam\left(G\right)$. In addition, $d_G(v_a,b_2)=diam\left(G\right)$. Thereby, $Lo{l}_{l+diam\left(G\right)+1,2l+1}$ is a diameter subgraph of G some $1\le l\le diam\left(G\right)$, where $diam\left(\mathcal{T}\right(G\left)\right)=diam\left(G\right)+1$, which is impossible. Otherwise, suppose $v_i$ is an edge of $G,$$i=1,2,\dots ,diam\left(\mathcal{T}\right(G\left)\right)-1$, with $v_{diam\left(\mathcal{T}\right(G\left)\right)-1}=\left(c{b}_1\right)$ then $d_G(v_a,b_1)\ge diam\left(\mathcal{T}\left(G\right)\right)-1$. Since $diam\left(G\right)<diam\left(\mathcal{T}\right(G\left)\right)$, then $d_G(v_a,b_1)=diam\left(\mathcal{T}\left(G\right)\right)-1=diam\left(G\right)$. Moreover, $d_G(v_a,b_2)=diam\left(G\right)$. Thus, $Lo{l}_{l+diam\left(G\right)+1,2l+1}$ is a diameter subgraph of G for some $1\le l\le diam\left(G\right)$, where $diam\left(\mathcal{T}\right(G\left)\right)=diam\left(G\right)+1$, which is impossible.
  That is, $d_{\mathcal{T}\left(G\right)}(u,v)<diam\left(\mathcal{T}\left(G\right)\right)$ for any pair of vertices $u,v$ in $\mathcal{T}\left(G\right)$, which is a contradiction.

☐

Before proceeding, we need to establish the following facts about the line graphs.

Lemma 2

([16]). If H is an induced subgraph of G, then $\mathcal{L}\left(H\right)$ is an induced subgraph of $\mathcal{L}\left(G\right)$.

Let us denote by $F_1^k$ the path of length $k+1$, $k\ge 2$. Let $v_1,v_2,\dots ,v_{k+2}$ be the vertices of $F_1^k$ so that for $i=1,2,\dots ,k+1,$$v_i$ is adjacent to $v_{i+1}$.

Let $F_2^k$ and $F_3^k$ be the graphs obtained from $F_1^{k+1}$ by adding the edge $\left(v_1{v}_3\right)$, and the edges $\left(v_1{v}_3\right)$ and $\left(v_{k+1}{v}_{k+3}\right),$ respectively. Note that $F_1^{k+1}$, $F_2^k$, and $F_3^k$ have diameter $k+1$ (see Figure 2).

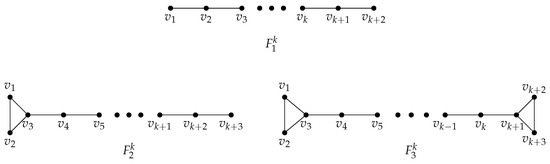
Figure 2. Graphs $F_1^k$, $F_2^k$, and $F_3^k$.

Theorem 2.

Let $k\ge 2$. Then, $diam\left(\mathcal{T}\right(G\left)\right)\le k$ if and only if all the following conditions fail to hold:

• $F_1^{k+1}$, ${F_2}^k$, and ${F_3}^k$ are induced subgraphs of G, and
• $F_1^k$ is a diameter path of G, and
• $Lo{l}_{l+k+1,2l+1}$ is a diameter subgraph of G for some $1\le l\le k$, where $diam\left(G\right)=k$.

Proof. 

The result can be easily verified for graphs of order $n\le 3$. Consequently, we assume that $n>3$. Let $k\ge 2$, and suppose that $diam\left(\mathcal{T}\right(G\left)\right)\le k$. If $F_1^k$ is a diameter path of G, by Lemma 1, $diam\left(\mathcal{T}\left(G\right)\right)\ge diam\left(F_1^k\right)=k+1>k$, which is a contradiction. Suppose that $F_2^k$ is an induced subgraph of G, by Lemma 2, $\mathcal{L}\left(F_2^k\right)$ is an induced subgraph of $\mathcal{L}\left(G\right)$. Thus, $\mathcal{L}\left(F_2^k\right)$ is an induced subgraph of $\mathcal{T}\left(G\right)$. Therefore, $diam\left(\mathcal{T}\left(G\right)\right)\ge diam\left(\mathcal{L}\left(F_2^k\right)\right)=k+1$, which is a contradiction. Similarly, we prove that $F_1^{k+1}$ and $F_3^k$ are not induced subgraphs of G. Moreover, if $Lo{l}_{l+k+1,2l+1}$ is a diameter subgraph of G for some $1\le l\le k$, where $diam\left(G\right)=k$, then $diam\left(\mathcal{T}\left(G\right)\right)\ge diam\left(\mathcal{T}\left(Lo{l}_{l+k+1,2l+1}\right)\right)=k+1$, which is a contradiction. Conversely, suppose that $k\ge 2$ and $diam\left(\mathcal{T}\right(G\left)\right)>k$. By Lemma 1, we have the following cases:

• Case 1: Suppose $diam\left(\mathcal{T}\right(G\left)\right)=diam\left(G\right)$. If $diam\left(G\right)=k+1$, then $F_1^k$ is a diameter path in G—a contradiction. If $diam\left(G\right)\ge k+2$, then $F_1^{k+1}$ is an induced subgraph of G—a contradiction.
• Case 2: Suppose $diam\left(\mathcal{T}\right(G\left)\right)=diam\left(\mathcal{L}\right(G\left)\right)$, then there must exist $k+2$ edges in G, say $e_1,e_2,\dots ,e_{k+2}$, such that $e_i$ is incident to $e_{i+1}$ in G, $i=1,2,\dots ,k+1$, and $d_{\mathcal{L}\left(G\right)}(e_1,e_{k+2})=k+1$. Let $e_i=\left(v_i{v}_{i+1}\right)$, $i=1,2,\dots ,k+1$. Then

  (i)

  If $v_1$ is not adjacent to $v_3$ and $v_{k+1}$ is not adjacent to $v_{k+3}$, then $F_1^{k+1}$ is an induced subgraph of G—a contradiction.

  (ii)

  If $v_1$ is adjacent to $v_3$ (or $v_{k+1}$ is adjacent to $v_{k+3}$), then $F_2^k$ is an induced subgraph of G—a contradiction.

  (iii)

  If $v_1$ is adjacent to $v_3$ and $v_{k+1}$ is adjacent to $v_{k+3}$, then $F_3^k$ is an induced subgraph of G—a contradiction.

• Case 3: Suppose that $Lo{l}_{l+diam\left(G\right)+1,2l+1}$ is a diameter subgraph of G for some $1\le l\le diam\left(G\right)$, where $diam\left(\mathcal{T}\right(G\left)\right)=diam\left(G\right)+1$. If $diam\left(\mathcal{T}\right(G\left)\right)=k+1$, then $Lo{l}_{l+k+1,2l+1}$ is a diameter subgraph of G for some $1\le l\le k$, where $diam\left(G\right)=k$—a contradiction. If $diam\left(\mathcal{T}\right(G\left)\right)=k+2$, then $F_1^k$ is a diameter path of G—a contradiction. If $diam\left(\mathcal{T}\right(G\left)\right)\ge k+3$, then $F_1^{k+1}$ is an induced subgraph of G—a contradiction.

☐

An equivalent result to Theorem 2 is given below.

Theorem 3.

Let $k\ge 2$. For a connected graph G, $diam\left(\mathcal{T}\right(G\left)\right)>k$ if and only if some of the following conditions are verified:

• $F_1^{k+1}$ or ${F_2}^k$ or ${F_3}^k$ is an induced subgraph of G, or
• $F_1^k$ is a diameter path of G, or
• $Lo{l}_{l+k+1,2l+1}$ is a diameter subgraph of G for some $1\le l\le k$, where $diam\left(G\right)=k$.

The following results characterize some subgraphs of $\mathcal{T}\left(G\right)$ according to the diameter of either $\mathcal{L}\left(G\right)$ or G. Evidently, $diam\left(\mathcal{T}\right(G\left)\right)=0$ if and only if $G\cong K_1$.

Lemma 3.

For a connected graph G, if $diam\left(\mathcal{L}\right(G\left)\right)=diam\left(G\right)=2$, then some of the following conditions are verified:

• $K_4-e$ or $Lo{l}_{4,3}$, or $C_4$ is an induced subgraph of G, or
• $C_5$ is a diameter subgraph of G.

Proof. 

Let G be a connected graph such that $diam\left(\mathcal{L}\right(G\left)\right)=2$, then there exists 4 vertices, say $u_1,u_2,u_3,u_4,$ such that $u_i$ is adjacent to $u_{i+1}$, for $i=1,2,3$.

(i)

If $u_1$ is not adjacent to $u_3$, $u_2$ is not adjacent to $u_4$ and $u_1$ is not adjacent to $u_4$, then $P_4$ is an induced subgraph of G. Moreover, since $diam\left(G\right)=2$, then $P_3:u_{1}v{u}_4$ is a diameter path of G for some v. Hence, $C_5$ is a diameter subgraph of G.

(ii)

If $u_1$ is adjacent to $u_3$ (or $u_2$ is adjacent to $u_4$) and $u_1$ is not adjacent to $u_4$, then $Lo{l}_{4,3}$ is an induced subgraph of G.

(iii)

If $u_1$ is adjacent to $u_3$, $u_2$ is adjacent to $u_4$ and $u_1$ is not adjacent to $u_4$, then $K_4-e$ is an induced subgraph of G.

(iv)

If $u_1$ is adjacent to $u_4$, $u_1$ is not adjacent to $u_3$ and $u_2$ is not adjacent to $u_4$, then $C_4$ is an induced subgraph of G.

☐

Corollary 1.

Let G be a connected graph. Then

a.

$diam\left(\mathcal{T}\right(G\left)\right)=1$ if and only if $G\cong K_2$.

b.

If the following conditions fail to hold:

• $K_4-e$, $Lo{l}_{4,3}$ and $C_4$ is an induced subgraph of G, and
• $C_5$ is a diameter subgraph of G,

then $diam\left(\mathcal{T}\right(G\left)\right)=2$ if and only if $G\cong K_n$ or $G\cong S_n$.

Proof. 

a.

If $G\cong K_2$, then all the vertices of $\mathcal{T}\left(G\right)$ are adjacent. That is, $\mathcal{T}\left(G\right)=K_3$. Thus, $diam\left(\mathcal{T}\left(G\right)\right)=diam\left(K_3\right)=1$.

Conversely, let $diam\left(\mathcal{T}\right(G\left)\right)=1$ and $G\cong K_2$. Then, there exists two different edges in G, say $e_i=\left(xy\right)$ and $e_j=\left(yz\right)$. Thus, $d_{\mathcal{T}\left(G\right)}(e_j,x)=2$. Therefore, $diam\left(\mathcal{T}\right(G\left)\right)>1$—a contradiction.

b.

Suppose that none of the three graphs $K_4-e$, $Lo{l}_{4,3}$, and $C_4$ are induced subgraphs of G, and that $C_5$ is not a diameter subgraph of G. By Lemma 3 it does not occur that $diam\left(\mathcal{L}\right(G\left)\right)=diam\left(G\right)=2$. Now, if $diam\left(\mathcal{T}\right(G\left)\right)=2$, by Lemma 1 some of the following cases are verified:

• Case 1: $diam\left(G\right)=2$. Then, $diam\left(\mathcal{L}\right(G\left)\right)=1$, thus any couple of edges of G are incidents. Consequently, $G\cong K_3$ or $G\cong S_n$. Since $diam\left(G\right)=2$, we concluded that $G\cong S_n$.
• Case 2: $diam\left(\mathcal{L}\right(G\left)\right)=2$. Then, $diam\left(G\right)=1$, thus any couple of vertices of G are adjacents. Therefore, $G\cong K_n$.
• Case 3: $Lo{l}_{3,3}$ is a diameter subgraph of G. Then, $diam\left(G\right)=1$. Thus, $G\cong K_n$.

Conversely, let $G\cong K_n$. Then, any couple of vertices in G are at distance 1. Let $e_i=\left(xy\right)$ and $e_j=\left(zw\right)$ be two different edges in G. If $e_i$ and $e_j$ are incident edges, then $d_{\mathcal{L}\left(G\right)}(e_i,e_j)=1$. Otherwise, since $e_k=\left(yz\right)$ is an edge in G, we have $d_{\mathcal{L}\left(G\right)}(e_i,e_j)=2$. Finally, let $e=\left(xy\right)$ be an edge of G and let v be a vertex of G. If $v=x$ or $v=y$, then $d_{\mathcal{T}\left(G\right)}(e,v)=1$. Otherwise, since $\left(xv\right)$ is an edge of G, then $d_{\mathcal{T}\left(G\right)}(e,v)=2$. Hence, $diam\left(\mathcal{T}\right(G\left)\right)=2$.

If $G\cong S_n$, then all the edges of G are incidents to a common vertex. Therefore, all vertices are pairwise incident in $\mathcal{L}\left(G\right)$ and thus $\mathcal{L}\left(G\right)\cong K_{n-1}$. Hence, $diam\left(\mathcal{L}\right(G\left)\right)=1$. Moreover, all $n-1$ vertices are adjacents to a common vertex in G. Then, $diam\left(G\right)=2$. Finally, since $diam\left(\mathcal{L}\right(G\left)\right)=1$, then any edge of G and any vertex of G are to distance less than or equal to 2. Therefore, $diam\left(\mathcal{T}\right(G\left)\right)=2$.

☐

2.2. Results for Iterated Total Graphs

Theorem 4.

Let $r\ge 1$ and $k\ge 4r+3$. Let G be a connected graph such that

$$diam\left({\mathcal{T}}^{r+1}\left(G\right)\right)>k-r.$$

Then, $F_1^{k-4r-1}$ is an induced subgraph of G.

Proof. 

Suppose $diam\left({\mathcal{T}}^{r+1}\left(G\right)\right)>k-r$. By Theorem 3, we have

• $F_1^{k-r+1}$ or ${F_2}^{k-r}$ or ${F_3}^{k-r}$ is an induced subgraph of ${\mathcal{T}}^r\left(G\right)$, or
• $F_1^{k-r}$ is a diameter path of ${\mathcal{T}}^r\left(G\right)$, or
• $Lo{l}_{l+k-r+1,2l+1}$ is a diameter subgraph of ${\mathcal{T}}^r\left(G\right)$ for some $1\le l\le k-r$, where $diam\left({\mathcal{T}}^r\left(G\right)\right)=k-r$.

Moreover,

(a)

If $F_1^{k-r+1}$ is an induced subgraph of ${\mathcal{T}}^r\left(G\right)$, then either $F_1^{k-r-2}$ or $F_1^{k-r+1}$ is an induced subgraph of ${\mathcal{T}}^{r-1}\left(G\right)$ or $F_1^{k-r+1}$ is an induced subgraph of $\mathcal{L}\left({\mathcal{T}}^{r-1}\left(G\right)\right)$. Since $\mathcal{L}\left(F_1^{k-r+2}\right)=F_1^{k-r+1}$, then $F_1^{k-r-2}$ is an induced subgraph of ${\mathcal{T}}^{r-1}\left(G\right)$.

(b)

If $F_2^{k-r}$ is an induced subgraph of ${\mathcal{T}}^r\left(G\right)$, then $F_1^{k-r}$ is an induced subgraph of ${\mathcal{T}}^r\left(G\right)$. By $\left(\mathrm{a}\right)$, $F_1^{k-r-3}$ is an induced subgraph of ${\mathcal{T}}^{r-1}\left(G\right)$.

(c)

If $F_3^{k-r}$ is an induced subgraph of ${\mathcal{T}}^r\left(G\right)$, then $F_1^{k-r-1}$ is an induced subgraph of ${\mathcal{T}}^r\left(G\right)$. By $\left(\mathrm{a}\right)$, $F_1^{k-r-4}$ is an induced subgraph of ${\mathcal{T}}^{r-1}\left(G\right)$.

(d)

If $F_1^{k-r}$ is a diameter path of ${\mathcal{T}}^r\left(G\right)$, then either $F_1^{k-r}$ or $F_1^{k-r-1}$ is a diameter path of ${\mathcal{T}}^{r-1}\left(G\right)$ or $F_1^{k-r}$ is a diameter path of $\mathcal{L}\left({\mathcal{T}}^{r-1}\left(G\right)\right)$. Since $\mathcal{L}\left(F_1^{k-r+1}\right)=F_1^{k-r}$, then $F_1^{k-r-1}$ is an induced subgraph of ${\mathcal{T}}^{r-1}\left(G\right)$.

(e)

If $Lo{l}_{l+k-r+1,2l+1}$ is a diameter subgraph of ${\mathcal{T}}^r\left(G\right)$, for some $1\le l\le k-r$, where $diam\left({\mathcal{T}}^r\left(G\right)\right)=k-r$. Then, $F_1^{k-r-1}$ is a diameter path of ${\mathcal{T}}^r\left(G\right)$. By $\mathrm{d})$, $F_1^{k-r-2}$ is a diameter path of ${\mathcal{T}}^{r-1}\left(G\right)$.

Therefore, $F_1^{k-r-4}$ is an induced subgraph of ${\mathcal{T}}^{r-1}\left(G\right)$. By (a), $F_1^{k-r-7}$ is an induced subgraph of ${\mathcal{T}}^{r-2}\left(G\right)$. Then, $F_1^{k-r-10}$ is an induced subgraph of ${\mathcal{T}}^{r-3}\left(G\right)$. Following this process, we concluded that $F_1^{k-4r-1}$ is an induced subgraph of G. ☐

Theorem 5.

Let $r\ge 1$, $k\ge 2r+2$ and G be a connected graph. If $F_1^{k-2r}$ be an induced subgraph of G, then

$$diam\left({\mathcal{T}}^{r+1}\left(G\right)\right)>k-r.$$

Proof. 

Suppose $F_1^{k-2r}$ is an induced subgraph of G, then $F_1^{k-2r+1}$ is an induced subgraph of $\mathcal{T}\left(G\right)$. Moreover, $F_1^{k-2r+2}$ is an induced subgraph of ${\mathcal{T}}^2\left(G\right)$. Following this process, we concluded that $F_1^{k-r-1}$ is an induced subgraph of ${\mathcal{T}}^{r-1}\left(G\right)$. Then, the graph with vertices

$$v_1,\left(v_1{v}_2\right),v_2,\dots ,v_{k-r},\left(v_{k-r}{v}_{k-r+1}\right),v_{k-r+1}$$

is an induced subgraph of ${\mathcal{T}}^r\left(G\right)$ isomorphic to $F_3^{k-r}$. By Theorem 3, $diam\left({\mathcal{T}}^{r+1}\left(G\right)\right)>k-r$.

2.3. Results for Iterated Line Graphs

Let $P_{k-1}$ be the path with vertices $v_1,v_2,\dots ,v_{k-1}$, where $v_i$ is adjacent to $v_{i+1}$, $i=1,2,\dots ,k-2$, $k\ge 3$. Let $F_4^k$ be the graph obtained from $P_{k-1}$ by joining two new vertices to the vertex $v_1$ and another two new vertices the vertex $v_{k-1}$. Thus, $F_4^k$ has $k+3$ vertices and $k+2$ edges. Let $P_{k+1}$ be a path on the vertices $v_1,v_2,\dots ,v_{k+1}$, where $v_i$ is adjacent to $v_{i+1}$, $i=1,2,\dots ,k$, $k\ge 1$. Let $F_5^k$ be the graph obtained from $P_{k+1}$ by joining two new vertices to the vertex $v_{k+1}$. Note that $F_4^k$ and $F_5^k$ have diameter $k+1$ (see Figure 3).

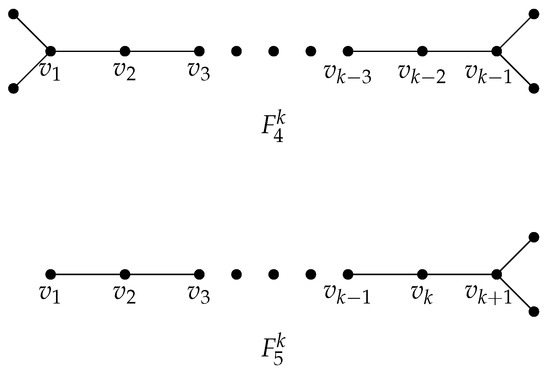
Figure 3. Graphs $F_4^k$ and $F_5^k$.

Lemma 4

([5]). Let G be a connected graph with $n\ge 3$ vertices. Let $k\ge 2$. Then, $diam\left(\mathcal{L}\right(G\left)\right)>k$, if and only if either $F_1^{k+1}$ or $F_2^k$ or $F_3^k$ is an induced subgraph of G.

Considering Lemma 4, the next result is obtained.

Corollary 2.

Let G be a connected graph.

a.

If $r\ge 1$ and $k\ge 2r+3$ such that

$$diam\left({\mathcal{L}}^{r+1}\left(G\right)\right)>k-r.$$

Then $F_1^{k-2r-1}$ is an induced subgraph of G.

b.

If $1\le r<k-1$ such that $F_1^{k+1}$ or $F_4^k$ or $F_5^k$ is an induced subgraph of G. Then

$$diam\left({\mathcal{L}}^{r+1}\left(G\right)\right)>k-r.$$

Proof. 

a.

Suppose $diam\left({\mathcal{L}}^{r+1}\left(G\right)\right)>k-r$. By Lemma 4, $F_1^{k-r+1}$ or $F_2^{k-r}$ or $F_3^{k-r}$ is an induced subgraph of ${\mathcal{L}}^r\left(G\right)$. Then, $F_1^{k-r-1}$ is an induced subgraph of ${\mathcal{L}}^r\left(G\right)$. Since $\mathcal{L}\left(F_1^{k-r}\right)=F_1^{k-r-1}$. Then, $F_1^{k-r-2}$ is an induced subgraph of ${\mathcal{L}}^{r-1}\left(G\right)$. Thus, $F_1^{k-r-3}$ is an induced subgraph of ${\mathcal{L}}^{r-2}\left(G\right)$. Then, $F_1^{k-r-4}$ is an induced subgraph of ${\mathcal{L}}^{r-3}\left(G\right)$. Following this process, we concluded that $F_1^{k-2r-1}$ is an induced subgraph of G.

b.

Suppose $F_1^{k+1}$ or $F_4^k$ or $F_5^k$ is an induced subgraph of G. By Lemma 2, ${\mathcal{L}}^r\left(F_1^{k+1}\right)$ or ${\mathcal{L}}^r\left(F_4^k\right)$ or ${\mathcal{L}}^r\left(F_5^k\right)$ is an induced subgraph of ${\mathcal{L}}^r\left(G\right)$. Moreover, ${\mathcal{L}}^r\left(F_1^{k+1}\right)=F_1^{k-r+1}$, ${\mathcal{L}}^r\left(F_4^k\right)=F_3^{k-r}$, and ${\mathcal{L}}^r\left(F_5^k\right)=F_2^{k-r}$. By Lemma 4, $diam\left({\mathcal{L}}^{r+1}\left(G\right)\right)>k-r$.

☐

3. Energy of Iterated Graphs

In this section, we derive bounds on the incidence energy of iterated total graphs of regular graphs. Furthermore, we construct new families of non-isomorphic cospectral graphs.

3.1. Incidence Energy of Iterated Graphs

The basic properties of iterated line graph sequences are summarized in References [17,18].

The line graph of a regular graph is a regular graph. In particular, the line graph of a regular graph of order $n_0$ and degree $r_0$ is a regular graph of order $n_1={\displaystyle \frac{1}{2}}{r}_0{n}_0$ and degree $r_1=2r_0-2$. Consequently, the order and degree of ${\mathcal{L}}^k\left(G\right)$ are (see [17,18]):

$n_k={\displaystyle \frac{1}{2}}{r}_{k-1}{n}_{k-1}$, and $r_k=2r_{k-1}-2$, where $n_{k-1}$ and $r_{k-1}$ stand for the order and degree of ${\mathcal{L}}^{k-1}\left(G\right)$. Therefore,

$$r_k=2^k{r}_0-2^{k+1}+2$$

and

$$n_k={\displaystyle \frac{n_0}{2^k}}\prod _{i=0}^{k-1}{r}_i={\displaystyle \frac{n_0}{2^k}}\prod _{i=0}^{k-1}\left(2^i{r}_0-2^{i+1}+2\right).$$

Theorem 6.

Let G be a regular graph of order $n_0$ and degree $r_0$, then for $k\ge 1$ the k-th iterated total graph of G is a regular graph of degree $r_k$ and order $n_k$, where

1.

$r_k=2r_{k-1}$, and

2.

$n_k=n_{k-1}\left({\displaystyle \frac{r_{k-1}+2}{2}}\right)$.

Proof. 

Let $k\ge 1$. Suppose that the $(k-1)$-th iterated total graph of G is a regular graph of order $n_{k-1}$ and degree $r_{k-1}$.

• Let v be a vertex of the k-th iterated total graph of G. Then
  • Case a: If v is a vertex of the $(k-1)$-th iterated total graph of G, then v is adjacent to $r_{k-1}$ vertices and incident to $r_{k-1}$ edges in ${\mathcal{T}}^{k-1}\left(G\right)$. Thus, the degree of v in ${\mathcal{T}}^k\left(G\right)$ is

    $$r_{k-1}+r_{k-1}=2r_{k-1}.$$
  • Case b: If v is an edge of the $(k-1)$-th iterated total graph of G, then v is adjacent in each extreme to $r_{k-1}-1$ edges and incident to its two extreme vertices in ${\mathcal{T}}^{k-1}\left(G\right)$. Thus, the degree of v in ${\mathcal{T}}^k\left(G\right)$ is

    $$(r_{k-1}-1)+(r_{k-1}-1)+2=2r_{k-1}.$$
  Therefore, the k-th iterated total graph of G is a regular graph of degree

  $$r_k=2r_{k-1}.$$
• Let ${\mathcal{T}}^{k-1}\left(G\right)$ be a regular graph with $m_{k-1}$ edges, then $m_{k-1}=\frac{n_{k-1}{r}_{k-1}}{2}$. Therefore, the order of the k-th iterated total graph of G is

  $$n_k=m_{k-1}+n_{k-1}={\displaystyle \frac{n_{k-1}{r}_{k-1}}{2}}+n_{k-1}=n_{k-1}\left(\frac{r_{k-1}+2}{2}\right).$$

☐

Repeated application of the previous theorem generates the following result.

Corollary 3.

Let G be a regular graph of order $n_0$ and degree $r_0$, then for $k\ge 1$ the k-th iterated total graph of G is a regular graph of degree $r_k$ and order $n_k$, where

$$r_k=2^k{r}_0,$$

(3)

and

$$n_k={\displaystyle \frac{n_0}{2^k}}\prod _{i=0}^{k-1}\left(2^i{r}_0+2\right).$$

(4)

The following result gives the eigenvalues of $\mathcal{T}\left(G\right)$ for a regular graph of order n and degree r.

Lemma 5

([19]). Let G be a regular graph of order n and degree r. Then, the eigenvalues of $\mathcal{T}\left(G\right)$ are

$$\left\{\begin{array}{cc}{\displaystyle \frac{2{\lambda }_i+r-2\pm \sqrt{4{\lambda }_i+r^2+4}}{2}}& i=1,2,\dots ,n,\mathit{and}\hfill \\ -2& {\displaystyle \frac{n(r-2)}{2}}\mathit{times},\hfill \end{array}\right.$$

(5)

where ${\lambda }_i$ is an eigenvalue of G.

Now we consider bounds for the incidence energy of the iterated total graph.

Theorem 7.

Let G be a regular graph of order n and degree r. Then

• $IE\left(\mathcal{T}\left(G\right)\right)<{\displaystyle \frac{n(r-2)\sqrt{2r-2}}{2}}+2n\sqrt{r}+(n-1)\sqrt{3r-2},$ and
• $IE\left(\mathcal{T}\left(G\right)\right)\ge {\displaystyle \frac{n(r-2)\sqrt{2r-2}}{2}}+(n+1)\sqrt{r}+\sqrt{3r-2}+(n-1)\sqrt{2r-2}$.

Equality holds if and only if $G\cong K_2$.

Proof. 

1. Let $r=1$, then G is union disjoint of copies of $K_2$ and $\mathcal{T}\left(G\right)$ is union disjoint of copies of $K_3$. That is, $G\cong \frac{n}{2}{K}_2$ and $\mathcal{T}\left(G\right)\cong \frac{n}{2}{K}_3$, where n is even. Since $IE\left(K_3\right)=4$, it follows that $IE\left(\mathcal{T}\right(G\left)\right)=2n$. Therefore, if $r=1$

$${\displaystyle \frac{n(r-2)\sqrt{2r-2}}{2}}+2n\sqrt{r}+(n-1)\sqrt{3r-2}=3n-1>2n$$

$${\displaystyle \frac{n(r-2)\sqrt{2r-2}}{2}}+(n+1)\sqrt{r}+\sqrt{3r-2}+(n-1)\sqrt{2r-2}=n+2\le 2n,$$

with equality if and only if $n=2,$ that is, $G\cong K_2$.

Let $r\ge 2$. Since G is a regular graph of degree r. From Theorem 6, $\mathcal{T}\left(G\right)$ is a regular graph of degree $2r$. From Lemma 5, the signless Laplacian eigenvalues of $\mathcal{T}\left(G\right)$ are

$$\left\{\begin{array}{cc}{\displaystyle \frac{5r+2{\lambda }_i-2\pm \sqrt{4{\lambda }_i+r^2+4}}{2}}& i=1,2,\dots ,n\mathrm{and}\hfill \\ 2r-2& {\displaystyle \frac{n(r-2)}{2}}\mathrm{times},\hfill \end{array}\right.$$

where ${\lambda }_i$ is an eigenvalue of G.

From Perron–Frobenius’s theory, ${\lambda }_1=r$ and $-r\le {\lambda }_i<r$ for $i=2,\dots ,n$. By definition of the incidence energy of a graph, we have

$$\begin{array}{ccc}\hfill IE\left(\mathcal{T}\right(G\left)\right)& =& {\displaystyle \frac{n(r-2)\sqrt{2r-2}}{2}}+2\sqrt{r}+\sqrt{3r-2}\hfill \\ & +& \sum _{i=2}^n\left(\sqrt{\frac{5r+2{\lambda }_i-2+\sqrt{4{\lambda }_i+r^2+4}}{2}}+\sqrt{\frac{5r+2{\lambda }_i-2-\sqrt{4{\lambda }_i+r^2+4}}{2}}\right).\hfill \end{array}$$

Let

$$g\left(t\right)=\sqrt{\frac{5r+2t-2+\sqrt{r^2+4t+4}}{2}}+\sqrt{\frac{5r+2t-2-\sqrt{r^2+4t+4}}{2}}$$

and

$$h\left(t\right)=\sqrt{r^2+4t+4},$$

where $-r\le t<r$. Thus,

$$g^{\prime }\left(t\right)={\displaystyle \frac{1}{\sqrt{2}h\left(t\right)}}\left(\frac{h\left(t\right)+1}{\sqrt{5r+2t-2+h\left(t\right)}}+\frac{h\left(t\right)-1}{\sqrt{5r+2t-2-h\left(t\right)}}\right).$$

It is clear that $g\left(t\right)$ is an increasing function for $-r\le t<r$.

$$\begin{array}{ccc}\hfill IE\left(\mathcal{T}\right(G\left)\right)& <& {\displaystyle \frac{n(r-2)\sqrt{2r-2}}{2}}+2\sqrt{r}+\sqrt{3r-2}+\sum _{i=1}^{n}g\left(r\right)\hfill \\ & =& {\displaystyle \frac{n(r-2)\sqrt{2r-2}}{2}}+2n\sqrt{r}+(n-1)\sqrt{3r-2}.\hfill \end{array}$$

$$\begin{array}{ccc}\hfill IE\left(\mathcal{T}\right(G\left)\right)& \ge & {\displaystyle \frac{n(r-2)\sqrt{2r-2}}{2}}+2\sqrt{r}+\sqrt{3r-2}+\sum _{i=1}^{n}g(-r)\hfill \\ & =& {\displaystyle \frac{n(r-2)\sqrt{2r-2}}{2}}+(n+1)\sqrt{r}+\sqrt{3r-2}+(n-1)\sqrt{2r-2}.\hfill \end{array}$$

Since $n\ge 3$, then there exists ${\lambda }_i>-r$ for some $i=2,3,\dots ,n$. Therefore, the equality does not hold. ☐

Corollary 4.

Let G be a regular graph of order $n_0$ and degree $r_0\ge 2$, and let for $k\ge 0$, the $k-th$ iterated total graph of G be of degree $r_k$ and order $n_k$. Then,

• $IE\left({\mathcal{T}}^{k+1}\left(G\right)\right)<{\displaystyle \frac{n_k(r_k-2)\sqrt{2r_k-2}}{2}}+2n_k\sqrt{r_k}+(n_k-1)\sqrt{3r_k-2}$, and
• $IE\left({\mathcal{T}}^{k+1}\left(G\right)\right)\ge {\displaystyle \frac{n_k(r_k-2)\sqrt{2r_k-2}}{2}}+(n_k+1)\sqrt{r_k}+\sqrt{3r_k-2}+(n_k-1)\sqrt{2r_k-2}$.

Equality holds if and only if $G\cong K_2$ and $k=0$.

Corollary 5.

Under the notation specified in Corollary 3, for any integer k

• $IE\left({\mathcal{T}}^k\left(G\right)\right)<(n_k-2n_{k-1})\sqrt{r_k-2}+n_{k-1}\sqrt{2r_k}+(n_{k-1}-1)\sqrt{r_k+r_{k-1}-2}$, and
• $IE\left({\mathcal{T}}^k\left(G\right)\right)\ge (n_k-2n_{k-1})\sqrt{r_k-2}+(n_{k-1}+1)\sqrt{r_{k-1}}+\sqrt{r_k+r_{k-1}-2}+(n_{k-1}-1)\sqrt{r_k-2}$.

Equality holds if and only if $G\cong K_2$ and $k=1$.

3.2. An Application: Constructing Non-isomorphic Cospectral Graphs

Many constructions of cospectral graphs are known. Most constructions from before 1988 can be found in [20], Section 6.1, and [21], Section 1.3; see also [22], Section 4.6. More recent constructions of cospectral graphs were presented by Seress [23], who gives an infinite family of cospectral 8-regular graphs. Graphs cospectral to distance-regular graphs can be found in [20,21,22,23,24,25,26]. Notice that the graphs mentioned are regular, so they are cospectral with respect to any generalized adjacency matrix, which in this case includes the Laplace matrix.

Let us consider the functions

$$f_1\left(x\right)={\displaystyle \frac{1}{2}}(2x+r-2+\sqrt{4x+r^2+4})$$

and

$$f_2\left(x\right)={\displaystyle \frac{1}{2}}(2x+r-2-\sqrt{4x+r^2+4}).$$

Theorem 8.

Let $G_1$ and $G_2$ be two regular graphs of the same order and degree $n_0$ and $r_0\ge 3$, respectively. Then, for any $k\ge 1$, the following hold

(a) 

${\mathcal{T}}^k\left(G_1\right)$ and ${\mathcal{T}}^k\left(G_2\right)$ are of the same order, and have the same edges number.

(b) 

${\mathcal{T}}^k\left(G_1\right)$ and ${\mathcal{T}}^k\left(G_2\right)$ are cospectral if and only if $G_1$ and $G_2$ are cospectral.

Proof. 

Statement (a) follows from Equations (2) and (3), and the fact that the number of vertices and edges of ${\mathcal{T}}^k\left(G\right)$ corresponds to the number of vertices of ${\mathcal{T}}^{k+1}\left(G\right)$. Statement (b) follows from relation (4) and the injectivity of the functions $f_1$ and $f_2$ on the segment $[-r,r],$ $r>2$, applied a sufficient number of times. ☐

4. Conclusions

In this article, in Section 2, necessary and sufficient conditions such that the diameter of the total graph of a graph are less than or equal to a given integer k are established, $k\ge 2$. Additionally, we introduce necessary and sufficient conditions such that the diameter of the $(r+1)$-th iterated line and total graph of a graph are greater than the difference between two given integers k and r. In Section 3, upper and lower bounds are determined for the incidence energy of the total graph of a regular graph, depending on the order and degree of the graph. Finally, we obtain an application for the construction of non-isomorphic cospectral graphs.