Weak Fault Detection for Gearboxes Using Majorization–Minimization and Asymmetric Convex Penalty Regularization
Abstract
1. Introduction
- (1)
- Unique dictionaries’ atoms and optimal wavelet basis cannot simultaneously match the natural structure of every real vibration signal well;
- (2)
- A large number of observed signals should be collected to form a training dictionary before diagnosis, which is always infeasible in practical applications;
- (3)
- Computational complexity and time-consuming problems occur simultaneously in dictionary training, such as with the K-SVD training and SI-K-SVD dictionaries training [31].
- (1)
- Generally, the penalty functions that are established in a low-rank matrix approximation (LRMA) model are symmetric functions, e.g., the absolute value function (AVF); the common drawback is that this penalty function is non-differentiable at the zero point, which can lead to some numerical issues, such as a local optimum and early termination of algorithm.
- (2)
- In a conventional low-rank matrix approximation (LRMA) method, the convex regularizer, such as the L1-norm, usually underestimates the sparse signal when the absolute value function (AVF) is used as a sparsity regularizer; the nonconvex regularizer suffers from several issues, such as a strict convexity problem of objective cost function (OCF), a non-convergence problem, etc. Additionally, both the convex and nonconvex regularizers shrink all the coefficients equally and remove too much energy from the useful signal, resulting in the estimation of the fault signal becoming more challenging.
- (3)
- When the useful fault characteristics signals are very weak but additive noise extremely strong, the conventional LRMA method cannot estimate low-dimensional feature distribution accurately.
2. Majorization–Minimization Algorithm
- (1)
- Initialize u0 and k = 0;
- (2)
- Construct a majorization function G(u, uk);
- (3)
- Operate the iteration ;
- (4)
- If the stopping criterion is satisfied, then output ; otherwise, k = k + 1, and go to step (2);
- (5)
- Output .
3. Asymmetric Convex Penalty Regularization Algorithm
3.1. Sparse Representation and Filter Banks
3.2. Asymmetric Convex Penalty Regularization Model
- (I)
- The M-term compound regularizers estimate the fault transient impulses;
- (II)
- The compound regularizers model consists of symmetric and asymmetric penalty functions, wherein the symmetric penalty function is a differentiable function, compared with the nondifferentiable function at i = 0.
- (III)
- The MM algorithm is introduced for the solution of the proposed compound regularization method.
3.3. The Solution of the Proposed Model Based on the Majorization–Minimization Algorithm
- (a)
- The majorizer of the symmetric and differentiable function based on the MM algorithm.
- (b)
- The majorizer of the asymmetric and differentiable function based on the MM algorithm.
- (c)
- The majorizer of the objective cost function F(x) based on the MM algorithm.
- (1)
- Input: signal y, r ≥ 1, matrix A, matrix B, , k = 0;
- (2)
- (3)
- Initialize x = y;
- (4)
- Repeat the following iterations:
- (5)
- If the stopping criterion is satisfied, then output signal x—otherwise, k = k + 1, and go to step (4).
- (6)
- Output: signal x.
3.4. Parameter Selection
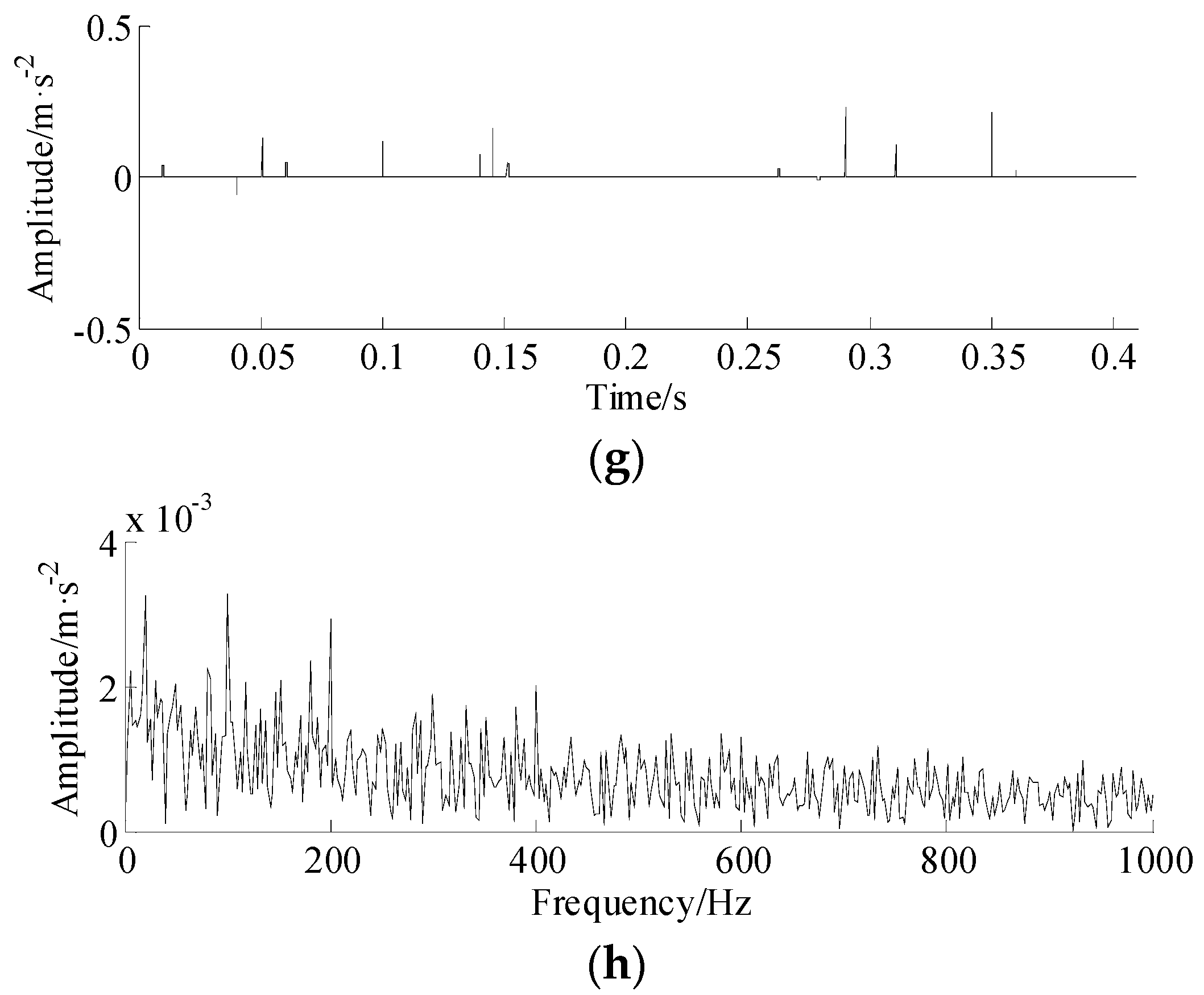
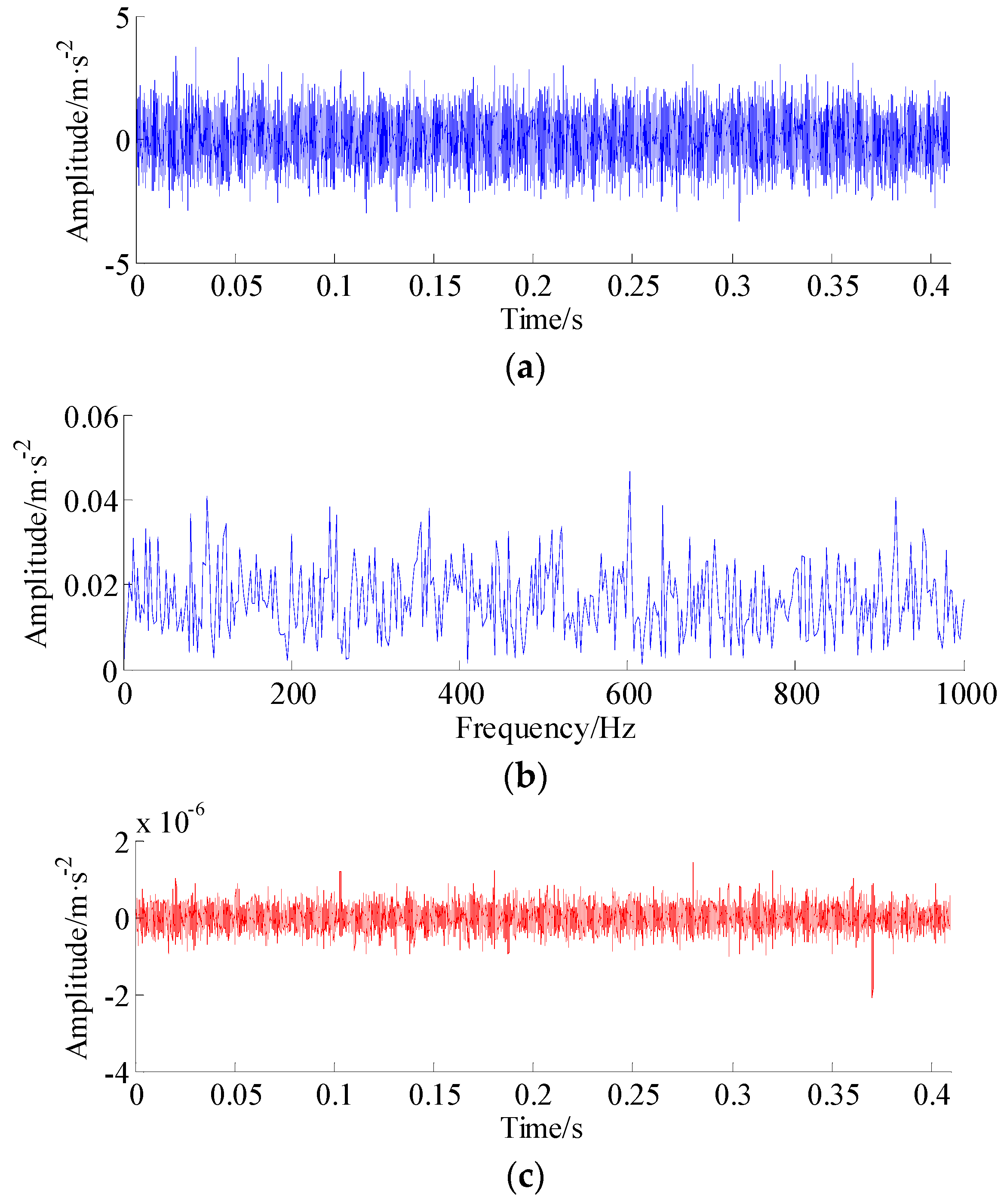
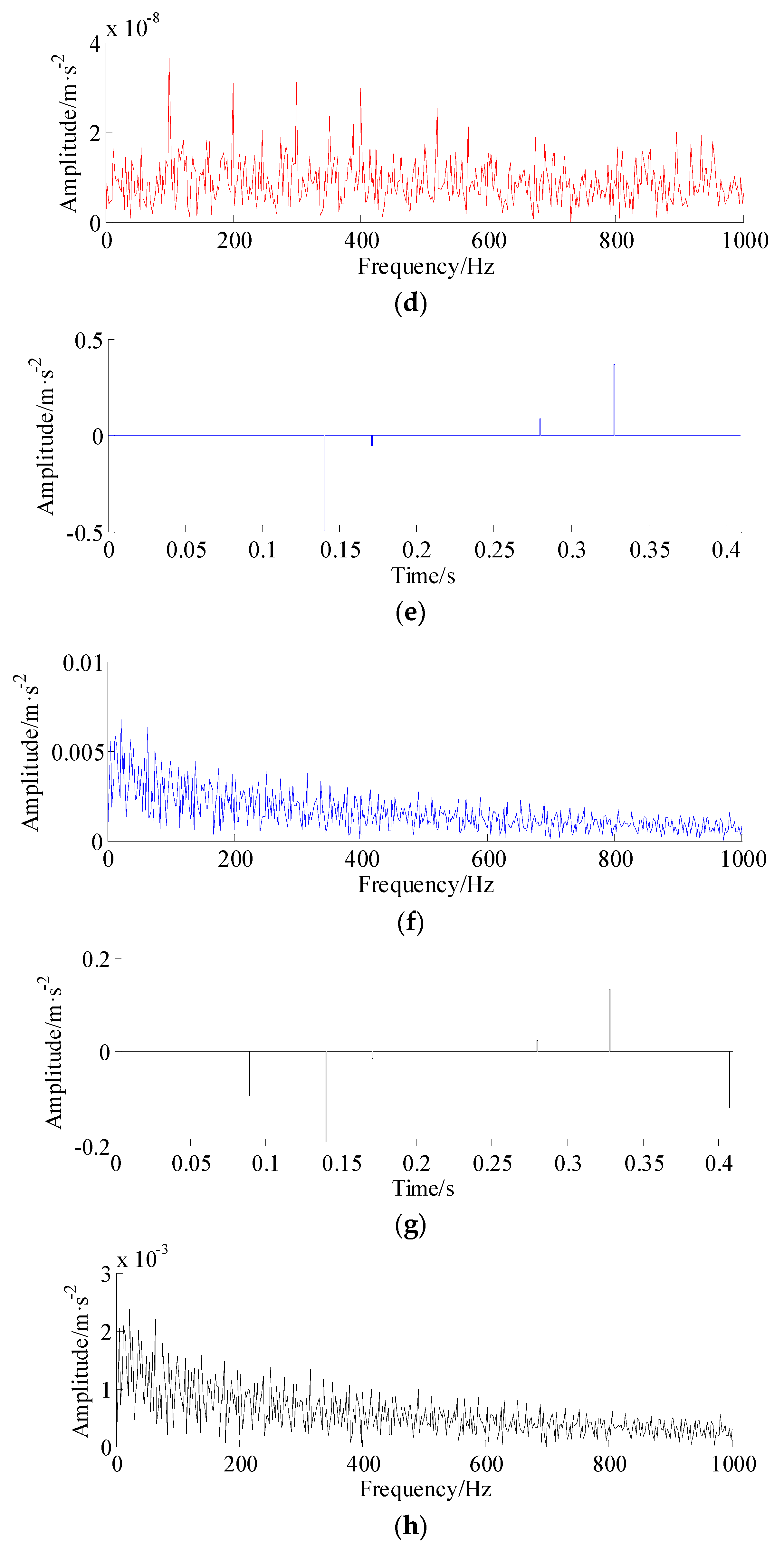
4. Numerical Simulation
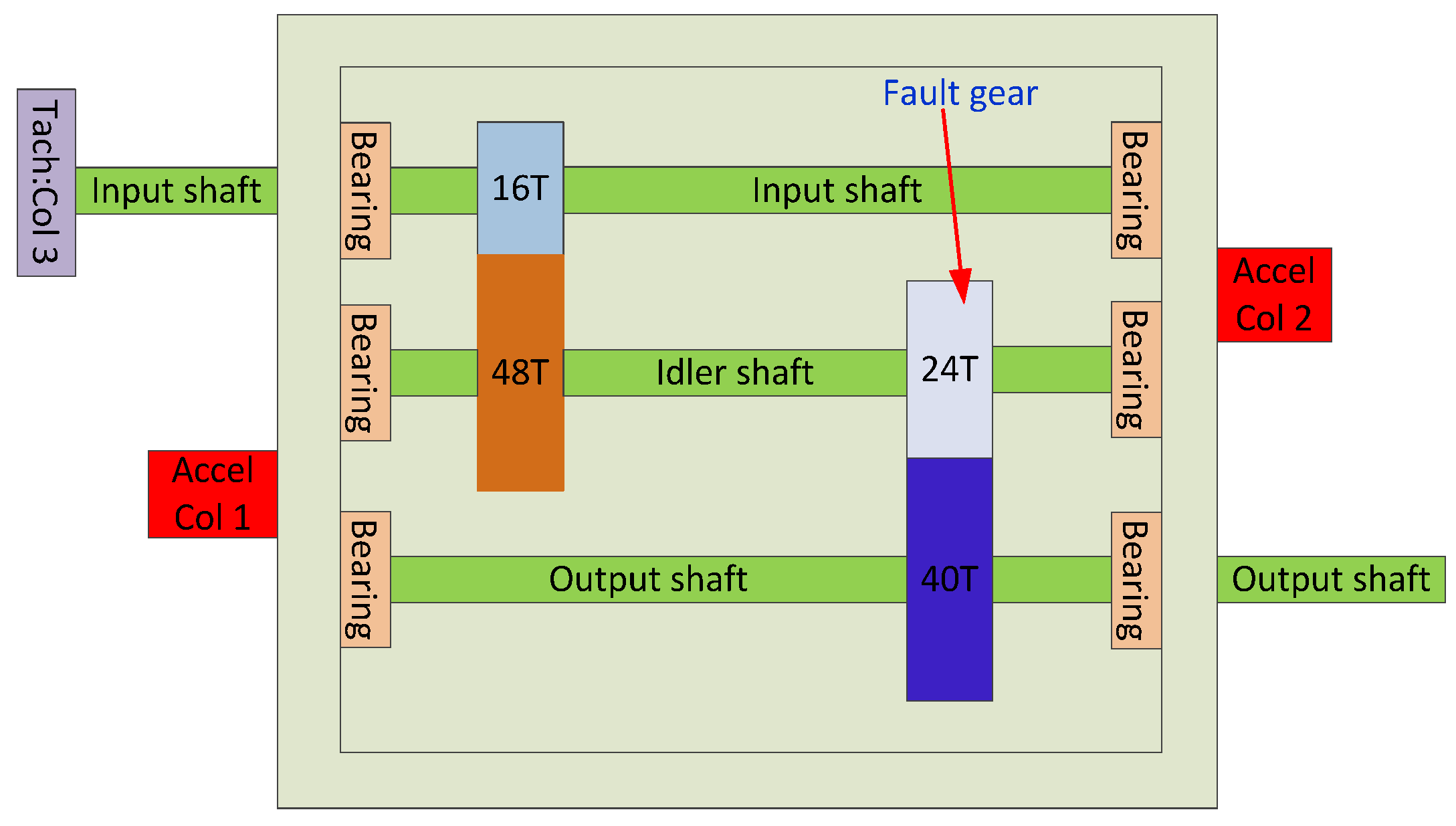
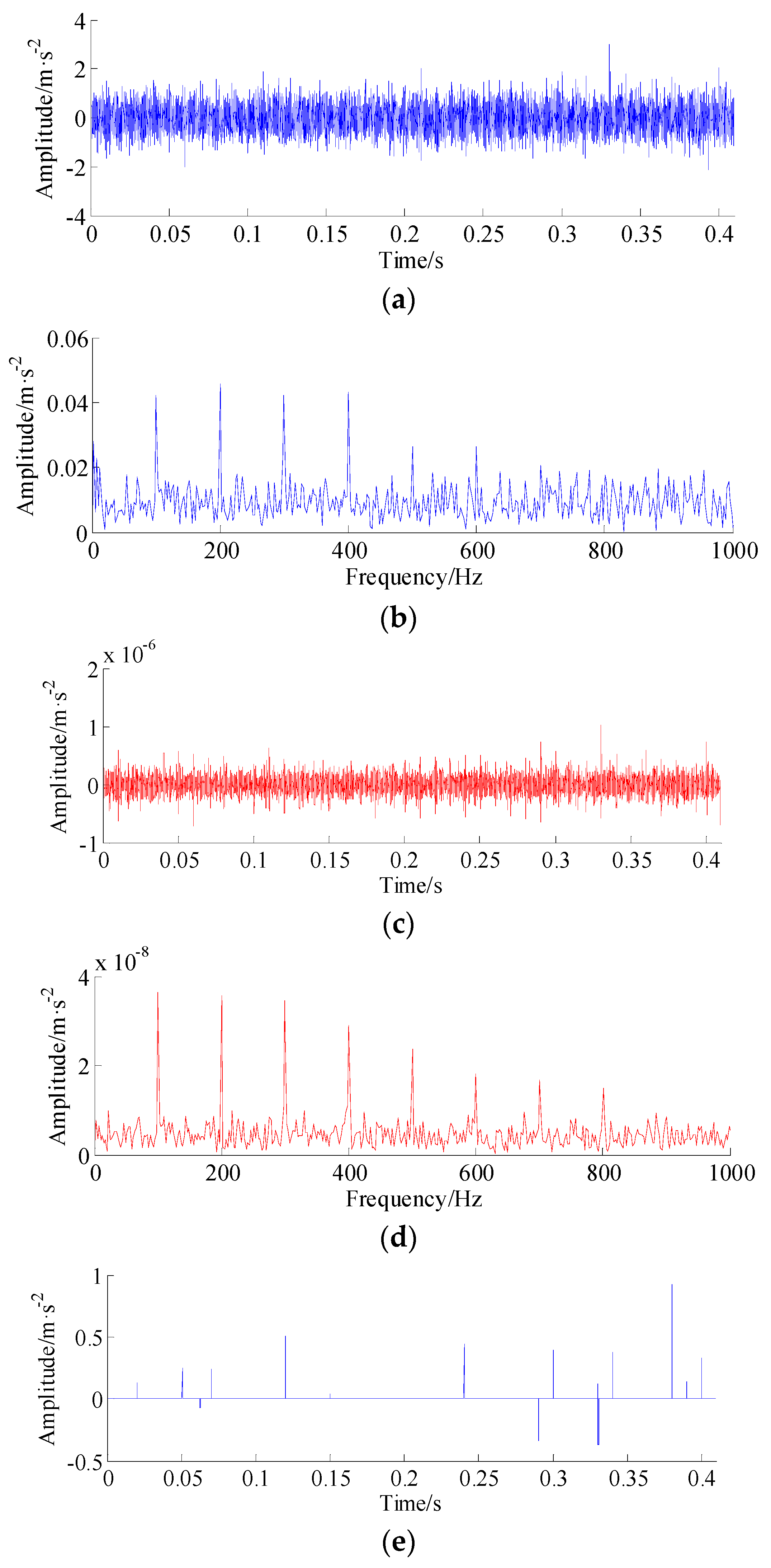
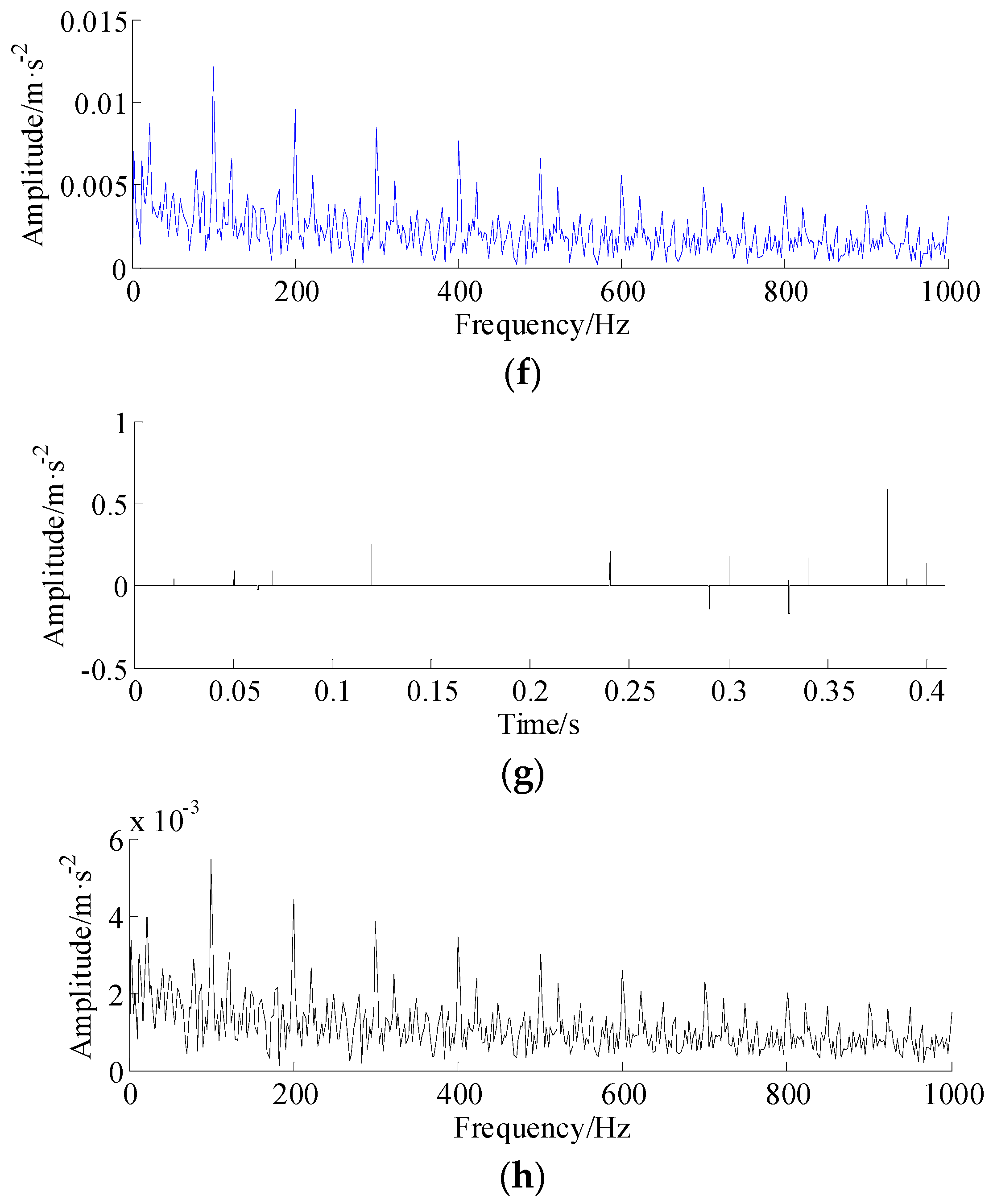
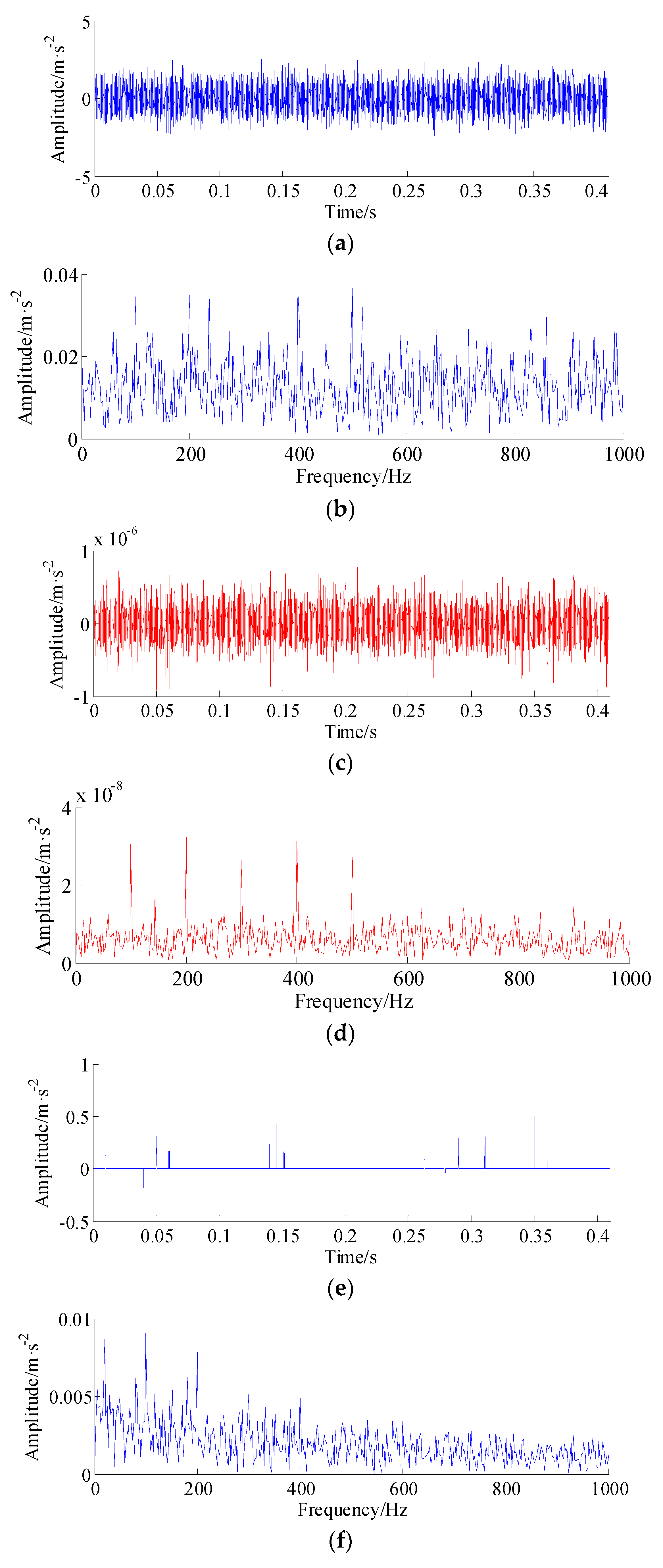
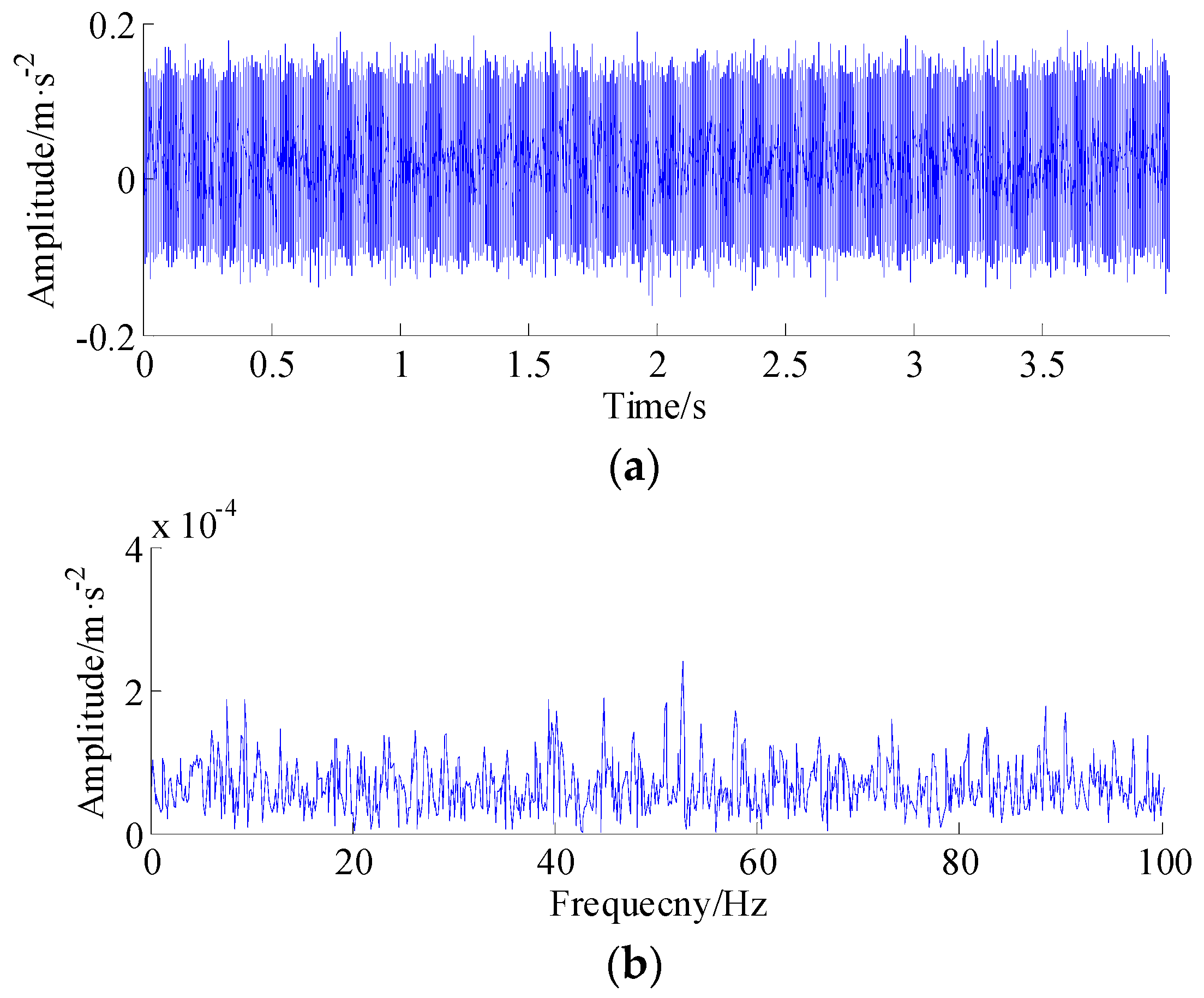
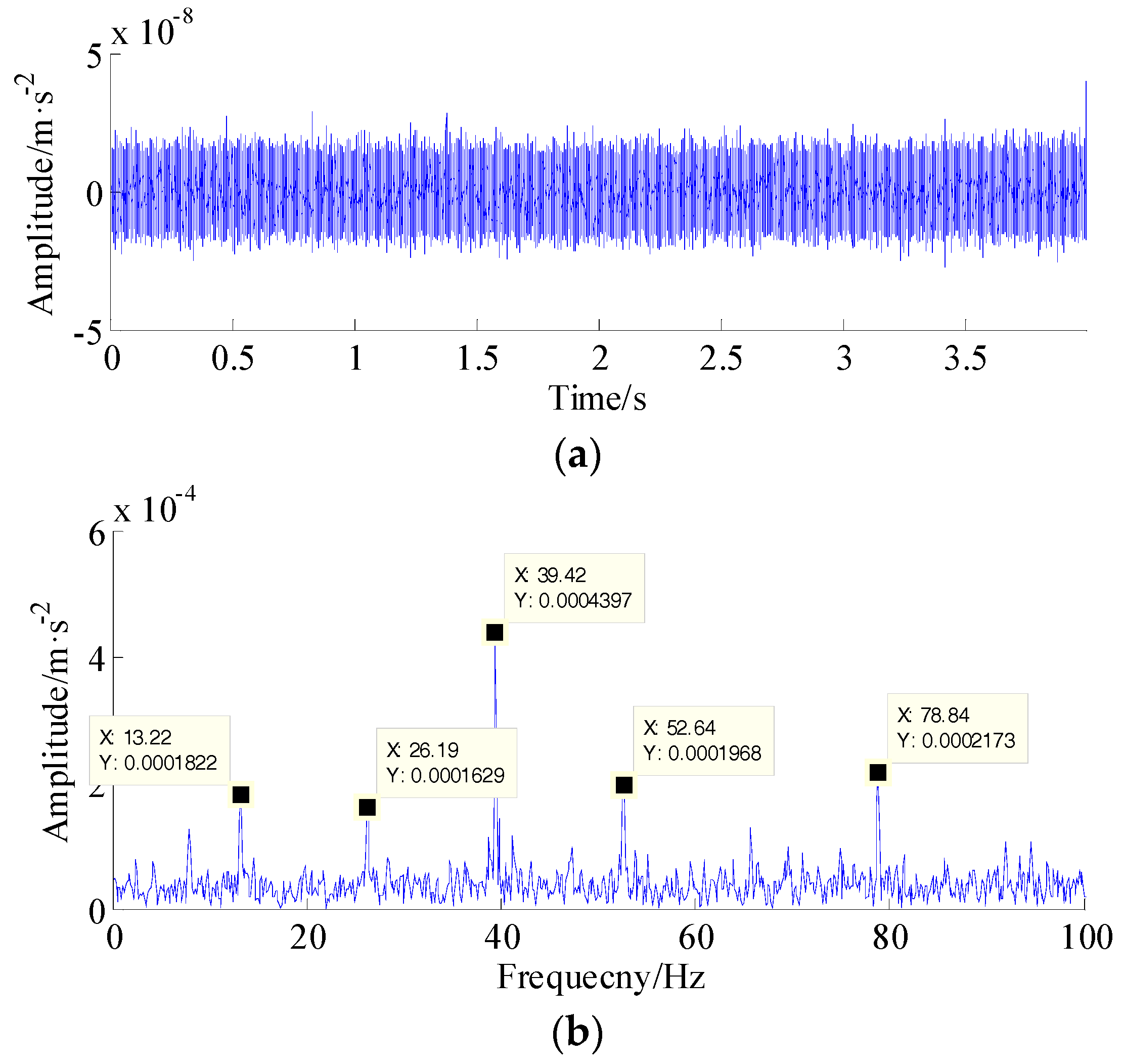
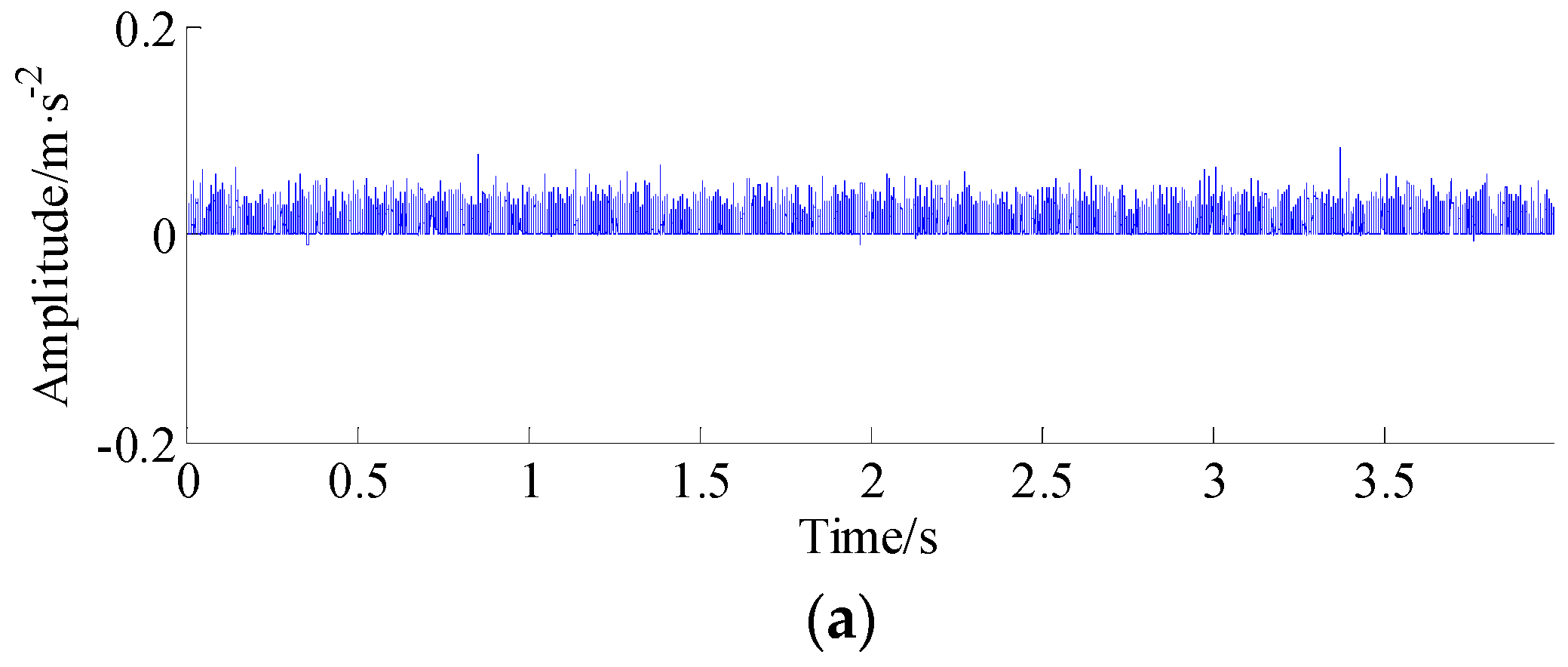
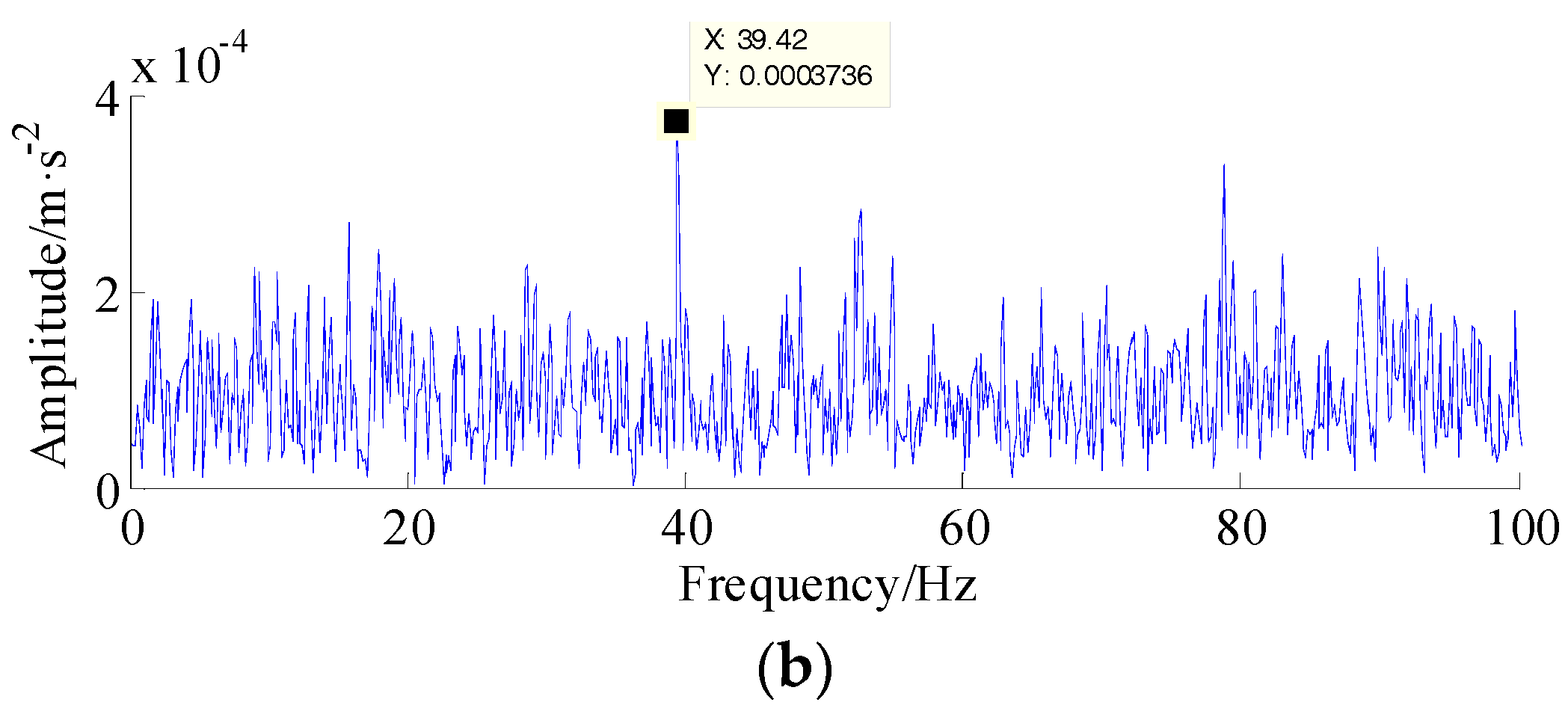
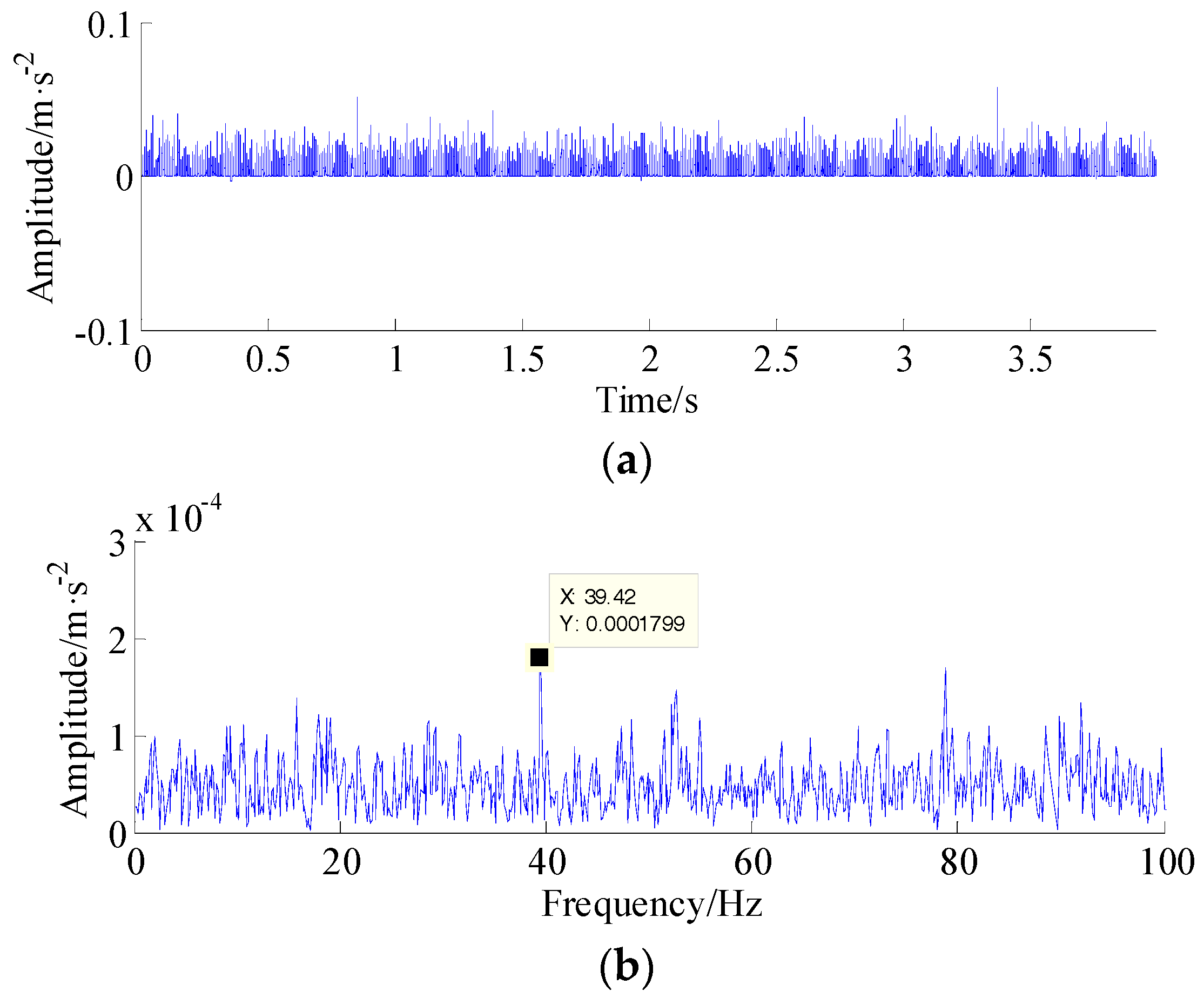
5. Experimental Validation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jing, L.Y.; Zhao, M.; Li, P.; Xu, X.Q. A convolutional neural network based feature learning and fault diagnosis method for the condition monitoring of gearbox. Measurement 2017, 111, 1–10. [Google Scholar] [CrossRef]
- Li, Y.B.; Li, G.Y.; Yang, Y.T.; Liang, X.H.; Xu, M.Q. A fault diagnosis scheme for planetary gearboxes using adaptive multi-scale morphology filter and modified hierarchical permutation entropy. Mech. Syst. Signal Process. 2018, 105, 319–337. [Google Scholar] [CrossRef]
- Kia, S.H.; Henao, H.; Capolino, G.A. Fault index statistical study for gear fault detection using stator current space vector analysis. IEEE Trans. Ind. Appl. 2016, 52, 781–4788. [Google Scholar] [CrossRef]
- Teng, W.; Ding, X.; Zhang, X.L.; Liu, Y.B.; Ma, Z.Y. Multi-fault detection and failure analysis of wind turbine gearbox using complex wavelet transform. Renew. Energy 2016, 93, 591–598. [Google Scholar] [CrossRef]
- Hemmati, F.; Orfali, W.; Gadala, M.S. Roller bearing acoustic signature extraction by wavelet packet transform, applications in fault detection and size estimation. Appl. Acoust. 2016, 104, 101–118. [Google Scholar] [CrossRef]
- Qu, J.X.; Zhang, Z.S.; Gong, T. A novel intelligent method for mechanical fault diagnosis based on dual-tree complex wavelet packet transform and multiple classifier fusion. Neurocomputing 2016, 171, 837–853. [Google Scholar] [CrossRef]
- Wang, L.H.; Zhao, X.P.; Wu, J.X.; Xie, Y.Y.; Zhang, Y.H. Motor fault diagnosis based on short-time Fourier transform and convolutional neural network. Chin. J. Mech. Eng. 2017, 30, 1357–1368. [Google Scholar] [CrossRef]
- Bouchikhi, E.H.E.; Choqueuse, V.; Benbouzid, M.E.H. Current frequency spectral subtraction and its contribution to induction machines bearings condition monitoring. IEEE Trans. Energy Convers. 2013, 28, 135–144. [Google Scholar] [CrossRef]
- Wang, H.C.; Chen, J.; Dong, G.M. Feature extraction of rolling bearing’s early weak fault based on EEMD and tunable Q-factor wavelet transform. Mech. Syst. Signal Process. 2014, 48, 103–119. [Google Scholar] [CrossRef]
- Li, Q.; Liang, S.Y. Bearing incipient fault diagnosis based upon maximal spectral kurtosis TQWT and group sparsity total variation de-noising approach. J. Vibroeng. 2018, 20, 1409–1425. [Google Scholar] [CrossRef]
- Li, R.Y.; He, D. Rotational machine health monitoring and fault detection using EMD-based acoustic emission feature quantification. IEEE Trans. Instrum. Meas. 2012, 61, 990–1001. [Google Scholar] [CrossRef]
- Yuan, J.; Ji, F.; Gao, Y.; Zhu, J.; Wei, C.J.; Zhou, Y. Integrated ensemble noise-reconstructed empirical mode decomposition for mechanical fault detection. Mech. Syst. Signal Process. 2018, 104, 323–346. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Z.W.; Miao, Q.; Zhang, X. Time-frequency analysis based on ensemble local mean decomposition and fast kurtogram for rotating machinery fault diagnosis. Mech. Syst. Signal Process. 2018, 103, 60–75. [Google Scholar] [CrossRef]
- Li, Q.; Liang, S.Y.; Song, W.Q. Revision of bearing fault characteristic spectrum using LMD and interpolation correction algorithm. Procedia CIRP 2016, 56, 182–187. [Google Scholar] [CrossRef]
- Li, Z.X.; Jiang, Y.; Guo, Q.; Hu, C.; Peng, Z.X. Multi-dimensional variational mode decomposition for bearing-crack detection in wind turbines with large driving-speed variations. Renew. Energy 2018, 116, 55–73. [Google Scholar] [CrossRef]
- Li, Q.; Ji, X.; Liang, S.Y. Incipient fault feature extraction for rotating machinery based on improved AR-minimum entropy deconvolution combined with variational mode decomposition approach. Entropy 2017, 19, 7. [Google Scholar] [CrossRef]
- Zhang, R.; Tao, H.Y.; Wu, L.F.; Guan, Y. Transfer learning with neural networks for bearing fault diagnosis in changing working conditions. IEEE Access 2017, 5, 14347–14357. [Google Scholar] [CrossRef]
- Masud, A.A.; Albarracín, R.; Rey, J.A.A.; Sukki, F.M.; Illias, H.A.; Bani, N.A.; Munir, A.B. Artificial Neural Network Application for Partial Discharge Recognition: Survey and Future Directions. Energies 2016, 9, 574. [Google Scholar] [CrossRef]
- He, M.; He, D. Deep learning based approach for bearing fault diagnosis. IEEE Trans. Ind. Appl. 2017, 53, 3057–3065. [Google Scholar] [CrossRef]
- Jia, F.; Lei, Y.G.; Guo, L.; Lin, J.; Xing, S.B. A neural network constructed by deep learning technique and its application to intelligent fault diagnosis of machines. Neurocomputing 2018, 272, 619–628. [Google Scholar] [CrossRef]
- Li, Q.; Liang, S.Y. Multiple faults detection for rotating machinery based on Bi-component sparse low-rank matrix separation approach. IEEE Access 2018, 6, 20242–20254. [Google Scholar] [CrossRef]
- Tang, H.F.; Chen, J.; Dong, G.M. Sparse representation based latent components analysis for machinery weak fault detection. Mech. Syst. Signal Process. 2014, 46, 373–388. [Google Scholar] [CrossRef]
- Zhou, H.T.; Chen, J.; Dong, G.M.; Wang, R. Detection and diagnosis of bearing faults using shift-invariant dictionary learning and hidden Markov model. Mech. Syst. Signal Process. 2016, 72–73, 65–79. [Google Scholar] [CrossRef]
- Yang, B.Y.; Liu, R.N.; Chen, X.F. Fault diagnosis for a wind turbine generator bearing via sparse representation and shift-invariant K-SVD. IEEE Trans. Ind. Inform. 2017, 13, 1321–1331. [Google Scholar] [CrossRef]
- Feng, Z.P.; Liang, M. Complex signal analysis for planetary gearbox fault diagnosis via shift invariant dictionary learning. Measurement 2016, 90, 382–395. [Google Scholar] [CrossRef]
- Qin, Y. A new family of model-based impulsive wavelets and their sparse representation for rolling bearing fault diagnosis. IEEE Trans. Ind. Electron. 2018, 65, 2716–2726. [Google Scholar] [CrossRef]
- Cui, L.L.; Wang, J.; Lee, S. Matching pursuit of an adaptive impulse dictionary for bearing fault diagnosis. J. Sound Vib. 2014, 333, 2840–2862. [Google Scholar] [CrossRef]
- Cui, L.L.; Gong, X.Y.; Zhang, J.Y.; Wang, H.Q. Double-dictionary matching pursuit for fault extent evaluation of rolling bearing based on the Lempel-Ziv complexity. J. Sound Vib. 2016, 385, 372–388. [Google Scholar] [CrossRef]
- Cui, L.L.; Wu, N.; Ma, C.Q.; Wang, H.Q. Quantitative fault analysis of roller bearings based on a novel matching pursuit method with a new step-impulse dictionary. Mech. Syst. Signal Process. 2016, 68–69, 34–43. [Google Scholar] [CrossRef]
- Ding, X.X.; He, Q.B. Time-frequency manifold sparse reconstruction: A novel method for bearing fault feature extraction. Mech. Syst. Signal Process. 2016, 80, 392–413. [Google Scholar] [CrossRef]
- Li, Q.; Liang, S.Y. Incipient fault diagnosis of rolling bearings based on impulse-step impact dictionary and re-weighted minimizing nonconvex penalty Lq regular technique. Entropy 2017, 19, 8. [Google Scholar] [CrossRef]
- Ding, Y.; He, W.P.; Chen, B.Q.; Zi, Y.Y.; Selesnick, I.W. Detection of faults in rotating machinery using periodic time-frequency sparsity. J. Sound Vib. 2016, 382, 357–378. [Google Scholar] [CrossRef]
- He, W.P.; Ding, Y.; Zi, Y.Y.; Selesnick, I.W. Sparsity-based algorithm for detecting faults in rotating machines. Mech. Syst. Signal Process. 2016, 72–73, 46–64. [Google Scholar] [CrossRef]
- He, W.P.; Ding, Y.; Zi, Y.Y.; Selesnick, I.W. Repetitive transients extraction algorithm for detecting bearing faults. Mech. Syst. Signal Process. 2017, 84, 227–244. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, X.F.; Du, Z.H.; Li, X.; Yan, R.Q. Nonlocal sparse model with adaptive structural clustering for feature extraction of aero-engine bearings. J. Sound Vib. 2016, 368, 223–248. [Google Scholar] [CrossRef]
- Du, Z.H.; Chen, X.F.; Zhang, H.; Yang, B.Y.; Zhai, Z.; Yan, R.Q. Weighted low-rank sparse model via nuclear norm minimization for bearing fault detection. J. Sound Vib. 2017, 400, 270–287. [Google Scholar] [CrossRef]
- Mourad, N.; Reilly, J.P.; Kirubarajan, T. Majorization minimization for blind source separation of sparse sources. Signal Process. 2017, 131, 120–133. [Google Scholar] [CrossRef]
- Qiu, T.Y.; Palomar, D.P. Undersampled sparse phase retrieval via majorization minimization. IEEE trans. Signal Process. 2017, 65, 5957–5969. [Google Scholar] [CrossRef]
- Ndoye, M.; Anderson, J.M.M.; Greene, D.J. An MM-based algorithm for ℓ1-regularized least-squares estimation with an application to ground penetrating radar image reconstruction. IEEE Trans. Image Process. 2016, 25, 2206–2221. [Google Scholar] [CrossRef] [PubMed]
- Donoho, D.L.; Elad, M.; Temlyakov, V.N. Stable recovery of sparse overcomplete representations in the presence of noise. IEEE Trans. Inform. Theory 2006, 52, 6–18. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inform. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Donoho, D.L.; Tsaig, Y. Fast solution of ℓ1-norm minimization problems when the solution may be sparse. IEEE Trans. Inform. Theory 2008, 54, 4789–4812. [Google Scholar] [CrossRef]
- Donoho, D.L. De-noising by soft-thresholding. IEEE Trans. Inf. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef]
- Selesnick, I.W. Total variation denoising via the Moreau envelope. IEEE Signal Process. Lett. 2017, 24, 216–220. [Google Scholar] [CrossRef]
- Selesnick, I.W.; Parekh, A.; Bayram, I. Convex 1-D total variation denoising with non-convex regularization. IEEE Signal Process. Lett. 2015, 22, 141–144. [Google Scholar] [CrossRef]
- Selesnick, I.W.; Graber, H.L.; Pfeil, D.S.; Barbour, R.L. Simultaneous low-pass filtering and total variation denoising. IEEE Trans. Signal Process. 2014, 62, 1109–1124. [Google Scholar] [CrossRef]
- Ning, X.R.; Selesnick, I.W.; Duval, L. Chromatogram baseline estimation and denoising using sparsity (BEADS). Chemom. Intell. Lab. 2014, 139, 156–167. [Google Scholar] [CrossRef]
- Donoho, D.L.; Johnstone, I.M. Ideal spatial adaptation by wavelet shrinkage. Biometrika 1993, 81, 425–455. [Google Scholar] [CrossRef]
- Annual Conference of the Prognostics and Health Management Society 2009. Available online: https://www.phmsociety.org/events/conference/phm/09 (accessed on 5 June 2018).
- Atat, H.A.; Siegel, D.; Lee, J. A systematic methodology for gearbox health assessment and fault classification. Int. J. Progn. Health Manag. 2011, 2, 1. [Google Scholar]


| Functions | ||
|---|---|---|
| Signal(x) | ||
| Regularization Parameter λ0 | Regularization Parameter λ1 | Regularization Parameter λ2 | M-Term | Iteration Times |
|---|---|---|---|---|
| λ0 = 0.35 | λ1 =1.125 | λ2 = 0.35 | 2 | 50 |
| Noise Standard Deviation | ACPR Algorithm | NCPR Algorithm | LFLO Algorithm |
|---|---|---|---|
| sigma = 0.5 | 0.288113 s | 0.05391 s | 0.000486 s |
| sigma = 0.7 | 0.283184 s | 0.073986 | 0.000743 s |
| sigma = 0.9 | 0.308288 s | 0.052860 s | 0.000524 s |
| Regularization Parameter λ0 | Regularization Parameter λ1 | Regularization Parameter λ2 | M-Term | Iteration Times |
|---|---|---|---|---|
| λ0 = 0.02863 | λ1 = 0.09203 | λ2 = 0.02863 | 2 | 50 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Liang, S.Y. Weak Fault Detection for Gearboxes Using Majorization–Minimization and Asymmetric Convex Penalty Regularization. Symmetry 2018, 10, 243. https://doi.org/10.3390/sym10070243
Li Q, Liang SY. Weak Fault Detection for Gearboxes Using Majorization–Minimization and Asymmetric Convex Penalty Regularization. Symmetry. 2018; 10(7):243. https://doi.org/10.3390/sym10070243
Chicago/Turabian StyleLi, Qing, and Steven Y. Liang. 2018. "Weak Fault Detection for Gearboxes Using Majorization–Minimization and Asymmetric Convex Penalty Regularization" Symmetry 10, no. 7: 243. https://doi.org/10.3390/sym10070243
APA StyleLi, Q., & Liang, S. Y. (2018). Weak Fault Detection for Gearboxes Using Majorization–Minimization and Asymmetric Convex Penalty Regularization. Symmetry, 10(7), 243. https://doi.org/10.3390/sym10070243