Group-Theoretic Exploitations of Symmetry in Novel Prestressed Structures
Abstract
1. Introduction
2. Group Theory and Its Matrix Representations
- Identity: , for any element , it satisfies .
- Inverses: .
- Closure: .
- Associativity: .
3. Stability Analysis on Prestressable Pin-Jointed Structures
3.1. Positive Definiteness of the Tangent Stiffness Matrix for a Prestressed Pin-Jointed Structure
3.2. Necessary Conditions for Structural Stability of Prestressed Pin-Jointed Structures
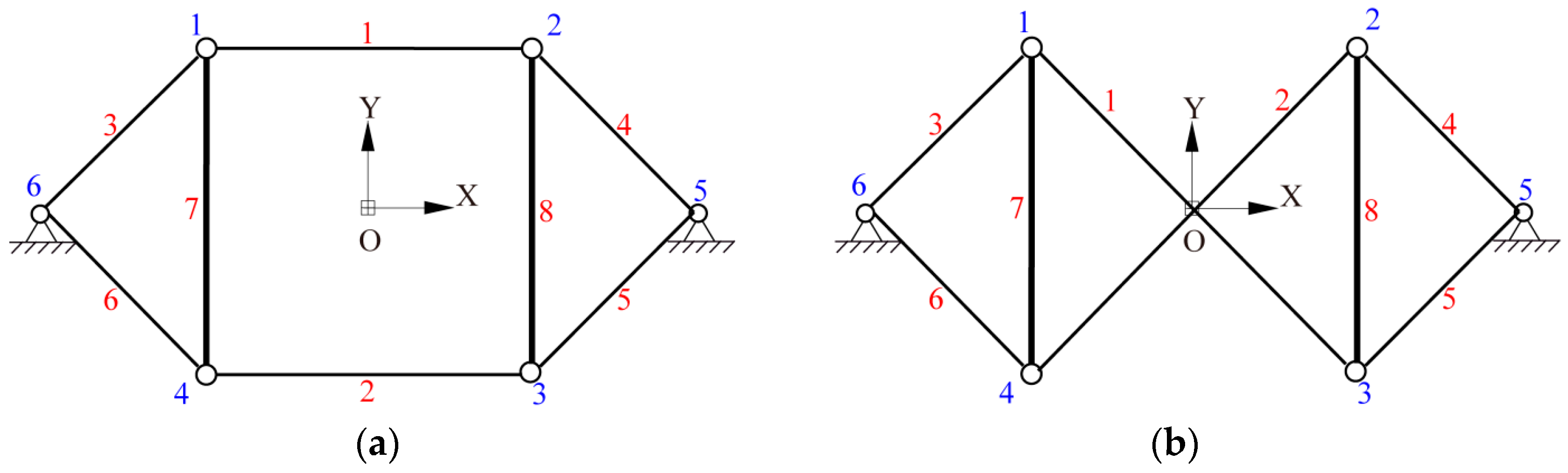
3.3. Example: C2v Symmetric Cable-Strut Structures
4. Form-Finding Analysis on Tensegrity Structures
4.1. Integral Self-Stress State Obtained from the Block with Full Symmetry
4.2. Example: A Symmetric Tensegrity Structure
5. Generalized Eigenvalue Problems of Symmetric Prestressed Structures
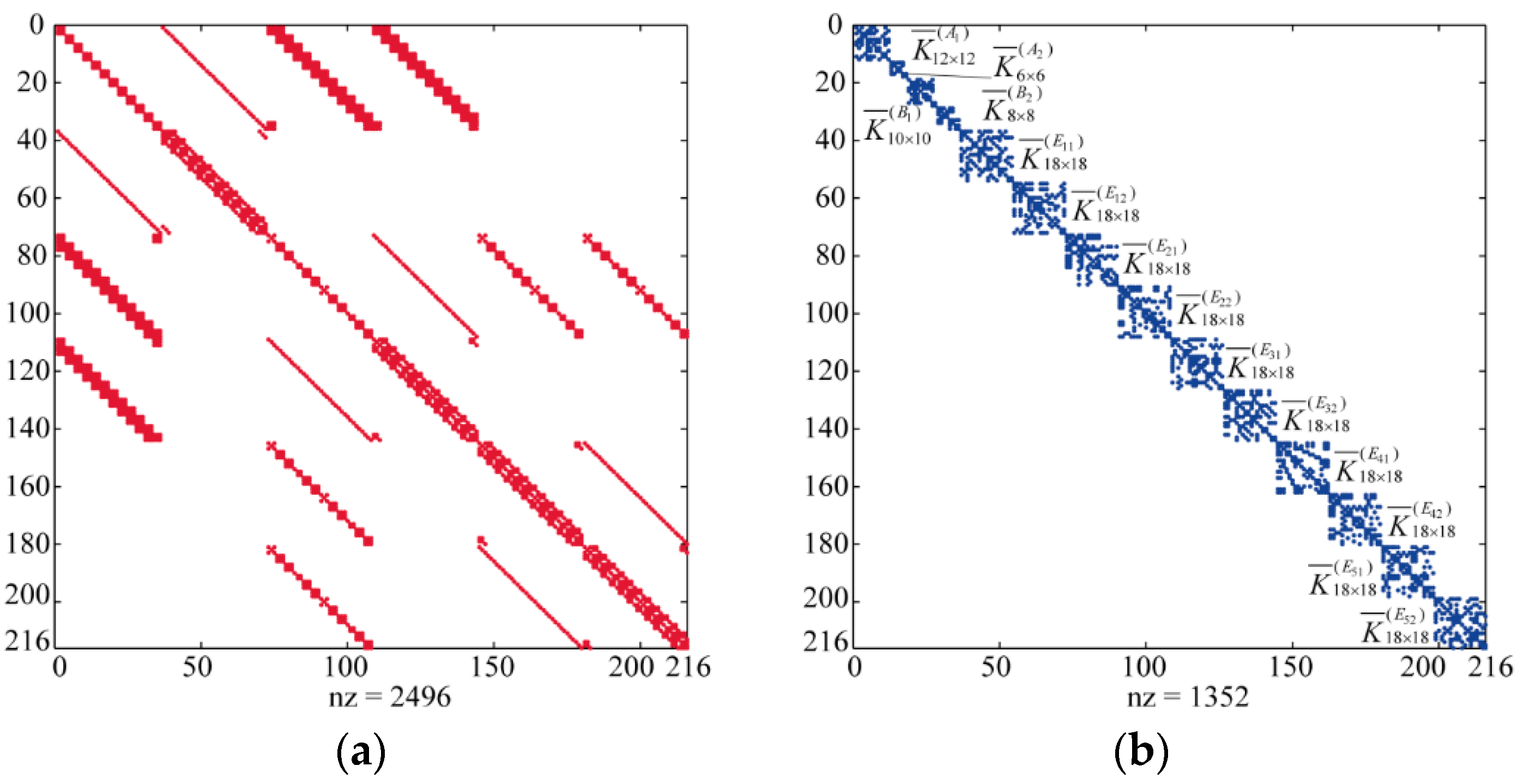
5.1. Symmetry-Adapted Frequency Analysis
5.2. Symmetry-Adapted Buckling Analysis
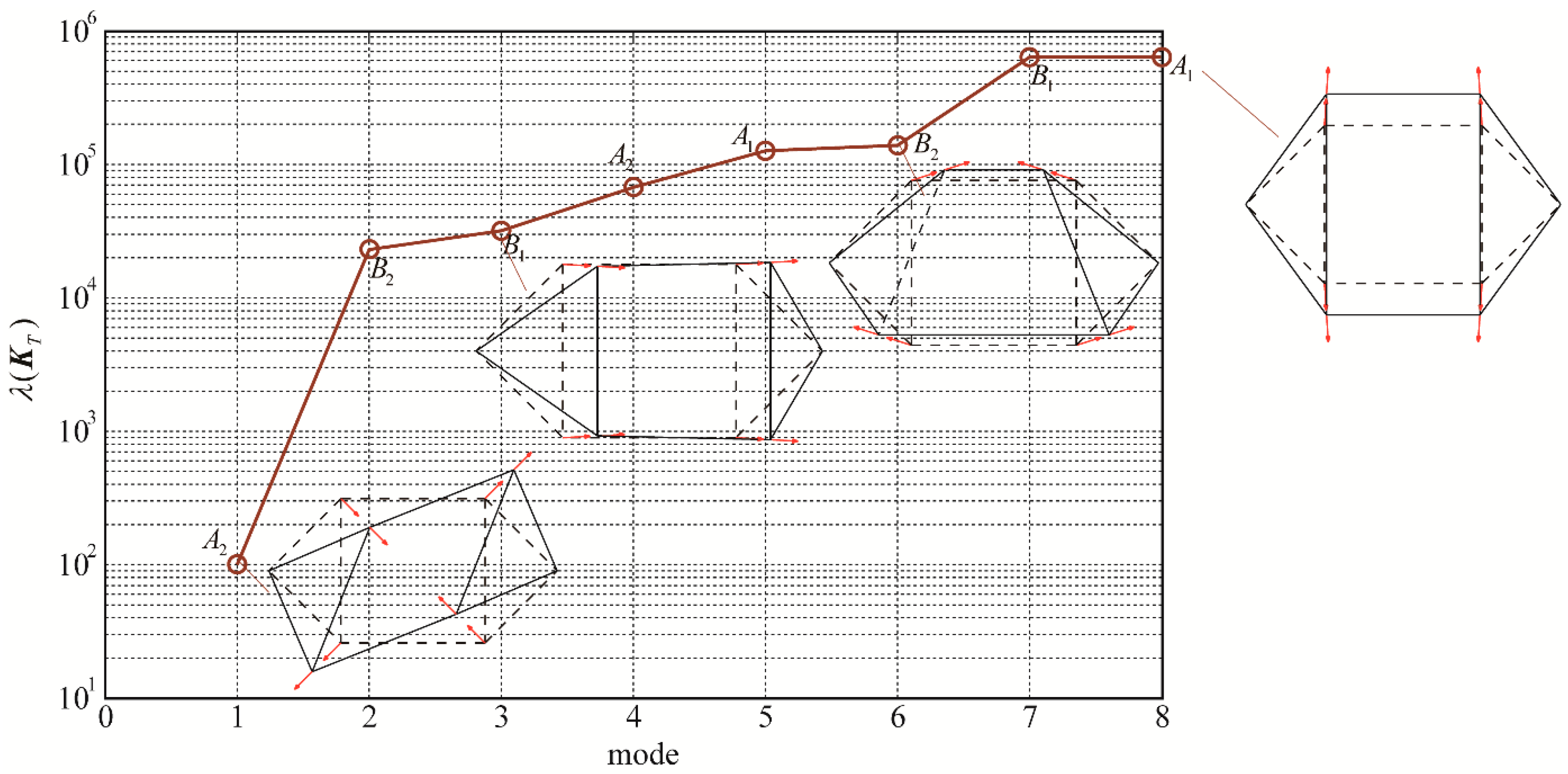
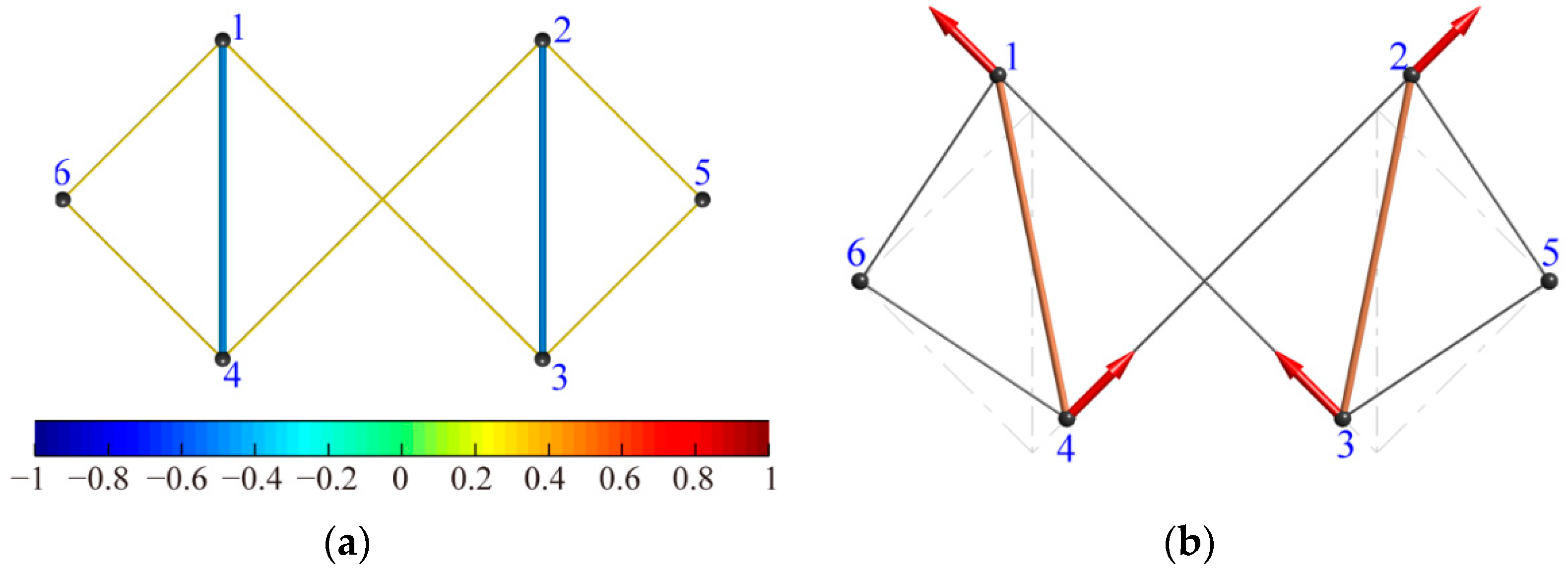
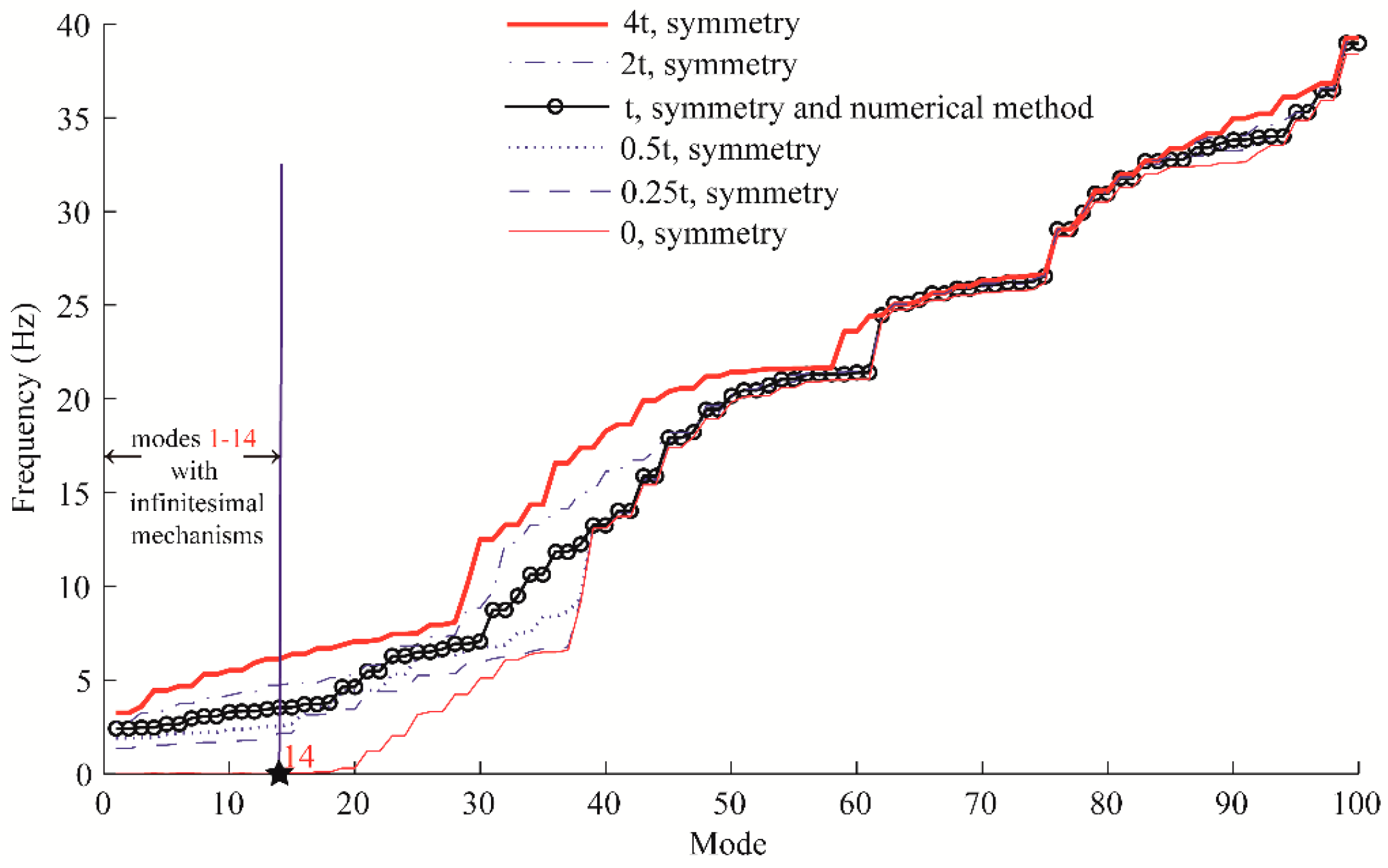
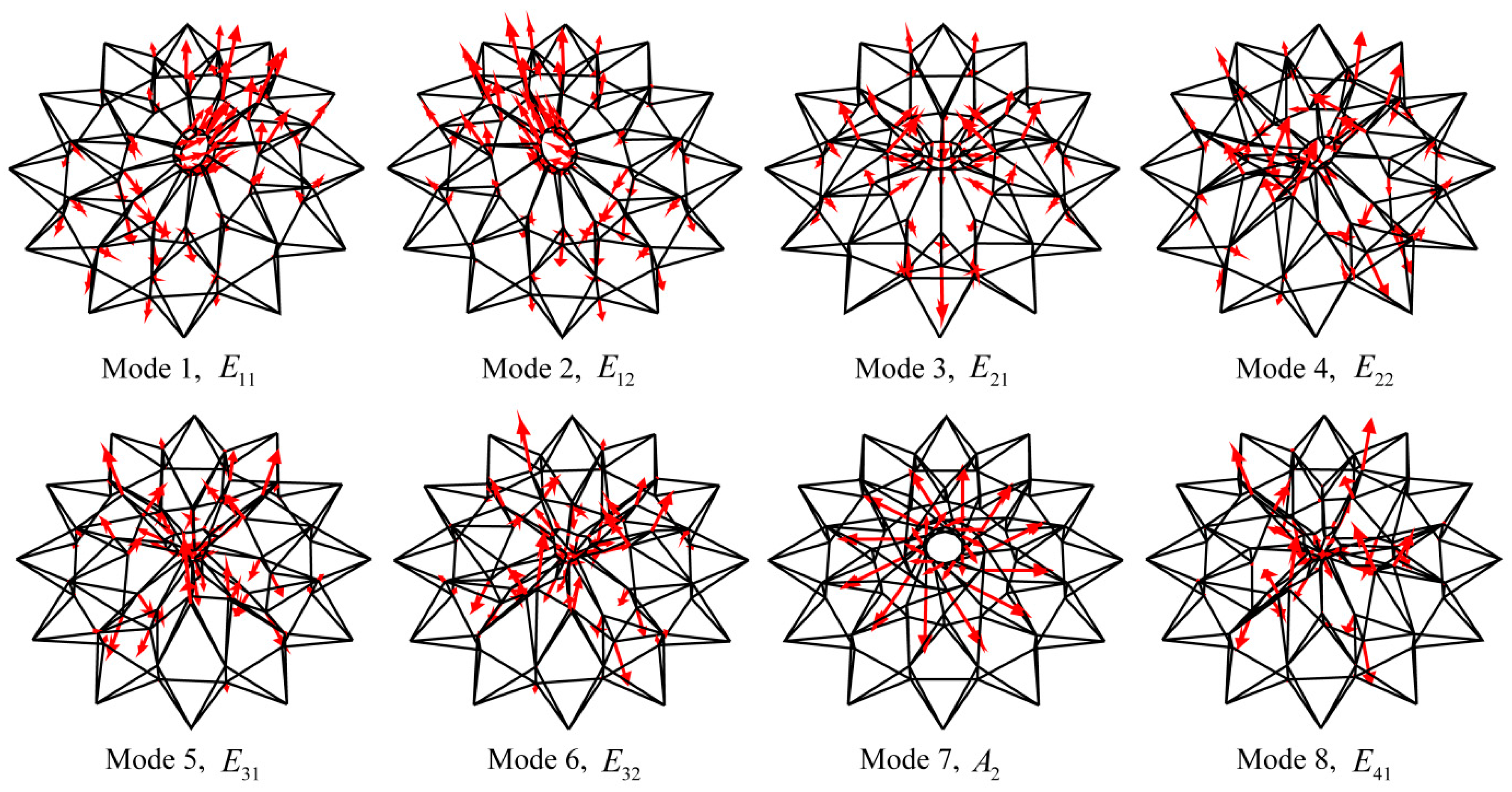
5.3. Illustrative Example: A Symmetric Cable Dome Structure
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kaveh, A. Optimal Analysis of Structures by Concepts of Symmetry and Regularity; Springer: Berlin, Germany, 2013. [Google Scholar]
- Fowler, P.W.; Guest, S.D.; Tarnai, T. Symmetry Perspectives on some Auxetic Body-Bar Frameworks. Symmetry 2014, 6, 368–382. [Google Scholar] [CrossRef]
- Kangwai, R.D.; Guest, S.D.; Pellegrino, S. An Introduction to the Analysis of Symmetric Structures. Comput. Struct. 1999, 71, 671–688. [Google Scholar] [CrossRef]
- Bishop, D.M. Group Theory and Chemistry; Clarendon Press: Oxford, UK, 1973. [Google Scholar]
- Peeters, K.; Taormina, A. Group Theory of Icosahedral Virus Capsid Vibrations: A Top-Down Approach. J. Theor. Biol. 2009, 256, 607–624. [Google Scholar] [CrossRef] [PubMed]
- Tarnai, T.; Kovacs, F.; Fowler, P.W.; Guest, S.D. Wrapping the Cube and Other Polyhedra. Proc. R. Soc. A Math. Phys. Eng. Sci. 2012, 468, 2652–2666. [Google Scholar] [CrossRef]
- Ceulemans, A.; Fowler, P.W. Extension of Euler’s Theorem to Symmetry Properties of Polyhedra. Nature 1991, 353, 52–54. [Google Scholar] [CrossRef]
- Kettle, S.F. Symmetry and Structure: Readable Group Theory for Chemists; John Wiley and Sons Ltd.: Chichester, UK, 2008. [Google Scholar]
- Kovacs, F.; Tarnai, T.; Fowler, P.W.; Guest, S.D. A Class of Expandable Polyhedral Structures. Int. J. Solids Struct. 2004, 41, 1119–1137. [Google Scholar] [CrossRef]
- Mohan, S.J.; Pratap, R. A Natural Classification of Vibration Modes of Polygonal Ducts Based on Group Theoretic Analysis. J. Sound Vib. 2004, 269, 745–764. [Google Scholar] [CrossRef]
- Healey, T.J. A Group-Theoretic Approach to Computational Bifurcation Problems with Symmetry. Comput. Methods Appl. Mech. Eng. 1988, 67, 257–295. [Google Scholar] [CrossRef]
- Zingoni, A. On Group-Theoretic Computation of Natural Frequencies for Spring-Mass Dynamic Systems with Rectilinear Motion. Commun. Numer. Methods Eng. 2008, 24, 973–987. [Google Scholar] [CrossRef]
- Kaveh, A.; Nikbakht, M. Improved Group-Theoretical Method for Eigenvalue Problems of Special Symmetric Structures, Using Graph Theory. Adv. Eng. Softw. 2010, 41, 22–31. [Google Scholar] [CrossRef]
- Zingoni, A. Symmetry Recognition in Group-Theoretic Computational Schemes for Complex Structural Systems. Comput. Struct. 2012, 94–95, 34–44. [Google Scholar] [CrossRef]
- Zlokoviâc, Ł. Group Theory and G-Vector Spaces in Structures: Vibrations, Stability, and Status; Ellis Horwood Ltd.: Chichester, UK; New York, NY, USA, 1989. [Google Scholar]
- Zingoni, A. Group-Theoretic Exploitations of Symmetry in Computational Solid and Structural Mechanics. Int. J. Numer. Methods Eng. 2009, 79, 253–289. [Google Scholar] [CrossRef]
- Pandia Raj, R.; Guest, S.D. Using Symmetry for Tensegrity Form-Finding. J. Int. Assoc. Shell Spat. Struct. 2006, 47, 245–252. [Google Scholar]
- Zhang, J.Y.; Guest, S.D.; Ohsaki, M. Symmetric Prismatic Tensegrity Structures. Part II: Symmetry-Adapted Formulations. Int. J. Solids Struct. 2009, 46, 15–30. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Guest, S.D.; Connelly, R.; Ohsaki, M. Dihedral ‘Star’ Tensegrity Structures. Int. J. Solids Struct. 2010, 47, 1–9. [Google Scholar] [CrossRef]
- Zingoni, A. A Group-Theoretic Formulation for Symmetric Finite Elements. Finite Elem. Anal. Des. 2005, 41, 615–635. [Google Scholar] [CrossRef]
- Zingoni, A. On the Symmetries and Vibration Modes of Layered Space Grids. Eng. Struct. 2005, 27, 629–638. [Google Scholar] [CrossRef]
- Liang, X.Q.; Gao, Q.; Yao, W.A. An Efficient Algorithm Based on Group Theory and the Woodbury Formula for the Dynamic Responses of Periodic Structures. Comput. Struct. 2017, 182, 238–251. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, J. Efficient Method for Moore-Penrose Inverse Problems Involving Symmetric Structures Based on Group Theory. J. Comput. Civ. Eng. ASCE 2014, 28, 182–190. [Google Scholar] [CrossRef]
- Kaveh, A.; Nikbakht, M. Stability Analysis of Hyper Symmetric Skeletal Structures Using Group Theory. Acta Mech. 2008, 200, 177–197. [Google Scholar] [CrossRef]
- Harth, P.; Michelberger, P. Determination of Loads in Quasi-Symmetric Structure with Symmetry Components. Eng. Struct. 2016, 123, 395–407. [Google Scholar] [CrossRef]
- Chen, Y.; Guest, S.D.; Fowler, P.W.; Feng, J. Two-Orbit Switch-Pitch Structures. J. Int. Assoc. Shell Spat. Struct. 2012, 53, 157–162. [Google Scholar]
- Chen, Y.; Sareh, P.; Feng, J.; Sun, Q. A Computational Method for Automated Detection of Engineering Structures with Cyclic Symmetries. Comput. Struct. 2017, 191, 153–164. [Google Scholar] [CrossRef]
- Altmann, S.L.; Herzig, P. Point-Group Theory Tables; Clarendon Press: Oxford, UK, 1994. [Google Scholar]
- Chen, Y.; Sareh, P.; Feng, J. Effective Insights into the Geometric Stability of Symmetric Skeletal Structures under Symmetric Variations. Int. J. Solids Struct. 2015, 69–70, 277–290. [Google Scholar] [CrossRef]
- Chen, Y.; Fan, L.; Feng, J. Automatic and Exact Symmetry Recognition of Structures Exhibiting High-Order Symmetries. J. Comput. Civ. Eng. ASCE 2018, 32, 04018002. [Google Scholar] [CrossRef]
- Quagliaroli, M.; Malerba, P.G.; Albertin, A.; Pollini, N. The Role of Prestress and its Optimization in Cable Domes Design. Comput. Struct. 2015, 161, 17–30. [Google Scholar] [CrossRef]
- Tran, H.C.; Park, H.S.; Lee, J. A Unique Feasible Mode of Prestress Design for Cable Domes. Finite Elem. Anal. Des. 2012, 59, 44–54. [Google Scholar] [CrossRef]
- Sultan, C.; Corless, M.; Skelton, R.E. The Prestressability Problem of Tensegrity Structures: Some Analytical Solutions. Int. J. Solids Struct. 2001, 38, 5223–5252. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Guest, S.D.; Ohsaki, M. Symmetric Prismatic Tensegrity Structures. Part I: Configuration and Stability. Int. J. Solids Struct. 2009, 46, 1–14. [Google Scholar] [CrossRef]
- Ohsaki, M.; Zhang, J.Y. Stability Conditions of Prestressed Pin-Jointed Structures. Int. J. Non-Linear Mech. 2006, 41, 1109–1117. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, J.; Zhang, Y.T. A Necessary Condition for Stability of Kinematically Indeterminate Pin-Jointed Structures with Symmetry. Mech. Res. Commun. 2014, 60, 64–73. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Ohsaki, M. Self-Equilibrium and Stability of Regular Truncated Tetrahedral Tensegrity Structures. J. Mech. Phys. Solids 2012, 60, 1757–1770. [Google Scholar] [CrossRef]
- Guest, S.D. The Stiffness of Prestressed Frameworks: A Unifying Approach. Int. J. Solids Struct. 2006, 43, 842–854. [Google Scholar] [CrossRef]
- Guest, S.D. The Stiffness of Tensegrity Structures. IMA J. Appl. Math. 2011, 76, 57–66. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, J. Generalized Eigenvalue Analysis of Symmetric Prestressed Structures Using Group Theory. J. Comput. Civ. Eng. ASCE 2012, 26, 488–497. [Google Scholar] [CrossRef]
- Calladine, C.R.; Pellegrino, S. First-Order Infinitesimal Mechanisms. Int. J. Solids Struct. 1991, 27, 505–515. [Google Scholar] [CrossRef]
- Koohestani, K.; Guest, S.D. A New Approach to the Analytical and Numerical Form-Finding of Tensegrity Structures. Int. J. Solids Struct. 2013, 50, 2995–3007. [Google Scholar] [CrossRef]
- Miki, M.; Adriaenssens, S.; Igarashi, T.; Kawaguchi, K. The Geodesic Dynamic Relaxation Method for Problems of Equilibrium with Equality Constraint Conditions. Int. J. Numer. Meth. Eng. 2014, 99, 682–710. [Google Scholar] [CrossRef]
- Lee, S.; Lee, J. Form-Finding of Tensegrity Structures with Arbitrary Strut and Cable Members. Int. J. Mech. Sci. 2014, 85, 55–62. [Google Scholar] [CrossRef]
- Yuan, X.F.; Dong, S.L. Integral Feasible Prestress of Cable Domes. Comput. Struct. 2003, 81, 2111–2119. [Google Scholar] [CrossRef]
- Zhang, P.; Kawaguchi, K.; Feng, J. Prismatic Tensegrity Structures with Additional Cables: Integral Symmetric States of Self-Stress and Cable-Controlled Reconfiguration Procedure. Int. J. Solids Struct. 2014, 51, 4294–4306. [Google Scholar] [CrossRef]
- Koohestani, K. Form-Finding of Tensegrity Structures via Genetic Algorithm. Int. J. Solids Struct. 2012, 49, 739–747. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, J.; Ma, R.; Zhang, Y. Efficient Symmetry Method for Calculating Integral Prestress Modes of Statically Indeterminate Cable-Strut Structures. J. Struct. Eng. ASCE 2015, 141, 04014240. [Google Scholar] [CrossRef]
- Tran, H.; Lee, J. Form-Finding of Tensegrity Structures with Multiple States of Self-Stress. Acta Mech. 2011, 222, 131–147. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, J.; Wu, Y. Prestress Stability of Pin-Jointed Assemblies Using Ant Colony Systems. Mech. Res. Commun. 2012, 41, 30–36. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, J. Initial Prestress Distribution and Natural Vibration Analysis of Tensegrity Structures Based on Group Theory. Int. J. Struct. Stab. Dyn. 2012, 12, 213–231. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, J. Group-Theoretic Method for Efficient Buckling Analysis of Prestressed Space Structures. Acta Mech. 2015, 226, 957–973. [Google Scholar] [CrossRef]
- Levy, M. Floating Fabric Over Georgia Dome. Civ. Eng. ASCE 1991, 61, 34–37. [Google Scholar]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Feng, J. Group-Theoretic Exploitations of Symmetry in Novel Prestressed Structures. Symmetry 2018, 10, 229. https://doi.org/10.3390/sym10060229
Chen Y, Feng J. Group-Theoretic Exploitations of Symmetry in Novel Prestressed Structures. Symmetry. 2018; 10(6):229. https://doi.org/10.3390/sym10060229
Chicago/Turabian StyleChen, Yao, and Jian Feng. 2018. "Group-Theoretic Exploitations of Symmetry in Novel Prestressed Structures" Symmetry 10, no. 6: 229. https://doi.org/10.3390/sym10060229
APA StyleChen, Y., & Feng, J. (2018). Group-Theoretic Exploitations of Symmetry in Novel Prestressed Structures. Symmetry, 10(6), 229. https://doi.org/10.3390/sym10060229




