Abstract
In recent years, group theory has been gradually adopted for computational problems of solid and structural mechanics. This paper reviews the advances made in the application of group theory in areas such as stability, form-finding, natural vibration and bifurcation of novel prestressed structures. As initial prestress plays an important role in prestressed structures, its contribution to structural stiffness has been considered. General group-theoretic approaches for several problems are presented, where certain stiffness matrices and equilibrium matrices are expressed in symmetry-adapted coordinate system and block-diagonalized neatly. Illustrative examples on structural stability analysis, force-finding analysis, and generalized eigenvalue analysis on cable domes and cable-strut structures are drawn from recent studies by the authors. It shows how group theory, through symmetry spaces for irreducible representations and matrix decompositions, enables remarkable simplifications and reductions in the computational effort to be achieved. More importantly, before any numerical computations are performed, group theory allows valuable and effective insights on the behavior or intrinsic properties of a prestressed structure to be gained.
1. Introduction
Symmetry is one of the most common and important features in nature. Different forms of symmetry can be easily observed from a microscopic view to macroscopic view, from atoms and crystals to large-scale space structures. At the same time, innovative methods that consider the inherent symmetry of a system will be systematic and effective [1,2,3]. As an important branch of mathematics and vector algebra, group theory is a powerful tool for systematic analysis on symmetric systems. It simplifies the complex computation process. Moreover, it has a direct and qualitative understanding on the intrinsic properties of the system. Thus, group theory has been extensively applied in many fields such as computational physics, electromagnetics, crystal chemistry [4,5] and molecular vibration [6,7].
Notably, applying group theory into structural analysis can significantly improve computational efficiency [8,9]. In recent years, group theory has been gradually adopted by some researchers from structural engineering to solve the involved computational mechanics of symmetric structures [10,11,12,13,14]. Based on group theory, Zlokoviâc [15] and Zingoni [16] showed how to evaluate irreducible representations and symmetry subspaces for symmetric structures. They also summarized the main advantage of group theory through its applications in structural stability, vibration and control. Kangwai et al. [3] briefly described how to utilize group theory to establish a symmetry-adapted coordinate system and perform static analysis on symmetric structures. They concluded that the Fourier method was a special case of the symmetry method using group theory. During nonlinear buckling analysis or frequency analysis of a symmetric structure, if symmetry subspaces associated with certain irreducible representations are established, the tangential stiffness matrix and mass matrix of the structure would be neatly block-diagonalized, and also different types of buckling modes and vibration shapes can be predicted without further computations [10,16]. Pandia Raj and Guest [17] successfully introduced group theory to the form-finding analysis of tensegrity structures. According to the distribution patterns of the symmetry-adapted equilibrium matrices, analytic solutions for the internal forces of different types of members were effectively obtained. Then, Zhang et al. [18,19] combined group theory and the force-density method to investigate prestress stability and super stability of symmetric tensegrity structures. Subsequently, considerable progress has been made, and important applications have arisen in areas such as vibration, stability, bifurcation and finite element analysis [20,21,22,23,24].
Unfortunately, group theory has not been widely adopted in structural analysis because it is abstract (i.e., mathematically represented) and not commonly used by most structural engineers. In addition, conventional symmetry mentioned in structural mechanics generally refers to mirror symmetry or cyclic symmetry [25]. However, many prestressed space structures are neither cyclically symmetric nor mirror-symmetric, such as the dihedral star tensegrity structures [19] and the two-orbit switch-pitch deployable structures [26]. It should be explained that, in this study, novel prestressed structures refer to a type of engineering structures whose stiffness would be dominated/improved by initial prestresses or similar measures. For example, cable-strut structures, tension structures, tensegrity and cable domes. In fact, many seemingly asymmetric structures still retain a number of symmetry operations [14,27], including proper rotations, reflections, improper rotations, and the inverse [28]. It should be pointed out that using group theory to investigate novel prestressed structures can make full use of all the inherent symmetry. Importantly, group-theoretic approaches can simplify the involved computations [23], and also get fruitful and effective conclusions that might be difficult to obtain from conventional methods [16,29]. Here, through different areas of structural mechanics and illustrative examples drawn from recent work of the authors, this study will describe important developments and applications of group theory for novel prestressed structures. As initial prestress plays an important role in prestressed structures, its contribution to structural stiffness is considered. General group-theoretic approaches for the involved problems are presented, where certain stiffness matrices and equilibrium matrices are expressed in symmetry-adapted coordinate system and block-diagonalized.
2. Group Theory and Its Matrix Representations
A symmetry group G describes all the inherent symmetry of a structure by a set of elements , where each element denotes an independent symmetry operation, and denotes the total number of symmetry operations. This group must obey the following four group properties:
- Identity: , for any element , it satisfies .
- Inverses: .
- Closure: .
- Associativity: .
where denotes the multiplication between different elements. In fact, each element in the symmetry group describes an independent symmetry operation for the structure [2]. Under every symmetry operation, the structure can be transformed into a new configuration that is equivalent or indistinguishable from the original configuration. For structures with finite nodes and members, all symmetry operations can be divided into the following five types [14,30]: (a) the identity ; (b) rotation about an n-fold symmetry axis; (c) reflection along a symmetry plane; (d) inverse ; and (e) improper rotation .
Mathematically speaking, each symmetry operation can be taken as a linear transformation in 2D/3D space, and thus the configuration can be expressed as a matrix form:
where the matrices and are the generalized nodal coordinates for the initial configuration and the transformed configuration by the symmetry operation , and is the corresponding transformation matrix. As the base vectors are variable for different coordinate systems, the transformation matrix is not unique. Fortunately, group theory can be utilized to neatly construct a symmetry-adapted coordinate system, and to decompose the reducible transformation matrix into a series of irreducible representations [23,29]:
where the parameters and are the coefficients for the first and second irreducible representations and . Generally, a symmetry group G has independent irreducible representations, (). The character for each irreducible representation keeps constant in different coordinate systems. Specific values associated with different kinds of symmetry operations can be directly read from group theory books [15,28].
3. Stability Analysis on Prestressable Pin-Jointed Structures
Note that novel prestressed structures described in this study refer to various types of prestressable pin-jointed structures, including cable domes, cable nets, tensegrity structures and cable-strut tension structures [31,32,33]. These structures have innovative and attractive geometries, and often contain internal mechanism modes. Thus, the stability of a prestressable pin-jointed structure, that is, whether it can keep a stable state by the initial prestresses, is the basic and key problem that structural engineers need to solve [29,34,35].
3.1. Positive Definiteness of the Tangent Stiffness Matrix for a Prestressed Pin-Jointed Structure
It is known that the potential energy of a stable structure states at a minimum [36]. In other words, for an arbitrary virtual nodal displacement vector , the second-order variation of the potential energy should satisfy
which is expressed by the quadratic form of the tangent stiffness matrix of the structure. Therefore, stability analysis of the structure is transformed into the positive definiteness problem of the tangent stiffness matrix [34,35,37]. Guest [38,39] has established a unifying approach for the tangent stiffness matrix of a general prestressed pin-jointed structure:
In Equation (4), is the elastic stiffness matrix, and is the geometric stiffness matrix contributed by the initial prestresses. Unlike conventional prestressed structures with positive definite matrix , novel prestressed structures have internal mechanisms , which come from the null space of the positive semi-definite matrix and satisfy
For a symmetric structure, the tangent stiffness matrix can be block-diagonalized in the symmetry-adapted coordinate system. According to the great orthogonal theorem [3], the transformation matrix for expressing generalized nodal displacements and external loads is established:
where denotes the symmetry subspace associated with the irreducible representation , is the number of irreducible representations of a symmetry group, and is the dimension of the irreducible representation . Then, the symmetry-adapted tangent stiffness matrix of the structure is
where diag [ ] denotes a diagonal matrix, and represents a typical small-sized block matrix along the diagonal of the matrix . Equation (7) shows that the original tangential stiffness matrix is decomposed into a series of block matrices, and the total number of the block matrices is computed by
On condition that the structural configuration and initial prestresses are fully symmetric, the stiffness matrices and can be similarly decomposed into the block-diagonalized ones:
where and are symmetry-adapted elastic stiffness matrix and geometric stiffness matrix. For a positive integer , the block stiffness matrices , , and are associated with the irreducible representation .
Therefore, to evaluate the positive definiteness of the original tangent stiffness matrix , each block matrix can be independently evaluated by numerical approaches, e.g., the eigenvalue decomposition
where and are the eigenvalue and eigenvector extracted from the symmetry subspace associated with the irreducible representation . Because any similarity transformations do not alter the eigenvalues of a matrix [16,40], the eigenvalues obtained from Equation (11) belong to the eigenvalues of the original tangent stiffness matrix
and the corresponding eigenvector can be expressed as
where the symmetry subspace (see Equation (6)) reveals that the eigenvector holds the same symmetry associated with the irreducible representation . Subsequently, the full eigenvector matrix can be obtained by
Hence, by using group theory, the positive definiteness problem of the original tangent stiffness matrix is transformed into many independent sub-problems. Consequently, the computational complexity required for eigenvalue decomposition will be significantly reduced.
3.2. Necessary Conditions for Structural Stability of Prestressed Pin-Jointed Structures
In the symmetry-adapted coordinate system, Equation (3) can be rewritten as
where is the symmetry-adapted nodal displacement vector, is the symmetry-adapted mechanism mode, and (refer to Equation (5)). To satisfy the structural stability, the matrix should be positive definite or positive semi-definite, i.e., . Then, a necessary condition for stability of the symmetric prestressed structure can be obtained [36]. The structure must have at least a single state of self-stress with full symmetry, given by
where is the symmetry representation of the self-stress states. On the other hand, when the structure has only self-stress states without full symmetry (), the symmetry of the self-stress states is associated with the i-th type irreducible representation , where . Thereafter, the symmetry-adapted geometric stiffness matrix cannot be decomposed into block-diagonalized matrices. However, it has certain regularity, and all the diagonal blocks are zero matrices. At this point, the trace of the matrix is 0, . Therefore, this matrix is neither a positive definite nor a negative definite matrix, and does not satisfy the necessary condition for the stability (see Equations (3) and (15)). In this case, the structure must be an unstable (finite) structure.
3.3. Example: C2v Symmetric Cable-Strut Structures
Stability analysis on two simple two-dimensional symmetric cable-strut structures is presented, to explain the basic group-theoretic process. As shown in Figure 1, both of the structures consist of two vertical struts and six cables. The length of struts is Lc = 2000 mm, the distance between the struts is 2000 mm, and the minimum distance from the boundary nodes (nodes 5 and 6) to the struts is 1000 mm. The elastic modulus of the cables and that of the struts is and ; the cross-sectional area of the cables and that of the struts is and . Both structures have a single mechanism mode () and a self-stress state (). Note that the initial prestress of the vertical struts is −100 kN, and prestresses of other members can be uniquely determined by the self-stress state.
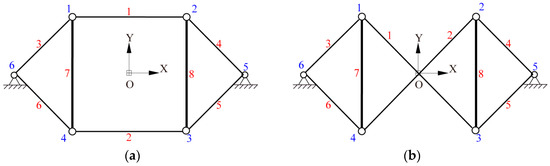
Figure 1.
Two-dimensional symmetric cable-structures (a) with horizontal cables; (b) with cross cables.
The structures are symmetric as they keep equivalent by the following four symmetry operations: Identity, rotation by , and the reflections along X and Y axes. These four symmetry operations constitute a symmetry group. The group has one-dimensional irreducible representations, , , , , and . Through Equations (6) and (7), the tangential stiffness matrices can be decomposed into four block matrices, as listed in Table 1.

Table 1.
Different blocks of symmetry-adapted tangent stiffness matrix .
Therefore, the eigenvalues and eigenvectors can be independently extracted from each of the block matrices. Figure 2 plots the eigenvalue decomposition results of the tangent stiffness matrix of the structure shown in Figure 1a. The endpoints of the polyline and the discrete dots are the solutions obtained by the symmetry method and the conventional method, respectively.
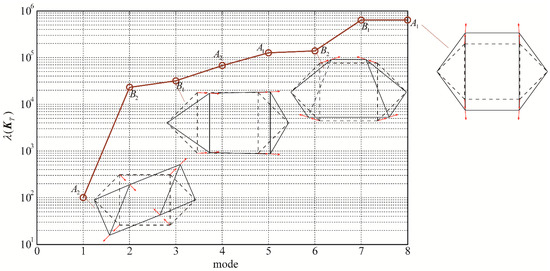
Figure 2.
Eigenvalues extracted from different symmetry subspaces for of the cable-strut structure shown in Figure 1a.
As the minimum eigenvalue is positive, , this structure is stable. However, the minimum eigenvalue is much smaller than the others, as shown in Figure 2. This is because the structure has an internal and infinitesimal mechanism mode, and the first-order eigenvalue is mainly determined by the initial prestress [40,41]. Besides, the results obtained by the symmetry method are exactly the same as those of the conventional method. Because the tangent stiffness matrix has been diagonalized into four small-sized blocks, computation cost of the symmetry method is only 0.004 s. However, the conventional method concerns the original matrix and takes 0.0156 s.
In Figure 2, the first, third, sixth, and eighth modes of the eigenvectors obtained from different symmetry spaces are also plotted, where A1 indicates full symmetry and the others indicate lower-order symmetry. The short arrows indicate the motion trend of the free nodes. It turns out the eigenvectors keep consistent with the inherent symmetry properties of specific symmetry subspaces. For instance, the fifth and eighth eigenvectors come from the full symmetry subspace and thus they have full symmetry of C2v. Similarly, since the first and fourth eigenvectors are from the symmetry subspace A2, they exhibit rotational symmetry of C2v. The third and seventh eigenvectors keeps Cv symmetry along the X axis, while the second and the sixth eigenvectors keeps Cv symmetry along the Y axis.
On the other hand, stability of the structure shown in Figure 1b is also studied, where the upper and lower horizontal cables are replaced by two cross cables. As shown in Figure 3, this structure has a single state of self-stress with full symmetry (i.e., C2v symmetry) and an internal mechanism mode with lower-order symmetry (i.e., Cv symmetry). However, it has been verified that the internal mechanism mode cannot be rigidified by prestressing (see Figure 3), as the minimum eigenvalue . Consequently, this structure is unstable, although it satisfies the necessary conditions given by Equation (16). It should be pointed out that the results for this structure are consistent with the reported ones [42].
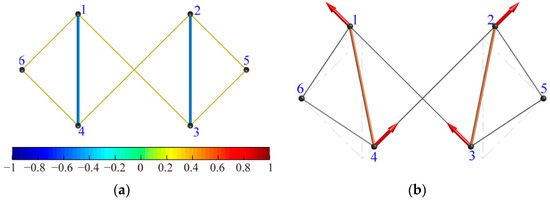
Figure 3.
Static and kinematic indeterminacy of the cable-strut shown in Figure 1b: (a) C2v symmetric self-stress state; (b) Cv symmetric mechanism mode.
4. Form-Finding Analysis on Tensegrity Structures
A significance of novel prestressed structures mentioned in this study is that these structures rely on initial prestresses to obtain or enhance the structural stiffness. Therefore, form-finding (or force-finding) analysis on these structures is important [43,44]. For a structure with multiple self-stress states and complex geometry, Yuan et al. [45] considered the symmetry of the structure and proposed the concepts of integral self-stress state and feasible prestress to seek an effective and proper distribution for initial prestresses. They proposed the double singular value decomposition(DSVD) method for form-finding, which manually classified the members into different types and imposed symmetry constraints on the internal forces in the members. Zhang et al. [46] have utilized the energy method to obtain the integral self-stress state. Recently, some researchers [17,18,32] have combined the force density method with the structural symmetry to simplify the form-finding analysis for novel prestressed structures.
Admittedly, these methods rely on the correct classification for the members. When the configuration becomes complicated or the number of members rises [47], the involved form-finding becomes difficult. Notably, in a symmetry-adapted coordinate system, each block matrix is associated with a certain symmetry subspace, and thus the null space of the block with full symmetry necessarily contains independent self-stress states that satisfy the requirements of full symmetry [36,48]. In this section, the authors will describe how to adopt group theory for computing the integral self-stress states.
4.1. Integral Self-Stress State Obtained from the Block with Full Symmetry
According to the force equilibrium condition for each node of a structure, the equilibrium equation of the structure can be established:
where is the equilibrium matrix, is the internal force vector, and is the external load vector. Because most novel prestressed structures are statically indeterminate, the self-stress states S come from the null space of the singular matrix (i.e., ). In the symmetry-adapted coordinate system, the symmetry-adapted equilibrium matrix can be transformed from the original matrix :
where is the transformation matrix associated with the load vector , and is the transformation matrix associated with the internal force vector ; the positive integer , , and and are the dimensions of the irreducible representations and . Equation (18) indicates that each block matrix corresponds to a symmetry subspace associated with the irreducible representation . The first block matrix is associated with full symmetry, while the last block indicates the lowest-order symmetry. Thus, integral self-stress states necessarily come from the first block matrix of the matrix . Notably, as each block matrix is independent, the first block matrix can be directly computed by
where and are the full symmetry subspaces for the load vector and the internal force vector, respectively. Both matrices are associated with the first irreducible representation . Then, the null space of the block matrix can be solved, which satisfies
The integral self-stress state of the structure is given by [48]
Note that the integral self-stress state in Equation (21) has considered the whole symmetry of the structure, which allows the members of the same type to retain equal prestress. Thus, the solution space for the form-finding problem of prestressed structures can be effectively reduced, especially for the structures with multiple self-stress states [48,49]. Moreover, this symmetry method does not need to manually classify the members into different groups in advance, and it avoids repeating calculations of conventional methods. Thus, the involved computation process is simple and convenient, and particularly suitable for structures with complex geometry [50].
4.2. Example: A Symmetric Tensegrity Structure
Figure 4 shows the geometric configuration and symmetry rotations for a simple prismatic tensegrity structure, which consists of six pin-joints, six tension cables and three compression struts. The twist angle between the bottom and top triangles is ; the radius of the circumcircle of the triangles is unit length, and the vertical height of the structure is unit length.
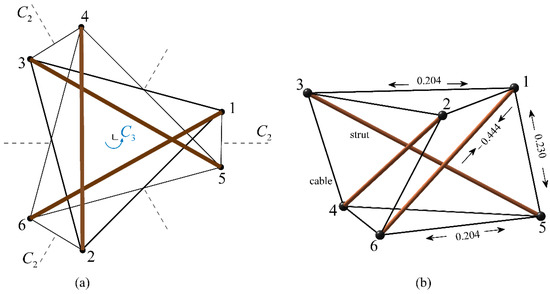
Figure 4.
A simple tensegrity structure with symmetry [48]: (a) three two-fold rotations; (b) integral prestress mode with full symmetry.
This symmetric structure has independent symmetry operations: the identity, two rotations around the vertical axis, and three two-fold rotations around the axes connecting the center of the structure and the mid-points of the diagonal cables (indicated by the dotted lines in Figure 4a). Thus, this structure belongs to the group [34,51]. Thereafter, the full symmetry subspaces corresponding to the internal force vector and the load vector are
Then, the first block matrix of the symmetry-adapted equilibrium matrix is obtained by Equation (19)
Because this matrix is a rank-deficient (its rank ), it has a -dimensional null space
Therefore, the integral self-stress state of the structure is:
As shown in Figure 4b, the obtained integral self-stress state satisfies the feasibility condition for the members, where six horizontal cables, three vertical cables, or three struts respectively belong to the same type. All the cables are in tension while the struts are in compression. It should be pointed out that this symmetry method just computes the null space of the first block matrix and extract integral self-stress states from all the independent self-stress. Because the dimension of the first block matrix is significantly smaller than that of the original matrix, the computational complexity is effectively reduced. In comparison with the conventional DSVD method, this method avoids manual classification on the members and repeated computations on the matrices. As far as a highly symmetric structure with many self-stress states and members is concerned, the computational efficiency of this symmetry method is considerably improved [48].
5. Generalized Eigenvalue Problems of Symmetric Prestressed Structures
5.1. Symmetry-Adapted Frequency Analysis
Generalized eigenvalue problems can be frequently found among structural analysis [16,40], which generally is a challenge from a computational perspective. For example, frequency analysis can be taken as a well-known generalized eigenvalue problem in terms of the tangent stiffness matrix and the mass matrix M
which describes free vibrations of a general structure. In Equation (27), denotes a circular frequency and is the corresponding mode shape. On condition that this structure is symmetric, group-theoretic process considers smaller block matrices rather than the full matrices. Using the transformation matrix U in Equation (7), the mass matrix M can be decomposed into similar block-diagonalized forms
where is a symmetry-adapted mass matrix. For any positive integer , the block matrices and come from the specific symmetry subspace associated with the irreducible representation . Therefore, to analyze the vibration characteristics of the structure, eigenvalue problems with smaller matrices can be independently solved. For the block matrices and , it satisfies
where and are the eigenvalues and eigenvectors extracted from the symmetry subspace associated with the irreducible representation . Since the similarity transformation does not change the eigenvalues of the matrix, the obtained generalized eigenvalues are included in the solutions to the original eigenvalue problem [40],
The corresponding mode shape can be expressed as
where the symmetry subspace associated with indicates the symmetry of the eigenvector . It is helpful for predicting the vibration modes for a symmetric structure. In addition, the complete vibration mode matrix can be obtained from
In summary, using the symmetry method based on group theory, the original frequency analysis has been transformed into a series of independent sub-problems.
5.2. Symmetry-Adapted Buckling Analysis
Buckling analysis of a structure is essentially about the generalized eigenvalue problem of the tangent stiffness matrix and the geometric stiffness matrix:
where the function f is defined to describe the buckling problem of the structure, is the eigenvalue and is the corresponding eigenvector. According to the inherent symmetry of the structure, the above equation satisfies [52]:
where is the transformation matrix for a symmetry operation S. According to the external loads and their symmetries, symmetry subspaces need to be established in a certain subgroup . Then, the stiffness matrices and in Equation (33) can be decomposed into a similar block-diagonal form:
where the matrix V is an orthogonal transformation matrix for expression in the symmetry-adapted coordinate system. Because each block matrix is independent, the original buckling problem can be solved by solving the subproblems in parallel [52]
Recall that similarity transformations do not alter the generalized eigenvalues of the original matrix, the eigenvalues obtained from Equation (37) are included in the solutions to the original buckling problem,
and the corresponding buckling shape can be expressed as
5.3. Illustrative Example: A Symmetric Cable Dome Structure
The well-known Levy cable dome is a typical prestressed cable-strut structure [40,53]. Figure 5 shows a highly symmetric Levy cable dome with a diameter of 100 m. This structure is composed of 84 pin-joints, 36 compression struts and 168 tension cables, where the boundary nodes 1–12 are constrained in three directions. Note that cross-sectional areas and initial prestresses of different types of members of this cable dome structure have been reported [40].
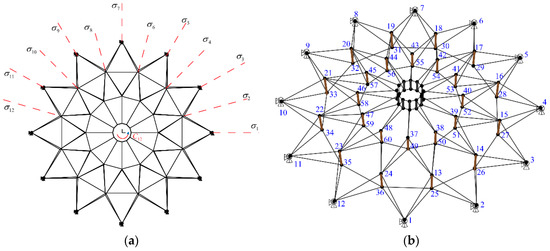
Figure 5.
A symmetric cable dome structures [40]: (a) twelve rotations and twelve reflections indicated in the plan view; (b) 3D geometric configuration.
In the view of symmetry, this cable dome structure keeps unshifted by twelve rotations along the 12-fold rotation axis , and twelve reflections , as shown in Figure 5a. Thus, this structure is symmetric. According to the point-group theory table [28], the symmetry group has four one-dimensional () irreducible representations and , and five two-dimensional () irreducible representations − . To establish the symmetry-adapted coordinate system, the orthogonal transformation matrix for the cable dome is obtained from Equation (6). This matrix is composed by independent vectors associated with fourteen symmetry subspaces, where the first vector for the full symmetry subspace is a matrix, is a matrix, is a matrix, is a matrix, and all the vectors – for the lower-order symmetry subspaces are matrices. These 14 independent symmetry subspaces are utilized to decompose the stiffness matrix or the mass matrix into 14 block matrices with smaller dimensions. For example, the distribution patterns of nonzero entries of the original tangent stiffness matrix and the block-diagonalized matrix are shown in Figure 6. As shown in Figure 6b, all the block matrices are independent and distribute along the main diagonal.
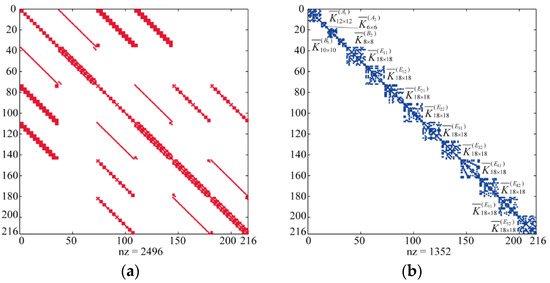
Figure 6.
Distribution patterns of nonzero entries of stiffness matrices of the symmetric cable dome: (a) original tangent stiffness matrix ; (b) block-diagonalized stiffness matrix .
As far as the frequency analysis is concerned, the original problem is neatly simplified into fourteen sub-problems involved with small-sized matrices. Figure 7 shows the first 100 frequencies obtained by the proposed symmetry method, which is compared with the results by the conventional numerical method. In addition, to study the influence of initial prestresses on the natural frequencies, the C12v symmetric cable dome with different prestress levels are analyzed by the proposed method (the symmetry subspaces keep invariant). The prestress levels are respectively 0, 0.25t, 0.5t, 2t and 4t, and the initial prestresses t are determined by the feasible prestress modes [40].
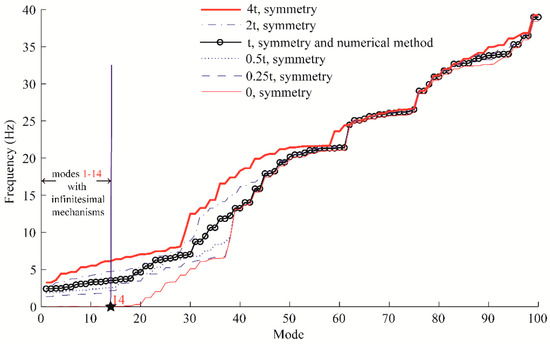
Figure 7.
First 100 frequencies of the C12v symmetric cable dome with different prestress levels [40].
It can be noticed from Figure 7 that the obtained results are in good agreement with those of the numerical method, where the maximum error is . Lower-order natural frequencies are low and intensively distributed. Notably, the first 14 frequencies are dominated by the prestress level, as they are associated with infinitesimal mechanism modes. In fact, the initial prestresses also improve the structural stiffness of the cable dome. After increasing the initial prestress level, the first 50 frequencies of this structure increase significantly.
On the other hand, Figure 8 depicts the first eight vibration shapes of the C12v symmetric cable dome [40]. It can be noticed that this symmetric dome structure has many repeated eigenvalues and equivalent eigenvectors, such as modes 1–2, modes 3–4, and modes 5–6. In fact, this phenomenon is ubiquitous for most symmetric structures. This is because the roots computed from the symmetry spaces for multi-dimensional irreducible representations are identical, and the generalized eigenvalues for these symmetry subspaces are exactly the same. In addition, each vibration shape obtained from lower-order symmetry subspace does not maintain its full symmetry (i.e., ). Then, it may be reduced to a low-order symmetry. Because the seventh vibration shape is obtained from the symmetry subspace , it has rotational symmetry (i.e., ). In other words, the symmetry of all the vibration modes can be predicted from symmetry subspaces in advance [16,29], without numerical computing.
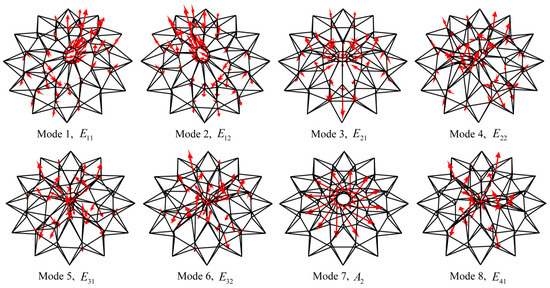
Figure 8.
First eight vibration shapes of the C12v symmetric cable dome [40].
6. Conclusions
This paper has described some new developments of symmetry analysis on novel prestressed structures using group theory. Through theoretical group-theoretic approaches and illustrative examples, basic process and key features of group-theoretic approaches in stability analysis, form-finding analysis, frequency analysis and buckling analysis have been identified. A significant advantage of these group-theoretic approaches is that the involved large-sized matrices can be neatly block-diagonalized into many smaller-sized and independent matrices. Thus, the computational complexity for dealing with the original problem will be significantly reduced. More importantly, these methods can qualitatively reveal certain physical meanings and obtain effective insights into the involved problems. It is worth mentioning that group-theoretic approaches are systematic and general. When a structure has only the lowest-order symmetry, the method still works and degenerates into a conventional method. This research is helpful for enriching developments in the field of symmetric structures.
Author Contributions
Conceptualization, Y.C. and J.F.; Methodology and Analysis, Y.C. and J.F.; Writing-Review & Editing, Y.C.; Supervision, J.F. Both authors participated in detailed discussion, drafting the paper and producing the final version.
Funding
This research was funded by the Natural Science Foundation of Jiangsu Province (Grant No. BK20150602), the National Natural Science Foundation of China (Grant No. 51508089 and No. 51578133), the Fundamental Research Funds for the Central Universities, and the Priority Academic Program Development of Jiangsu Higher Education Institutions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kaveh, A. Optimal Analysis of Structures by Concepts of Symmetry and Regularity; Springer: Berlin, Germany, 2013. [Google Scholar]
- Fowler, P.W.; Guest, S.D.; Tarnai, T. Symmetry Perspectives on some Auxetic Body-Bar Frameworks. Symmetry 2014, 6, 368–382. [Google Scholar] [CrossRef]
- Kangwai, R.D.; Guest, S.D.; Pellegrino, S. An Introduction to the Analysis of Symmetric Structures. Comput. Struct. 1999, 71, 671–688. [Google Scholar] [CrossRef]
- Bishop, D.M. Group Theory and Chemistry; Clarendon Press: Oxford, UK, 1973. [Google Scholar]
- Peeters, K.; Taormina, A. Group Theory of Icosahedral Virus Capsid Vibrations: A Top-Down Approach. J. Theor. Biol. 2009, 256, 607–624. [Google Scholar] [CrossRef] [PubMed]
- Tarnai, T.; Kovacs, F.; Fowler, P.W.; Guest, S.D. Wrapping the Cube and Other Polyhedra. Proc. R. Soc. A Math. Phys. Eng. Sci. 2012, 468, 2652–2666. [Google Scholar] [CrossRef]
- Ceulemans, A.; Fowler, P.W. Extension of Euler’s Theorem to Symmetry Properties of Polyhedra. Nature 1991, 353, 52–54. [Google Scholar] [CrossRef]
- Kettle, S.F. Symmetry and Structure: Readable Group Theory for Chemists; John Wiley and Sons Ltd.: Chichester, UK, 2008. [Google Scholar]
- Kovacs, F.; Tarnai, T.; Fowler, P.W.; Guest, S.D. A Class of Expandable Polyhedral Structures. Int. J. Solids Struct. 2004, 41, 1119–1137. [Google Scholar] [CrossRef]
- Mohan, S.J.; Pratap, R. A Natural Classification of Vibration Modes of Polygonal Ducts Based on Group Theoretic Analysis. J. Sound Vib. 2004, 269, 745–764. [Google Scholar] [CrossRef]
- Healey, T.J. A Group-Theoretic Approach to Computational Bifurcation Problems with Symmetry. Comput. Methods Appl. Mech. Eng. 1988, 67, 257–295. [Google Scholar] [CrossRef]
- Zingoni, A. On Group-Theoretic Computation of Natural Frequencies for Spring-Mass Dynamic Systems with Rectilinear Motion. Commun. Numer. Methods Eng. 2008, 24, 973–987. [Google Scholar] [CrossRef]
- Kaveh, A.; Nikbakht, M. Improved Group-Theoretical Method for Eigenvalue Problems of Special Symmetric Structures, Using Graph Theory. Adv. Eng. Softw. 2010, 41, 22–31. [Google Scholar] [CrossRef]
- Zingoni, A. Symmetry Recognition in Group-Theoretic Computational Schemes for Complex Structural Systems. Comput. Struct. 2012, 94–95, 34–44. [Google Scholar] [CrossRef]
- Zlokoviâc, Ł. Group Theory and G-Vector Spaces in Structures: Vibrations, Stability, and Status; Ellis Horwood Ltd.: Chichester, UK; New York, NY, USA, 1989. [Google Scholar]
- Zingoni, A. Group-Theoretic Exploitations of Symmetry in Computational Solid and Structural Mechanics. Int. J. Numer. Methods Eng. 2009, 79, 253–289. [Google Scholar] [CrossRef]
- Pandia Raj, R.; Guest, S.D. Using Symmetry for Tensegrity Form-Finding. J. Int. Assoc. Shell Spat. Struct. 2006, 47, 245–252. [Google Scholar]
- Zhang, J.Y.; Guest, S.D.; Ohsaki, M. Symmetric Prismatic Tensegrity Structures. Part II: Symmetry-Adapted Formulations. Int. J. Solids Struct. 2009, 46, 15–30. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Guest, S.D.; Connelly, R.; Ohsaki, M. Dihedral ‘Star’ Tensegrity Structures. Int. J. Solids Struct. 2010, 47, 1–9. [Google Scholar] [CrossRef]
- Zingoni, A. A Group-Theoretic Formulation for Symmetric Finite Elements. Finite Elem. Anal. Des. 2005, 41, 615–635. [Google Scholar] [CrossRef]
- Zingoni, A. On the Symmetries and Vibration Modes of Layered Space Grids. Eng. Struct. 2005, 27, 629–638. [Google Scholar] [CrossRef]
- Liang, X.Q.; Gao, Q.; Yao, W.A. An Efficient Algorithm Based on Group Theory and the Woodbury Formula for the Dynamic Responses of Periodic Structures. Comput. Struct. 2017, 182, 238–251. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, J. Efficient Method for Moore-Penrose Inverse Problems Involving Symmetric Structures Based on Group Theory. J. Comput. Civ. Eng. ASCE 2014, 28, 182–190. [Google Scholar] [CrossRef]
- Kaveh, A.; Nikbakht, M. Stability Analysis of Hyper Symmetric Skeletal Structures Using Group Theory. Acta Mech. 2008, 200, 177–197. [Google Scholar] [CrossRef]
- Harth, P.; Michelberger, P. Determination of Loads in Quasi-Symmetric Structure with Symmetry Components. Eng. Struct. 2016, 123, 395–407. [Google Scholar] [CrossRef]
- Chen, Y.; Guest, S.D.; Fowler, P.W.; Feng, J. Two-Orbit Switch-Pitch Structures. J. Int. Assoc. Shell Spat. Struct. 2012, 53, 157–162. [Google Scholar]
- Chen, Y.; Sareh, P.; Feng, J.; Sun, Q. A Computational Method for Automated Detection of Engineering Structures with Cyclic Symmetries. Comput. Struct. 2017, 191, 153–164. [Google Scholar] [CrossRef]
- Altmann, S.L.; Herzig, P. Point-Group Theory Tables; Clarendon Press: Oxford, UK, 1994. [Google Scholar]
- Chen, Y.; Sareh, P.; Feng, J. Effective Insights into the Geometric Stability of Symmetric Skeletal Structures under Symmetric Variations. Int. J. Solids Struct. 2015, 69–70, 277–290. [Google Scholar] [CrossRef]
- Chen, Y.; Fan, L.; Feng, J. Automatic and Exact Symmetry Recognition of Structures Exhibiting High-Order Symmetries. J. Comput. Civ. Eng. ASCE 2018, 32, 04018002. [Google Scholar] [CrossRef]
- Quagliaroli, M.; Malerba, P.G.; Albertin, A.; Pollini, N. The Role of Prestress and its Optimization in Cable Domes Design. Comput. Struct. 2015, 161, 17–30. [Google Scholar] [CrossRef]
- Tran, H.C.; Park, H.S.; Lee, J. A Unique Feasible Mode of Prestress Design for Cable Domes. Finite Elem. Anal. Des. 2012, 59, 44–54. [Google Scholar] [CrossRef]
- Sultan, C.; Corless, M.; Skelton, R.E. The Prestressability Problem of Tensegrity Structures: Some Analytical Solutions. Int. J. Solids Struct. 2001, 38, 5223–5252. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Guest, S.D.; Ohsaki, M. Symmetric Prismatic Tensegrity Structures. Part I: Configuration and Stability. Int. J. Solids Struct. 2009, 46, 1–14. [Google Scholar] [CrossRef]
- Ohsaki, M.; Zhang, J.Y. Stability Conditions of Prestressed Pin-Jointed Structures. Int. J. Non-Linear Mech. 2006, 41, 1109–1117. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, J.; Zhang, Y.T. A Necessary Condition for Stability of Kinematically Indeterminate Pin-Jointed Structures with Symmetry. Mech. Res. Commun. 2014, 60, 64–73. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Ohsaki, M. Self-Equilibrium and Stability of Regular Truncated Tetrahedral Tensegrity Structures. J. Mech. Phys. Solids 2012, 60, 1757–1770. [Google Scholar] [CrossRef]
- Guest, S.D. The Stiffness of Prestressed Frameworks: A Unifying Approach. Int. J. Solids Struct. 2006, 43, 842–854. [Google Scholar] [CrossRef]
- Guest, S.D. The Stiffness of Tensegrity Structures. IMA J. Appl. Math. 2011, 76, 57–66. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, J. Generalized Eigenvalue Analysis of Symmetric Prestressed Structures Using Group Theory. J. Comput. Civ. Eng. ASCE 2012, 26, 488–497. [Google Scholar] [CrossRef]
- Calladine, C.R.; Pellegrino, S. First-Order Infinitesimal Mechanisms. Int. J. Solids Struct. 1991, 27, 505–515. [Google Scholar] [CrossRef]
- Koohestani, K.; Guest, S.D. A New Approach to the Analytical and Numerical Form-Finding of Tensegrity Structures. Int. J. Solids Struct. 2013, 50, 2995–3007. [Google Scholar] [CrossRef]
- Miki, M.; Adriaenssens, S.; Igarashi, T.; Kawaguchi, K. The Geodesic Dynamic Relaxation Method for Problems of Equilibrium with Equality Constraint Conditions. Int. J. Numer. Meth. Eng. 2014, 99, 682–710. [Google Scholar] [CrossRef]
- Lee, S.; Lee, J. Form-Finding of Tensegrity Structures with Arbitrary Strut and Cable Members. Int. J. Mech. Sci. 2014, 85, 55–62. [Google Scholar] [CrossRef]
- Yuan, X.F.; Dong, S.L. Integral Feasible Prestress of Cable Domes. Comput. Struct. 2003, 81, 2111–2119. [Google Scholar] [CrossRef]
- Zhang, P.; Kawaguchi, K.; Feng, J. Prismatic Tensegrity Structures with Additional Cables: Integral Symmetric States of Self-Stress and Cable-Controlled Reconfiguration Procedure. Int. J. Solids Struct. 2014, 51, 4294–4306. [Google Scholar] [CrossRef]
- Koohestani, K. Form-Finding of Tensegrity Structures via Genetic Algorithm. Int. J. Solids Struct. 2012, 49, 739–747. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, J.; Ma, R.; Zhang, Y. Efficient Symmetry Method for Calculating Integral Prestress Modes of Statically Indeterminate Cable-Strut Structures. J. Struct. Eng. ASCE 2015, 141, 04014240. [Google Scholar] [CrossRef]
- Tran, H.; Lee, J. Form-Finding of Tensegrity Structures with Multiple States of Self-Stress. Acta Mech. 2011, 222, 131–147. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, J.; Wu, Y. Prestress Stability of Pin-Jointed Assemblies Using Ant Colony Systems. Mech. Res. Commun. 2012, 41, 30–36. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, J. Initial Prestress Distribution and Natural Vibration Analysis of Tensegrity Structures Based on Group Theory. Int. J. Struct. Stab. Dyn. 2012, 12, 213–231. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, J. Group-Theoretic Method for Efficient Buckling Analysis of Prestressed Space Structures. Acta Mech. 2015, 226, 957–973. [Google Scholar] [CrossRef]
- Levy, M. Floating Fabric Over Georgia Dome. Civ. Eng. ASCE 1991, 61, 34–37. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).