A Bi-Level Programming Model for the Railway Express Cargo Service Network Design Problem
Abstract
1. Introduction
2. Literature Review
3. Problem Description
- (1)
- ABE;
- (2)
- ACE;
- (3)
- ABE;
- (4)
- ABE;
- (5)
- ABE;
- (6)
- ABE;
- (7)
- ACE;
- (8)
- ACE;
- (9)
- ABCE.
4. Mathematical Model
4.1. Notations
4.2. Mathematical Formulation
4.3. Linearization Technique
5. Numerical Example
5.1. Parameters of the Model
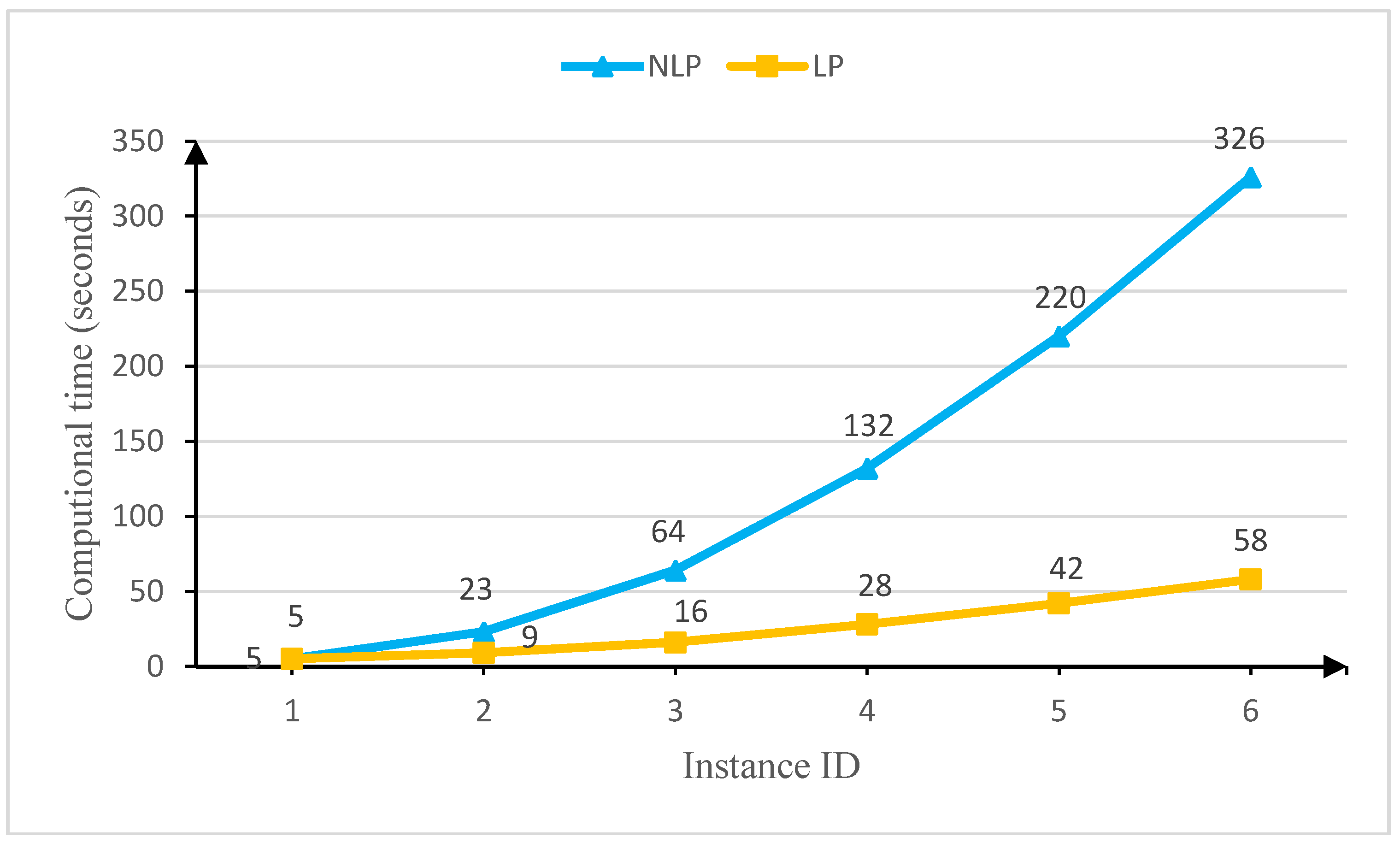
5.2. Computational Performance of the Proposed Model
5.3. Computational Results and Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Plan | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I | H1 | H4 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| H1 | H4 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H5 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| H1 | H5 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | |
| H1 | H3 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H5 | 2 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 2 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |
| H1 | H6 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 3 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| II | H1 | H3 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| H1 | H4 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H5 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| H1 | H5 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H3 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H5 | 2 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 3 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| III | H1 | H3 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| H1 | H4 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H4 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H5 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| H1 | H5 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H3 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H5 | 2 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 3 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| IV | H1 | H4 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| H1 | H4 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H5 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| H1 | H5 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |
| H1 | H6 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H3 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H5 | 2 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |
| H1 | H6 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | |
| H1 | H6 | 3 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| V | H1 | H3 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| H1 | H4 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H4 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H5 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| H1 | H5 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |
| H1 | H6 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H3 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H5 | 2 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |
| H1 | H6 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | |
| H1 | H6 | 3 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| VI | H1 | H4 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| H1 | H4 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H5 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| H1 | H5 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H3 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H5 | 2 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 2 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |
| H1 | H6 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 3 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| VII | H1 | H4 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| H1 | H4 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H5 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| H1 | H5 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H3 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H5 | 2 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 2 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |
| H1 | H6 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 3 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| VIII | H1 | H4 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| H1 | H4 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H5 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| H1 | H5 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | |
| H1 | H3 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H5 | 2 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |
| H1 | H6 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 3 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 3 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |
| H1 | H6 | 3 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | |
| IX | H1 | H4 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| H1 | H4 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H5 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| H1 | H5 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | |
| H1 | H3 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H5 | 2 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 2 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |
| H1 | H6 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 2 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | |
| H1 | H6 | 3 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 3 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |
| X | H1 | H4 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| H1 | H4 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H5 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| H1 | H5 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | |
| H1 | H5 | 2 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 2 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |
| H1 | H6 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 2 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | |
| H1 | H6 | 3 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| H1 | H6 | 3 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
References
- Liu, C.; Lin, B.L.; Wang, J.X.; Liu, S.; Wu, J.; Li, J. Flow assignment model for quantitative analysis of diverting bulk freight from road to railway. PLoS ONE 2017, 12, e0182179. [Google Scholar] [CrossRef] [PubMed]
- Ahuja, R.; Magnanti, T.; Orlin, J. Network flows: Theory, algorithms, and applications. J. Oper. Res. Soc. 1993, 45, 791–796. [Google Scholar] [CrossRef]
- Crainic, T.G.; Kim, K.H. Chapter 8 intermodal transportation. In Transportation: Handbooks in Operations Research and Management Science; Barnhart, C., Laporte, G., Eds.; Elsevier: Amsterdam, The Netherlands, 2006; Volume 14, pp. 189–284. ISBN 9780080467436. [Google Scholar]
- Crainic, T. Long-Haul Freight Transportation. In Handbook of Transportation Science, International Series in Operations Research & Management Science; Hall, R.W., Ed.; Springer: Boston, MA, USA, 2003; Volume 56, pp. 451–516. ISBN 9781402072468. [Google Scholar]
- Crainic, T.; Ferland, J.A.; Rousseau, J.M. A tactical planning model for rail freight transportation. Transp. Sci. 1984, 18, 165–184. [Google Scholar] [CrossRef]
- Campetella, M.; Lulli, G.; Pietropaoli, U.; Ricciardi, N. Freight Service Design for the Italian Railways Company. In Proceedings of the ATMOS 6th Workshop on Algorithmic Methods and Models for Optimization Railways, Zurich, Switzerland, 14 September 2006. [Google Scholar]
- Ahuja, R.K.; Jha, K.C.; Liu, J. Solving real-life railroad blocking problems. Interfaces 2007, 47, 404–419. [Google Scholar] [CrossRef]
- Ceselli, A.; Gatto, M.; Lübbecke, M.E.; Nunkesser, M. Optimizing the Cargo Express Service of Swiss Federal Railways. Transp. Sci. 2008, 42, 450–465. [Google Scholar] [CrossRef]
- Lin, B.L.; Wang, Z.M.; Ji, L.J.; Tian, Y.M.; Zhou, G.Q. Optimizing the freight train connection service network of a large-scale rail system. Transp. Res. B Meth. 2012, 46, 649–667. [Google Scholar] [CrossRef]
- Zhu, E.; Cranic, T.G.; Gendreau, M. Scheduled Service Network Design for Freight Rail Transportation. Oper. Res. 2014, 62, 383–400. [Google Scholar] [CrossRef]
- Newton, H.N.; Barnhart, C.; Vance, P.H. Constructing railroad blocking plans to minimize handling costs. Transport. Sci. 1998, 32, 330–345. [Google Scholar] [CrossRef]
- Barnhart, C.; Jin, H.; Vance, P. Railroad blocking: A network design application. Oper. Res. 2000, 48, 603–614. [Google Scholar] [CrossRef]
- Barnhart, C.; Krishnan, N.; Kim, D.; Ware, K. Network design for express shipment delivery. Comput. Optim. Appl. 2002, 21, 239–262. [Google Scholar] [CrossRef]
- Kim, D.; Barnhart, C.; Ware, K.; Reinhardt, G. Multimodal express package delivery: A service network design application. Transp. Sci. 1999, 33, 391–407. [Google Scholar] [CrossRef]
- Armacost, A.P.; Barnhart, C.; Ware, K.A. Composite variable formulations for express shipment service network design. Transp. Sci. 2002, 36, 1–20. [Google Scholar] [CrossRef]
- Yang, T.H.; Chen, C.C. Air Freight Service Network Design for Stochastic Demand. In Proceedings of the IEEE/INFORMS, International Conference on Service Operations, Logistics and Informatics, Chicago, IL, USA, 22–24 July 2009; IEEE: Washington, DC, USA, 2009. [Google Scholar]
- Christiansen, M.; Fagerholt, K.; Nygreen, B.; Ronen, D. Chapter 4 maritime transportation. In Handbooks in Operations Research and Management Science; Barnhart, C., Laporte, G., Eds.; Elsevier: Amsterdam, The Netherlands, 2006; Volume 14, pp. 189–284. ISBN 9780080467436. [Google Scholar]
- Wang, D.Z.W.; Lo, H.K. Multi-fleet ferry service network design with passenger preferences for differential services. Transp. Res. B Meth. 2008, 42, 798–822. [Google Scholar] [CrossRef]
- Nourbakhsh, S.M.; Ouyang, Y. A structured flexible transit system for low demand areas. Transp. Res. B Meth. 2012, 46, 204–216. [Google Scholar] [CrossRef]
- Bai, R.; Wallace, S.W.; Li, J.; Chong, A.Y.L. Stochastic service network design with rerouting. Transp. Res. B Meth. 2014, 60, 50–65. [Google Scholar] [CrossRef]
- Ji, S.F.; Luo, R.J. A hybrid estimation of distribution algorithm for multi-objective multi-sourcing intermodal transportation network design problem considering carbon emissions. Sustainability 2017, 9, 1133. [Google Scholar] [CrossRef]
- Di, X.; Ma, R.; Liu, H.X.; Ban, X.G. A link-node reformulation of ridesharing user equilibrium with network design. Transp. Res. B Meth. 2018, 112, 230–255. [Google Scholar] [CrossRef]
- Liu, J.T.; Zhou, X.S. Capacitated transit service network design with boundedly rational agents. Transp. Res. B Meth. 2016, 93, 225–250. [Google Scholar] [CrossRef]
- Lin, B.L. A study of car-to-train assignment problem for rail express cargos on scheduled and unscheduled train service network. arXiv 2018, arXiv:1803.05760v1. [Google Scholar]
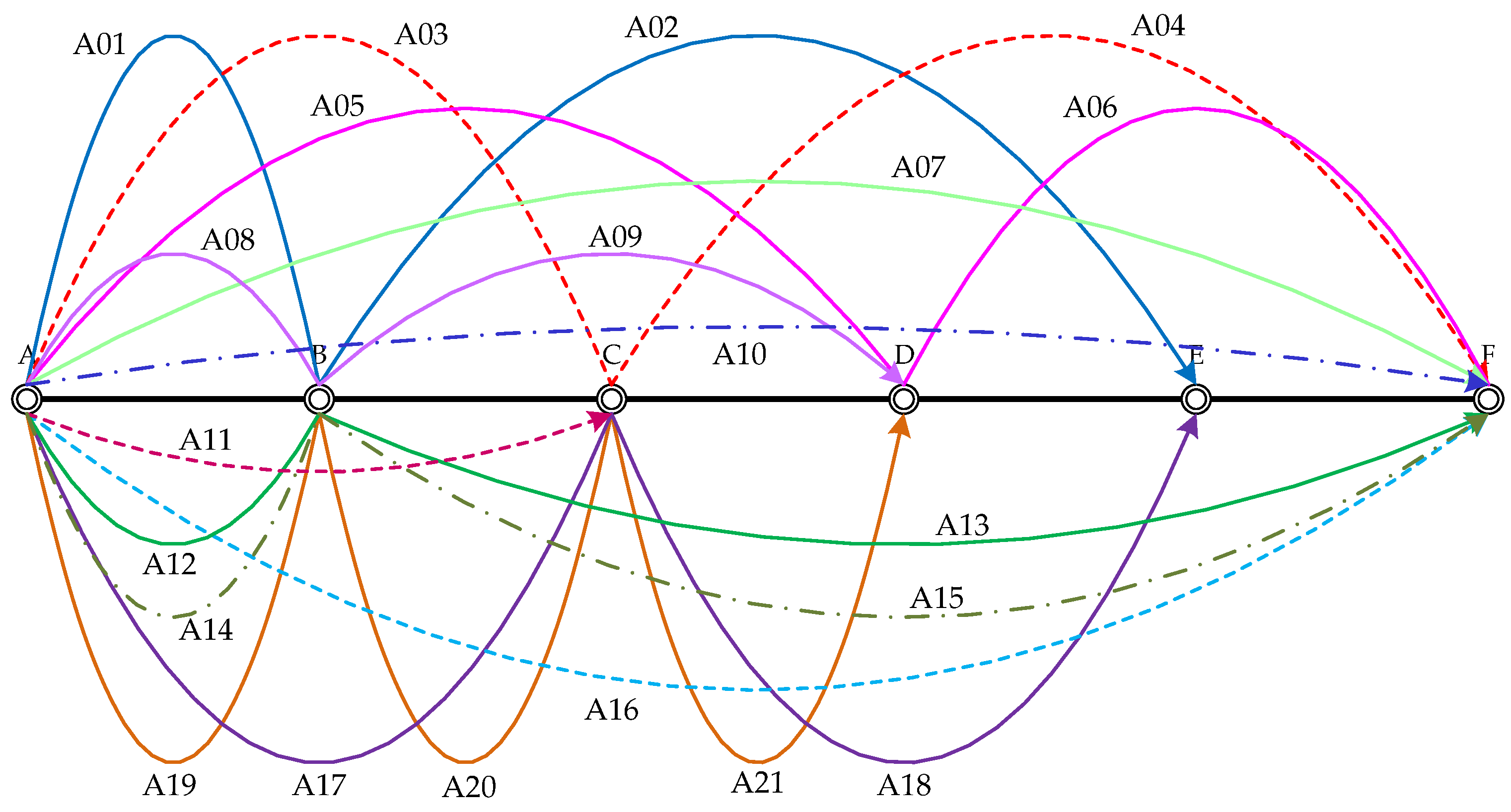
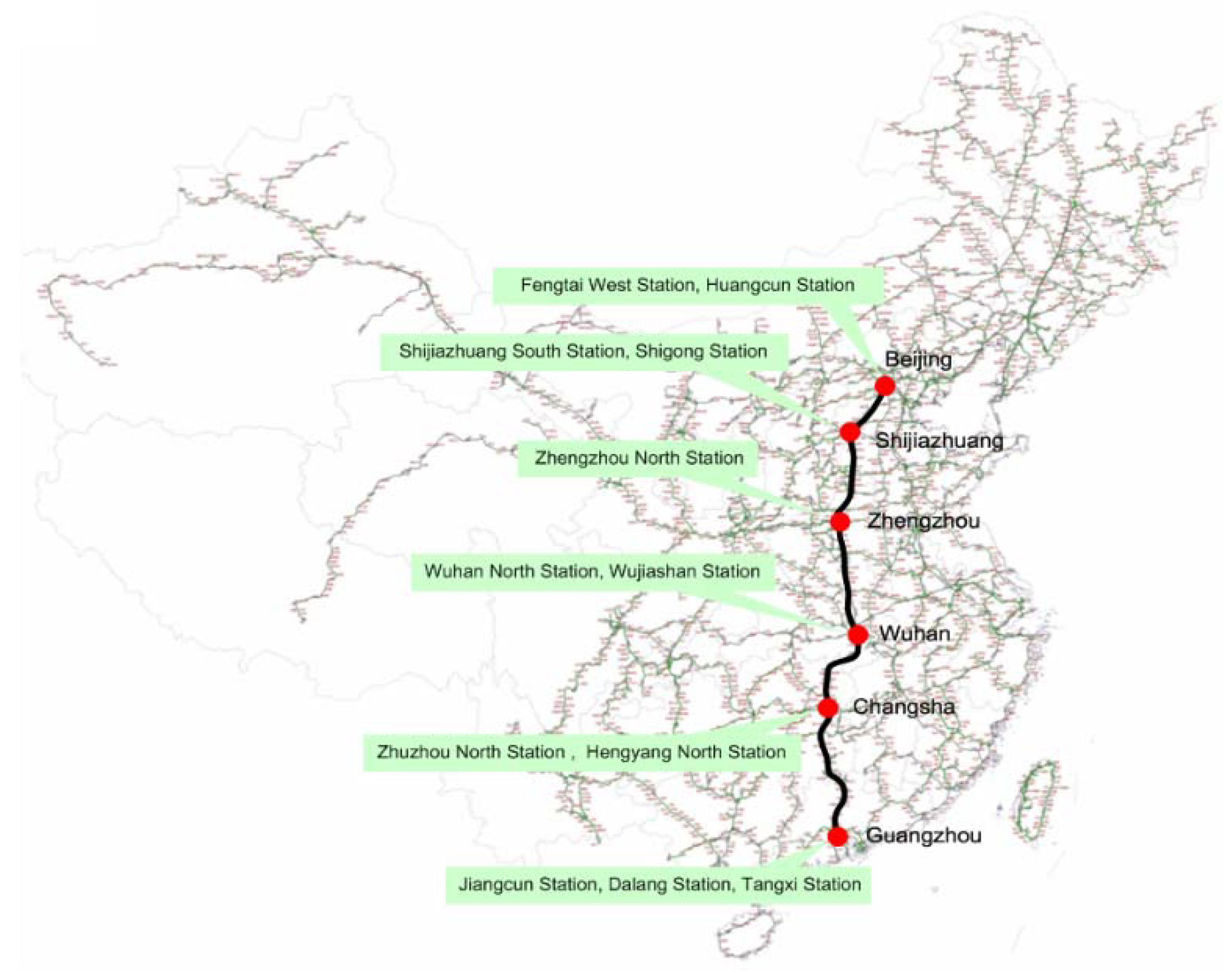
| Train | Speed (km/h) | A ↓ B | A ↓ C | A ↓ D | A ↓ E | A ↓ F | B ↓ C | B ↓ D | B ↓ E | B ↓ F | C ↓ D | C ↓ E | C ↓ F | D ↓ E | D ↓ F | E ↓ F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 80 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 120 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 3 | 80 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 4 | 80 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 80 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 160 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | 120 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | 80 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 9 | 160 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 10 | 120 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 11 | 80 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 12 | 80 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| Notations | Definition |
|---|---|
| Indices | |
| Index of railway hubs; | |
| Index of train stopping patterns; | |
| Index of train service arcs; | |
| Index of shipments; | |
| Index of speed levels of the trains. | |
| Sets | |
| Set of all railway hubs; | |
| Set of all stopping patterns for the train from hub to hub ; | |
| Set of all train service arcs that are generated from the upper-level model; | |
| Set of all shipments; | |
| Set of all speed levels. | |
| Input Parameters | |
| The fixed costs of the train (,,,), where denotes the origin station, denotes the destination station, denotes the speed level, and denotes the stopping patterns; | |
| Binary parameters, if the service arc is provided by the train (,,,), = 1, otherwise, = 1; | |
| The costs associated with stopping at hub for a train; | |
| Unit transportation income obtained by railway operators from carrying goods ; | |
| Volume of the shipment in cars; | |
| Time consumption for train through the service arc at speed level ; | |
| The transfer time for cargo from service arc to at hub ; | |
| The prescribed transit time for transporting cargo ; | |
| The origin station of train service arc ; | |
| The destination station of train service arc ; | |
| The unit capacity of service arc come from train (,); | |
| A sufficiently large positive number; | |
| The origin of the shipment ; | |
| The destination of the shipment ; | |
| The service arc provided by train . | |
| Decision Variables | |
| Binary variables, if a train (,,,) = 1; otherwise, = 1; | |
| Continuous variable, the operating frequency of train (,,,); | |
| Binary variables, if the shipment passes through the arc = 0; | |
| Continuous variable, the proportion of shipment that can be transported. | |
| F01 | H1 | H2 | 4.72 | 20 | 5598 | F30 | H1 | H6 | 5.28 | 72 | 19892 |
| F02 | H1 | H2 | 14.64 | 72 | 19770 | F31 | H1 | H6 | 4.48 | 72 | 19808 |
| F03 | H1 | H2 | 4.48 | 26 | 9201 | F32 | H2 | H3 | 3.76 | 24 | 5211 |
| F04 | H1 | H3 | 29.44 | 36 | 9567 | F33 | H2 | H3 | 4.56 | 24 | 5577 |
| F05 | H1 | H3 | 13.76 | 34 | 13146 | F34 | H2 | H4 | 4.24 | 29 | 9157 |
| F06 | H1 | H3 | 7.76 | 60 | 16363 | F35 | H2 | H4 | 3.76 | 48 | 12373 |
| F07 | H1 | H3 | 9.04 | 60 | 16603 | F36 | H2 | H5 | 13.68 | 60 | 12614 |
| F08 | H1 | H3 | 2.36 | 72 | 28534 | F37 | H2 | H5 | 7.76 | 45 | 14434 |
| F09 | H1 | H3 | 7.68 | 72 | 19929 | F38 | H2 | H5 | 5.2 | 72 | 16645 |
| F10 | H1 | H4 | 17.52 | 72 | 19854 | F39 | H2 | H5 | 5.04 | 60 | 16561 |
| F11 | H1 | H4 | 2.15 | 72 | 28428 | F40 | H2 | H6 | 25.92 | 24 | 19892 |
| F12 | H1 | H4 | 11.28 | 24 | 5673 | F41 | H2 | H6 | 19.6 | 43 | 19808 |
| F13 | H1 | H5 | 8.56 | 36 | 9276 | F42 | H2 | H6 | 10.4 | 46 | 5211 |
| F14 | H1 | H5 | 5.36 | 48 | 9642 | F43 | H2 | H6 | 7.28 | 60 | 5577 |
| F15 | H1 | H5 | 5.12 | 36 | 13222 | F44 | H2 | H6 | 4.96 | 65 | 9157 |
| F16 | H1 | H5 | 3.76 | 60 | 16439 | F45 | H2 | H6 | 3.68 | 56 | 12373 |
| F17 | H1 | H5 | 3.84 | 60 | 16679 | F46 | H3 | H5 | 26.96 | 24 | 12614 |
| F18 | H1 | H5 | 7.28 | 72 | 19694 | F47 | H3 | H5 | 4.8 | 32 | 14434 |
| F19 | H1 | H6 | 4.16 | 72 | 19853 | F48 | H3 | H5 | 5.76 | 26 | 16645 |
| F20 | H1 | H6 | 8.72 | 72 | 28427 | F49 | H3 | H5 | 18.4 | 48 | 16561 |
| F21 | H1 | H6 | 3.64 | 72 | 28321 | F50 | H3 | H6 | 12.24 | 48 | 8119 |
| F22 | H1 | H6 | 17.44 | 72 | 19779 | F51 | H3 | H6 | 7.6 | 36 | 11336 |
| F23 | H1 | H6 | 37.68 | 24 | 5560 | F52 | H3 | H6 | 6.64 | 24 | 11576 |
| F24 | H1 | H6 | 25.84 | 36 | 9163 | F53 | H3 | H6 | 5.92 | 36 | 13396 |
| F25 | H1 | H6 | 19.36 | 65 | 9529 | F54 | H3 | H6 | 5.92 | 48 | 13322 |
| F26 | H1 | H6 | 18.88 | 48 | 13108 | F55 | H3 | H6 | 4.72 | 36 | 13237 |
| F27 | H1 | H6 | 14.72 | 58 | 16325 | F56 | H4 | H6 | 4.72 | 36 | 7732 |
| F28 | H1 | H6 | 8.72 | 48 | 16565 | F57 | H4 | H6 | 4.48 | 36 | 7973 |
| F29 | H1 | H6 | 5.52 | 72 | 19966 | F58 | H4 | H6 | 3.84 | 36 | 9793 |
| Distance (km) | ||||||
|---|---|---|---|---|---|---|
| A01 | H1 | H2 | 10.8 | 6.9 | 5 | 648 |
| A02 | H1 | H3 | 18.4 | 11.6 | 8.5 | 1101 |
| A03 | H1 | H4 | 26.7 | 16.9 | 12.3 | 1599 |
| A04 | H1 | H5 | 33.4 | 21.1 | 15.4 | 2000 |
| A05 | H1 | H6 | 38.2 | 24.2 | 17.7 | 2290 |
| A06 | H2 | H3 | 7.6 | 4.8 | 3.5 | 453 |
| A07 | H2 | H4 | 15.9 | 10.1 | 7.4 | 951 |
| A08 | H2 | H5 | 22.6 | 14.3 | 10.4 | 1352 |
| A09 | H2 | H6 | 27.4 | 17.3 | 12.7 | 1642 |
| A10 | H3 | H4 | 8.3 | 5.3 | 3.9 | 498 |
| A11 | H3 | H5 | 15 | 9.5 | 7 | 899 |
| A12 | H3 | H6 | 19.9 | 12.6 | 9.2 | 1189 |
| A13 | H4 | H5 | 6.7 | 4.3 | 3.1 | 401 |
| A14 | H4 | H6 | 11.6 | 7.3 | 5.4 | 691 |
| A15 | H5 | H6 | 4.9 | 3.1 | 2.3 | 290 |
| H1 | 12.2 | 2.4 |
| H2 | 11.1 | 1.9 |
| H3 | 7.8 | 1.3 |
| H4 | 10 | 2.3 |
| H5 | 17.7 | 3.5 |
| H6 | 9.9 | 1.6 |
| Instance ID | The Number of the Flows |
|---|---|
| 1 | 10 (F01–F10) |
| 2 | 20 (F01–F20) |
| 3 | 30 (F01–F30) |
| 4 | 40 (F01–F40) |
| 5 | 50 (F01–F50) |
| 6 | 58 (F01–F58) |
| Plan | ||
|---|---|---|
| I | −12,285,301.68 CNY | 100% |
| II | −10,829,293.23 CNY | 87.41% |
| III | −11,426,699.99 CNY | 91.36% |
| IV | −12,091,374.86 CNY | 98.91% |
| V | −12,282,876.71 CNY | 100% |
| VI | −11,953,287.68 CNY | 97.20% |
| VII | −11,953,287.68 CNY | 97.20% |
| VIII | −12,281,774.42 CNY | 100% |
| IX | −12,284,106.74 CNY | 100% |
| X | −12,284,004.98 CNY | 100% |
| Service Arc | Service Arc | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| F01 | H1 | H2 | 100% | (H1, H2, 10.8, t4) | F30 | H1 | H6 | 100% | (H1, H6, 17.7, t13) |
| F02 | H1 | H2 | 100% | (H1, H2, 6.9, t12) | F31 | H1 | H6 | 100% | (H1, H6, 17.7, t13) |
| F03 | H1 | H2 | 100% | (H1, H2, 6.9, t12) | F32 | H2 | H3 | 100% | (H2, H3, 7.6, t2) |
| F04 | H1 | H3 | 100% | (H1, H3, 18.4, t3) | F33 | H2 | H3 | 100% | (H2, H3, 7.6, t2) |
| F05 | H1 | H3 | 100% | (H1, H3, 18.4, t3) | F34 | H2 | H4 | 100% | (H2, H4, 15.9, t1) |
| F06 | H1 | H3 | 100% | (H1, H3, 18.4, t3) | F35 | H2 | H4 | 100% | (H2, H4, 15.9, t1) |
| F07 | H1 | H3 | 100% | (H1, H3, 11.6, t11) | F36 | H2 | H5 | 100% | (H2, H5, 22.6, t4) |
| F08 | H1 | H3 | 100% | (H1, H3, 11.6, t11) | F37 | H2 | H5 | 100% | (H2, H5, 22.6, t4) |
| F09 | H1 | H3 | 100% | (H1, H3, 11.6, t8) | F38 | H2 | H5 | 100% | (H2, H5, 22.6, t4) |
| F10 | H1 | H4 | 100% | (H1, H4, 26.7, t7) | F39 | H2 | H5 | 100% | (H2, H5, 22.6, t4) |
| F11 | H1 | H4 | 100% | (H1, H2, 10.8, t1) (H2, H4, 15.9, t1) | F40 | H2 | H6 | 100% | (H2, H6, 27.4, t6) |
| F12 | H1 | H4 | 100% | (H1, H2, 10.8, t2) (H2, H3, 7.6, t2) (H3, H4, 8.3, t2) | F41 | H2 | H6 | 100% | (H2, H6, 27.4, t6) |
| F13 | H1 | H5 | 100% | (H1, H3, 18.4, t3) (H3, H5, 15.0, t3) | F42 | H2 | H6 | 100% | (H2, H6, 27.4, t6) |
| F14 | H1 | H5 | 100% | (H1, H2, 10.8, t4) (H2, H5, 22.6, t4) | F43 | H2 | H6 | 100% | (H2, H6, 17.3, t12) |
| F15 | H1 | H5 | 100% | (H1, H5, 21.1, t9) | F44 | H2 | H6 | 100% | (H2, H6, 17.3, t12) |
| F16 | H1 | H5 | 100% | (H1, H5, 21.1, t9) | F45 | H2 | H6 | 100% | (H2, H6, 17.3, t12) |
| F17 | H1 | H5 | 100% | (H1, H5, 21.1, t9) | F46 | H3 | H5 | 100% | (H3, H5, 15.0, t3) |
| F18 | H1 | H5 | 100% | (H1, H5, 21.1, t9) | F47 | H3 | H5 | 100% | (H3, H5, 15.0, t3) |
| F19 | H1 | H6 | 100% | (H1, H6, 38.2, t5) | F48 | H3 | H5 | 100% | (H3, H5, 15.0, t3) |
| F20 | H1 | H6 | 100% | (H1, H2, 10.8, t6) (H2, H6, 27.4, t6) | F49 | H3 | H5 | 100% | (H3, H5, 15.0, t3) |
| F21 | H1 | H6 | 100% | (H1, H4, 26.7, t7) (H4, H6, 11.6, t7) | F50 | H3 | H6 | 100% | (H3, H6, 12.6, t11) |
| F22 | H1 | H6 | 100% | (H1, H6, 24.2, t10) | F51 | H3 | H6 | 100% | (H3, H4, 8.3, t2) (H4, H6, 11.6, t6) |
| F23 | H1 | H6 | 100% | (H1, H2, 6.9, t12) (H2, H6, 17.3, t12) | F52 | H3 | H6 | 100% | (H3, H6, 12.6, t11) |
| F24 | H1 | H6 | 100% | (H1, H3, 11.6, t11) (H3, H6, 12.6, t11) | F53 | H3 | H6 | 100% | (H3, H6, 12.6, t11) |
| F25 | H1 | H6 | 100% | (H1, H6, 24.2, t10) | F54 | H3 | H6 | 100% | (H3, H6, 12.6, t11) |
| F26 | H1 | H6 | 100% | (H1, H6, 17.7, t13) | F55 | H3 | H6 | 100% | (H3, H6, 12.6, t11) |
| F27 | H1 | H6 | 100% | (H1, H6, 17.7, t13) | F56 | H4 | H6 | 100% | (H4, H6, 11.6, t7) |
| F28 | H1 | H6 | 100% | (H1, H6, 17.7, t13) | F57 | H4 | H6 | 100% | (H4, H6, 11.6, t7) |
| F29 | H1 | H6 | 100% | (H1, H6, 17.7, t13) | F58 | H4 | H6 | 100% | (H4, H6, 11.6, t7) |
| Train | t1 | t2 | t3 | t4 | t5 | t6 | t7 | t8 | t9 | t10 | t11 | t12 | t13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.88 | 0.27 | 1.56 | 1.23 | 0.55 | 1.22 | 0.73 | 0.11 | 0.91 | 1.20 | 1.33 | 0.85 | 1.19 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, B.; Wu, J.; Wang, J.; Duan, J.; Zhao, Y. A Bi-Level Programming Model for the Railway Express Cargo Service Network Design Problem. Symmetry 2018, 10, 227. https://doi.org/10.3390/sym10060227
Lin B, Wu J, Wang J, Duan J, Zhao Y. A Bi-Level Programming Model for the Railway Express Cargo Service Network Design Problem. Symmetry. 2018; 10(6):227. https://doi.org/10.3390/sym10060227
Chicago/Turabian StyleLin, Boliang, Jianping Wu, Jiaxi Wang, Jingsong Duan, and Yinan Zhao. 2018. "A Bi-Level Programming Model for the Railway Express Cargo Service Network Design Problem" Symmetry 10, no. 6: 227. https://doi.org/10.3390/sym10060227
APA StyleLin, B., Wu, J., Wang, J., Duan, J., & Zhao, Y. (2018). A Bi-Level Programming Model for the Railway Express Cargo Service Network Design Problem. Symmetry, 10(6), 227. https://doi.org/10.3390/sym10060227






