1. Introduction
Pawlak raised rough set theory (RST) [
1] in 1982, which has become a relatively complete system after more than thirty years of rapid development. Since the advent of this theory, its strong qualitative analysis [
2] makes it a great success in many science and technology fields. As an effective tool for handling ambiguity and uncertainty, the RST has been widely applied in many areas based on its preliminary knowledge. For instance, artificial intelligence, machine learning, data mining, medical diagnosis, algebra [
3,
4,
5,
6,
7,
8,
9] and so on. The RST has extended rapidly in recent years and has a lot of fruitful research results [
10,
11,
12,
13,
14,
15,
16,
17], which is concerned by domestic and foreign scholars and peers.
A subset of universe be often referred to as a concept. The set of these subsets is called knowledge with regard to
U. An information system (IS) can represent knowledge and information. Many scholars have studied a variety of rough set problems about information system. Initially, attribute values of the information system are characteristic values or single-values. Later, due to some scholars have different practical needs during their researches, the attribute values are gradually extended to interval numbers, set values, intuitionistic fuzzy numbers, lattice values, etc. and relevant information systems are correspondingly produced [
18,
19,
20,
21,
22,
23]. However, data obtained from real world may exist the phenomena of missing, measurement errors, data noise or other situations. It is inevitable that these reasons will cause the incompleteness of information system. In general, this information system is called an incomplete information system. At first, attribute values studied in the incomplete information system were discrete. Subsequently, the discrete attribute values were extended to continuous values or even other values (such as interval numbers, set values and so on). The classical rough set theory cannot handle problems in incomplete information systems [
24,
25,
26]. Hence many professors pretreated the data, and then used the ideology of the classical RST to solve the problem. These articles [
27,
28] adopted complete methods to study and deal with the incomplete information system. Nevertheless, these approaches may changed the original data and increased new human uncertainty of information system. Therefore, many scholars provided some relations that were distinct from equivalence relation to avoid changing the original data in the incomplete information system. Zhang [
29] studied a method of acquisition rules in incomplete decision tables in the light of similarity relation. The literature [
30] calculated the core attribute set based on ameliorative tolerance relationship. Wei [
31] optimized the dominance relation and proposed a valued dominance relationship that was negatively/positively concerned in classification analysis. The essay [
32] raised
-dominance relationship by using the dominant degree between interval values and gave methods for solving approximate reductions. Gao [
33] gave the concept of approximate set based on
-improved limited tolerance relation. Some researchers [
34,
35,
36,
37] took into account preference orders in incomplete ordered information system, and put forward methods to acquire reductions or rules. To study incomplete interval-values information system, Dai [
38,
39] defined two different similar relations to further explore system uncertainty.
The classification is the foundation of research in RST. From this perspective, a discourse is divided into knowledge granules [
40,
41,
42,
43] or concepts. An equivalence relation on the discourse can be considered as a granularity. The partition induced by equivalence relation is treated as a granular space. The classical RST can be seen as a theory that is formed by a single granularity under the equivalence relation. To better apply and promote RST, a new multi-view data analysis method was emerged in recent years, which was data modeling method in multi-granulation rough set (MGRS). Between 1996 and 1997, Zadeh first proposed the concept of granular computing [
44]. Qian [
45] advanced multi-granulation rough set, which has been researched by many scholars and specialists. However, in practical problems, a discourse is not only divided by one relation, sometimes it will be divided by multiple relations. Faced with this problem, the previously studied single-granularity rough set theory was powerless. It is necessary to consider multiple granularities. Some professors consider fuzzy logic and fuzzy logic inference in [
46,
47,
48]. The literature [
49] extended two MGRS models into an incomplete information system. Yang [
50] mainly researched several characteristics of MGRS in interval-valued information systems. Xu [
51] used the order information system as their investigative object and discussed some measurement methods. Wang [
52] introduced the similarity dominance relation for studying MGRS in incomplete ordered decision systems. Yang [
53] mainly discussed the relationships among several of multigranulation rough sets in incomplete information system. However, experts and professors have less researches on MGRS in incomplete interval-valued information systems.
To facilitate our discussion,
Section 2 mainly introduces some essential notions about RST and incomplete interval-valued decision information system. A single granularity rough set model is established based on the multi-threshold tolerance relation that is defined as the connection degree of Zhao’s [
54] set pair analysis.
Section 3 establishes two MGRS models (namely, OMRGS model and PMGRS model), and discusses their properties in accordance with the multi-threshold tolerance relation and the viewpoint of multiple granularities.
Section 4 explores the uncertainty measure of MGRS in IIVDIS, which are the roughness and the degree of dependence of MGRS in IIVDIS to measure uncertainty of rough set.
Section 5 exhibits two algorithms for computing the roughness and the degree of dependence in single granularity rough set and MGRS, respectively. In addition, several UCI data sets are used to verify the correctness of proposed theorems in
Section 6. The article ends up with conclusion in
Section 7.
2. Preliminaries about RST and IIVDIS
In many cases, we utilize a table to collect data and knowledge. This table regards the universe (that is, objects of discussion) as rows, attributes features represented by objects as columns, which is usually called an information system. For the convenience of the discussion later, this section first gives a few basic definitions [
24,
38,
39].
In general, an information system is denoted as a quadruple . When and hold simultaneously, is known as a decision table. It also can be called a decision information system. In here, U is called universe/discourse that represents objects of discussing. Set of characteristics represented by discourse is usually called attribute set A, which contains two parts: the set of condition attributes C and the set of decision attributes D. is a subset of V that is the domain of attributes. It can be written as . is a mapping to transform an ordered pair to a value for each . In addition, the mapping is called an information function. Especially, is single-valued for every .
In mathematics, any subset R of the product of the universe U can be known as a binary relation on U. R is usually referred to as an equivalence relation on U if and only if R satisfies reflexivity, symmetry and transitivity. Pawlak approximation space can be denoted by a binary group U, R. Another mathematical object is the partition on the universe U, which is closely related to the equivalence relation. Specifically, a quotient set is the set of all equivalence classes obtained from the equivalence relation R. It can be easily verify that the quotient set is a partition on U, written down as . Where equivalence class for .
If for , , attribute value () is an interval number, then is an interval-valued information system, referred to as . Particularly, if , is a real number, so the interval-valued information system is the generalization of classical information system. Where , R is the set of real number.
Let , if at least one of lower bound and upper bound is an unknown value, thus we will write down as . In addition, is an incomplete interval-valued information system. is an incomplete interval-valued decision information system or incomplete interval-valued decision table. In the following discussion, we only discuss the situation where .
Definition 1. Given an incomplete interval-valued information system , for ∀ , . The attribute values of two objects are not *. Let , , then the similarity degree [55] with reference to under the attribute is In the above equation, represents the length of the closed interval. The similarity degree can also be transformed as Remark 1. - (1)
The length of the empty set and the single-point set are equal to zero;
- (2)
Assume that two attribute values are single-point set. If , then ; if , then .
- (3)
If or or , , then set the similarity degree with respect to equals ▲.
Definition 2. [54] Let two sets Q, G constitute a set pair . According to the need of the problem W, we can analyze the characteristics of set pair H, and obtain N characteristics (attributes). For two sets Q, G, which have same values on S attributes, different values on P attributes, and the rest of attribute values are ambiguous. is called the identical degree of these two sets under problem W. Referred to as the identical degree. is called the opposite degree of these two sets under problem W. Referred to as the opposite degree. is called the difference degree of these two sets under problem W. Referred to as the difference degree. Then the connection degree with respect to two sets Q, G can be defined as Denoted as . Where , . In the calculation, set , i and j also participate in the operation as coefficients. However, the function of i, j are just markings in this paper. i is the marking of the difference degree, j is the marking of the opposite degree.
Given an incomplete interval-valued information system (IIIS), the similarity degree of the two objects can be calculated in the light of the values of Definition 1. There are three possible cases:
- (1)
The two attribute values are both not equal to *, and their similarity degree is greater than or equal to a given threshold;
- (2)
The two attribute values are both not equal to *, and their similarity degree is less than a given threshold;
- (3)
At least one of the two attribute values is equal to *, and their similarity degree is considered to be ▲.
Definition 3. [56] Given an incomplete interval-valued information system , , . Let is a set of the attributes that the similarity degree of under the attribute is not less than a similar level λ. is a set of the attributes that the similarity degree of under the attribute is less than a similar level λ. is a set of the attributes that the similarity degree of under the attribute is equal to ▲.
Where shows the tolerance degree of the two objects with regard to B. shows the opposite degree of the two objects with regard to B. shows the difference degree of the two objects with regard to B. Then the relationship of is known as indicates similar connection degree of the two objects . Referred to as . Where , , the function of i, j are just markings. i is the marking of the difference degree, j is the marking of the opposite degree.
It is unreasonable to put two objects in the same class only if the tolerance degree of the two objects under the attribute subset is equal to 1. In [56], the paper considers the tolerance degree and the opposite degree but is unaware of difference degree. Whether two objects should be classified as the same class, the article [56] defines the tolerance relation based on similarity connection degree to solve this problem. In there, we assume that and there are five attributes, that is . If attribute values of under the attribute set B are and , respectively. We can see from the calculation that ( is the tolerance relation based on similarity connection degree in [56]). However, it is obvious that the attribute values of under attribute are absolutely different. Therefore, in order to better study the information system containing multiple unknown values or missing parts. Based on the above discussion, this article also considers the difference degree apart from the tolerance degree and the opposite degree. The concrete method is: the tolerance degree of the two objects under the attribute subset is greater than or equal to α and the opposite degree of the two objects under the attribute subset is less than or equal to β. Moreover, the difference degree of the two objects under the attribute subset is less than or equal to γ. In summary, the multi-threshold tolerance relation is given below. Definition 4. In the incomplete interval-valued decision information system (IIVDIS) , for any , . , . The multi-threshold tolerance relation can be referred as represent, respectively, the tolerance degree, the difference degree and the opposite degree of objects with reference to B. α is the threshold of the tolerance degree, β is the threshold of the opposite degree, γ is the threshold of the difference degree.
The multi-threshold tolerance class can be defined as In addition, a binary relation under decision attribute d is remembered as . Decision class and quotient set can be alluded to as , , respectively. Obviously, relation is an equivalence relation and constitutes a partition on U.
Remark 2. - (1)
It obviously observes that the multi-threshold tolerance relation is reflexive and symmetrical rather than transitive, which is a tolerance relation; is a cover on U.
- (2)
It is reasonable to put two objects in the same class if the tolerance degree of the two objects under the attribute subset is not less than α and the opposite degree, the difference degree of the two objects under the attribute subset is less than or equal to β, γ, respectively.
- (3)
If we don’t consider parameter γ and the range of , the multi-threshold tolerance relation is degraded into the tolerance relation in [56]. Therefore, the tolerance relation in [56] can be regarded as a specific situation of multi-threshold tolerance relation. - (4)
When , can be replaced by a. The following paper will denote , , .
Definition 5. In the , for each , . The approximations of X concerning a multi-threshold tolerance relation can be represented by , are called lower and upper approximation operator of X concerning a multi-threshold tolerance relation .
Moreover, similar to classical rough set, positive region is recorded as negative region is known as what boundary region represents the difference between the lower approximation and upper approximation of X concerning is denoted by
Some relationships between upper and lower approximation are similar to the properties of upper and lower approximation of the classical rough set. Detailed results are as follows.
Theorem 1. In the , for any , . There have| (1) | . | (Boundedness) |
| (2) | ; . | (Duality) |
| (3) | ; . | (Normality) |
| (4) | ; . | (Multiplicativity and Additivity) |
| (5) | If holds, then and . | (Monotonicity) |
| (6) | ; . | (Inclusion) |
Proof. For , have . If , thus hold. So . For . must be hold on account of satisfies reflexivity, so . That is . Hence
From the above, we can prove that .
For
, according to Definition 5 (Equation (
8)), there have
⇔
⇔
⇔
.
In summary, . Obviously, , therefore, .
It can be known from of this theorem that , moreover, it is evident that , so
Suppose that , then there must be exists s.t. , which is a contradiction with . Hence
From the proof of of this theorem, we can see .
For , have ⇔ and ⇔ and ⇔ .
For , have ⇔ or ⇔ or ⇔ .
Since , so . Under the equation of this theorem, . Therefore, . In other words,
Since , so . Under the equation of this theorem, . Therefore, . In other words,
For , . In the light of the equation of this theorem, we can acquire So
For . According to the equation of this theorem, we can obtain So
Inspired by the roughness of X with regard to the classical approximation space. Following definition describes the roughness and the degree of dependence of X based on the multi-threshold tolerance relation in single granularity rough set. ☐
Definition 6. In the , for any , . Then the roughness of X is Moreover, what the quality of approximation of d is decided by B is referred to as the degree of dependence. It can be denoted as 4. The Uncertainty Measure of MGRS in IIVDIS
Section 3 presents the concepts and properties of the optimistic and pessimistic multi-granulation rough set in IIVDIS, which are studied based on single granularity rough set. Then, this section will mainly explore tools for measuring uncertainty of MGRS. Firstly, we study the relationship between single granularity and multi-granulation rough set in IIVDIS.
Theorem 4. In the , (), . There have:
(1) (2)
Proof. (1) For , then or ⇔ or ⇔ . Therefore,
(2) For , then and ⇔ and ⇔ . Therefore, ☐
Theorem 5. In the , (), . There have:
Proof. For , then and ⇔ and ⇔ . Therefore,
For , then or ⇔ or ⇔ . Therefore, ☐
Theorem 6. In the , (), . Then:
Proof. These two formulas is effortless to demonstrate owing to the Theorem 4 and the Theorem 1 (4). ☐
Theorem 7. In the , (), . Then:
Proof. These two formulas is effortless to demonstrate owing to the Theorem 5 and the Theorem 1 (4). ☐
Theorem 8. In the , (), . Then:
Proof. These two formulas is effortless to demonstrate owing to the Theorem 4 and the Theorem 5. ☐
In the following, we will investigate the roughness and the degree of dependence of MGRS and their properties in IIVDIS as well as classical single granularity rough set.
Definition 9. In the , (), . The optimistic roughness of X can be defined aswhere . In particularly, if , then we can say . Definition 10. In the , (), . The pessimistic roughness of X iswhere . In particularly, if , then we can say . Theorem 9. In the , (), . Then
Proof. It can be obtained by the Theorem 8 that
Moreover, in the light of Equations (
9), (
15) and (
16), we can acquire
Let is decision class that is induced by decision attribute d. When all objects are classified by attribute set, we mainly study the degree of dependence in IIVDIS, which represents the percentage of objects that can be exactly classified into optimistically/pessimistically. ☐
Definition 11. In the , (). Then decided by , the optimistic degree of dependence of d is Definition 12. In the , (). Then decided by , the pessimistic degree of dependence of d is Theorem 10. In the , (). Then
Proof. For all
,
. From the Theorem 8, we will obtain that
Therefore,
Besides, according to the Equations (
10), (
17) and (
18), we will prove
☐
Example 1. Just as revealed in Table 1, which is an incomplete interval-valued decision information system. It represents situation of treating wart of 20 people, which is selected from Immunotherapy data set in Section 6. Here, . Where universe , represent the ith people (). , () represent sex, age, time, number of warts, type, area, induration diameter, respectively. d shows the result of treatment. . In this example, let . It is easy to know decision attribute divides discourse into two parts, . Where , . Assume that , then . Let , , . It can be obtained by Equations (11) and (13):
In what follows, the approximation sets of based on single multi-threshold tolerance relation are displayed by Equation (8):
Apparently, the following properties hold:
Then it also can be acquired that: In addition, by Equations (9), (15) and (16): Analogously, by Equations (8), (11) and (13), we can gain: ,
,
,
.
6. Experimental Section
We download six data sets from UCI database (
http://archive.ics.uci.edu/ml/datasets.html) in this section. Namely, “Immunotherapy”, “User Knowledge Modeling”, “Blood Transfusion Service Center”, “Wine Quality-Red”, “Letter Recognition (randomly selecting 3400 objects)” and “Wine Quality-White”, which are outlined in
Table 2. The testing results are running on personal computer with processor (2.5 GHz Intel Core i5) and memory (4 GB, 2133 MHz). The platform of algorithms is Matlab2014a.
In fact, the downloaded data sets are real numbers. However, what we are investigating is IIVDIS. So we need utilizing error precision and missing rate to process the data and change the data from real numbers to incomplete interval numbers. Let be a decision information system. Where . All attribute values are single-valued. For any , , the attribute value of under the attribute can be written as . Firstly, we randomly choose ( is the meaning of taking an integer down) attribute values and turn them into missing values in order to construct an incomplete information system. These missing values are written as *. However, the attribute value of under the decision attribute d remains unchanged. Secondly, the interval number can be obtained by formula . In summary, an IIVDIS is gained by this way.
Because attribute set
C have
attribute subsets, so we only select two subsets as granularities and a decision class for facilitating comparison of experimental results in IIVDIS, which are denoted as
and
,
and
. In all experiments, we discuss three rough set models, which are the single granularity rough set (it can be written as Single Granularity RS) model, the OMGRS model and PMGRS model. In the following, OMGRS and PMGRS consider granularities
and
while single granularity rough set discusses a granularity
in IIVDIS. In addition, we respectively select a decision value from six data sets when the roughness is calculated. There are 0, 1, 0, 3, 1, 3. The computation results both Algorithms 1 and 2 are displayed in
Table 3. Here we set allowable error scope is 0.0001.
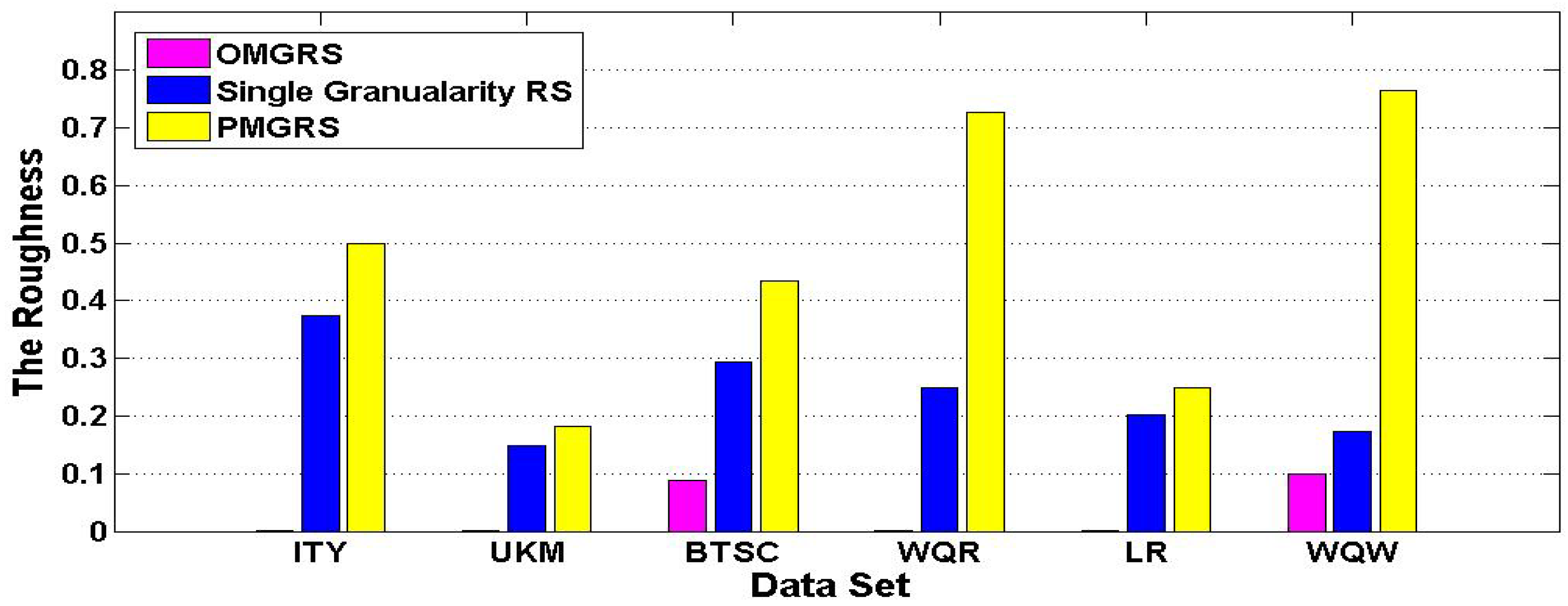
We can draw a histogram
Figure 1 based on the results of the roughness in
Table 3. As illustrated in
Figure 1, the roughness of three rough set models is increasing in each data set according to the order of OMGRS, Single Granularity RS, and PMGRS. Where the roughness in OMGRS is the smallest, the roughness in PMGRS is the largest and the roughness in Single Granularity RS falls in between the roughness in OMGRS and the roughness in PMGRS in each data set, which show the concept become increasingly rough in the light of the order of OMGRS, Single Granularity RS, and PMGRS.
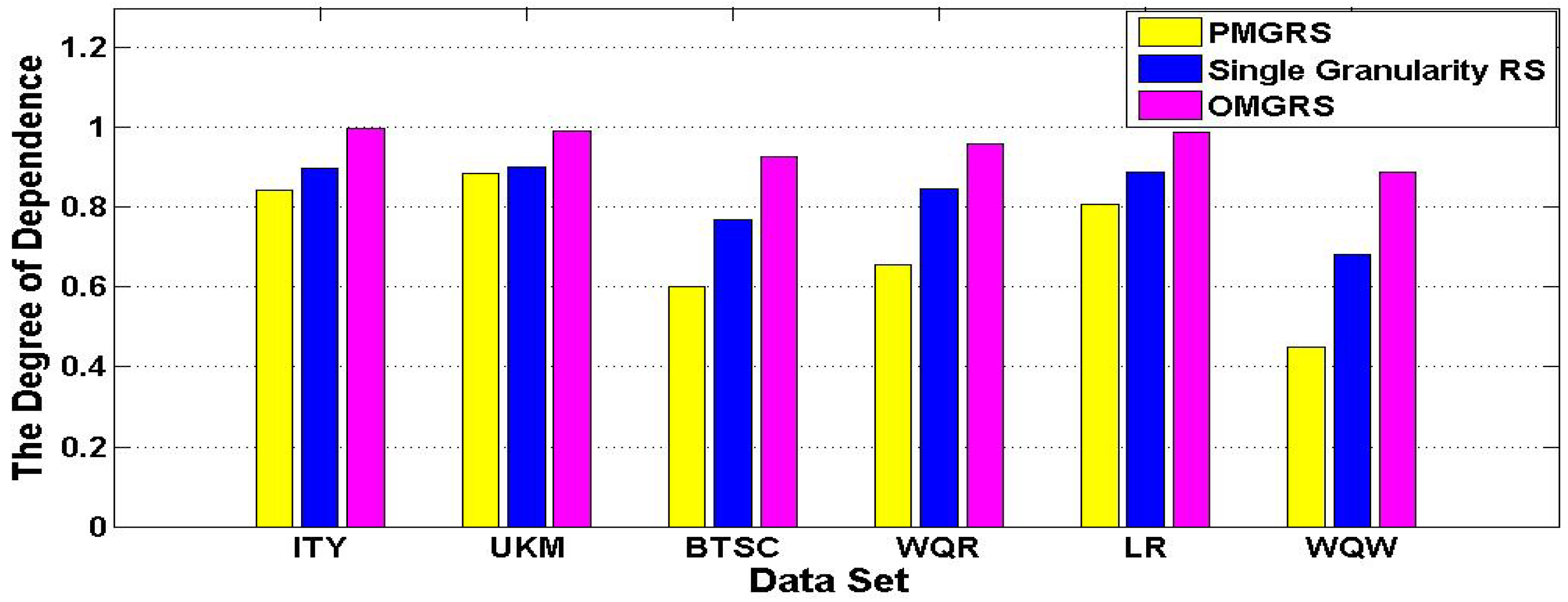
Similarly, we plot the histogram
Figure 2 by experimental results about the degree of dependence in
Table 3. We can obtain that the degree of dependence of three rough set models is increasing for every data set considering the order of PMGRS, Single Granularity RS, and OMGRS from
Figure 2. Where the degree of dependence in PMGRS is the smallest, the degree of dependence in OMGRS is the largest and the degree of dependence in Single Granularity RS falls in between the degree of dependence in PMGRS and the degree of dependence in OMGRS, which reveal the percentage of objects that can be definitely divided into decision classes become increasing in accordance with the order of PMGRS, Single Granularity RS, and OMGRS in every data sets.